Abstract
Measurement of the size of anatomic regions of interest in medical images is used to diagnose disease, track growth, and evaluate response to therapy. The discrete nature of medical images allows for both continuous and discrete definitions of region boundary. These definitions may, in turn, support several methods of area calculation that give substantially different quantitative values. This study investigated several boundary definitions (e.g., continuous polygon, internal discrete, and external discrete) and area calculation methods (pixel counting and Green’s theorem). These methods were applied to three separate databases: A synthetic image database, the Lung Image Database Consortium database of lung nodules and a database of adrenal gland outlines. Average percent differences in area on the order of 20% were found among the different methods applied to the clinical databases. These results support the idea that inconsistent application of region boundary definition and area calculation may substantially impact measurement accuracy.
Keywords: lung nodule, measurement, area, image processing, Green’s theorem, Lung Image Database Consortium (LIDC)
INTRODUCTION
Quantitative measurement of disease on medical images is an established practice for both diagnosis and tracking of disease progression or response to therapy.1, 2 Lung nodules,3 mesothelioma,4, 5 and pulmonary arterial size,6 for example, are all routinely measured on one or several axial images of a computed tomography (CT) scan. Widespread application of modalities such as CT and magnetic resonance make size in two dimensions (with potential extension to three dimensions) a natural choice for quantitative disease measurement, despite the routine use of unidimensional measurements in clinical practice.7 Furthermore, computerized methods for analyzing medical images are often applied to two-dimensional (2D) representation of structures when processing data (i.e., section-by-section analysis). Even three-dimensional (3D) measurements (e.g., volume) are often obtained from the analysis of stacked 2D regions.
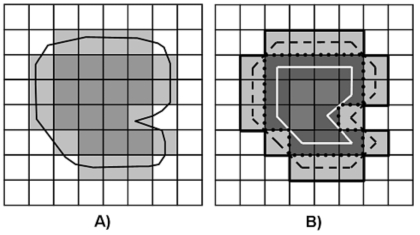
Although the concept of area is easily defined for abstract 2D structures in continuous space, the quantitative assessment of area for continuous structures represented in digital images is not. Two broad concepts of area exist and primarily differ with regard to whether the region boundaries are defined in continuous or discrete space. Digital medical images are 2D matrices formed from discrete samples of an underlying continuous distribution (the patient). It is therefore a matter of choice when calculating 2D size metrics whether to restrict the definition of the region and its boundary to the discrete space of the image or to allow the region to be defined in the continuous space “between” pixels in an attempt to better approximate the underlying continuous structure of the region (Fig. 1).
Figure 1.
A) Discrete boundary (light gray pixels) and continuous boundary (black line) of an object (medium gray pixels) in a digital image. Note that the continuous boundary is not constrained to the discrete image pixels. B) The discrete boundary can be defined as an external boundary (light gray pixels) or an internal boundary (dark gray pixels). Discrete-to-continuous conversion can be defined by the pixel centers of the discrete boundaries (solid white line and dashed black line) or the pixel edges of a discrete boundary (solid black line and dotted black line).
In 2D continuous space, any solid region can be approximated to arbitrary accuracy by a simple polygon. The error between the polygonal approximation and the actual structure may be made arbitrarily small by appropriately adding vertices to the polygon. Defining the boundary of a region with a polygon is widely used in medical image analysis when observers manually outline regions of interest. Typically, an observer is shown a digital image and, using a mouse-driven interface, places vertex points along the perceived boundary of the region of interest. The boundary of the region is then defined by connecting the vertices with straight line segments. The region is considered to be defined in continuous space because neither the vertex points nor the points along the lines connecting the vertices are constrained to the integer coordinates of the image pixels. The boundary of a 2D region in continuous space is a closed one-dimensional (1D) piecewise-continuous, linear curve that does not contribute to the area of the region. Given a polygon defined in continuous space, the area may be calculated from the vertices by means of Green’s theorem.8, 9 This method of area calculation is exact, computationally efficient, expandable to higher dimensions (through Stokes’ theorem), and is a standard method of polygon area calculation in continuous space.10
An image region defined in continuous space sometimes must be converted to the discrete space of a digital image matrix. Such a conversion is necessary when applying computerized methods that combine image processing techniques typically native to discrete space (e.g., morphological operators11, 12) with those native to continuous space (e.g., active contours13, 14) or when using semi-automated segmentation methods that integrate the continuous-space boundary defined by an observer with discrete-space image processing techniques. The conversion between continuous-space and discrete-space representations may cause changes in the area due to the conversion process. This study investigated three methods for conversion from continuous space to discrete space and measured the differences in the resulting area.
Continuous-to-discrete space conversions and many automated and semiautomated segmentation methods generate regions restricted to the discrete coordinates defined by the pixels of the image. In discrete space, the boundary of a 2D region is not the 1D curve that defines boundaries in continuous space; instead, the discrete boundary is defined by a set of small 2D regions (the individual pixels that comprise the region boundary). Since the discrete boundary of the region is no longer one dimensional, two possibilities exist when calculating the area of a region defined in discrete space (Fig. 1). First, the boundary could be considered part of the region (an “internal boundary”) and thus the area of the boundary itself is included in the region area calculations. Second, the boundary is not part of the region (an “external boundary”) and is excluded from area calculation. Given a region defined in discrete space, the area may be calculated by counting the number of pixels in the region. This calculation of area is fast and is the standard method of area calculation in discrete space.
It should be noted that differences in the discrete-space boundary may exist due to the choice of discrete boundary connectivity. A region boundary may be defined in four-neighbor connectivity or in eight-neighbor connectivity. The choice of connectivity can cause differences in area calculation since more pixels will be present in the four-connected boundary and different region representations may result. All discrete boundaries in this study were set to eight-connectivity to prevent connectivity issues from contributing to differences in area.
For reasons similar to the continuous-to-discrete space conversion, conversion from discrete space to continuous space may be necessary. Several methods for discrete-to-continuous space conversion exist and may result in substantially different boundaries and thus different area values. First, the centers of the discrete boundary pixels may be connected to form a polygon (Fig. 1), a technique that can be applied to either the internal or external discrete boundary. Second, the outer edges of boundary pixels may be connected to form a polygon (Fig. 1). If the discrete boundary is defined to be an internal boundary, the area calculated by application of Green’s theorem to the continuous polygon constructed in this manner will be equal to the discrete area calculated from pixel counting with the boundary pixels included; if the discrete boundary is defined to be an external boundary, the area calculated by application of Green’s theorem to the continuous polygon constructed in this manner will be an overestimation of the discrete area calculated from pixel counting with the boundary pixels excluded. Finally, the inner edges of the boundary pixels may be connected to form a polygon (Fig. 1). If the discrete boundary is an external boundary, the area calculated by application of Green’s theorem to the continuous polygon constructed in this manner will be the same as the discrete area calculated from pixel counting with boundary pixels excluded; if the discrete boundary is an internal boundary, the area calculated by application of Green’s theorem to the continuous polygon constructed in this manner will underestimate the discrete area calculated from pixel counting with boundary pixels included.
Previous studies investigated size discrepancies due to inter- and intraobserver variability when defining a region boundary15 and variability due to the manner in which size is quantified from a given region boundary.16 This study examined the impact of region boundary definitions and continuous-to-discrete and discrete-to-continuous conversion methods on subsequent area calculation. The boundary definitions and conversion methods were applied to a synthetic-image database and two clinical databases: Adrenal glands with boundaries defined in continuous space and lung nodules with boundaries defined in discrete space.
MATERIALS AND METHODS
Green’s theorem
The standard method for calculating the area of a polygon is Green’s theorem. Let R be a simple polygon with no holes and vertices ordered in a counterclockwise manner. If functions P and Q and derivatives ∂P∕∂y and ∂Q∕∂x are continuous over R, then Green’s theorem states that: ∮Pdx+Qdy=∫∫(∂Q∕∂x−∂P∕∂y)dxdy. The area of a polygon with n vertices of position (x,y) is calculated by settingP=−y∕2 and Q=x∕2 and converting the integral to a summation: Area=1∕2∑nxiyi+1−xi+1yi with xn+1=x1 and yn+1=y1. Thus, the area of a polygon with vertices defined in continuous space may be exactly calculated from the coordinates of the vertices.9, 10
Methods for continuous-to-discrete conversion
A polygon in continuous space is a series of line segments joined at their endpoints, thus conversion of a polygon from continuous to discrete space is completely determined by the method applied to convert the continuous line segments to line segments composed of pixels in discrete space. Let v1 and v2 in R2 define the endpoints of a line segment to be converted from continuous space to discrete space. First, the equation defining the line segment is determined from v1 and v2. Next, this line equation is used to determine the image pixels composing the corresponding discrete line segment. This process is repeated for all continuous line segments composing the polygon boundary. It should be noted that instead of discretizing the boundary to the image pixels, the boundary can be descretized to a supersampled version of the image. The supersampled version of the image is constructed by dividing each pixel into several subpixels. This article does not consider this technique for two reasons. First, supersampling forces the boundary to the subpixels of the supersampled image. Although the boundary is still discrete, it is no longer restricted to the discrete image pixels. Second, as the number of subpixels goes to infinity, the boundary created on the supersampled image becomes the continuous polygon boundary (note that in this case the size of the supersampled image becomes infinite).
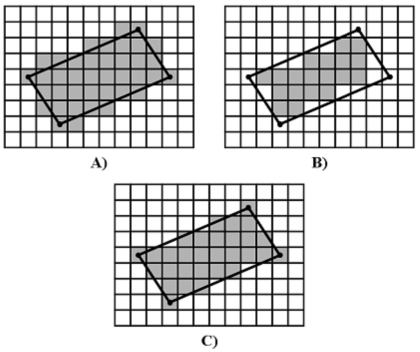
Given a continuous polygon converted to a discrete boundary by the line equation method, the discrete representation of polygon area may be computed. If polygon area is calculated by counting the discrete boundary pixels and those pixels enclosed within the discrete boundary, the resulting area will be larger than the corresponding area calculated in continuous space by Green’s theorem. This is the boundary-included pixel-counting area (BIPCA). Similarly, area may be calculated by counting only those pixels enclosed within the discrete boundary. This boundary-excluded pixel-counting area (BEPCA) will result in an area lower than the area calculated in continuous space by Green’s theorem. Finally, a compromise between the boundary-included and boundary-excluded pixel counting methods may be applied by only including the discrete boundary pixels whose centers lie within the continuous polygon. This is the pixel-center pixel-counting area (PCPCA). All continuous-to-discrete conversion methods are demonstrated in Fig. 2.
Figure 2.
Continuous-to-discrete line conversion methods applied to a parallelogram (black lines). A) Converted region with boundary included. B) Converted region with boundary excluded. C) Pixel-center conversion.
Synthetic image database
A database containing continuous ellipses, continuous isosceles triangles, discrete ellipses, and discrete isosceles triangles was created to test the impact of shape on boundary and area definition. Three ellipse parameters were individually varied in the continuous ellipse portion of the database. The major axis (which is proportional to area) was varied keeping the tilt (i.e., angle between the major axis and the horizontal) at 0 deg and aspect ratio at 1 (i.e., a circle), the tilt was varied keeping the major axis length at 40 pixels and aspect ratio at 0.25, and aspect ratio was varied keeping the area at 800 pixels2 and the tilt at 0 deg. A set of discrete ellipse images was also created using the same parameters. Three triangle parameters were individually varied in the continuous triangle portion of the database. The height was varied keeping the tilt (i.e., angle between the horizontal axis and the vertex between sides of equal length) at 0 deg and the interior angle (i.e., the angle between sides of equal length) at 20 deg, the tilt was varied keeping the height at 80 pixels and the interior angle at 20 deg, and the interior angle was varied keeping the area at 800 pixels and the tilt at 0 deg. A set of discrete triangle images was also created using the same parameters.
For each continuous synthetic isosceles triangle and ellipse created, four region boundary and area definitions were applied: (1) Green’s theorem applied to the originally constructed continuous boundary, (2) direct conversion to discrete space and calculation of the BEPCA, (3) direct conversion to discrete space and calculation of the BIPCA, and (4) pixel-center conversion to discrete space and calculation of the PCPCA. The percent differences of the area were calculated among the different definitions. Similarly, for each discrete synthetic isosceles triangle and ellipse created, four region boundary and area definitions were applied: (1) BEPCA, which is the method that is most consistent with the boundary data provided by the Lung Image Database Consortium (LIDC), (2) BIPCA, (3) Green’s theorem applied to vertices defined by the center of each boundary pixel, where the boundary has been defined as an outer boundary (Green’s outer area), and (4) Green’s theorem applied to vertices defined by the center of each inner boundary pixel (Green’s inner area). Finally, analytic expressions for the dependence of percent difference on the different shape parameters were derived (see the Appendix). The percent difference for Quantity1 versus Quantity2 was calculated as %Diff=200*(Quantity1−Quantity2)∕(Quantity1+Quantity2). Thus, positive percent difference implies Quantity1 is greater than Quantity2 and negative percent difference implies Quantity1 is less than Quantity2.
Adrenal gland database
A database of patients enrolled in adrenal gland perfusion studies at The University of Chicago Medical Center was collected. Each of 11 patients underwent a contrast-enhanced helical CT scan with images reconstructed as a 512×512-pixel image matrix. A single observer outlined both adrenal glands in every CT section in which they appeared through the manual placement of vertices along the boundary of the adrenal gland (Fig. 3). These vertices and the lines connecting the vertices were not constrained to the discrete space of the image pixels. This resulted in a total of 71 adrenal outlines (6±6 per patient). For each adrenal region, the area was calculated by four methods: (1) Green’s theorem applied to the originally constructed continuous boundary, (2) direct conversion to discrete space and calculation of the BEPCA, (3) direct conversion to discrete space and calculation of the BIPCA, and (4) pixel-center conversion to discrete space and calculation of the PCPCA. The percent differences between the different area calculation methods were computed. The percent differences between the different area calculation methods were computed using the same method and sign convention applied to the synthetic image database.
Figure 3.
Observer-defined region boundaries. A) Adrenal gland boundaries defined in continuous space (black). B) Zoomed adrenal boundary illustrating line segments connected by manually positioned vertices (black boxes). C) External boundary of a lung nodule defined in discrete space (black). Note the large spur present in the boundary (white arrows).
LIDC database
The LIDC public database of lung nodules17 was selected to evaluate region boundaries defined in discrete space. For each scan of the 85-patient LIDC database (one scan per patient), between one and four experienced thoracic radiologists provided boundaries for each nodule with longest diameter greater than 3 mm and less than 30 mm (Fig. 3).18 Nodule boundaries were constructed in every section in which the nodule was demonstrated, as individually determined by each radiologist who chose to mark that lesion as a nodule ⩾3 mm. Boundaries of internal cavities were not considered for this study. Per LIDC protocol, all nodule regions were defined on the discrete pixel grid by an exterior boundary. All boundaries were then converted to eight-connectivity for this study. These conditions resulted in 371 nodule instances composed of 1764 boundaries (28±55 per patient) defined across 64 patients. Four separate area metrics were then calculated for each radiologist-defined boundary instance (Fig. 1): (1) BEPCA, which is the method that is most consistent with the boundary data provided by the LIDC; (2) BIPCA, (3) Green’s theorem applied to vertices defined by the center of each boundary pixel, where the boundary has been defined as an outer boundary (Green’s outer area), and (4) Green’s theorem applied to vertices defined by the center of each inner boundary pixel (Green’s inner area). The percent differences between the different area calculation methods were computed using the same method and sign convention applied to the synthetic image database. In clinical practice, linear measurements are used to represent nodule size.19 To obtain a more clinically meaningful analysis, the diameter of the area-equivalent circle was calculated for each of the four area metrics, and the percent differences among the different methods were computed.
RESULTS
Synthetic image database
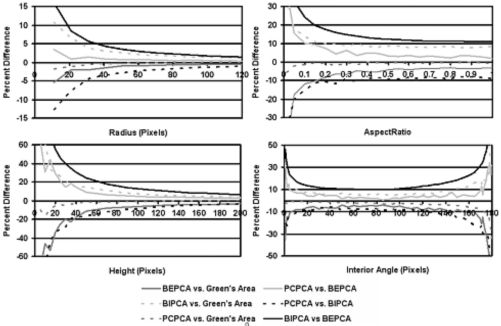
Four region boundary and area definitions were applied to each continuous-space ellipse and triangle. The percent differences of the area were calculated among the definitions and plotted as a function of (1) major axis length and aspect ratio for ellipses and (2) height and internal angle for isosceles triangles (Fig. 4). Analytic expressions for the dependence of percent difference on the different shape parameters were derived (see the Appendix) and demonstrated trends similar to those graphed in Fig. 4. Though the shape of the analytic expressions demonstrated similarities with those graphed in Fig. 4, the deviations from this shape were substantial (this is both due to the approximate nature of the analytic expressions and the impact of the discretizing of the continuous structure). Dependence on ellipse and triangle tilt was also investigated and demonstrated sinusoidal dependence on the tilt angle.
Figure 4.
Comparison of continuous-to-discrete conversion methods applied to the synthetic database. Top-left: Circles of varying radius. Top-right: Ellipses with constant area and varying aspect ratio. Bottom-left: Isosceles triangles with constant interior angle and varying height. Bottom-right: Isosceles triangles of constant area and varying interior angle.
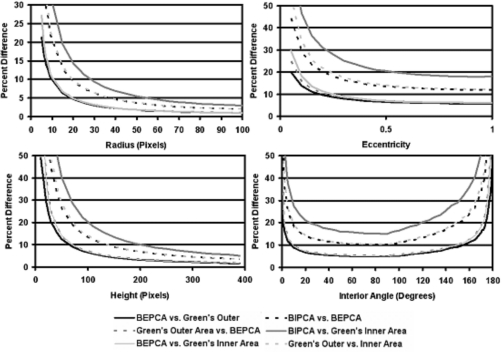
Four region boundary and area definitions were applied to each discrete-space ellipse and triangle image. The percent differences of the area were calculated among the definitions and plotted as a function of (1) major axis length and (2) aspect ratio for ellipses and height and internal angle for isosceles triangles (Fig. 5). Deviations of graph shape (Fig. 5) with the calculated analytic expressions were similar to those of the continuous case. The dependence on ellipse and triangle tilt also demonstrated sinusoidal dependence on the tilt angle.
Figure 5.
Comparison of discrete-to-continuous conversion methods and discrete boundary and area definitions applied to the synthetic database. Top-left: Circles of varying radius. Top-right: Ellipses with constant area and varying aspect ratio. Bottom-left: Isosceles triangles with constant interior angle and varying height. Bottom-right: Isosceles triangles of constant area and varying interior angle.
Adrenal database
Four area calculation methods were applied to each continuous-space, observer-defined adrenal gland boundary. Mean adrenal gland area ranged from 85.11±35.42 pixels2 to 126.24±42.76 pixels2 depending on the method of calculation. The percent differences between the different area-calculation methods are collected in Table 1. PCPCA resulted in the closest match to the area of the continuous region calculated by Green’s theorem. The percent differences between the different area calculation methods are graphed as a function of Green’s theorem area in Fig. 6. The presence of negative values for percent difference are a consequence of the formula used to calculate the percent differences and were purposely made negative to provide better visualization of the different comparisons being graphed.
Table 1.
Percent differences among area calculation methods applied to the adrenal database.
| BIPCA vs Green’s area | BEPCA vs Green’s area | PCPCA vs Green’s area | BIPCA vs BEPCA | PCPCA vs BIPCA | PCPCA vs BEPCA | |
|---|---|---|---|---|---|---|
| Mean | 22.83±5.23 | −19.27±5.62 | 2.87±3.58 | 41.59±8.94 | −25.64±7.70 | 16.41±6.75 |
| Max | 35.23 | −9.78 | 12.34 | 63.16 | −10.81 | 28.57 |
| Min | 5.23 | −31.27 | −3.82 | 26.33 | −47.06 | 4.65 |
Figure 6.
Percent difference vs Green’s theorem area calculated on the adrenal database.
LIDC database
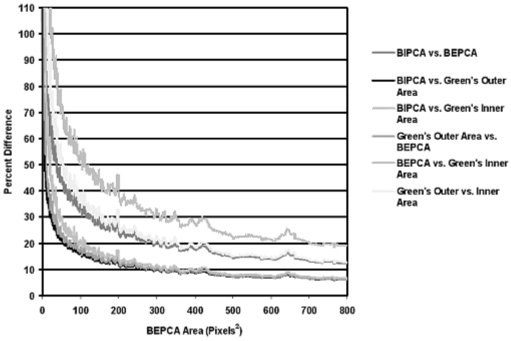
Four area calculations and four corresponding diameter of the area-equivalent circle calculations were performed for each boundary. Mean nodule region area ranged from 146.95±212.14 pixels2 to 208.78±251.71 pixels2 depending on the method of calculation. The mean diameter of the area equivalent circle ranged from 10.96±8.19 pixels to 14.08±8.23 pixels depending on the area used for calculation. The percent difference between each set of area calculations and between each set of area-equivalent diameter calculations was recorded (Table 2). The percent differences between the different area calculation methods are graphed as a function of BEPCA in Fig. 7. The graph illustrates a trend-line with a 10-bin mean smoothing kernel for each set of data. This trend-line and smoothing were used to better demonstrate the dependence of percent differences on structure area and to improve the readability of the graphs. Almost identical trends as demonstrated in Fig. 7 were also found for the diameter of the area equivalent circle differences. Forty-six nodule boundary instances (2.6%) demonstrated zero area when calculated using BEPCA. A total of 199 boundary instances (11.3%) included one or more spurs in which a portion of the boundary surrounds zero area when calculated using BEPCA (Fig. 5). It should be noted that if the boundaries were not converted to eight-connectivity then the total number of spurs increased to 786 boundary instances (44.6%).
Table 2.
Percent differences among area calculation methods applied to the LIDC database.
| BIPCA vs Green’s outer area | Green’s outer area vs BEPCA | BEPCA vs Green’s inner area | BIPCA vs BEPCA | BIPCA vs Green’s inner area | Green’s outer area vs Green’s inner area | |
|---|---|---|---|---|---|---|
| Mean | 24.32±27.59 | 24.23±24.28 | 30.55±32.36 | 46.09±35.92 | 69.75±44.37 | 50.98±39.49 |
| Percent differences among diameters of the area equivalent circle | ||||||
| Mean | 13.94±25.48 | 13.24±20.55 | 17.51±28.28 | 26.36±31.99 | 41.53±40.52 | 29.42±34.25 |
Figure 7.
Percent difference vs BEPCA calculated on the LIDC database.
DISCUSSION
Inconsistent definition of area and changes in area due to continuous-discrete conversion are possible sources of systematic error in both the experimental and clinical analysis of medical images. The positional differences at any boundary vertex or boundary pixel will usually differ by less than 2 pixels among the different definitions of region boundary; however, the resulting percent differences in area may become substantial. Figures 4567 demonstrate these differences and their strong dependence on the size of the image region. This dependence on size is twofold. First, the percent differences are essentially ratios of boundary length with area (see the Appendix). This implies that the percent difference will always decrease as the structure size increases because area will always grow faster than perimeter for a 2D region. This effect is present both when converting from continuous-to-discrete space and if the incorrect method of boundary representation and area calculation are applied within either the continuous or discrete space (i.e., applying BEPCA when the boundary was formed using boundary representation and area calculation of BIPCA). Second, as a structure becomes smaller relative to the discrete image pixel size, the approximation to the image edge becomes less accurate and begins to show substantial pixelation. This pixelation translates into an increase in the differences between discrete and continuous calculations of area. A similar effect is seen when considering the curvature of the structure boundary. If continuous-to-discrete conversion is applied to a polygonal representation of an ellipse of constant area (as calculated by Green’s theorem), the percent differences increase with aspect ratio. This is because areas of high curvature cannot be correctly converted to the discrete image space (Fig. 4). Similarly, differences were observed when converting continuous-space triangles to the discrete image depend on how well the triangle vertices are approximated by the discrete image pixels. Percent error will also increase with the number of high curvature boundary points. Thus, while a circular structure (such as a benign lesion) may only see a modest impact from differing boundary and area representations, structures with many high curvature points (such as spiculated malignant lesions) will see more substantial percent errors.
Differences among the different methods were generally higher for triangles than for ellipses in both the continuous and discrete spaces due to the conversion errors present in high curvature portions of the object boundary (e.g., triangular corners). It should also be noted that ordering the method comparisons by percent error produced the same ordering at almost all points for graphs in Figs. 45. For example, in the continuous-to-discrete graph BIPCA versus BEPCA had the highest percent error and PCPCA versus Green’s area had the lowest percent error across almost all radius and height values in graphs illustrated in Fig. 4. Considering the substantial shape differences between an ellipse and an isosceles triangle, this implies that such orderings are insensitive to the specific shape and can be expected from a range of similar shapes. The orderings observed in the synthetic image database for percent difference versus height and percent difference versus radius are also the same as those seen in both the adrenal database and LIDC database results of percent difference versus area.
When studies are conducted by a single observer, consistent application of a single definition of the region boundary and area calculation will eliminate this source of error. However, the relatively abstract reasons behind this error and its perceived size (on the order of pixels per boundary vertex or boundary pixel) make it unlikely to be seriously discussed and considered in clinical practice. Further, such differences may actually happen in the internal processing of a semiautomated method making its presence unknown to the clinician. It is also a potentially serious problem in large multi-institutional studies and in the clinical setting where several individuals independently provide boundary definitions and area measurements. In large collaborative research studies involving several institutions, the definition of boundary and calculation of area may be carried out independently at each institution. In such a case, if the collaborating institutions do not explicitly agree upon a single definition of region boundary and area, substantial measurement differences may arise. Similarly, it is important for researchers to clearly specify measurement protocols in published studies and especially in publicly available databases where multiple, unrelated researchers will be analyzing and processing the same data.
The differences demonstrated in this study for region boundaries native to both discrete and continuous space support the idea that inconsistent application of boundary definition and area calculation may potentially impact both research results and clinical patient care. Even when single definitions of boundary and area are agreed upon, an observer’s preconceived idea of area may cause the application of differing definitions in practice. For example, the LIDC protocol defines all boundaries as external boundaries in discrete space and area as boundary-excluded pixel counting area. However, LIDC radiologists still created nodule boundaries of zero area and boundaries that contained spurs (Fig. 5). Strict application of the BEPCA definition would not allow the creation of spurs or boundaries of zero area since such structures do not make logical sense. Such inconsistencies may occur when an observer attempts to outline the continuous underlying distribution without recognizing the inconsistencies that may arise during creation of a discrete region boundary and subsequent calculation of area.
In the clinical setting, tracking of disease progression and response to therapy is often quantified by measurements made on images acquired serially in time. In this case, several possibilities exist for inconsistent application of boundary and area definitions. First, different observers within the same institution (applying differing definitions of region boundary and area) may analyze the images of the same patient at different time periods. Second, the patient may change to a new hospital that applies a different measurement protocol. If previous scans are not remeasured under the new protocol, the new area values may give a false impression of disease evolution. Finally, as automated and semiautomated techniques are introduced into the clinic, there is the possibility that separate systems (with differing definitions of boundary and area) will be applied to the same patient, thus resulting in inconsistent area values.
As technology advances, the problems associated with defining region boundary and size metrics will continue to become more complicated. The addition of another dimension increases the number of possible methods for calculating size metrics (e.g., volume). An extension of Green’s theorem (Stokes’ theorem) allows for the direct calculation of volume from the vertices of a bounding polygon. This calculation is fast and exact; however, it is currently of limited use because it requires the construction of a 3D polygon. The inability of human observers to easily view and manipulate 3D structures in digital datasets limits the application of Stokes theorem to two scenarios. First, automated and semiautomated methods can construct a 3D structure from user-defined 2D boundaries. Unfortunately, this is an ill-posed problem and only heuristic methods currently exist to do this.20 Second, if the segmentation of a 3D structure is performed through image processing methods (e.g., active surfaces), the resulting vertices of the surface will be known and Stokes’ theorem could be applied. Further work will be necessary to assess the potential errors that may arise in 3D size metrics for surface boundary and volume definitions.
CONCLUSION
This study investigated the possible impact of applying inconsistent definitions of region boundary and area to medical images for the purpose of computerized patient analysis. Region boundary definitions and area calculation methods were categorized as native to discrete space or native to continuous space. Motivation for converting between these two paradigms and appropriate conversion methods were also presented and investigated in calculations. Methods were tested on two clinical databases: One with region boundaries defined in continuous space and one with region boundaries confined to discrete pixel space. Substantial differences were demonstrated among the various area calculation methods supporting the necessity, in both the research and clinical settings, to consistently apply boundary definition and area calculation methods. Further, these differences also support the importance of reporting boundary definition and area calculation methods in written protocols and published manuscripts.
ACKNOWLEDGMENT
Supported in part by USPHS Grant No. CA 102085.
APPENDIX: DERIVATION OF FUNCTIONAL DEPENDENCIES FOR THE SYNTHETIC DATABASE
A. Functional dependencies of percent difference for isosceles triangles
Let an isosceles triangle be defined by the distance from the origin to a vertex connecting the sides of equal length (height) and the angle between the sides of equal length (internal angle). The area of this triangle is then given by:A=1∕2bh=h2tan(θ∕2) where h is the height, b is the base, and θ is the internal angle. The perimeter of the triangle is: P=b+2S=b+2(b∕2)csc(θ∕2)=b[1+csc(θ∕2)] where S is the length of a side of equal length. This implies that if the differences occur only along the boundary of the structure, the percent difference will be of the functional form:P∕A∝b[1+csc(θ∕2)]∕A=2[1+csc(θ∕2)]∕h.
B. Functional dependencies of percent difference for ellipses
Let an ellipse be defined by the length of the major axis and the ratio of minor axis to major axis (aspect ratio). The area of the ellipse is then given by A=πab=πa2e where a is the major axis length, b is the minor axis length, and e is the aspect ratio. This implies the percent differences for circles will have a functional form: P∕A∝2πa∕πa2=2∕a. Unfortunately, the perimeter of an ellipse of arbitrary size does not have a simple and exact formulation. An approximation developed by Ramanujan21 estimates the perimeter as
where h=(a−b)∕(a+b)=(1−e)∕(1+e). This implies a percent difference estimated as
References
- Jaffe C. C., “Measures of response: RECIST, WHO, and new alternatives,” J. Clin. Oncol. 24, 3245–3251 (2006). [DOI] [PubMed] [Google Scholar]
- Schwartz L. H., Ginsberg M. S., Decorato D., Rothenberg L. N., Einstein S., Kijewski P., and Panicek D. M., “Evaluation of tumor measurements in oncology: Use of film-based and electronic techniques,” J. Clin. Oncol. 18, 2179–2184 (2000). [DOI] [PubMed] [Google Scholar]
- Tran L. N., Brown M. S., Goldin J. G., Yan X., Pais R. C., McNitt-Gray M. F., Gjertson D., Rogers S. R., and Aberle D. R., “Comparison of treatment response classifications between unidimensional, bidimensional, and volumetric measurements of metastatic lung lesions on chest computed tomography,” Acad. Radiol. 11, 1355–1360 (2004). [DOI] [PubMed] [Google Scholar]
- S. G.ArmatoIII and Oxnard G. R., “The radiologic measurement of mesothelioma,” Hematol. Oncol. Clin. North Am. 19, 1053–1066 (2005). [DOI] [PubMed] [Google Scholar]
- Nowak A. K., “CT, RECIST, and malignant pleural mesothelioma,” Lung Cancer 49, S37–S40 (2005). [DOI] [PubMed] [Google Scholar]
- Edwards P. D., Bull R. K., and Coulden R., “CT measurement of main pulmonary artery diameter,” Br. J. Radiol. 71, 1018–1020 (1998). [DOI] [PubMed] [Google Scholar]
- Dachman A. H., Maceneaney P. M., Adedipe A., Carlin M., and Schumm L. P., “Tumor size on computed tomography scans: Is one measurement enough?” Cancer 91, 555–560 (2001). [PubMed] [Google Scholar]
- Edwards C. H., Advanced Calculus of Several Variables (Academic, New York, 1973). [Google Scholar]
- Brlek S., Labelle G., and Lacasse A., “The discrete green theorem and some applications to discrete geometry,” Theor. Comput. Sci. 346, 200–225 (2005). [Google Scholar]
- Bockman S. F., “Generalizing the formula for areas of polygons to moments,” Am. Math. Monthly 96, 131–132 (1989). [Google Scholar]
- Heijmans H. J. A. M., “Mathematical morphology: A modern approach in image processing based on algebra and geometry,” SIAM Rev. 10.1137/1037001 37, 1–36 (1995). [DOI] [Google Scholar]
- Sonka M., Hlavac V., and Boyle R., Image Processing: Analysis and Machine Vision (Thomson-Engineering, Toronto, 1998). [Google Scholar]
- Kass M., Witkin A., and Terzopoulos D., “Snakes—Active contour models,” Int. J. Comput. Vis. 10.1007/BF00133570 1, 321–331 (1987). [DOI] [Google Scholar]
- Osher S. and Sethian J. A., “Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations,” J. Chem. Phys. 10.1063/1.445571 79, 12–49 (1988). [DOI] [Google Scholar]
- Meyer C. R., Johnson T. D., Mclennan G., Aberle D. R., Kazerooni E. A., Macmahon H., Mullan B. F., Yankelevitz D. F., Van Beek E. J., S. G.ArmatoIII, McNitt-Gray M. F., Reeves A. P., Gur D., Henschke C. I., Hoffman E. A., Bland P. H., Laderach G., Pais R., Qing D., Piker C., Guo J., Starkey A., Max D., Croft B. Y., and Clarke L. P., “Evaluation of lung MDCT nodule annotation across radiologists and methods,” Acad. Radiol. 13, 1254–1265 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeves A. P., Biancardi A. M., Apanasovich T. V., Meyer C. R., MacMahon H., vanBeek E. J., Kazerooni E. A., Yankelevitz D., McNitt-Gray M. F., McLennan G., S. G.ArmatoIII, Henschke C. I., Aberle D. R., Croft B. Y., and Clarke L. P., “The Lung Image Database Consortium (LIDC): A comparison of different size metrics for pulmonary nodule measurements,” Acad. Radiol. 14, 1475–1485 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- S. G.ArmatoIII, McLennan G., McNitt-Gray M. F., Meyer C. R., Yankelevitz D., Aberle D. R., Henschke C. I., Hoffman E. A., Kazerooni E. A., MacMahon H., Reeves A. P., Croft B. Y., Clarke L. P., and The LIDC Research Group, “Lung Image Database Consortium: Developing a resource for the medical imaging research community,” Radiology 10.1148/radiol.2323032035 232, 739–748 (2004). [DOI] [PubMed] [Google Scholar]
- McNitt-Gray M. F., S. G.ArmatoIII, Meyer C. R., Reeves A. P., Mclennan G., Pais R. C., Freymann J., Brown M. S., Engelmann R. M., Bland P. H., Laderach G. E., Piker C., Guo J., Towfic Z., Qing D. P.-Y., Yankelevitz D. F., Aberle D. R., Van Beek E. J. R., Macmahon H., Kazerooni E. A., Croft B. Y., and Clarke L. P., “The Lung Image Database Consortium (LIDC) data collection process for nodule detection and annotation,” Acad. Radiol. 14, 1464–1474 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Therasse P., Arbuck S. G., Eisenhauer E. A., Wanders J., Kaplan R. S., Rubinstein L., Verweij J., Van Glabbeke M., Van Oosterom A. T., Christian M. C., and Gwyther S. G., “New guidelines to evaluate the response to treatment in solid tumors. European Organization for Research and Treatment of Cancer, National Cancer Institute of the United States, National Cancer Institute of Canada,” J. Natl. Cancer Inst. 10.1093/jnci/92.3.205 92, 205–216 (2000). [DOI] [PubMed] [Google Scholar]
- Cong G. and Parvin B., “Surface reconstruction from sparse fringe contours,” Proceedings of the Fourth IEEE Workshop on Applications of Computer Vision, 19–21 October, 1998, Princeton, NJ, p. 140.
- Aiyangar S. Ramanujan and Berndt B. C., Ramanujan’s Notebooks (Springer, New York, 1985). [Google Scholar]