Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2008 Jun 12;35(7):3054–3061. doi: 10.1118/1.2938519

A feasibility study to calculate unshielded fetal doses to pregnant patients in 6-MV photon treatments using Monte Carlo methods and anatomically realistic phantoms

Bryan Bednarz 1, X George Xu 1,a)
PMCID: PMC2809713  PMID: 18697528

Abstract

A Monte Carlo-based procedure to assess fetal doses from 6-MV external photon beam radiation treatments has been developed to improve upon existing techniques that are based on AAPM Task Group Report 36 published in 1995 [M. Stovall et al., Med. Phys. 22, 63–82 (1995)]. Anatomically realistic models of the pregnant patient representing 3-, 6-, and 9-month gestational stages were implemented into the MCNPX code together with a detailed accelerator model that is capable of simulating scattered and leakage radiation from the accelerator head. Absorbed doses to the fetus were calculated for six different treatment plans for sites above the fetus and one treatment plan for fibrosarcoma in the knee. For treatment plans above the fetus, the fetal doses tended to increase with increasing stage of gestation. This was due to the decrease in distance between the fetal body and field edge with increasing stage of gestation. For the treatment field below the fetus, the absorbed doses tended to decrease with increasing gestational stage of the pregnant patient, due to the increasing size of the fetus and relative constant distance between the field edge and fetal body for each stage. The absorbed doses to the fetus for all treatment plans ranged from a maximum of 30.9 cGy to the 9-month fetus to 1.53 cGy to the 3-month fetus. The study demonstrates the feasibility to accurately determine the absorbed organ doses in the mother and fetus as part of the treatment planning and eventually in risk management.

Keywords: Monte Carlo, TG-36, fetal dose, radiation protection

INTRODUCTION

The number of pregnant patients who undergo radiation therapy has been increasing partially due to the improvements in cancer detection and the tendency for women to delay their pregnancy until later reproductive ages. Radiation safety of the fetus implemented in treatment planning is of particular concern because of the relatively high radiosensitivity and potentially secondary exposure levels. The Task Group 36 (TG-36) of the American Association of Physicists in Medicine (AAPM) summarized a number of adverse radiation effects of the fetus for absorbed doses as low as 10 cGy.1 The TG-36 also recommended procedures and data that can help medical physicist plan and execute radiation treatment of a pregnant patients. Measurement data were provided for dose outside the treatment beam in water phantoms for a variety of beam energies and field sizes. Different types of shielding structures in terms of their complexity, ease of use, cost, and usefulness with other aids were also recommended.

As part of the recommended procedures, the physicist would need to estimate the unshielded dose to the fetus by taking out-of-field dose measurements. The task group also provided reference dose data to accompany the fetal dose measurements. However, data for only a few field sizes were considered by the TG-36 leading to difficulty when approximating fetal dose from treatment plans with irregular fields. Kry et al.2 compared fetal dose estimates from TG-36 to measurements for irregular treatment fields and determined that on average the TG-36 calculations underestimated the measured dose by 31%. In addition, the task group recommended a phantom arrangement in which an anthropomorphic phantom is coupled to a small sized water or solid phantom to approximate anatomical details of the pregnant patient.

Pregnant patients have been treated for tumors in a variety of sites including the brain,3, 4 breast,5 nasopharynx,6 and knee,7 as well as Hodgkin’s disease.8, 9 Treatment plans are developed with additional consideration for the fetal exposure. Simple techniques have been used to reduce the dose outside the treatment field by adjusting the gantry angle,1, 3 field size,1 treatment beam energy,1 and patient position.1, 3 Furthermore, defining the field edge that is located nearest to the fetus using the lower collimator components, such as the multileaf collimator (MLC) and jaws, have been found to reduce the dose outside the field.1, 10 Many have reported that the use of shielding structures have advantages in avoiding the stray radiation4, 5, 6, 7, 8, 9 and a factor of 2 or more in fetal dose reduction can be achieved.11, 12, 13 The majority of these past studies, however, were based on experimental measurements in physical phantoms that are anatomically simplified and the dose to the fetus contained considerable uncertainty.3, 4, 5, 7, 8, 9, 12

Recently, there has been a renewed concern about the increase in latent effects, most importantly secondary cancer induction, in cancer survivors who were treated by radiation.14, 15, 16, 17 Such concern can be extended to the fetus which is much more radiosensitive than the mother. In utero irradiation can lead to both cell killing and the induction of cancers.1 Effects caused by cell killing have a practical threshold below which the effect is not seen; however, the severity of these effects is dose dependent. Cell killing effects include lethality, central nervous system abnormalities, cataracts, growth retardation, malformations, and even behavioral disorders.1 In addition to cell killing, in utero irradiation elevates the risk of developing potential carcinogenic effects postdelivery, most notably childhood leukemia.1 The fetus has an elevated cancer risk, owing to the higher proportion of dividing cells and the longer lifespan for a potential cancer to develop. Clearly, an accurate dosimetry method is needed to both reduce the uncertainty in the derived dose-response relationship and better manage the risk in such treatment procedures.

This article describes a Monte Carlo dosimetry study to demonstrate the feasibility of calculating the absorbed dose to the fetus of a pregnant patient for selected external beam treatment plans. This procedure utilizes a set of newly developed anatomical models of the pregnant patient that are realistic and compatible with International Commission on Radiological Protection (ICRP) reference values for average pregnant females at the end of 3-, 6-, and 9-month gestational periods.18 Coupled with a detailed medical accelerator model, these computational tools offer an opportunity to quickly and accurately estimate the absorbed organ doses in the mother and fetus as part of the treatment planning.

MATERIAL AND METHODS

Pregnant patient models

To calculate the secondary radiation to organs outside of the treatment volume, a whole-body model is required because computed tomography (CT) images are typically obtained only for partial body and are rarely available for a pregnant patient. The first generation of whole-body anthropomorphic models were developed nearly 40 years ago at Oak Ridge National Laboratory (ORNL) for the Medical Internal Radiation Dose Committee of the Society of Nuclear Medicine.19, 20, 21 To accommodate the computer capabilities in the 1970s–1980s, these models were designed with simple quadric equations for the organs using descriptive and schematic anatomy references of the so-called “reference man.”22 Later improvements at ORNL led to a family of stylized models representing both genders at various ages that became widely adopted by the radiation dosimetry community.23 Adopting the model that represents both a 15-year-old male and an adult female, Stabin et al.24 added the fetus and placenta to create stylized models of a pregnant female at the end of each trimester of pregnancy, the 3-, 6-, and 9-month models, for various internal nuclear medicine applications. Later, Chen25 extended the stylized pregnant female models into four pregnancy periods, 8 week, 3, 6, and 9 months, for external ionizing radiation dosimetry. Using whole-body medical images, the so-called voxel or tomographic models gradually emerged in the past two decades.26 A partial-body 30-week pregnant female model was developed from a set of CT images that were taken when the pregnancy was unknown.27, 28 However, the poor image resolution (0.94 mm×0.94 mm×7 mm) compromised the anatomical detail. Due to a lack of whole-body images for pregnant females, “hybrid” approaches have also been taken to create pregnant models using simplified geometry for the fetus.29, 30, 31

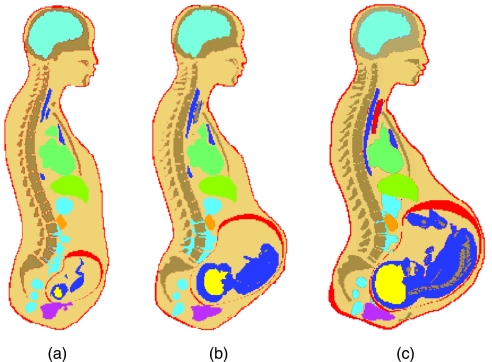
To improve upon existing models of pregnant patients, Xu et al.18 recently developed a set of models using a boundary-representation method. The models are represented in an organ-based surface geometric domain involving a mixture of data structures represented by voxels,32 meshes, and NURBS. Using this novel approach, individual organs and the fetus were assembled in the body of an adult female to form a pregnant female. In addition, the organ volumes (and masses) were easily adjusted to match with the recommended anatomical parameters for an average pregnant female at the end of 3-, 6-, and 9-month gestational stages, respectively.33 The RPI-P3, P6, and P9 models are converted to voxels for Monte Carlo calculations using the Binvox software.34, 35 Given the resolution information, Binvox can change the mesh surface to voxels organ by organ. Binvox performs the conversion from a polygonal mesh surface to an object that consists of less than 1024×1024×1024 voxels. To cover the entire body, the pregnant female was divided into three sections: the head and neck, body trunk, and the legs and feet. Finally, the voxelized organs were assembled into a whole-body model and overlapping voxels were cleaned. For the first time, 35 organs including fetal organs were adjusted to agree with ICRP reference organ masses and sizes representing a typical pregnant patient. Figure 1 shows the RPI-P3, P6, and P9 models plotted in MCNPX.

Figure 1.

Figure 1

Open in a new tab

Pregnant patient models plotted in MCNPX: (a) RPI-P3 representing the first trimester of pregnancy, (b) RPI-P6 representing the second trimester of pregnancy, and (c) RPI-P9 representing the third trimester of pregnancy.

Accelerator modeling

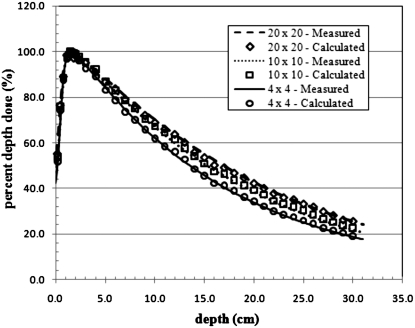
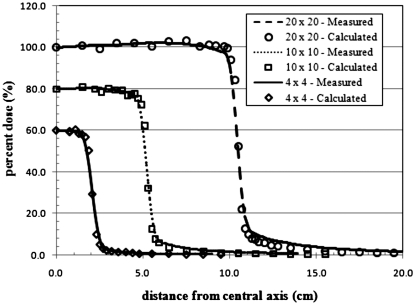
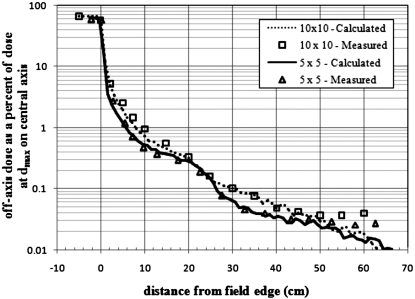
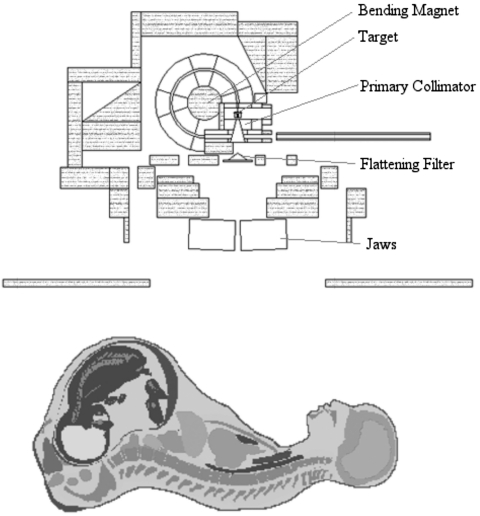
A detailed representation of a Varian Clinac 2100C (Varian Medical Systems Inc., Palo Alto, CA) accelerator head was developed for Monte Carlo calculations of secondary radiation to the pregnant patient. The primary components such as the target, primary collimator, flattening filter, and jaws, were based on detailed drawings provided by the manufacturer, while additional components of the accelerator head were taken from the combinational geometry input of the same accelerator type published by Kase et al.36 These components are important when considering the leakage radiation that emanates from the accelerator. The MLC was left out of the model in order to be consistent with the accelerator setup used by Kry et al.2 whose treatment plans were adopted for this study. All calculations in this work used a 6-MV photon beam to treat the patient. The 6-MV beam was created by an electron beam with a 1.3-mm full width half maximum (FWHM) Gaussian spatial spread and a mean energy of 6.2 MeV with a Gaussian spread of 3% FWHM. The accelerator model was benchmarked with previously measured in-field and out-of-field data. For the in-field benchmarking, field sizes of 4 cm×4 cm, 10 cm×10 cm, and 20 cm×20 cm were considered. A comparison of measured and calculated depth dose and dose profile data is provided in Figs. 23, respectively. The accelerator was also benchmarked with measured out-of-field data provided by Stovall et al.1 A comparison of measured and calculated out-of-field dose data for field sizes of 5 cm×5 cm and 10 cm×10 cm is provided in Fig. 4. For both field sizes the calculated out-of-field dose agrees well with the measured data. For the 5 cm×5 cm field, the average difference was 11% with differences never exceeding 20% for distances less than 50 cm from the field edge. For the 10 cm×10 cm field, the average difference was 10% with differences never exceeding 25% for distances less than 50 cm from the field edge. Larger differences between measured and calculated dose for both field sizes appear beyond 50 cm. These discrepancies have been reported in previous studies.37

Figure 2.

Figure 2

Open in a new tab

Calculated and measured percent depth dose curves from 4 cm×4 cm, 10 cm×10 cm, and 20 cm×20 cm fields in water.

Figure 3.

Figure 3

Open in a new tab

Cross-plane dose profile from 4 cm×4 cm, 10 cm×10 cm, and 20 cm×20 cm fields. Calculated and measured data at 5 cm depth in water. For clarity, the calculated and measured lateral doses for the 10 cm×10 cm and 4 cm×4 cm field sizes were reduced by 20% and 40%, respectively.

Figure 4.

Figure 4

Open in a new tab

Out-of-field dose profile in the in-plane direction. Calculated and measured data from 5 cm×5 cm and 10 cm×10 cm fields at 10 cm depth in water.

Monte Carlo calculation procedures

Monte Carlo calculations in this study were performed using the Monte Carlo code package MCNPX which is a multiparticle, all-energy (eV–TeV) general purpose transport code from Los Alamos National Laboratory.38 The absorbed dose to the fetus was calculated using the track length cell energy deposition tally (F6:p). This tally theoretically provides the collision kerma throughout the fetus. However, It has been shown that for a 10 cm×10 cm treatment field at depths below 2 cm, the conditions of electronic equilibrium are satisfied and the dose and kerma inside and outside the treatment field are nearly the same.37 To test this assumption, we compared the collision kerma to absorbed dose using the pulse height tally modified to provide energy deposition divided by the fetal mass (*F8:e). For each treatment plan the collision kerma was well within the statistical uncertainty range of the absorbed dose. The advantage of calculating the collision kerma is that for the same number of initial source particles, the relative error of the collision kerma is 2–3 times lower than the absorbed dose. The lower relative error for the collision kerma is due to the difference in how MCNPX records the photon track length energy deposition tally compared to the modified pulse height tally. The track length energy deposition tally uses a track length estimator to calculate the energy deposition in a cell. The modified pulse height tallies are made at source points and at surface crossings. Consequently, for small tally volumes, nonzero scores occur much less frequently using the modified pulse height tally than the track length tally, since the probability of interaction in the tally volume is low.

For all simulations, electrons were tracked with the Integrated Tiger Series energy indexing, which has been shown to provide more accurate results than the default indexing method.37, 39 The values of the photon and electron cut-off energies were set to 0.01 and 0.1 MeV, respectively.

Treatment setup

In this study, we adopted treatment plans involving a total of ten different treatment fields that were previously reported by Kry et al.2 and were developed at The University of Texas M.D. Anderson Cancer Center for pregnant patients who received radiation treatment between 1999 and 2001. An example of a typical treatment setup in MCNPX is provided in Fig. 5. One treatment plan was not considered in this article since the distance from the nearest fetal point to the field edge was too great to obtain statistically reliable results. Table 1 provides information on the treatment plans used in this study including the treatment field, prescribed dose, field size, gantry position, and treatment depth. Table 2 provides the distance from the fields edge to the nearest fetal point in each patient model for all treatment fields. The distance to the nearest fetal point was kept consistent with those values given by Kry et al.2 for the 3-month pregnant patient. One limitation of the pregnant patient phantoms was the inability to adjust the position of the arms for field 8. The pregnant patient is fixed in the supine position with her arms resting near her sides. Therefore, the arms were inside the treatment field for field 8, which is an atypical patient setup for a 270° field.

Figure 5.

Figure 5

Open in a new tab

Plot of a typical treatment setup of the pregnant patient (RPI-P9) and accelerator model in MCNPX. All secondary shielding components are shaded gray.

Table 1.

Parameters for the seven treatment plans adopted from Kry et al. (Ref. 2).

Plan No. Field No. Treatment field Prescribed dose (cGy) Field size (cm2) Gantry position Treatment depth (cm)
1 1 Right parotid gland 5000 12.6×13.6 0° 4
2 2 Super clavicle and mediastinum 3060 26.5×20 0° 3
3 3 Mantle 2520 23×25.5 0° 8
  4 Mantle 540 23×25.5 0° 8
  5 Right neck 900 12×16.5 0° 4
4 6 Mantle 3960 25×29.5 0°∕90° (matched) 8
5 7 Mantle 3960 25.5×32.5 0° 8
6 8 Upper neck 6000 9×7.5 270° 4
  9 Super clavicle 6000 20×10 0° 3
7 10 Right tibia 4500 39.6×12 0°∕90° (matched) 1.5
Open in a new tab

Table 2.

Distance from nearest fetal point to field edge for the ten different treatment fields.

Field No. Distance from nearest fetal point to field edge (cm)
RPI-P3 phantom RPI-P6 phantom RPI-P9 phantom
1 35 25 21
2 11 1 −3
3 20 10 6
4 22 12 8
5 25 15 11
6 22.5 12.5 8.5
7 20 10 6
8 32 22 18
9 22 12 8
10 38 37 35
Open in a new tab

Following the treatment plans provided in Table 1, absorbed dose to the fetus was calculated using the 3-, 6-, and 9-month pregnant patient models. All calculations were performed with enough initial electron histories, at least 1×108 electrons, in order to achieve reasonable statistics in the tally results. More initial electron histories were needed for the RPI-P3 phantom, which has a smaller fetus than both the RPI-P6 and RPI-P9 phantoms.

The tally result provided by MCNPX is normalized per source history. In order to determine the absolute fetal dose from each treatment plan, the dose per source electron in MCNPX was converted to dose per cGy in the following manner. First, a water tank was modeled at 100 cm source-to-surface distance, and the number electrons needed to deliver 1 cGy at dmax in the tank under reference conditions (i.e., 10 cm×10 cm field without MLCs) was determined. This number was then scaled to account for the increase in the number of electrons needed to deliver the prescribed dose to the desired treatment depth. As seen in Table 1, all plans had a scaling factor larger than 1. The resulting value gives a conversion factor between dose per source particle and dose per cGy. Next, the dose per cGy was multiplied by the prescribed dose to determine the total dose to the fetus from the given treatment plan. The number of source electrons required to produce 1 cGy at dmax was kept constant for all field sizes. Keeping this value constant for all field sizes introduces error, since the dose at dmax changes with different field sizes. However, as pointed out by Kry et al.,18 the dependence of dose at dmax on field size is rather insignificant when calculating dose outside the treatment field.

RESULTS AND DISCUSSION

Absorbed dose to the fetus using pregnant patient models

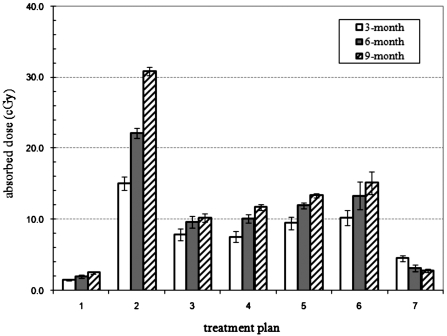
The calculated absorbed dose to the fetus for all three pregnant patient models (3-, 6-, and 9-month) using the seven treatment plans are summarized in Table 3. The relative statistical errors for all treatment plans were equal to or below 10%. For the same number of histories, the relative error for all treatment plans improved with increasing stage of gestation as more particles will interact with the fetus. Figure 6 compares the calculated fetal absorbed doses from each treatment plan for 3-, 6-, and 9-month fetus, respectively. The fetal absorbed dose ranged from a maximum of 30.9 cGy to the 9-month fetus to 1.53 cGy to the 3-month fetus. For all treatment plans except treatment plan 7 the absorbed dose to the fetus increased with increasing stage of gestation. This increase in dose with gestational stage can be attributed to the decrease in the distance between the fetal body and the field edge as the fetus increases in size, as seen in Table 1. Therefore, the 9-month fetus is the closest to the field edge for each treatment followed by the 6-month fetus and then the 3-month fetus. For treatment plan 7, in which the treatment field was below the fetus, the fetal dose decreased from 4.82 to 2.90 cGy with gestational stage increasing from 3 to 9 months. In this case, unlike treatment fields above the fetus, the distance between the nearest fetal point and field edge is relatively constant between gestational stages. Therefore, the decrease in dose is due to mainly the increase in fetal body mass during the pregnancy and the distance now is a minor factor.

Table 3.

Calculated absorbed dose to the fetus from various treatments plans using RPI-P3, RPI-P6, and RPI-P9 phantoms. Accompanying each value is the percent relative error calculated for each value. The relative error is the variance of the calculated dose divided by the value itself.

Treatment plan RPI-P3 phantom RPI-P6 phantom RPI-P9 phantom
(field No.) Dose (cGy) Dose (cGy) Dose (cGy)
1 1.53 8% 2.04 8% 2.47 6%
2 15.07 6% 22.11 3% 30.86 2%
3 7.89 10% 9.62 8% 10.23 5%
4 7.58 10% 10.09 5% 11.72 3%
5 9.51 9% 12.00 3% 13.34 2%
6 10.23 10% 13.34 9% 15.13 7%
7 4.54 10% 3.13 9% 2.90 7%
Open in a new tab

Figure 6.

Figure 6

Open in a new tab

Comparison of calculated fetal dose values from treatment plans for three different gestational stages of the pregnant patient.

Differences between calculated and measured fetal dose values

Here it is necessary to consider the TG-36 recommendations and its difficulties in practice. The TG-36 report provides guidelines to help physicists develop safe treatment plans for pregnant patients. The report recommends that the fetal dose be estimated by taking measurements without special shielding at selected points that will reflect the range of dose throughout the fetus. More than one measurement with an ionization chamber is recommended to estimate the dose averaged over the entire fetal volume. Once the dose is measured and recorded, shielding should be designed to lower the fetal dose below the recommended dose range of 5–10 cGy. This range of dose limits was determined by the TG-36 after a careful evaluation of the epidemiological data of risks to the fetus after radiation exposure. While this dose range is conservative,1 it takes into account the therapeutic nature of the exposure and it is more reasonable than the occupational dose limit of 0.5 cGy recommended by the ICRP.40 With regard to the recommended limit, the measurements used to estimate the fetal dose strongly impact the treatment plan and choice of shielding to lower the dose below 5–10 cGy. However, there are many physical restraints in performing these measurements.

The above recommendations are difficult to implement in clinical situations because there is currently no physical phantom representing the pregnant female. As a compromise, medical physicist often use an anthropomorphic phantoms attached to water or solid phantoms to approximate the fetus.1, 2 Although anthropomorphic adult male phantoms provide photon scattering, such phantoms do not include important female anatomical features. In addition to the lack of realistic physical phantoms for the pregnant patient, determining the fetal dose using point-wise measurements is also challenging. Three fetal points commonly used are the fundus, symphysis pubis, and umbilicus, and it is not certain that these three points are optimal locations for estimating the average dose to the fetus. In order to evaluate the range of dose throughout the fetus, measurement locations should consider the initial size of the fetus and the gestational change of fetal size throughout the course of treatment and shielding should be modified to account for this variation.

Furthermore, the ICRP has repeatedly recommended the use of organ-averaged equivalent doses as the most suitable quantity to accompany epidemiological data to evaluate radiation effects to patients, instead of point-wise dose estimates such as the dose index.40 Ultimately, organ-averaged equivalent doses need to be measured or calculated using physical or computational (e.g., RPI-P series) phantoms that contain clearly labeled organs. The computational approach to obtaining organ-averaged equivalent dose, as demonstrated in this study, is obviously more convenient and versatile than measurements involving dosimeters such as TLDs or metal–oxide–semiconductor field effect transistors placed in several cavity locations that correspond to individual organs.

The RPI-P series computational phantoms represent the detailed female anatomy of the pregnant mother and fetuses at three different gestational periods, thus the radiation scattering and energy deposition in different parts of the mother and fetus will be determined for different gestational stages more accurately than measurements. The RPI-P series phantoms contain organs that have been carefully adjusted to match ICRP organ data for “average” pregnant females in three gestational periods. These new phantoms provide organ-averaged equivalent doses that can eventually allow for epidemiological assessment of the radiation risk to the fetus. The Monte Carlo procedure described above provides an alternative and potentially better way of estimating the unshielded fetal dose than those provided by the TG-36.

CONCLUSION

In this study, a Monte Carlo based computational procedure for calculating unshielded fetal absorbed dose for an average pregnant patient during 3-, 6-, and 9-month gestations has been described. The approach demonstrates the feasibility of a more flexible yet accurate initial fetal dose assessment than that obtained from using TG-36 recommendations. In addition, newly developed pregnant patient models provide anatomical detail that can be useful in treatment planning and ultimately risk assessment. The anatomical position and posture of the fetus in utero varies with patient and time of treatment. Therefore, point measurements in a water phantom, as suggested by the TG-36, could significantly overestimate or underestimate the unshielded fetal dose depending on the chosen measurement points. In our calculations, the absorbed dose to the fetus is the averaged value over the entire fetal volume, thus is more representative of the true anatomy. Both the patient and accelerators models in this study can be adopted for routine treatment planning and risk communication with the patient as well as the design of appropriate fetal shielding for specific treatment plans in a quick and accurate manner. In on-going research, we are developing tools for users to model various shielding materials for common clinical practice to assess the reduction in the dose to the fetus. Over the long term, accurate radiation dose estimates for the pregnant patients and fetuses will provide an opportunity for epidemiological studies to improve the dose-response functions for the fetus in dose levels that are not available in other exposure scenarios.

ACKNOWLEDGMENTS

This project was funded in part by the National Cancer Institute Grant No. R01CA116743. The authors would like to thank Dr. Valery Taranenko for assistance with the use of MCNPX code and Dr. Stephen Kry from MD Anderson Cancer Center for helpful discussions on treatment plans.

References

  1. Stovall M. et al. , “Fetal dose from radiotherapy with photon beams: Report of AAPM Radiation Therapy Committee Task Group No. 36,” Med. Phys. 10.1118/1.597525 22, 63–82 (1995). [DOI] [PubMed] [Google Scholar]
  2. Kry S. F., Starkschall G., Antolak J. A., and Salehpour M., “Evaluation of the accuracy of fetal dose estimates using TG-36 data,” Med. Phys. 10.1118/1.2710332 34, 1193–1197 (2007). [DOI] [PubMed] [Google Scholar]
  3. Magne N., Marcie S., Pignol J., Casagrande F., and Lagrange J., “Radiotherapy for a solitary brain metastasis during pregnancy: A method for reducing fetal dose,” Br. J. Radiol. 74, 638–641 (2001). [DOI] [PubMed] [Google Scholar]
  4. Mazonakis M., Damilakis J., Theoharopoulos N., Varberis H., and Gourtsoyiannis N., “Brain radiotherapy during pregnancy: An analysis of conceptus dose using anthropomorphic phantoms,” Br. J. Radiol. 72, 274–278 (1999). [DOI] [PubMed] [Google Scholar]
  5. Antypas C., Sandilos P., Kouvaris J., Balafouta E., Karinou E., Kollaros N., and Vlahos L., “Fetal dose evaluation during breast cancer radiotherapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(97)00909-7 40, 995–999 (1998). [DOI] [PubMed] [Google Scholar]
  6. Yan J. H., Liao C. S., and Hu Y. H., “Pregnancy and nasopharyngeal carcinoma: A prognostic evaluation of 27 patients,” Int. J. Radiat. Oncol., Biol., Phys. 10, 851–855 (1984). [PubMed] [Google Scholar]
  7. Nair R. P., Nair T. K. M., and El-Akkad S., “Evaluation of fetal dose from megavoltage irradiation of the knee and neonate followup,” Med. Phys. 10.1118/1.595349 10, 862–865 (1983). [DOI] [PubMed] [Google Scholar]
  8. Cygler J., Ding G. X., Kendal W., and Cross P., “Fetal dose for a patient undergoing mantle field irradiation for Hodgkin’s Disease,” Med. Dosim. 22, 135–137 (1997). [DOI] [PubMed] [Google Scholar]
  9. Woo S. Y. et al. , “Radiotherapy during pregnancy for clinical stages of IA–IIA Hodgkin’s disease,” Int. J. Radiat. Oncol., Biol., Phys. 23, 407–412 (1992). [DOI] [PubMed] [Google Scholar]
  10. Mutic S. and Klein E., “A reduction in the AAPM TG-36 reported peripheral dose distributions with tertiary multileaf collimators,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(99)00092-9 44, 947–953 (1999). [DOI] [PubMed] [Google Scholar]
  11. Antolak J. A. and Storm E. A., “Fetal dose estimates for electron-beam treatment to the chest wall of a pregnant patient,” Med. Phys. 10.1118/1.598449 25, 2388–2391 (1998). [DOI] [PubMed] [Google Scholar]
  12. Roy S. C. and Sandison G. A., “Shielding for neutron scattered dose to the fetus in patients treated with 18 MV x-ray beams,” Med. Phys. 10.1118/1.1287438 27, 1800–1803 (2000). [DOI] [PubMed] [Google Scholar]
  13. Islam M. K., Saeedi F., and Al-Rajhi N., “A simplified shielding approach for limiting fetal dose during radiation therapy of pregnant patients,” Int. J. Radiat. Oncol., Biol., Phys. 49, 1469–1473 (2001). [DOI] [PubMed] [Google Scholar]
  14. Followill D., Geis P., and Boyer A., “Estimates of whole-body dose equivalent produced by beam intensity modulated conformal therapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(97)00012-6 38, 667–672 (1997). [DOI] [PubMed] [Google Scholar]
  15. Hall E. and Wuu C. S., “Radiation induced second cancers: The impact of 3D-CRT and IMRT,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/S0360-3016(03)00073-7 56, 83–89 (2003). [DOI] [PubMed] [Google Scholar]
  16. Kry S. F., Salehpour M., Followill D. S., Stovall M., Kuban D. A., White R. A., and Rosen I., “The calculated risk of fatal secondary malignancies from intensity-modulated radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 10.1016/j.ijrobp.2005.03.053 62, 1195–1203 (2005). [DOI] [PubMed] [Google Scholar]
  17. Paganetti H., Bortfeld T., and Delaney T. F., “Neutron dose in proton radiation therapy: in regard to Eric J. Hall,” Int. J. Radiat. Oncol., Biol., Phys. 66, 1594–1595 (2006). [DOI] [PubMed] [Google Scholar]
  18. Xu X. G., Taranenko V., Zhang J., and Shi C., “A boundary-representation method for designing whole-body radiation dosimetry models: pregnant females at the ends of three gestational periods—RPI-P3, -P6, and -P9,” Phys. Med. Biol. 10.1088/0031-9155/52/23/017 52, 7023–7044 (2007). [DOI] [PubMed] [Google Scholar]
  19. Snyder W. S., Ford M. R., Warner G. G., and H. L.Fisher, Jr., Medical Internal Radiation Dose Committee (MIRD) Pamphlet No. 5, Supplement No. 3, J. Nuclear Med. Vol. 10 (Society of Nuclear Medicine, New York, 1969). [Google Scholar]
  20. Snyder W. S., Ford M. R., Warner G. G., and Watson S. B., “‘S’ absorbed dose per unit cumulated activity for selected radionuclides and organs,” Medical Internal Radiation Dose Committee (MIRD) Pamphlet No. 11 (The Society of Nuclear Medicine, New York, 1975). [Google Scholar]
  21. Snyder W. S., Ford M. R., Warner G. G., and H. L.Fisher, Jr., “Estimates of absorbed fractions for monoenergetic photon source uniformly distributed in various organs of a heterogeneous phantom,” Medical Internal Radiation Dose Committee (MIRD) Pamphlet No. 5, Revised (The Society of Nuclear Medicine, New York, 1978). [PubMed] [Google Scholar]
  22. ICRP, Report of the task group on Reference Man, ICRP Publication 23, 1975. [DOI] [PubMed]
  23. Cristy M. and Eckerman K. F., “Specific absorbed fractions of energy at various ages from internal photon sources,” Report No. ORNL/TM-8381Nl (Oak Ridge National Laboratory, Oak Ridge, TN, 1987). [Google Scholar]
  24. Stabin M. G., Watson E. E., Cristy M., Ryman J. C., Eckerman K. F., Davis J. L., Marshall D., and Gehlen M. K., “Mathematical models and specific absorbed fractions of photon energy in the nonpregnant adult female and at the end of each trimester of pregnancy,” Oak Ridge National Laboratory Report No. ORNL/TM-1907, 1995. (unpublished).
  25. Chen J., “Mathematical models of the embryo and fetus for use in radiological protection,” Health Phys. 86, 285–295 (2004). [DOI] [PubMed] [Google Scholar]
  26. Zaidi H. and Xu X. G., “Computational anthropomorphic models of the human anatomy: The path to realistic Monte Carlo modeling in radiological sciences,” Annu. Rev. Biomed. Eng. 10.1146/annurev.bioeng.9.060906.151934 9, 471–500 (2007). [DOI] [PubMed] [Google Scholar]
  27. Shi C. and Xu X. G., “Development of a 30-week-pregnant female tomographic model from CT-images for Monte Carlo organ dose calculations,” Med. Phys. 10.1118/1.1778836 31, 2491–2497 (2004). [DOI] [PubMed] [Google Scholar]
  28. Shi C. Y., Xu X. G., and Stabin M. G., “Specific absorbed fractions calculated from a tomographic model of pregnant woman for internal photon emitters using Monte Carlo method,” Health Phys. 10.1097/01.HP.0000133364.55155.09 87, 507–511 (2004). [DOI] [PubMed] [Google Scholar]
  29. Dimbylow P., “Development of pregnant female, hybrid voxel-mathematical models and their application to the dosimetry of applied magnetic and electric fields at 50 Hz,” Phys. Med. Biol. 51, 2383–2394 (2006). [DOI] [PubMed] [Google Scholar]
  30. Dimbylow P., “SAR in the mother and foetus for RF plane wave irradiation,” Phys. Med. Biol. 52, 3791–3802 (2007). [DOI] [PubMed] [Google Scholar]
  31. Cech R., Leitgeb N., and Pediaditis M., “Fetal exposure to low frequency electric and magnetic fields,” Phys. Med. Biol. 10.1088/0031-9155/52/4/001 52, 879–888 (2007). [DOI] [PubMed] [Google Scholar]
  32. Xu X. G., Chao T. C., and Bozkurt A., “VIP-MAN: An image-based whole-body adult male model constructed from color photographs of the visible human project for multi-particle Monte Carlo calculations,” Health Phys. 10.1097/00004032-200005000-00003 78, 476–86 (2000). [DOI] [PubMed] [Google Scholar]
  33. ICRP, “Basic anatomical and physiological data for use in radiological protection: Reference values,” ICRP Publication 89, 2002. [PubMed]
  34. Binvox, http://www.cs.princeton.edu/~min/binvox/, last accessed August 2007; http://www.cs.princeton.edu/~min/binvox/, last accessed August 2007.
  35. Nooruddin F. and Turk G., “Simplification and repair of polygonal models using volumetric techniques,” IEEE Trans. Vis. Comput. Graph. 9, 191–205 (2003). [Google Scholar]
  36. Kase K. R., Mao X. S., Nelson W. R., Liu J. C., Kleck J. H., and Elsalim M., “Neutron fluence and energy spectra around the Varian clinac 2100C/2300C medical accelerator,” Health Phys. 74, 38–47 (1998). [DOI] [PubMed] [Google Scholar]
  37. Kry S. F. et al. , “A Monte Carlo model for calculating out-of-field dose from a Varian 6 MV beam,” Med. Phys. 10.1118/1.2360013 33, 4405–4413 (2006). [DOI] [PubMed] [Google Scholar]
  38. Pelowitz D. B., “MCNPX User’s Manual, Version 2.5.0,” Los Alamos National Laboratory, Report No. LA-UR-02–2607, 2005. (unpublished).
  39. Jeraj R., Keall P., and Ostwald P., “Comparison between MCNP, EGS4, and experiment for clinical electron beams,” Phys. Med. Biol. 10.1088/0031-9155/44/3/013 44, 705–717 (1999). [DOI] [PubMed] [Google Scholar]
  40. ICRP, “Recommendations of the International Commission on Radiological Protection,” Publication 103, 2007, Vol. 37. [DOI] [PubMed]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES