On the accuracy of a moving average algorithm for target tracking during radiation therapy treatment delivery

Abstract

Real-time tumor targeting involves the continuous realignment of the radiation beam with the tumor. Real-time tumor targeting offers several advantages such as improved accuracy of tumor treatment and reduced dose to surrounding tissue. Current limitations to this technique include mechanical motion constraints. The purpose of this study was to investigate an alternative treatment scenario using a moving average algorithm. The algorithm, using a suitable averaging period, accounts for variations in the average tumor position, but respiratory induced target position variations about this average are ignored during delivery and can be treated as a random error during planning. In order to test the method a comparison between five different treatment techniques was performed: (1) moving average algorithm, (2) real-time motion tracking, (3) respiration motion gating (at both inhale and exhale), (4) moving average gating (at both inhale and exhale) and (5) static beam delivery. Two data sets were used for the purpose of this analysis: (a) external respiratory-motion traces using different coaching techniques included 331 respiration motion traces from 24 lung-cancer patients acquired using three different breathing types [free breathing (FB), audio coaching (A) and audio-visual biofeedback (AV)]; (b) 3D tumor motion included implanted fiducial motion data for over 160 treatment fractions for 46 thoracic and abdominal cancer patients obtained from the Cyberknife Synchrony. The metrics used for comparison were the group systematic error (M), the standard deviation (SD) of the systematic error (Σ) and the root mean square of the random error (σ). Margins were calculated using the formula by Stroom et al. [Int. J. Radiat. Oncol., Biol., Phys. 43(4), 905–919 (1999)]: 2Σ+0.7σ. The resultant calculations for implanted fiducial motion traces (all values in cm) show that M and Σ are negligible for moving average algorithm, moving average gating, and real-time tracking (i.e., M and Σ=0 cm) compared to static beam (M=0.02 cm and Σ=0.16 cm) or gated beam delivery (M=−0.05 and 0.16 cm at both exhale and inhale, respectively, and Σ=0.17 and 0.26 cm at both exhale and inhale, respectively). Moving average algorithm σ=0.22 cm has a slightly lower random error than static beam delivery σ=0.24 cm, though gating, moving average gating, and real-time tracking have much lower random error values for implanted fiducial motion. Similar trends were also observed for the results using the external respiratory motion data. Moving average algorithm delivery significantly reduces M and Σ compared with static beam delivery. The moving average algorithm removes the nonstationary part of the respiration motion which is also achieved by AV, and thus the addition of the moving average algorithm shows little improvement with AV. Overall, a moving average algorithm shows margin reduction compared with gating and static beam delivery, and may have some mechanical advantages over real-time tracking when the beam is aligned with the target and patient compliance advantages over real-time tracking when the target is aligned to the beam.

INTRODUCTION

Radiation therapy treatment using real-time tumor targeting offers several advantages towards the improvement of accuracy during radiotherapy, especially for lung cancer patients where the tumor moves continuously throughout the treatment.^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16} During real-time tracking, the treatment beam continuously realigns to the tumor throughout the treatment.^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38} The advantages to such a treatment technique include improved accuracy of tumor treatment and reduced dose to surrounding tissue by reducing the margin added for tumor motion. However, currently there are certain practical limitations to this technique.

Bortfeld et al.³⁹ showed that if the systematic error component of interfraction motion can be removed; according to margin formulas the residual random error is not significantly deleterious to the dose delivered to the patient. The problem of the above conclusions is that the systematic error component correction, i.e., mean target position of the intrafraction motion, cannot be known a priori before commencing each fraction of treatment. Thus, the most accurate static beam delivery scenario of online pretreatment target-beam alignment may still result in systematic errors. However, by tracking using a continuously updated estimate of the mean target position during treatment the systematic error could possibly be reduced to negligible levels.⁴⁰ This reasoning prompted the investigation of a moving average algorithm.

Van Herk et al.⁴¹ have described systematic errors as errors mainly due to the preparation of the treatment and random errors as errors during the delivery of the treatment on every treatment day. Using patient measurements taken on a daily basis for a number of patients over a number of fractions, three parameters were quantified: group systematic error, systematic error, and random error. Group systematic error, M, is a mean of all the means of the daily measurements and is expected to be very small. It deviates often from mean because of imprecision in equipment and procedure. Systematic error, Σ, is the standard deviation (SD) of the means and is an assessment of reproducibility of the treatment preparation. Random error, σ, is the root mean square of the SD of the daily measurements.⁴¹

Though motion exceeding mechanical constraints is possible for motion parallel and perpendicular to the leaf motion direction, motion parallel to the leaf direction is clearly the most sensitive. There are several options where multileaf collimator (MLC) tracking in any direction is not possible. An obvious solution is to ignore the motion or use gating. An approach to essentially eliminate the systematic tracking error and treat the respiration motion as residual random error is to use a moving average algorithm with a time scale of several breathing periods. This approach significantly reduces the mechanical requirements on the MLC, and can also be combined with respiration gating.

The moving average algorithm may be appropriate in situations of significant target motion to either:

• (1)account for either mechanical limitations of MLC, linac or treatment couch (from a number of manufacturers whose mechanical limitations may vary) to deliver motion compensated radiotherapy where the beam and tumor are continuously aligned, or
• (2)for practical considerations, such as for couch tracking, moving the patient with the negative velocity of the tumor motion may be uncomfortable for the patient.

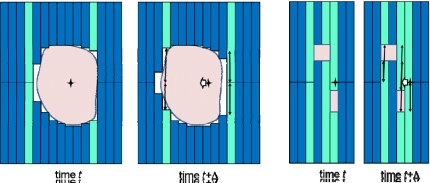
For one MLC type, Wijesooriya et al.⁴² estimated that target motion parallel to leaf motion could be achieved for up to 97% of respiratory motion, however no attempt was made to investigate the efficiency for motion perpendicular to the leaf direction—or the real case of motion parallel and perpendicular to the leaf direction. A demonstration of the challenge of using a MLC to track motion perpendicular to the leaf direction is shown in Fig. 1. If a target being tracked at time t moves perpendicular to the leaf motion (in this case ∼1.5 leaf widths) at time t+Δ, then a given target motion can result in a much larger motion of some of the individual leaves. If the difference in position of individual leaves divided by the time to achieve the motion is greater than the maximum leaf velocity (∼3.5 cm s⁻¹), a beam hold will occur. Any one leaf not being in position will cause a beam hold, and thus MLC tracking efficiency is governed not by the average maximum velocity of the leaves, but the maximum velocity of an individual leaf. If there are a significant number of beam holds, the delivery efficiency will be substantially decreased, to the point of not being able to complete a given treatment. This problem can be further exaggerated by IMRT delivery, where the leaf sequencing process can result in adjacent leaves having positions several centimeters apart.

Figure 1.

A demonstration of the challenge of using a multileaf collimator to track motion perpendicular to the leaf direction for conformal radiotherapy (left) and IMRT (right). If a target being tracked at time t moves perpendicular to the leaf motion (in this case ∼1.5 leaf widths for the conformal case and 1 leaf for the IMRT case) at time t+Δ, then the target motion can result in a much larger motion of some of the individual leaves. The leaves with the largest motion are light shaded, and the magnitude of motion of these leaves is shown with arrows. This problem can be further exaggerated by IMRT delivery (right), where the leaf sequencing process can result in adjacent leaves having positions several centimeters apart.

The study of Wijesooriya et al.⁴² was for only one MLC type. It is likely that there will be variability between manufacturers, and even individual MLCs, so that in general it is not valid to state that MLCs are capable of real-time tracking of respiratory-induced target motion.

The moving average algorithm was chosen since, despite its simplicity, the moving average algorithm is optimal for a common task: reducing random noise while retaining a sharp step response. This makes it the premier filter for time domain encoded signals.⁴³ Though there are other options for such filters, the moving average algorithm achieves the desired goal, to essentially eliminate systematic error caused by any nonstationary signals (e.g., base line drift) and the motion of each respiration cycle is treated as a residual random error. Moving average can be considered as an intermediate state between real-time tumor tracking and static beam delivery. While the moving average algorithm does not follow the tumor on a moment by moment basis it does follow the general trend of the tumor motion. This is an important advantage over static beam delivery especially during period of base line drift where based on the theory of moving average algorithm the beam would follow the general trend of the motion pattern.

The advantages and disadvantages of a moving average algorithm compared with real-time tracking and static beam delivery with pretreatment correction are:

Advantages of moving average algorithm for tracking:

• (1)More accurate than pretreatment correction.
• (2)Less mechanical motion and therefore possibly longer motor life than real-time tracking.
• (3)Less issue of moving MLC leaves,^{19, 20, 22, 23} linac^{1, 17, 33, 34} or couch⁴⁴ at high velocities since an average period is used. The couch motion may also affect patient compliance and secondary-induced skeletal motion.
• (4)An additional issue for DMLC IMRT real-time tumor tracking is that the mechanical limitations of MLC⁴⁵ motion may be exceeded, and motion perpendicular to the MLC leaf travel direction can also cause beam holds during delivery and therefore the moving average algorithm may be more efficient than real-time tumor tracking in terms of delivery time.

Disadvantages of moving average algorithm for tracking:

• (1)Less precise than continuous tracking.
• (2)Still requires feedback mechanism for target motion registration to align the beam and the target during treatment.

Given the advantages (and disadvantages) of the moving average algorithm listed above, the aim of this study is to quantify the accuracy and precision of radiation therapy treatment delivery using a moving average algorithm for tracking in comparison with real-time tracking algorithm, gated beam delivery, moving average gating, and static beam delivery with online pretreatment target-beam alignment.

METHOD AND MATERIALS

Data acquisition

Two sets of respiration motion data were used for the purpose of analyzing the accuracy of moving average algorithm.

External respiratory motion

This motion data consisted of 331 4 min abdominal wall (respiratory) anterior-posterior motion traces from 24 lung cancer patients using the Varian RPM system. Each patient was initially asked to breathe without instructions called free breathing (FB) and the respiration motion was recorded. Then audio (A) instructions were given followed by audio-visual (AV) biofeedback based on the frequency and displacement of respiration motion during the FB session. For each type of instruction the respiration motion was recorded. The respiration rate for this set of patients varied between 6 and 24 breaths per minute. The displacement for this set of patients varied between 0.6 and 3 cm peak-to-peak motion. The process was repeated five times for each patient with each session typically spaced a week apart. Further details on the data collected can be found in George et al.^{46, 47, 48} The main application of these data was to study the link between the systematic and random error and the breathing training types, and it is important to note that the data are not tumor motion, for which a separate data set described below was used.

Implanted fiducial motion

This 3D target motion were was acquired from 46 thoracic and abdominal cancer patients treated with stereotactic body radiotherapy using the Cyberknife Synchrony (Accuray Inc. Sunnyvale, CA) system at Georgetown University Hospital and shared under an IRB-approved protocol. Between July 2005 and January 2006 implanted fiducial motion data were acquired for patients with the following tumor locations: lung (30 patients), retroperitoneum (11), liver (two), chest wall (two) and internal mammary nodes (one). The number of fractions for each patient was anywhere from one to seven treatment fractions with a total of 160 treatment fractions. The Synchrony system, which was used to acquire the implanted fiducial motion information, is a subsystem of respiration tumor tracking in the Cyberknife system.^{33, 34, 49, 50} The Synchrony system estimates the tumor positions by a correlation between the external patient motion and implanted fiducial locations and a prediction algorithm. The data contained patient 4D target motion information (3D target positions versus time) and its duration time was 31.4 min (5.0–106.4 min).⁵¹ For each of 160 treatment fractions, overall mean of the means of motion extent was 0.47 cm (0.02–1.44 cm), and overall means of the means of percent contributions from left-right, anterior-posterior, and superior-inferior motion to 3D motion were 26.6%, 30.5%, and 42.9%, respectively.

Data analysis

Comparison of treatment scenarios

A depiction of the five treatment delivery scenarios is shown in Fig. 2. The study assumes a real-time target position monitoring system is present for all five delivery scenarios. The target motion information is used to investigate five treatment scenarios:

Figure 2.

Five different treatment scenarios are displayed in this figure depicting the comparison performed in this study. Gating and moving average gating were evaluated at both exhale and inhale.

(i) Moving average algorithm for tracking: In this case the position of the beam at time t is calculated as the mean of the position during the past m seconds. The value for m is assumed to be 15 s for this analysis. The number of points included in the moving average was m×f, where f is the sampling frequency (30 Hz for the respiratory signals and 25 Hz for the tumor motion data). Thus, for moving average algorithm the equation was

$$x_{\mathrm{est}}\left(t\right)=\frac{{\sum }_{i=t-m\times f-RT}^{t-RT}{x}_{\mathrm{act}}\left(i\right)}{m\times f},$$

where x_est(t) is the estimated position at time t, x_act is the actual position, and RT is the number of sample points in the system response time, assumed here to be 0.16 s.⁵² From the equation above, the beam position x_est(t) has been calculated as the average of the past 15 seconds of position information.

(ii) Real-time tracking: The treatment beam responds to the target position after a system response time RT, which is assumed to be 0.16 s as above. No motion prediction algorithm is assumed, and thus the estimated tumor position is

$$x_{\mathrm{est}}\left(t\right)=x_{\mathrm{act}}(t-RT).$$

Therefore from the equation for real-time tracking above it can be seen that x_est(t) is the beam position after a system response time of RT.

(iii) Gated beam delivery at inhale and exhale: Clinically it has been suggested and also studied by various institutions that the standard range of duty cycle for a gated patient should be between 30% and 50%.^{48, 53} This is in order to provide the benefits of gating while mitigating the effects of intra fraction motion by limiting the treatment time. Thus for the purpose of studying respiration motion gating along with the other techniques, a duty cycle of 40% was utilized. The phase information for the purpose of this analysis was obtained from the RPM phase file for the external respiratory motion data. For the Cyberknife Synchrony data, the phase was obtained by finding the motion peak for each respiratory cycle and linearly assigning phase from 0 to 2π between successive motion peaks. Ruan et al.⁵⁴ have, however, noted the nonstationary nature of respiration motion. Ruan et al.⁵⁴ observed that various phases of respiration were predicted with various accuracies. Similarly, in Fig. 2, which displays the effect of the moving average algorithm with respect to other techniques, we can see that during the base line shift the gating window is less accurate (very slightly) as compared to when the base line is constant. In terms of percentage, inhale gating used phases from 80% to 20%, and exhale gating 30%–70%. The real-time calculation of phase has an associated uncertainty, particularly in the presence of varying base line, changing period, and peak-to-trough magnitude, and may not be centered about the peak, but is generally close to the peak.

The position of the beam at time t is calculated as the mean of the position during the first n seconds of gated motion. Gating beam position is calculated at both inhale and exhale. The position of the beam is determined by

$$x_{\mathrm{est}}\left(t\right)=\frac{{\sum }_{i=1}^{n\times f}{x}_{\mathrm{act}}\left(i\right)\times H}{{\sum }_{i=1}^{n\times f}H},$$

where H is the Heavyside function that equals 1 when the respiratory phase is within the gate and 0 otherwise. From equation for gated beam delivery at inhale and exhale above, the beam position x_est(t) has been calculated as the average of the first n seconds of beam position within the 40% duty cycle information.

In spite of issues during base line drift, phase-based gating was used in this study for the gating techniques. Displacement-based gating also has a problem with baseline drift, as the gating thresholds need to be adjusted during treatment which takes extra time, particularly if imaging verification is required. In a previous work,⁴⁸ we found a slight advantage to displacement-based gating, however the difference was less than 0.5 mm. Hence phase based gating is used as it is the more viable and also currently clinically used with the RPM system. From the study by George et al.⁴⁸ comparing phase with displacement-based gating, there was little difference in the overall uncertainty of these two approaches thus justifying the use of phase-based gating.

(iv) Moving average gating at inhale and exhale: The moving average gating technique involves using a moving average algorithm over the respiration motion in the gated window (obtained from iii above) and is given by

$$x_{\mathrm{est}}\left(t\right)=\frac{{\sum }_{i=t-m\times f-RT}^{t-RT}{x}_{\mathrm{act}}\left(i\right)\times H}{{\sum }_{i=1-m\times f-RT}^{t-RT}H}.$$

In this treatment scenario the position is updated every 15 s similar to moving average tracking algorithm (Sec. II.B.1.i). From equation for gated beam delivery at inhale and exhale above, the beam position x_est(t) has been calculated as the average of the most recent n seconds (i.e., from t−RT−m×f to t−RT) of beam position within the 40% duty cycle information.

This technique will reduce the systematic error and random error. The velocity can be similarly calculated as for the moving average. However, as only respiratory points at a given breathing phase (Fig. 2) are included, the overall velocity will be less for moving average gating than for the moving average algorithm.

(v) Static beam delivery with online pretreatment target-beam alignment: The first n seconds of target position information is used to align the beam with the target pretreatment, but the beam does not respond to target motion. Thus the position of the beam is determined as the mean of the position during the first n seconds. The position of the beam is determined by:

$$x_{\mathrm{est}}\left(t\right)=\frac{{\sum }_{i=1}^{n\times f}{x}_{\mathrm{act}}\left(i\right)}{n\times f}.$$

From equation for static beam delivery with online pretreatment target-beam alignment above, the beam position x_est(t) has been calculated as the average of the first n seconds of position information.

Evaluation metrics

The metrics evaluated for each of the five motion compensation scenarios: the group systematic error, M, the SD of the systematic error, Σ, and the root mean square of the random error, σ, were calculated as shown in Table 1.⁴¹

Table 1.

The formalism used to calculate the metrics M, Σ and σ, where Δ is the displacement between the beam and target at a given time, and Δ(P_j,F_l) is the set of displacements for a given fraction F_i for patient P_j (see Ref. 41) (M: mean; SD: standard deviation; RMS: root mean square).

	Patient 1	Patient 2	…
Fraction 1	Δ(P1,F1)	Δ(P2,F2)
Fraction 2	Δ(P1,F2)	Δ(P2,F2)
…
			↗	$M=\overline{\Delta (P_1\dots P_M,F_1\dots F_N)}$
Mean	$\overline{\Delta (P_1,F_1\dots F_N)}$	$\overline{\Delta (P_2,F_1\dots F_N)}$	→	Σ=SD(Δ(P1…PM,F1…FN))
SD	SD(Δ(P1,F1…FN))	SD(Δ(P2,F1…FN))	→	σ=RMS(Δ(P1…PM,F1…FN))

The displacement of the beam and the target at a given time is indicated as Δ. Δ for the purpose of this analysis was evaluated for a given fraction F_i for a given patient P_j and is represented as Δ(P_j,F_i). To calculate the group systematic error, M, Δ(P_j,F_i) was averaged over all fractions and over all patients

$$M=\overline{\Delta (P_1\dots P_N,F_1\dots F_M)}.$$

For the SD of the systematic error, Σ, the first SD was obtained over all fractions of each patient Δ(P_j,F_i), and then SD was obtained over all patients

$$\Sigma =SD\left[\Delta (P_1\dots P_N,F_1\dots F_M)\right].$$

Finally, to obtain root mean square of the random error, σ, the root mean square was calculated overall patients over all fractions

$$\sigma =RMS\left[\Delta (P_1\dots P_N,F_1\dots F_M)\right].$$

These terms were defined by van Herk,⁴¹ however, are clarified here as multiple error values corresponding to each time point instead of single error values for a given treatment.

Margin calculations

Margins were calculated for the implanted fiducial motion data using the formula 2Σ+0.7σ by Stroom et al..⁵⁵ The two assumptions were

• (1)no other error contributions (optimistic case) and
• (2)0.3 cm systematic and random error contributions from other sources (realistic case). The margins that included the 0.3 cm systematic and random errors were calculated in quadrature 2(Σ²+0.3²)+0.7(σ²+0.3²).

Averaging period and higher order algorithms

Different choices of windows for averaging between 5 and 25 s were also explored and compared against each other. In addition to the zeroth order (moving average filter), a first and a second order filter were investigated. There are a number of additional filter choices that could be investigated to obtain an algorithm which has the requirements of reducing systematic error and treating the respiratory signal as a random error. These algorithms include adaptive filters, neural networks, and template matching algorithms. However, as the results demonstrate, the simple moving average algorithm fulfils the above requirements.

RESULTS AND DISCUSSION

In this study we analyzed the feasibility delivery techniques using a moving average algorithm. Though the results obtained show a potential advantage by using moving average algorithm over static beam delivery, the need for feedback mechanism for target motion registration to align the beam and the target during treatment is a current barrier to the clinical implementation of this algorithm.

Comparison of treatment scenarios

The results for the five treatment scenarios for both external and implanted fiducial motion are shown in Table 2. These results were obtained using n=15 s. Table 2 quantifies the geometric uncertainty using three metrics for the evaluation of the treatment scenarios being investigated.

Table 2.

The values for M, Σ and σ as calculated for the different treatment scenarios for each of respiration motion (see Ref. 41). The table includes the external respiration motion obtained from 24 lung cancer patients. In parentheses are the minimum and maximum values for systematic and random error.

Tracking algorithm	Group systematic error, M (cm)
	External			Implanted fiducial motion
	FB	A	AV
Moving average algorithm	−0.01	−0.01	0.00	0.00
Real-time tracking	0.00	0.00	0.00	0.00
Gating exhale	−0.11	−0.05	−0.03	−0.05
Gating inhale	−0.16	−0.12	−0.02	0.16
Moving average gating at exhale	−0.01	−0.01	0.00	0.00
Moving average gating at inhale	−0.01	0.00	0.00	0.00
Static beam delivery	−0.13	−0.17	−0.06	0.02
Tracking algorithm	SD of systematic error, ∑ (cm)
	External			Implanted fiducial motion
	FB	A	AV
Moving average algorithm	0.01  (−0.03–0.02)	0.01  (−0.03–0.01)	0.01  (−0.03–0.01)	0.00  (−0.01–0.01)
Real-time tracking	0.00  (0.00–0.00)	0.00  (0.00–0.00)	0.00  (0.00–0.00)	0.00  (0.00–0.00)
Gating at exhale	0.18  (−0.52–0.48)	0.12  (−0.28–0.25)	0.06  (−0.18–0.11)	0.17  (−0.73–0.60)
Gating at inhale	0.23  (−0.64–0.41)	0.18  (−0.52–0.21)	0.07  (−0.19–0.15)	0.26  (−0.53–1.23)
Moving average gating at exhale	0.01  (−0.03–0.04)	0.01  (−0.03–0.01)	0.01  (−0.03–0.01)	0.00  (−0.01–0.01)
Moving average gating at inhale	0.02  (−0.04–0.05)	0.01  (−0.03–0.02)	0.01  (−0.02–0.03)	0.00  (−0.02–0.01)
Static beam delivery	0.21  (−0.52–0.45)	0.24  (−0.55–0.36)	0.18  (−0.77–0.12)	0.16  (−0.56–0.84)
Tracking algorithm	Random error, σ (cm)
	External			Implanted fiducial motion
	FB	A	AV
Moving average algorithm	0.46  (0.14–0.80)	0.53  (0.22–0.90)	0.54  (0.23–0.88)	0.22  (0.01–0.63)
Real-time tracking	0.13  (0.07–0.25)	0.14  (0.06–0.26)	0.16  (0.08–0.32)	0.07  (0.00–0.18)
Gating at exhale	0.30  (0.11–0.58)	0.29  (0.14–0.50)	0.27  (0.13–0.49)	0.15  (0.01–0.75)
Gating at inhale	0.44  (0.15–0.77)	0.44  (0.21–0.67)	0.36  (0.13–0.68)	0.23  (0.01–0.83)
Moving average gating at exhale	0.21  (0.08–0.43)	0.21  (0.09–0.31)	0.22  (0.12–0.37)	0.10  (0.00–0.53)
Moving average gating at inhale	0.35  (0.13–0.57)	0.35  (0.17–0.58)	0.32  (0.12–0.61)	0.17  (0.01–0.68)
Static beam delivery	0.47  (0.18–0.81)	0.54  (0.21–0.86)	0.55  (0.23–0.88)	0.24  (0.01–0.82)

External respiratory motion

For external respiratory motion, the group systematic error and SD of systematic error are negligible for moving average algorithm, moving average gating, and real-time tracking. For real-time tracking as shown by Murphy et al.⁵⁶ the errors can be reduced to zero by using a good prediction algorithm. The result of a moving average algorithm over the gated respiration motion, i.e., moving average gating, was an improvement to the gated respiration motion for both inhale and exhale. The random error for real-time tracking and moving average algorithm has a slightly lower random error than static beam delivery. For random error, moving average gating results showed an improvement when compared to the moving average algorithm. AV has a lower group systematic error and SD of systematic error for static beam delivery over the other training types. However, for random errors σ the AV is higher. This result could be explained by the definition of random error which is the root mean square of the SD of all the patients. Hence what we see here could be possibly the variation of respiration motion with AV across the patient population.

Implanted fiducial motion

Implanted fiducial motion data showed similar results to external respiration motion. Moving average results for group systematic error and SD of systematic error are negligible compared to static beams. The trend for the moving average gated respiration motion was also similar to the external respiration motion data where the random error component was a lesser magnitude compared to the moving average algorithm over the entire respiration trace. Values for this data set are listed in Table 2.

For implanted fiducial motion, the different treatment techniques can be ranked based on the margin calculation without error as follows:

• (1)Real-time tracking;
• (2)Moving average gating at exhale;
• (3)Moving average gating at inhale;
• (4)Moving average algorithm for tracking;
• (5)Gated beam delivery at exhale;
• (6)Static beam delivery with online pretreatment target-beam alignment;
• (7)Gated beam delivery at inhale.

The Kuka robot used by the Cyberknife has mechanical specifications exceeding that of respiratory motion, and this has also been the clinical experience in that beam holds are rare during Synchrony treatments. When beam holds occur, it is typically due to an unacceptable variation in the internal-external correlation model from irregular breathing. Thus the moving average algorithm is not recommended for the Cyberknife as real-time tracking works well. Real-time tracking has not been clinically implemented for MLC or couch tracking and there are potential limitations with respect to efficiency and patient motion from these techniques. The moving average algorithm may be an acceptable path to clinical implementation.

Margin calculations

Margins for the implanted fiducial motion are shown in Fig. 3 and quantified in Table 3. Table 3 shows the population margins for the implanted fiducial motion obtained from the 46 thoracic and abdominal cancer patients. The overall population Σ and σ values are provided in Table 2 for the comparison of the various techniques.

Figure 3.

Margins calculated using the five treatment scenarios for implanted fiducial motion (seven traces because gating and moving average gating are split into inhale and exhale). (a) Indicates margin calculated without other error components while (b) indicates the addition of 0.3 cm systematic and random error contribution from other sources. The x axis is the margin in cm and they y axis is the cumulative probability of the number of patients.

Table 3.

Population margins using equation 2Σ+0.7σ (see Ref. 55) (assuming no other error components) and $2\sqrt{{\Sigma }^2+{0.3}^2}+0.7\sqrt{{\sigma }^2+{0.3}^2}$ (addition of 0.3 cm systematic and random error contribution from other sources) for the implanted fiducial motion obtained from the 46 thoracic and abdominal cancer patients. Individual margins are shown in Fig. 3.

Tracking algorithm	Margin without errors added (cm)	Margins with error added (cm)
Moving average algorithm	0.15	0.86
Real-time tracking	0.05	0.82
Gating exhale	0.45	0.92
Gating inhale	0.68	1.06
Moving average gating at exhale	0.07	0.82
Moving average gating at inhale	0.12	0.84
Static beam delivery	0.49	0.95

Cumulative margins are shown in Fig. 3. These cumulative probability plots indicate the appropriate margin for each individual. The cumulative plots show how appropriate (or in some cases inappropriate) applying a population margin to an individual is. The cumulative probability plots are useful to determine what percentage of the patients fell into a particular margin range.

Averaging period and higher order algorithms

The insensitivity of three errors to different averaging period validates the use of 15 s for the other analyses performed in the study. Since there was no significant differences across these windows 15 s was chosen. Fifteen seconds also represents and average amount of time that the patient takes to settle on the table and breathe normally. Along the same lines, the simplest of the three techniques, i.e., the average of the previous n seconds or moving average, would give the best value for the new beam position as the higher order algorithms did not show any benefit.

CONCLUSIONS

A technique for tumor tracking based on a moving average algorithm for tracking has been investigated. Moving average algorithm has accuracy advantages over online correction with static delivery and practical advantages over real-time tracking as the motion is slower and smoother. This has mechanical advantages when the beam is aligned to the target and patient compliance advantages when the target is aligned to the beam. The main findings of this work can be summarized as:

• (1)The moving average algorithm reduces the group systematic error and SD of the systematic error compared with static beam delivery. The random error is modestly reduced.
• (2)There is a group systematic error caused by intrafraction motion during FB (1.5 mm) and A (1 mm).
• (3)The margins required for moving average algorithm lie between those of real-time tracking and static delivery with pretreatment beam-target alignment. The margin reduction for moving average algorithm compared with online pretreatment correction delivered with a static beam delivery is significant for FB and A, but less noticeable for AV.
• (4)The margins required for moving average algorithm are in most cases less than those of gated respiration motion.
• (5)For moving average algorithm and static beam delivery the systematic error using AV is less than that for FB and A.
• (6)The margins required for real-time tracking as studied here are independent of breathing training type.
• (7)AV and the moving average algorithm have a similar characteristic in that they both effectively remove the base line variations or nonstationary signal behavior.
• (8)The moving average algorithm can add a further advantage to gated respiration motion by reducing margins making the margin values comparable to real-time tracking.