Implementation of a computationally efficient least-squares algorithm for highly under-determined three-dimensional diffuse optical tomography problems

Abstract

Three-dimensional (3D) diffuse optical tomography is known to be a nonlinear, ill-posed and sometimes under-determined problem, where regularization is added to the minimization to allow convergence to a unique solution. In this work, a generalized least-squares (GLS) minimization method was implemented, which employs weight matrices for both data-model misfit and optical properties to include their variances and covariances, using a computationally efficient scheme. This allows inversion of a matrix that is of a dimension dictated by the number of measurements, instead of by the number of imaging parameters. This increases the computation speed up to four times per iteration in most of the under-determined 3D imaging problems. An analytic derivation, using the Sherman–Morrison–Woodbury identity, is shown for this efficient alternative form and it is proven to be equivalent, not only analytically, but also numerically. Equivalent alternative forms for other minimization methods, like Levenberg–Marquardt (LM) and Tikhonov, are also derived. Three-dimensional reconstruction results indicate that the poor recovery of quantitatively accurate values in 3D optical images can also be a characteristic of the reconstruction algorithm, along with the target size. Interestingly, usage of GLS reconstruction methods reduces error in the periphery of the image, as expected, and improves by 20% the ability to quantify local interior regions in terms of the recovered optical contrast, as compared to LM methods. Characterization of detector photomultiplier tubes noise has enabled the use of the GLS method for reconstructing experimental data and showed a promise for better quantification of target in 3D optical imaging. Use of these new alternative forms becomes effective when the ratio of the number of imaging property parameters exceeds the number of measurements by a factor greater than 2.

INTRODUCTION

Diffuse optical tomography (DOT) uses near infrared wavelengths (600–1000 nm) to obtain optical absorption and scattering images for characterizing functional properties of the tissue under investigation.^{1, 2, 3, 4} The most important step in forming these images is solving the inverse problem, i.e., estimating the optical properties by matching the experimental data with modeled results in the least-squares sense.^{3, 5, 6} This problem is typically ill posed and ill determined depending on the noise in the data, the number of measurements, and the dimensions of the parameter space.⁶ Even though light travels in three dimensions (3D), most of the numerical models reported in the literature have been two dimensional (2D) because of computational considerations. Moreover, the 3D DOT imaging problem is more under-determined relative to the 2D case and has been found to generate poor quantitative estimates of the optical properties when compared to 2D results.^{7, 8, 9, 10, 11, 12, 13, 14, 15} Several methods have appeared in the literature describing efficient 3D computations,^{11, 14, 16} but no unified approach to the problem has been discussed. Recently, a generalized least-squares (GLS) minimization scheme was presented for 2D DOT image reconstruction.¹⁷ This article reports a computationally efficient approach for implementing GLS minimization in 3D which shows an improvement in the quantification of optical properties relative to earlier studies. Even though the focus is on GLS implementation, equivalent forms for other methods are also presented in light of the GLS framework.

The inverse problem in DOT is solved by minimizing the objective function (Ω) over the range of optical properties (μ). Methods based on gradient optimization, which do not require an explicit inversion of the Hessian matrix (here, Hessian approximates the second derivative; this can be some form equivalent to J^TJ or JJ^T, in general some form of J^TJ, J being the Jacobian) are known to be computationally efficient.^{18, 19} But these methods require an optimization scheme, which can be thought of as an inner iteration, for choosing the step size, and are not as straightforward as a direct inversion of the matrix. Alternatively, the full-Newton methods require calculation of the Jacobian (J), the forward data, and inversion of the dense Hessian matrix at each iteration. Because full-Newton methods are relatively easy to implement, they are widely used for DOT image reconstruction even though they require large matrix inversions at every iteration. Thus, while the full-Newton method is ideal for small problems, it rapidly becomes intractable for larger domains, such as those encountered in 3D imaging problems. This manuscript presents a formal approach, using the Sherman–Morrison–Woodbury identity, to construct a more efficient alternative form of update equations of GLS and Levenberg–Marquardt (LM) minimization schemes, which generates a Hessian matrix to invert. The dimension of this Hessian is dictated by the number of measurements, rather than the number of parameter estimates which can be considerably lower for highly under-determined problems, and therefore, much more efficient computationally. This equivalent form is also shown for other common minimization methods, namely Tikhonov.

The later part of this article describes a way to characterize the systematic noise using a simple analytical formula, when the photomultiplier tube (PMT) is used as a detector. Characterizing noise behavior of the experimental data leads to the use of the GLS technique in the experimental data case and it is also shown that usage of noise characteristics will lead to better quality and quantification of target in a experimental test case.

DIFFUSE OPTICAL TOMOGRAPHY: FORWARD PROBLEM

Near-infrared (NIR) light propagation in a biological tissue like breast can be modeled using the diffusion equation (DE)^{6, 20} which in the frequency domain becomes

$$-\nabla \cdot D\left(r\right)\nabla \Phi (r,\omega )+({\mu }_a\left(r\right)+i\omega ∕c)\Phi (r,\omega )=Q_o(r,\omega ),$$ (1)

where the optical diffusion and absorption coefficients are given by D(r) and μ_a(r), respectively. The light source, represented by Q_o(r,ω), is modeled as isotropic. Φ(r,ω) is the photon fluence rate at a given position r. The light modulation frequency is denoted by ω, where ω=2πf, (here f=100 MHz). The velocity of light in tissue is represented by c, which is assumed to be constant. Note that

$$D\left(r\right)=\frac{1}{3[{\mu }_a\left(r\right)+{\mu }_s^{\prime }\left(r\right)]},$$ (2)

where ${\mu }_s^{\prime }\left(r\right)$ is the reduced scattering coefficient which is defined as ${\mu }_s^{\prime }={\mu }_s(1-g)$; μ_s is the scattering coefficient and g is the anisotropy factor. The finite element method (FEM) is used to solve Eq. 1 to generate modeled data (G(μ)) for a given distribution of optical properties (μ),^{11, 13, 21} where $\mu =\left[{\mu }_s^{\prime }\right(r);{\mu }_a(r\left)\right]$. A Type-III boundary condition is employed to account for the refractive-index mismatch at the boundary.²² Under the Rytov approximation, the data (y) becomes the natural logarithm of the amplitude (A) and phase (θ) of the frequency-domain signal; y=[lnA;θ].

DIFFUSE OPTICAL TOMOGRAPHY: INVERSE PROBLEM

Levenberg–Marquardt (LM) minimization

The most-common approach for solving the inverse problem in DOT is LM minimization.^{1, 6, 11, 13, 17, 20, 23, 24} A detailed discussion of this method is available in Ref. 17 and it is only briefly reviewed here.

The objective function^{25, 26} for this approach is defined as

$$\Omega ={\Vert y-G\left(\mu \right)\Vert }^2,$$ (3)

where y is the experimental data and G(μ) is the modeled response. Minimization of this objective function with respect to μ is achieved by setting the first-order derivative equal to zero

$$\frac{\partial \Omega }{\partial \mu }={\mathbf{J}}^T\delta =0,$$ (4)

where δ is the data-model misfit, δ=y−G(μ), and J represents the Jacobian (J=∂G(μ)∕∂μ). Due to the ill-conditioned nature of the problem, the update equation for the optical properties at iteration “i” is regularized to be

$$\mathrm{\Delta }{\mu }_i={[{\mathbf{J}}^T\mathbf{J}+\alpha \mathbf{I}]}^{-1}{\mathbf{J}}^T{\delta }_{i-1}$$ (5)

or equivalently (See Appendix 2)

$$\mathrm{\Delta }{\mu }_i={\mathbf{J}}^T{[{\mathbf{JJ}}^T+\alpha \mathbf{I}]}^{-1}{\delta }_{i-1},$$ (6)

where Δμ_i represents the update of the optical property parameters at the ith step; α is the regularization parameter, which monotonically decreases with increasing iteration (always>0).²⁶ In this approach (Eq. 5), the Jacobian is normalized by its optical properties. Moreover, α is chosen empirically (it typically starts at 10 and reduced by a factor of 10^0.25 at every following iteration after being multiplied by the maximum of the diagonal values of JJ^T.^{17, 27}). The iterative procedure is stopped when the L2 norm of the data-model misfit (δ) does not improve (in our experience, by more than 1% because beyond these values the LM procedure can become unstable¹⁷).

Even though LM minimization or its modified versions have been used successfully for DOT image reconstruction,^{1, 6, 11, 13, 17, 20, 23, 24, 27} the final image depends on the choice of α due to the ill-conditioned nature of the problem. Moreover, the approach ignores the noise characteristics of the data and optical properties. A more systematic and generalized method for image reconstruction can be based on GLS minimization. The GLS scheme is discussed extensively in Ref. 17 and is only briefly reviewed here.

Generalized least squares (GLS) minimization

In GLS, the objective function is given by^{17, 28}

$$\Omega ={(y-G\left(\mu \right))}^T{\mathbf{W}}_{\delta }(y-G\left(\mu \right))+{(\mu +{\mu }_0)}^T{\mathbf{W}}_{\mu -{\mu }_0}(\mu -{\mu }_0),$$ (7)

where W_δ and W_μ−μ0 are the weight matrices for the data-model misfit (δ) and optical properties (μ−μ₀), respectively. Note that W_δ=(C_δ)⁻¹, where C represents the covariance matrix and similarly W_μ−μ0=(C_μ−μ0)⁻¹ (see Appendix A-4 of Ref. 28). These weight matrices; are symmetric and positive definite (because they are, inverses of covariance matrices). No regularization parameter is involved because the weight matrices include the noise characteristics of the experimental data and optical properties.¹⁷ Similarly to the LM approach, minimization of Ω (Eq. 7) is accomplished by setting the first derivative of Ω with respect to μ equal to zero:

$$\frac{\partial \Omega }{\partial \mu }={\mathbf{J}}^T{\mathbf{W}}_{\delta }\delta -{\mathbf{W}}_{\mu -{\mu }_0}(\mu -{\mu }_0)=0.$$ (8)

Linearizing the problem leads to the iterative update equation (for ith iteration)¹⁷

$$\mathrm{\Delta }{\mu }_i={[{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J}+{\mathbf{W}}_{\mu -{\mu }_0}]}^{-1}({\mathbf{J}}^T{\mathbf{W}}_{\delta }{\delta }_{i-1}-{\mathbf{W}}_{\mu -{\mu }_0}({\mu }_{i-1}-{\mu }_0)).$$ (9)

Explicit definitions of the weight matrices (W_δ and W_μ−μ0) are given in Ref. 17. Although any number of forms for W_μ−μ0 can exist, only one is considered here, specifically, where the covariance matrix is defined as¹⁷

$${\left[{\mathbf{C}}_{\mu -{\mu }_0}\right]}_{ij}={\left({\sigma }_{\mu -{\mu }_0}\right)}^2(1+\frac{r_{ij}}{l})e^{-(r_{ij}∕l)}$$ (10)

with l being the correlation length (here l=15 mm) and r_ij being the distance between the FEM nodes i and j(σ_μ−μ0)² is the expected variance of μ−μ₀. Strategies for calculating the expected variances are given in Ref. 17. In this work, the expected variance is determined from the prior knowledge that the expected contrast between tumor and normal tissue is about 50%–400%. To demonstrate the robustness of the GLS reconstruction procedure, for the results discussed here, the variance was chosen to be (4*μ)². Both weight matrices, W_δ and W_μ−μ0, are computed before the reconstruction procedure begins, whereas the Jacobian (J), and modeled data, G(μ), are calculated at each iteration. The iterative procedure is stopped when the L2 norm of the data-model misfit (δ) does not improve by more than 0.001%. Beyond these values, the round-off error dominates.

GLS implementation

The parameters recovered in the case of this GLS scheme are $({\mu }_s^{\prime };{\mu }_a)$, which is different from some previous approaches that estimate (D;μ_a). The later case has a mismatch because the units of D are mm whereas those of μ_a are mm⁻¹. In its implementation typically the whole equation is normalized by the optical properties (outlined in Ref. 17) which becomes computationally intensive especially for GLS in 3D because the update equation must be left and right multiplied by the optical properties at every iteration. Here, the GLS problem was reformulated in terms of $({\mu }_s^{\prime };{\mu }_a)$, so that both parameters have the same units (mm⁻¹). While this is a relatively minor alteration in the form of the algorithm, it has important implications for the computational time required for matrix preconditioning.

A simple transformation converts the diffusion part of the Jacobian (∂G(μ)∕∂D) to its scattering component $(\partial G\left(\mu \right)∕\partial {\mu }_s^{\prime })$:

$$\frac{\partial G\left(\mu \right)}{\partial {\mu }_s^{\prime }}=\frac{\partial G\left(\mu \right)}{\partial D}\frac{\partial D}{\partial {\mu }_s^{\prime }}.$$ (11)

Using Eq. 2

$$\frac{\partial D}{\partial {\mu }_s^{\prime }}=\frac{1}{3}\left(\frac{-1}{{\left[({\mu }_a+{\mu }_s^{\prime })\right]}^2}\right)=-3D^2$$ (12)

and substituting Eq. 12 in Eq. 11, leads to

$$\frac{\partial G\left(\mu \right)}{\partial {\mu }_s^{\prime }}=\frac{\partial G\left(\mu \right)}{\partial D}(-3D^2).$$ (13)

After this transformation (Eq. 13), the Jacobian (J) has the form

$$\mathbf{J}=\left[\begin{array}{cccccccc}\hfill \frac{\partial ln{A}_1}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_1}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_1}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_1}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial ln{A}_1}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_1}{\partial {\mu }_{aNN}}\hfill \\ \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_1}{\partial {\mu }_{aNN}}\hfill \\ \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_2}{\partial {\mu }_{aNN}}\hfill \\ \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_2}{\partial {\mu }_{aNN}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \dots \hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \dots \hfill & \hfill ⋮\hfill \\ \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial ln{A}_{NM}}{\partial {\mu }_{aNN}}\hfill \\ \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{s1}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{s2}^{\prime }}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{sNN}^{\prime }}\hfill & \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{a1}}\hfill & \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{a2}}\hfill & \hfill \cdots \hfill & \hfill \frac{\partial {\theta }_{NM}}{\partial {\mu }_{aNN}}\hfill \end{array}\right],$$ (14)

where NM and NN represent the number of measurements and number of property parameters associated with the FEM mesh, respectively. The implementation of the GLS update equation (Eq. 9) requires assembly of the weight matrix (W_μ−μ0) for simultaneous reconstruction of ${\mu }_s^{\prime }$ and μ_a and is accomplished by writing Eq. 9 in block matrix form

$$\{\left[\begin{array}{cc}\hfill H_{{\mu }_s^{\prime }2}\hfill & \hfill H_{{\mu }_s^{\prime }{\mu }_a}\hfill \\ \hfill H_{{\mu }_s^{\prime }{\mu }_a}\hfill & \hfill H_{{\mu }_a^2}\hfill \end{array}\right]+\left[\begin{array}{cc}\hfill W_{{\mu }_s^{\prime }-{\mu }_{s0}^{\prime }}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill W_{{\mu }_a-{\mu }_{a0}}\hfill \end{array}\right]\}\left[\begin{array}{c}\hfill \mathrm{\Delta }{\mu }_{si}^{\prime }\hfill \\ \hfill \mathrm{\Delta }{\mu }_{ai}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\left(J^T\right)}_{{\mu }_s^{\prime }}{W}_{\delta }{\delta }_{i-1}\hfill \\ \hfill {\left(J^T\right)}_{{\mu }_a}{W}_{\delta }{\delta }_{i-1}\hfill \end{array}\right]-\left[\begin{array}{c}\hfill W_{{\mu }_s^{\prime }-{\mu }_{s0}^{\prime }}\left({\mu }_{s_{i-1}^{\prime }-{\mu }_{s0}^{\prime }}\right)\hfill \\ \hfill W_{{\mu }_a-{\mu }_{a0}}\left({\mu }_{a_{i-1}-{\mu }_{a0}}\right)\hfill \end{array}\right],$$ (15)

where H represents the Hessian matrix (J^TW_δJ). Here, the cross terms in the weight matrix (W_μ−μ0) are zero because ${\mu }_s^{\prime }$ and μ_a are independent parameters in the estimation procedure. Note that the dimensions of the matrices in Eq. 9 are: J:2NM×2NN, W_μ−μ0:2NN×2NN, W_δ:2NM×2NM, δ=2NM×1, and Δμ=2NN×1. Most 3D-D0T problems are ill determined, i.e., NM⪡NN.

Computing an update of the optical properties (Δμ_i, from Eq. 9) requires an inversion (or its equivalent) of a large matrix with dimensions 2NN×2NN. Inverting a matrix of dimension N×N typically requires an order of N³ operations and N² memory.²⁸ Hence, any gain in reducing the dimensionality of the matrix to be inverted will reduce the computation time cubically and the memory requirement quadratically. An alternative form of Eq. 9, which requires few operations, is

$$\mathrm{\Delta }{\mu }_i=[\mathbf{I}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T+{\mathbf{C}}_{\delta })}^{-1}\mathbf{J}]\{{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{\mathbf{W}}_{\delta }{\delta }_{i-1}-({\mu }_{i-1}-{\mu }_0)\}.$$ (16)

Full derivation of this alternative form is given in the Appendix 1, along with the equivalent expressions for other minimization methods. Equation 16 requires an inversion of a matrix with dimensions 2NM×2NM (same is true for Eq. 6).

Note that the covariance∕weight matrices are calculated before the start of the iterative procedure and are used throughout the iteration. For nodes where the sensitivity (column sum of Jacobian) fell below 1% of the maximum sensitivity, the expected variance of the optical properties were chosen to be 1% of background μ (in Eq. 10).

SIMULATION STUDIES: THREE-DIMENSIONAL TEST PROBLEM

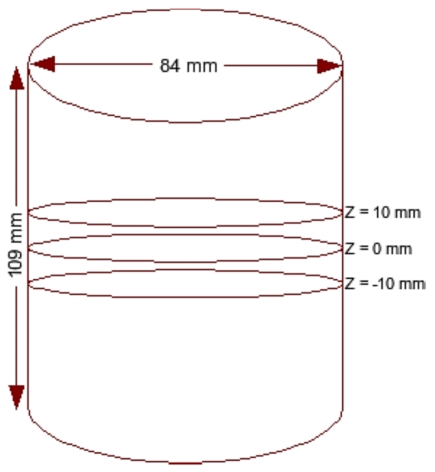
For all numerical experiments discussed here, the imaging domain was chosen to be cylindrical (as shown in Fig. 1) with a diameter of 84 mm and height of 109 mm. The background optical properties were μ_a=0.01 mm⁻¹ and ${\mu }_s^{\prime }=1.0{\mathrm{mm}}^{-1}$. Two meshes were used: (1) a cylinder consisting of 21 440 nodes corresponding to 110 483 linear tetrahedral elements for the forward model and (2) a cylinder having 9211 nodes corresponding to 45 980 linear tetrahedral elements for the reconstruction. The data-collection geometry consisted of 48 fibers that were arranged in a circular, equally spaced fashion in three layers spaced 10 mm apart (Fig. 1), with 16 fibers per plane. One fiber was used at a time as the source while the fibers in the same “source fiber plane” were used as detectors to generate 720 (3×16×15) measurement locations or a total of 1440 values (720 lnA data points and 720 θ data points). The sources were modeled as a Gaussian profile with a full width at half maximum of 3 mm to represent the distribution used in an experimental setup.²⁹ The source was also placed one mean transport length inside the boundary.

Figure 1.

Schematic diagram of the three-dimensional cylindrical imaging domain.

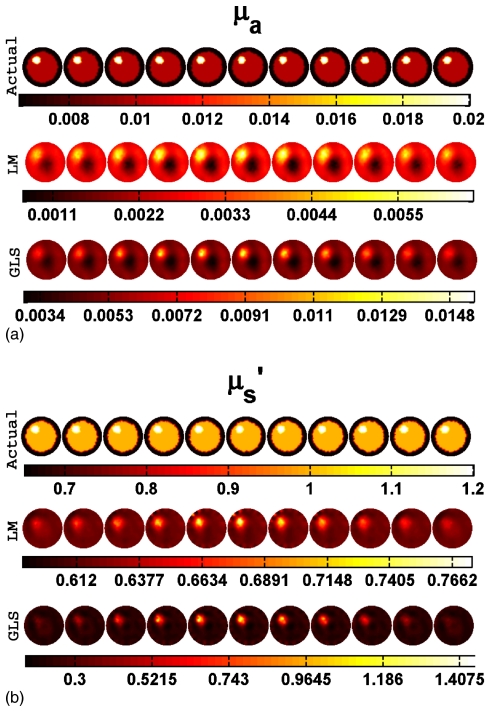
Both spherical and cylindrical objects were considered as targets. The cylindrical target had a contrast of 2:1 with the background in both μ_a and ${\mu }_s^{\prime }$ and a diameter of 15 mm. It extended in Z direction throughout the domain (height of 109 mm) and was placed at the center (at (0,0), first row of Fig. 5) and near the boundary (at (30,0)). Two-dimensional cross sections of both reconstructed and actual 3D volumes, displayed in increments of 5 mm spanning from z=−25 mm to z=25 mm (from left-hand side to right-hand side), are shown in Figs. 356. Cross section below z=−25 mm and beyond z=25 mm did not show any deviation from the starting values of iterations as the sensitivity in this region is almost negligible compared to the rest of the domain, so these cross sections are omitted for display purposes. Measurements with a noise level of 1% were assumed as the experimental data (y) in most of the cases discussed here. The noise variance was also used with GLS reconstruction algorithm.¹⁷ The background optical properties were selected as starting values for the iterative image reconstruction procedures discussed in Sec. 3. All computations were carried out on a Linux work station with an AMD Dual Core Opteron 280 processor (2.2 GHz) with 8 GB of random access memory (RAM).

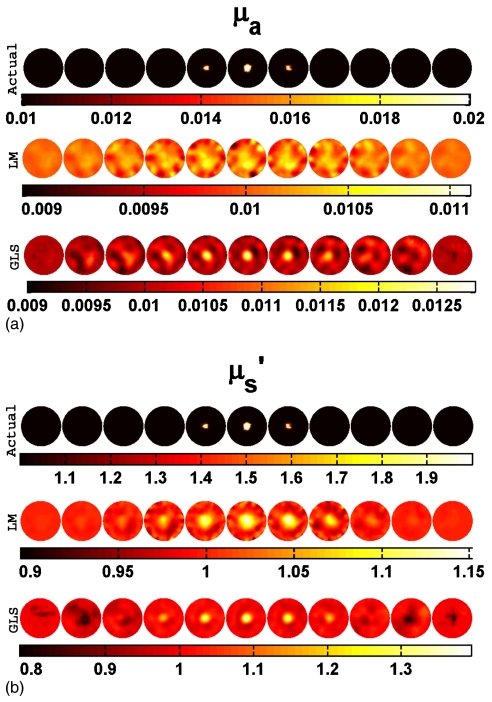
Figure 5.

Actual and reconstructed (a) μ_a and (b) ${\mu }_s^{\prime }$ distributions of a cylindrical target located at the center (diameter — 15 mm) using 5% noisy data. Two-dimensional cross sections of the 3D volume in 5 mm increments spanning from z=−25 mm to z=25 mm (from left to right) are shown. Actual distributions are given in the first row. Reconstructed distribution using the LM minimization scheme and GLS minimization scheme are presented in the middle and last rows, respectively.

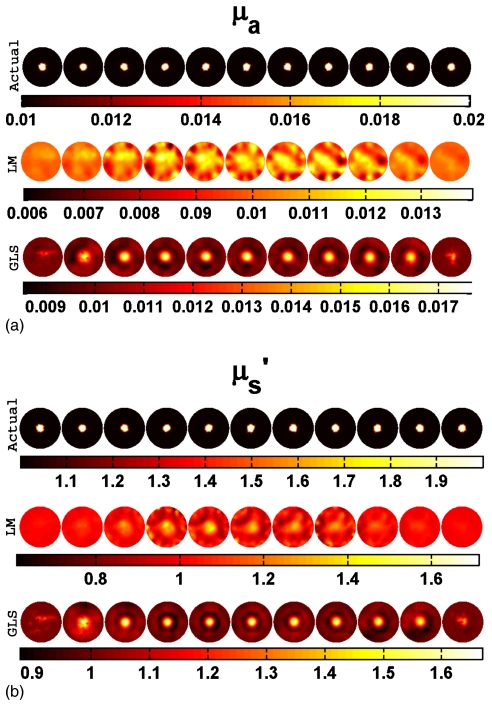
Figure 3.

Actual and reconstructed (a) μ_a and (b) ${\mu }_s^{\prime }$ distributions of a spherical target having a diameter of 15 mm located at the center (at (0,0,0)) using 1% noisy data. Two-dimensional cross sections of the 3D volume in 5 mm increments spanning from z=−25 mm to z=25 mm (from left to right) are shown. Actual distributions are given in the first row. Reconstructed distribution using the LM minimization scheme and GLS minimization scheme are presented in the middle and last rows, respectively.

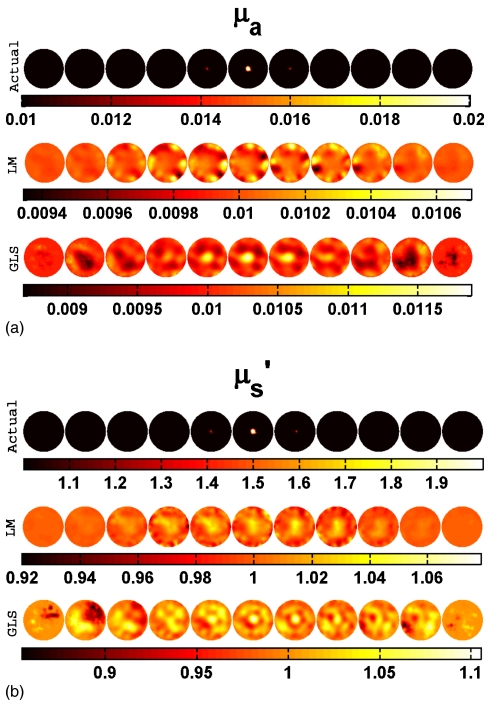
Figure 6.

Actual and reconstructed (a) μ_a and (b) ${\mu }_s^{\prime }$ distributions of a spherical target having a diameter of 10 mm located at the center (at (0,0,0)) using 1% noisy data. Two-dimensional cross sections of the 3D volume in 5 mm increments spanning from z=−25 mm to z=25 mm (from left to right) are shown. Actual distributions are given in the first row. Reconstructed distribution using the LM minimization scheme and GLS minimization scheme are presented in the middle and last rows, respectively.

PHANTOM STUDIES

Data variance estimation

Use of weight matrices in the GLS scheme (W_δ in Eq. 9) requires an estimation of data variance, which requires experimental characterization of the expected values, prior to patient∕phantom imaging. This was achieved by tracking the detected voltage measured at the photomultiplier tube (PMT). PMTs are used as a detectors in the experimental system at Dartmouth, details of the experimental system are given in Ref. 29. Note that this characterization includes only systematic errors associated with low signal levels, but errors due to poor fiber-tissue coupling are not accounted for in this model.

Starting from the assumption that the detected signal at the PMT in diffuse optical imaging is shot noise limited leads to

$$\sigma \left(N\right)=\sqrt{N},$$ (17)

where σ is the standard deviation of N and N is the number of photons reaching the PMT. The voltage (V; representing the detected ac intensity signal²⁹) measured at the PMT is directly proportional to N, which also implies that measured amplitude (A) of the detected frequency domain signal (y) is proportional to this voltage (V). This is written as

$$A\propto V\Rightarrow A=kV$$ (18)

$$\sigma \left(A\right)=k\sigma \left(V\right).$$

Here, k acts as a proportionality constant. In the reconstruction procedure, the Rytov approximation is used, leading to data being represented as lnA rather than A. If f(x) is a function of x and is continuous and differentiate, then

$$\sigma \left(f\left(x\right)\right)=\frac{\partial f\left(x\right)}{\partial x}\sigma \left(x\right).$$ (19)

Similar to the previous equation (Eq. 19), writing the standard deviation of InA leads to

$$\sigma \left(lnA\right)=\frac{1}{A}\sigma \left(A\right).$$ (20)

now using Eq. 18 leads to

$$\sigma \left(lnA\right)=\frac{\sigma \left(V\right)}{V}.$$ (21)

From the above equation (Eq. 21), it can be concluded that the variance in data (σ²) can be known by measuring the deviation in the PMT voltage (V).

To measure the deviation in the measured signal, a series of light signal measurements were taken through homogeneous intra-lipid phantom experiments which were conducted with increasing levels of blood (HbT) concentration, varying from 7.3 to 36 μM, leading to a decrease in the measured PMT voltage. To achieve this, the gain of the PMT was kept at 0.9. A concise discussion of the PMT gain setting in the system characterization is given in Ref. 29. A single source and the farthest detector was used for these transmission measurements. For every concentration, 200 data points were collected to estimate the deviation in the measured voltage using the same gain settings. The approach for the characterization is similar to the one described in Ref. 29, except the raw detected voltage was used here for estimation of the error (or deviation σ). Note also that two sets of diameters, 56 and 84 mm, were used to get the voltage in the range of 0–1 V. This was repeated for all the wavelengths to ensure uniformity of performance in the signal, and to ensure that the observed trend was independent of wavelength and gain setting.

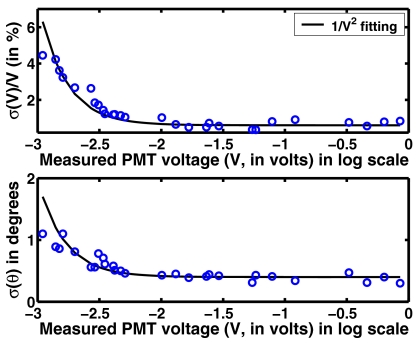
Figure 9 gives a plot of error (σ(V)∕V) as a function of measured PMT voltage for 785 nm wavelength. A similar trend was observed for other wavelengths. This plot also gives a deviation in phase (σ(θ)) in degrees for the same voltage. Each of these points represents a sample size of 200. The lowest measured voltage of PMT was 0.001 V. The measured deviations were 1% for lnA and 0.5° for θ for PMT voltages above 0.005 V. These values are similar to the ones reported in the literature (Mcbride et al.²⁹ reported 0.32% for the PMT voltage and 0.48° in phase). A solid line in Fig. 9 shows these average deviation using 1∕V² fitting (following the shot-noise model). From this plot, the weight matrix for the data-model misfit (W_δ in Eq. 9) can be written as

$${\left[{\mathbf{W}}_{\delta }\right]}_{ij}=\{\begin{array}{cc}0\hfill & \mathrm{if}i\ne j\hfill \\ \frac{1}{{[(5.7∕V^2)+0.6]}^2}forlnAwithV⩾0.001\hfill & \mathrm{if}\mathrm{i}=\mathrm{j}\hfill \\ \frac{1}{{[(1.3∕V^2)+0.4]}^2}for\theta withV⩾0.001\hfill & \mathrm{if}\mathrm{i}=\mathrm{j}\hfill \\ 1forlnAwithV<0.001\hfill & \mathrm{if}\mathrm{i}=\mathrm{j}\hfill \\ \frac{1}{{\left(\theta \right)}^2}for\theta withV<0.001\hfill & \mathrm{if}\mathrm{i}=\mathrm{j}\hfill \end{array}.$$ (22)

This implies that if the PMT voltage is below 0.001 V, the signal is considered to be in the noise floor. For the signals above 0.001 V, the variance can be estimated using 1∕V² fitted curve (Eq. 22). This characterization enables the usage of the GLS scheme in the case of experimental data, with a requirement that the voltage measured at the PMT is available.

Figure 9.

An error (deviation, σ) plot of the measured voltage and phase (θ) as a function of mean of measured PMT voltage. The legend of the figure represents the fitting model used. Each data point corresponds to a sample size of 200.

Gelatin phantom

A multilayer cylindrical gelatin phantom of diameter 86 mm, height 25 mm was fabricated using different mixtures of India ink for absorption and Titanium oxide (TiO₂) for scattering. These different layers of gelatin were fabricated by successively hardening heated gelatin solutions (typically 80% deionized water and 20% gelatin (G2625, Sigma Inc)) along with different amounts of ink and TiO₂ (Sigma Inc). A cylindrical hole extending in Z direction (diameter of 16 mm and height of 24 mm) filled with intra-lipid mixed with India ink acted as a target having the optical properties μ_a=0.02 mm⁻¹ and ${\mu }_s^{\prime }=1.2{\mathrm{mm}}^{-1}$. The outer layer with optical properties μ_a=0.0065 mm⁻¹ and ${\mu }_s^{\prime }=0.65{\mathrm{mm}}^{-1}$ had a thickness of 10 mm mimicking the typical fatty layer of the breast.³⁰ The middle layer with 76 mm diameter, mimicking fibro-glandular layer, had optical properties μ_a=0.01 mm⁻¹ and ${\mu }_s^{\prime }=1.0{\mathrm{mm}}^{-1}$. Validation of individual layer optical properties was performed by the data collected on large cylindrical samples of each layer using 785 nm wavelength laser diode as the source. Two-dimensional cross sections of this gelatin phantom optical properties are displayed in increments of 2.5 mm spanning from z=−12.5 mm to z=12.5 mm (from left-hand side to right-hand side) in top rows of Figs. 10a, 10b. In this phantom case, dater were collected using only one layer of fibers (at z=0 mm) leading to 240 lnA data points and 240 θ data points. A cylindrical mesh consisting 8990 nodes corresponding to 44 803 linear tetrahedral elements was used and the experimental data were also calibrated using a reference homogenous phantom data. The outer layer (mimicking fatty layer) optical properties were used as initial guess for reconstruction procedures. A second mesh with the same geometry containing 3718 nodes (16 627 linear tetrahedral elements) was used as a reconstruction mesh.

Figure 10.

Actual and reconstructed (a) μ_a and (b) ${\mu }_s^{\prime }$ distributions of a cylindrical target using experimental multilayered phantom data. Two-dimensional cross sections of the 3D volume in 2.5 mm increments spanning from z=−12.5 mm to z=12.5 mm (from left to right) are shown. Actual distributions are given in the first row. Reconstructed distribution using the LM minimization scheme and GLS minimization scheme are presented in the middle and last rows, respectively.

RESULTS

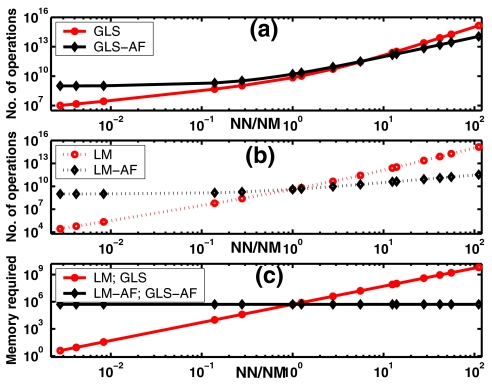
The number of operations required to produce an optical property update (Δμ_i) for both the original and alternative GLS update equations (Eqs. 9, 16, respectively) was compared as a function of the ratio of the number of estimation parameters (NN) to the number of measurements (NM). A similar comparison for LM update equations (Eqs. 5, 6) was also performed. The results are plotted in Figs. 2a, 2b, respectively. The expressions used for calculating the number of operations are given in Appendix 4. Memory required for implementing these inversions is presented in Fig. 2c. To relate the analysis to existing experiments, NM was chosen to be 720. The number of nodes (equivalently estimation parameters) was varied from 2 to 80 000. The number of computations increases for both LM and GLS cases as NN increases, but the alternative form for GLS (GLS-AF) has a lower computational cost when NN∕NM is greater than 6. In the case of alternative form LM (LM-AF), this is when NN∕NM is greater than 2. In terms of memory, as soon as NN>NM, both GLS-AF and LM-AF requirement is less than GLS and LM counterparts.

Figure 2.

Comparison of the number of operations required for the original update equation and its alternative form (a); for GLS (Eq. 9, represented by GLS) and its alternative form (Eq. 16, represented by GLS-AF) (b); for LM (Eq. 5, represented by LM) and its alternative form (Eq. 6, represented by LM-AF) as a function of the ratio of number of estimation parameters to number of measurements (represented by NN∕NM). Memory required for implementing the inversion procedure is plotted in (c).

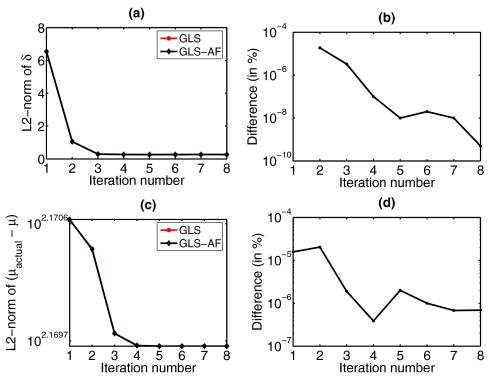
In order to assess algorithm performance, a series of test reconstructions were evaluated. Data with 1% noise from the cylinder containing a 15-mm-diam spherical target (first rows of Figs. 3a, 3b) was reconstructed for the optical properties using LM and GLS techniques (middle and last rows and Figs. 3a, 3b). In the case of the GLS scheme, the reformulated update equation (alternative form - Eq. 16) was used (last rows of Figs. 3a, 3b). However, it was also important to confirm that the two forms of the update equation (Eqs. 9, 16) produced numerically equivalent solutions. Figure 4 shows a comparison of results generated with the original GLS update equation (Eq. 9) and its alternative form (Eq. 16) in terms of data-model misfit (δ) and reconstructed optical properties. The difference plots (Figs. 4b, 4d) demonstrate that Eqs. 9, 16 are equal within the limits of the numerical precision to be expected (<10⁻⁸ of the L2-norm value, after the first few iterations). A similar analysis between the original LM update equation (Eq. 5) and its alternative form (Eq. 6) was performed and gave similar results (not shown here). These results indicate that there were no unexpected numerical difficulties in proving that these alternative forms of update equations (GLS: Eq. 16; LM: Eq. 6) are equivalent to its original forms (GLS: Eq. 9; LM: Eq. 5). Reconstruction results with different target shapes and positions are summarized in Table 1 which reports the mean and standard deviation of recovered μ_a and ${\mu }_s^{\prime }$ values in the background and target areas. Note that the recovered optical properties between Z=15 mm and Z=−15 mm were used because the reconstructed optical properties were equal to the actual background value and the standard deviation was zero (within round-off error limits) above∕below these Z values.

Figure 4.

Comparison of results from the GLS update equation (Eq. 9, represented by GLS) and its alternative form (Eq. 16, represented by GLS-AF). (a) L2 norm of data-model misfit (δ) as a function of iteration, (b) difference (in %) in the curves in (a), (c) L2-norm of the solution space (μ_actual−μ) as a function of iteration, (d) difference (in %) in the curves in (c).

Table 1.

Mean and standard deviation of the reconstructed μ_a and ${\mu }_s^{\prime }$ values in mm⁻¹ for the background and target with LM and GLS techniques using data with 1% noise. The spherical target had a diameter of 15 mm. One set of reconstructed images for the target in the center is presented in Fig. 3. The cylindrical target diameter was 15 mm and extended throughout the imaging domain in the z direction.

		Target		Target		Background
Methods	Shape	Position	μa	${\mu }_s^{\prime }$	μa	${\mu }_s^{\prime }$
Actual	⋯	⋯	0.01	1.0	0.02	2.0
LM	Spherical	(0,0,0)	0.0101±0.003	1.0079±0.0322	0.0104±0.0002	1.1259±0.0160
		(30,0,0)	0.0101±0.0006	1.0063±0.0500	0.0126±0.0009	1.4514±0.1152
	Cylindrical	(0,0)	0.0102±0.0010	1.0120±0.0874	0.0151±0.0012	1.4308±0.0854
		(30,0)	0.0101±0.006	1.0030±0.0663	0.0148±0.0015	1.8406±0.2470
GLS	Spherical	(0,0,0)	0.0101±0.0001	1.0100±0.0212	0.0122±0.0004	1.2903±0.0326
		(30,0,0)	0.0100±0.0004	1.0108±0.0250	0.0241±0.0006	1.4498±0.0853
	Cylindrical	(0,0)	0.0102±0.0008	1.0055±0.0500	0.0159±0.0009	1.4750±0.0941
		(30,0)	0.0101±0.0008	1.0043±0.0588	0.0170±0.0012	1.6793±0.1848

To show the robustness of the GLS procedure, data with 5% noise was used in the reconstruction of a cylindrical target located in the center (as shown in first rows of Figs. 5a, 5b). The reconstruction results using the LM and GLS schemes are presented in middle and last rows of Figs. 5a, 5b, respectively. The GLS minimization technique was able to localize the target more clearly than the LM method.

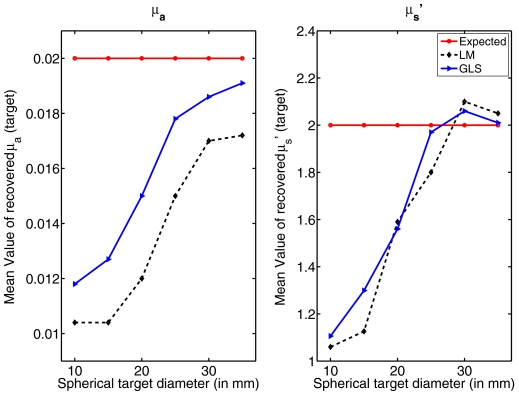
To see the effect of target size on the recovery of its contrast using these reconstruction techniques, a series of simulations were performed where the diameter of the spherical target located at the center was varied (from 10 to 35 mm). One set of results is presented for the 15-mm-diam target in Fig. 3. Another sample set for a target with diameter of 10 mm is shown in Fig. 6. A comparison plot is given in Fig. 7. The data noise level for the cases considered here is 1%. Increase in the diameter of the spherical target increases the contrast recovery.

Figure 7.

Comparison of recovered optical properties as a function of inclusion size (diameter) for the spherical target located at (0,0,0) using both LM and GLS techniques. Standard deviations were of the same order as given in Table 1.

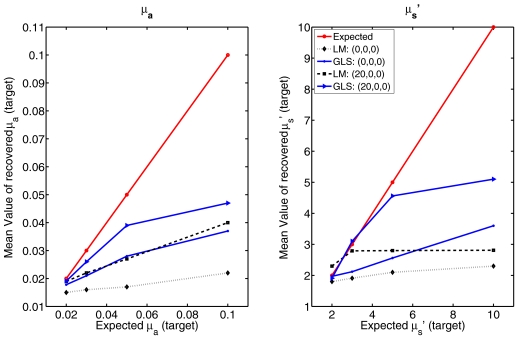
A performance comparison of these reconstruction techniques with increases in target (spherical object with diameter of 25 mm) contrast (from 2 to 10 with respect to background optical properties) located at the center (0,0,0) and (20,0,0) is presented in Fig. 8. Again, the noise level in the data was 1%. The recovery of contrast is much lower in the case of the centered target compared to the off-centered location in both LM and GLS techniques. Between the LM and GLS methods, the latter performs better in terms of recovery of contrast.

Figure 8.

Comparison of recovered optical properties with respect to expected values in a spherical target located at (0,0,0) and (20,0,0) having a diameter of 25 mm using both LM and GLS reconstruction techniques. Observed standard deviations are of similar order to that reported in Table 1.

A study was conducted to evaluate estimation parameter independence (cross-talk) in these reconstruction procedures. The spherical target having a contrast of 2:1 only in μ_a was considered at the center and near the boundary of the imaging domain. Synthetic data with 1% noise were used in the reconstructions, and the results are presented in Table 2 in terms of recovered mean and standard deviation of the optical properties. The recovery of contrast was higher in the GLS case and the amount of cross-talk was less (roughly 50% in the LM case compared to 30% in the GLS case). A similar study with a contrast of only in ${\mu }_s^{\prime }$ was also conducted (not shown) and it also showed a similar trend in terms of cross-talk.

Table 2.

Mean and standard deviation of reconstructed μ_a and ${\mu }_s^{\prime }$ in mm⁻¹ values for the background and a spherical target with no scattering contrast using the LM and GLS techniques. The diameter of the spherical inclusion was 15 mm. Data with 1% noise were used.

	Target position	Background		Target
Methods		μa	${\mu }_s^{\prime }$	μa	${\mu }_s^{\prime }$
Actual	⋯	0.01	1.0	0.02	1.0
LM	(0,0,0)	0.0101±0.0003	1.0025±0.0211	0.0109±0.0001	1.0500±0.0071
	(30,0,0)	0.0101±0.0004	1.0009±0.0205	0.0119±0.0004	1.0934±0.0269
GLS	(0,0,0)	0.0101±0.0001	1.0016±0.0269	0.0126±0.0002	1.0924±0.0253
	(30,0,0)	0.0100±0.0004	1.0029±0.0189	0.0136±0.0003	1.1002±0.0294

Finally, using the experimental data (Sec. 5B) collected using a multilayered gelatin phantom, reconstructions using both LM and GLS techniques were performed. For the GLS technique, experimental data variance was estimated (Sec. 5A) using an analytical equation, given in Eq. 22. Two-dimensional cross sections of the actual and reconstructed optical properties distribution are plotted in Figs. 10a, 10b. The middle and bottom rows correspond to the reconstruction results obtained by LM and GLS techniques. The variance in the data (noise charters tics) is embedded in the GLS reconstruction procedure, resulting in optimal weighting (highly noisy data points get less weightage and vice versa for less noisy data points), leading to better quantification of tumor region.

DISCUSSION

Appendix 1 presents a computationally efficient form for implementing an iterative GLS reconstruction scheme which reduces the dimensionality of the matrix to be inverted. The alternative forms for other minimization methods are also developed in the appendices (Sec. 2, 3). Appendix 4 presents expressions for estimating the operations count of both forms of the GLS update equations (Eqs. 9, 16) for a single iteration. Appendix 4 also gives operations count for both LM and its alternative form (Eqs. 5, 6) as well. Figure 2 shows a log-log plot of operations count as a function of the ratio of number of optical property parameters (NN) to number of measurements (NM) which determines the form of the GLS and LM update equation to be preferred (given that both produce numerically equivalent results as reported in Fig. 4). For example, when spatial priors are available, the number of optical unknowns can be reduced to the number of regions that can be segmented³¹ which in the case of breast tissue is typically NN=3 (assuming fatty, fibro-glandular and tumor regions).³¹ Here, since NM⪢NN, the original LM and GLS update equation (Eqs. 5, 9, respectively) is effective. In under-determined problems, such as the cases considered in this article, where NM⪡NN (NN∕NM ratio of 12 in the test problems), the GLS alternative form reduces the number of operations (by up to two times in Fig. 2a when NN∕NM=12). In fact, the alternative form of the GLS update equation (Eq. 16) becomes effective once NN∕NM>6 and the number of operations decreases by an order of magnitude when NN∕NM reaches 100. For the LM minimization scheme, alternative form reduces the number of operations by a factor of 6 in Fig. 2b when NN∕NM=12. The memory required for inverting such matrices is plotted in Fig. 2c as a function of NN∕NM. It is also important to recognize that the memory required to complete these operations can become critical because the cache sizes and RAM available on different architectures is variable but influences the efficiency of the computational processes executing on a given platform.

Under-determinedness of the imaging problem (i.e., NN∕NM>1) leads to nonuniqueness in the solution space, but regularization helps to give a unique solution in these cases. Typically NN∕NM values are between 2 and 10 for a typical two-dimensional (2D) problem, as the choice depends on the expected resolution in the reconstructed image, imaging domain size, shape, data-collection geometry, and prior information available. For a 3D problem, this choice (NN∕NM values) also depends on these factors, but one expects this ratio to be higher than the 2D case as the imaging domain size is bigger reflecting in the number of imaging parameters (NN) to be larger [Typical example: NN=600 (in 2D) and 6000 (in 3D)]. Ideally, one would like to have this ratio (NN∕NM) constant between 2D and 3D; this implies that the number of measurements has to increase by the same factor (typical case requires a factor of 10), which might not be feasible due to instrumentation constrains.²⁴ This leads to choice of NN∕NM greater than 6 at least, where the derived forms are effective (even though in the case of LM, the alternative form is effective when NN∕NM>2). It is also important to note that, ideally one would like mesh the volume where the sensitivity is greater (for the imaging domain discussed here z between −25 and 25 mm) finer and rest of the domain coarser, to keep NN∕NM in the same range as in 2D (typically 3–8). This adaptive meshing gets trickier when the patients are imaged, in our experience. We could not find appropriate tools that could be used in real time for this meshing problem, even though efforts to solve this patient-specific adaptive meshing are being pursued.^{32, 33} Even when NN∕NM=3 (lowest ratio one expects in a 3D imaging problem), from Fig. 2b, the alternative form (LM-AF, Eq. 6) in the case of LM minimization scheme becomes effective.

Figure 4 demonstrates that the two GLS update forms (Eqs. 9, 16) are equivalent numerically (within the numerical precision of the L2 norm value). For the cases considered here, the computation time for each iterative update using Eq. 16 was approximately 46 min, which was three times faster than with Eq. 9 (computation time ∼126 min per iteration). In terms of operations count, a factor of 2 reduction would be estimated from Fig. 2a for the NN∕NM ratio involved. The deviation in run time that occurs in practice is likely due to the cost of memory management alluded to above in the case of Eq. 9. It is also important to note that implementation of Eq. 9 requires an inversion of the covariance matrix (Eq. 10), whereas this matrix can be used directly in Eq. 16. In the case of LM update equations, computation time for an iteration using Eq. 6 was approximately 21 min and for Eq. 5 was 91 min. The deviation from factor of 6 (from Fig. 2b) is mainly due to the memory required to perform these operations; this affects run time in turn.

The middle and last rows of Figs. 3a, 3b indicate that with 1% noise in the data, LM has failed to recover μ_a in a spherical target with a diameter of 15 mm located at the center, whereas GLS was able to identify the target very well. The failure of LM minimization is indicative of a lack of sensitivity at the center of the domain²⁴ which is improved through the GLS approach by including the noise characteristics and covariances associated with the problem. When the same target is located near the boundary (at (30,0,0)), both techniques were able to recover the contrast approximately 20% better relative to the center position (Table 1).

When 1% noisy data generated from a centered cylindrical target with a diameter of 15 mm (first rows of Figs. 5a, 5b) were used in the reconstruction, both LM and GLS techniques were able to recover approximately 50% of the expected contrast (Table 1). For the same type of target located near the boundary (at (30,0)), the recovery of contrast was approximately 70% in the case of GLS. For LM, the recovery was only 50% for μ_a and 85% for ${\mu }_s^{\prime }$ under these conditions. The reconstruction results also show that recovery of the centered target is always poor relative to an object near the boundary. This is primarily due to the hypersensitivity at the boundary in these cases.²⁴ The extended cylindrical target is essentially equivalent to the two-dimensional case of a circular inclusion and the trend observed in 3D of recovering more contrast for a target near the boundary is similar to the behavior found in 2D.²⁴

When 5% noisy data were used, LM reconstruction (middle rows of Figs. 5a, 5b) performs poorly in terms of localization of the target, whereas GLS was able to reconstruct optical images with better quality and quantitation (up to 70%). Even though the reconstructed results using very noisy data were presented here from only one type of target, similar trends were also observed in other cases that mimic the 2D reconstructions reported in Ref. 17. These results show that GLS outperforms LM even though the data noise level is high because stability is retained by including the noise characteristics into the weight matrices used for normalization.

Accuracy in contrast recovery of local targets increases as the size of the target increases, as shown in Fig. 7. For example, the contrast recovered for a centered target below 20 mm in diameter is only about 30% of the true value and as low as 10% for the LM algorithm (Fig. 7), whereas increasing the size of target to 30 mm leads to quantitative accuracy near 100%. The GLS approach provides maximal contrast recovery and superior image quality at all sizes relative to LM (example: Fig. 6). Even when the target size is as low as 5 mm (Fig. 6), the object was well localized in the GLS case, but not with LM (Fig. 6).

The performance comparison of the algorithms in terms of contrast recovery (Fig. 8) confirms that the position of the target dictates the response. When the target had 10:1 contrast in comparison to the background, the maximum recovery of contrast was ∼5:1. GLS outperformed LM in this regard but there is a plateau in recovery of contrast at 400% of the background value.

Table 2 shows that estimation parameter dependence (cross-talk) is lower (by 20%) for GLS compared to LM, by reinforcing the independence of μ_a and ${\mu }_s^{\prime }$ through elimination of any cross terms in the weight matrix W_μ−μ0 (Eq. 15). The inter-parameter dependence is complex because of the non-unique relationship between the optical property distribution and the incomplete boundary data, indicating that different formulations of the inversion tend to perform differently. Nonetheless, the estimation parameter dependence is substantially higher in 3D data-limited situations, relative to when the ratio of data to number of estimates is less skewed.

In the case of phantom data (Fig. 10), as expected, GLS reconstructions showed more promising results in this test case. Characterization of the data collection system, leading to variance estimation depending on the voltage measure at PMT (Fig. 9) enabled the employment of the GLS technique for experimental data reconstructions. Both techniques (LM and GLS) were able to give qualitative information about the target, in terms of quantification the GLS technique overtakes the LM technique (Fig. 10). It should be noted that this type of characterization of the experimental system does not take into account coupling errors between the light collection∕delivery fiber and tissue surface. These kinds of unsystematic errors are difficult to estimate as it depends on many parameters, such as tissue surface roughness, tissue elastic properties, design of tissue-fiber coupling interface, repeatability, and alignment of fibers. Recent advances, such as inclusion of coupling errors as a part of reconstruction scheme by making them as unknowns and iteratively solving for them along with optical parameters, are possible.^{34, 35, 36, 37} But this makes the reconstruction problem more computationally complex in nature as the number of unknowns of this procedure are larger than the techniques considered here. As the main focus of this article is about presenting a computationally efficient algorithm for reconstructing optical parameters, this issue was not considered as a part of this work. Development of methods, which were presented as a part of this work, that can include systematic noise characteristics in the reconstruction procedure, will be taking a step in the right direction. Moreover, as can be seen from Eq. 22, covariances among the data points were ignored, making the data weight matrix (W_δ) a simple diagonal matrix. Inclusion of covariances can offer a better weighting in case of experimental data; this is under investigation as of now. Even though this test case showed very promising results, in our experience, in cases where coupling errors are dominant in the data, the GLS scheme did not yield any meaningful results. In these cases, the LM technique was able to give reasonable results.

Even though the data used here are generated by using in-plane data, it was collected only from the source fiber plane. Previous investigations indicate that the use of out-of-plane data (when the data were collected from rest of the fibers in all three planes when one fiber was used as source) may not give enough advantage in terms of reconstructed image quality given an increase in the data-acquisition time and computational cost compared to in-plane data (in this case the data were collected only from those fibers which lie in the same plane as the source fiber).²⁴ So for all the simulation studies conducted here, in-plane data collection scheme is used. The experimental phantom study uses only one plane of data, as the phantom optical properties were not varying in Z direction. Even though considering a experimental phantom where the optical properties are varying in Z direction might have been ideal to demonstrate the depth resolution of reconstruction procedures, in here only a simple case was considered as the main aim is to prove that the techniques developed here can be used in experimental data reconstruction. It is also important to note that the studies conducted here are generic in nature, especially in terms of proving the computational efficiency of alternative forms (Fig. 2), as NN∕NM was changed over a range of 0.0028–100 (spanning from well-determined to highly under-determined problems).

Partial volume effects can be observed in the recovery of contrast as a function of target size. The recovery of contrast was much higher for the extended cylinder target compared to the spherical inclusion (Table 1). The quantitative accuracy of reconstructed images increases with an increase in target size (Fig. 7). GLS reconstruction results of the data from a centered cylindrical object are encouraging, demonstrating recovery of more than 30% contrast in this case (other Newton-type algorithms have reported a maximum of 10% contrast recovery^{7, 11, 13, 14, 24}).

CONCLUSIONS

Three-dimensional diffuse optical tomography is more computationally intensive because of the size of the parameter space to be reconstructed. Newton-based inversion methods that operate on a Hessian matrix, which has dimensions of the number of measurements rather than the number of parameters, can be derived using the Sherman–Morrison–Woodbury identity and become computationally more efficient once the number of estimation parameters exceeds two times the number of measurements. Representative examples demonstrate that this form of update equation can be at least six times faster in practice in the highly under-determined problems which commonly occur in 3D. Three-dimensional diffuse optical tomographic reconstruction algorithms also suffer from partial volume effects that significantly degrade the accuracy with which optical properties can be quantified. The GLS approach which incorporates structured weight matrices consisting of the variance and covariance of the data-model misfit and the optical properties, improves the quantification of optical properties by at least 20% in 3D. The GLS estimate is also robust to data noise as high as 5%—conditions under which other algorithms fail when the problem is highly under-determined. By characterizing the detector noise for systematic errors, using a multi-layered gelatin phantom data, the GLS technique can be easily employed for reconstructing experimental data and can yield better quantification of targets compared to conventional reconstruction methods. Future investigations will include thorough examination of the GLS technique when applied to phantom and clinical data and extension of the technique to direct-spectral reconstruction. The test data used in this article, along with computer algorithms, are available on a web page.³⁸

APPENDIX

Alternative form for GLS update equation

Before deriving the alternative form, it is useful to catalog several properties of the weight matrices and their inverses²⁸

$${\mathbf{W}}_{\delta }={\left({\mathbf{C}}_{\delta }\right)}^{-1};{\mathbf{W}}_{\mu -{\mu }_0}={\left({\mathbf{C}}_{\mu -{\mu }_0}\right)}^{-1}$$ (A1)

$${\left({\mathbf{W}}_{\delta }\right)}^T={\mathbf{W}}_{\delta };{\left({\mathbf{W}}_{\mu -{\mu }_0}\right)}^T={\mathbf{W}}_{\mu -{\mu }_0}$$

$${\left({\mathbf{C}}_{\delta }\right)}^T={\mathbf{C}}_{\delta };{\left({\mathbf{C}}_{\mu -{\mu }_0}\right)}^T={\mathbf{C}}_{\mu -{\mu }_0}.$$

If a square matrix A has block form

$$\mathbb{A}=\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }\hfill & \hfill \mathbf{J}\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}\hfill \end{array}\right]$$ (A2)

with dimensions (2NM+2NN)×(2NM+2NN), it is readily shown to be symmetric by invoking the relationships in Eq. A1:

$$\left({\mathbb{A}}^T\right)={\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }\hfill & \hfill \mathbf{J}\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}\hfill \end{array}\right]}^T=\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }^T\hfill & \hfill {\left({\mathbf{J}}^T\right)}^T\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}^T\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }\hfill & \hfill \mathbf{J}\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}\hfill \end{array}\right]=\mathbb{A}.$$ (A3)

Since inverses of both C_δ and W_μ−μ0 exist, then A⁻¹ also exists and can be expressed in block form as well

$${\mathbb{A}}^{-1}=\left[\begin{array}{cc}\hfill \mathbf{P}\hfill & \hfill \mathbf{Q}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{S}\hfill \end{array}\right]$$ (A4)

in which case

$$\mathbb{A}{\mathbb{A}}^{-1}=\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }\hfill & \hfill \mathbf{J}\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}\hfill \end{array}\right]\left[\begin{array}{cc}\hfill \mathbf{P}\hfill & \hfill \mathbf{Q}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{S}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right]$$ (A5)

requires that

$$-{\mathbf{C}}_{\delta }\mathbf{P}+\mathbf{JR}=\mathbf{I}$$ (A6)

$$-{\mathbf{C}}_{\delta }\mathbf{Q}+\mathbf{JS}=\mathbf{0}$$ (A7)

$${\mathbf{J}}^T\mathbf{P}+{\mathbf{W}}_{\mu -{\mu }_0}\mathbf{R}=\mathbf{0}$$ (A8)

$${\mathbf{J}}^T\mathbf{Q}+{\mathbf{W}}_{\mu -{\mu }_0}\mathbf{S}=\mathbf{I}.$$ (A9)

These relationships can be manipulated through a series of substitutions to express the blocks of A⁻¹ in terms of combinations of the block components of A. Specifically, Eqs. A7, A8 along with the weight matrix properties in Eqs. A1 imply that

$$\mathbf{Q}=W_{\delta }\mathbf{JS}$$ (A10)

and

$$\mathbf{R}=-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T\mathbf{P}.$$ (A11)

Substituting Eq. A11 into Eq. A6 to form the expression

$$\mathbf{P}=-{({\mathbf{C}}_{\delta }+{\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T)}^{-1},$$ (A12)

which is put back into Eq. A11 produces

$$\mathbf{R}={\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{C}}_{\delta }+{\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T)}^{-1}.$$ (A13)

A similar series of steps starting with Eqs. A10, A9 to write

$$\mathbf{S}={({\mathbf{W}}_{\mu -{\mu }_0}+{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J})}^{-1},$$ (A14)

which is combined again with Eq. A10 yields

$$\mathbf{Q}={\mathbf{W}}_{\delta }\mathbf{J}{({\mathbf{W}}_{\mu -{\mu }_0}+{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J})}^{-1}.$$ (A15)

Since A is symmetric and invertible, A⁻¹ is symmetric as well.

$${\left({\mathbb{A}}^{-1}\right)}^T={\left[\begin{array}{cc}\hfill \mathbf{P}\hfill & \hfill \mathbf{Q}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{S}\hfill \end{array}\right]}^T=\left[\begin{array}{cc}\hfill {\mathbf{P}}^T\hfill & \hfill {\mathbf{R}}^T\hfill \\ \hfill {\mathbf{Q}}^T\hfill & \hfill {\mathbf{S}}^T\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \mathbf{P}\hfill & \hfill \mathbf{Q}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{S}\hfill \end{array}\right]={\mathbb{A}}^{-1}$$ (A16)

in which case

$${\mathbf{Q}}^T=\mathbf{R}.$$ (A17)

Substituting the forms of Q and R (Eqs. A15, A13, respectively) into Eq. A17 results in

$${\left[{\mathbf{W}}_{\delta }\mathbf{J}{({\mathbf{W}}_{\mu -{\mu }_0}+{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J})}^{-1}\right]}^T={\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{C}}_{\delta }+{\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T)}^{-1}$$ (A18)

Equation A16 also requires S^T=S, where S is given by Eq. A15, which when identified in the term on the left side of Eq. A18 allows it to be rewritten as

$${({\mathbf{W}}_{\mu -{\mu }_0}+{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J})}^{-1}{\mathbf{J}}^T{\mathbf{W}}_{\delta }={\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{C}}_{\delta }+{\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T)}^{-1}.$$ (A19)

Alternately,

$${\mathbb{A}}^{-1}\mathbb{A}=\left[\begin{array}{cc}\hfill \mathbf{P}\hfill & \hfill \mathbf{Q}\hfill \\ \hfill \mathbf{R}\hfill & \hfill \mathbf{S}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill -{\mathbf{C}}_{\delta }\hfill & \hfill \mathbf{J}\hfill \\ \hfill {\mathbf{J}}^T\hfill & \hfill {\mathbf{W}}_{\mu -{\mu }_0}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill \mathbf{I}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \end{array}\right]$$ (A20)

or

$$\mathbf{RJ}+{\mathbf{SW}}_{\mu -{\mu }_0}=\mathbf{I}.$$ (A21)

Solving for S

$$\mathbf{S}={\mathbf{C}}_{\mu -{\mu }_0}-{\mathbf{RJC}}_{\mu -{\mu }_0}$$ (A22)

and substituting Eqs. A13, A14 for R and S in Eq. A22 produces

$${({\mathbf{W}}_{\mu -{\mu }_0}+{\mathbf{J}}^T{\mathbf{W}}_{\delta }\mathbf{J})}^{-1}={\mathbf{C}}_{\mu -{\mu }_0}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{C}}_{\delta }+{\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T)}^{-1}{\mathbf{JC}}_{\mu -{\mu }_0}.$$ (A23)

Note that this derivation was adapted from Liebelt.³⁹ A variant of Eq. A23 exists in the literature with many names, the most common being the Sherm–Morrison–Woodbury identity.⁴⁰, ⁴¹, ⁴², ⁴³, ⁴⁴, ⁴⁵, ⁴⁶, ⁴⁷ It is also known as the matrix inversion lemma.⁴⁸, ⁴⁹ Even though one can start from this equation and derive the alternative forms, the complete derivation is presented here for completeness.

Substituting Eq. A23 back into Eq. 9 yields

$$\mathrm{\Delta }{\mu }_i=[{\mathbf{C}}_{\mu -{\mu }_0}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T+{\mathbf{C}}_{\delta })}^{-1}{\mathbf{JC}}_{\mu -{\mu }_0}]\{{\mathbf{J}}^T{\mathbf{W}}_{\delta }{\delta }_{i-1}-{\mathbf{W}}_{\mu -{\mu }_0}({\mu }_{i-1}-{\mu }_0)\}$$ (A24)

or

$$\mathrm{\Delta }{\mu }_i=[\mathbf{I}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T+{\mathbf{C}}_{\delta })}^{-1}\mathbf{J}]\{{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{\mathbf{W}}_{\delta }{\delta }_{i-1}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{W}}_{\mu -{\mu }_0}({\mu }_{i-1}-{\mu }_0)\}$$ (A25)

which results in

$$\mathrm{\Delta }{\mu }_i=[\mathbf{I}-{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{({\mathbf{JC}}_{\mu -{\mu }_0}{\mathbf{J}}^T+{\mathbf{C}}_{\delta })}^{-1}\mathbf{J}]\{{\mathbf{C}}_{\mu -{\mu }_0}{\mathbf{J}}^T{\mathbf{W}}_{\delta }{\delta }_{i-1}-({\mu }_{i-1}-{\mu }_0)\}$$ (A26)

as the alternative form for the update equation (Eq. 16).

The next two subsections show the alternative forms of other least-squares minimization techniques, namely LM and Tikhonov minimizations.

Alternative form for LM update equation

The LM update equation (Eq. 5) is a special case of the GLS update equation (Eq. 9) when W_μ−μ0=αI and W_δ=I (see Sec. III.V.4 in Ref. 17). Using these forms in Eq. A19 leads to an alternative form to Eq. 5

$$\mathrm{\Delta }{\mu }_i={\left(\alpha \mathbf{I}\right)}^{-1}{\mathbf{J}}^T{(\mathbf{J}{\left(\alpha \mathbf{I}\right)}^{-1}{\mathbf{J}}^T+{\mathbf{I}}^{-1})}^{-1}{\delta }_{i-1}.$$ (A27)

Rearranging the terms in Eq. A27 leads to

$$\mathrm{\Delta }{\mu }_i=\frac{{\mathbf{J}}^T}{\alpha }{\left(\frac{{\mathbf{JJ}}^T+\alpha \mathbf{I}}{\alpha }\right)}^{-1}{\delta }_{i-1}$$ (A28)

which can be simplified to produce

$$\mathrm{\Delta }{\mu }_i={\mathbf{J}}^T{({\mathbf{JJ}}^T+\alpha \mathbf{I})}^{-1}{\delta }_{i-1}.$$ (A29)

Equation A29 is also known as under-determined form in the literature.¹¹, ¹⁴

Alternative form for Tikhonov update equation

The objective function¹⁷, ⁵⁰ for the Tikhonov scheme is

$$\Omega ={\Vert \mathbf{y}-G\left(\mu \right)\Vert }^2+\lambda {\Vert \mathbf{L}(\mu -{\mu }_0)\Vert }^2.$$ (A30)

Minimization of Eq. A30 and linearizing the problem leads to update equation¹⁷, ³¹

$$\mathrm{\Delta }{\mu }_i={[{\mathbf{J}}^T\mathbf{J}+\lambda {\mathbf{L}}^T\mathbf{L}]}^{-1}({\mathbf{J}}^T{\delta }_{i-1}-\lambda {\mathbf{L}}^T\mathbf{L}({\mu }_{i-1}-{\mu }_0)).$$ (A31)

Equation A31 is a special case of the GLS update equation (Eq. 9) with weight matrices (see Sec. III.B.4 in Ref. 17)

$${\mathbf{W}}_{\delta }=\mathbf{I};{\mathbf{W}}_{\mu -{\mu }_0}=\lambda {\mathbf{L}}^T\mathbf{L}.$$ (A32)

From Eq. A26 one can write

$$\mathrm{\Delta }{\mu }_i=[\mathbf{I}-{\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T{(\mathbf{J}{\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T+{\mathbf{I}}^{-1})}^{-1}\mathbf{J}]\{{\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T\mathbf{I}{\delta }_{i-1}-({\mu }_{i-1}-{\mu }_0)\}.$$ (A33)

This leads to

$$\mathrm{\Delta }{\mu }_i=[\mathbf{I}-{\left({\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T{(\mathbf{J}{\left({\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T+\lambda \mathbf{I})}^{-1}\mathbf{J}]\{{\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T{\delta }_{i-1}-({\mu }_{i-1}-{\mu }_0)\}.$$ (A34)

Assuming μ_i−1=μ₀, the single-step Tikhonov update equation (or its equivalent)¹⁴, ³⁰, ⁵¹ becomes

$$\mathrm{\Delta }{\mu }_i={({\mathbf{J}}^T\mathbf{J}+\lambda {\mathbf{L}}^T\mathbf{L})}^{-1}{\mathbf{J}}^T{\delta }_{i-1}.$$ (A35)

Using Eqs. A19, A32 leads to

$$\mathrm{\Delta }{\mu }_i={\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T{(\mathbf{J}{\left(\lambda {\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T+{\mathbf{I}}^{-1})}^{-1}{\delta }_{i-1},$$ (A36)

which can be rearranged to

$$\mathrm{\Delta }{\mu }_i={\left({\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T{(\mathbf{J}{\left({\mathbf{L}}^T\mathbf{L}\right)}^{-1}{\mathbf{J}}^T+\lambda \mathbf{I})}^{-1}{\delta }_{i-1}.$$ (A37)

Equation A37 is also known as the under-determined Tikhonov single-step update equation.¹¹, ¹⁴, ¹⁶

Calculation of number of operations for LM and GLS update equations

The number of operations was estimated by assuming that divisions∕multiplications consume most of the processor cycles. Note that Gaussian elimination was used in computing matrix inversion. Typically, Gaussian elimination for an N×N matrix requires ((N³∕3)+N²−(N∕3)) operations.⁴⁷ The memory required to invert a matrix of dimension N×N is N².⁴⁷ The number of operations only includes solution of the update equation and does not account for the number of operations required to form the matrices∕vectors used in these equations.

For the GLS update equation (Eq. 9), the number of operations required for iteration i is (using the dimensions defined after Eq. 15)

$$Numberofoperations=[(2NM*2NM*2NN)+(2NN*2NM*2NN)+(\frac{\left(2NN\right)}{3}+{\left(2NN\right)}^2-\frac{2NN}{3})]+(2NN*2NN*1)+[(2NN*2NM*1)+(2NN*2NN*1)+(2NN*2NN*1)].$$ (A38)

For the alternative form for the GLS update equation (Eq. 16), the number of operations is

$$Numberofoperations=[(2NN*2NN*2NM)+(2NM*2NN*2NM)+(2NN*2NN*2NM)+(\frac{{\left(2NM\right)}^3}{3}+{\left(2NM\right)}^2-\frac{2NM}{3})+(2NM*2NM*2NN)]+(2NN*2NN*1)+[(2NN*2NN*2NM)+(2NN*2NM*1)+(2NM*2NM*1)].$$ (A39)

Similarly, for the LM update equation (Eq. 5), the number of operations required for iteration i is

$$Numberofoperations=[(2NN*2NM*2NN)+(\frac{{\left(2NN\right)}^3}{3}+{\left(2NN\right)}^2-\frac{2NN}{3})]+(2NN*2NM*1).$$ (A40)

The number of operations for the alternative form for the LM update equation (Eq. 6) is

$$Numberofoperations=(2NN*2NM*1)+[(2NM*2NN*2NM)+(\frac{{\left(2NM\right)}^3}{3}+{\left(2NM\right)}^2-\frac{2NM}{3})]+(2NM*2NM*1).$$ (A41)

Note that the computation time for these update equations is not only dependent on the number of operations needed to be performed, but also on the memory required for implementing the operations.