Tumor trailing strategy for intensity-modulated radiation therapy of moving targets

Abstract

Internal organ motion during the course of radiation therapy of cancer affects the distribution of the delivered dose and, generally, reduces its conformality to the targeted volume. Previously proposed approaches aimed at mitigating the effect of internal motion in intensity-modulated radiation therapy (IMRT) included expansion of the target margins, motion-correlated delivery (e.g., respiratory gating, tumor tracking), and adaptive treatment plan optimization employing a probabilistic description of motion. We describe and test the tumor trailing strategy, which utilizes the synergy of motion-adaptive treatment planning and delivery methods. We regard the (rigid) target motion as a superposition of a relatively fast cyclic component (e.g., respiratory) and slow aperiodic trends (e.g., the drift of exhalation baseline). In the trailing approach, these two components of motion are decoupled and dealt with separately. Real-time motion monitoring is employed to identify the “slow” shifts, which are then corrected by applying setup adjustments. The delivery does not track the target position exactly, but trails the systematic trend due to the delay between the time a shift occurs, is reliably detected, and, subsequently, corrected. The “fast” cyclic motion is accounted for with a robust motion-adaptive treatment planning, which allows for variability in motion parameters (e.g., mean and extrema of the tidal volume, variable period of respiration, and expiratory duration). Motion-surrogate data from gated IMRT treatments were used to provide probability distribution data for motion-adaptive planning and to test algorithms that identified systematic trends in the character of motion. Sample IMRT fields were delivered on a clinical linear accelerator to a programmable moving phantom. Dose measurements were performed with a commercial two-dimensional ion-chamber array. The results indicate that by reducing intrafractional motion variability, the trailing strategy enhances relevance and applicability of motion-adaptive planning methods, and improves conformality of the delivered dose to the target in the presence of irregular motion. Trailing strategy can be applied to respiratory-gated treatments, in which the correction for the slow motion can increase the duty cycle, while robust probabilistic planning can improve management of the residual motion within the gate window. Similarly, trailing may improve the dose conformality in treatment of patients who exhibit detectable target motion of low amplitude, which is considered insufficient to provide a clinical indication for the use of respiratory-gated treatment (e.g., peak-to-peak motion of less than 10 mm). The mechanical limitations of implementing tumor trailing are less rigorous than those of real-time tracking, and the same technology could be used for both.

INTRODUCTION

Internal organ motion, associated with respiration or cardiac cycles, is known to compromise the conformality of the therapeutic dose distribution delivered to thoracic and abdominal tumors.^{1, 2, 3, 4, 5} The most common effect of the target motion on the dose distribution is smearing of the gradients, which results in smoothing of the dose inhomogeneities within the target, and dose washout beyond the target edges. Commonly, increased planning margins have been used to ensure desired irradiation of the target.⁶ The margin solution, however, inevitably results in an increased dose to the uninvolved tissues surrounding the tumor. In addition, since the therapeutic dose in IMRT is often delivered dynamically, as a sequence of treatment segments, the exact effect of target motion (even in the hypothetical case of a highly reproducible motion pattern and delivery) will be determined by a number of factors, such as the start time of treatment, and of each segment, with respect to the phase of motion, and the rate of dose delivery.⁷ Due to this effect, commonly referred to as the “interplay,” the dosimetric outcome of each particular fraction of the treatment course may be quite different from the plan. It has been shown, however, that cumulative dose distribution will be largely insensitive to the fraction-to-fraction variations in treatment delivery, and will approach the “expectation” value for the interplay of the given delivery sequence with the realized pattern of target motion.⁸

Advances in imaging allow for a more detailed and precise observation and description of the target motion due to respiration. Target motion can be observed directly by means of respiratory-correlated computed tomography (4D-CT),^{9, 10, 11, 12, 13} and, in real time, with fluoroscopy.³ Alternatively, it can be inferred from monitoring of external markers. Correlation between the internal motion and its external surrogates has been investigated extensively.^{14, 15, 16, 17}

Several approaches, which employ real-time target monitoring, have been proposed to mitigate the effect of internal target motion on the dosimetric outcome. In respiratory-gated treatments the dose is delivered only during a part of the motion cycle (typically less than half of the cycle), when the tumor is believed to be sufficiently well localized within a gating window.^{18, 19, 20} In tumor tracking, the delivery sequence is continuously adjusted so that the radiation field and the target move in synchrony. Such motion synchronization may be achieved by tracking with multileaf collimator (MLC),²¹ stereotactic beam,²² scanning of particle beams,²³ or setup adjustment. The example of the latter implementation, described by D’Souza et al.,^{24, 25} involves adjustments of the treatment couch position to counter the motion of the target.

While motion-correlated delivery strategies allow for an increased precision in dose delivery to the target, they have a number of disadvantages. In the case of gating, the reduction in the duty cycle leads to a substantial lengthening of the treatment session. Additionally, the efficiency of gating is reduced by the residual motion within the gate window.^{26, 27} Delays in motion detection, as well as any possible lag between the internal motion and the surrogate-marker motion may have a strong effect on the precision of targeting in gating, and especially tracking delivery. In the case of couch tracking,^{24, 25} the main difficulty arises from implementing fast couch motion and associated position verification uncertainties.

Alternatively, the effect of the target motion can be mitigated by means of adaptive treatment planning, which employs a probabilistic description of motion. Probability distribution functions (PDFs) have been previously used in treatment planning, primarily as the means of estimating the effect of target motion on the delivered dose distribution,^{28, 29, 30, 31, 32} uncertainty in the patient setup,^{33, 34, 35} and, more recently, uncertainties in gated intensity-modulated radiation therapy (IMRT) treatments.³⁶ Planning methods based on the PDF have been proposed by several groups of authors.^{37, 38, 39, 40} Since the PDF does not include explicit time dependence, the probabilistic planning approaches relax (compared to the motion-correlated delivery) the requirements for the precision of monitoring of the target motion and speedy intervention to adjust the treatment accordingly. However, probability-based planning has its own weaknesses. First, it relies on the motion pattern being both predictable and reproducible, and, second, the PDF sampling during delivery needs to be sufficiently dense to ensure the dose convergence to the expectation. The uncertainty in realization of the “planned” breathing patterns is the main obstacle to successful implementation of motion-robust treatment planning.

Making IMRT more robust, namely, reducing the sensitivity of the outcome of IMRT optimization to the uncertainties and deviations from the plan during delivery, has recently been a focus of several publications.^{41, 42, 43} The robust IMRT optimization method formulated by Chan et al.⁴⁴ considers uncertainty bounds that encompass all (or at least, the most likely) possible realizations of the PDF during treatment. As the result, the delivered dose will be acceptable (will fulfill the planning objectives) for any realized PDF, which is contained within the bounds. The outcome of robust optimization converges to the single-PDF solution of Refs. ^{37, 39, 40} in the case of minimal uncertainty (largely reproducible motion), and approximates the margin solution in the case of large uncertainties.⁴⁵ Thus, a reduction in the uncertainties of the PDF realization leads to the fuller engagement of the potential of robust planning methods to reduce the unwanted dose deposition in healthy tissues. Among the major factors that negatively influence the reproducibility of PDF are the long-term aperiodic changes in the respiratory base line, which have been reported by various investigators.^{17, 46, 47}

In this article, we formulate a radiotherapy delivery strategy which combines elements of motion-adaptive treatment planning and image-guided delivery and describe its application to a test case.

METHODS

We propose and test the strategy of “trailing” the trend in the change of the target position, on the scale which is longer than that of a typical breathing cycle. In this approach, the motion of the internal target is regarded as a superposition of the “fast” cyclic component (respiratory) and the, generally, aperiodic trends occurring on the time scale beyond that of a breathing cycle: the ultracyclic motion. The trailing strategy requires real-time monitoring of the target motion to detect the ultracyclic motion and corrects for it by applying setup adjustments whenever the accumulated shifts exceed the predetermined tolerance level. Delivery does not track the target position exactly but trails the relatively slow ultracyclic trend due to the delay that exists between the time a shift occurs and the time it can be reliably identified based on the marker data, followed by setup correction.

Unlike the couch tracking which aims to correct for the fast periodic motion exactly,^{24, 25} the trailing strategy relies on other means to manage the cyclic component. This can be accomplished, for example, with robust motion-adaptive planning methods, which allow for variability in motion parameters (tidal volume, period, expiratory duration). Thus, the trailing approach, in combination with robust planning, embraces the fact that, in certain tumor sites, target motion occurs continuously, and, generally, is not stable or reproducible. However, it also requires that certain generalizations be made about the character of motion: namely, an expected (average) probabilistic position description based on relatively long-term observation of the target, as well as statistically expected deviation from that average.

The original motivation to introduce the trailing method in delivery was indeed to improve the efficiency of the robust planning approach, by minimizing the detrimental effect of the ultracyclic motion. Nevertheless, the trailing strategy can be synergistically combined with other motion mitigation techniques, such as gating, or the use of planning margins.

Respiratory motion-surrogate data

At Massachusetts General Hospital (MGH), a considerable body of data is available for investigation of both the intersubject and intrafractional variability of respiratory motion. Respiratory-correlated 4D-CT scanning is routinely performed in cases where tumor motion is of concern. Respiratory-gated radiotherapy treatments at MGH are administered to patients who exhibit target motion of over 10 mm peak-to-peak (based on 4D-CT scans).

The position of an infrared reflector attached to a patient surface is being recorded, with a sampling frequency of f_s=30 Hz, during gated treatments,⁴⁸ as well as 4D-CT data acquisition.¹² The recorded data (marker traces) serve as a surrogate source of information for the internal tumor motion. The length of traces varies between 100 and 480 s. At least one trace is recorded for each 4D-CT acquisition session, or a fraction of gated IMRT treatments. Fluoroscopic imaging is used as part of the setup procedure but not for target monitoring during treatments.

The external marker motion data were anonymized, and IRB approval was procured for their use in this study. Most results presented here used data sets collected during fractionated IMRT courses. The data recorded during 4D-CT acquisition were used to evaluate the interobserver PDF variation.

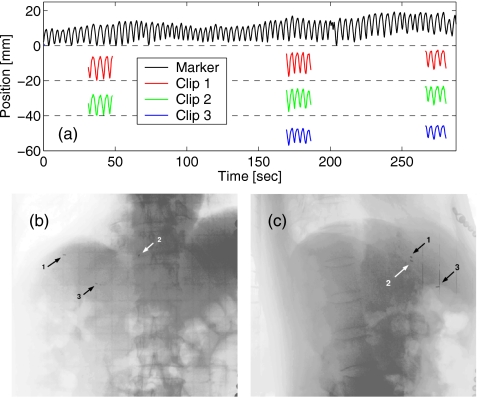
For the purposes of this study, it will be assumed that a stable correlation between the external and internal motion exists and can be readily established and parameterized. Of note is that while a correlation between the drift of an external marker and a systematic change in the target position has been documented (e.g, see Ref. 17 and also see Fig. 1), the proportionality between the two is generally different from that between the periodic motion of the marker and the target. The most common underlying cause of ultracyclic motion is a change in the residual (expiratory) tidal volume of the lung, related to psychological and physiological causes, such as variations in the state of the central nervous system and hormonal balance.⁴⁹ However, a systematic shift in the external marker position may as well reflect the relaxation or flexing of surface muscles, or inadequate immobilization of the marker, both of which are generally unrelated to the internal motion. The correlation coefficients can be estimated by comparing data from internal (e.g., radio-opaque seeds observed with fluoroscopy) and external marker traces collected simultaneously, as illustrated in Fig. 1.

Figure 1.

(a) The drift in the position of the external marker (black line) reflects the change in position of three radio-opaque clips implanted in patient’s liver, as detected in three 20-s long sessions of fluoroscopic imaging. Location of the clips is shown in (b) coronal and (c) sagittal fluoroscopic view of the patient.

Decoupling of the motion components

The respiratory traces from gated-IMRT patients were used to test algorithms aimed to detect and extract the ultracyclic motion component in the regime approximating real-time acquisition. Two methods to extract the ultracyclic component of the marker motion were applied and compared.

One method employed digital filtering, which is an established method of separating frequency-band components in time-dependent data.⁵⁰ A Fourier transformation (FT) was applied to a complete trace and the low-frequency motion component was separated by application of bandpass filtering. The portion of the original transform data that passed through the filter was then transferred back into the time domain with the inverse FT.

The FT of a trace l(t) of length t_max (s), sampled at f_s (Hz), represents the spectrum of frequencies between 0 and f_s, with the resolution of 1∕t_max (Hz),

$$L\left(f\right)=\sum _{\left[n=t\cdot f_s\right]=0}^{N-1}l\left(t\right)\cdot e^{-2\pi ift},$$ (1)

where n is the index variable, and N=(t_max⋅f_s+1) is the length of the data set. Since the FT is symmetric in frequency (the real part is an even, and the imaginary part is an odd function), the frequencies of f and f_s−f are indistinguishable in the spectrum. Thus, in order to extract the low-frequency component of the data below the pass frequency of f_p, it is necessary to consider both of the bands: [0,f_p] and [f_s−f_p,f_s]. For simplicity of calculation, a step-like transfer function was chosen for the filter

$$F\left(f\right)=\{\begin{array}{ll}1,\hfill & \text{for}f\le f_p\hfill \\ 0,\hfill & \text{for}{f}_p<f<\left(f_s-f_p\right)\hfill \\ 1,\hfill & \text{for}\left(f_s-f_p\right)\le f.\hfill \end{array}\phantom{\}}$$ (2)

The ultracyclic motion component, l_u(t), is then obtained with the inverse transform

$$l_u\left(t\right)=\sum _{\left[n=f\cdot t_{\text{max}}\right]=0}^{N-1}L\left(f\right)\cdot F\left(f\right)\cdot e^{2\pi ift}.$$ (3)

For ease of exposition, below, we will refer to the approach described by Eqs. 1, 2, 3 as the FT method.

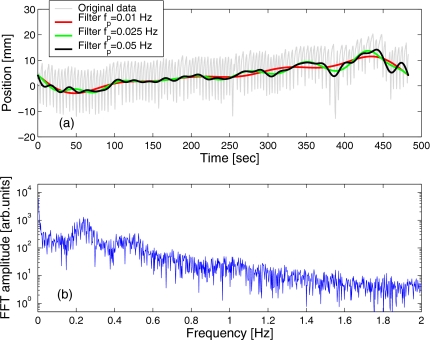
The low-pass cutoff frequency should be chosen sufficiently below the frequency of the respiration, which varies between observers, and is typically in the range between 0.15 and 0.4 Hz. The result of the filter application is obviously dependent on the choice of f_p, as illustrated in Fig. 2.

Figure 2.

(a) A sample marker trace overlaid with the curves designating the ultracyclic component of the marker motion, extracted using the FT method [Eqs. 1, 2, 3] with different low-pass cutoff frequencies f_p. The Fourier transform spectrum of the original data is shown in (b).

While the high-frequency component in the data is typically associated with noise, it has an important role in fulfilling the boundary conditions, i.e., the start and end values in the data sample. Because the filtering eliminates the high-frequency component from the data, l_u(0)=l_u(t_max) in the filtered trace [see, e.g., Fig. 2a]. Due to this feature, the FT method is not capable of approximating the ultracyclic component of motion within the “blind spots” that cover the first and last 1∕(2f_p) seconds of the trace. Practically, this means that the FT method cannot detect ultracyclic shifts immediately as they occur but with a delay that is determined by the cutoff frequency. Additionally, FT is a relatively computationally intensive process and, arguably, it may not be practical to perform the transform repeatedly in real-time during the data acquisition. This point notwithstanding, when applied to completed data sets, the FT method can provide the reference base line solution to which the results obtained with other methods can be compared.

Another method, that provides a simple approximation of the FT result, in real-time, is based on observation of the running mean (RM) of the marker position within a moving time window (e.g., most recent T s). For t>T, the RM method gives

$$l_u\left(t\right)=\frac{1}{T}{\int }_{t-T}^{t}l\left(t\right)\cdot dt\simeq \frac{1}{T{f}_s}\sum _{n=\left(t-T\right)f_s}^{t{f}_s}l\left(\frac{n}{f_s}\right).$$ (4)

Since the mean time over the sample corresponds to the middle of the window t−T∕2, the detection of shifts in the mean marker position with the RM method is delayed by T∕2 s.

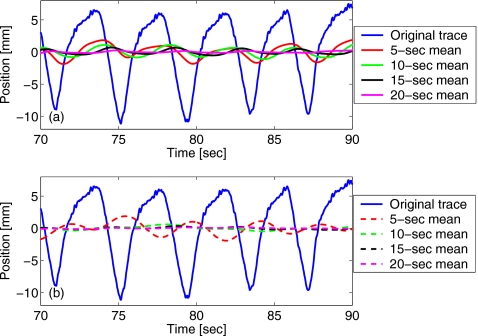
Notably, the result of the RM method is affected by “phase pulling” from incomplete cycles [Fig. 3a]. Since the relative contribution from incomplete cycles grows as the width of the time window is reduced, so does the amplitude of phase pulling. One way to limit this effect is, therefore, to increase the width of the time window used for calculating the RM. Alternatively, the effect may be reduced if weighted average values are considered

$$l_u\left(t\right)={\int }_{t-T}^{t}l\left(t\right)\cdot w\left(t,T\right)\cdot dt,$$ (5)

$$\text{with}{\int }_{t-T}^{t}w\left(t,T\right)\cdot dt=1,$$

where w(t) is a function [e.g., a Gaussian, see Fig. 3b], normalized over the time window of T. [Obviously, uniform weighting with a constant w(t)=1∕T, produces the mean value, as in Eq. 4.] The phase pulling effect can be further reduced with the application of a median filter (over a smaller time window, of the order of the respiratory period) to the results obtained with Eqs. 4, 5.

Figure 3.

The phase-pulling effect on the running mean value of the marker position is illustrated for different settings of the time window used for weighted averaging. The values are shown for the window widths of T=5, 10, 15, and 20 s for (a) no weighting (true mean) and (b) a Gaussian weighting function (with ⟨t⟩=t−T∕2, σ=T∕4).

Subtraction of the ultracyclic component from the original data yields the cyclic component of the marker motion l_c(t),

$$l_c\left(t\right)=l\left(t\right)-l_u\left(t\right).$$ (6)

Framework formulation for robust planning

The effect of the cyclic component of motion can be mitigated with motion-adaptive treatment planning. The optimization framework developed by Chan et al.⁴⁴ requires a “nominal” probability distribution function, $p\left(\vec{x}\right)$, which is a normalized function (∫p=1) that describes the probability of the target position characterized by a shift, $\vec{x}$, from the reference position. The PDF of the cyclic motion is obtained by time binning of l_c over the time interval of interest

$$p\left(x\right)=\frac{\int \delta \left(l_c\left(t\right)-x\right)dt}{\int dt}.$$ (7)

The nominal PDF can be defined based on pretreatment data, e.g., those acquired during respiratory-correlated CT scan or treatment simulation.

Furthermore, the framework requires definition of the expected variability of the target motion, in the form of upper $\left(p+\overline{p}\right)$ and lower $\left(p-\underset{̱}{p}\right)$ bounds for the PDF to be realized during treatment fractions. This formulation implies equal likelihood of realizations of any motion PDF $\tilde{p}$ entirely contained within the bounds. Of note is that all $\tilde{p}$ are time independent and normalized to the same unit probability, therefore the bounds $\left(p+\overline{p}\right)$ and $\left(p-\underset{̱}{p}\right)$ themselves are not among the realizable PDF, assuming $\underset{̱}{p}\ne 0$, $\overline{p}\ne 0$. The variability bounds $\overline{p}\left(x\right)$, $\underset{̱}{p}\left(x\right)$ may be estimated from multiple traces or, if the available data are limited, based on the intrafractional variability of motion (e.g., within a single trace). Alternatively, the variability bounds may be designed based on observations from different patients, assuming that a cohort of patients exhibits similar respiratory characteristics.⁴⁵ (Strictly speaking, even in the same instance of beam delivery, the motion of various subvolumes within the patient will be described by different functions $\tilde{p}$, thus, the model can be broadened to counter the effects of deformation of the internal anatomy, in addition to the variability of respiratory parameters.)

Solving the robust optimization problem requires identifying the set of non-negative weights (integrated intensities), w_b≥0, of pencil beams (bixels), b, that minimize the integral dose to all subvolume elements (voxels), v, within the volume of interest

$$\sum _{\forall v}\sum _{\forall b}\sum _{\forall x}\left[{\Delta }_{v,b,x}\cdot p\left(x\right)\cdot w_b\right],$$ (8)

subject to the appropriate lower and upper dose constraints, $\underset{̱}{d}$ and $\overline{d}$,

$$\underset{̱}{d_v}\le \sum _{\forall b}\sum _{\forall x}\left[{\Delta }_{v,b,x}\cdot \tilde{p}\left(x\right)\cdot w_b\right]\le \overline{d_v}\text{for}\forall v\forall \tilde{p}\in \left[\left(p-\underset{̱}{p}\right),\left(p+\overline{p}\right)\right].$$ (9)

Here Δ_v,b,x is the shift-differentiated dose influence matrix, the elements of which represent the dose delivered by a unit-weight beam, b, to an anatomical voxel, v, which is displaced by x from its location in the reference grid. The Δ matrix is a more general form of the dose-influence matrix D_ij,^{40, 51} applied to a variable anatomy.

Design and delivery of test treatment plans

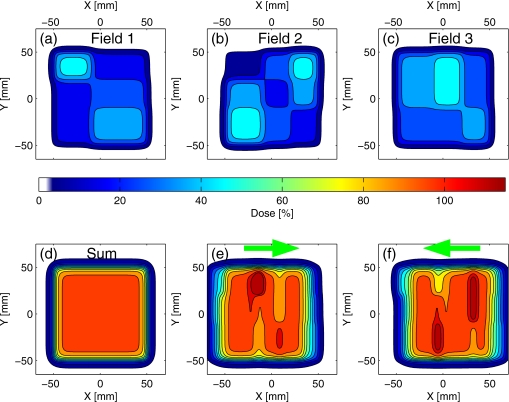
Since the ultracyclic drift in the target position would result in a mismatch between the IMRT fields delivered consecutively, a simple IMRT plan was designed to evaluate and emphasize the potential of the trailing strategy in countering this effect. In the test plan, the dose from three inhomogeneous fields, consisting of rectangular areas of level intensity, alternating in a checkerboard pattern [Figs. 4a, 4b, 4c], adds to a uniform dose distribution when the fields are delivered to a target from the same direction, in the absence of ultracyclic motion [Fig. 4d]. However, if the ultracyclic motion is not negligible, a mismatch would occur as illustrated in Figs. 4c, 4f. The exact pattern of mismatch and the resulting deviation from the planned dose will depend on the direction and time dependence of the drift.

Figure 4.

Test IMRT plan (calculation): two-dimensional dose distributions from three fields shown in (a)–(c) combine to a uniform distribution (d), when delivered consecutively to the target from the same direction. In the presence of the target position drift, the distributions will not match as planned: plots (e), (f) show possible patterns of inhomogeneities for the scenarios in which the target drifted (in the beam’s eye view) in the direction indicated by arrows.

Robust optimization of the test plan was performed with the software package CPLEX-9 (ILOG SA, Gentilly, France). The unoptimized checkerboard-pattern intensity maps were input as the initial guess, and the weights of individual pencil beams were adjusted in iterative optimization with the aim to deliver a uniform combined dose to the moving target. The dose deposited from pencil beams was modeled based on the measurements performed during clinical commissioning of the linear accelerator, on which the test plans were later delivered.

The treatment plans were sequenced for a MLC of 5×5 mm² resolution at the isocenter and delivered to a programmable moving phantom in several fractions. The phantom utilized in this test has been previously used for target motion studies.⁵² The programmable phantom is capable of reproducing motion patterns in three dimensions, according to the input. The precision of the phantom motion had been tested previously and was found to be within 1 mm. In this study, only one of the three modes of motion was used to reproduce selected marker traces previously acquired during IMRT treatments. No traces were recorded during the test delivery.

Dose measurements were performed with a commercial ion-chamber array, with the resolution of 7.6 mm. The detector was attached to the phantom in the “home” position (no displacement), under 10 cm of water-equivalent material. The center of the active area of the detector was aligned with the isocenter of the accelerator, at a source-to-detector distance of 1 m.

Test fields were delivered, at the dose rate of 300 monitor units (MU) per minute, while the phantom moved according to selected traces, with and without the correction for the ultracyclic motion. The drift-detection analysis (using the RM method) for the traces selected for the delivery was done offline, before the test. The RM within a 20-s time window was evaluated at 1 s intervals, and a minimum detected drift of 1 mm was set to trigger a setup correction. The trigger threshold value may be chosen arbitrarily small or large, depending on the notion of what shift should be deemed manifestly systematic to warrant a correction.

In approximation of trailing delivery, the correction was applied to the phantom motion itself (modified trace), instead of the treatment couch. Couch correction is technically implementable, as was shown by D’Souza et al.²⁴ but is not currently available at our institution.

RESULTS

Detection of the ultracyclic motion

A sample marker motion trace and the spectrum of its Fourier transform are shown in Fig. 2. The peak corresponding to the main respiratory frequency is clearly visible, centered at 0.24 Hz (4.2 s period), while the strong second harmonic is also present at 0.48 Hz. The pass frequency can be chosen rather arbitrarily, for example, depending on the limitation in the speed with which the shifts may be corrected. However, f_p needs to be sufficiently below the respiratory frequency, to allow for good separation of the fast respiratory motion from slower trends. The examples of the form of the ultracyclic component, extracted with different settings of the pass frequency [Fig. 2a] show increased oscillations in the result with the increasing f_p. The pass cutoff of f_p=25 mHz, an order of magnitude below the typical respiratory frequency, was selected for comparison with the RM method in this study.

The results of the comparison are illustrated in Figs. 56, for two data sets that exhibited ultracyclic drift in opposite directions. The analysis was done off-line, however, it approximated the regime of real-time data acquisition. That is, the analyzer program considered only the data acquired prior to the time for which the mean position was evaluated. For the RM method, the ultracyclic component was calculated as the mean over a time window of width T=1∕(2f_p)=20 s, preceding the time of evaluation. The detection of ultracyclic motion with the RM method was effectively delayed by 10 s (half of the averaging window), compared to the reference result given by the FT method applied to the complete trace. This delay is visible in Figs. 5a, 6a. The maximum peak-to-peak excursion of the detected drift in the two sample traces was 16 and 15 mm, respectively.

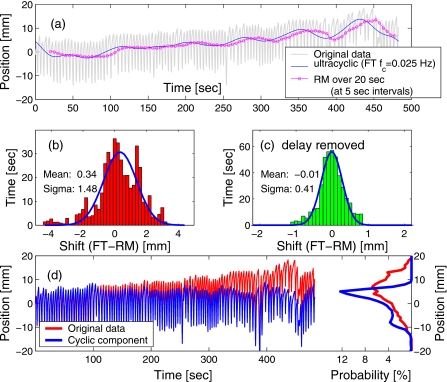
Figure 5.

(a) A sample marker trace is overlaid with curves showing the ultracyclic component of motion, extracted with FT and RM methods. The RM curve is delayed with respect to the FT curve by 10 s: half of the averaging time window. The distribution of differences in the values given by the two methods is shown (b) in real time, and (c) with the 10-s delay removed (RM curve shifted back in time). The parameter values are shown for the fit to a normal distribution. Plot (d) shows the original trace, the cyclic component (after the drift detected with the RM method was subtracted), and their respective PDFs.

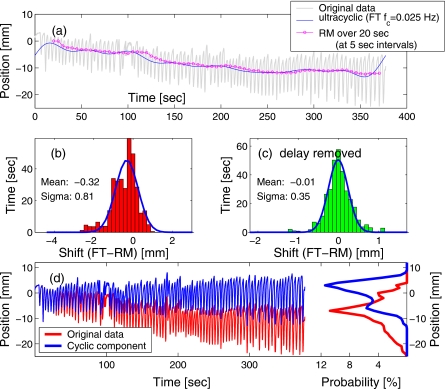
Figure 6.

Similar to Fig. 5, but with the drift direction reversed. (a) The marker trace is overlaid with the ultracyclic motion components obtained with FT and RM methods. The distribution of differences in the values given by the two methods is shown (b) in real time, and (c) with the 10-s delay removed. Plot (d) shows the original trace, the cyclic component alone, and their respective PDFs.

The distribution of the difference in the target position produced by the two methods reveals both a systematic shift due to the relatively stable direction of the drift in the selected examples and a spread in values due to the delay in detection with the RM method [see Figs. 5b, 6b]. However, when the time scales were synchronized by removing the 10-s delay in the result of the RM method, it approximated the FT result rather well [e.g., Figs. 5c, 6c], with the standard deviation of below 0.5 mm.

While, because of the delay in the shift detection, the RM method is not suitable for target tracking, it fits well with the objective of the trailing strategy to reduce the variability of the PDF, both intra- and interfractionally. Figures 5d, 6d show the cyclic component of the marker motion, obtained by subtracting the ultracyclic motion, detected with RM analysis, from the original marker data, and the corresponding PDF. Not surprisingly, the excursion in the cyclic component was reduced: in the original data set of Fig. 5, the excursion interval in which the marker spent 95% of the time spanned over 26 mm, while after the ultracyclic component was subtracted, the 95%-excursion window was reduced to 19 mm. Similarly, for the data set of Fig. 6, the 95%-excursion window was reduced from 23 mm in the original data to 16 mm in the extracted cyclic component of the motion. The variance of the exhale and inhale positions was reduced after the drift was removed. As the result, after the ultracyclic components were subtracted, in both examples, two distinct peaks appeared in the PDF, which correspond to the exhale (the larger peak) and inhale (smaller, due to higher variation in the exhale position).

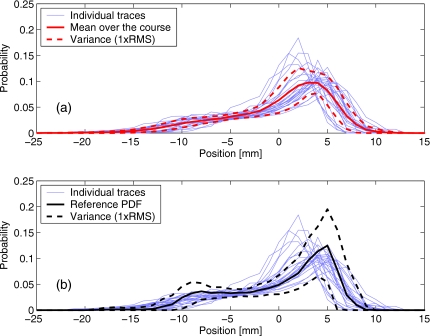
To evaluate the intrafractional variation in the marker motion, the cyclic component of the trace was broken-up into individual respiratory cycles, and the PDFs were constructed for each cycle separately, as well as for the whole trace. The reduction in the intrafractional variability of the PDF for the reference trace is illustrated in Fig. 7, as manifested in the reduced variance bounds. The variance was estimated as the standard deviation of the PDF values from different respiratory cycles, for a given marker position x.

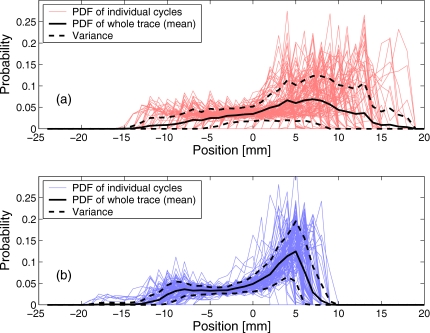
Figure 7.

For the data plotted in Fig. 5d, intrafractional variability of PDF is illustrated for: (a) the original data and (b) the cyclic component of the trace. Thin lines show the PDFs of 94 individual respiratory cycles, thick solid line is the PDF averaged over the entire data set, and dashed lines show the variance (1×RMS). The mean PDFs (solid lines) are the same as in Fig. 5d

The marker data from multiple treatment fractions for the selected patient were used to evaluate the applicability of the PDF model for the robust optimization. The distribution of the ultracyclic component from 25 fractions of gated IMRT treatments is shown in Fig. 8. While drift of as much as 15 mm away from the starting position of the marker was detected during one fraction, its excursion and predominant direction changed from day to day. The approximately Gaussian shape of the drift distribution [Fig. 8b] can be interpreted as an indication of a certain degree of randomness in the drift. The positive bias of 1.31 mm in the fit curve implies that the marker drift “upwards” (presumably, reflecting the tumor drift in the cranial direction) was somewhat more prevalent for this particular patient.

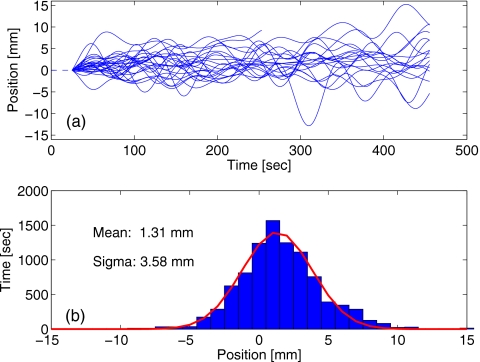
Figure 8.

(a) Ultracyclic motion components extracted from traces recorded during 25 fractions of a treatment course (for the same patient). The start position is set to 0 for all data sets. The distribution of drift positions is shown in (b), fitted to the normal distribution.

Figure 9 shows 25 individual PDFs of the cyclic components from different fractions, overlaid with (a) the mean PDF and variance over the whole treatment course, and (b) the mean and variance of the reference trace (the data set of Fig. 5). Of note is that the intrafractional variance estimated for the reference trace exceeds the variance between PDFs from multiple fractions for the same patient. A likely explanation is that the intrafractional variation reflects a variety of respiratory wave forms (varying by the amplitude, expiratory duration, etc.) that are customary to the given patient, while the interfractional variability is mostly due to the variation in the likelihood of these different wave forms being realized within the time interval of the recording. Figure 9b shows that while the bounds $p-\underset{̱}{p}$ and $p+\overline{p}$ do not contain some of the fraction PDF completely, they represent a reasonable guess for the probabilistic description of motion that was recorded throughout the treatment course.

Figure 9.

Interfractional variation of PDF is illustrated for the patient who received 25 fractions of respiratory-gated treatment: (a) the PDFs of individual fractions are shown as thin lines, as well as the mean PDF (solid line) and its variance (dashed line) over the course. For comparison, plot (b) shows the same data overlaid with the mean of the reference trace and its intrafractional variance [same as in Fig. 7b].

Test of trailing strategy for IMRT delivery

The framework for robust optimization of the test plan was built based on the intrafractional variability within the reference trace. The mean PDF of the cyclic component [Fig. 7b] was used as the nominal PDF, and its variance, σ(x), was used to define the variability boundaries $p-\underset{̱}{p}$, $p+\overline{p}$ with $\underset{̱}{p}=\overline{p}=\sigma \left(x\right)$. The negative parts of $\left(p-\underset{̱}{p}\right)$ were reset to 0.

Three types of test plans were generated: (A) unoptimized IMRT fields that consisted of rectangular areas of level intensity, adding up to deliver a uniform photon fluence within a square field of 10×10 cm² (as in Fig. 4); (B) same with planning margins of 10 mm added to the edges of the field in the direction of motion (fields expanded to 12×10 cm²); and (C) fields optimized with the robust approach.

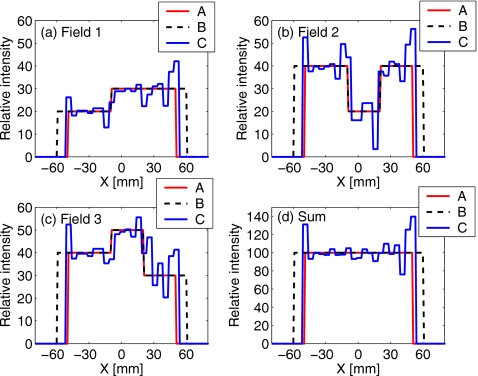
Figure 10 shows sample intensity profiles for different types of plans, for the individual fields and for their sum. The “horns” of excess intensity at the edges of the field aim to compensate for the dose washout due to motion. In the first approximation, the profile from a motion-compensated plan is the deconvolution of the standard-planned profile (here, uniform for the sum of three fields) with the asymmetric average motion PDF. Such controlled, iterative “deconvolution” in the process of robust optimization is the source of asymmetric oscillations (known as ringing, or Gibbs effect) in the profiles. (This phenomenon has been previously illustrated in articles that described motion-compensated planning.^{38, 44})

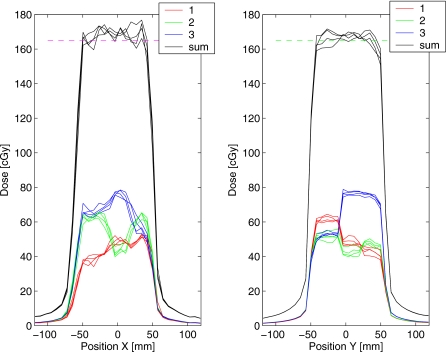
Figure 10.

Intensity profiles through the isocenter, along the direction of target motion, from (a)–(c) three test fields, and (d) their sum. Profiles are shown for three types of plans described in Sec. 2: unoptimized (A) without margins, (B) with a 1-cm margin added in the direction of motion, and (C) the robust-optimized plan.

The intensity maps from each field within a plan were sequenced for delivery on a MLC-equipped clinical linear accelerator. Table 1 summarizes some of the parameters of the test MLC sequences. The sequence parameters of fields in unoptimized plans with and without margins were identical, since the only difference was the increase in the treatment field size. Combined, the three fields of each plan would deliver (to a static target) a roughly uniform photon fluence of 200 MU throughout a rectangular area.

Table 1.

Parameters of the MLC sequences for the test fields. Bixel designates a 5×5 mm² element of the MLC field.

Field label	Dose distribution	No. of segments	Total MU per field	Average MU per bixel	Maximum MU per bixel
Unoptimized 1	Fig. 11a	4	100	60	100
Unoptimized 2	Fig. 11b	6	120	66	100
Unoptimized 3	Fig. 11c	4	100	74	100
Robust 1	Fig. 12a	137	294	61	146
Robust 2	Fig. 12b	163	358	68	160
Robust 3	Fig. 12c	133	314	75	136

Sets of three test fields were delivered consecutively to the moving phantom, for each of three types of plans. The delivery was repeated four times (fractions) to approximate (a part of) a fractionated treatment course. The phantom reproduced different motion traces for each fraction of delivery. The 95%-excursion amplitude of the cyclic motion in test traces was between 15 and 19 mm. [The 10-mm margin width for the test plan (B) was chosen based on this information, with the aim to achieve nearly complete coverage of the target excursions.]

For delivery of unoptimized fields, the phantom was set to reproduce the drift wherever it was present in the original marker trace. The delivery of robust fields approximated the trailing strategy: the trace was analyzed off-line to extract the ultracyclic component of motion, using the RM method, and the appropriate corrections were applied. Thus, the phantom reproduced only the cyclic component of the trace during delivery of robust-optimized fields.

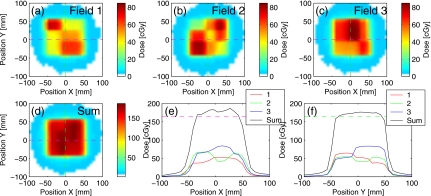
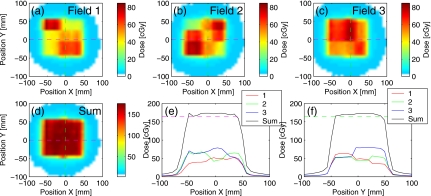
The results of the dose measurements from a single fraction of delivery are shown in Fig. 11 for the unoptimized plan (no margins). The mismatch in the field position due to target drift resulted in visible inhomogeneities in the dose profiles along the direction of motion [Fig. 11e]. In contrast, the delivery of the robust plan with the trailing strategy (Fig. 12) reduced inhomogeneities within the target: the maximum hot spot was below 111% of the prescription, compared to 117% without trailing.

Figure 11.

Results of dose measurement from delivery of the unoptimized test plan to the phantom that moved according to the trace in Fig. 5a. The doses from three fields are shown separately in (a)–(c). The combined dose (d) shows the distribution of inhomogeneities similar to that in Fig. 4f, due to the drift in the target position. Dose profiles through the isocenter are shown for (e) X and (f) Y directions. Both the phantom and MLC leaves moved in the X direction. The resolution of the dose measurement is 7.62 mm.

Figure 12.

Similar to Fig. 11, for the test plan optimized using the robust method and delivered to a moving target using the trailing strategy: the drift was corrected by adjusting the phantom position.

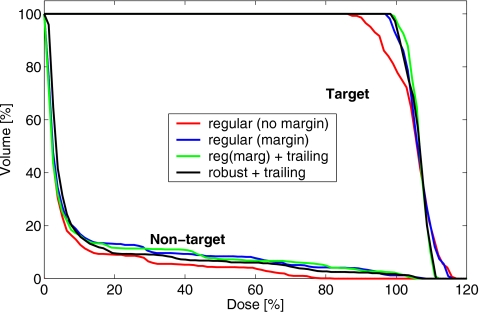
Dose-volume histograms (DVHs) were calculated for the delivered test plans. For the DVH calculation, the target was defined as the rectangular area covered by the set of 12×12 ionization chambers (approximately 91×91 mm²) in the middle of the array used for dose measurements. The rest of the active area of the chamber array was labeled as “nontarget.”

Figure 13 shows DVHs from the sum of four delivery fractions, for a selection of courses delivered with and without the trailing correction. The unoptimized plan with no margins delivered the least dose to the nontarget area, however, the target coverage was severely compromised due to motion, with the cold spots of below 85% of the planned dose. While the margin expansion compensated for the dose washout close to the target boundaries in the direction of motion, the hot and cold spots that arose inside the target volume due to the field mismatch were of comparable magnitude regardless of the use of the margin.

Figure 13.

DVHs from the measurement of the dose delivered in four fractions with the regular plans without and with margins, and the robust plan. The margin plan was delivered without and with the trailing correction for the target drift. The robust plan was delivered with the trailing correction.

These internal inhomogeneities were minimized, and the target coverage improved with the trailing delivery strategy, which corrected for the drift in the mean target position. For the margin plan, trailing delivery reduced the nontarget integral dose by 2%, compared to the standard delivery. With trailing, the target coverage in the robust plan, was comparable to that in the plan that used 1-cm margin expansion, and the integral nontarget dose was reduced by 5% with the robust plan. The improvement was mostly in the penumbra region in the direction of motion, while the low-dose part of the nontarget DVH (which represents the contribution from interleave leakage) is higher for the robust plan, due to the increased number of monitor units.

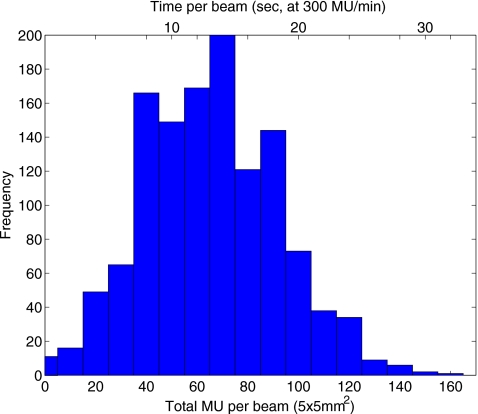
For the robust plan, the sum of distributions delivered in four fractions showed better uniformity, than any of the individual fraction doses. This is because the single-fraction inhomogeneity patterns in the robust plan are designed to mutually cancel out as the density and uniformity of PDF sampling increase with each delivery in a fractionated course. The interplay of the motion of the MLC leaves and the target resulted in deviations of up to 6% of the prescribed dose, as shown for the robust plan in Fig. 14. The amplitude of the interplay effect is affected by the rate of dose delivery, which determines the exposure time for individual pencil beams. Figure 15 shows the distribution of the number of monitor units per 5×5 mm² element (bixel) in the robust-optimized IMRT fields, and the corresponding “beam-on” time for the rate of delivery of 300 MU∕min, with the mean at 13 s. (The beam-on time is inversely proportional to the rate of the dose delivery.)

Figure 14.

The dose profiles through the isocenter, show inhomogeneities produced by the interplay of the MLC sequence with the target motion, during four fractions of delivery of the robust test plan from Fig. 12. The profiles are shown for each of the three fields, as well as for the fraction total.

Figure 15.

Distribution of the bixels, 5×5 mm² beam elements of the MLC field, by the number of delivered monitor units. The scale on top of the plot shows the corresponding beam-on times for the delivery rate of 300 MU∕min.

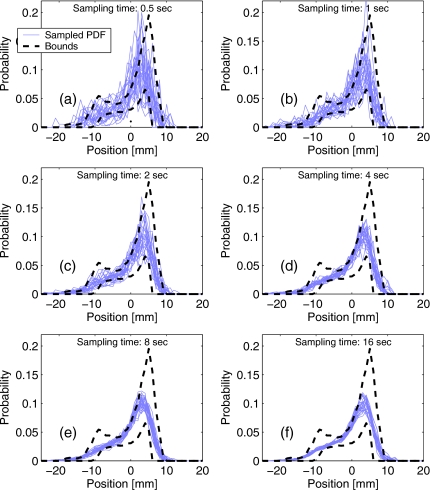
The relatively small effect of the interplay is explained by the high sampling of the motion PDF by each of the bixels. Figure 16 shows the result of the simulation using motion traces recorded during 25 fractions of a gated IMRT course. Random segments of a certain length, corresponding to a bixel “on” time, were sampled, one from each trace, and combined to approximate the total PDF of target position sampled by that bixel throughout the whole course. The results show that for 25 different random seeds, the effective sampled PDFs were, with a high probability, within the expected variation bounds for the beam-on time as low as 4 s (of the order of the typical respiratory cycle).

Figure 16.

Simulation of the effective PDF sampling by individual bixels, with beam-on times between 0.5 and 16 s per fraction. Motion traces from 25 fractions were sampled randomly: thin lines show possible PDF as would be sampled by individual bixels (using different seeds for random number generator). Thick dashed lines designate the PDF variance bounds, designed based on the reference trace [see Fig. 7b]. For longer beam-on times, the sampled PDF approaches the mean PDF overall fractions [Fig. 9a].

DISCUSSION

The purpose of this study was to evaluate the utility of combining the trailing strategy, that corrected for the slow systematic changes in the average target position (ultracyclic motion), with the robust motion-adaptive treatment planning method, that aimed to improve the dose coverage by including the variable target motion into consideration.

Arguably, there is more than one possible answer to the question of what constitutes the “average position” of the target, or how ultracyclic motion should be defined. However, for the purposes of the trailing strategy for treatment delivery, the exact definition is not of high relevance as long as the position correction helps reduce the variability of the cyclic component of the motion. The RM method is one possible way to achieve that goal. It is a relatively simple and computationally light method to detect slow-scale trends in the target during the data acquisition. By reducing intrafractional variability of the PDF of the residual cyclic motion, trailing enhances the relevance and applicability of probabilistic motion-adaptive planning methods.

Motion-robust optimization produces a plan that, when delivered to a moving target, results in a clinically acceptable dose distribution, provided the variation in the motion does not grossly exceed the expectation of the model. Delivery of such robust plans does not require any modification to the MLC-based IMRT procedure. In addition, the technique is largely independent of the temporal effects of motion, such as the variation in the respiratory frequency, or phase shift between the external (marker) and internal motion. However, the trailing approach, and robust treatment planning require that certain generalizations be made about the character of motion: namely, an the expected probabilistic position description based on reasonably long-term observation of the target, as well as statistically expected deviation from that average. The potential advantage that robust optimization can provide increases as the variability bounds in the model are decreased, which puts the emphasis on the development of techniques to extract reliable motion models from the limited body of data in the most optimal way.

In radiotherapy research, the average tumor trajectory⁵⁴ and other similar concepts have been widely used to describe internal motion. Previously, the variability and reproducibility of respiratory patterns has been studied extensively by investigators in respiration physiology. It has been stated that variations in the respiratory patterns are governed by psychological and physiological impulses, thus they are generally not random,^{46, 49} and, indeed, often periodic (on a time scale orders of magnitude larger than that of respiration).⁵³ While variability in the tidal volume (respiration amplitude) is commonly observed, it has been noted that individuals do tend to follow rather particular, customary respiratory patterns selected from among the seemingly “infinite number of possible combinations of ventilatory variables and airflow profile.”⁴⁹ Therefore, certain characteristics of breathing, such as tidal volume variation, inspiratory, and expiratory duration are in fact rather stable within individual subjects. Classification of subjects into relatively stable categories, or “ventilatory personalities” according to the specifics of their breathing patterns has been proposed (e.g., by Dejours et al., as cited by Benchetrit⁴⁹).

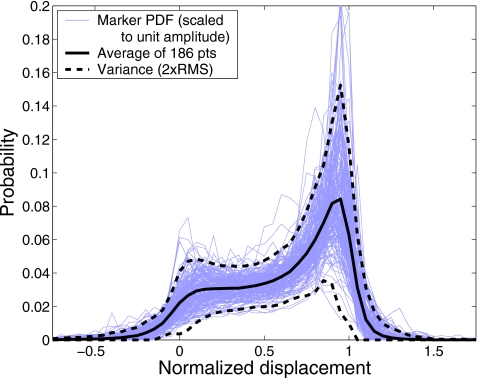
The data collected at our institution indicate that intrafractional variability of PDFs is typically larger than either interfraction or interobserver variability, as a wide variety of customary waveforms are typically realized within each trace. In multiple instances of observation (e.g., different days throughout the treatment course) these same wave forms are being repeated, although the rate of their occurrence may vary. This limits the observed variability between PDFs of data sets that cover dozens of respiratory cycles over time periods of several minutes. We find that the external marker position PDF and its variability bounds, constructed based on a single trace (e.g., pretreatment 4D-CT), may serve as a reliable estimate of the expected variability in the PDF realized during a fractionated treatment. The simulation results (Fig. 16) based on the data available from multiple treatment fractions speak in favor of the validity of this approach. Thus, for this test, we employed a variability model for predicting the patient respiratory behavior during treatment was based on a single data set. Further, our data from 186 observers showed a remarkable similarity of PDFs (see Fig. 17), when the variation in the motion amplitude was not considered (i.e., if the marker motion data are normalized to the mean amplitude of individual traces). In light of this, it appears possible to use a shared motion variability model for certain classes of patients, provided the necessary adjustments to the amplitude of motion are made depending on the observer and disease site.

Figure 17.

Probability distribution functions from traces collected during 4D-CT acquisition from 186 patients are shown as thin lines. The traces were scaled to unit amplitude (with 0 displacement corresponding to mean inhalation and 1 to mean exhalation position), after the ultracyclic component of motion was subtracted. The mean PDF is shown as the thick solid line and the variance bounds as dashed lines.

If the internal motion cannot be monitored continuously, maintaining the correlation of the external marker to the internal motion is of high importance. It has been demonstrated that reliable models of correspondence between external and internal motion can be built based on series of x-ray images in the beginning of the treatment.¹⁷

Since the trailing delivery follows the slow-changing component of the motion, it is less constrained by the technical limitations, e.g., the maximum speed of the compensating treatment couch motion during correction (named as an obstacle for fast tracking by D’Souza et al.²⁴). While real-time couch or MLC corrections are not yet available on clinical machines, many commercial linacs would allow for the couch position to be corrected during a short pause, either between fields, or if a field delivery had been interrupted (e.g., if the detected systematic shift exceeds a certain interlock-threshold value). In this discretized “shift-and-shoot” version, trailing strategy can be implemented with only minimal modifications to software and equipment already in place for respiratory-gated treatments.

A combination of trailing correction with gated radiotherapy delivery can help deal with the issues of the trigger delay, phase shift and poor predictability of the breathing motion that affect the precision of targeting^{55, 48, 56} during treatment. Potentially, it may allow one to better describe the dose deposited within the gating window, reduce the associated errors, and increase the duty cycle of gating, while weakening (or eliminating) the reliance on breath coaching. Additionally, when applied to standard IMRT treatments, robust planning and trailing will improve dose conformity in cases with small amplitude of motion (e.g., less than 10 mm), which is often deemed too small to warrant a gated treatment. The approach may also be useful in addressing the issues related to minor inter-fractional changes in the patient anatomy,⁵⁷ which also affect the precision of targeting in image-guided radiotherapy.

The time delay in the detection of the ultracyclic drift with the use of the RM method described here is a notable limitation of the correcting strategy. However, as the results show, the effect is limited to a mean systematic shift of less than 0.5 mm and standard deviation of below 1.5 mm. This roughly translates into a 2×σ confidence interval of 6 mm, which is comparable to the typical size of the gating window in respiratory-correlated IMRT delivery. The distribution of delayed corrections may be modeled as a Gaussian [Figs. 5b, 6b] and accounted for within the robust uncertainty framework, or treated otherwise similarly to a random setup error.

The precision of detection of the ultracyclic motion component can be improved, and the intrinsic delay can be reduced with the use of predictive methods. Prediction algorithms have been proposed that rely on, e.g., the use of neural networks,⁵⁸ wavelet-based autoregression.⁵⁹ Recently, it has been documented that a method using ellipse fitting⁶⁰ with certain parameters reduced the delay in the detection of the target drift, compared to the moving average filter (which is equivalent to the unweighted RM method, Eq. 4 of this article).

The proposed trailing strategy is not intended to replace the common-sense approach to treatment delivery. We believe that, not unlike in, e.g., gated IMRT, in trailing delivery, the target monitoring should be performed continuously by a trained operator, and decisions on how to deal with sudden changes in the respiratory pattern should be made on a case-by-case basis. Generally, if a sudden and significant shift occurs, it would not be unreasonable to pause the delivery and investigate the source of that shift. Certain perturbations may be temporary (e.g., patient coughing) in which case it might be possible to resume delivery after the breathing pattern stabilizes (and, presumably, returns to the preperturbation state). In other cases, in which sudden shifts in the breathing base line occur, it may be necessary to reevaluate the relationship between the external marker and target position, and, possibly, repeat the setup.

CONCLUSIONS

The trailing strategy for radiotherapy delivery to moving targets, combines robust probabilistic treatment planning with dynamic tracking of relatively slow aperiodic trends in the target motion. The mechanical limitations of implementing tumor trailing are less rigorous than those of real-time tracking, and the same technology could be used for both. A discretized shift-and-shoot version of trailing delivery can be implemented with only minimal modifications to the equipment and software in place for respiratory-gated treatments. In the presence of systematic changes in the average position of the target (ultracyclic motion), trailing improves matching of IMRT fields delivered consecutively, where standard approaches using planning margins fail. By increasing the reproducibility of the probability distribution of intrafractional motion, trailing increases the relevance of robust probabilistic treatment planning, and its reliability in managing the effect of cyclic motion on the dose delivered distribution. By better accounting for residual motion during therapy delivery, robust optimization, in combination with trailing delivery, can improve dose conformality in treatments with and without the use of respiratory gating. In gated treatments, additionally, the strategy may allow for an increase in the duty cycle.