Geometric calibration for a dual tube∕detector micro-CT system

Abstract

The authors describe a dual tube∕detector micro-computed tomography (micro-CT) system that has the potential to improve temporal resolution and material contrast in small animal imaging studies. To realize this potential, it is necessary to precisely calibrate the geometry of a dual micro-CT system to allow the combination of projection data acquired with each individual tube∕detector in a single reconstructed image. The authors present a geometric calibration technique that uses multiple projection images acquired with the two imaging chains while rotating a phantom containing a vertical array of regularly spaced metallic beads. The individual geometries of the imaging chains are estimated from the phantom projection images using analytical methods followed by a refinement procedure based on nonlinear optimization. The geometric parameters are used to create the cone beam projection matrices required by the reconstruction process for each imaging chain. Next, a transformation between the two projection matrices is found that allows the combination of projection data in a single reconstructed image. The authors describe this technique, test it with a series of computer simulations, and then apply it to data collected from their dual tube∕detector micro-CT system. The results demonstrate that the proposed technique is accurate, robust, and produces images free of misalignment artifacts.

INTRODUCTION

Micro-computed tomography (micro-CT) is a noninvasive imaging modality used to assess morphology and function in small animals.^{1, 2} Dual tube∕detector micro-CT, in which two imaging chains consisting of an x-ray tube and a detector image the same object in parallel, offers several advantages over more conventional micro-CT. Dual simultaneous imaging can acquire the same amount of images as a conventional micro-CT in half the time, which facilitates functional imaging studies such as in cardiac,^{3, 4} pulmonary,^{5, 6} or perfusion investigations in small animals.⁷ Dual tube∕detector micro-CT also facilitates dual energy imaging, in which two different absorption coefficients at two different energies are recorded for the same location simultaneously, enhancing sensitivity and material differentiation.⁸

To realize these advantages of dual tube∕detector micro-CT imaging, it is necessary to reconstruct the images from the individual systems in one shared geometry. To accomplish this, geometric calibration must be performed, in which a set of parameters describing the geometry of the system is calculated from a set of images acquired of some ideal object. The calibration parameters can then be provided to the CT reconstruction algorithm to map data from the pixels in the detector to voxels in the object.

Several techniques have been proposed over the years for finding these calibration parameters in individual micro-CT systems for various geometries. These techniques have generally fallen into two categories: those based on iterative nonlinear optimization^{9, 10, 11, 12, 13} and those based on the direct solution of geometric equations.^{14, 15, 16, 17, 18} The latter category has become favored in recent years because of superior performance and ease of implementation. Both categories entail the imaging of phantoms containing point-like structures, such as various arrangements of small metal beads, with varying requirements about the a priori knowledge of the phantom and the geometry.

Although similar work has been done with multiple detectors in SPECT and PET,¹² we have not found any prior work on the calibration of dual tube∕detector x-ray micro-CT. Therefore, in the construction of our dual tube∕detector system, it was necessary to develop a new geometric calibration method. In this method we first employ an analytic algorithm to find estimates of the most important calibration parameters and then use nonlinear optimization to find additional parameters and refine the results. Once this is done for both tube∕detector chains, we use the parameters to create the cone beam projection matrices required by the reconstruction process for each imaging chain. We then find a transformation between the two projection matrices to combine the two sets of projection data in a single reconstructed image. In this work we describe this method and test it in computer simulations and then apply it to data collected from our dual tube∕detector system.

MATERIALS AND METHODS

Projection matrices

Our approach is based on the use of projection matrices.^{19, 20, 21, 22} A cone beam projection matrix A has a 4×3 dimension and relates the mapping of a point in three-dimensions (3D) (x,y,z) to its projection (u,v) on a two-dimensional detector in homogeneous coordinates

$$\left[\begin{array}{c}uw\\ vw\\ w\end{array}\right]=\mathbf{A}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right],$$

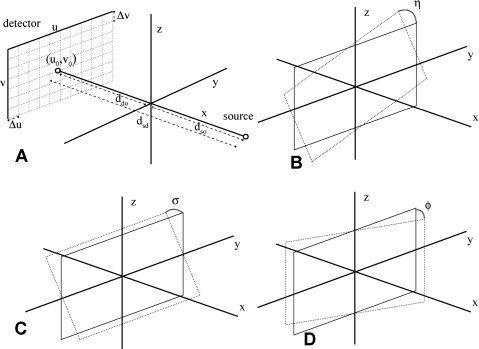
where w is an arbitrary scale factor. Each projection matrix is constructed from seven geometric parameters that define the cone beam geometry of a single imaging chain made of one x-ray source and one detector (see Fig. 1). These are d_so, d_do, u₀, v₀, η, σ, and φ, where d_so and d_do are the source-to-origin and detector-to-origin distances (for simplicity, we will often use the source-to-detector distance d_sd=d_so+d_do instead of d_do); (u₀,v₀) is the pixel location where the central ray intersects the detector plane [see Fig. 1a]; and η, σ, and φ are the detector rotation angles around each of the x, y, and z axes, respectively [see Figs. 1b, 1c, 1d]. Additionally, the horizontal pixel distance Δu and vertical pixel distance Δv of the detector must be known in advance.

Figure 1.

The geometry of an x-ray CT system, defined by (a) d_so, d_do, u₀, v₀, (b) η, (c) σ, and (d) φ.

The rotation of the detector around the three axes is described by the three rotation matrices R_η, R_σ, and R_ϕ,

$${\mathbf{R}}_{\eta }=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \text{cos}\eta & -\text{sin}\eta & 0\\ 0& \text{sin}\eta & \text{cos}\eta & 0\\ 0& 0& 0& 1\end{array}\right],$$

$${\mathbf{R}}_{\sigma }=\left[\begin{array}{cccc}\text{cos}\sigma & 0& \text{sin}\sigma & 0\\ 0& 1& 0& 0\\ -\text{sin}\sigma & 0& \text{cos}\sigma & 0\\ 0& 0& 0& 1\end{array}\right],$$

$${\mathbf{R}}_{\varphi }=\left[\begin{array}{cccc}\text{cos}\varphi & -\text{sin}\varphi & 0& 0\\ \text{sin}\varphi & \text{cos}\varphi & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].$$

With these matrices we construct the vectors u and v which describe the displacement of a pixel from the detector origin, and the detector normal vector n,

$$\mathbf{u}=\Delta u{\mathbf{R}}_{\eta }^{-1}{\mathbf{R}}_{\sigma }^{-1}{\mathbf{R}}_{\varphi }^{-1}\left[\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right],$$

$$\mathbf{v}=\Delta v{\mathbf{R}}_{\eta }^{-1}{\mathbf{R}}_{\sigma }^{-1}{\mathbf{R}}_{\varphi }^{-1}\left[\begin{array}{c}0\\ 0\\ 1\\ 1\end{array}\right],$$

$$\mathbf{n}=\mathbf{v}\times \mathbf{u}.$$

We can now construct the projection matrix A,

$$\mathbf{A}=\left[\begin{array}{cccc}0& 1∕\Delta u& 0& 0\\ 0& 0& 1∕\Delta v& 0\\ 0& 0& 0& 1\end{array}\right]{\mathbf{R}}_{\varphi }{\mathbf{R}}_{\sigma }{\mathbf{R}}_{\eta }\left[\begin{array}{cccc}1& 0& 0& u_0{\mathbf{u}}_1+v_0{\mathbf{v}}_1-d_{\text{sd}}\\ 0& 1& 0& u_0{\mathbf{u}}_2+v_0{\mathbf{v}}_2\\ 0& 0& 1& u_0{\mathbf{u}}_3+v_0{\mathbf{v}}_3\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}{\mathbf{n}}_1{d}_{\text{sd}}& 0& 0& {\mathbf{n}}_1{d}_{\text{sd}}{d}_{\text{so}}\\ 0& {\mathbf{n}}_1{d}_{\text{sd}}& 0& 0\\ 0& 0& {\mathbf{n}}_1{d}_{\text{sd}}& 0\\ {\mathbf{n}}_1& {\mathbf{n}}_2& {\mathbf{n}}_3& {\mathbf{n}}_1{d}_{\text{so}}\end{array}\right].$$ (1)

To describe the planar circular trajectory of the source and detector by angle θ around the rotation axis, in this case z axis, we multiply A, given by Eq. 1, by a rotation matrix to obtain the projection matrix for each sampling angle A_θ,

$${\mathbf{A}}_{\theta }=\mathbf{A}\left[\begin{array}{cccc}\text{cos}\theta & -\text{sin}\theta & 0& 0\\ \text{sin}\theta & \text{cos}\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].$$

The tomographic reconstruction algorithm uses the A_θ matrices to perform the 3D backprojection process. We note that with our dual tube∕detector micro-CT system, the scanned object is rotating and the tubes∕detectors are stationary. Nevertheless, the two geometries with rotating tube∕detector or rotating object are equivalent. Therefore, to calibrate a dual tube∕detector system, it is necessary first to find the parameters describing the cone beam geometry for each individual tube∕detector and to construct the projection matrices [see Eq. 1]. Next, we find a transformation that relates these two projection matrices in one shared geometry.

Geometric calibration for a single imaging chain

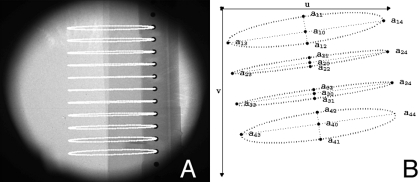
To find d_so, d_do, u₀, v₀, η, σ, and φ for a single imaging chain, we have taken a two-step approach. First, we obtain initial estimates following the method described by Yang et al.,¹⁸ and then we refine the values with a nonlinear optimization procedure. We use a phantom consisting of 20 metallic beads with a 2 mm diameter inserted in an acrylic rod and arranged along a vertical axis with distance l=5 mm between each adjacent pair of beads. The phantom is scanned through one complete rotation [see Fig. 2a] of 360° using both imaging chains and projection images acquired every 1°. Following scanning, the phantom’s projection images are processed in MATLAB (The MathWorks, Inc., Natick, MA) to compute the trajectories of the center of mass of each imaged bead. Finding the beads’ centers of mass is a semiautomatic process that requires the user to select rectangular regions of interest (ROIs) around each bead only in the first projection image. In each ROI, the bead is segmented using adaptive local thresholding. An initial threshold is chosen halfway between the maximum and minimum brightness values, and this threshold is iteratively improved. At each iteration, the threshold divides the pixels inside each ROI into two sets corresponding to the bead and background. The bead set is assigned the connected component containing the central pixel. The background set is assigned the corner pixels, and the threshold is recalculated to be halfway between the averages of these two sets. The iterations stop when the threshold no longer changes. After segmentation, the center of mass (u_c,v_c) for each bead is found using the bead pixel values of the segmented bead image I(u,v),

$$u_c=\frac{{\Sigma }_{\text{bead}}I\left(u,v\right)\cdot u}{{\Sigma }_{\text{bead}}I\left(u,v\right)},$$

$$v_c=\frac{{\Sigma }_{\text{bead}}I\left(u,v\right)\cdot v}{{\Sigma }_{\text{bead}}I\left(u,v\right)}.$$

Figure 2.

(a) An x-ray image of the calibration phantom, with the centers of the projections of the beads overlaid in white, and (b) the ellipses that are fit to the centers.

The radius of the bead projection is found by calculating the average distance from the perimeter to the center

$$r=\frac{{\Sigma }_{\text{perimeter}}\sqrt{{\left(u-u_c\right)}^2+{\left(v-v_c\right)}^2}}{{\Sigma }_{\text{perimeter}}1}.$$ (2)

Unlike in the first projection image, the ROIs in subsequent projections are constructed automatically by predicting the location of the bead center using a linear fit of the most recent locations and setting a square around the predicted location with a side length equal to twice the radius given by Eq. 2.

For each bead i, an ellipse is fitted to the set of all centers of mass over all projection images. Point p in ellipse i is denoted a_ip=(u_ip,v_ip), and the distance between pointsa_ip and a_jp is denoted $\overline{a_{ip}{a}_{jp}}$. The center, a_i0=(u_i0,v_i0), and four principal corners, a_i1, a_i2, a_i3, and a_i4, are recorded for each ellipse [see Fig. 2b]. The centers of the ellipses, a_i0, are computed as the mean of all points, a_ip, on the ellipse. The major axis line is obtained by linear regression on all the points, and the minor axis line is the line perpendicular to the major axis that passes through the center. The angle of the major axis is obtained as the inverse tangent of the slope. All points a_ip are then projected onto the ellipse axes, and the corners are the extreme points of the projections. With these ellipse parameters we now calculate the calibration parameters, using geometric relations derived by Yang et al.¹⁸

Calculation ofd_sd and v₀

For each bead i, we construct

$$x_i=\frac{v_{i1}-v_{i2}}{\overline{a_{i3}{a}_{i4}}},$$

$$y_i=\frac{v_{i1}+v_{i2}}{2}.$$

The x_i and y_i are related by the linear function

$$y_i=v_0+d_{\text{sd}}\Delta v{x}_i.$$

We find v₀ and d_sd by linear regression over all i.

Calculation ofη and u₀

For each bead i, u_i0, and v_i0 are related by the linear function

$$u_{i0}=a+b{v}_{i0}.$$

We find a and b by linear regression over all i, and then calculate

$$u_0=a+b{v}_0,$$

$$\eta =\text{arctan}b.$$

Calculation ofd_so

For each pair of beads i and j,

$$d_{\text{so}}=\frac{l}{\overline{a_{i0}{a}_{j0}}\Delta v}{d}_{\text{sd}}.$$

We average d_so for each adjacent pair i and j. This formula is simpler than the one described by Yang et al.,¹⁸ since we assume that our phantom is placed parallel to the z axis. While this assumption may not always be valid, we note that the geometric parameters obtained by this analytic approach are just initial estimates that are further refined through an optimization procedure.

Nonlinear optimization

The method described by Yang et al.¹⁸ does not determine the out-of-plane detector rotations σ and φ, since it is claimed that careful mechanical placement can reduce these parameters to less than 5°, below which these values have little impact on reconstruction. However, in an imaging system with components that are frequently moved, as in our case, we cannot guarantee that the detectors will always be so well aligned. Furthermore, in a dual tube∕detector system, the small changes caused by erroneous values for σ and φ will be amplified, since overlapping systems with slight independent misalignments will produce pronounced double contours in the reconstruction. These rotations may be present in our system and should be addressed, so we use a nonlinear optimization program to move from an initial estimate of [d_sdd_sou₀v₀ η 0 0] to [d_sdd_sou₀v₀ η σ φ].

For the objective function, we must first construct the projection lines from the x-ray source to the beads’ projection centers of mass using the initial estimates of the geometric parameters. These projection lines are constructed for all beads in all projections. For each bead the minimum pairwise distance between all its associated projection lines is computed. The objective function returns a vector with an entry for each bead representing the sum of the minimum pairwise distances between projection lines.

We pass this objective function to a nonlinear least-squares minimization function which successively recomputes selected parameters in order to minimize the distances between projection lines. We run the program in two steps. First, we allow σ and φ to vary while holding the other parameters fixed since these parameters have no values and would distort the other parameters. Next, we allow all parameters d_sd, d_so, u₀, v₀, η, σ, and φ to vary together. This technique estimates σ and φ accurately and refines the estimates of the other parameters.

Geometric calibration for a dual tube∕detector system

After computing the geometric parameters for each individual imaging chain, we can construct their respective projection matrices A₁ and A₂ using Eq. 1. However, these matrices describe projection in two different systems of reference. We need a transformation matrix T that will allow us to transform projection matrix A₂ into ${\mathbf{A}}_2^{\prime }={\mathbf{A}}_2\mathbf{T}$ in the coordinate system of A₁.

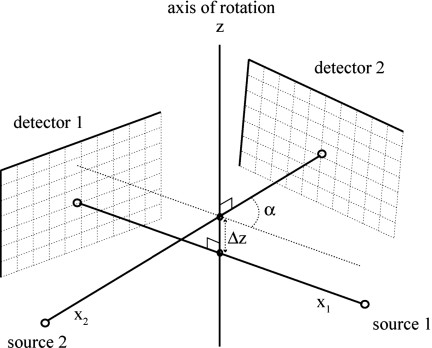
Since both systems image the same rotating object, they must share the same axis of rotation, i.e., the z axis. Consequently, the transform between the two systems of coordinates can consist only of rotation α around the z axis and translation Δz along the z axis and thus the transformation matrix T is given by

$$\mathbf{T}=\left[\begin{array}{cccc}\text{cos}\alpha & -\text{sin}\alpha & 0& 0\\ \text{sin}\alpha & \text{cos}\alpha & 0& 0\\ 0& 0& 1& \Delta z\\ 0& 0& 0& 1\end{array}\right].$$

Therefore, once we calibrate the individual systems, we need an additional step to find Δz and α to calibrate the entire dual system (see Fig. 3).

Figure 3.

The geometry of a dual micro-CT system, defined by Δz and α in addition to the parameters of the individual systems.

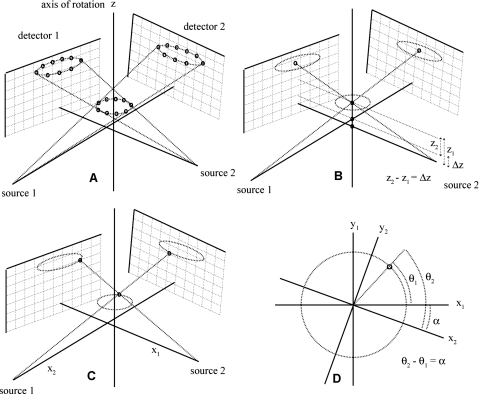
We first compute Δz, using the sets of projections of the same calibration phantom described previously which were acquired with both imaging chains simultaneously. The movement of each bead of the phantom is described by rotation around the z axis, therefore we expect the z coordinate to remain constant at each rotation step, and a single z value for each bead can be found in each system of geometry [see Fig. 4a]. The same beads should be matched in the two sets of projection images from the two imaging chains. Knowing the system parameters allows us to write the expressions of vectors s for the x-ray source and p for a detector point (u,v) in the object system of reference

$$\mathbf{s}=\left[\begin{array}{c}-d_{\text{so}}\\ 0\\ 0\\ 1\end{array}\right],$$ (3)

$$\mathbf{p}=\left[\begin{array}{c}{\mathbf{p}}_1\\ {\mathbf{p}}_2\\ {\mathbf{p}}_3\\ 1\end{array}\right]=\left[\begin{array}{c}{d}_{\text{do}}\\ 0\\ 0\\ 1\end{array}\right]+\Delta u\left(u-u_0\right){\mathbf{R}}_{\eta }^{-1}{\mathbf{R}}_{\sigma }^{-1}{\mathbf{R}}_{\varphi }^{-1}\left[\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right]+\Delta v\left(v-v_0\right){\mathbf{R}}_{\eta }^{-1}{\mathbf{R}}_{\sigma }^{-1}{\mathbf{R}}_{\varphi }^{-1}\left[\begin{array}{c}0\\ 0\\ 1\\ 1\end{array}\right].$$

In a rotating object geometry as in our dual micro-CT system, the point at the center of the rotation of a bead should project to the center of the ellipse trajectory that we found in the individual system calibration, and therefore we set (u,v) in Eq. 3 to be equal to (u_i0,v_i0) for ellipse i [see Fig. 4b]. The line from the x-ray source s to the pixel p is constructed and its intersection with the z axis is given by

$$\left[\begin{array}{c}-d_{\text{so}}\\ 0\\ 0\\ 1\end{array}\right]+k\left(\left[\begin{array}{c}{\mathbf{p}}_1\\ {\mathbf{p}}_2\\ {\mathbf{p}}_3\\ 1\end{array}\right]-\left[\begin{array}{c}-d_{\text{so}}\\ 0\\ 0\\ 1\end{array}\right]\right)=\left[\begin{array}{c}0\\ 0\\ z\\ 1\end{array}\right],$$

$$k=\frac{d_{\text{so}}}{{\mathbf{p}}_1+d_{\text{so}}},$$

$$z={\mathbf{p}}_{3}k,$$

where k is the parameter describing the location of a point along the line. This gives us the z value for each bead in each geometry. The vertical displacement Δz between the two systems is the difference between the z coordinates for the same bead in the two different systems. We compute this value for each bead i and report the average value as Δz [see Fig. 4b].

Figure 4.

(a) The projection of beads onto detectors in the dual system calibration technique, (b) the method for finding Δz using the line segments from the x-ray sources through the axis of rotation to the centers of the ellipses, (c) the lines from the x-ray sources through a bead to the ellipses, and (d) the method for finding α using the different x and y values found from the lines through the same bead.

Following the computation of the z coordinate for each bead, we proceed to determine the x and y coordinates at each rotation step by constructing the line from s to p as described before, where the pixel location (u,v) is now the center of the projection of the bead [see Fig. 4c]. The x and y coordinates for each bead at each rotation step are computed

$$k=\frac{z}{{\mathbf{p}}_3},$$

$$x=k\left({\mathbf{p}}_1+d_{\text{so}}\right)-d_{\text{so}},$$

$$y=k{\mathbf{p}}_2.$$

We can now compute the angle α around the z axis between the two imaging chains. For this purpose, we first find the angle of rotation θ of each (x,y) from some arbitrary starting point. Since tan θ=(y∕x), we find θ=arctan(y∕x). There are two values of θ, i.e., θ₁ and θ₂, corresponding to each imaging chain [see Fig. 4d]. The rotation angle α is computed as α=θ₂−θ₁. We perform this calculation for each bead in each simultaneous projection and report the average value as α [see Fig. 4d].

Finally, we refine these estimates with the same nonlinear optimization program used for the individual calibrations, by constructing the transformed projection lines from the different detectors through the same beads and minimizing the pair-wise distances between the lines.

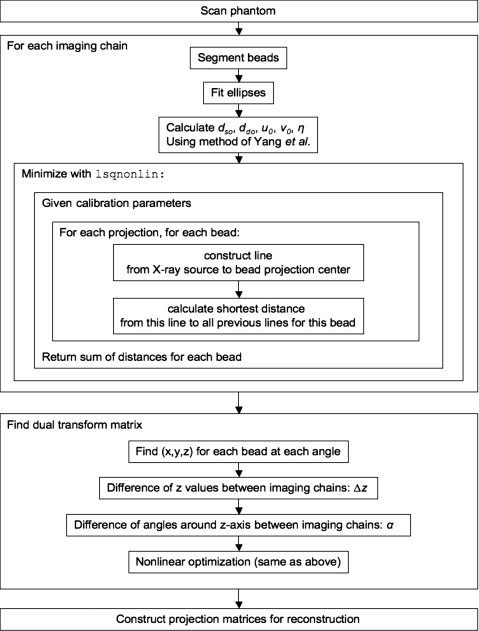
A flowchart of the complete calibration process is shown in Fig. 5.

Figure 5.

A flowchart of the complete calibration process.

Implementation

The above equations are implemented in MATLAB (Version 7.0). The optimization function used is lsqnonlin, part of the MATLAB Optimization Toolbox, which uses preconditioned conjugate gradients constrained by a subspace trust region. The ray-tracing programs called in the optimization process were written in C to reduce computation time.

For our in-house developed dual tube∕detector system (see Fig. 6), we use two Varian A197 x-ray tubes with dual focal spots fs=0.6∕1.0 mm. The tubes are designed for angiographic studies with high instantaneous flux and total heat capacity. Two high frequency x-ray generators (EPS 45-80, EMD Technologies, Quebec, Canada) are used to control the x-ray tubes. The system has two identical detectors with a Gd₂O₂S phosphor (XDI-VHR 2 115 mm, Photonic Science, East Sussex, UK) with pixels of 22 μm, 115 mm input taper size, and 4008×2672 image matrix. Both detectors allow on-chip binning of up to 8×8 pixels, and subarea readout to allow high speed readout of more than 10 frames∕s, i.e., a time resolution of 100 ms. Both tubes and detectors are mounted on a table together with the rotation stage. The vertically positioned animal is placed in a cradle that is rotated via an Oriel model 13049 digital stepping motor. The x-ray generators, tubes, detectors and the rotation are controlled by a sequencer application written in LABVIEW (National Instruments, Austin, TX) that also allows for in vivo studies, the flexible integration of cardiac and respiratory physiology with the imaging sequence.²³ Images of the rotating object are acquired with a step-and-shoot acquisition scheme.

Figure 6.

Our in-house implemented dual tube∕detector micro-CT system.

For geometric calibration, the phantom described previously, containing an array of steel beads placed in an acrylic rod, is attached to the imaging cradle and scanned prior to the animal experiments. The projections and the computed projection matrices are used with the COBRA EXXIM software package (EXXIM Computing Corp, Livermore, CA) that implements Feldkamp’s algorithm²⁴ to reconstruct tomographic data as 3D image arrays (512³). The projection matrices computed with our method are written to a geometry file containing one line for each angle, which is read by COBRA.

Experiments

To test our geometric calibration method we used both simulated and experimental data. Using Eq. 1 we simulated the projection operation on the calibration phantom in MATLAB and performed the calibration method. Since our method first involves finding the geometric parameters for each imaging chain, it made sense to compare our results with those from previous articles for single chain micro-CT systems. We used the same parameters as in Yang et al.,¹⁸ with the same number of projections and beads, and the same noise conditions: 48 μm×48 μm pixel pitch, 500 projection images over 360°, eight beads, distance between beads l=2 mm, d_sd=400 mm, d_so=150 mm, u₀=1005, v₀=480, η=−1°, σ=1.2°, and φ=1.5°. We ran ten simulations with Gaussian noise with standard deviation 0.4 pixels added to the simulated bead projection centers.

We then simulated the projection operations with two orthogonal imaging chains as in our dual tube∕detector system in which the parameters for the first chain were the same as before, and the parameters for the second chain were d_sd=420 mm, d_so=160 mm, u₀=900, v₀=500, η=2°, σ=2°, and φ=−2°. The dual parameters were Δz=5 mm for the z-axis displacement and α=90° between the central rays of the two systems. We again performed ten simulations with Gaussian noise with standard deviation 0.4 pixels added to the simulated bead projection centers.

For the validation of our calibration method, experiments involving our dual tube∕detector system were also performed. We performed three sets of scans with the system, with the parameters of 80 kVp, 100 mA, and 10 ms per exposure. The small focal spot of 0.6 mm was used, and we set the sampling distances to approximately d_sd=750 mm and d_so=650 mm to ensure that the penumbral blurring caused by focal spot is less than the detector pixel size of 0.88 mm. In the first scan, we acquired 360 images with each imaging chain over a 360° rotation of the calibration phantom. Next we acquired 372 projections with each imaging chain over a 186° (180°+fan angle of 6°) scan angle of a cylindrical phantom containing water. Finally, we acquired 372 projections over a 186° scan angle of a dead C57BL∕6 mouse.

The images from the first scan were provided as input to the calibration program, and the system parameters were obtained. These parameters were then used to reconstruct the objects in the next two scans. Single detector images were reconstructed using 372 projections acquired with the same imaging chain. For dual tube∕detector reconstructions we used 186 projections acquired with the first imaging chain over 93° and 186 projections over the other 93° acquired with the second imaging chain. All projection images are corrected for distortions by the acquisition software of the detectors. The reconstructed data of the cylinder phantom was used to calculate the modulation transfer function of the individual and dual systems according to the method described in the ASTM.²⁵

RESULTS

The values estimated in the simulation by our calibration program for the geometric parameters of an individual system are shown alongside the values found by Yang et al.¹⁸ in Table 1. Overall the two sets of results compare well and they show similar performance in the noise-affected situation. Unlike Yang’s method, note that our method also gives estimates of two detector rotation angles σ and φ. This is possible due to the refinement part based on optimization.

Table 1.

Calibration results for the single system parameters, compared with results in similar conditions by Yang et al. (Ref. ¹⁸), from ten computer simulations, with Gaussian noise of standard deviation 0.4 pixels added to simulated bead projection centers, 500 images, eight beads.

	True values	Our method	Yang’s method
dsd (mm)	400.00	399.99±0.06	401±1
dso (mm)	150.00	149.62±0.06	150.2±0.5
u0 (pixel)	1005.0	1005.0±0.0	1005.9±0.3
v0 (pixel)	480.00	479.90±0.15	480±1
η (°)	−1.0000	−1.0001±0.0002	−0.99±0.03
σ (°)	1.2000	1.1961±0.0116
φ (°)	1.5000	1.5018±0.0046

Next, the values estimated for the dual tube∕detector system parameters are shown in Table 2. Again, the results provided by the calibration procedure match the known values quite well.

Table 2.

Calibration results for the dual system parameters from ten computer simulations, with Gaussian noise of standard deviation 0.4 pixels added to simulated bead projection centers, 500 images, eight beads.

System 1	True values	Estimates	System 2	True values	Estimates
dsd (mm) dsd (mm)	400.00	399.99±0.06	dsd (mm)	420.00	419.84±0.14
dso (mm)	150.00	149.62±0.06	dso (mm)	160.00	159.96±0.10
u0 (pixel)	1005.0	1005.0±0.0	U0 (pixel)	900.00	899.99±0.01
v0 (pixel)	480.00	479.90±0.15	V0 (pixel)	500.00	500.19±0.18
η (°)	−1.0000	−1.0001±0.0002	η (°)	2.0000	2.0000±0.0002
σ (°)	1.2000	1.1961±0.0116	σ (°)	2.0000	1.9997±0.0065
φ (°)	1.5000	1.5018±0.0046	φ (°)	−2.0000	−1.9985±0.0029
Dual	True values	Estimates
Δz (mm)	5.0000	4.9947±0.0062
α (°)	90.000	4.9947±0.0062

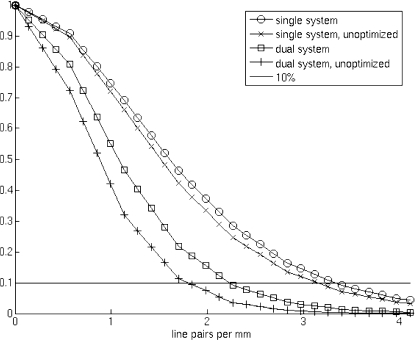
The geometric parameters estimated for our dual tube∕detector system are shown in Table 3. While the real values of these variables are unknown, we can judge the performance of the calibration results by the image quality of the reconstructions. We know that imperfect calibration would cause double contours, and blur the reconstructed images. Therefore, we used the modulation transfer functions (MTFs) as a more quantitative figure of merit to assess the performance of the calibration. Figure 7 presents the MTFs plots for the following: single detector reconstruction using refined parameters; single detector reconstruction using unrefined parameters as in Yang’s method, i.e., without the two angles σ and φ; dual tube∕detector reconstruction using refined parameters; and dual tube∕detector reconstruction using unrefined parameters. The MTF at 10% appears to be about 3.4 lp∕mm for refined single detector reconstructions and 3.3 lp∕mm for unrefined single detector reconstructions, 2.3 lp∕mm for refined dual tube∕detector reconstructions, and 1.9 lp∕mm for unrefined dual tube∕detector reconstructions.

Table 3.

Calibration results for our dual micro-CT system.

System 1	Estimates	System 2	Estimates	Dual	Estimates
dsd (mm)	808.80	dsd (mm)	753.22	Δz (mm)	1.2357
dso (mm)	706.41	dso (mm)	653.32	α (°)	−90.846
U0 (pixel)	543.95	u0 (pixel)	459.43
v0 (pixel)	326.80	v0 (pixel)	356.20
η (°)	1.9983	η (°)	1.4183
σ (°)	−4.4962	σ (°)	2.1522
φ (°)	1.1031	φ (°)	2.7240

Figure 7.

A plot of the modulation transfer functions for the reconstructions with different calibration parameters for the single and dual micro-CT systems.

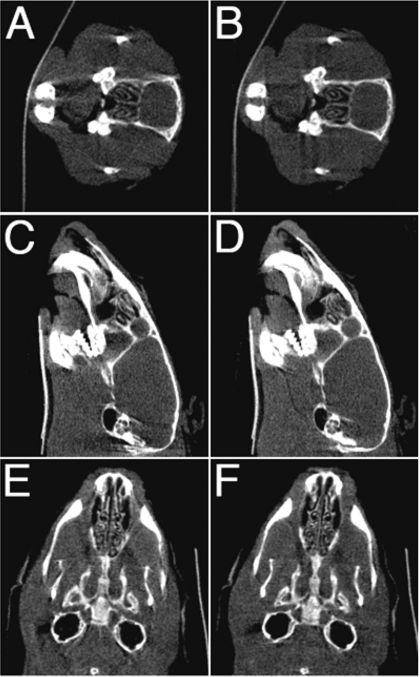
Finally, Fig. 8 displays micro-CT images of slices in axial, coronal and sagittal orientations of the mouse head using the single and dual tube∕detector reconstructions. Although projections from both imaging chains were used in the reconstruction of the dual tube∕detector micro-CT images, they show no misalignment artifacts and the image quality of single and dual chain micro-CT are comparable, visual proof that the calibration method performed well.

Figure 8.

Axial [(a), (b)], sagittal [(c), (d)], and coronal [(e), (f)] slices from a reconstruction of a mouse from a single chain micro-CT system [(a), (c), (e)] and a dual micro-CT system [(b), (d), (f)].

DISCUSSION

We have presented here a geometric calibration method suitable for a dual tube∕detector micro-CT system. We are not aware of other published prior work on this subject. Since our method involves the geometric calibration of each individual chain, we could compare part of our results with the previous work.¹⁸ Table 1 demonstrates that our method finds the calibration parameters with good accuracy and precision, and improves upon the results of previous work for single chain imaging systems. We find values for d_sd, u₀, v₀, and η that are both closer to the correct values and have less variance in the presence of noise than the method of Yang et al.¹⁸ The values for d_so are within the margin of error of previous methods, but are not improved by the optimization, so we typically exclude d_so from the optimization process. The values for angles σ and φ that were not estimated with other methods are now found accurately. Although we partially use the same formulas as Yang et al.¹⁸ to initially estimate five of the geometric parameters, our method for single chain calibration shows advantages due to added refinement based on optimization. Table 2 demonstrates that we also find accurate and precise values for the dual tube∕detector system parameters including Δz and α. The discrepancy between the two chains in the accuracy of estimation of d_so further indicates the fragility of this parameter estimation.

The optimization-based refinements improve the quality of reconstruction as shown by the MTF plots (see Fig. 7). The dual tube∕detector system does not match the quality of the single chain, but is reasonably close. We suspect that this loss in quality is due to the compounding of slight errors in the separate single chain calibrations, since the impact of optimization is much stronger on the dual tube∕detector MTF than the single tube∕detector MTF. Further reductions in image quality are caused by detector distortion, which is not completely corrected by the imaging software. We will address this issue in future work.

Figure 8 demonstrates that reconstructions from the dual micro-CT system look very much like the reconstructions from a single micro-CT system, and both reconstructions show few misalignment artifacts.

In our step-and-shoot acquisition scheme, with each tube∕detector acquiring one quadrant, the radiation dose should be the same as in the single tube∕detector system.

Although the method shown here was tested for our dual tube∕detector micro-CT system that is built with a rotating object geometry, we believe that the method could be adapted for rotating gantry geometry and could be used with other cone beam CT systems. We hypothesize that our method could be extended to correct for other sources of misalignment artifacts, such as reproducible wobbling gantry motion in C-arm-based systems.²⁶ This could be accomplished by adding an angle-dependent perturbation parameter that could be found in the optimization step in the same manner as σ and ϕ. Further work would be required for the validation of this hypothesis.

CONCLUSIONS

We have developed a method that accurately finds the parameters necessary to perform reconstruction with dual micro-CT imaging systems. The method is currently used with a newly developed dual micro-CT system and is robust. The accuracy of the parameters estimated for the individual sources and detectors is equal to or higher than the accuracy of previous single micro-CT methods, and the parameters found for the combined system enable accurate reconstructions free of misalignment artifacts.