Geometric calibration of a mobile C-arm for intraoperative cone-beam CT

Abstract

A geometric calibration method that determines a complete description of source-detector geometry was adapted to a mobile C-arm for cone-beam computed tomography (CBCT). The non-iterative calibration algorithm calculates a unique solution for the positions of the source (X_s,Y_s,Z_s), detector (X_d,Y_d,Z_d), piercing point (U_o,V_o), and detector rotation angles (ϕ,θ,η) based on projections of a phantom consisting of two plane-parallel circles of ball bearings encased in a cylindrical acrylic tube. The prototype C-arm system was based on a Siemens PowerMobil modified to provide flat-panel CBCT for image-guided interventions. The magnitude of geometric nonidealities in the source-detector orbit was measured, and the short-term (∼4 h) and long-term (∼6 months) reproducibility of the calibration was evaluated. The C-arm exhibits large geometric nonidealities due to mechanical flex, with maximum departures from the average semicircular orbit of ΔU_o=15.8 mm and ΔV_o=9.8 mm (for the piercing point), ΔX and ΔY=6–8 mm and ΔZ=1 mm (for the source and detector), and Δϕ∼2.9°, Δθ∼1.9°, and Δη∼0.8° (for the detector tilt∕rotation). Despite such significant departures from a semicircular orbit, these system parameters were found to be reproducible, and therefore correctable by geometric calibration. Short-term reproducibility was <0.16 mm (subpixel) for the piercing point coordinates, <0.25 mm for the source-detector X and Y, <0.035 mm for the source-detector Z, and <0.02° for the detector angles. Long-term reproducibility was similarly high, demonstrated by image quality and spatial resolution measurements over a period of 6 months. For example, the full-width at half-maximum (FWHM) in axial images of a thin steel wire increased slightly as a function of the time (Δ) between calibration and image acquisition: FWHM=0.62, 0.63, 0.66, 0.71, and 0.72 mm at Δ=0 s, 1 h, 1 day, 1 month, and 6 months, respectively. For ongoing clinical trials in CBCT-guided surgery at our institution, geometric calibration is conducted monthly to provide sufficient three-dimensional (3D) image quality while managing time and workflow considerations of the calibration and quality assurance process. The sensitivity of 3D image quality to each of the system parameters was investigated, as was the tolerance to systematic and random errors in the geometric parameters, showing the most sensitive parameters to be the piercing point coordinates (U_o,V_o) and in-plane positions of the source (X_s,Y_s) and detector (X_d,Y_d). Errors in the out-of-plane position of the source (Z_s) and detector (Z_d) and the detector angles (ϕ,θ,η) were shown to have subtler effects on 3D image quality.

INTRODUCTION

Cone-beam computed tomography (CBCT) using a flat-panel detector (FPD) offers an important advance for image-guided interventions. Flat-panel CBCT provides three-dimensional (3D) image reconstructions from two-dimensional (2D) projections acquired in a single orbit about the patient within an open geometry and demonstrates sub-mm 3D spatial resolution and soft-tissue detectability with a field of view sufficient for volumetric imaging of large anatomical sites. CBCT is becoming well established in image-guided radiation therapy (IGRT), where integration on the gantry of a medical linear accelerator provides soft-tissue localization at the time of treatment delivery.^{1, 2, 3, 4} Implementation of CBCT on a mobile isocentric C-arm has been recently investigated for 3D intraoperative guidance.^{5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16} Gantry rotation for such systems is subject to geometric nonidealities, with motion of the x-ray source and detector differing significantly from a simple circular orbit due, for example, to gravity-induced mechanical flex.² CBCT reconstruction algorithms that assume a circular source-detector trajectory (e.g., FDK filtered backprojection¹⁷) therefore require an accurate calibration method to account for geometric nonidealities. Failure to correct for such nonidealities in the source-detector orbit can result in misregistration, a loss of detail, and image artifacts.²

In general, geometric calibration relates the 3D coordinates (x,y,z) of voxels in the reconstructed image to the 2D coordinates (u,v) of pixels in the projection domain.^{18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} Geometric calibration consists of two stages: (i.) characterization of pose across the range of source-detector orbit; and (ii.) correction of geometric nonidealities in the process of 3D reconstruction. Methods of pose characterization include the use of stereoscopic tracking systems to monitor mechanical motion²⁵ and, more commonly, image-based methods that operate directly on projection data acquired either from a prior calibration^{2, 18, 23, 24} or simultaneous with imaging.^{20, 28} The form of the geometric characterization can consist of a projection matrix describing the linear relationship between 3D voxel coordinates and 2D pixel coordinates,^{19, 24} or a set of geometric parameters describing degrees of freedom in the imaging system (e.g., source and detector positions, detector rotation angles, etc.).¹⁸

Perhaps the simplest method for image-based geometric calibration of a CBCT system uses a single ball bearing (BB) placed near the isocenter of the rotational gantry to characterize the location of the “piercing point” (i.e., the point at which the isocenter projects on the detector plane) as a function of gantry angle.^{6, 23} The “single-BB” (or piercing point) method has been shown to provide a first-order correction of geometric nonidealities by applying in-plane translations of the detector position during 3D reconstruction. However, the method does not fully account for deviations from a circular orbit – e.g., displacements of the x-ray source, rotation∕tilt of the detector, or changes in source-to-detector distance (SDD).¹⁸ A more sophisticated method uses a helical pattern of BBs from which projection matrices are computed using an iterative approach.^{7, 24, 25} More recently, an analytical (noniterative) calibration method that determines all nine degrees of freedom in source-detector geometry has been reported in the context of IGRT.¹⁸ The method uses a phantom consisting of two plane-parallel circles of BBs and calculates a complete pose determination for each projection view, including the 3D positions of the source and detector, location of the piercing point, and the rotation angles of the detector.

In this paper, we report on the adaptation of the geometric calibration method of Cho et al.¹⁸ to a prototype C-arm for intraoperative CBCT. The short- and long-term reproducibility of the calibration and the magnitude of geometric nonidealities on the C-arm were measured, and the sensitivity and tolerance of 3D reconstructions to each of the geometric parameters were investigated quantitatively and qualitatively. The imaging system was a mobile isocentric C-arm (Siemens PowerMobil) modified in collaboration with Siemens Medical Solutions (Erlangen, Germany).^{5, 6, 7} This prototype has been shown to offer sub-mm 3D spatial resolution and soft-tissue visibility and is currently being deployed in preclinical applications across a broad range of image-guided interventions, including head and neck surgery,^{8, 9, 10, 11, 12, 13} orthopedics,^{14, 15} spine surgery,⁷ thoracic surgery, breast surgery, and brachytherapy.⁶ The reproducibility, sensitivity, and tolerance of geometric calibration were evaluated in terms of spatial resolution, image artifacts, and bony anatomy visualization in an anthropomorphic head phantom. Implications for geometric calibration of the C-arm in image-guided surgery are discussed.

MATERIALS AND METHODS

Mobile isocentric C-arm for flat-panel cone-beam CT

The main modifications to the C-arm (PowerMobil, Siemens Medical Solutions, Erlangen, Germany) to provide CBCT imaging capability include: a large-area FPD (Pax Scan 4030CB, Varian Imaging Products, Palo Alto, CA) in place of the x-ray image intensifier; a custom-built collimator with an expanded field of view; added filtration (2 mm Al+0.1 mm Cu) to reduce beam-hardening effects; a motorized orbital drive for C-arm rotation; and a computer control system for synchronized pulsed fluoroscopy x-ray exposure, image readout, and 3D reconstruction, as shown in Fig. 1a. The FPD was designed for real-time radiographic∕fluoroscopic imaging²⁹ and consists of a 2048×1536 (∼40×30 cm²) active matrix of a-Si:H photodiodes and thin-film transistors with a 194 μm pixel pitch, 70% fill factor, and 600-μm-thick CsI:Tl scintillator. The detector can be read at frame rates up to 15 fps at full resolution and up to 30 fps at half-resolution (1024×768 pixels at 388 μm pitch). The detector supports a variety of multiple-gain readout modes, with “dynamic gain”²⁹ read at half-resolution utilized for all image acquisitions below.

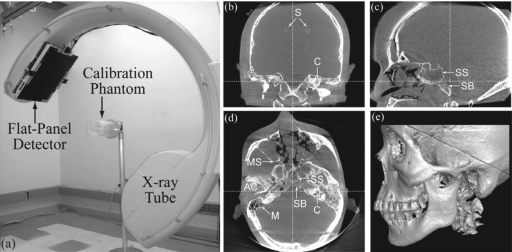
Figure 1.

(a) Experimental setup for geometric calibration of the prototype C-arm. (b) Coronal, (c) sagittal, (d) axial, and (e) volumetric renderings illustrating CBCT image quality over the (∼20×20×15 cm³) volumetric field of view. The anthropomorphic head phantom contains soft-tissue simulating spheres (denoted S) and a natural human skeleton, with anatomical regions of interest denoted SB (skull base), SS (sphenoid sinus), MS (maxillary sinus), C (cochlea), M (mastoid air cells), and AC (auditory canal).

CBCT imaging involved collection of 2D projections (100–500 total) acquired under continuous rotation of the C-arm. The FPD was read at either 3.33 or 6.66 fps, allowing the following acquisition modes: “Nominal” (200 projections acquired in ∼60 s); “Slow” (500 projections acquired in ∼150 s); “Fast” (100 projections acquired in ∼30 s); and “Fast-HiQ” (200 projections acquired in ∼30 s at ∼6.66 fps). The orbital range was ∼178°, which is less than the 180°+ fan angle (∼18°) required for accurate tomographic reconstruction; therefore, image artifacts related to a limited angle orbit are expected.⁷ Radiation doses for CBCT-guided head and neck surgery have been previously reported,¹² with a dose (measured at the center of a 16 cm water-equivalent cylinder) of 2.9 mGy (0.10 mSv) sufficient for visualization of bony detail and 9.6 mGy (0.35 mSv) for visualization of soft-tissue structures. For all studies below, CBCT acquisition consisted of 200 projections over ∼178° at 9.6 mGy. The system geometry has a nominal source-to-isocenter distance (SAD) of 63.7 cm and source-to-detector distance (SDD) of 125.5 cm, yielding a magnification factor of ∼1.97. The field of view (FOV) is ∼(20×20×15) cm³ at isocenter.

Volume reconstructions were formed using a modified FDK algorithm¹⁷ for 3D filtered backprojection which accommodates variations in the source position, detector position, and detector angles at each gantry angle. Nominal volume reconstructions were (256×256×192) voxels at 0.8 mm voxel pitch with a Hanning function apodization filter. Image acquisition and reconstruction were performed on a Dell Precision 650 (dual 2.0 GHz Xeon CPUs, 3 GB RAM).

Image quality evaluation

Reconstructions of a thin steel wire (0.16 mm diameter) placed within the geometric calibration phantom were used to evaluate spatial resolution quantitatively [e.g., full-width at half-maximum (FWHM) of the point spread function] and qualitatively (e.g., symmetry of the wire profile as well as magnitude of image artifacts). FWHM was analyzed from a 2D gaussian fit to axial images of the wire, taking the average of the FWHM in the x and y directions as the reported value, unless otherwise specifically noted. CBCT image quality was assessed in reconstructions of an anthropomorphic head phantom³⁰ containing soft-tissue simulating contrast-detail spheres (11–103 HU; 1.6–12.7 mm diameter) and a natural human skeleton. Figures 1b, 1c, 1d, 1e illustrate CBCT image quality in coronal, sagittal, axial, and volume renderings from a full FOV 3D reconstruction of the head phantom using the geometric calibration method. Two regions within the head phantom were selected to illustrate image quality: the skull base region and the temporal bone region, which contain anatomical structures of interest including the skull base, sphenoid sinus, maxillary sinus, cochlea, mastoid air cells, and auditory canal. To evaluate subtle differences in spatial resolution and visualization of fine anatomical details, high-resolution reconstructions were generated using voxel sizes of: (i.) 0.1 mm for analysis of FWHM in reconstructions of the wire phantom; and (ii.) 0.2 mm for regions of interest in the head phantom. Throughout the paper, axial images of the steel wire are 31×31 voxels (∼3×3 mm²) and images of regions within the head phantom are 401×401 voxels (∼8×8 cm²).

Geometric calibration

The calibration method of Cho et al.¹⁸ was adapted to the CBCT C-arm. Based upon a phantom containing two plane-parallel circles of BBs, the method gives complete pose determination at each projection angle and is guaranteed to produce a unique solution by linear parameter-estimation techniques. The algorithm assumes that the dimensions of the calibration phantom are known to a high degree of accuracy and that the detector presents no spatial distortion and is of known scale. Previous investigation on a high-precision CBCT benchtop system and a CBCT-capable linear accelerator for IGRT have shown the method to provide submillimeter accuracy and precision in the characterization of source-detector geometry.¹⁸

System geometry

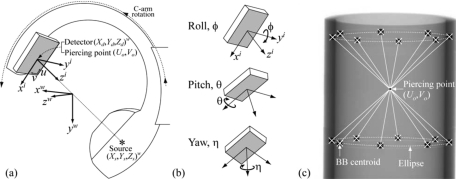
The system geometry of the CBCT C-arm is illustrated in Figs. 2a, 2b, and Table 1 includes a glossary of all the geometric system parameters. All geometric parameters are defined according to three right-handed Cartesian coordinate systems: the world (w), virtual detector (i), and real detector (I) reference frames. In Fig. 2a, the world coordinate system (w) provides a fixed reference frame (x^w,y^w,z^w) around which the C-arm gantry rotates and within which the CT reconstruction volume [denoted simply (x,y,z) in all figures] is computed. The positions of source and detector are denoted (X_s,Y_s,Z_s)^w and (X_d,Y_d,Z_d)^w, respectively. [Coordinate axes are denoted using lower case (e.g., x^w) and coordinates of a specific object are denoted using upper case (e.g., X_d).] The z axis of the world coordinate system (z^w) points along the rotation axis of the C-arm gantry, the x^w axis points to the source at a gantry angle of zero, and the y^w axis points to the source at a gantry angle of 90°. The virtual coordinate system (i) refers to a model detector that is perfectly aligned, while the real detector coordinate system (I) describes possible detector roll (ϕ, about the yⁱ axis), pitch (θ, about a rotated xⁱ axis), and yaw (η, about the detector normal axis) relative to the virtual detector system as shown in Fig. 2b. Both the virtual and real detector coordinate systems have their origin at the piercing point, which is defined as the projection of the world coordinate system origin on the detector plane. The 3D position of the detector is defined as the position of the piercing point relative to the world coordinate system. The yⁱ axis of the virtual detector system is antiparallel to the z^w axis of the world coordinate system, and the xⁱ axis is perpendicular to the yⁱ axis and to the vector from the piercing point to the source. The position of the piercing point on the real detector plane is described by the distances U_o and V_o from the origin of the u and v axes.

Figure 2.

(a) System geometry of the CBCT C-arm. The world coordinate system (w) is the reference frame for object positions (e.g., source and detector) and CBCT volume reconstructions. The piercing point (U_o,V_o) is the projection of the origin of the world coordinate system (i.e., the C-arm isocenter) on the detector plane (u,v). The positions of the source (X_s,Y_s,Z_s) and detector (X_d,Y_d,Z_d) with respect to the world coordinate system are shown. (b) Illustration of detector tilt (ϕ and θ) and rotation (η) angles applied on the virtual detector coordinate system (i) to produce the real detector coordinate system (I) (not shown), which results after rotation by η. (c) Example projection image of the calibration phantom, illustrating the relationship between diametrically opposed BB locations and the piercing point. The geometric system parameters are computed analytically based on two five-parameter fits to the ellipses defined by centroids of the 16 BBs as shown.

Table 1.

Glossary of geometric parameters computed by the calibration algorithm, along with results summarizing the magnitude of geometric nonideality on the CBCT C-arm and the reproducibility of geometric parameters. Geometric nonideality is reported as the maximum deviation from the average semicircular orbit over the gantry motion. Geometric reproducibility is computed as the average of the angle-dependent standard deviations evaluated for ten calibrations of the C-arm.

Description	Symbol	Geometric nonideality (Maximum departure from zero or mean value)	Geometric reproducibility (Average standard deviation across orbit)
Piercing point	Uo	15.8 mm	0.160 mm
	Vo	9.8 mm	0.097 mm
X-ray source position	Xs	7.7 mm	0.250 mm
	Ys	6.0 mm	0.260 mm
	Zs	1.2 mm	0.035 mm
Detector position	Xd	6.0 mm	0.240 mm
	Yd	6.7 mm	0.250 mm
	Zd	1.2 mm	0.033 mm
Detector tilt∕rotation	ϕ	2.9°	0.0190°
	θ	1.9°	0.0089°
	η	0.8°	0.0036°
Source-to-detector distance	SDD	13.8 mm	0.150 mm
Source-to-axis distance	SAD	7.7 mm	0.097 mm
Axis-to-detector distance	ADD	7.4 mm	0.084 mm

The geometry of the C-arm was characterized in terms of the following 12 system parameters: the source position (X_s,Y_s,Z_s)^w, the detector position (X_d,Y_d,Z_d)^w, the detector rotation (ϕ,θ,η), the piercing point location (U_o,V_o), and the gantry angle (γ). The 12 parameters can be reduced to nine degrees of freedom by characterizing the detector position using only one independent variable specifying the distance from the detector origin to the world origin along the line that connects the source and piercing point, and by computing the gantry angle based on the source position. Other derived parameters are also used to provide insight into the characteristics of C-arm geometry, including the source-to-axis distance (SAD), source-to-detector distance (SDD), and axis-to-detector distance (ADD).

Calibration phantom

A modified version of the calibration phantom¹⁸ was constructed appropriate to the C-arm FOV. The phantom consists of 16 steel BBs precisely located (within 25 μm machining tolerance) in two circular patterns encased in a cylindrical acrylic tube. Each circular pattern contains 8 BBs of 4.7 mm diameter spaced evenly over 360°. The diameter of each circular pattern is 100 mm, and the spacing between the two parallel circles is 90 mm. As shown in Fig. 2c, the calibration method operates on projection images of the calibration phantom and computes the geometric system parameters based on the estimated BB centroids at each gantry angle.

The calibration phantom was placed near isocenter with the phantom longitudinal axis aligned roughly with the C-arm axis of rotation to ensure that the phantom was visible in all projections. Precise placement of the phantom relative to the C-arm is not necessary, since the world coordinate system is defined relative to the calibration phantom.

Because the geometric parameters resulting from the calibration are determined with respect to the world coordinate system attached to the phantom (as placed in the calibration scan), a method was implemented to convert the parameters to an alternate, consistent reference frame. For example, such was required for intercomparison of geometric parameters acquired with different phantom placements in the long-term reproducibility studies. In the results reported below, a consistent reference frame was chosen that minimizes the discrepancy to the mean circular orbit. A three-dimensional circular least-squares fit to the x-ray source trajectory was computed, and the optimized circle center and rotation angles of the plane passing through the circle were used to determine the transformation (i.e., translation and rotation) to the new coordinate system. All the calibration parameters were converted to this coordinate system to minimize the effect of phantom location on the calibration.

Calibration algorithm

The key aspects of the analytical geometric calibration algorithm of Cho et al.¹⁸ are briefly summarized below. Cone-beam projections of the two circular BB patterns in the calibration phantom define two ellipses in the detector plane,²² as illustrated in Fig. 2c. All geometric system parameters are analytically computed from an intermediate set of parameters describing the two ellipses, which guarantees a stable and unique solution. The centroid positions of the BBs in each projection image are determined by fitting circles to the edges of the BBs (determined using a Canny edge detector), and are used to fit two five-parameter ellipses of the form:

$$a{(m-m_o)}^2+b{(n-n_o)}^2+2c(m-m_o)(n-n_o)=1,$$ (1)

where (m_o,n_o) is the ellipse center. The parameters a, b, c, m_o, and n_o, are determined analytically using a linear least-squares method.²² The calculation of the piercing point (U_o,V_o) is provided as an example to illustrate the general approach of deriving system parameters from the parameterized ellipses. The origin of the world coordinate system is located at the center of the calibration phantom (i.e., at the point bisecting the line connecting the centers of the two circular BB patterns) and can be found from the intersection of lines connecting diametrically opposed BBs across the two circles. Since an intersection of lines in 3D is projected onto an intersection of projected lines in 2D, the piercing point (the projection of the world coordinate system origin on the detector plane) can be determined from the intersection of diametrically opposed BBs across the two ellipses as shown in Fig. 2c.

The calibration algorithm was implemented using MATLAB (MathWorks, Natick, MA), requiring ∼3.5 min to compute a calibration based on a sequence of 200 projections over ∼178° (Dell Precision 470, dual 2.8 GHz Xeon CPUs, 2 GB RAM). The majority of the processing time (∼70%) is associated with the BB centroid search algorithm (∼60% for numerical optimization of the circular fit and ∼10% for edge detection). The analytical calculations of geometric parameters (aside from image handling and display) constitute <5% of the total computing time (∼10 s). With appropriate changes to the algorithm (e.g., implementation in C∕C++ operating in parallel with image acquisition), the full set of geometric calibration parameters could potentially be available immediately after the calibration scan.

Geometric reproducibility

Short-term and long-term reproducibility

The geometric calibration method requires that nonidealities due to mechanical flex of the C-arm are reproducible. Short-term reproducibility of the C-arm gantry motion was tested using ten CBCT acquisitions of the calibration phantom repeated over a 4 h time period during which the phantom was not moved between scans. The standard deviation of each system parameter across the ten repeats was computed at each gantry angle and averaged over all angles to summarize the geometric reproducibility.

Long-term reproducibility of the C-arm geometry was evaluated from five calibrations obtained over a period of ∼6 months, during which time the C-arm was used regularly and significantly perturbed for purposes of other experiments. To permit intercomparison of geometric parameters acquired with different phantom setup positions, a simple correction was applied to convert the parameters into an alternate, consistent world reference frame that minimized the deviation from a circular orbit. The robustness of the correction for phantom position was tested by acquiring ten scans over a 4 h time period with the calibration phantom repositioned after each scan. Random perturbations in phantom setup were achieved using five participants (engineers) who were familiar with the system and were asked independently to position the phantom (with two repeats, giving a total of ten scans).

Effect of C-arm position

The C-arm allows gross movement of the gantry in horizontal (in-out) and vertical (up-down) directions relative to the support armature. For example, the “in-out” adjustment is used in bedside setup to center the FOV along the patient’s sagittal line (PA view), and the vertical adjustment is used to accommodate various bed heights and to center the FOV along the patient’s medial line (LAT view). The effect of C-arm position on CBCT image quality was evaluated to verify that system geometric parameters obtained at a nominal position provide robust calibration across the extent of horizontal and vertical motion. The effect of C-arm angulation has been reported previously.⁷ A reference calibration acquisition was obtained with the C-arm positioned at (x,y)=(0,0), defined as the horizontal position at the center of the in-out range of motion and a vertical height of 1 m (floor-to-isocenter distance). CBCT images of the wire and head phantoms were acquired at nine C-arm positions across a broad range of in-out and vertical motion, including three horizontal positions (x=−10, 0, 10 cm) and three vertical positions (y=−5, 0, 10 cm). The image sets obtained at each position (x,y) were compared to those obtained at the reference position [(x,y)=(0,0)]. Furthermore, CBCT images of the wire phantom acquired at each of these nine positions were reconstructed based on the calibration achieved at the reference position, and the images were evaluated quantitatively (FWHM) and qualitatively (visualization of artifacts).

Calibration sensitivity and tolerance

Sensitivity: Parameter knockout

The sensitivity of the geometric calibration to each of the system parameters was evaluated by neglecting geometric nonidealities associated with each parameter in volume reconstruction, essentially “knocking out” any one of the following 11 system parameters: the source coordinates (X_s,Y_s,Z_s), the detector coordinates (X_d,Y_d,Z_d), the detector offsets (U_o,V_o), and the detector angles (ϕ,θ,η). Although the detector position can be described by a single independent variable, all three coordinates were considered as individual variables to provide a convenient presentation of the sensitivity analysis. To systematically neglect the geometric nonideality associated with a given system parameter, the parameter values computed in the full calibration method were replaced with values corresponding to the average over the semicircular orbit. Thus, the source and detector (X,Y) positions were taken as sinusoidals:

$$X_s=\overline{\mathrm{SAD}}\cos \left(\gamma \right),Y_s=\overline{\mathrm{SAD}}\sin \left(\gamma \right),$$ (2a)

$$X_d=-\overline{\mathrm{ADD}}\cos \left(\gamma \right),Y_d=-\overline{\mathrm{ADD}}\sin \left(\gamma \right),$$ (2b)

whereas the Z positions of the source and detector, detector offsets, and detector angles were individually set to their average over the semicircular orbit.

Calibration comparison: Full, single-BB, and semicircular

The full geometric calibration was compared to two other methods: (i.) a single-BB (“piercing point”) calibration; and (ii.) a calibration assuming an ideal semicircular orbit. Both methods were implemented by modifying system parameters returned from the full calibration method. As described in the Introduction, the first method supposes a single BB placed near isocenter to characterize the angle-dependent location of the piercing point, a fairly common approach in early implementations of CBCT for IGRT. This technique was simulated from the full calibration by applying corrections for the piercing point location based on the U_o and V_o parameters, but setting the remaining parameters (source position, detector position, and detector angles) to values corresponding to the average semicircular orbit in Eq. 2 or their average value over the gantry rotation as described above. For the second method (semicircular orbit), there was no attempt to correct geometric nonidealities, applying instead corrections for all system parameters based on the average semicircular orbit. CBCT images of the wire and head phantoms reconstructed according to each of these simpler calibration methods were quantitatively and qualitatively compared to those obtained using the full calibration method.

Tolerance: Systematic and random perturbations

The effect of systematic and random errors in the geometric system parameters was evaluated. Systematic perturbations were introduced by adding a constant value (δ) to the measured angle-dependent parameters. Random perturbations were introduced at each angle by adding a gaussian distributed random variable with zero-mean and variance σ. For each geometric parameter, wire and head phantom reconstructions were performed for four systematic and four random perturbations across a broad range of δ and σ. For the detector offsets (U_o and V_o), the systematic and random perturbations were δ=σ=0, 0.4, 0.8, and 1.6 mm (i.e., δ=σ=0, 1, 2, and 4 pixels). Perturbations for the source and detector positions were δ=σ=0, 1, 5, and 10 mm for the positions (X_s, Y_s, X_d, and Y_d) and δ=σ=0, 1, 2, and 4 mm for the positions (Z_s and Z_d). Detector angle (ϕ, θ, and η) perturbations were δ=σ=0°, 1°, 2°, and 4°. CBCT image quality was evaluated over the range of δ and σ in each case.

RESULTS

Geometric reproducibility

Short-term and long-term reproducibility

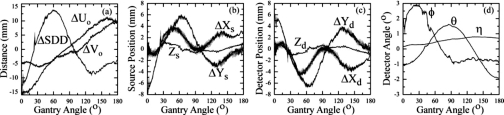
Figure 3 displays geometric system parameters computed as a function of gantry angle from ten CBCT scans repeated over ∼4 h. To illustrate the magnitude of geometric nonideality, and also to plot parameters on a common scale, parameters preceded by “Δ” are plotted as a difference from the average semicircular orbit (e.g., $\Delta X_s=X_s-\overline{\mathrm{SAD}}\cos \left(\gamma \right)$, $\Delta U_o=U_o-{\overline{U}}_o$, etc.). The C-arm is seen to display significant geometric nonidealities. The maximum deviation from a semicircular orbit over the gantry rotation is summarized for each parameter in Table 1. The piercing point displays a maximum departure from the mean of ΔU_o=15.8 mm and ΔV_o=9.8 mm, and the SDD departs from the mean by up to 13.8 mm over the orbit. Source and detector X and Y positions display large deviations of up to 6–8 mm from a semicircular orbit, while smaller departures of 1 mm were found in the Z positions. The detector angles exhibited significant fluctuation over the orbit, with roll (ϕ) varying ∼(−1°–2.9°), pitch (θ) varying ∼(−1.9°–1.6°), and yaw (η) varying ∼(0.2°–0.8°).

Figure 3.

Geometric parameters from ten repeat CBCT scans over ∼4 h, with one of the scans (selected arbitrarily) highlighted by the thicker black line. The system parameters computed as a function of the gantry angle include: (a) the piercing point (U_o,V_o) and source-to-detector distance (SDD), (b) source position (X_s,Y_s,Z_s), (c) detector position (X_d,Y_d,Z_d), and (d) detector tilt (ϕ and θ) and rotation (η) angles. Parameters prefixed by “Δ” are plotted as a difference from their average value over the semicircular orbit.

Table 1 also summarizes the reproducibility of each geometric parameter. The parameters exhibiting the highest levels of geometric nonideality also exhibit larger standard deviations (e.g., >0.1 mm for U_o and V_o, and >0.24 mm for X_s, Y_s, X_d, and Y_d), while parameters that deviate less significantly from the ideal orbit demonstrate smaller standard deviations (e.g., <0.035 mm for Z_s and Z_d, <0.02° for ϕ, θ, and η). Slightly higher variability was observed in all parameters during the first 4–5 projections due to variations in acceleration of the C-arm from the start position. Overall, the geometry of the C-arm was found to be highly reproducible as characterized by the standard deviation across ten scans, which permits use of a geometric correction based on a prior calibration scan to be accurately applied during subsequent 3D reconstructions.

Figures 4a, 4b, 4c, 4d, 4e, 4f, 4g, 4h, 4i, 4j illustrate the short- and long-term reproducibility of CBCT image quality in axial images of the wire as a function of time (Δ=t−t_cal), where t is the time of the wire phantom scan and t_cal is the time of the calibration phantom scan. Figure 4k displays the corresponding FWHM and normalized maximum signal (i.e., the maximum voxel value of the wire divided by the maximum value at Δ=0 s). The logarithmic scale of the Δ axis allows visualization of individual data points over short-term and long-term time scales. (Data points for Δ=0 are plotted at Δ=0.01 so they appear on the log scale.) The logarithmic fits to the FWHM and maximum signal data shown in Fig. 4k are intended as guides to the eye, and do not represent a physical model. Three vertical dotted lines are superimposed on the Δ axis at ∼0.01, 1 day, and 1 month to highlight key time points, as discussed below. The top row of wire images [Figs. 4a, 4b, 4c, 4d, 4e] were calibrated from system parameters obtained over a 4 h time period with random perturbations in phantom setup, and are seen to be qualitatively reproducible, with FWHM and maximum signal degrading by 0.025 and 0.08 mm, respectively, over the 4 h. The most evident degradation in performance over the 4 h time period was between Δ=0 (simultaneous geometric calibration and wire acquisition) and Δ=1 h (and also verified for smaller delays), as highlighted by the first vertical line in Fig. 4k. This suggests that simultaneous calibration may account for any nonreproducible characteristics of C-arm motion (e.g., random noise), although the effect is seen to be small (<0.015 mm increase in FWHM from Δ=0 to Δ=1 h). A second drop in calibration performance is observed after a delay of 1 day, which shows FWHM and maximum signal degraded (relative to Δ=0) by 0.05 and 0.014 mm, respectively. The corresponding image in Fig. 4f presents more visible streaks and demonstrates the loss of peak signal intensity. The wire images for Δ=1, 4, and 6 months in Figs. 4h, 4i, 4j, respectively, show increasing distortion and a corresponding loss of symmetry, although these qualitative observations are not strongly reflected in the measures of FWHM and maximum signal in Fig. 4k.

Figure 4.

Geometric reproducibility of the C-arm calibration over a six-month time period. (a)–(j) Axial images of a steel wire (0.16 mm diameter) placed within the two-circle calibration phantom shown as a function of the time interval, Δ, between scanning of the wire and calibration phantom. The calibration phantom was repositioned between each scan. (k) Plots of FWHM and normalized maximum signal in axial wire images as a function of Δ (logarithmic time scale).

The correction for variability in phantom setup position was found to reduce variability in the computed system parameters, with residual differences associated with slight rotation and translation of the world reference frame attached to the phantom. As a result, the standard deviations of each system parameter across ten repeat scans with the phantom repositioned after each scan were ∼40% higher than for ten repeats with the phantom fixed in position; however, no appreciable differences in CBCT image quality were found between the two cases [e.g., FWHM=(0.64±0.0013) mm over ten trials for a fixed phantom position compared to FWHM=(0.63±0.0011) mm for variable phantom setup].

Effect of C-arm position

CBCT image quality was found to be insensitive to movement of the C-arm gantry along horizontal and vertical directions, allowing for a single calibration scan obtained at a nominal C-arm position to be applied across the range of C-arm “in-out” and “table-height” motion. Wire and head phantom images acquired at nine positions across the range of horizontal and vertical C-arm motion displayed no appreciable differences in spatial resolution (<0.018 mm FWHM standard deviation), soft-tissue visibility, bony detail visualization, or image artifacts.

Calibration sensitivity and tolerance

Sensitivity: Parameter knockout

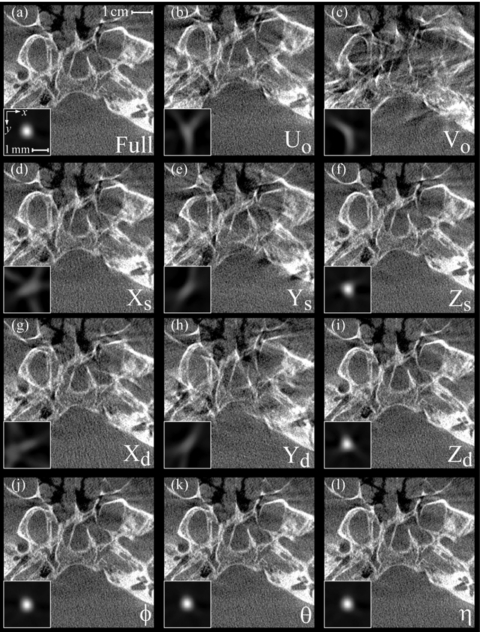
Figure 5 displays images of the wire and head phantom reconstructed using the full calibration method [Fig. 5a] and the 11 sensitivity studies [Figs. 5b, 5c, 5d, 5e, 5f, 5g, 5h, 5i, 5j, 5k, 5l] in which nonideality of a given geometric parameter was neglected. To permit visual comparison of voxel values in the wire images, all wire images in Fig. 5 have identical grayscale window and level settings that correspond to the complete range of values in Fig. 5a. Similarly, the head phantom images have a common window and level based on that of the full calibration image. Images reconstructed using the full calibration method [Fig. 5a] demonstrate a symmetric wire profile (FWHM=0.62 mm) and visualization of fine bony details in the head phantom, including delineation of the skull base and the posterior bony aspect of the sphenoid sinus. The results in Fig. 5 suggest two groups of parameters based on the level of image quality degradation relative to the full calibration: (i.) first-order parameters; and (ii.) second-order parameters.

Figure 5.

Sensitivity analysis of each geometric system parameter on the spatial resolution and image quality of CBCT reconstructions. Each case shows an axial image of the anthropomorphic head phantom in the region of the skull base, with axial images of a steel wire shown as insets to demonstrate the effect on the point-spread function. (a) Image reconstructed using the complete geometric calibration. (b)–(l) Image reconstructions for which a given geometric parameter was replaced by its average value over the semicircular orbit.

The first-order parameters exhibit a considerable loss in image quality and include the piercing point offsets (U_o and V_o) and the X and Y positions of the source and detector [Figs. 5b, 5c, 5d, 5e, 5g, 5h, respectively]. The wire images for these parameters demonstrate distorted, asymmetric profiles with pronounced artifact and >50% loss in peak signal compared to the full calibration. The distortion present in these wire profiles prevents accurate and meaningful calculation of a FWHM, but the signal intensity of the wire has clearly been spread over a region far exceeding that of the full calibration method in Fig. 5a. The corresponding head phantom images similarly suffer distortion and loss of detail, which diminish accurate identification and delineation of anatomical structures of interest (e.g., skull base and sphenoid sinus).

The second-order parameters display subtler image degradation and include the source and detector Z positions and the detector angles [Figs. 5f, 5i, 5j, 5k, 5l, respectively]. For each of these parameters, the wire and head phantom images suffer comparatively little distortion. For Z_s and Z_d, the maximum wire signal decreased by ∼3% and the FWHM increased by ∼2%. For ϕ, θ, and η, the degradation was ∼0.1% in maximum signal and ∼0.01% in FWHM.

Calibration comparison: Full, single-BB, and semicircular

Figure 6 shows the comparison of three geometric calibration methods. In Fig. 6a, the full calibration method produces a symmetric wire profile (FWHM=0.62 mm) and provides visualization of fine bony details in the region of the temporal bone, including delineation of the matrix of air cells within the mastoid bone. In Fig. 6b, the single-BB method demonstrates a subtle degradation in image quality compared to the full calibration, as seen in the artifacts introduced in the wire image and the loss of detail in the mastoid air cells. The visible loss in image quality demonstrates the second-order effects associated with neglecting the nonidealities in the source position, detector position, and detector angles. As shown in Fig. 6c, the semicircular calibration results in a significant degradation in image quality, as evident in the distortion and artifact in the wire image, and the loss of detail and streak artifacts in the head image. These examples clearly illustrate the need for accurate geometric calibration to correct for the significant nonidealities of the C-arm gantry.

Figure 6.

Comparison of three geometric calibration methods. (a) The full geometric calibration method, which accounts for nonidealities in the positions of the source and detector and the tilt and rotation angles of the detector. (b) A “single-BB” calibration method simulated by correcting only the detector offsets of the piercing point. (c) Calibration assuming a semicircular orbit. The inset images are axial slices of a wire, and the full images are axial views of the temporal bone region within an anthropomorphic head phantom.

Tolerance: Systematic and random perturbations

For brevity, the tolerance studies shown below were limited to three parameters (X_s, U_o and η) indicative of overall results. Figure 7 presents tolerance analysis for the system parameter X_s, which is also representative of the trends for the other source coordinates (Y_s and Z_s) as well as the detector coordinates (X_d, Y_d, and Z_d). Figure 7a illustrates the set of systematic shifts (δ_Xs) introduced into X_s, and Figs. 7b, 7c, 7d, 7e show the corresponding wire and head phantom reconstructions. The results show that a systematic error in X_s produces a volume reconstruction that is unaffected in image quality, but is translated along the x direction, as illustrated by the arrow marking the cochlea in the skull images of Figs. 7b, 7c, 7d, 7e. (The wire image insets throughout were centered on the maximum signal intensity, and therefore do not reflect translations imparted by systematic shifts.) The translation distance along x was measured to be ∼δ_Xs∕M_s, where M_s=SDD∕ADD (e.g., for the C-arm a systematic shift of δ_Xs=10 mm in X_s introduces a volume shifted by ∼5 mm). The measured translation agreed with the expected value for the other source coordinates (Y_s and Z_s) as well. For the detector coordinates (X_d, Y_d, and Z_d), the translation distance along any axis of the reconstruction volume is given by ∼δ∕M, where M=SDD∕SAD is the magnification of the imaging system. Random errors in X_s, on the other hand, as shown in Fig. 7f, cause distortion (stretching) of the wire profiles along the x direction and a decrease in the peak signal intensity, as shown in Figs. 7g, 7h, 7i, 7j. Random error of σ_Xs=0, 1, 5, and 10 mm resulted in peak signal intensity of 1.0, 0.48, 0.11, and 0.07, respectively. The FWHM_x (FWHM in the x direction) doubled from 0.60 mm for σ_Xs=0 mm up to 1.2 mm at σ_Xs=1 mm, and for σ_Xs=5 and 10 mm the severe distortion in the wire profile prevented meaningful calculation of FWHM.

Figure 7.

Tolerance to (a–e) systematic and (f–j) random errors in the source position, X_s. Plots of X_s as a function of gantry angle are shown for (a) systematic offsets of δ_Xs=[0,1,5,10] mm and (f) zero-mean gaussian perturbations with variance σ_Xs=[0,1,5,10] mm. Images in (b)–(e) and (g)–(j) are axial reconstructions of a steel wire (inset) and a head phantom in the region of the skull base, with the position of the cochlea (C) marked by the arrow.

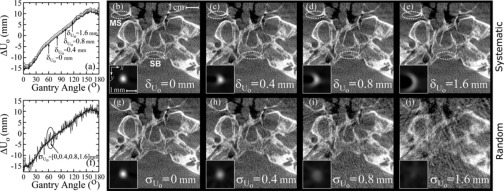
Tolerance analysis for the detector offset U_o is shown in Fig. 8. Systematic errors as shown in Fig. 8a produce wire profiles with a progressively more semicircular shape, illustrated in Figs. 8b, 8c, 8d, 8e, which would become “donut-shaped” in the case of a 360° source-detector orbit. The head phantom images illustrate the distortion and loss of detail introduced by systematic shifts, highlighted by the loss in delineation of the two anatomical structures circled (the posterior aspect of the skull base and the posterior wall of the right maxillary sinus). FWHM and peak signal intensity are not reported for systematic errors in U_o (and the remaining parameters below) since they do not provide meaningful insight into the magnitude of the semicircular and∕or fully 3D distortion introduced with increased δ. Random errors in U_o shown in the graph in Fig. 8b and the corresponding images in Figs. 8g, 8h, 8i, 8j impart a distortion (stretching) of wire signal intensity along x and y and a loss of peak signal intensity. Random error of σ_Uo=0, 0.4, 0.8, and 1.6 mm (i.e., 0, 1, 2, and 4 pixels) resulted in FWHM of 0.62, 0.78, 1.1, and >10 mm, respectively, and peak signal intensity of 1.0, 0.66, 0.33, and 0.17, respectively. The other detector offset V_o was less sensitive to both systematic and random perturbations, as expected, since error in U_o (tangential to orbital motion) introduces angle-dependent reconstruction error along both x and y, while error in V_o (parallel to the axis of rotation) introduces reconstruction error along only z that is independent of the gantry angle. Systematic errors in V_o produced reconstruction volumes translated by ∼δ_Vo∕M_d, along the z direction with no significant change in image quality for shifts up to δ_Vo=4 mm. Random errors of σ_Vo=0, 0.4, 0.8, and 1.6 mm caused distortion (stretching) along the z direction, and resulted in FWHM of 0.62, 0.63, 0.67, and 0.81 mm, respectively, and peak signal intensity of 1.0, 0.96, 0.86, and 0.58, respectively.

Figure 8.

Tolerance to (a–e) systematic and (f–j) random errors in the detector offset, U_o. Plots of U_o as a function of gantry angle are shown for (a) systematic offsets of δ_Uo=[0,0.4,0.8,1.6] mm (i.e., 0, 1, 2, and 4 pixels) and (f) zero-mean gaussian perturbations with variance σ_Uo=[0,0.4,0.8,1.6] mm. Corresponding axial wire profiles and head phantom images are shown in (b)–(e) and (g)–(j), with the posterior aspects of the skull base (SB) and maxillary sinus (MS) circled.

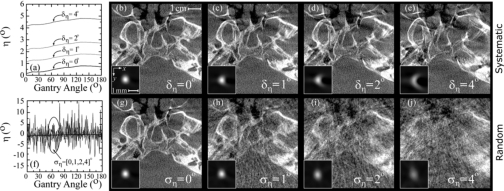
Figure 9 shows tolerance analysis for the detector rotation angle η. The axial wire images shown as a function of the systematic shift in Figs. 9b, 9c, 9d, 9e present similar semicircular distortion as observed for U_o in Fig. 8 (although flipped along x); however, the head phantom images in Figs. 9b, 9c, 9d, 9e display a more severe degradation than those in Figs. 8b, 8c, 8d, 8e. This is the result of fully 3D distortion, including degradation along the z direction (variation in the diameter of the semicircular wire images across axial slices) imparted by error in the detector rotation angle η, causing both in-plane and out-of-plane distortion. Random errors of σ_η=0°, 1°, 2° and 4° produced wire images with fully 3D distortion and a loss of signal intensity, and for the central slice resulted in FWHM of 0.62, 0.65, 0.72, and 0.91 mm, respectively, and peak signal intensity of 1.0, 0.93, 0.77, and 0.50, respectively. Systematic and random shifts in the other detector angles ϕ and θ (not shown) were found to impart truncation-like artifacts that progressively limit the effective FOV of the reconstruction volume with increasing δ and σ, and for δ=σ=4° almost completely encompassed the axial slices for both detector angles. Systematic errors in ϕ also produced in-plane distortion along x and y (semicircular wire images), and in θ caused a smaller degree of out-of-plane distortion. The parameter θ was also found to be less sensitive than ϕ to random perturbations, with random errors of σ_θ=0°, 1°, 2° and 4° producing FWHM of 0.62, 0.62, 0.63, and 0.67 mm, respectively, and peak signal intensity of 1.0, 1.0, 0.97, and 0.80, respectively, while random errors of σ_ϕ=0°, 1°, 2° and 4° produced FWHM of 0.62, 0.63, 0.66, and 0.84 mm, respectively, and peak signal intensity of 1.0, 0.98, 0.86, and 0.23, respectively.

Figure 9.

Tolerance to (a–e) systematic and (f–j) random errors in the detector rotation, η. Plots of η as a function of gantry angle are shown for (a) systematic offsets of δ_η=[0,1,2,4]° and (f) zero-mean gaussian perturbations with variance σ_η=[0,1,2,4]°. Corresponding axial wire profiles and head phantom images are shown in (b)–(e) and (g)–(j).

DISCUSSION AND CONCLUSIONS

The geometric calibration method of Cho et al.¹⁸ was adapted to a prototype mobile C-arm for CBCT. The method uses a calibration phantom consisting of two plane-parallel circles of BBs encased in a cylindrical tube and analytically computes a complete description of source-detector geometry, including the positions of the source (X_s,Y_s,Z_s) and detector (X_d,Y_d,Z_d), the piercing point (U_o,V_o), and detector rotation and tilt angles (ϕ,θ,η). The method was previously implemented on an experimental CBCT benchtop system and a clinical CBCT-capable linear accelerator for IGRT. Implementation on the CBCT C-arm (which exhibits larger geometric nonidealities due to mechanical flex of the gantry) provided high 3D image quality and demonstrated further the generality, robustness, and ease of implementation of the calibration algorithm. Short- and long-term stability of the calibration was investigated quantitatively (wire phantom) and qualitatively (head phantom), as was the sensitivity and tolerance of the calibration to each of the geometric parameters.

The short-term geometric reproducibility of the calibration was investigated in a series of intraoperative CBCT images acquired over a ∼4 h procedure. Although the C-arm exhibits large geometric nonidealities (>15 mm departure from a perfect semicircular orbit), such were found to be sufficiently reproducible to allow precise correction based on a calibration obtained prior to the procedure. The calibration algorithm provided CBCT image quality with sub-mm spatial resolution (e.g., ∼0.62 mm FWHM) and visualization of fine anatomical details in an anthropomorphic head phantom. The effect of gross movement of the C-arm gantry along horizontal (in-out) and vertical (up-down) directions relative to the support armature was shown to have a negligible effect on image quality, allowing the C-arm to be freely moved during an interventional procedure (e.g., adjusting the horizontal and vertical positions to image a specific region of interest, moving the C-arm in and out of the operating field, etc.). Previous work⁷ demonstrated the extent to which a single calibration may also be used for various angulations of the C-arm (i.e., rotation about the axis of the armature).

The long-term geometric reproducibility of the calibration was similarly high, demonstrated by image quality and spatial resolution measurements over a period of 6 months. CBCT image quality degraded slightly as the delay (Δ) between calibration and image acquisition increased, with delays of Δ=0 s, 1 h, 1 day, 1 month, and 6 months resulting in FWHM of 0.62, 0.63, 0.66, 0.71, and 0.72 mm, respectively, in axial images of a 0.16 mm diameter wire. Qualitative evaluation of images in Fig. 4 suggests a subtle increase in distortion and a loss of symmetry in the wire profiles at 4–6 months that are not strongly reflected in the FWHM metric. In practice, we have observed that geometric calibration parameters obtained up to ∼1–6 months apart from imaging (during which time the C-arm was used regularly and significantly perturbed) provided sufficient image quality for other image-guided surgery experiments. For ongoing clinical trials in CBCT-guided procedures at our institution, geometric calibration is conducted monthly to provide accurate calibration parameters, yield sufficient 3D image quality, and limit the calibration time introduced into the quality assurance (QA) process. Such a schedule is consistent with clinical IGRT systems that incorporate monthly geometric calibration of the CBCT system in QA programs.^{31, 32} More frequent calibration (e.g., daily or weekly) is certainly possible, depending on the requirements of a particular application, but will add to the time and resources required for calibration and QA.

In addition to providing high 3D image quality, accurate and precise determination of geometric parameters also provides insight into characteristics of the imaging system (e.g., nonidealities in the mechanical flex and orbital drive) and the process of 3D image reconstruction itself (e.g., sensitivity and tolerance to each of the parameters). The sensitivity results suggest two general classes of parameters distinguished by the extent to which neglecting a given parameter degrades image quality: (i.) first-order parameters, exhibiting significant loss in image quality [viz., the piercing point coordinates (U_o,V_o) and in-plane positions of the source (X_s,Y_s) and detector (X_d,Y_d)]; and (ii.) second-order parameters, exhibiting subtler effects on 3D image quality [viz., the out-of-plane positions of the source (Z_s) and detector (Z_d) and the detector angles (ϕ,θ,η)]. These results provide insight into the effectiveness of various geometric calibration methods. For example, the single-BB (“piercing point”) calibration provides reasonable calibration of in-plane translations (first-order parameters); however, the combined effect of ignoring nonidealities in the out-of-plane source-detector positions and detector rotation∕tilt angles (second-order parameters) results in a subtle, but appreciable, loss in image quality.

The tolerance results can be employed to identify sources of error in CBCT geometric calibrations. For example, systematic errors in the detector rotation angle η (about the detector normal axis) produced subtle but visibly detrimental 3D distortion,^{18, 22} with axial images of a wire phantom displaying semicircular profiles that vary in diameter between slices. Images displaying such characteristics may be indicative of uncalibrated detector rotation present in the imaging system, which in some cases may be corrected by adjusting the detector mount, or may require the use of a more comprehensive calibration method (such as the one described here) to characterize detector rotation resulting from complex source-detector geometry.

The tolerance analysis can also be used to reveal the sensitivity of other CBCT systems to specific types of calibration errors. For example, systematic errors in the positions of the source and detector produced systematic shifts in the reconstruction volume that were dependent on the imaging geometry (e.g., SDD, SAD, ADD). For the C-arm (for which SAD≈ADD, giving a magnification of M∼2), errors in the source coordinates produced approximately equal shifts of the volume reconstruction as did errors in the detector coordinates. For an IGRT system with a typical magnification factor of M∼1.55,³³ errors in the detector position would produce larger shifts than would errors in the source position. Conversely, small animal imaging systems with larger magnification factors (e.g., M∼3) would be more sensitive to errors in the source location. In each case, it should be recognized that calibration errors in these source and detector positions result not in degradation of image quality, but in the accuracy of image-based localization—an important consideration for systems using CBCT for image guidance.

In the context of CBCT-guided interventions, the high reproducibility of the C-arm geometry permits the use of geometric calibration parameters obtained as part of a monthly QA procedure, such that geometric calibration does not introduce any additional complexity or time to the image-guided procedure. The precision, accuracy, and reproducibility of the geometric calibration provide CBCT images with sub-mm spatial resolution and soft-tissue visibility,¹² and the calibration method has been adopted in ongoing clinical trials in CBCT-guided procedures.