Adult Height and Childhood Disease

Abstract

Taller populations are typically richer populations, and taller individuals live longer and earn more. In consequence, adult height has recently become a focus in understanding the relationship between health and wealth. We investigate the childhood determinants of population adult height, focusing on the respective roles of income and of disease. Across a range of European countries and the United States, we find a strong inverse relationship between postneonatal (ages 1 month to 1 year) mortality, interpreted as a measure of the disease and nutritional burden in childhood, and the mean height of those children as adults. Consistent with these findings, we develop a model of selection and stunting in which the early-life burden of undernutrition and disease not only is responsible for mortality in childhood but also leaves a residue of long-term health risks for survivors, risks that express themselves in adult height and in late-life disease. The model predicts that at sufficiently high mortality levels, selection can dominate scarring, leaving a taller population of survivors. We find evidence of this effect in the poorest and highest-mortality countries of the world, supplementing recent findings on the effects of the Great Chinese Famine.

Height has long been of interest to biologists, but it has recently become an important focus in demographers’ and economists’ attempts to understand the relationship between health and wealth. It is a direct and readily available measure of long-run, life-course health. Taller populations are generally richer populations, sufficiently so that height has been used to infer historical living standards (Floud, Wachter, and Gregory 1990; Fogel 2004; Steckel 1995, 2004). On average, taller individuals live longer and earn more, perhaps reflecting their superior cognitive abilities (Case and Paxson 2008; Jousilhati et al. 2000; Leon et al. 1995; Waaler 1984). Understanding the determinants of adult height is therefore important for both public health and economic policy.

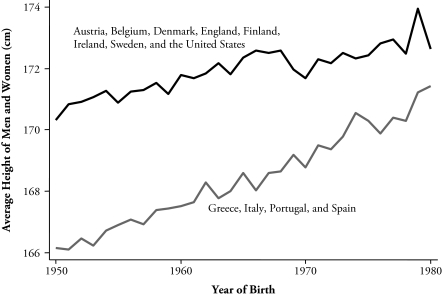
We examine the adult heights of 31 cohorts (born between 1950 and 1980) from England, the United States, and 10 continental European countries. We show that there is a close link between average heights and childhood mortality and that this relationship helps explain both the pattern of heights across countries and the shapes of country-specific trends within countries. In particular, the national rate of postneonatal mortality, which is the fraction of newborn infants who survive for at least 28 days but die before their first birthday, predicts the average adult height of the relevant birth cohort. Postneonatal mortality (PNM) is a measure of childhood disease; while many children suffer from respiratory or gastrointestinal infections, for example, and only a few die, the mortality rate is a measure of the prevalence of disease in a particular country. In our pooled panel data, the simple correlation between PNM and average height is −.79. While the size of this correlation is largely attributable to trends in PNM and in average height, the shapes of the trends differ across countries, and there is a marked country-by-country relationship between the shapes of the country trends in the two variables. In the richer, more northerly countries (Austria, Belgium, Denmark, England, Finland, Sweden, and the United States), PNM at first fell and then flattened out as it reached an irreducible minimum; in the poorer, more southerly countries (Greece, Italy, Spain, and Portugal), PNM continued to fall through 1980. Average adult heights show the mirror image of this pattern, rising to a plateau in the north and continuing to rise in the south, so that average southern heights are catching up with those in the north.

In spite of it being the richest country in the analysis, the United States had a level of PNM in 1970 that was three times as large as that of Sweden; according to our estimates, this difference in childhood disease can account for 20% to 30% of the 2-cm shortfall of 30-year-old Americans compared with 30-year-old Swedes in 2000.

Conditional on PNM, our analysis finds no relationship between adult height and GDP per capita in the year and country of birth. This is the case for GDP itself as well as for its trend and cyclical components taken separately. Disease, not income, appears to have been the constraining factor in these rich countries, at least after 1950.

We start by presenting these findings. We then discuss the broader literature that links childhood circumstance to adult height, and we develop a simple model of population height based on selection and stunting. This model provides a stripped-down and much simplified account of ideas that have long been familiar in the demographic and epidemiological literatures. The model is consistent with the relationship between PNM and average height, essentially by construction, but it also delivers a number of predictions—in particular, that the relationship between childhood mortality and adult height is not necessarily monotonic. Where mortality is sufficiently high, increases in mortality might either leave no net effect on the average height of the population of survivors, or even increase it, a proposition that is consistent with recent examination of the effects of the Chinese famine on the height of survivors (Gørgens, Meng, and Vaithianathan 2007). We extend this literature by examining adult heights of women in 43 higher-mortality countries, including 27 in sub-Saharan Africa. Africans are much taller than might be expected from their levels of economic development, and some of this can be explained by the selection caused by high mortality in childhood.

PNM AND HEIGHTS IN EUROPE AND THE UNITED STATES

Table 1 summarizes the height data for the United States, England, and 10 continental European countries. Although we use yearly observations in the analysis, there is substantial sampling error that induces year-to-year variation, so here we present five-year averages (or six-year averages for the birth cohorts 1950 to 1955.) These are averages over native-born (except Swedish) men and women, calculated as half the average male height plus half the average female height. The data come from the European Community Household Panel, from the Health Survey of England, and from the National Health Interview Survey in the United States; details are given in the notes to the table.

Table 1.

Mean Heights (in cm) of Men and Women in 2000 (h) and Postneonatal Mortality per 1,000 births (p) for Selected Birth Cohorts

Year of Birth	1950–1955		1956–1960		1961–1965		1966–1970		1971–1975		1976–1980
	h	p	h	p	h	p	h	p	h	p	h	p
Austria	171	23	172	16	173	8	172	7	173	6	173	5
Belgium	170	18	171	13	171	9	173	7	173	6	174	4
Denmark	174	10	173	6	174	5	175	4	175	3	176	3
England	169	9	170	6	170	6	170	6	170	6	170	5
Finland	171	14	172	9	173	4	172	3	172	2	172	2
Greece	169	—	170	27	171	18	171	12	172	7	172	5
Ireland	169	18	169	11	170	9	170	9	171	—	171	5
Italy	167	31	168	23	169	16	169	11	170	6	172	4
Portugal	164	61	165	57	165	48	165	35	167	21	168	11
Spain	166	47	166	—	167	—	169	—	170	6	171	5
Sweden	172	5	173	4	174	3	174	2	174	2	174	2
United States	171	8	172	7	172	7	172	6	172	5	172	4

Notes: A dash indicates that averages are not available for any year in the span; otherwise averages are taken over all available data. See Appendix A and Appendix Table B1. Except for Sweden, where data on heights are unavailable, only native-born persons are included. European and U.S heights are self-reported, while those from England are measured by nurses. Thomas and Frankenberg (2002: Figure 1) and Ezzati et al. (2006: Figure 2) showed that in the United States, self-reported heights exaggerate actual heights, on average, and that the difference is close to constant for ages 20 to 50; if this effect holds in England, the English heights will be understated relative to the others.

Sources: Heights data are from authors’ calculations from the National Health Interview Survey for the United States, the Health Survey of England, and Garcia and Quintana-Domeque (2007) for the other countries whose data come from the European Community Household Panel, as described in Peracchi (2002). PNM data are from World Health Organization (1953–1964–1965–1982), supplemented by the WHO mortality database.

Denmark and Sweden are the two tallest countries in this sample, and Spain and Portugal are the shortest. There is a distinct north-south gradient in this aspect of health, and inhabitants of richer and more-equal countries are taller than the inhabitants of poorer and less-equal countries. The cross-country correlation between average height (average height averaged over all birth cohorts from 1950 to 1980) and the logarithm of real GDP per capita (from the Penn World Table, and similarly averaged over year of birth) is .76. We have no reliably consistent time series on income inequality, but the cross-country correlation between averaged average heights and the Gini coefficients for 1997 or 2000 reported in World Bank (2007) and United Nations Development Program (2006) is −.68. This correlation rises to −.86 if we exclude the United States, where people are 5 cm taller than would be predicted by the regression of mean height on the Gini coefficient for the other 11 countries. The correlation between average height and geographical latitude is .58; northern countries are taller (and much less unequal) than southern countries and in this the United States is no exception.

Table 1 also shows that in the poorer and more southerly countries of Europe, height has been increasing across the birth cohorts from 1950 through to 1980, whereas in the richer and more northerly countries, height has either stagnated or increased for the earlier birth cohorts and leveled off later. Figure 1 shows this pattern more clearly. The lower curve shows the average height by birth cohort for Greece, Italy, Portugal, and Spain (each given equal weight), while the higher curve shows the unweighted average over the other eight countries. (The picture looks essentially the same if Ireland is moved to the lower group.)

Figure 1.

Average Height for Two Groups of Countries

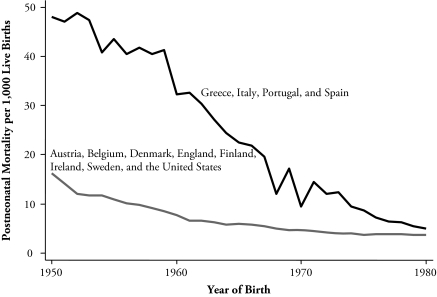
Table 1 also shows the five-year averaged data for PNM for the countries and periods for which we have been able to locate the data; again, see the table notes for sources. In 1950–1955, PNM varied from 61 per 1,000 live births in Portugal to 5 per 1,000 live births in Sweden. By 1976–1980, it had fallen in all countries—for example, to 11 in Portugal and to 2 in Sweden, a value that had also been attained by Finland, with Denmark not far behind. A rate of 2 deaths per thousand is presumably close to the minimum attainable. Already in 1950, Sweden was close to this figure, while Portugal, Spain, Italy, and (presumably) Greece, still had a long way to go. Figure 2 shows the annual pattern of PNM averaged over the same groups of countries as for heights in Figure 1, and shows its mirror image. Adults in the countries with high PNM were relatively short, on average, and as their PNM rate fell, children born in the years of lower PNM were taller as adults. In the richer countries, with lower PNM to start and smaller improvements to make, heights were taller to start but did not grow over time. In the next section, we explore whether the timing of these changes in trend in PNM and adult height match one another on a country-by-country basis and whether the relationship is robust to the introduction of other variables.

Figure 2.

Postneonatal Mortality for Two Groups of Countries

If Figure 2 is redrawn for neonatal mortality (NNM), which is the mortality rate in the first 28 days of life, the two lines are much less far apart in the early years and fall in parallel (not shown). There has been a great deal of progress in reducing NNM—for example, through the use of neonatal intensive care units that help the survival of low-birth-weight babies—and this progress had shown no signs of slowing by 1980. PNM by contrast, is driven less by technological improvements than by improving the disease environment, more-complete vaccination, and the ready availability of hospital care, something that had already been largely accomplished in the richer countries by the early 1950s.

Table 2 presents a series of regressions in which mean population height is the dependent variable. Column 1 shows that in the 316 pooled time-series cross-section observations for the 12 countries over 31 years of birth, variation in PNM explains 62% of the variation in average height. The parameter estimate is −0.16, so that a reduction in PNM by 20 per thousand—a modest improvement by historical standards—has been associated with an increase in average height by 3.2 cm, which is more than most of the actual increases shown in Table 1. The coefficient on PNM is identical if we replace PNM by the average of PNM in the first three years of life, which is one of the most crucial periods for human growth.

Table 2.

Regressions of Population Height on Postneonatal Mortality (PNM) and Other Variables

Variable	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PNM	−0.161 (0.007)	−0.100 (0.007)	−0.057 (0.009)	−0.057 (0.009)	−0.121 (0.012)	−0.048 (0.013)	−0.052 (0.014)	−0.044 (0.017)
NNM	—	—	—	—	−0.029 (0.026)	−0.080 (0.028)	−0.069 (0.030)	−0.047 (0.035)
Ln(GDP)	—	—	—	—	0.993 (0.299)	0.542 (0.517)	0.149 (0.678)	0.833 (0.809)
Year of Birth	—	—	0.054 (0.008)	—	—	—	0.018 (0.018)	—
Country Dummy Variables?	No	Yes	Yes	Yes	No	Yes	Yes	Yes
Year Dummy Variables?	No	No	No	Yes	No	No	No	Yes
R2	.623	.898	.914	.923	.640	.916	.916	.924
Sample Size	316	316	316	316	316	316	316	316

Notes: Heteroskedasticity-robust standard errors are reported in parentheses.

Source: Authors’ calculations. GDP per capita is the chained real per capita GDP series from version 6.2 of the Penn World Table (Heston, Summers, and Aten 2006).

These first estimates force the effects of PNM on heights to be identical across and within countries, and it is important to check that the coefficient remains significant when country fixed effects are included. Column 2 includes country dummy variables, and the estimated effect is cut by a third to −0.10. The pooled estimate in column 1 is a weighted average of the between estimate and the within estimate in column 2; since the former is larger in absolute magnitude than the latter, the within estimate can be interpreted as an underestimate of the effect of PNM by whatever fraction of the between estimate is actually assignable to PNM. Column 3 shows the results of another check: the inclusion of a time trend. According to this, there is a secular increase in heights in all countries of 0.05 cm per year, or 1.5 cm over the 30-year period; allowing for this reduces the estimated effect of PNM by another third, to −0.06. Column 4 includes, in addition to the country fixed effects, a set of year fixed effects. This adds little to the explained variance over the time trend in column 3 and does not further change the size or significance of the estimated effect of PNM on height.

Our purpose in these regressions, as in those that follow, is not to provide a precise estimate of the effect of PNM on adult height; presumably some of the fixed country differences in heights and some of the common time trend are in fact attributable to the international and time-series variation in PNM, or at least to the variation in childhood disease that it indicates. What is important is the demonstration that the effects of PNM remain significant when we (over)control for country and year fixed effects. The cross-country patterns of the timing of the fall and stabilization of PNM match (inversely) the cross-country patterns of the timing of the rise and stabilization of heights.

The right panel of Table 2 looks at what happens when we introduce two other possible determinants of height: real income per head (measured by the log of real per capita GDP in purchasing power parity dollars) and NNM, both in the year of birth. Otherwise, we follow the same procedure as in the left side of the table, sequentially introducing country effects, a time (year of birth) trend, and a set of time effects. Column 8 shows that column 4 is essentially unaffected by the introduction of income and NNM. In the pooled time-series and cross-section, neither (the logarithm of) per capita GDP nor NNM are significantly different from zero, and neither the size nor the significance of PNM is much affected. For real GDP per capita, the insignificance persists in all specifications that contain country fixed effects, although in column 5, it plays a role in explaining cross-country variation in heights. Across columns 5 through 8, the size of the estimated income coefficient is unstable from one specification to another. In columns 6 and 7, NNM attracts a significant coefficient, and it is possible that it, along with PNM, is linked to adult height.

As is shown in Figures 1 and 2, the link that we are documenting is a low-frequency relationship between PNM and adult height; the shape of the country trends, rising (or falling) and flattening, are matched country by country, and this low-frequency relationship is presumably also responsible for at least part of the cross-country correlation between PNM and height. Even so, we have also checked to see whether there is any relationship between height and PNM at higher frequencies—for example, over business cycles. Our data, however, are not well-suited to this task. First, the height data are sample averages whose standard errors are substantial, 0.3 to 0.5 cm, depending on the country and cohort. In consequence, the year-to-year fluctuations in average height are dominated by sampling error, making it hard to detect high-frequency patterns if they indeed exist. Second, we have only 30 years of international-price GDP data for each country, which makes it difficult to reliably distinguish cycles from trends, especially in data that have in some cases been created by extrapolation around a few benchmarks. Contrast this situation with the century of data for one country (Holland) used in the study of the business cycle position at birth on later-life mortality by van den Berg, Lindeboom, and Portrait (2006). Finally, our matching of date of birth to PNM and GDP is inevitably imprecise at the level of a single year, if only because the income and disease environments that are relevant for adult mortality operate not just in the year of birth; thus, our data should pick up trends and changes in trends, not year-to-year or business cycle frequencies.

In line with these concerns, the results in Table 2 do not show anything of interest when we break up series into trend and cyclical components, using the standard Hodrick–Prescott filter to make the decompositions country by country.1 In spite of this, we remain agnostic about the existence of high-frequency relationships between adult height, PNM, or GDP. Our data are simply not suitable for investigating the issue. Our main concern here is something else: the matching of PNM and adult height, both across countries, and the shapes of trends within countries.

Although not shown in Table 2, the (1997 or 2000) Gini coefficient attracts a significant negative sign if introduced into either columns 1 or 5, but the country fixed effects remain significant even when the Gini (or geographical latitude) is introduced. The rationale for the role of income inequality in explaining height is the concavity of the height-to-income relationship at the individual level (see Steckel 1995, 2008), but it is not clear how to reconcile this rationale with the insignificance of national income in columns 6 through 8, nor is it obvious how to investigate the issue further without reliable and consistent cross-country time-series data on income inequality. We note also that Deaton (2008) found no consistent effect of consumption inequality on mean adult heights in India.

We now turn to the causes of PNM and identify four components: mortality from pneumonia, mortality from intestinal disease, mortality from congenital anomalies, and mortality from other causes. Appendix A provides the definitions of each category, and Appendix Table B1 and Appendix C provide information on missing causes. Data on the components of PNM are not always available, so the number of observations falls to 297, and the loss includes most of the Spanish data. Data on cause of death are also much more prone to error than are data on the timing of death, and this should be borne in mind when interpreting our results. Classification systems change over time and are not always the same across countries. For example, some countries list multiple causes on death certificates, from the immediate cause to the fundamental cause or underlying condition, yet only one is incorporated into the WHO international data. Indeed, Rosano et al. (2000) noted that in England, the introduction of a new format of death certificate in 1986 coincided with an immediate large decline in reports of neonatal deaths from anencephaly, a congenital malformation. In consequence, our analysis of cause data should be treated with great caution.

The large differences between high-PNM and low-PNM countries—for example, Portugal and Italy on the one hand, and Sweden and the United States on the other—lie in mortality from intestinal disease, followed by mortality from pneumonia. The Swedish PNM rate from intestinal disease has been zero (or at least less than 0.5 per 1,000) since 1972. There are also substantial differences in the “other” category. International differences in mortality rates from congenital anomalies are the smallest. Over time and within countries, all categories of PNM have fallen, except those from congenital anomalies. PNM from this last category fell in most countries after about 1960, though it rose for most of the period in Italy and for the entire period in Greece and Portugal. Mortality from pneumonia and intestinal disease fell most rapidly and in about equal measure, from about 8 and 6 per thousand for the 1950 birth cohort to 0.4 and 0.2, respectively, for the 1980 birth cohort.

Table 3 shows the same sequence of regressions as in Table 2 but with PNM split into its four components. PNM from pneumonia in infancy is the only consistently significant predictor of adult height across all of the specifications, with the size of the estimated effect varying over specifications in much the same way as did the estimated effect of overall PNM in Table 2. Mortality from congenital diseases has a significant effect on adult height in the regressions with dummy variables for country, provided that there are no time effects. This effect is worth further comment, even bearing in mind the lack of consistency of the estimated effects across specifications and the degree of measurement error in these data. Starting around 1960, the richer countries increasingly adopted prenatal testing for anomalies using amniocentesis and ultrasound technologies. Once a condition is discovered, termination rates are very high; Mansfield, Hopfer, and Marteau (1999) surveyed the literature back to the early 1980s, where many studies show termination rates greater than 80% for Down syndrome, spina bifida, and anencephaly. These terminations reduce the potential for postnatal mortality and might conceivably increase the height of the adult population.

Table 3.

Regressions of Height on Postneonatal Mortality (PNM) by Cause and Other Variables

Variable	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
PNM
Pneumonia	−0.531 (0.053)	−0.228 (0.041)	−0.126 (0.042)	−0.137 (0.046)	−0.408 (0.066)	−0.099 (0.046)	−0.101 (0.048)	−0.105 (0.053)
Intestinal	−0.082 (0.037)	0.004 (0.028)	−0.014 (0.026)	−0.008 (0.027)	−0.099 (0.038)	−0.021 (0.027)	−0.021 (0.027)	−0.014 (0.027)
Congenital	−0.110 (0.161)	−0.406 (0.176)	−0.165 (0.090)	−0.168 (0.098)	0.097 (0.150)	−0.248 (0.099)	−0.242 (0.099)	−0.207 (0.106)
Other	−0.034 (0.046)	−0.125 (0.034)	−0.083 (0.032)	−0.8083 (0.034)	0.014 (0.049)	−0.082 (0.040)	−0.084 (0.041)	−0.063 (0.043)
NNM	—	—	—	—	−0.028 (0.030)	−0.089 (0.027)	−0.085 (0.031)	−0.063 (0.036)
Ln(GDP)	—	—	—	—	0.832 (0.347)	0.006 (0.574)	−0.102 (0.752)	0.585 (0.916)
Year of Birth	—	—	0.042 (0.009)	—	—	—	0.005 (0.020)	—
Country Dummy Variables?	No	Yes	Yes	Yes	No	Yes	Yes	Yes
Year Dummy Variables?	No	No	No	Yes	No	No	No	Yes
R2	.651	.907	.913	.922	.658	.915	.915	.923
F Test	16.78	12.26	2.95	3.03	11.67	2.48	2.46	1.87
Sample Size	297	297	297	297	297	297	297	297

Notes: Heteroskedasticity-robust standard errors are reported in parentheses. The F tests in the bottom panel are tests of the hypothesis that the coefficients on the four categories of PNM are identical; those in columns 1, 2, and 5 are significant at better than 1%, those in columns 3 and 4 are significant at better than 5%, and those in the last three columns are insignificant.

THE LONG-TERM CONSEQUENCES OF CHILDHOOD DISEASE

The literature on human growth has established that adult height is determined by cumulative net nutrition over the growing period, where net nutrition is the difference between the intake of nutrition (food) and the claims on it through activity and disease (see Bogin 2001; Evelyth and Tanner 1990; or Silventoinen 2003). Although adult height is not attained until around age 18 in the rich countries today, many authors have argued that much of the programming of adult height occurs in the first three years and that it is difficult to make up shortfalls in growth. The correlation of child’s height with ultimate height, which is between .25 and .30 at birth, rises to between .70 and .80 at age 2 and increases only slowly thereafter (Schmidt, Jorgensen, and Michaelsen 1995). Because we can probably ignore cross-population variations in activity for children younger than 3, our primary concerns here are two: the availability of food—as set by income, prices, and local patterns of food consumption—and the effects of childhood disease.

In the regressions in Tables 2 and 3, per capita national income in the year of birth plays no role in predicting subsequent adult height once we condition on PNM and country fixed effects. This finding is consistent with the view that in these now rich countries, per capita income has not been a constraint on child growth in the years since 1950 because year-to-year variations in income are not associated with year-to-year variations in adult height. Of course, this says nothing about the possibility that income was such a constraint in those countries in the past—as argued, for example, by Fogel (2004)—or that it is still a constraint today in many poor countries. Nor does it deny that height should be related to non-income-related fluctuations in nutrition, such as seasonal variations in the availability of some foods, as indicated by Doblhammer and Vaupel’s (2001) findings on the seasonal variation of life expectancy at age 50, or national differences in the mix of foods consumed, as suggested by the positive effects on Irish heights of a diet of skim milk and potatoes (Mokyr and Ó Gráda 1996).

Childhood disease levels, as measured by PNM, still appear to be relevant for adult heights today, at least for those born in these European and North American countries between 1950 and 1980. It was not the lack of nutritional inputs but the effect of disease on the absorption of those nutrients that was important. Perhaps surprisingly, Table 3 shows no evidence for effects of diarrheal disease, which places an obvious tax on nutritional inputs. Yet, our findings on the importance of respiratory and other diseases are consistent with the results of Finch and Crimmins (2004) and Crimmins and Finch (2006), who argued that a wide range of childhood infectious diseases lead to inflammatory responses. These responses are well-adapted for short-term survival, but they divert energy from growth and diminish adult stature and, beyond that, increase the risk of cardiovascular disease in late life.

Finch and Crimmins (2004) and Crimmins and Finch (2006) used long-run data from nineteenth-century England, France, Sweden, and Switzerland to confirm a relationship between mean adult height (at age 20–21) for a birth cohort and its infant mortality rate, the latter interpreted as an indicator of the general disease environment in childhood. Their work, as well as our work described in this article, complements that by Schmidt et al. (1995), who used modern data to document a relationship between the average height of 18-year-old (male) conscripts in 11 European countries and PNM in the year of their birth.

In the demographic literature, the effects of childhood disease on adult health, including height, are typically thought of in terms of (normally) offsetting effects of scarring and selection (see, e.g., Elo and Preston 1992; Preston, Hill, and Drevenstedt 1998; and Schultz 2001). Scarring is the direct long-term effect of the disease on survivors. This effect is usually negative, so that the disease causes long-term damage. A similar, positive effect can occur when a childhood disease provides acquired immunity for the rest of life; we could perhaps stretch the meaning and think of this as “negative scarring.” While acquired immunity is important for health in general, it is likely of limited relevance for height, which is set over a limited period. Selection occurs through the indirect positive effect of the removal of the least healthy (or shorter) members of the population by mortality, so that the survivors are healthier (or taller). To see how these familiar effects might work in different mortality contexts, a simplified illustrative model of selection and stunting is useful.

Suppose that each child is born with some physiological characteristic h_i. This characteristic, which we can think of as (potential) adult height, is distributed in the population with distribution function F(h). Newborn children with height less than a cutoff z cannot survive, so that the baseline infant mortality rate, which we can think of as mortality from factors (such as congenital anomalies) that operate up to and including birth, is F(z).

Into this baseline situation, we introduce an environmental disease or nutritional burden that varies from year to year. Write this as v_t, with larger values indicating heavier disease burden. We think of these as epidemics of childhood disease, smallpox and whooping cough in the seventeenth and eighteenth centuries, and measles and scarlet fever in the early to mid-twentieth century. They could also cover nutritional deficiencies, whether through famine-induced lack of food or through infectious disease reducing net nutritional intake.

The disease burden is assumed to reduce the endowed physiological characteristic, increasing the infant mortality rate; here, and in contrast to the empirical work, we draw no distinction between infant and postneonatal mortality. Children die if the reduced characteristic is less than z, if

$$h_i-v_t\le z,$$ (1)

so that the mortality rate, taking account the disease burden, is now given by

$$m_t=F(z+v_t),$$ (2)

which varies from year to year. If we knew the distribution and the value of z, we could recover the disease burden from knowledge of the infant mortality rate using

$$v_t=F^{-1}(m_t)-z.$$ (3)

In this sense, infant mortality is an indicator of the burden of disease, which justifies its frequent treatment as such in the literature, including the empirical work above. Note that z is measured in the same units as h and, in the empirical results below, will typically be presented as a “z score,” the number of standard deviations below the mean at which survival becomes impossible.

Note that the cutoff z might itself vary over time or from one country to another with variations in the ability to keep children alive through variations in medical care or public health. We shall allow for this in the empirical work.

We need to add long-term effects—“scarring” or “stunting”—to this story. Those who survive the epidemic are assumed to pay some permanent price in their long-term health. For example, scarring might come from an infection acquired in childhood that is carried through the rest of life—for example, respiratory tuberculosis or Helicobacter pylorii in times before the availability of effective chemical prophylaxis. Rheumatic heart disease in childhood might predispose to rheumatic heart disease in old age. This scarring might affect adult mortality or, in the analysis here, adult height, in which case the effect is stunting. We assume that some fraction θ of v_t is permanently deducted from the physiological parameter of the survivors. Hence, for the survivors,

$${\tilde{h}}_{it}=h_i-\theta v_t.$$ (4)

We shall typically assume that θ is positive because the negative θ associated with acquired immunity is of limited relevance for heights. The size of θ, which has the dimension of a pure number, measures the extent to which the forces that shift down the health endowment and that lead to infant mortality persist into final adult height. If the effects of early damage are permanent, θ will be unity; with some transitory effect or some recovery, it will be less.

Given the adult height of the survivors from Eq. (4), the average adult height of the survivors of the cohort born in t is given by

$${\overline{h}}_t=\frac{{\int }_{z+v_t}^{\infty }hdF(h)}{1-F(z+v_t)}-\theta v_t.$$ (5)

The first term is increasing in the burden of disease v_t; childhood disease selects out the shorter people, leaving people who are taller, on average, and who are taller by more the greater the severity of the disease. The second term, which is negative if θ is positive, is the stunting effect of the disease.

The effects of v_t on cohort height can be assessed by differentiating (5), which can be written as

$$\frac{\partial {\overline{h}}_t}{\partial v_t}=\left(\overline{h}-z-(1-\theta )v_t\right)\frac{f(z+v_t)}{1-F(z+v_t)}-\theta .$$ (6)

Since height has to be larger than z + v_t in order to survive, the shortest survivor has adult height z + v_t − θv_t, so that the first term on the right side of (6) is positive. This is the effect of childhood mortality selecting out the infants and children who have the lowest potential adult height. Depending on the values of the parameters and the size of the burden v_t, the net effect can go in either direction, and the derivative in (6) can change sign over the range of v_t.

Given that the shock v_t is not observable but that the mortality rate is, it is useful to combine (3) and (5) so as to link the average height of the survivors to the mortality rate of the birth cohort. This yields

$${\overline{h}}_t=\frac{\underset{F^{-1}(m_t)}{\overset{\infty }{\int }}hdF(h)}{1-m_t}-\theta (F^{-1}(m_t)-z).$$ (7)

Eq. (7) is more straightforward to handle if we assume that the (untruncated) original distribution of heights is normal with mean μ and variance σ². Substituting into (7) and performing the integration, we obtain

$$\frac{{\overline{h}}_t-\mu }{\sigma }=\frac{\phi \left[{\Phi }^{-1}(m_t)\right]}{1-m_t}-\theta \left[{\Phi }^{-1}(m_t)-\frac{z-\mu }{\sigma }\right],$$ (8)

where φ and Φ are the standard normal density and distribution functions, respectively. Eq. (8) provides a relationship for the z score of height (in relation to the standard that would prevail in the absence of mortality) in terms of the mortality rate, the survival cutoff (expressed in standard deviations from the mean), and the stunting parameter θ.

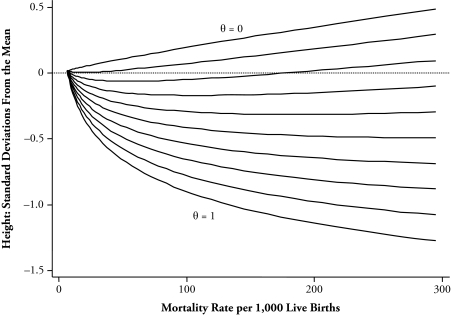
Figure 3 shows plots of average height from (8) against the mortality rate for a range of values of θ. We have assumed a value of z that is 2.5 standard deviations below the mean, so that the baseline mortality rate (when v_t is zero) is only 0.6%. Each graph therefore starts from a value of 6 for the mortality rate, with the resulting mild selection giving an average height of 1.8% of a standard deviation above the unselected mean. In these graphs, higher mortality is associated with higher height when the stunting effect is unimportant (low θ) and with lower height when the stunting is important (high θ). As the figure shows, for intermediate values of θ, the graph is nonmonotonic in mortality, with stunting effects predominating at low mortality and selection effects predominating at high mortality. The figure also shows that, at low mortality levels, stunting effects can make average heights extremely sensitive to changes in mortality patterns, and even if there is no reversal, the stunting effects are gradually attenuated by selection as mortality rises.

Figure 3.

Theoretical Deviation of Height in Standard Deviations From the Mean of the Parent Distribution in Relation to Mortality Rate

SELECTION, STUNTING, AND THE WORLD DISTRIBUTION OF HEIGHTS

The European and American results can be directly interpreted in terms of the model of selection and stunting. In particular, if we maintain the assumption that the underlying distribution of potential heights is normal, we can use Eq. (8). We assume that in the absence of infant mortality, adult heights would have a mean of 176 cm and a standard deviation of 6.0, which were the actual figures for Denmark for the cohorts born between 1976 and 1980. Given this, and given that the first term on the right side of Eq. (8) is parameter free and so can be subtracted from the normalized mean height on the left side, we can estimate the parameters θ and z by estimating (8) by linear regression. Given our previous findings on the importance of country fixed effects, we extend (8) to allow the cutoffs z to vary across countries and to have a random component. With these additions, the model to be estimated uses data on average heights h̄_t and postneonatal mortality m_t to estimate the equation

$$\frac{{\overline{h}}_{it}-\mu }{\sigma }-\frac{\phi [{\Phi }^{-1}(m_{it})]}{1-m_{it}}={\alpha }_i-\theta {\Phi }^{-1}(m_{it})+{\epsilon }_{it},$$ (9)

where i denotes a country, t is a birth year, and the country fixed effects α_i + ε_it can be interpreted as θ (z_i − μ) / σ. The parameter θ is recovered as the coefficient on Φ⁻¹(m_it).

Without fixed effects, the stunting parameter θ is estimated to be 1.18, and the disease-free cutoff for mortality is 3.12 standard deviations below the untruncated mean. A value of θ near 1 implies that the disease- or famine-based shift in potential heights in childhood persists unmodified into adulthood. Although some later magnification of the childhood effect seems theoretically possible, we expect θ to be less than the full persistence value. Once we add in country fixed effects, the estimate of the stunting parameter falls to 0.77. With a time trend, which can be thought of as a common international reduction in the mortality cutoff, the estimate of θ falls to 0.64, which is little further affected if we add (common) year effects. As was the case for the regressions in Table 2, the time trend (or year effects) almost certainly absorbs some of the effect of mortality decline, causing the stunting effect to be underestimated. The fits of these equations are only slightly inferior to those obtained by adding a quadratic in PNM to the original regressions. When the logarithm of real income is added, it is insignificantly different from zero in the absence of country fixed effects, though it becomes significant in their presence, essentially because within-country year-to-year fluctuations in income are correlated with within-country variations in cohort heights.

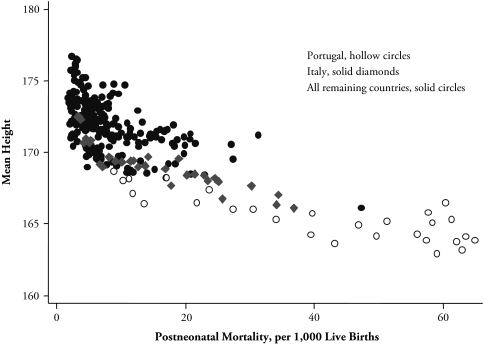
Given the skeletal nature of the stunting and selection model, these results are encouraging in that they enable us to interpret the original results within a parsimonious model. Even so, these data cannot provide a thoroughgoing test of the model. The problem is that the stunting effect, which we knew in advance was important, is built into the model by construction, and the selection effect and the possible nonmonotonicity of the relationship between height and infant mortality, which are the interesting predictions of the analysis, are unlikely to be apparent in low-mortality environments. Indeed, the curvature of the relationship between adult height and PNM rests heavily on the experience of the (then) highest mortality countries—particularly Portugal and, to a lesser extent, Italy (see Figure 4). To investigate the model further, we turn to a different source of data with a much wider range of mortality experience.

Figure 4.

Mean Height and Postneonatal Mortality: Europe and the United States, 1950 to 1980

We use information on the heights of women who were measured in the international system of Demographic and Health Surveys (DHS). These surveys, whose main subject is reproductive and child health, have measured the heights of women aged 15 through 49 in more than 40 countries since the late 1990s. The countries that we use are listed in Appendix D; there are 27 in Africa, 8 in Latin America and the Caribbean, 3 (India, Bangladesh, and Nepal) in South Asia, and 5 in Central Asia (which we group with the Egyptian and Moroccan surveys from Africa to form a Middle East and North African region.) As is to be expected, the availability of other data for these countries is not as good as for Europe and the United States. Although we have annual data on income per capita in international purchasing power parity dollars from the Penn World Table that can be matched to the adult height of each birth cohort in most of the surveys, we do not have any consistent international data on PNM, and for many of these countries, such data do not exist. Instead, we turn to the infant mortality rates provided by the United Nations population division, which are available for five-year intervals after 1950. (Childhood mortality up to age 5 is often more accurately measured than infant mortality rates because of uncertainty about birth dates, but this information is not available from the United Nations, and World Bank data begin only in 1960.)

We also note that, compared with the rich countries of Europe and North America, the poorer countries have much greater mortality between infancy and adulthood, when heights are measured. In consequence, there is a case for measuring mortality not only in infancy but at least through to early adulthood, and the model of the previous section can be thought of in this way. For the rich, northern countries, this adjustment makes very little difference because there is so little mortality between, say, age 1 and age 15; for most of the poorer countries in other regions, there are no good data on mortality after childhood. One approach is simply to ignore the problem and use the infant mortality rates, and we have calculated all the results below on that basis. However, the results we actually report are based on scaling up each country’s own infant mortality rates by our own estimates of the ratio of 0–15 mortality to 0–1 mortality, where the ratios are estimated by region and five-year periods. This approach, which is akin to the use of model life tables, uses partial U.N. data on 0–15 mortality rates to estimate the set of period and regional correction factors listed in Table 4, whose footnotes detail the data sources. The models with these corrected mortality rates give very similar results to the models using the original infant mortality rates, though the fit is always slightly superior. Given this, and the desirability of making some correction for later mortality, these are the results that we report.

Table 4.

Estimated Ratios of 0–15 Mortality to 0–1 Mortality

Birth Cohort	Latin America and the Caribbean	Middle East and North Africa	Europe and the United States	South Asia	Sub-Saharan Africa
1950–1954	1.21	1.46	1.08	1.46	1.16
1955–1959	1.19	1.47	1.08	1.46	1.22
1960–1964	1.18	1.50	1.08	1.46	1.30
1965–1969	1.17	1.52	1.08	1.46	1.38
1970–1974	1.17	1.55	1.08	1.46	1.46
1975–1979	1.16	1.58	1.08	1.47	1.54
1980–1984	1.15	1.60	1.09	1.47	1.61

Source: Authors’ calculations from regressions with period and regional effects of incomplete U.N. data, accessed online (http://unstats.un.org/unsd/demographic/products/dyb/dybhist.htm) and from United Nations (1986).

Both the switch from postneonatal to pre-adult mortality and the move from rich to poor countries change the way in which we need to think about the effects of income and disease on mortality rates, as well as on adult heights. For the rich countries after 1950, PNM was largely a reflection of the disease environment, not of gross nutritional adequacy in terms of food intake, which was unlikely to have been a limiting factor. Infant mortality includes both neonatal and postneonatal mortality, and in poor countries in Africa and South Asia, it is almost certainly affected by the availability of food, by disease, and by interactions between them (Scrimshaw, Taylor, and Gordon 1968). Food inadequacy makes children more likely to succumb to at least some infections, and the growth inhibition from the infection will be made up later only if there is adequate nourishment. Hence, unlike the case in the rich countries, infant mortality rates capture the effects both of disease and of food inadequacy (or low income), while food inadequacy itself is likely to affect adult height even conditional on infant or childhood mortality.

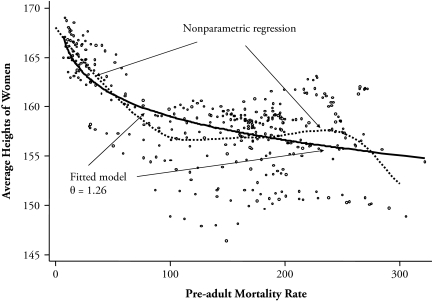
Figure 5 shows a plot of women’s heights against the pre-adult mortality rate (pooling the DHS with the European and North American data); there are 320 observations across countries and five-year periods. Each point is the mean of women’s height in a five-year birth cohort versus the pre-adult mortality rate for the same period; we use data only on women aged 20 or older because women in poor countries sometimes attain adult height at later ages than in rich countries. (Indeed, age 20 is too young for South Asia, but an older cutoff would eliminate many otherwise valid data points.) Imposed on the scatter-plot, we show two lines. The broken line is a nonparametric regression fit, which shows height declining with infant mortality in the year of birth throughout most of the range, but with an upturn beginning at levels of pre-adult mortality above 100 per thousand; this regression eventually declines again in recognition of the few points on the bottom right. The solid line shows the fitted values of the selection and stunting model, again using the Danish standard, without country fixed effects and with fitted estimates for θ and z of 1.26 and 3.69 standard deviations below the mean, respectively. This value of θ is too high to give nonmonotonicity, even at high values of infant mortality, but it otherwise provides a reasonable fit to the general pattern of the data.

Figure 5.

Women’s Average Heights and Pre-adult Mortality Rates Around the World

As was the case for Europe and the United States, the fit is improved and the estimate of θ is reduced (to 0.69) if we include dummy variables for five regions of the world (Europe/United States, Middle East and North Africa, South Asia, Latin America and the Caribbean, and sub-Saharan Africa). The regional dummy variables are important, and given the cohort pre-adult mortality levels, women in Latin America and in South Asia are shorter and women in sub-Saharan Africa are taller than would be expected from the selection and stunting alone. This is the adult version of the child malnutrition–child mortality puzzle previously noted by Klasen (2006). Within the model, the regional effects are interpretable as regional differences in medical treatment or public health. In this global context, they might also reflect genetic variations in potential height, although it is perhaps more likely that there are no genetic differences and the variation in heights comes from the fact that the adaptation of height to the tightening or loosening of environmental constraints takes many generations. There are limits to the size of children that small women can bear, and it has been argued that the century and a half of secular increase in heights in Europe, which was both large and too rapid to be genetically based, was simply the time taken to adjust to the better environment after 1850 (Cole 2000).

It is also useful to estimate less tightly specified regressions in which we can include both income and infant mortality rates. Table 5 shows quadratic regressions with log income alone, pre-adult mortality alone, or both, in which case we include an interaction between log income and pre-adult mortality. Year of birth effects (or, in the pre-adult mortality regressions, five-year period of birth effects) are always included, and the columns show results with and without regional and country fixed effects. For both income (columns 1–3) and infant mortality (columns 4–6), the quadratic effects are strongly significant; income decreases height in the poor countries and increases it among the rich, and infant mortality increases height in poor countries and decreases it in the rich ones. The inclusion of regional or country effects much diminishes the role of either income or infant mortality, but the quadratic shape is preserved.

Table 5.

Regressions of Height on Log Income and Pre-adult Mortality

Variable	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)
lny	−32.30 (1.66)	−4.20 (1.05)	−5.12 (0.94)				−18.90 (5.50)	6.86 (3.90)	−1.85 (3.42)
lny2	2.16 (0.103)	0.31 (0.067)	0.40 (0.059)				1.02 (0.28)	−0.31 (0.20)	0.20 (0.19)
mr (÷10)				−1.023 (0.10)	−0.53 (0.11)	−0.67 (0.08)	−2.54 (0.96)	0.32 (0.60)	−0.11 (0.50)
mr2 (÷100)				0.003 (0.000)	0.001 (0.000)	0.001 (0.000)	0.004 (0.000)	0.001 (0.001)	0.001 (0.000)
lny × mr							0.127 (0.09)	−0.112 (0.05)	−0.036 (0.052)
Region	No	Yes	No	No	Yes	No	No	Yes	No
Country	No	No	Yes	No	No	Yes	No	No	Yes
R2	.40	.78	.97	.46	.78	.99	.58	.82	.99
F(y)	495	24	56	—	—	—	9.83	1.66	5.30
F(mr)	—	—	—	245	12	41	57.6	18.3	6.65
N	1,514	1,514	1,514	360	360	360	288	288	288

Notes: Heteroskedasticity-robust standard errors are reported in parentheses. The F tests in the last panel are tests of the hypothesis that the coefficients involving either lny, for F(y), or mr, for F(mr) are zero; for example, in columns 7, 8, and 9, the former is the test that the coefficients on log income, log income squared, and the interaction of log income and pre-adult mortality rate are jointly zero. In these regressions, for presentational clarity, mr has been divided by 10, and is expressed in deaths per 100. Region refers to a set of region dummy variables representing North (the rich, developed countries), Latin American and the Caribbean, Middle East and North Africa, South Asia, and sub-Saharan Africa. Country refers to a set of country dummy variables, one for each country. All regressions include a set of dummy variables for birth cohort.

Columns 6–9 fail to provide any clear adjudication between income and infant mortality. In these regressions, the coefficients are often individually insignificant, and the importance of different sets of variables is best seen from the F statistics at the bottom of the table. In all specifications, the loss of fit to excluding pre-adult mortality is larger than the loss of fit to excluding income, but the income effects are significant in two out of the three specifications. The safest conclusion is perhaps that for this broader range of countries, both income and disease are important in determining adult height.

The introduction of income into the regressions does nothing to reduce the marked heteroskedasticity in Figure 5, with the scatter of adult heights around the regression much larger in the countries with high mortality. Again, much of this comes from Africa, where there is enormous diversity of average heights across countries, presumably reflecting local nutritional, environmental, and disease conditions (or even genetic differences) that are not captured either by income per capita or by infant mortality rates.

We view the results in Figure 5 and Table 5 as supportive of the idea that the balance between selection and stunting may change as the mortality rate falls. However, we also note the considerable uncertainties induced by the weak data for the high-mortality countries, and the fact that our model is a skeletal one, with only one key parameter. Such stripped-down models are better for clarifying concepts than for fitting the data. Yet, there is support for the idea that selection may offset stunting at very high levels of mortality from a remarkable study of the Great Chinese Famine of 1959–1961 by Gørgens et al. (2007). Although the famine caused 20 to 30 million excess deaths, most of them children, so that perhaps as much as half of the relevant birth cohorts died, the adult heights of the survivors are no different from those of cohorts born immediately before or after the famine. Gørgens et al. provided creative and convincing evidence that this “nonfinding” is in fact the result of a close to exact offset between selection and stunting. According to the theory, the survivors are in fact potentially taller than average but were reduced to average by malnutrition in childhood. That this is in fact the case is demonstrated by examining the heights of their children, who inherited their parents’ genetic propensity to be tall but did not experience the famine and who indeed are taller than the children of those born immediately before or after the famine.

SUMMARY AND CONCLUSIONS

We used data on 31 birth cohorts from 11 European countries and from the United States to investigate the early childhood determinants of adult height. We found that infant mortality, specifically PNM, predicts the adult height of the birth cohort that survives it. Given that PNM is a sensitive indicator of the disease environment in the first year of life, these results support accounts in which some form of “scarring” in infancy negatively affects lifetime health, as marked by adult height. In these low-mortality countries, the stunting effect of childhood disease dominates any possible height-based selective mortality in childhood that would induce a positive relationship between disease in early life and adult health.

In our pooled cross-section and time-series data from Europe and the United States, variations in PNM can explain more than 60% of the variation in adult heights, and the fall in PNM can account for almost all of the increase in adult heights between those born in 1950 and those born in 1980. More importantly, PNM displays a distinct historical pattern, falling to its minimum attainable level and then flattening out. This pattern is common across countries, but the timing of the flattening out differs from country to country. The international variation in the timing of the pattern of PNM matches the country-by-country timing in the rise and flattening out of average heights. Fluctuations in national income play no such role, even though national income and average height are closely correlated in the cross section.

We also find that the component of PNM that most closely predicts adult heights is mortality from pneumonia, not mortality from congenital anomalies, mortality from intestinal disease, or mortality from other causes. Our finding is consistent with the literature that argues that childhood diseases elicit inflammatory responses that make heavy demands on nutrition and that compromise ultimate growth. The lack of any response to per capita GDP, albeit at best a weak measure of nutrition, suggests a relatively weak role for gross nutrition.

The situation is different once we examine poor and rich countries simultaneously. Among the poorest, highest mortality countries, we find evidence for distinct effects on adult height of both disease and of food availability, as represented by income; these results suggest that early childhood development is constrained both by food and by disease in poor countries, whereas the food constraint has not been important since 1950 in countries that are now rich. More notably, albeit with evidence that is best viewed as suggestive, we find that selection may be stronger than stunting at high levels of mortality and low levels of income, which would explain at least part of the African height paradox—that Africans are relatively tall in spite of extremely unfavorable income and disease environments. It is also consistent with the effect of the 1959–1961 Chinese famine on the heights of the survivors (Gørgens et al. 2007). There is much stronger evidence that the effect of pre-adult mortality on adult height is weaker at higher mortality rates, which we attribute to the fact that selection is stronger at high mortality. Even so, remarkably little is understood about global patterns of height, which are difficult to account for even in loosely parameterized models involving income and mortality, even allowing for regional effects (Deaton 2007).

Our results are also relevant for understanding the link between adult height and late-life chronic disease, and how that correlation might change historically and geographically. There is evidence that height is protective against cardiovascular disease in late life (Jousilahti et al. 2000; Leon et al. 1995; Waaler 1984), which is consistent with an interpretation in which both adult height and late-life disease are caused by childhood disease. It is also possible that childhood disease, the quantity v_t in the model, has a different effect on adult height from its effect on late-life disease, although there will still be an apparently protective effect of height on disease, reflecting the role of childhood disease on both. If so, and if it is true that selection outweighs stunting on adult heights in the highest-mortality environments, the negative correlation between adult height and late-life chronic disease may be eliminated or even reversed. In rich countries with low infant mortality, taller people have a survival advantage, even conditional on obesity and other risk factors, but this advantage may not exist in poor, high-mortality countries now, and may not have existed historically in the now rich countries. This is because the survivors of extreme negative environments, although selected for both height and health, are still heavily scarred by their childhood environment, and it may be the scarring more than the selection that predicts late-life chronic disease, even though both affect height in the same way. Unfortunately, we do not have data on mortality from cardiovascular disease from sub-Saharan Africa on which this prediction might be tested. Even so, recent work by Costa (2002, 2004) and by Costa, Helmchen, and Wilson (2007) has shown or inferred very high levels of late-life morbidity among veterans of the nineteenth-century Union Army in the United States, including morbidity associated with arteriosclerosis and ischemic heart disease, at least some of which the authors attribute to early-life infections. Interestingly, and consistently with our account here, Costa et al. (2007) found that adult height at enlistment did not predict arteriosclerosis in late life among the survivors. In the historical record, as in the poorest countries now, the prevalence of late-life chronic disease is masked by the importance of infectious diseases. But it is quite possible that the age-specific prevalence of chronic disease was higher in the past than now and is currently high in some of the currently poorest countries of the world.

APPENDIX A. CLASSIFICATIONS OF PNM CAUSES

PNM From Pneumonia (Cause 1)

ICD5: Bronchopneumonia (107); lobar pneumonia (108); pneumonia (unspecified) (109).

ICD7: Bronchopneumonia (491); lobar pneumonia (490); primary atypical pneumonia (492); pneumonia, other and unspecified (493).

ICD7A: Bronchopneumonia (A090); lobar pneumonia (A089); primary atypical, other, and unspecified pneumonia (A091).

ICD8A: Viral pneumonia (A091); other pneumonia (A092).

ICD9B: Pneumonia (B321).

PNM From Intestinal Disease (Cause 2)

ICD5: Enteritis and diarrhea with/without mention of ulceration of the intestines (except duodenum) (119); enteritis and diarrhea without mention of ulceration, or ulceration of the intestines (except duodenum) (120).

ICD7: Gastritis and duodenitis (543); gastro-enteritis and colitis, except ulcerative, age 4 weeks and over (571); chronic enteritis and ulcerative colitis (572).

ICD7A: Gastritis and duodenitis (A101); gastro-enteritis and colitis, except diarrhea of the newborn (A104).

ICD8A: Enteritis and other diarrhoeal diseases (A005).

ICD9B: Intestinal infectious diseases (B01) (cholera, typhoid fever, shigellosis, food poisoning, amoebiasis, intestinal infections due to other specified organism, ill-defined intestinal infections, other).

PNM From Congenital Anomalies (Cause 3)

ICD5: Congenital hydrocephalus (157a); spina bifida and meningocele (157b); congenital malformation of heart (157c); monstrosities (157d); congenital pyloric stenosis (157e); cleft palate and harelip (157f); imperforate anus (157g); cystic disease of kidney (157h); congenital malformations of the central nervous system (157ia); congenital malformations of the circulatory system (157ib); congenital malformations of the digestive system (157ic); congenital malformations of the genitor-urinary system (157id); other stated malformations (157ie); congenital malformations (unspecified) (157j).

ICD7: Monstrosity (750); spina bifida and meningocele (751); congenital hydrocephalus (752); other congenital malformations of the nervous system and sense organs (753); congenital malformations of the circulatory system (754); cleft palate and harelip (755); congenital malformations of the digestive system (756); congenital malformations of the genitor-urinary system (757); congenital malformations of bone and joint (758); other and unspecified congenital malformations, not elsewhere classified (759).

ICD7A: Spina bifida and meningocele (A127); congenital malformations of circulatory system (A128); all other congenital malformations (A129).

ICD8A: Spina bifida (A126); congenital anomalies of heart (A127); other congenital anomalies of circulatory system (A128); cleft palate and cleft lip (A129); all other congenital anomalies (A130).

ICD9B: Congenital anomalies (B44) (spina bifida and hydrocephalus, other deformities of central nervous system, congenital anomalies of heart and circulatory system, cleft palate and cleft lip, other deformities of digestive system, undescended testicle, congenital dislocation of hip, other congenital anomalies of musculoskeletal system, other).

Sweden 1950

Causes of death according to the Swedish list of 1931 are as follows:

• PNM from pneumonia: pneumonia and bronchopneumonia (3520–3530).

• PNM from intestinal disease: diarrhea and enteritis (1150, 4020).

• PNM from congenital anomalies: congenital malformations (0001).

Appendix Table B1.

Missing Causes

Country	1950	1951	1952	1953	1954	1955	1956	1957	1958	1959	1960	1961	1962	1963	1964	1965	1966	1967	1968	1969	1970	1971	1972	1973	1974	1975	1976	1977	1978	1979	1980
Austria	A	A	A	B	B	B	C	C	C	C	C	—	—	—	—	C	C	C	C	D	D	D	D	D	D	D	D	D	D	D′	E
Belgium	—	—	—	—	B	B	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	D′	—	—	—
Denmark	A	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	—	D′	D′
England and Wales	B	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	D	D′	E	E
Finland	B	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D′	D′	D′	—	—
Greece	—	—	—	—	—	—	—	—	—	—	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	D	D	E	—
Ireland	B	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	—	—	—	—	—	—	—	—	D′	D′	D′	—	—
Italy	A	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D′	D′	D′	—	—
Portugal	A′	A′	A	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	—	C	—	D	D	D	D	D	D′	D′	D′	D′	—
Spain	A	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	—	D	D′	D′	—	—
Sweden	S	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	D	D′	D′
United States	B	B	B	B	B	B	C	C	C	C	C	C	C	C	C	C	C	C	D	D	D	D	D	D	D	D	D	D	D′	—	—

Notes: A = list of 1938; A′ = list of 1929; B = list of 1948; C = list of 1955; D = list of 1965; D′ = ICD 8A; E = ICD 9; S = Swedish list of 1931; and a dash indicates missing data.

APPENDIX C. NOTES ON MISSING CAUSES

1950

Austria: Causes of death are only available at the Infant Mortality Rate level. Spain: “congenital malformations” (157) and “diseases peculiar to the first year of life” (158–161) are reported together; hence, this observation is discarded. Portugal: “congenital Malformations” (157) and “diseases peculiar to the first year of life” (158–161) are reported together; hence, this observation is discarded.

1951

Austria: Causes of death are available only at the infant mortality rate level. Portugal: “congenital malformations” (157) and “diseases peculiar to the first year of life” (158–161) are reported together; hence, this observation is discarded.

1952

Finland: Cause 2 is available only at the infant mortality rate level. Ireland: Cause 2 is available only at the infant mortality rate level.

1955

Austria: Cause 2 is missing. England and Wales: Cause 2 is available only at the infant mortality rate level.

1956

Austria and Ireland: Cause 2 is missing.

1961 and 1964

Ireland: Cause 2 is available only at the infant mortality rate level.

1965

Austria and Ireland: Cause 2 is available only at the infant mortality rate level.

1966

Ireland: Cause 2 is available only at the infant mortality rate level.

1967

England and Wales: Cause 2 is available only at the infant mortality rate level.

1972, 1973, and 1975

Portugal: Cause 3 is available only at the infant mortality rate level.

APPENDIX D. COUNTRY AND YEAR LISTING OF DHS SURVEYS

Sub-Saharan Africa

Benin 2001, Burkina Faso 2003, Cameroon 2004, Central African Republic 1994, Chad 2004, Comoros 1996, Cote d’Ivoire 1998, Ethiopia 2000, Gabon 2000, Ghana 2003, Guinea 1999, Kenya 2003, Lesotho 2004, Madagascar 1997, Malawi 2004, Mali 2001, Mozambique 2003, Niger 1998, Nigeria 2003, Rwanda 2000, Tanzania 1998, Togo 1998, Uganda 1995 and 2000, Zambia 2001, Zimbabwe 1999.

Middle-East and North Africa

Armenia 2000, Egypt 1995 and 2000, Kazakhstan 1999, Kyrgyz Republic 1997, Morocco 2003, Turkey 1998, Uzbekistan 1996.

Latin America and the Caribbean

Bolivia 1993, 1998 and 2003, Brazil 1996, Colombia 1995, 2000 and 2004, Dominican Republic 1996, Guatemala 1998, Haiti 1994 and 2000, Nicaragua 2001, Peru 1996 and 2000.

South Asia

Bangladesh 2004, India 1999, Nepal 2001.