Recrossing and Dynamic Matching Effects on Selectivity in a Diels-Alder Reaction

Abstract

The products from the hetero-Diels-Alder reaction of acrolein with methyl vinyl ketone arise from a single transition state and trajectory studies accurately predict the selectivity. In an extension of the dynamic matching idea of Carpenter, the product formed is determined by the direction of motion passing through the transition state. Recrossing of the cycloaddition transition state occurs extensively and decreases formation of the minor product.

The products and selectivities of some organic reactions cannot be explained within the normal framework of reaction barriers and transition state theory. In these cases, explicit consideration of the detailed motions and momenta of the atoms can often rationalize the experimental results.[1] Such reactions may be described as involving “dynamic effects.” The recognition of the breadth of reactions involving dynamic effects and the detailed understanding of experimental observations in these reactions remains a substantial challenge in chemistry.

Dynamic effects can arise in several ways. In reactions involving “dynamic matching,” the selectivity after passing through a shallow intermediate is related to the momentum of atoms crossing an initial transition state.[2–4] Other reactions involve “bifurcating energy surfaces,” in which reactions that pass through a rate-limiting transition state can proceed downhill to two or more products.[5–11] A third dynamic effect involves the recrossing of barriers; much recrossing is predictable and handled well by variational transition state theory, but some recrossing is not readily predictable statistically,[12] and such “non-statistical recrossing” can affect observations in organic reactions.[9] Reactions can involve a complex combination of dynamic effects.[9–13]

A number of cycloadditions involve bifurcating energy surfaces,[7–10] and the understanding of selectivity in unsymmetrical examples is a difficult problem. In general terms, the effects influencing the selectivity between products on a bifurcating surface may be artificially divided into “static factors,” i.e., the geometry of the initial transition state and the shape of the energy surface beyond the transition state, and “dynamic factors,” i.e., effects associated specifically with the momenta of atoms. The latter category would include both dynamic matching and non-statistical recrossing. Previous studies of Diels-Alder reactions have focused on static factors,[7,10] and this has provided qualitative guidance in rationalizing the major products and which reactions are highly selective versus unselective. The role of dynamic factors is much less easily assessed, even with the aid of trajectory studies. Trajectory studies inherently incorporate dynamic factors affecting the selectivity and have proven highly successful in predicting product ratios,[3b,3c,6b,7,8c,9] but provide little direct guidance to intuitive understanding.

We describe here a combined experimental and theoretical study of diene/dienophile role selectivity in a synthetically useful hetero-Diels-Alder reaction. The results demonstrate the importance of dynamic factors, particularly non-statistical recrossing and a new form of dynamic matching, in controlling the selectivity of Diels-Alder reactions involving bifurcating surfaces.

The simple hetero-Diels-Alder reaction of acrolein (1) with methyl vinyl ketone (2) has found synthetic application including the total synthesis of brevicomin.[14,15] Aside from homodimers, this cycloaddition affords two cross products: 3, in which methyl vinyl ketone has acted as the dienophile, and 4, in which acrolein has acted as the dienophile. The 3 : 4 ratio was previously reported as 10 : 1, but the product ratio changes with time as these isomers interconvert by what was proposed to be a Cope-type rearrangement.[14,16]

The formation of mixtures of products complicates the direct determination of the reaction kinetics, so we opted for an indirect process. Looking at the simple Diels-Alder dimerization of 1, the activation energy was 21.9 ± 1.2 kcal/mol, based on initial rates over a temperature range from 100 – 180 °C. In the mixed reaction of 1 with 2 at 80 °C, the cross products 3 and 4 are formed in sum with a rate constant 5.1 ± 0.5 times greater than the rate constant for dimerization of 1. Assuming that this difference is due to activation energy, the barrier for the cross reaction is ≈20.8 kcal/mol.

The 3 : 4 ratio varies at a significant rate even at 80 °C. On prolonged heating, ketone 3 is favored and less than 2% of 4 was observed. Pyrolyses of the Diels-Alder cycloadducts did not afford observable monomers up to 180 °C. From the rate of the slow decomposition of 3 in a pyrolysis at 180 °C in dibenzyl ether, an upper limit for the rate of the retro-Diels-Alder reaction of 2.5 × 10⁻⁶ s⁻¹ could be estimated. This is at least 10 times slower than the loss of 4 at this temperature. The complete reaction composition versus time was kinetically modeled in a series of experiments up to 160 °C (see the Supporting Information) assuming bimolecular kinetics for the Diels-Alder reactions, unimolecular isomerization of 4 to 3, and negligible rates for conversion of 3 to 4 and retro-Diels-Alder steps. From this analysis, the best-fit relative rate for formation of 3 : 4 was 2.5 ± 0.4 : 1.

Conventional theoretical analysis of this reaction does not account for the product ratio. Ignoring non-observed regioisomers and considering all possible combinations of endo versus exo approach, s-cis versus s-trans dienophile conformation, and 1 versus 2 acting as the diene, a total of eight transition structures (TSs) for the reaction of 1 with 2 may be considered. TS 5 (Figure 1) was by far the lowest in energy in a variety of calculations (B3LYP, MPW1K, and MP2 with various basis sets, either in the gas phase or with full optimization using a PCM solvent model for benzene, and including CCSD(T)/6-31+G** gas phase and PCM single-point energies, see the Supporting Information for a full list). The predicted activation energy for TS 5 in the best calculation (CCSD(T)/6-31+G**/PCM//MP2/6-311+G**/PCM + zpe + thermal energy for 25 °C) was 19.9 kcal/mol, within the uncertainty of the experimental barrier above.

Figure 1.

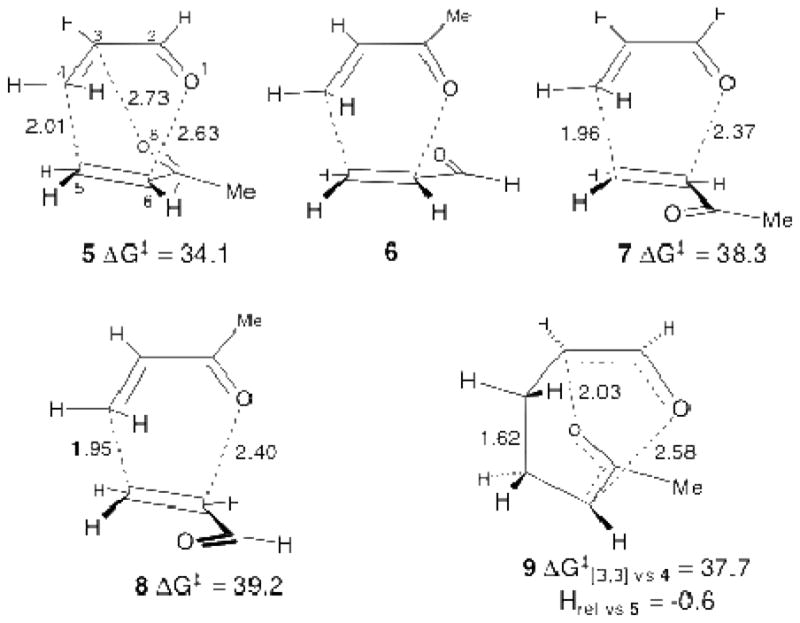
TSs of relevance to the reaction of 1 with 2. Four additional high-energy structures are shown in the Supporting Information. Distances shown refer to the MP2/6-311+G**/PCM TSs. Free energies are CCSD(T)/6-31+G**/PCM//MP2/6-311+G**/PCM + a harmonic free-energy estimate for 298 K in kcal/mol. No TS corresponding to 6, defined as an endo s-cis TS leading by MEP to 4, could be located in high-level calculations. TS 9 is for the [3,3]-sigmatropic rearrangement interconverting 4 and 3.

Of the seven remaining possible TSs, only six are actually present. Four s-trans TSs were quite high in energy (>6.9 kcal/mol above 5) and these are shown in the Supporting Information. The remaining three possibilities are structures 6 through 8 in Figure 1. However, no TS corresponding to 6 could be located in the MP2 or DFT calculations despite substantial effort. All searches for 6 instead afforded 5. Steepest descent paths in both mass-weighted coordinates (the minimum-energy path, MEP) and Cartesian coordinates starting from TS 5 lead to 3, and 5 is greatly favored over the lowest-energy TS leading to 4 (TS 8) in all of the calculations. At the CCSD(T)/6-31+G**/PCM//MP2/6-311+G**/PCM level, a harmonic free-energy estimate for 100 °C favored 5 over 8 by 4.9 kcal/mol. This predicts that 3 should be formed 700 times faster than 4, in clear contrast to experiment. A hidden assumption in this analysis, however, was that TS 5 could only afford 3.

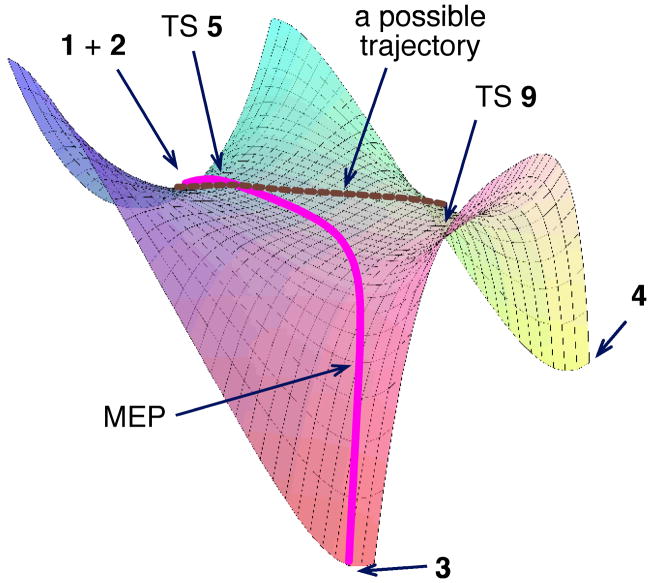
The absence of TS 6 and the inability of transition state theory to account for the product mixture support the involvement of a bifurcating energy surface in this reaction, as qualitatively depicted in Figure 2. On this surface, the two idealized endo s-cis pathways through TSs 5 and 6 have merged to give a single cycloaddition TS. The resulting structure 5 is then poised to form both 3 and 4; the C3 O8 distance in 5 is only slightly longer than the C6 O1 distance. In this regard, TS 5 closely resembles a C₂-symmetric bispericyclic TS found by Caramella for the dimerization of methacrolein.[8] We postulated that the experimental selectivity results from trajectories passing through 5 to both 3 and 4.

Figure 2.

Qualitative potential energy surface in the reaction of 1 with 2. The products 3 and 4 are both downhill from the rate-limiting TS. Trajectories can lead to either product, but the MEP only leads to 3.

To explore this issue, transition structure 5 was used as the starting point for quasiclassical direct dynamics trajectories[17] on the MP2/6-311+G** energy surface. While MP2 calculations generally underestimate pericyclic barriers, the MP2 surface was chosen for this study because it most accurately depicts the shape of the energy surface on the product side of 5. In particular, the DFT methods incorrectly place 9, the [3,3]-sigmatropic rearrangement TS for interconversion of the two products, higher than 5, in conflict with our experimental observations above.

With all atomic motions freely variable, the trajectories were initialized by giving each mode its zpe plus a Boltzmann sampling of additional energy appropriate for 80 °C, with a random phase and sign for its initial velocity. The transition vector was given a Boltzmann sampling of translational energy ‘forward’ from the col. Employing a Verlet algorithm, 1-fs steps were taken until either 3 and 4 were formed (median time 116 fs) or recrossing occurred to afford the starting materials (median time 101 fs).

Strikingly, the trajectory results (Table 1) not only account for the formation of both 3 and 4, but also quite accurately predict the experimental ratio. The precision of this prediction is limited by a practical limit on the number of trajectories calculated. Considering also the experimental uncertainty, the close agreement is to some degree fortuitous. It should be noted that a qualitative consideration of the static potential energy surface could only predict that 3 would be favored, not distinguishing whether the preference would be slight or exclusive. The agreement between the experimental and calculated ratios supports the idea that the trajectories accurately represent the underlying physics engendering the selectivity.

Table 1.

Outcome of quasiclassical trajectories starting from 5.

Trajectories affording 3	Trajectories affording 4	Trajectories recrossing to 1 + 2
89	33	174
ratio 3 : 4 = 2.7
95% confidence: 1.9 – 4.3

A remarkable observation is the large number of trajectories that undergo recrossing of the transition state. Greater than 50% of the trajectories fully form the C4 C5 bond (to <1.6 Å), passing geometrically through the area of [3,3]-sigmatropic rearrangement TS 9, then run into a potential energy “wall” associated with a short C4 C5 internuclear distance and bounce back to starting materials. The recrossing trajectories may not be understood as a statistical partitioning from 9; of 10 trajectories started statistically from the area of 9, none afforded 1 + 2. To check that the high recrossing was not a spurious result of intramolecular vibrational-energy redistribution (IVR) in the quasiclassical trajectories, a limited number of fully classical trajectories, not subject to the IVR problem, were carried out. Of 38 such trajectories, 19 recrossed.

To understand the nature of the selectivity in the reaction, the relationship of the starting atomic positions and momenta to the outcome of individual trajectories was examined in detail. Surprisingly, there was no substantial correlation between the trajectory outcomes and the starting position for trajectories (i.e., the starting geometry along the transition state ridge arising from the random phases for the modes). However, a strong correlation was observed between the trajectory outcomes and the initial velocity in a 98-cm⁻¹ internal vibrational normal mode in 5. When the initial velocity in this mode was “negative” (the sign is arbitrary), 3 is formed. The same is true when the velocity is slightly positive (< 1200 meters/s), as a small positive velocity does not overcome the energy surface’s bias toward 3. A more positive velocity in this mode leads to the formation of 4. This criterion predicts the outcome of 86% of the productive trajectories!

The origin of this correlation may be understood by considering the motion associated with the 98-cm⁻¹ mode. As shown in Figure 3, a negative motion in this mode closes the C6–O1 distance and distorts the transition structure toward 3. A strongly positive motion in this mode closes the C3–O8 distance and leads toward 4, but if this velocity is small a general bias in the system for the formation of 3 still dominates.

Figure 3.

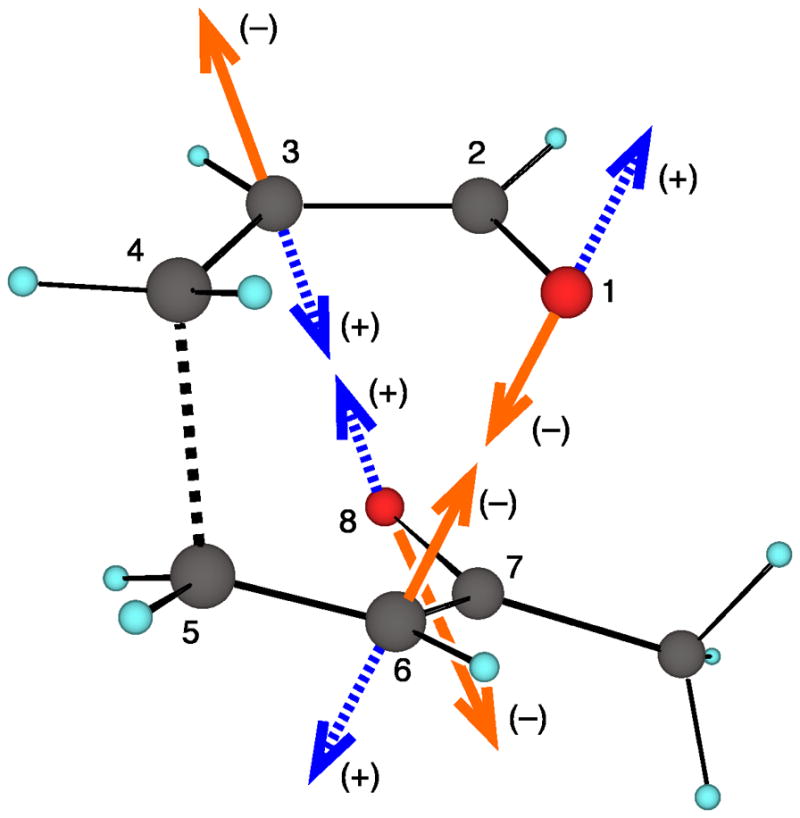
Heavy-atom motion associated with the 98-cm⁻¹ mode of 5. Motion in the negative direction moves the structure toward 3 while a positive motion approaches 4.

This close correlation of the product outcome with the motions of atoms at the transition state may be viewed as a form of dynamic matching. In its original formulation, dynamic matching referred to a correlation of the dynamics of atoms at an initial transition state with the choice of exit channels from a shallow intermediate.[2b] There is no intermediate in the current system, and the correlation that exists is defined by subsets of the motions at the transition state, rather than the transition state as a whole. However, in the absence of molecular energetic equilibration the presence versus absence of an intermediate is a semantic question and structures are better defined by their lifetime. The lifetime here is very short, but the relationship of the product selectivity to motion at the transition state fits clearly within the dynamic matching idea.

The critical role of dynamic matching in the selectivity here, along with the negligible role of the starting position for trajectories crossing the transition state ridge, contrasts sharply with results we reported in a previous study of Diels-Alder reactions of cyclopentadienones.[7] In retrospect, the previous work emphasized a minor trend while missing the major role of dynamic matching.

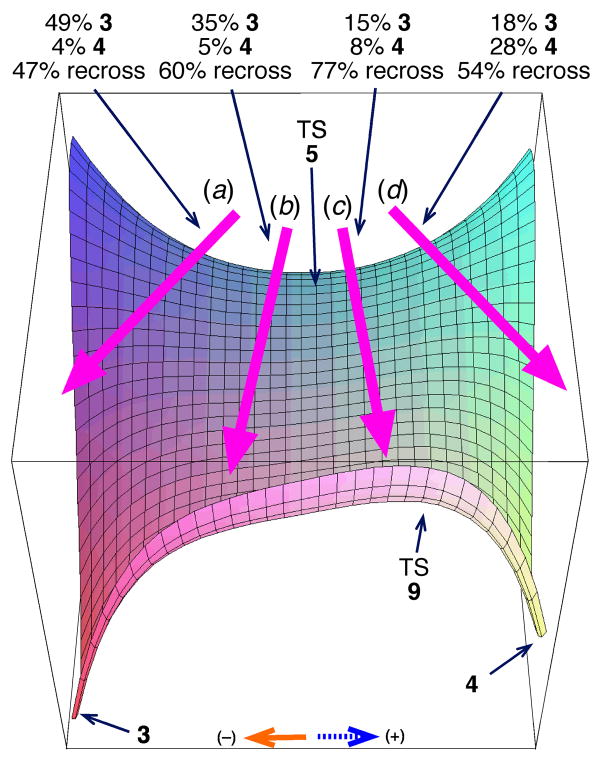
Recrossing also plays a significant role in determining the observed product mixture. Figure 4 illustrates the differing outcomes of trajectories depending on the “angle” at which the trajectories leave the transition state (defining the angle from the momentum in the 98-cm⁻¹ mode compared to the momentum in the transition vector, ignoring other normal modes). Recrossing is substantial at all angles; the trajectories must thread a multidimensional needle to bring C6 and O1 or C3 and O8 together during the few dozen femtoseconds that C4 and C5 are bonded. However, a significantly higher proportion of the trajectories angled toward 4 (c and d in Figure 4) recross compared to those angled toward 3 (a and b). Trajectories that avoid the middle of the surface are more likely to be productive; the category c trajectories aimed roughly toward TS 9 recross at a particularly high rate. Without recrossing, 3 would still be favored but the ratio of products would be lower by about 20%. Our previous work showed that non-statistical recrossing affected experimental observations in ketene cycloadditions,[9] but the current results suggest that the impact of this effect will be much broader.

Figure 4.

Outcome of trajectories versus the angle (see text) at which they leave the transition state. On this qualitative potential energy surface, the horizontal axis corresponds to motion along the 98-cm⁻¹ vibrational mode and the orthogonal axis is motion along the transition vector. The arrows labeled a, b, c, and d refer to trajectories within a range of angles: a: <−26°; b: between −26° and 0°; c: between 0° and 26°; d: >26°.

In reactions where transition state theory is applicable, product ratios are simple to understand qualitatively from the properties of transition states, following rules that are closely analogous to those well understood for stable structures. In contrast to the simplicity of transition state theory, the dynamic factors governing selectivity here are foreign to everyday understanding. Transition state theory surely governs the kinetic selectivity observed in most reactions, but for a growing number of reactions recognizably involving dynamic effects, consideration of the kinds of ideas encountered here will be necessary to understand the selectivity.