Abstract
Identification and characterization of ensembles of intermediate states remains an important objective in describing protein folding in atomic detail. The 67-residue villin headpiece, HP67, consists of an N-terminal subdomain (residues 10–42) that transiently unfolds at equilibrium under native-like conditions and a highly stable C-terminal subdomain (residues 43–76). The transition between folded and unfolded states of the N-terminal domain has been characterized previously by 15N NMR relaxation dispersion measurements [Grey et al., J. Mol. Biol. (2006) 355, 1078]. In the present work, 13C spin relaxation was used to further characterize backbone and hydrophobic core contributions to the unfolding process. Relaxation of 13Cα spins was measured using the Hahn echo technique at five static magnetic fields (11.7, 14.1, 16.4, 18.8, and 21.1 T) and the Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion method at a static magnetic field of 14.1 T. Relaxation of methyl 13C spins was measured using CPMG relaxation dispersion experiments at static magnetic fields of 14.1 and 18.8 T. Results for 13C and 15N spins yielded a consistent model in which the partially unfolded intermediate state of the N-terminal subdomain maintains residual structure for residues near the unprotonated His41 imidazole ring and in the interface between the N- and C-terminal subdomains. In addition, a second faster process was detected that appears to represent local dynamics within the folded state of the molecule and is largely confined to the hydrophobic interface between the N- and C-terminal subdomains.
Keywords: Carr-Purcell-Meiboom-Gill, chemical exchange, Hahn echo, NMR spectroscopy, protein folding
Introduction
Most small globular proteins or protein domains appear to fold and unfold in a cooperative two-state fashion. In these cases, protein-folding intermediates are difficult to detect experimentally because they form rapidly and have low equilibrium populations. However, growing evidence from highly sensitive experimental techniques suggests that the free energy surfaces of small globular proteins are more complex than suggested by simple two-state models and that a number of intermediate states can be populated along the folding pathway [for a recent review, see (Dill, et al., 2008)]. Nuclear magnetic resonance (NMR) spin relaxation dispersion measurements, based on R1ρ(Akke and Palmer, 1996, Vugmeyster, et al., 2000) or relaxation-compensated Carr-Purcell-Meiboom-Gill (CPMG) (Loria, et al., 1999, Hill, et al., 2000) techniques, are particularly powerful approaches for studying protein folding because spin probes are available at a large number of sites, site-specific kinetic rate constants allow multi-state kinetic processes to be resolved, and chemical shifts or residual dipolar coupling constants provide structural information for otherwise unobservable sparsely populated intermediates (Neudecker, et al., 2009).
The 67-residue villin headpiece domain (HP67) has been the subject of a number of experimental and theoretical investigations of structure and folding kinetics (Vardar, et al., 1999, Vardar, et al., 2002, Meng, et al., 2005, Grey, et al., 2006, Tang, et al., 2006, Khandogin, et al., 2007, Smirnov, et al., 2007, Meng and McKnight, 2008, Meng and McKnight, 2009). The structure of HP67 is shown in Figure 1. HP67 conventionally is numbered from residue Pro10 to Phe76 and consists of two structural domains: a N-terminal subdomain (Pro10–Leu42) notable for a buried His41 side chain and a largely helical C-terminal subdomain (Ser43–Phe76). Equilibrium unfolding of HP67 is a multi-state process. At equilibrium in H2O under native conditions (pH 7.0 and 293 K), (1.11 ± 0.09)% of the molecules populate a partially folded intermediate in which the N-terminal subdomain samples a distribution of (partially) unfolded conformations, while the C-terminal subdomain retains a predominantly native-like fold (Grey, et al., 2006, Tang, et al., 2006). Previous NMR R1ρ and CPMG spin relaxation dispersion measurements for backbone amide 15N spins established that the N-terminal subdomain unfolds cooperatively with unfolding and refolding rate constants of 63 ± 5 s−1 and 5,640 ± 100 s−1, respectively (Grey, et al., 2006). Evidence from chemical shift differences between the native and intermediate species suggested that most residues in the N-terminal subdomain sample primarily random coil distributions of conformations. However, both native and non-native residual structure persists for residues in the vicinity of His41 when the imidazole ring is neutral, but not when protonated. A His41Tyr mutant of HP67 exhibited reduced magnitudes of the 15N secondary shifts in the intermediate, indicating that residual structure was absent in the mutant and providing additional evidence for the importance of His41. However, the 15N chemical shifts measured for wild-type or His41Tyr HP67 were not sufficient to precisely define the characteristics of these residual structural interactions. In addition, a second kinetic process with a chemical exchange rate constant of (4.2 ± 0.5) × 104 s−1, given by the sum of forward and reverse transition rate constants, was identified that affects spins located in the interface between the N- and C-terminal subdomains of HP67.
Figure 1.

Structure of HP67 (PDB 2RJX, chain A). The N-terminal subdomain (residues 10–42) is colored in magenta; the C-terminal subdomain (residues 43–76) is brown. The side chain of His41 is depicted in pink stick format. The N-terminal subdomain consists mostly of turns and loops with regular secondary structure defined for three short helices: alpha helix h1 (residues 18–23), and 3–10 helices h2 and h3 (residues 26–28 and 35–41, respectively). The N-terminal loop (residues 10–17) contains the conserved residue Phe16 that forms part of the hydrophobic core. The V-loop (residues 22–28), so named for the sequence variability among headpiece homologues in the stretch of amino acids situated between conserved residues Leu21 and Leu29, encompasses h2 and is important for positioning residues in h1 and Leu29 in the hydrophobic core. B-factors for x-ray crystallographic structures and NMR generalized order parameters indicate that the V-loop is more mobile than other non-terminal residues in HP67; in addition, residues 26–28 have been shown to adopt either a 3–10 helix or an extended turn conformation under identical crystallization conditions (Meng and McKnight, 2009). The loop succeeding h2 also plays a role in positioning of conserved residues in the N-terminal subdomain hydrophobic core. Residues 30–33 form a β-turn that enables Val33 and Asp 34 to pack close to and interact with His41. The C-terminal subdomain consists of threeα-helices, h4, h5 and h6 defined by residues 44–51, 55–59 and 63–73, respectively. A triad of phenylalanine residues, 47, 51 and 58 comprise the hydrophobic core. The hydrophobic cores of the two subdomains are bridged by an interfacial hydrophobic cluster including Leu18, Leu42, Val50 and Leu75. Additional bridging contacts between the N-terminal loop and h4 further stabilizes the N-terminal subdomain and occludes His 41 from the solvent. Regions of HP67 involved in F-actin binding include residues 37–39, 63–65 and 70–76; most residues lie in the C-terminal subdomain near the actin binding surface with the exception of 37–39. The binding surface is comprised of a hydrophobic patch (63–64) encircled by a ring of mostly positive surface charge (37, 65, 71 and 73) that is situated above a distinct isolated of positive charge (38) (Vardar, et al., 1999, Meng, et al., 2005). Glu39 and Lys70 form a buried salt-bridge between subdomains that is required for high-affinity binding.
In the present work, 13Cα and methyl 13C NMR spin relaxation measurements were used to further characterize chemical exchange kinetic processes in HP67. Relaxation experiments were performed in D2O solution to minimize difficulties with water suppression. As previously observed by 15N relaxation dispersion measurements (Grey, et al., 2006), HP67 unfolded to a partially structured intermediate. Owing to an isotope effect, the unfolding and folding kinetic rate constants in D2O solution differed slightly from those measured in H2O and were 35.4 ± 3.5 s−1 and 3150 ± 180 s−1, respectively; however, the equilibrium population of the intermediate was not statistically different from that measured in H2O solution. The ensemble of structures of the folding intermediate of HP67 exhibited four distinct features: the N-terminal face is nearly completely unfolded; residues in the N-terminal subdomain at the interface between the N- and C-terminal subdomains and in the vicinity of His41 maintain residual native-like interactions; residues Val33, Asn40, and His41 have non-native-like conformations in the partially folded intermediate; and the C-terminal domain, with the exception of the most C-terminal residues, remains folded. The faster kinetic processes detected in the 15N relaxation dispersion experiments also was observed by 13Cα and methyl 13C relaxation dispersion and may arise from repacking of hydrophobic side chains in the core of the N-terminal subdomain and in the interface between the N- and C-terminal subdomains. The results from 13C spin relaxation are consistent with previous 15N measurements, but provide a more detailed description of the conformational states of HP67.
HP67 is the minimal villin domain that retains high-affinity binding to actin in vitro (Friederich, et al., 1992, Doering and Matsudaira, 1996, Vardar, et al., 1999). Most residues that contribute favorably to actin-binding (residues 38, 39, 64, 65, 70–76) map to the C-teminal subdomain. Transient unfolding of HP67 to the partially folded intermediate perturbs the structure of residues in the C-terminal helix h6, particularly residues Leu75 and Phe76, and thereby may affect actin binding by villin.
Materials and Methods
Sample preparation
Wild-type HP67 constructs of the chicken villin headpiece domain (Pro10 – Phe76) were expressed and purified as described previously (Vardar, et al., 1999). Isotopically labeled samples were prepared using 18% random fractionally 13C enriched glucose as a carbon source and 99% 15NH4Cl as a nitrogen source (Cambridge Isotopes, Inc.). NMR experiments were performed on a 0.5 mM [18%-13C, U-15N] isotopically enriched HP67 sample buffered at pH/pD 7.0 (uncorrected for isotope effects) in 10 mM sodium phosphate (100% D2O or 90%H2O/10%D2O). Sodium 2,2-dimethyl-2-silapentane-5-sulfonate (DSS) was included in the sample at a concentration of 100 μM as an internal chemical shift reference.
NMR spectroscopy
NMR experiments were recorded on a Bruker DRX600 NMR spectrometer (Columbia University) or Bruker Avance 500, 600, 700, 800, and 900 NMR spectrometers (New York Structural Biology Center). All spectrometers were equipped with CryoProbes. Sample temperatures of 293 K were calibrated using neat methanol or 99.9% d4-methanol. Post-acquisition spectral processing was performed using the NMRPipe software package (Delaglio, et al., 1995), spectral analysis was performed with the Sparky 3 software package (Goddard, T D, and Kneller, D G, University of California, San Francisco), and analysis of relaxation data was performed using Grace (http://plasma-gate.weizmann.ac.il/Grace/), Mathematica (v4.1, Wolfram Research, Inc.), Igor Pro 6 (WaveMetrics, Inc.), CurveFit (www.palmer.hs.columbia.edu) and CPMGFit (www.palmer.hs.columbia.edu) or other in-house software programs.
Chemical shift assignments
Chemical shift assignments of 13Cα resonances were transferred from 1H resonance assignments (Vardar, et al., 1999) deposited in the Biological Magnetic Resonance Data Bank (BMRB) (Ulrich, et al., 2008) with accession number 15097 using 15N-edited TOCSY HSQC and HNCA experiments (Cavanagh, et al., 2007). The 15N-edited TOCSY HSQC was recorded at a static magnetic field strength of 14.1 T (600 MHz) with (90 × 16 × 358) complex points and spectral widths of (7.56 × 1.64 × 8.99) kHz in the (t1× t2× t3) dimensions, respectively. 1H and 15N radiofrequency (rf) carrier frequencies were set to 4.70 ppm and 118.5 ppm, respectively. Following 1H frequency labeling in t1, isotropic mixing was achieved using a DIPSI-2RC sequence (Cavanagh and Rance, 1992) applied with a 6.94 kHz field strength and a duration of 45.6 ms. The HNCA experiment was recorded at a static magnetic field strength of 14.1T (600 MHz) with (80 × 48 × 512) complex points and spectral widths of (7.55 × 2.50 × 8.99) kHz in the (t1× t2× t3) dimensions, respectively. 1H, 13C, and 15N rf carrier frequencies were set to 4.70 ppm, 55.0 ppm, and 118.0 ppm, respectively.
Stereospecific assignments of methyl 13C resonances were obtained by McKnight and coworkers (Smirnov, et al., 2007). These assignments were confirmed and corrected using a 13C-edited TOCSY HSQC experiment and an experiment measuring 2JCH and 3JCH scalar coupling constants for Leu methyl 13C spins (Vuister, et al., 1993). The former experiment was recorded at a static magnetic field strength of 11.7 T (500 MHz) with (64 × 64 × 512) complex points and spectral widths of (5.75 × 1.76 × 8.01) kHz in the (t1 × t2 × t3) dimensions, respectively. 1H and 13C rf carrier frequencies were set to 4.83 ppm and 22.8 ppm, respectively. Following 1H frequency labeling in t1, isotropic mixing was achieved using a DIPSI-2RC sequence (Cavanagh and Rance, 1992) applied with a 12.5 kHz field strength and a duration of 79.4 ms. The latter experiment was recorded at a static magnetic field strength of 16.4 T (700 MHz) with (80 × 64 × 512) complex points and spectral widths of (3.65 × 3.70 × 10.0) kHz in the (t1 × t2 × t3) dimensions, respectively. 1H and 13C rf carrier frequencies were set to 2.16 ppm and 27.7 ppm, respectively.
The 13Cα and methyl 13C secondary chemical shifts, Ωsec, were calculated as the difference between observed chemical shifts and the random coil values reported by Wright and coworkers (Schwarzinger, et al., 2000).
13Cα Hahn echo relaxation experiments
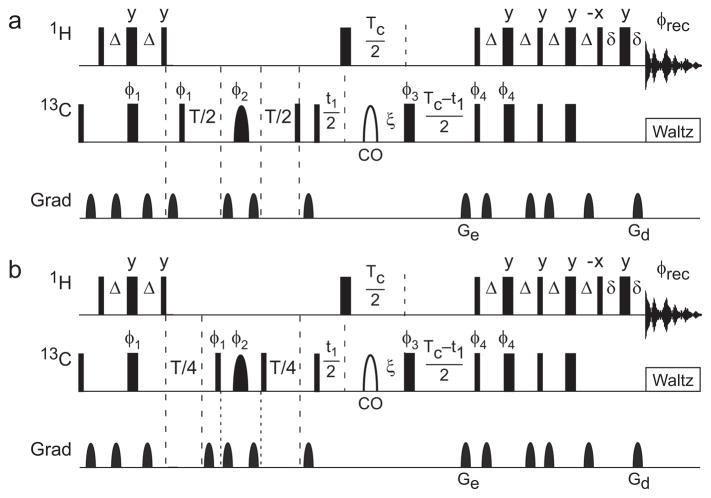
The pulse sequence for the 13Cα R2−½R1 Hahn echo relaxation experiment is shown in Figure 2. The experiment shown in Fig. 2a measures relaxation of single quantum S spin magnetization and the experiment shown in Fig. 2b measures relaxation of longitudinal two-spin order, 2IzSz (I = 1H and S = 13C). Two-dimensional 1H-13C correlation spectra for spin relaxation measurements were recorded for the sample prepared in D2O at static magnetic field strengths of (11.7, 14.1, 16.4, 18.8, 21.1) T with (95, 60, 70, 95, 80) × 512 complex points, spectral widths of (8.3, 5.3, 6.1, 8.3, 7.9) kHz × (10, 8.9, 10, 14, 14) kHz in the (t1 × t2) dimensions and 1H and 13C rf carrier frequencies of 4.83 ppm and 59.8 ppm, respectively. Interleaved two-dimensional correlation spectra were recorded with the sequences of Figure 2a and 2b and T = 34.5 ms. Relaxation rate constants were determined as R2,HE= ln[Ib/Ia]/T, where Ia and Ib are the peak intensities for the experiments of Figs. 2a and 2b, respectively. The experiment of Fig. 2a was repeated between 9–15 times and the experiment of Fig. 2b was repeated 4–6 times per field. Uncertainties were calculated from duplicate measurements. A conventional Hahn echo experiment is obtained by setting T = 0 in Fig. 2b.
Figure 2.
Hahn spin echo pulse sequence for fractionally 13Cα labeled proteins. Narrow and wide solid rectangular bars represent 90° and 180° pulses, respectively. The shaped pulse represented by a solid semi-ellipse is a Reburp 180° 13Cα refocusing pulse, and the shaped pulse represented by a open semi-ellipse is an off-resonance 4% truncated Gaussian pulse applied at the carbonyl 13C frequency. The power of the rectangular 180° pulse during the constant time period is adjusted to have a null at the carbonyl 13C frequency. Delays are defined as follows: Δ = 1/(4JCH) = 1.75 ms, ξ = 1/(4JCC′) = 4.54 ms, T is the relaxation delay, TC = 1/2JCC = 14.28 ms is the constant time period, t1 is the indirect carbon-frequency labeling delay, and δ is long enough to encompass the final gradient pulse. Pulse phases are x unless otherwise illustrated. Phase cycles are φ1 = x, −x; φ2 = 8(y), 8(−x). 8(−y), 8(x); φ3 = 2(x), (2y), 2(−x), 2(−y); φ4 = x; φrec = 2(x, −x, −x, x), 2(−x, x, x, −x). Unlabeled gradients are employed to suppress unwanted coherences and artifacts while Ge and Gd are encoding and decoding gradients, respectively, for echo/anti-echo coherence selection; selection is obtained by inverting the signs of φ4 and Ge (Palmer, et al., 1991, Kay, et al., 1992).
13Cα relaxation compensated CPMG experiments
The pulse sequence for 13Cα R2−½R1 relaxation-compensated CPMG experiments is very similar to Fig. 2, except that the Hahn echo relaxation period was replaced by a relaxation-compensated spin echo pulse train; the pulse sequence is provided as Figure S1 in the Supplementary Information (SI) (Loria, et al., 1999, Wang, et al., 2001, Yip and Zuiderweg, 2004). Two-dimensional 1H-13C correlation spectra for spin relaxation measurements were recorded for the sample prepared in D2O at a static magnetic field strength of 14.1 T with (512 × 60) complex points, spectral widths of (8.9 × 5.3) kHz in the (t1× t2) dimensions, and 1H and 13C rf carrier frequencies of 4.83 ppm and 59.8 ppm, respectively. Interleaved two-dimensional correlation spectra were recorded with T = 48 ms. Relaxation rate constants were determined as R2,rc (1/τcp) = ln[Ib/Ia]/T, where Ia and Ib are the peak intensities for the experiments shown in Figs. S1a and S1b, analogous to those of Figs. 2a and 2b, respectively. The Fig. 2a analogue was repeated 5 times and the Fig. 2b analogue was repeated 4 times per value of τcp, where τcp is the duration between CPMG refocusing pulses. Uncertainties were calculated from duplicate measurements. Relaxation dispersion profiles were obtained by measuring R2,rc(1/τcp) relaxation rate constants for seven different CPMG pulsing rates, 1/τcp, in the range of (0.17 – 2.0) × 103 s−1 by varying the number of 13C 180° rf pulses applied during the CPMG relaxation periods. Temperature compensation was achieved by varying the number of 180° pulses applied during the recycle delay to keep the total number of 180° pulses constant for each experiment (Wang and Bax, 1993, Yip and Zuiderweg, 2005).
Methyl 13C relaxation-compensated CPMG experiments
Methyl 13C R2,rc(1/τcp) relaxation rate constants were measured for the sample prepared in D2O in a constant-relaxation-time manner using the relaxation-compensated CPMG experiments reported by Kay and coworkers (Skrynnikov, et al., 2001). Two-dimensional 1H-13C correlation spectra for spin relaxation measurements were recorded at static magnetic field strengths of 14.1 T and 18.8 T with (256 × 512) complex points, spectral widths of (2.1 × 10.0) kHz in the (t1× t2) dimensions, and 1H and 13C rf carrier frequencies of 4.83 ppm and 22.8 ppm, respectively. Pairs of interleaved two-dimensional correlation spectra were recorded with relaxation delays of 0 ms and T = 40 ms. The relaxation rate constants were determined as R2,rc(1/τcp) = ln[I (0)/I(T)]/T, where I(t) is the corresponding peak intensity at time t. Uncertainties were estimated by propagating the uncertainty in the measured peak height, which was taken as the baseline noise in the spectra. Relaxation dispersion profiles were obtained by measuring R2,rc(1/τcp) relaxation rate constants for 30 different CPMG pulsing rates, 1/τcp, in the range of (0.1 – 5.0) × 103 s−1 by varying the number of 13C 180° rf pulses applied during the CPMG relaxation periods.
Temperature compensation was achieved by varying the number of 180° pulses applied during the recycle delay to keep the total number of 180° pulses constant for each experiment (Wang and Bax, 1993, Yip and Zuiderweg, 2005). A control CPMG experiment was performed at 14.1 T using the sample prepared in 90%H2O/10%D2O solution to assess isotope effects on the chemical exchange kinetics.
Relaxation dispersion analysis
In the relaxation-compensated CPMG experiments used herein, refocusing rf pulses applied with a frequency 1/τcp during the relaxation period are used to suppress chemical exchange contributions to transverse relaxation. The 1/τcp-dependence of apparent transverse relaxation rate constants is described as
| (1) |
in which is the limiting relaxation rate constant in the absence of exchange broadening, and Rex(1/τcp) is the chemical exchange contribution to transverse relaxation. The transverse relaxation rate constant observed in the free-precession limit is
| (2) |
and is approximated by R2, HE. In conventional Hahn echo and relaxation-compensated CPMG experiments for IS spin systems, the apparent transverse relaxation rate constant is the average of the relaxation rate constants for in-phase and anti-phase coherences owing to evolution under the scalar coupling Hamiltonian (Cavanagh, et al., 2007). As such, the limiting relaxation rate constant contains a contribution from 1H dipolar spin-lattice relaxation: . In the R2− ½R1 experiments utilized herein, relaxation of the operator 2IzSz is directly incorporated into the pulse sequence and the limiting rate constant is modified to . This modification has two advantages: the contribution from 1H relaxation is eliminated and the dependence on the static magnetic field is simplified (vide infra).
For fast-limit exchange among n-sites in the CPMG experiment, is the population-averaged value of the limiting rate constants for individual sites and
| (3) |
in which φi and κi are obtained from the eigenvalues and eigenvectors of the kinetic rate matrix as described elsewhere (Allerhand and Thiele, 1966). For two-site exchange that is fast on the chemical shift time-scale, Eq. 3 reduces to
| (4) |
in which , κ2 = kex = k12 + k21, klm are kinetic rate constants for transitions between sites l and m, pm is the equilibrium population of site m, Δωlm = Ωl − Ωm, and Ωm is the resonance offset of a nuclear spin in site m. For simplicity in the following, subscripts designating sites will be omitted if the context is clear; for example, Δω may be written instead of Δωlm.
In many situations of practical interest, only the initial decay of a dispersion curve can be recorded because one or more kinetic processes are very fast and the pulsing rate cannot be made arbitrarily large owing to limitations on sample heating or pulse duty cycle. In these cases, the initial decay of the dispersion curve for an n-site exchange process may be fit well by an apparent two-site process (Eq. 3) with average parameters defined by
| (5) |
| (6) |
Equations 5 and 6 are obtained by requiring that the average two-site equation match the initial value and first derivative of the n-site dispersion curve. If site 1 has a much larger equilibrium population than the other sites and if the different values of κi are well-separated (by a factor of 3–10), then Eq. 3 reduces approximately to the sum of n−1 independent two-state processes for exchange between site 1 and the n−1 other sites. In this limit for a three-site process, κ2 ≈ kex,2 = k12+ k21 and κ3 ≈ kex,3 = k13 + k31. If values of kex,2 and kex,3 are obtained from relaxation dispersion data for spins affected only by one of the two processes, then the measured value of φ̄ex for spins affected by both processes can be deconvoluted into individual contributions for each exchange process using:
| (7) |
| (8) |
with and .
For completeness, although not utilized in the present work, the situation also arises in which the full dispersion curve for an n-site exchange process is measurable, but the individual eigenvalues are too close together to allow the individual processes to be resolved. In these cases, the dispersion curves can be described by an apparent two-site exchange process (Eq. 3) with average parameters given by:
| (9) |
| (10) |
obtained by requiring that the average two-site equation match the initial value and first moment of the n-site dispersion curve.
The static magnetic field dependence of R2,HE in Hahn echo R2−½R1 experiments
For fast exchange on the chemical shift time scale in the R2−½R1 Hahn-echo experiments used for 13Cα spins, the relaxation rate constant is given by,
| (11) |
in which dCH is the dipolar coupling constant, Δσ is the 13C chemical shift anisotropy, ωC is the 13C Larmor frequency, and J(ω) is the spectral density function at frequency ω (Cavanagh, et al., 2007). Equation 11 does not depend on J(ωC) and small high frequency spectral density terms J(ωH ± ωC) have been neglected (Phan, et al., 1996). For 13Cα, Δσ ~ 25 ppm and the contribution of chemical shift anisotropy is < 3% even at a static magnetic field of 21.1 T. The last line of Eq. 11 is specialized to two-site exchange and Δδ = Δδ12 is the frequency difference between sites 1 and 2 measured in units of parts per million. Thus, the intercept and slope of a graph of R2, HE versus allows measurement of both and p1p2Δδ2/kex or more generally (i.e., is expressed in ppm2, rather than s−2). Spins for which the fitted slopes were significantly greater than zero were included in analysis of CPMG relaxation dispersion data (vide infra). Values of obtained from this analysis were used to constrain the corresponding limiting values of R2,rc (1/τcp → ∞)when fitting the CPMG relaxation dispersion curves.
Analysis of CPMG relaxation dispersion curves
For exchange broadened 13Cα and methyl 13C spins in HP67, except possibly His41, the field dependence of either the Hahn echo or CPMG relaxation rate constants indicates that exchange is fast on the chemical shift time scale and use of Eqs. 3 and 4 is valid. The 13Cα resonance for His41 is severely broadened and relaxation dispersion could not be measured precisely enough for detailed analysis. A sufficiently precise Hahn echo relaxation rate constant could be measured for His41 only at a static field of 11.7 T.
The 13Cα R2,rc(1/τcp) relaxation dispersion data recorded at a static magnetic field strength of 14.1 T were analyzed individually for those residues subject to chemical exchange broadening as judged by the field dependence of R2,HE and for which Rex > 2.5s−1 at a static magnetic field strength of 14.1 T. The inequality approximately requires that Rex > 0.1 R2,rc(0). Data were analyzed using Eq. 4 for a two-site chemical exchange model that is fast on the chemical shift time scale. Values of were fixed from the Hahn echo data and Rex = φex/kex and kex were optimized using the Levenberg-Marquardt algorithm in the in-house program CPMGFit. Uncertainties in fitted exchange parameters were estimated by jackknife simulations. As noted previously, relaxation dispersion measured for a limited range of τcp values at a single static magnetic field and a single temperature usually is insufficient to distinguish three-site from two-site models by direct curve fitting (Grey, et al., 2003),
The methyl 13C R2,rc(1/τcp) relaxation dispersion data recorded at static magnetic field strengths of 14.1 T and 18.8 T were analyzed individually to select the appropriate chemical exchange model that adequately describes the experimental data. For each methyl group, the set of dispersion data were analyzed using exchange models that assume (model 1) no chemical exchange with Rex(1/τcp) = 0, (model 2) two-site chemical exchange that is fast on the chemical shift time scale, and (model 3) three-site chemical exchange that is fast on the chemical shift time scale. For each exchange model, nonlinear least squares optimization of the parameters (model 1) ; (model 2) , Rex, and kex; or (model 3) , Rex,1, Rex,2, kex,2, and kex,3 against experimental R2,rc(1/τcp) relaxation rate constants was performed with the Levenberg-Marquardt algorithm using routines in the in-house program CPMGFit or written in Mathematica. In some analyses, one of the exchange rate constants was fixed at (4.2 ± 0.5) × 104 s−1 (vide infra). Incorporation of the chemical exchange terms in models 2 and 3 required (i) a significantly improved χ2 based on the F-statistic comparing fits with model 2 versus model 1 or model 3 versus model 2 at the 95% confidence level and (ii) Rex > 1 s−1 at a static magnetic field strength of 14.1 T. The inequality approximately requires that Rex > 0.1 R2,rc(0). Uncertainties in fitted exchange parameters were estimated by jackknife simulations.
Results
Two-dimensional 13C-1H correlation spectra for Cα-Hα and side chain C-H3 groups are shown in SI Figures S2 and S3. Representative relaxation data are shown in Figure 3 for 13Cα spins and Figure 4 for methyl 13C spins. Significant chemical exchange contributions to Hahn echo or CPMG relaxation dispersion data were detected for 23 of 50 resolved 13Cα spins of amino acid residues other than Gly. The pulse sequences utilized were optimized for IS spin systems and Gly residues are not characterized in the present study. Significant chemical exchange contributions to CPMG relaxation dispersion data were detected for 17 of 33 resolved methyl 13C spins.
Figure 3.
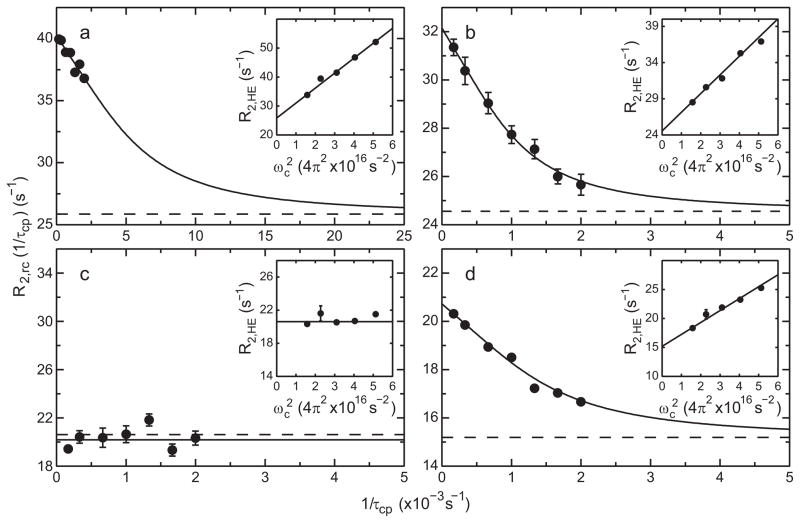
Exchange broadening of 13Cα spins in HP67. CPMG relaxation dispersion profiles R2,rc(1/τcp) measured at a static magnetic field strength of 14.1 T for (a) Leu21, (b) Arg37, (c) Asn60, and (d) Phe76. The solid lines are fits to the data using (a) model 2, (b) model 2, (c) model 1, and (d) model 2 (see text for details). The dashed line corresponds to the value of used to constrain the data in the limit of infinitely fast pulsing. The corresponding R2,HE dispersion data are plotted versus ωc2 in the insets; the solid lines are linear fits to the data.
Figure 4.
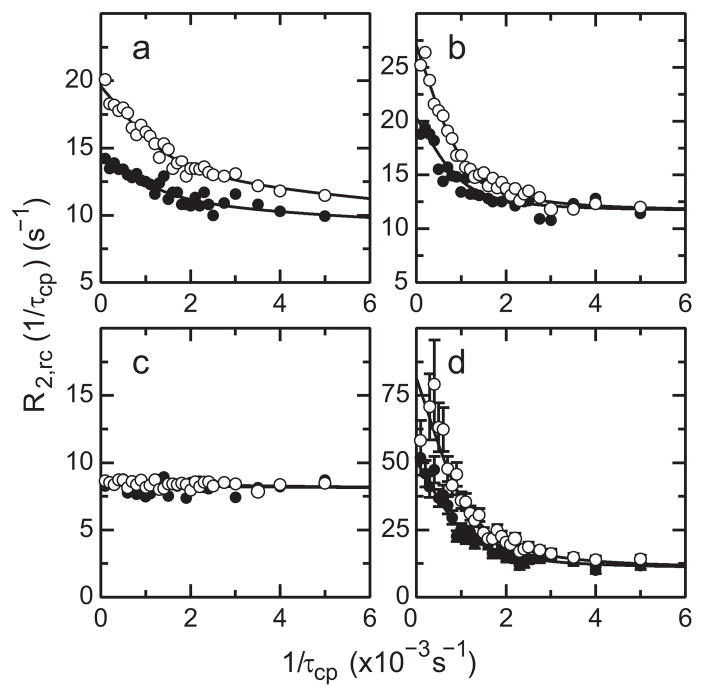
Exchange broadening of methyl 13C spins in HP67. 13C R2,rc(1/τcp) relaxation dispersion profiles measured at static magnetic field strengths of (○) 14.1 T and (●) 18.8 T for (a)Val20 Cγ2, (b) Leu21 Cδ1, (c) Val22 Cγ1, and (d) Val33 Cγ2. The solid lines are fits to the data using (a) model 3, (b) model 2, (c) model 1, and (d) model 2 (see text for details).
Most of the 13Cα spins exhibiting significant relaxation dispersion were fit with a two-site model with kex < 7,000 s−1, ranging from 1,160 ± 220 s−1 to 6,910 ± 570 s−1, and three spins, Leu21, Val22, and Leu75 were fit with a two-site model with kex > 10,000 s−1. The relaxation dispersion data for 13Cα spins with kex < 7,000 s−1 were summed and a global average kex = 3,190 ± 180 s−1 determined by fitting a two-site model to the combined data. Data for the 13Cα spins of Leu21, Val22, and Leu75 contain contributions from the faster process detected previously from 15N spin relaxation; however, the relaxation dispersion curves recorded at a single static magnetic field strength were fit adequately by a two-site model. The results from the two-site fit for these residues were deconvoluted into values of φex for each exchange process using global values of the slow and fast exchange processes and Eq. 7; the deconvoluted values are shown in Table 1. Residues with 5,000 s−1 < kex < 7,000 s−1 may contain some contributions from the faster process detected previously from 15N spin relaxation dispersion; however, the effects of this faster process are relatively minor on subsequent data analysis and are not considered further. Residues with kex < 2000 s−1 may be affected by a process slower than the unfolding transition; however, the present data are not sufficient to resolve such a process or processes using a three-site model. Furthermore, as has been discussed previously (Millet, et al., 2000, Kovrigin, et al., 2006), fitted parameters for relaxation dispersion curves recorded at single static magnetic fields are correlated. In the present case, data for residues that are independently fit with values of kex < 2000 s−1 or 5,000 s−1 < kex < 7,000 s−1 also are fit adequately by constraining kex to global value of 3,190 s−1 if is allowed vary by less than 5% of the value derived from the Hahn echo relaxation measurements. The fitted parameters for the Hahn echo and CPMG experiments are provided in SI Tables S1 and S2, respectively.
Table 1.
Deconvolution of average two-site parameters
| Name | k̄ex (s−1) | (ppm) | (ppm) | (ppm) |
|---|---|---|---|---|
| L21 | 16,900 ± 1,700 | 0.470 ± 0.023 | 0.079 ± 0.008 | 0.772 ± 0.013 |
| V22 | 10,500 ± 800 | 0.385 ± 0.016 | 0.110 ± 0.007 | 0.697 ± 0.017 |
| L75 | 18,000 ± 7100 | 0.196 ± 0.049 | 0.041 ± 0.036 | 0.42 ± 0.13 |
The methyl 13C relaxation data exhibiting significant dispersion fell into three categories: spins described by a two-site model with kex < 7,000 s−1; spins described by a two-site model with kex > 10,000 s−1, and spins with a three-site model with one kex < 7,000 s−1 and the other kex > 10,000 s−1. The rate constants < 7,000 s−1 for methyl 13C spins were consistent with the global value determined from the 13Cα data. The rate constants > 10,000 s−1 for methyl 13C spins were not well determined by individual curve fits, owing to the limited maximum pulsing rate and because Rex < 5 s−1 for these spins. These data were fit equally well using a value for kex fixed at (4.2 ± 0.5) × 104 s−1, determined previously from 15N relaxation dispersion; consequently the final parameters were obtained by fitting the dispersion curves with a fixed value for the faster kinetic process in either models 2 and 3 as required. Fitted parameters are provided in SI Table S3.
The global average kex is attributed to a chemical exchange process in which the N-terminal subdomain transiently unfolds to a partially structured intermediate, as previously observed using 15N spin relaxation dispersion. The value of kex = 3,190 ± 180 s−1 is smaller than the value of 5,700 ± 100 s−1 measured by backbone amide 15N spin relaxation dispersion (Grey, et al., 2006). This difference represents an isotope effect on the kinetic process rather than a difference between 13C and 15N experiments or the different protein preparations. As a control, values of kex = 2,810 ± 260 s−1 and 6,540 ± 740 s−1 are obtained in D2O and H2O solutions for Val33 13Cγ2 and are in good agreement with the global values measured for 13C in D2O and 15N in H2O, respectively.
Values of for slow unfolding process, determined from individual fitted values of Rex and the global value of kex, are plotted versus |Ωsec| in Figure 5. Previous analysis of 15N spin relaxation dispersion data indicated that most residues in the N-terminal subdomain are largely unstructured in the intermediate state. Under this assumption, Δω = Ωsec and the slope of a graph of versus |Ωsec| is linear through the origin with a slope of (p1p2)1/2. A line fitted to the data points depicted in black for 13Cα in Figure 5a yields a slope of 0.101 ± 0.007 and therefore an estimated intermediate population of (1.02 ± 0.14)%. A line fitted to the points for methyl 13C spins depicted in black in Fig. 5b yields a slope of 0.114 ± 0.007 and therefore an estimated intermediate population of (1.30 ± 0.16)%. Points selected for inclusion in the final fits shown in Figs. 5a and 5b were determined by sequential rounds of fitting in which large outliers were excluded from the data set with a bias for excluding data points with large negative residuals. Given the good overall consistency between these two estimates of the site populations and the close agreement with the value of (1.11 ± 0.09)% obtained from 15N relaxation dispersion, subsequent analyses of the data used the value of p2 = (1.11 ± 0.09)% for population of the intermediate state. The pooled 13Cα and methyl 13C data is shown in Figure 5c with both the fitted line with slope of 0.104 ± 0.005, corresponding to a population of (1.09 ± 0.11)%, and the line drawn with the slope obtained from the square root of the assumed population. Values of |Δδ| obtained from the relaxation dispersion measurements and values of Ωsec are shown as functions of amino acid sequence in Figure 6.
Figure 5.
Analysis of φex 13Cα and methyl 13C spins in HP67. Values determined from individual fits of Rex and the global value of kex are plotted versus |Ωsec| for (a) 13Cα (●, ○) and (b) methyl 13C (■, □) spins in HP67. Solid symbols in (a) and (b) represent data for residues that are assumed to be fully unfolded in the intermediate ensemble; in each plot, the solid line depicts the linear least-squares fit of these data points. In (a) the fit is computed using only 13Cα data and the line has a slope of 0.101 ± 0.007 and therefore an estimated population of the intermediate of (1.01 ± 0.14)%. Similarly, in (b) the fit of the methyl 13C data yields a slope of 0.114 ± 0.007 and therefore an estimated population of the intermediate of (1.30 ± 0.16)%. In (c) the data from both molecular probes are combined and fit collectively for points colored green. The global fit of the fully disordered residues, shown as a dashed green line, yields a slope of 0.104 ± 0.005, corresponding to a population of (1.09 ± 0.11)% for intermediate. The solid line has a slope of 0.0105, corresponding to p2 = (1.11 ± 0.09)% observed previously for 15N spin relaxation dispersion. Data points that were excluded from the fit are grouped into two categories: (i) those that lie above and to the left of the fitted are presumed to adopt non-native conformations in the intermediate and (ii) those that lie below and to the right of the fit are presumed to maintain residual native-like interactions in the intermediate. Residues in (i) and (ii) are colored with brown and blue gradients, respectively, with the color of the data points becoming lighter as the ratio |Δδ/Ωsec| deviates from unity, in which Δδ was obtained from φex assuming p2 = (1.11 ± 0.09)%.
Figure 6.
Values of Δδ for 13Cα spins in HP67. (a) 13Cα secondary shifts, Ωsec, are plotted versus residue number. A schematic of the protein secondary structure colored to reflect the subdomains defined in Fig. 1 is provided for reference. In (b) the absolute value of the chemical shift difference, |Δδ|, between the intermediate and native state 13Cα resonances are plotted versus residue number as solid bars colored to match the color coding in Fig. 5. Values of Δ δ were calculated from φex assuming a population p2 = (1.11 ± 0.09)% for the intermediate. White bars represent values of Δδ that are likely to be negative based on the corresponding sign of Ωsec. For residues in the N-terminal domain, Δδ is large due to the change in chemical environment associated with the unfolding transition. Residues in the C-terminal domain show very little change in chemical shift with the exception of Leu75 and Phe76.
The 13Cα resonance of His41 is too broadened to obtain relaxation dispersion curves. A value of R2,HE = 59.8 ± 2.7 s−1 was obtained at a static magnetic field strength of 11.74 T. Assuming that for His41 is similar to the values for the flanking residues Asn40 (23.6 ± 0.3 s−1) and Leu42 (26.0 ± 0.5 s−1) yields a value of Rex = 35.4 ± 2.7 s−1 for His41 Taken together with the global estimates of kex and p2, ppm and the chemical shift difference of His41 is estimated to be |Δδ| = 4.7 ± 0.6 ppm, compared to Ωsec = 0.5 ppm. Alternatively, the large value of Rex for His41 suggests that this residue may be in intermediate to slow exchange; thus, |Δδ| > 4 ppm because Δω12 ~ kex. Insight to the sign of Δδ can be gained by comparing the observed 13Cα chemical shift of His41 to the distribution of histidine 13Cα chemical shifts in BMRB. The histogram of deposited shifts is bimodal with one maximum at 55.6 ppm and another at 59.6 ppm; the highly populated region of chemical shift space spans 52–62 ppm. In the native state of HP67, His41 has backbone (φ, ψ) dihedral angles of (−104, 9.5), which are outside the favored region for an α-helical conformation, and its 13Cα spin has a chemical shift of 55.9 ppm. Therefore, the His41 13Cα spin resonates at either ~52 or ~60 ppm in the intermediate state. Because 52 ppm is in the tail of the chemical shift distribution, His41 13Cα more likely resonates at 60 ppm in the intermediate, indicating that the backbone dihedral angles of His41 adopt more helical values in the partially folded state.
Discussion and Conclusion
Chemical exchange broadening of 13Cα and methyl 13C spins provides a sensitive probe for characterizing the disruption of the secondary structure and the hydrophobic core during protein folding transitions. Measurements of chemical exchange broadening of 13Cα and 15N spins are complementary in that both report on dynamics of the protein backbone, but 13Cα chemical shifts are more easily interpreted (Spera and Bax, 1991) to provide insight into structural features of intermediate states with low populations. In the present work, the experimental design for 13Cα spins used CPMG relaxation dispersion measured at one static magnetic field coupled to Hahn spin echo measurements at five static magnetic fields. This strategy was adopted for two reasons: (i) the limiting value of is obtained from the Hahn echo data and used as an independent constraint in fitting the CPMG relaxation dispersion data, and (ii) the Hahn echo experiment is less demanding of rf and probe performance than the CPMG experiment. The former is particularly useful when τcp cannot be made short enough to define the limiting value of the relaxation rate constant, R2,rc (1/τcp → ∞), and the latter is particularly advantageous for implementation on cold probes. Both Hahn echo and CPMG measurements for 13Cα spins used the R2 − ½R1 constant-relaxation-time approach (Akke and Palmer, 1996) to suppress contributions to transverse relaxation arising from 1H longitudinal spin relaxation of antiphase coherences and from spectral density functions at non-zero frequencies (Phan, et al., 1996). An established CPMG approach (Skrynnikov, et al., 2001) was used to measure methyl 13C spin relaxation dispersion at two static magnetic field strengths.
The sample of HP67 utilized was randomly fractionally enriched with 13C to a level of 18% as a compromise between sensitivity and the fraction of spins with one-bond 1JCC scalar coupling interactions. Two approaches were used to suppress the residual effects of 1JCC scalar coupling interactions. The 13Cα spectra were acquired using constant-time labeling in the t1 dimension to convert coherences for 13Cα spins with a 13CO or 13Cβ coupling partner into unobservable two-spin coherences. The methyl 13C spectra, owing to the narrower linewidths of methyl resonances, simply were recorded to high enough digital resolution to resolve doublets arising from 1JCC interactions. The data shown in Figures 3 and 4 demonstrate that the use of a randomly 18% 13C enriched sample along with either constant-time labeling or high digital resolution in the indirect dimension of 1H-13C correlation spectra is adequate to suppress the effects of one-bond 13C-13C scalar coupling interactions and yield flat relaxation dispersion profiles in the absence of chemical exchange broadening. The 18% isotopic labeling scheme reduces overall sensitivity compared with schemes for obtaining higher degrees of labeling of isolated 13Cα and methyl 13C spins (Lundstrom, et al., 2007), and necessitate the use of high-sensitivity cold probes for all experiments. However, this approach has the advantage that measurements can be made for essentially all 13C spins using a single sample.
The Hahn echo and CPMG relaxation data for 13Cα spins and CPMG relaxation data for 13C methyl spins of HP67, like the 15N relaxation data acquired previously (Grey, et al., 2006), demonstrate that the N-terminal subdomain transiently unfolds to form a partially structured intermediate. The population of the intermediate is identical within experimental uncertainties for the 13C-labeled sample of HP67, prepared in D2O solution, and the 15N-labeled sample in H2O solution; however, the chemical exchange rate constant, kex, is reduced in D2O solution, suggesting that a small isotope effect raises the free energy of the transition state by ~0.6 kT in D2O.
The values of φex and Δδ obtained from the relaxation dispersion data provide information on the structure of the intermediates contributing to chemical exchange broadening. Values of |Δδ/Ωsec| are coded in pseudocolor in Fig. 6 and on the structure of HP67 in Figure 7. Residues with values of on or near the solid line defining the intermediate population in Fig. 5 have chemical shifts very close to random coil values and are presumed to be highly disordered in the intermediate; data for these residues are colored green in Figs. 6 and 7. Notably, only Val33, which packs against the imidazole ring of His41, Asn40, and His41 have 13C spins with values of that are substantially above the solid line in Fig. 5; data for these residues are colored using a gradient from dark to light brown as |Δδ/Ωsec| increases above unity. Thus, Val33, Asn40, and His41 appear to have non-native-like interactions in the intermediate state. As discussed above, the large shift for His41 only can be rationalized if the backbone conformation becomes more helical in the intermediate state. The value of Δδ for Asn40 also is consistent with a more helical state in the intermediate, although such an interpretation is not unique. In contrast, values of for a number of other residues lie below and to the right of the solid line in Fig. 5; data for these residues are colored using a gradient from dark to light blue as |Δδ/Ωsec| decreases below unity. The simplest interpretation of the data in this region of the plot is that these residues are not completely disordered and maintain a degree of native-like interactions in the intermediate state.
Figure 7.
Structural dependence of conformational dynamics in HP67. Exchange broadened 13Cα and 13C methyl groups are mapped onto the structure of HP67. (a) Atoms are colored to correlate with the classifications depicted in Figs. 5 and 6; thus, green, blue and brown spheres represent residues that are fully disordered, retain native-like interactions and have non-native-like conformations in the intermediate, respectively. As can be seen, two regions of residual interactions are maintained the intermediate: (i) at the interface of the N- and C-terminal subdomains and (ii) in the vicinity of His41. (b) 13Cα and 13C methyl groups affected by the fast process with kex = (4.2 ± 0.5) × 104 s−1 are mapped to the structure and color coded to reflect the magnitude of exchange broadening. Atoms for which Rex > 2.5 s−1are colored red, atoms for which 1 s−1 < Rex < 2.5 s−1 are orange, and atoms for which Rex < 1 s−1are colored yellow.
The ensemble of conformations sampled by the N-terminal subdomain of HP67 is heterogenous and complex. Different sites in the partially folded N-terminal subdomain exhibit one of three conformational preferences in the intermediate as determined by φex or |Δδ/Ωsec|: the most distal N-terminal face is fully unfolded; a subset of residues, including those located in the interface between N- and C-terminal subdomains, maintain some native-like interactions; and residues Val33, Asn40, and His41 form non-native interactions. The majority of residues in the C-terminal subdomain are fully folded in the intermediate; however, exchange broadening is observed for the most C-terminal residues, particularly Phe76, suggesting that fraying of helix 6 occurs upon disruption of the interaction between the N- and C-terminal subdomains. Therefore, a minimal model of the intermediate consists of two interconverting substates for the N-terminal subdomain: a nearly unfolded ensemble in which Val33, Asn40, and His41 maintain stable non-native interactions while the residues depicted in green and blue in Fig. 7 are disordered, and a partially structured ensemble in which Val33, Asn40, His41 and the residues depicted in blue in Fig. 7 maintain stable non-native and native interactions, respectively, and the residues depicted in green are disordered. A line through the origin fitted to the data points shown in blue in Fig. 5 has a slope of 0.053 ± 0.003; this value indicates that the fully unfolded subpopulation of these residues is (0.28 ± 0.032)%, and suggests that disordered conformations are sampled with a relative frequency of (0.28/1.11)% = 25% within the intermediate ensemble for these residues. Thus, populations of the nearly fully unfolded ensemble and partially structured ensemble are 1.11 (0.25)% = 0.28% and 1.11 (0.75)% = 0.83%, respectively.
In HP67, the hydrophobic core of the N-terminal subdomain is composed of methyl groups of Leu21, Leu29, and Val33; methyl groups of Leu18, Leu42, Val50, and Leu75 line the interface between the N- and C-terminal subdomains; and the remaining N-terminal methyl groups are solvent exposed. The number of contacts formed by a particular methyl group significantly contributes to the observed 13C chemical shift. Therefore, perturbations of methyl 13C chemical shifts and concomitant exchange broadening report directly on the disruption of the hydrophobic core upon unfolding of the N-terminal subdomain. The consistency between the 13Cα and methyl 13C data suggests that the secondary structure and hydrophobic core of HP67 unfold cooperatively to form the partially folded intermediate.
This interpretation of the 13C relaxation data is consistent with previous 15N relaxation dispersion data (Grey, et al., 2006). Exchange broadening of the 15N spin of Asp34 suggests that the native hydrogen bond to the His41 imidazole ring is maintained within ~75% of the ensemble. Exchange broadening observed for the 15N spins of Thr15, Phe16, and Gly32 also suggest that non-native interactions are formed for residues in the vicinity of the His41 ring. Alternatively, the small secondary shifts for these residues may reflect two opposing dominant contributions to the observed shifts, only one of which is disrupted in the intermediate. The 15N relaxation dispersion measurements also identified a pH-dependent shift from partially folded to completely disordered conformations of Asp34 in the intermediate state and demonstrated that non-native interactions of Thr15, Phe16, and Gly32 are only fully disrupted when the imidazole ring is protonated (Grey, et al., 2006). The 13C and 15N relaxation data for HP67, considered together with structural (Meng and McKnight, 2008) and theoretical (Khandogin, et al., 2007) investigations suggests that the most highly populated state within the intermediate ensemble arises from disruption of the Glu14-His41 hydrogen bond (disrupting the residues depicted in green in Fig. 7), and the second state arises by additional disruption of the Asp34-His41 hydrogen bond (additionally disrupting the residues depicted in blue in Fig. 7). The analysis of the 15N data for the His41Tyr mutant of HP67 also supports this conclusion (Grey, et al., 2006).
Although the minimal model is sufficient to explain the relaxation data qualitatively, the present data cannot rigorously distinguish whether the intermediate state ensemble consists of a small or large number of distinct conformations; that is whether the free energy surface contains a limited number of well-defined local minima separated by small barriers or consists of a relatively broad local minimum. The present data also cannot exclude the presence of non-native interactions for some residues with values of that are below and to the right of the solid line in Fig. 5; chemical shifts for other spins, such as 1HN, 1Hα, and 13CO, in the intermediate state must be determined in order to more fully describe the conformational ensemble (Neudecker, et al., 2009).
The 13Cα relaxation dispersion curves indicate that residues Leu21 and Val22 are sensitive to both the slow unfolding process and the second faster process. Both of these residues occupy the helical region of Ramachandran space, but have chemical shifts that are upfield of those expected for helical conformations. One possible explanation of the faster process is that the chemical shifts for these residues in the native state are determined by two additive factors: the secondary shift and a second contribution that partially offsets the secondary shift. If the fast chemical exchange process arises from transitions to a conformational state in which the second interaction is disrupted, then the chemical shift for residues in this state would manifest the full secondary shift. If this model is correct, then Δδ for the fast process is given by the difference between the observed shift and the shift expected for a canonical helical conformation. For Leu21 and Val22, this approach suggests that Δδ = 1.9 and 3.0 ppm respectively and a population of the second species of ~6–20%. As shown in Fig. 7b, this process also is sensed by multiple methyl groups in the interface between the N- and C-terminal subdomains of HP67, including Leu18, Val20, Leu21, Val22, Leu42 and Leu75, and consequently is likely to reflect repacking of the hydrophobic core within the native ensemble of structures. This hypothesis is supported by molecular dynamics simulations that detect enhanced disorder of many of the methyl-bearing sidechains in HP67 (Khandogin, et al., 2007); however, whether the process observed in simulations corresponds to the transition to the partially folded intermediate or to this faster intramolecular process remains to be elucidated.
The 13C relaxation dispersion results presented herein, coupled with backbone amide 15N relaxation dispersion measurements reported previously, provide a unique view of the unfolding of a globular protein domain. These results support the view that folding and unfolding transitions of even small proteins and protein domains, such as HP67, occur on rather complex free energy surfaces that may result in the formation of multiple intermediate states along the folding pathway.
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health (NIH) grants T32 GM008281 (N. E. O) and GM59273 (A. G. P.) and by National Science Foundation Grant MCB 0614365 (D. P. R.). A. G. P. and D. P. R. are members of the New York Structural Biology Center supported by NIH grant GM66354. We thank Jaehyun Cho (Columbia University) for helpful discussions.
Footnotes
Supplementary Information Available: HSQC spectra illustrating 13Cα and methyl 13C chemical shift assignments, figure describing the 13Cα CPMG experiment, three tables of relaxation parameters for 13Cα and methyl 13C spins, and the Bruker pulse sequence and acquisition files for the 13Cα Hahn echo and CPMG experiments.
References
- Akke M, Palmer AG. Monitoring macromolecular motions on microsecond to millisecond time scales by R1ρ-R1 constant relaxation time NMR spectroscopy. J Am Chem Soc. 1996;118:911–912. [Google Scholar]
- Allerhand A, Thiele E. Analysis of Carr---Purcell spin-echo NMR experiments on multiple-spin systems. II. The effect of chemical exchange. J Chem Phys. 1966;45:902–916. [Google Scholar]
- Cavanagh J, Rance M. Suppression of cross-relaxation effects in TOCSY spectra via a modified DIPSI-2 mixing sequence. J Magn Reson. 1992;96:670–678. [Google Scholar]
- Cavanagh J, Fairbrother WJ, Palmer AG, Rance M, Skelton NJ. Protein NMR Spectroscopy: Principles and Practice. Academic Press; San Diego, CA: 2007. [Google Scholar]
- Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 1995;6:277–293. doi: 10.1007/BF00197809. [DOI] [PubMed] [Google Scholar]
- Dill KA, Ozkan SB, Shell MS, Weikl TR. The protein folding problem. Annu Rev Biophys. 2008;37:289–316. doi: 10.1146/annurev.biophys.37.092707.153558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doering DS, Matsudaira PT. Cysteine scanning mutagenesis at 40 of 76 positions in villin headpiece maps the F-actin binding site and structural features of the domain. Biochemistry. 1996;35:12677–12685. doi: 10.1021/bi9615699. [DOI] [PubMed] [Google Scholar]
- Friederich E, Vancompernolle K, Huet C, Goethals M, Finidori J, Vandekerckhove J, Louvard D. An actin-binding site containing a conserved motif of charged amino acid residues is essential for the morphogenic effect of villin. Cell. 1992;70:81–92. doi: 10.1016/0092-8674(92)90535-k. [DOI] [PubMed] [Google Scholar]
- Grey MJ, Wang C, Palmer AG. Disulfide bond isomerization in basic pancreatic trypsin inhibitor: Multisite chemical exchange quantified by CPMG relaxation dispersion and chemical shift modeling. J Am Chem Soc. 2003;125:14324–14335. doi: 10.1021/ja0367389. [DOI] [PubMed] [Google Scholar]
- Grey MJ, Tang Y, Alexov E, McKnight CJ, Raleigh DP, Palmer AG. Characterizing a partially folded intermediate of the villin headpiece domain under non-denaturing conditions: contribution of His41 to the pH-dependent stability of the N-terminal subdomain. J Mol Biol. 2006;355:1078–1094. doi: 10.1016/j.jmb.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Hill RB, Bracken C, DeGrado WF, Palmer AG. Molecular motions and protein folding: Characterization of the backbone dynamics and folding equilibrium of α2D using 13C NMR spin relaxation. J Am Chem Soc. 2000;122:11610–11619. [Google Scholar]
- Kay LE, Keifer P, Saarinen T. Pure absorption gradient enhanced heteronuclear single quantum correlation spectroscopy with improved sensitivity. J Am Chem Soc. 1992;114:10663–10665. [Google Scholar]
- Khandogin J, Raleigh DP, Brooks CL., III Folding intermediate in the villin headpiece domain arises from disruption of a N-terminal hydrogen-bonded network. J Am Chem Soc. 2007;129:3056–3057. doi: 10.1021/ja0688880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovrigin EL, Kempf JG, Grey MJ, Loria JP. Faithful estimation of dynamics parameters from CPMG relaxation dispersion measurements. J Magn Reson. 2006;180:93–104. doi: 10.1016/j.jmr.2006.01.010. [DOI] [PubMed] [Google Scholar]
- Loria JP, Rance M, Palmer AG., III A relaxation-compensated Carr-Purcell-Meiboom-Gill sequence for characterizing chemical exchange by NMR spectroscopy. J Am Chem Soc. 1999;121:2331–2332. [Google Scholar]
- Lundström P, Teilum K, Carstensen T, Bezsonova I, Wiesner S, Hansen DF, Religa TL, Akke M, Kay LE. Fractional 13C enrichment of isolated carbons using [1-13C]- or [2-13C]-glucose facilitates the accurate measurement of dynamics at backbone Cα and side-chain methyl positions in proteins. J Biomol NMR. 2007;38:199–212. doi: 10.1007/s10858-007-9158-6. [DOI] [PubMed] [Google Scholar]
- Meng J, Vardar D, Wang Y, Guo HC, Head JF, McKnight CJ. High-resolution crystal structures of villin headpiece and mutants with reduced F-actin binding activity. Biochemistry. 2005;44:11963–11973. doi: 10.1021/bi050850x. [DOI] [PubMed] [Google Scholar]
- Meng J, McKnight CJ. Heterogeneity and dynamics in villin headpiece crystal structures. Acta Cryst D. 2009;65:470–476. doi: 10.1107/S0907444909008646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng JM, McKnight CJ. Crystal structure of a pH-stabilized mutant of villin headpiece. Biochemistry. 2008;47:4644–4650. doi: 10.1021/bi7022738. [DOI] [PubMed] [Google Scholar]
- Millet O, Loria JP, Kroenke CD, Pons M, Palmer AG. The static magnetic field dependence of chemical exchange linebroadening defines the NMR chemical shift time scale. J Am Chem Soc. 2000;122:2867–2877. [Google Scholar]
- Neudecker P, Lundström P, Kay LE. Relaxation dispersion NMR spectroscopy as a tool for detailed studies of protein folding. Biophys J. 2009;96:2045–2054. doi: 10.1016/j.bpj.2008.12.3907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer AG, Cavanagh J, Wright PE, Rance M. Sensitivity improvement in proton-detected two-dimensional heteronuclear correlation NMR spectroscopy. J Magn Reson. 1991;93:151–170. [Google Scholar]
- Phan IQH, Boyd J, Campbell ID. Dynamic studies of a fibronectin type I module pair at three frequencies: Anisotropic modelling and direct determination of conformational exchange. J Biomol NMR. 1996;8:369–378. doi: 10.1007/BF00228140. [DOI] [PubMed] [Google Scholar]
- Schwarzinger S, Kroon GJA, Foss TR, Wright PE, Dyson HJ. Random coil chemical shifts in acidic 8 M urea: Implementation of random coil shift data in NMRView. J Biomol NMR. 2000;18:43–48. doi: 10.1023/a:1008386816521. [DOI] [PubMed] [Google Scholar]
- Skrynnikov NR, Mulder FAA, Hon B, Dahlquist FW, Kay LE. Probing slow time scale dynamics at methyl-containing side chains in proteins by relaxation dispersion NMR measurements: Application to methionine residues in a cavity mutant of T4 lysozyme. J Am Chem Soc. 2001;123:4556–4566. doi: 10.1021/ja004179p. [DOI] [PubMed] [Google Scholar]
- Smirnov SL, Isern NG, Jiang ZG, Hoyt DW, McKnight CJ. The isolated sixth gelsolin repeat and headpiece domain of villin bundle F-actin in the presence of calcium and are linked by a 40-residue unstructured sequence. Biochemistry. 2007;46:7488–7496. doi: 10.1021/bi700110v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spera S, Bax A. Empirical correlation between protein backbone conformation and Cα and Cβ 13C nuclear magnetic resonance chemical shifts. J Am Chem Soc. 1991;113:5490–5492. [Google Scholar]
- Tang Y, Grey MJ, McKnight J, Palmer AG, Raleigh DP. Multistate folding of the villin headpiece domain. J Mol Biol. 2006;355:1066–1077. doi: 10.1016/j.jmb.2005.10.066. [DOI] [PubMed] [Google Scholar]
- Ulrich EL, Akutsu H, Doreleijers JF, Harano Y, Ioannidis YE, Lin J, Livny M, Mading S, Maziuk D, Miller Z, Nakatani E, Schulte CF, Tolmie DE, Kent Wenger R, Yao H, Markley JL. BioMagResBank. Nucl Acids Res. 2008;36:D402–408. doi: 10.1093/nar/gkm957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vardar D, Buckley DA, Frank BS, McKnight CJ. NMR structure of an F-actin-binding “headpiece” motif from villin. J Mol Biol. 1999;294:1299–1310. doi: 10.1006/jmbi.1999.3321. [DOI] [PubMed] [Google Scholar]
- Vardar D, Chishti AH, Frank BS, Luna EJ, Noegel AA, Oh SW, Schleicher M, McKnight CJ. Villin-type headpiece domains show a wide range of F-actin-binding affinities. Cell Motil Cytoskel. 2002;52:9–21. doi: 10.1002/cm.10027. [DOI] [PubMed] [Google Scholar]
- Vugmeyster L, Kroenke CD, Picart F, Palmer AG, Raleigh DP. 15N R1ρ measurements allow the determination of ultrafast protein folding rates. J Am Chem Soc. 2000;122:5387–5388. [Google Scholar]
- Vuister GW, Yamazaki T, Torchia DA, Bax A. Measurement of two- and three- bond 13C-1H J couplings to the Cδ carbons of leucine residues in staphyloccocal nuclease. J Biomol NMR. 1993;3:297–306. doi: 10.1007/BF00212516. [DOI] [PubMed] [Google Scholar]
- Wang AC, Bax A. Minimizing the effects of radio-frequency heating in multidimensional NMR experiments. J Biomol NMR. 1993;3:715–720. doi: 10.1007/BF00198374. [DOI] [PubMed] [Google Scholar]
- Wang CY, Grey MJ, Palmer AG. CPMG sequences with enhanced sensitivity to chemical exchange. J Biomol NMR. 2001;21:361–366. doi: 10.1023/a:1013328206498. [DOI] [PubMed] [Google Scholar]
- Yip GN, Zuiderweg ER. Improvement of duty-cycle heating compensation in NMR spin relaxation experiments. J Magn Reson. 2005;176:171–178. doi: 10.1016/j.jmr.2005.06.003. [DOI] [PubMed] [Google Scholar]
- Yip GNB, Zuiderweg ERP. A phase cycle scheme that significantly suppresses offset-dependent artifacts in the R2-CPMG 15N relaxation experiment. J Magn Reson. 2004;171:25–36. doi: 10.1016/j.jmr.2004.06.021. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.