Comparing and ranking hospitals based on outcome: results from The Netherlands Stroke Survey

Abstract

Background: Measuring quality of care and ranking hospitals with outcome measures poses two major methodological challenges: case-mix adjustment and variation that exists by chance.

Aim: To compare methods for comparing and ranking hospitals that considers these.

Methods: The Netherlands Stroke Survey was conducted in 10 hospitals in the Netherlands, between October 2002 and May 2003, with prospective and consecutive enrolment of patients with acute brain ischaemia. Poor outcome was defined as death or disability after 1 year (modified Rankin scale of ⩾3). We calculated fixed and random hospital effects on poor outcome, unadjusted and adjusted for patient characteristics. We compared the hospitals using the expected rank, a novel statistical measure incorporating the magnitude and the uncertainty of differences in outcome.

Results: At 1 year after stroke, 268 of the total 505 patients (53%) had a poor outcome. There were substantial differences in outcome between hospitals in unadjusted analysis (χ² = 48, 9 df, P < 0.0001). Adjustment for 12 confounders led to halving of the χ² (χ² = 24). The same pattern was observed in random effects analysis. Estimated performance of individual hospitals changed considerably between unadjusted and adjusted analysis. Further changes were seen with random effect estimation, especially for smaller hospitals. Ordering by expected rank led to shrinkage of the original ranks of 1–10 towards the median rank of 5.5 and to a different order of the hospitals, compared to ranking based on fixed effects.

Conclusion: In comparing and ranking hospitals, case-mix-adjusted random effect estimates and the expected ranks are more robust alternatives to traditional fixed effect estimates and simple rankings.

Introduction

Measuring quality of care receives increasing attention. Specifically, ranking of hospitals may be attempted to compare their quality of care. Such ranking is currently very popular, especially in the lay press.^1,2

Measuring quality of care and ranking hospitals has the potential to enable health care financers to identify poor performance. In addition, patients (or 'consumers') might choose the best hospital for their health problem, and hospitals may learn from best practices. All these applications can have huge consequences for hospitals on, for example, their budget and reputation, which makes reliability of results extremely important.

Quality of care is often measured with outcomes such as mortality, an approach that is surrounded by many methodological problems.³ The first major issue is case-mix adjustment.⁴ Case-mix adjustment should appropriately capture differences between hospitals in-patient characteristics that are outside the influence of actions in the hospital.

The second issue is drawing proper conclusions from the hospital-specific case-mix-adjusted outcomes. There will always be some variation in outcome between hospitals, caused just by chance. Disregarding this chance variation may lead to over-interpretation of differences between hospitals since especially smaller hospitals can have an extreme outcome, caused more by chance than by their underlying quality.

Variation between hospitals in binary outcomes is traditionally modelled as fixed effects in a logistic regression model. We can also use a random effect logistic regression model which accounts for variation by chance at the hospital level.^3,5–10

Ranking hospitals according to their outcome causes the problem that one hospital has to be first and the other has to be last. Simple ranking disregards both the magnitude of the relative differences between the hospitals and the variation that exists by chance, and can hence put hospitals in needless jeopardy.

In this study, we use data from the Netherlands Stroke Survey to compare methods for assessment of quality of care that takes into account case-mix and variation by chance.

Methods

The Netherlands Stroke Survey

The Netherlands Stroke survey was conducted in 10 hospitals in the Netherlands: two in the north, four in the middle and four in the southern regions. The participating hospitals comprised one small (<400 beds), four intermediate (400–800 beds) and five large hospitals (>800 beds). Two hospitals were university hospitals.

All patients who were admitted to the neurology department with suspected acute brain ischaemia between October 2002 and May 2003 were screened. Patients were enrolled consecutively and prospectively if the initial diagnosis of first or recurrent acute brain ischaemia was confirmed by the neurologist’s assessment. Trained research assistants collected data from the patients’ hospital charts, within 5 days after discharge. At 1 year, survival status was obtained through the Civil Registries. A telephone interview was conducted and it is based on a structured questionnaire, which was sent in advance. Follow-up was complete in 96% of the patients. More details on the study population and methods of data collection were reported previously.^11,12

Case-mix adjustment

The primary outcome was whether patients were dead or disabled at 1 year after admission, i.e. a score on the modified Rankin scale of 3 or higher. We used a logistic regression model to adjust for case-mix, because we consider case-mix as confounders since it may be related to the setting and to the outcome and is outside the influence of actions in the hospital. The model we used included 12-patient characteristics: age, sex, stroke subtype [transient ischaemic attack (TIA) or ischaemic stroke], stroke severity, lowered consciousness level at hospital arrival, Barthel Index 24 h from admission, previous stroke, atrial fibrillation, ischaemic heart disease, diabetes mellitus, hypertension and hyperlipidaemia. These variables were selected in previous work on the same data set with stepwise logistic regression analysis with backward elimination of possible confounders with the Akaike information criterion (AIC) for inclusion (equivalent to P < 0.157 for confounders with one degree of freedom).¹³ In the first step, age, sex and stroke subtype were entered and in the second step the other patient characteristics were added. The model is described in more detail elsewhere.¹²

Hospital effects

We estimated the variation between the hospitals with two different models. The first was a standard fixed effect logistic regression model, with hospital as a categorical variable. We estimated the coefficient for each hospital, compared with the average using an offset variable. We also calculated the chi-square for the model as the difference in −2 log likelihood for a model with and without hospital, to indicate the total variation between the hospitals. Both the individual coefficients and the variation were calculated with and without adjustment for case-mix. We refer to the results of the fixed effect models as fixed effect estimates.

Since the fixed effect estimates do not account for variation by chance, we also fitted a random effect logistic regression model. Random effect models account for the fact that part of the variation between hospitals is just chance. They estimate the hospital effects and the total variation ‘beyond chance’. This total variation is indicated by the model parameter τ². We refer to the results of the random effect models as random effect estimates and these were also fitted with or without adjustment for case-mix.

Ranking and rankability

To also account for the variation by chance in rankings, we calculated the expected rank (ER); this is the probability that the performance of a hospital is worse than another randomly selected hospital. The ER incorporates both the magnitude and the uncertainty of the difference of a particular hospital with other hospitals. We can scale the ERs between 0% and 100% with percentiles based on expected rank (PCER) for easy interpretation and to make the ranks independent of the number of hospitals. The PCER can be interpreted as the probability (as a percentage) that a hospital is worse than a randomly selected hospital, including itself.

To see whether it makes sense to rank the hospitals, we calculated the ‘rankability’. The rankability relates the total variation from the random effect models (How large are the differences between the hospitals?) to the uncertainty of the individual hospital differences from the fixed effect model (How certain are the differences?). The rankability can be interpreted as the part of variation between the hospitals that is not due to chance.

More details on the statistical analysis and formulas can be found in Appendix 1 and in a previous, more detailed work on this topic.¹⁴

The statistical analysis was performed with R (version 2.5, R foundation for statistical computing, Vienna). The random effect analysis was repeated in SAS (version 9, SAS Inc, Cary, NC, USA) with compatible results. R programming code can be found in Appendix 2.

Results

Study population

The study population consisted of 579 patients who were admitted to the hospital because of acute ischaemic stroke or TIA. Of these, 505 patients (87%) with complete data on potential confounders and outcome were used in the analysis. The lowest numbers enrolled were 22 and 24 patients in hospitals 5 and 6 and the highest numbers 92 and 99 in hospitals 2 and 7, respectively (Table 1).

Table 1.

Patient characteristics and poor outcome (modified Rankin scale ≥ 3), and multivariable OR of patient characteristics in the adjustment model on poor outcome

Hospital	1	2	3	4	5	6	7	8	9	10	Total	OR (P-value)
n	39	92	31	40	22	24	99	36	50	70	505
Mean age (years)	77	73	69	65	74	65	68	70	71	72	71	1.5 (< 0.001)a
Male sex (%)	46	54	61	59	55	67	65	41	56	47	55	0.7 (0.092)
Stroke subtype (% stroke vs. TIA)	97	95	97	80	91	63	94	92	88	81	90	1.1 (0.853)
Severe strokeb (%)	28	17	16	13	9	8	15	17	14	10	15	3.5 (< 0.001)
Lowered consciousness levelc (%)	21	21	10	15	18	4	2	17	12	11	13	3.5 (0.001)
ADL dependentc,d (%)	90	92	100	85	82	54	64	100	84	64	80	2.8 (0.001)
Previous stroke (%)	26	18	26	33	27	33	21	28	26	17	24	1.9 (0.012)
Atrial fibrillation (%)	23	21	16	15	27	8	17	11	22	14	18	1.7 (0.072)
Ischaemic heart disease (%)	13	23	29	18	36	21	13	31	26	21	21	2.0 (0.012)
Diabetes mellitus (%)	15	30	23	20	9	21	17	17	16	20	20	2.1 (0.008)
Hypertension (%)	56	47	58	58	59	75	81	50	58	50	59	0.6 (0.018)
Hyperlipedaemia (%)	54	46	68	53	73	50	58	44	70	79	59	0.6 (0.040)
Poor outcome (%)	59	72	35	44	73	29	39	78	54	46	53

^aOR per decade.

^bParesis of arm, leg and face, homonymous hemianopia and aphasia or other cortical function disorder.

^cAt hospital arrival.

^dBarthel index = 20.

Mean age was 71 (SD = 13 years), 278 patients (55%) were male, and the majority [450 (90%)] was diagnosed with cerebral infarction (Table 1).

At 1 year, 143 patients (28%) had died and of the remaining 362 patients, 125 (35%) were disabled (modified Rankin scale scores 3, 4 or 5). Thus, the total number of patients with poor outcome at 1 year after stroke was 268 (53%). This percentage varied substantially between hospitals from 29% poor outcome in hospital 6 to 78% poor outcome in hospital 8 (Table 1).

Case-mix adjustment

The strongest predictors of poor outcome were indicators of stroke severity [severe stroke: OR (odds ratio) = 3.5, P ⩽ 0.001; lowered consciousness level: OR = 3.5, P = 0.001; activities of daily living (ADL) dependency: OR = 2.8, P = 0.001] and age (OR = 1.5/decade, P = 0.001) (Table 1).

The area under the curve (AUC) of the total model was 0.804. Sex and stroke subtype were not significant anymore after adding all the confounders in the second step of the model development.

Although the differences in outcome between hospitals were highly significant in unadjusted fixed effects analysis (χ² = 48, 9 df, P < 0.0001, Table 2), they were partly explained by confounders. For example, hospitals 2, 5 and 8 had over 70% poor outcomes but mean ages of 73, 74 and 70 years. On the other hand, hospitals with mostly good outcomes had younger patients (e.g. hospital 6, mean age 65 years, 29% poor outcome, Table 1). Adjusting the fixed effect analysis for all 12 potential confounders led to halving of the χ² seen in unadjusted analysis (χ² = 24 instead of 48, Table 2). This pattern was also seen in the random effects analysis (τ² = 0.18 vs. 0.38, Table 2).

Table 2.

Heterogeneity between hospitals in fixed and random effect logistic regression analysis

	Fixed effect	Random effect
Unadjusted	χ2 = 48, 9 df, P < 0.0001	τ2 = 0.38, χ2 = 24, 1 df, P < 0.0001
Twelve confounders	χ2 = 24, 9 df, P = 0.0042	τ2 = 0.18, χ2 = 4, 1 df, P = 0.0275

χ²: Difference on −2 log likelihood scale of model with and without hospital. τ²: Variance of the random effects on log odds scale.

Estimation of differences between hospitals

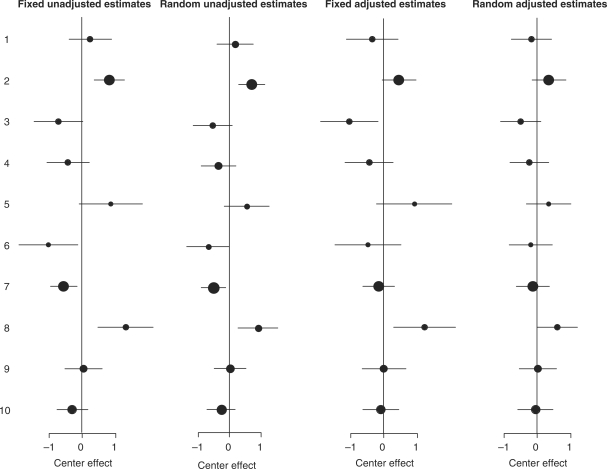
The apparent performance of the individual hospitals changed considerably between unadjusted and adjusted fixed analysis (Table 3, Figure 1).

Table 3.

Fixed and random effect estimates for differences between hospitals

Hospital	n	Fixed effect Unadjusted	Random effect Unadjusted	Fixed effect Adjusted	Random effect Adjusted
1	39	0.24	0.18	−0.36	−0.18
2	92	0.81	0.70	0.45	0.35
3	31	−0.72	−0.54	−1.04	−0.50
4	40	−0.43	−0.35	−0.44	−0.24
5	22	0.86	0.53	0.91	0.34
6	24	−1.01	−0.68	−0.47	−0.21
7	99	−0.55	−0.51	−0.15	−0.13
8	36	1.39	0.90	1.23	0.60
9	50	0.04	0.02	0.00	0.01
10	70	−0.29	−0.27	−0.09	−0.05

Values are logistic regression coefficients, compared to the overall average outcome. A positive number means a higher probability on poor outcome.

Figure 1.

Differences between centres with unadjusted fixed effect estimates, unadjusted random effect estimates, adjusted fixed effects estimates and adjusted random effect estimates. A positive numbers means a higher probability on poor outcome. Dot size indicates sample size per centre.

Hospital 1 seemed to perform relatively poorly in unadjusted analysis (positive coefficient) while adjusted analysis indicated that the hospital performed relatively well (negative coefficient). This suggests that the positive coefficient was attributable to the unfavourable case-mix of the hospital. Changes for other hospitals were only quantitative, without change of sign, with adjusted differences generally closer to zero.

Further changes were seen after accounting for variation by chance with adjusted random effect models (Table 3 and Figure 1). As expected random effect estimation did not affect estimates for the larger hospitals, such as 2 and 7. However, for the smaller hospitals, such as hospitals 5, 6 and 8, the point estimates were shrunken considerably. None of the hospitals had a deviation significantly different from the average in the random effect model but the overall heterogeneity was still statistically significant (Table 2).

Ranking and rankability

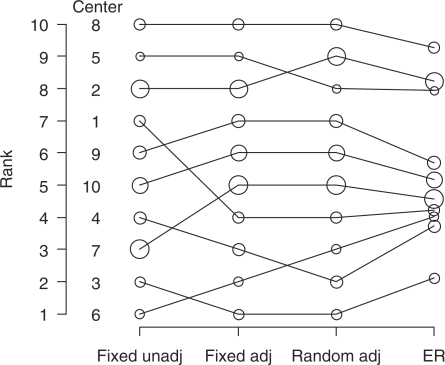
We first ranked hospitals based on unadjusted and adjusted fixed effect estimates and adjusted random effect estimates. Figure 2 shows that some hospitals such as 1, 3 and 4 change rank after adjustment for patient characteristics, and some small hospitals such as 5 and 6 again change rank after accounting for variation by chance with random effect estimation.

Figure 2.

Ranks (left y-axis) of 10 centres in fixed effect unadjusted, fixed effect adjusted, and random effects adjusted analyses and ER. Dot size indicates sample size per centre.

Subsequently, we calculated the ER and PCER. Figure 2 shows that the ER led to shrinkage of the ranks towards the median rank of 5.5 with 6 hospitals having an ER close to this median. Hospital 6 seemed to do best with rank 1 in unadjusted analysis, shifted to rank 2 in adjusted analysis, to rank 3 in random effects analysis and had an ER around 4, meaning that at most 4 out of 10 hospitals are expected to do better than this hospital.

With the PCER, we can express the ERs on a 0–100% scale. Hospital 8 had a PCER of 86%, meaning there is an 86% probability that a randomly selected hospital does better than hospital 8. Hospital 3 had the best PCER (17%), meaning that there was only a 17% probability that a randomly selected hospital does better than hospital 3.

The rankability was 55%. This means that of the total variation between hospitals after adjustment, 55% was not due to chance.

Discussion

In this study, we found large differences in the proportion of patients with poor outcome after stroke between hospitals. Adjusting for 12 potential confounders led to halving of the chi-square seen in unadjusted analysis, and considerable changes in performance estimates for individual hospitals. Further changes were seen after accounting for uncertainty in the random effect estimation, especially for smaller hospitals. Ordering the hospitals by means of the ER led to shrinkage of the simple ranks of 1–10 towards the median rank of 5.5 and to a different order of the hospitals.

A limitation of our study is that we are unable to do power calculations as we did not define a formal hypothesis on the difference between the hospitals. Our results should be considered as part of a larger debate on measuring quality of care. Measuring quality of care can have multiple purposes. A first broad distinction can be made between internal and external purposes. The first can, for example, be an internal quality system, or ‘benchmarking’, with the initiative at the side of the hospital. The second includes increasing accountability to governments, patients and insurance companies. These purposes are related, since a relatively poor performance might be an incentive for a hospital to stimulate improvements. Such feedback can lead to a continuous quality improvement. The results of this study apply more to external than to internal quality measurement.

If we want to compare hospitals, we can debate what to measure and how to measure it. In this study, we focused on outcome (in this case the combination of mortality and disability), but quality of care measures may also include, for example, patient satisfaction, and organizational issues such as procedures and processes of delivering care.^15,16 It is known that outcome is not always a valid indicator of quality of care.¹² Therefore some argue that we should concentrate on direct measurement of adherence to clinical and managerial standards.⁶ Moreover, measuring adherence to guidelines provides clear directions for improvement of care in all hospitals in those with poor outcome. Examples of such an approach in stroke are the ‘Get With The Guidelines’ program in the USA and the Scottish Stroke Care Audit.^17,18 Those in favour of outcome assessment, however, advocate that quality assessment on process level requests a too detailed data collection, and conclusions on quality depend largely on the selection of process measures.¹⁹

In debates around measuring quality of care based with outcome the issue of case-mix adjustment has received substantial attention.^20,21 Our study shows that this is indeed very important for stroke outcomes, since half of the differences, in terms of chi-square, between hospitals was explained by differences in case-mix. One hospital even seemed to perform poorly but appeared to perform well after adjustment for their unfavourable case-mix. We used a relatively simple model without any interaction terms for adjustment. In previous work, we showed that age, sex and stroke subtype alone have only a moderate predictive strength (AUC: 0.690; AUC of total model: 0.804).¹² The choice for an adjustment model should be a trade-off between the performance of the model and available data. It was surprising that in our model hypertension and hyperlipidaemia were protective for poor outcome (OR = 0.6). Both were scored if noted in medical history or if diagnosed during hospitalization. Most patients with one of these conditions were already diagnosed before their stroke and thus treated with antihypertensive drugs or statins; this may cause the protective effect.

A second issue in comparing hospitals is variation that exists just by chance. If there are hospitals involved with small samples sizes, using fixed effect models that disregard the variation by chance could lead to exploding estimates of the hospital effects, and over-interpretation of the differences. Random effect models do account for variation by chance; they allow imprecisely estimated outcomes from small hospitals to ‘borrow’ information from other hospitals, causing their estimates to be shrunk towards the overall mean. Random effect models are thus more robust.^3,5–10,20 Our study shows that the random effect estimates are indeed more conservative. In random effect analyses, none of the hospitals had an effect that was significantly different from zero, while some had in the fixed effect analyses. The variation by chance had a large impact on the conclusions drawn about the hospitals. Individual hospitals are often too small to reliably determine whether they are an outlier.²² Small hospitals are more likely to suffer more from variation just by chance than large hospitals.²³

We derived the random effect estimates directly from the fitted model as it is easily available now in statistical packages (such as R) and also since we were able to reproduce our results with other fitting methods and with other software. The random effect estimates can also be calculated in two steps.²⁴

Although random effect analyses are preferable for estimation of differences between hospitals, simple integer ranking based on these random effect estimates disregards uncertainty, and may lead to over-interpretation again. With the ER, uncertainty of the hospital effect estimates is also incorporated in the ranking. For example, we found that 6 of the 10 hospitals were close to the median rank. ERs are a better representation of the random effect estimates. Approaches similar to the ER have been proposed by others.^4,5,25–27 For ease of interpretation, we calculated the percentile based on expected rank, which is independent from the number of hospitals in the sample and indicates the probability that a hospital is worse than a randomly selected hospital, including itself.

A practical approach to ranking based on risk standardized mortality rates with 95% confidence intervals, estimated with hierarchical (random effects) modelling, was recently been proposed by Krumholz et al.²⁸ However, interpreting the magnitude and clinical significance of differences between hospitals with overlapping 95% confidence intervals is difficult.²⁹ The PCER consists of only one number. Although there is an almost universal agreement that a confidence interval is more informative than just an estimate, we believe that for lay people (patients who want to choose between hospitals) it is easier to interpret one number compared to an estimate and its confidence interval. On the other hand, the PCER does not show directly the degree of variation by chance, although it is included in the calculation of the single number. In our perspective, the PCER approach could be a useful extension to reporting of provider performance, since it combines the attractiveness of a ranking, provides a single number and is easy to interpret.

Some guidelines have recently been published with respect to statistical methods for public reporting of health outcomes, which suggest seven preferred attributes of statistical modelling for provider profiling: (i) clear and explicit definition of patient sample, (ii) clinical coherence of model variables, (iii) sufficiently high-quality and timely data, (iv) designation of a reference time before which covariates are derived and after which outcomes are measured, (v) use of an appropriate outcome and a standardized period of outcome assessment, (vi) application of an analytical approach that takes into account the multilevel organization of data and (vii) disclosure of the methods used to compare outcomes, including disclosure of performance of risk-adjustment methodology in derivation and validation samples.³⁰ In this study, we have focused mainly on attribute 6. We have also adjusted for case-mix (attribute 7) but the model we used was quite simple and not externally validated. We suggest adding an attribute: consider a measure of rankability to judge what part of the observed differences is not due by chance. It remains, however, a value judgment when ranking is appropriate. We would suggest that any ranking is meaningless when rankability is low (< 50%), that the ER should be used when rankability is moderate (> 50% and < 75%) and that simple integer ranks are appropriate when rankabilty is high (> 75%). ERs and integer ranks will then be very similar.

We label the remaining between hospital differences ‘unexplained’, since there can be many explanations to differences in outcome, including process of care, hospital characteristics, and more (unknown) patient characteristics. We will probably never know how large the ‘true’ differences are, or be able to completely explain them.¹⁸

To conclude, this study shows that adjustment for case-mix is crucial in measuring quality of care and ranking hospitals. Case-mix-adjusted random effect estimates and the ER are more robust alternatives to traditional fixed effect estimates and simple rankings and may assist to prevent over-interpretation.

Funding

The Netherlands Heart Foundation (2000T101); The National Institutes of Health (NS-01923521).

Conflict of interest. None declared.

Appendix 1: Formulas

Fixed effect logistic regression

with

Xij:	the regression coefficients describing the effect of the covariates and the intercept,
β:	the covariates (in this case the confounders) describing the patients characteristics of patient j in hospital i, including the constant term,
θ:i:	the effect of hospital i, that is the coefficient with respect to some overall mean.

Random effect logistic regression

with

Xij:	the covariates (in this case the confounders) describing the patients characteristics of patient j in hospital i, including the constant term,
β:	the regression coefficients describing the effect of the covariates and the intercept,
θi:	the effect of hospital i, that is the coefficient with respect to some overall mean, drawn from a normal distribution with mean µ and variance

Expected rank

with

F:	the normal distribution function,
θi–θk:	magnitude of the difference of a particular hospital with other hospitals and,
var(θi)+var(θk):	the uncertainty in this difference.

Percentiles based on expected ranks:

with

ERi:	the expected rank of a particular hospital and,
N:	the number of hospitals.

Rankability

with

τ2:	the variance of the random effects,
s2i:	the variance of the fixed effect individual hospital effect estimates.

Appendix 2: R Code