Direction Discrimination Thresholds of Vestibular and Cerebellar Nuclei Neurons

Abstract

To understand the roles of the vestibular system in perceptual detection and discrimination of self-motion, it is critical to account for response variability in computing the sensitivity of vestibular neurons. Here we study responses of neurons with no eye movement sensitivity in the vestibular (VN) and rostral fastigial nuclei (FN) using high-frequency (2 Hz) oscillatory translational motion stimuli. The axis of translation (i.e., heading) varied slowly (1°/s) in the horizontal plane as the animal was translated back and forth. Signal detection theory was used to compute the threshold sensitivity of VN/FN neurons for discriminating small variations in heading around all possible directions of translation. Across the population, minimum heading discrimination thresholds averaged 16.6° ± 1° SE for FN neurons and 15.3° ± 2.2° SE for VN neurons, severalfold larger than perceptual thresholds for heading discrimination. In line with previous studies and theoretical predictions, maximum discriminability was observed for directions where firing rate changed steeply as a function of heading, which occurs at headings approximately perpendicular to the maximum response direction. Forward/backward heading thresholds tended to be lower than lateral motion thresholds, and the ratio of lateral over forward heading thresholds averaged 2.2 ± 6.1 (geometric mean ± SD) for FN neurons and 1.1 ± 4.4 for VN neurons. Our findings suggest that substantial pooling and/or selective decoding of vestibular signals from the vestibular and deep cerebellar nuclei may be important components of further processing. Such a characterization of neural sensitivity is critical for understanding how early stages of vestibular processing limit behavioral performance.

Introduction

For decades, the neural processes underlying vestibular function have been studied primarily in relationship to reflexes. In contrast, the neural basis of perceptual functions related to self-motion and spatial orientation have remained relatively unexplored. Fundamental to sensory perception is that neuronal activity, even in response to a single repeated stimulus, is inherently variable (Seung and Sompolinsky, 1993; Shadlen and Newsome, 1994; Abbott and Dayan, 1999; Pouget et al., 2000; Dayan and Abbott, 2001; Averbeck et al., 2006; Ma et al., 2006). The issue of neuronal variability is particularly important for understanding perception around psychophysical threshold. Yet, little is currently known about the sensory detection and discrimination properties of vestibular neurons.

Only a few studies have characterized neuronal variability, and these have focused on spike timing of semicircular canal afferents (Paulin and Hoffman, 1999, 2001; Sadeghi et al., 2007a). Following the classic approach of studies in the vestibular periphery (Fernández and Goldberg, 1971, 1976a,b,c; Goldberg and Fernandez, 1971a,b; Fernandez et al., 1972; Goldberg et al., 1990; Dickman et al., 1991; Si et al., 1997; Purcell et al., 2003; Haque et al., 2004; Sadeghi et al., 2007b), responses of central vestibular neurons have only been characterized in terms of average gain and phase measurements and transfer-function approaches (for review, see Angelaki, 2004; Cullen and Roy, 2004; Angelaki and Cullen, 2008). These mean gain and phase measures have been critical for understanding the role of the vestibular system in reflexes, yet they are rather limited in helping us to understand how the sensitivity of neurons at different levels of the vestibular pathways place limits on perception (MacNeilage et al., 2008).

The first attempts to compare neuronal responses to vestibular stimulation with self-motion perception used animals trained to report their heading direction around straight-forward in a two-alternative-force-choice (2AFC) task (Gu et al., 2007, 2008). Macaques could accurately discriminate small changes in heading direction based on vestibular cues, with thresholds in the range from 1 to 5°. By comparison, cortical neurons recorded in the dorsal medial superior temporal area (MSTd) during performance of the task were tenfold less sensitive than behavior, on average, and only the most sensitive neurons rivaled behavioral performance (Gu et al., 2007). Vestibular heading discrimination thresholds have never been measured for subcortical neurons. Thus, it is not clear whether vestibular signals in area MSTd are more or less sensitive than those seen in earlier stages of the vestibular pathways.

We have used signal detection theory (Siebert, 1965; see also Green and Swets, 1966; Barlow et al., 1971; Newsome et al., 1989; Britten et al., 1992, 1996; Uka and DeAngelis, 2003) to characterize the heading discrimination thresholds of neurons in the vestibular nuclei (VN) and rostral fastigial nuclei (FN). We focused on these areas because they represent early levels of processing of otolith signals, with output projections to the thalamus (Lang et al., 1979; Meng et al., 2001, 2007) and spinal cord (Asanuma et al., 1983; Boyle et al., 1996; McCrea et al., 1999).

Materials and Methods

Subjects and surgery.

One fascicularis monkey (Macaca fascicularis) and two rhesus monkeys (Macaca mulatta) were used for these experiments. The animals were chronically and stereotaxically implanted with a plastic head-restraint ring and a guide tube platform, as well as with eye coils for monitoring eye movements. Additional details are provided in previous publications (Meng et al., 2005; Gu et al., 2006; Yakusheva et al., 2008). All surgical procedures were performed under sterile conditions in accordance with institutional and National Institutes of Health guidelines.

Electrophysiological recordings.

We recorded extracellularly the activities of single neurons in the vestibular and deep cerebellar nuclei using epoxy-coated tungsten microelectrodes (FHC, 5–7 MΩ impedance). Cerebellar nuclei recordings concentrated on the rostral fastigial nucleus, but some more laterally directed penetrations (up to 4.5 mm from the midline) encountered vestibular-responsive cells that are likely located in the anterior interposed nucleus (Shaikh et al., 2005). Vestibular nuclei recordings were made from the rostral medial part (Meng et al., 2005). Electrodes were inserted into 26-gauge transdural guide tubes and advanced by a remote-controlled microdrive (FHC). Raw neural activity was amplified, filtered (0–10 kHz, with notch filter at 60 Hz) and passed through a dual time-amplitude window discriminator (BAK Electronics). Single units were identified based on waveform shape, latency, and amplitude. Times of discriminated spikes were stored to disk for offline analyses through the event channel of a CED Power 1401 interface.

Experimental protocol.

We targeted the non-eye movement neurons in the FN/VN because they represent an early stage of processing of otolith information and because they are both strongly modulated during translation (Angelaki and Dickman, 2000; Zhou et al., 2001, 2006; Shaikh et al., 2005). While searching for responsive cells, animals were oscillated sinusoidally in complete darkness, either along their interaural axis or naso-occipital axis. Once a cell was satisfactorily isolated and found to be sensitive to translational movements, it was further tested with eye movement protocols. Monkeys were trained to follow a target, back-projected onto a screen located at a distance of 33 cm from the animal. The target was moved at 0.5 Hz, eliciting ±10° horizontal and vertical smooth-pursuit eye movements. Neurons were also tested during fixation and saccades to multiple horizontal and vertical targets. Only cells without eye movement sensitivity [typically referred to as “vestibular-only” (VO) cells] were further tested in these experiments.

In the main test, the animal was translated sinusoidally (2 Hz, ±0.3G) while simultaneously being rotated in yaw at a constant leftward or rightward velocity of 1°/s. Thus, the animal translated back and forth rapidly while the axis of translation changed very gradually over time (see Fig. 1A for a schematic). These motion stimuli were presented in complete darkness. Each “run” consisted of slightly more than a complete yaw revolution (i.e., a rotation that was always >360° but <540°, lasting 6–9 min), and each cell was tested with as many runs as possible (typically 5, with a minimum of 2 and a maximum of 10–11). For each pair of adjacent sinusoidal cycles (each cycle lasting 0.5 s), the axis of translation had only changed by 0.5°, considerably less than perceptual thresholds for vestibular heading discrimination (Gu et al., 2007, 2008). Thus, by comparing responses to nearby cycles we could measure the discriminability of each neuron; i.e., the smallest difference in heading direction that an ideal observer could discriminate based on the firing rate of the particular neuron. Moreover, since the heading axis varied continuously over all 360°, we could quantify neuronal discriminability around all possible reference directions to examine whether neurons were more sensitive in discriminating among forward vs lateral directions, for example.

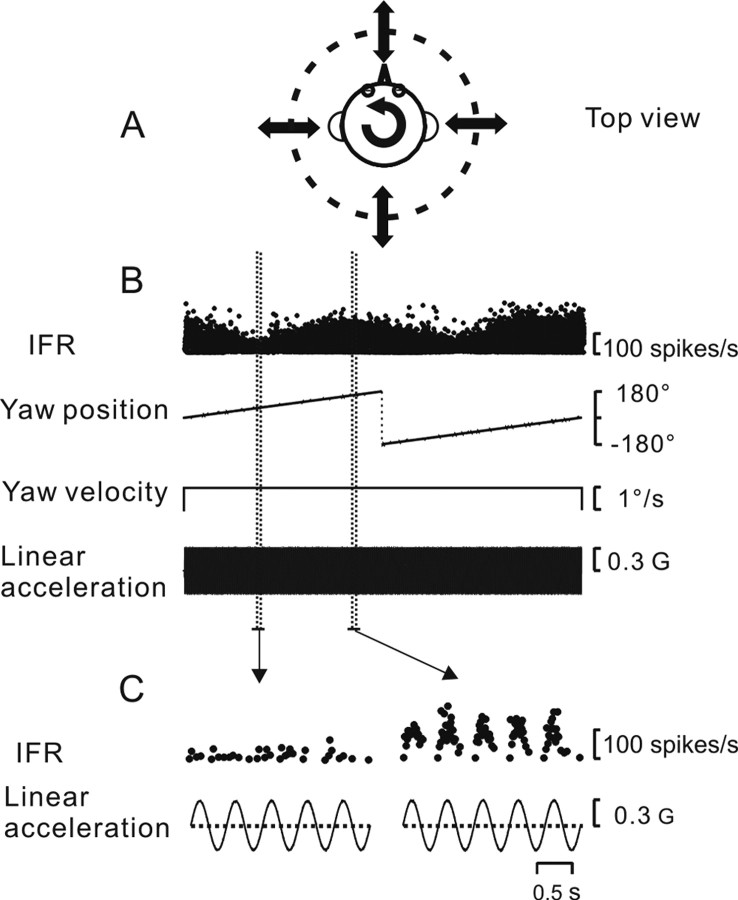
Figure 1.

Experimental protocol and neuronal responses. A, Schematic of the continuous linear acceleration stimulus around the head horizontal plane. B, IFR of a FN cell during combined sinusoidal translation (2 Hz; ±0.3G) and constant velocity rotation (1°/s). C, Enlarged time scale near the minimum and maximum response modulation, respectively.

Data analysis.

Sinusoidal responses were quantified using instantaneous firing rate (IFR), computed as the inverse of the interspike interval (Fig. 1B,C). First, peak sinusoidal modulation amplitude (half the peak-to-trough modulation) and phase were determined for each cycle by fitting a sinusoid (clipped off at zero response) to both the IFR and the stimulus using a nonlinear least-squares minimization algorithm (Levenberg-Marquardt). Second, we plotted the cycle-by-cycle response amplitude and phase as a function of translation direction (Fig. 2), collapsing data across all cycles of yaw rotation (i.e., all runs). To obtain a reliable estimate of the mean modulation amplitude and phase for all possible directions of translation, we subsequently fitted a spatiotemporal (STC, Angelaki, 1991, 1992) tuning model to both gain and phase data simultaneously.

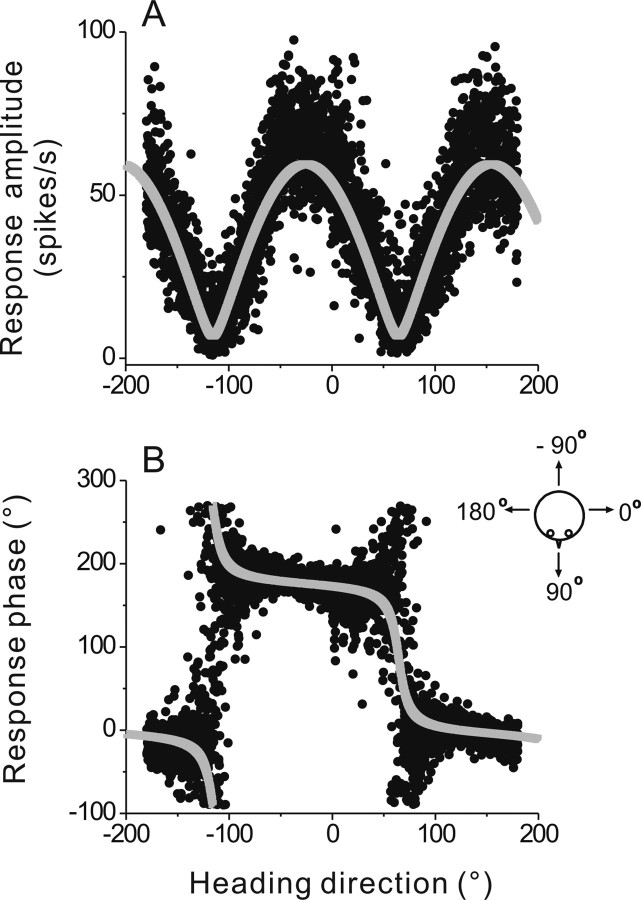
Figure 2.

Quantification of response tuning, including response amplitude and phase as a function of heading direction. A, Response amplitude is plotted as a function of heading direction for each cycle of translation (filled symbols). The best fit of a spatiotemporal model is shown as the gray curve. B, Response phase values (obtained from sinusoidal fits to each cycle response) are plotted as a function of heading direction (filled symbols), along with the model fit (gray curve). The tuning ratio for this cell was 0.12. Data shown are superimposed from five runs (yaw revolutions) for the same FN cell as illustrated in Figure 1.

Note that the raw amplitude and phase data that are fit by the STC model (Fig. 2, filled symbols) are noisier when a particular direction of motion elicits little response modulation. The raw phase data can be especially noisy near response nulls (Fig. 2B). However, because the STC model was fitted to gain and phase data from all cycles and directions simultaneously (Fig. 2), it provided a good way to interpolate phase and amplitude estimates through regions where the raw data were noisy. Thus, although the smaller the modulation amplitude the higher the variability of the phase (Fig. 2), the fits introduce no systematic bias and provide an average description of the phase dependence on stimulus direction, even for parts of the tuning curve that modulated little with the linear acceleration stimulus (Fig. 1C, left).

The STC model has four parameters; three parameters characterize the properties of the cell's preferred stimulus: i.e., preferred direction, as well as response magnitude and phase for stimulation along the preferred direction. The fourth parameter is the “tuning ratio,” which characterizes the ratio of the response along an axis perpendicular to the preferred direction over the response along the preferred direction. The larger the tuning ratio, the larger is the departure from the traditional cosine-tuning and the larger the dependence of phase on stimulus direction. Note that the spatiotemporal model has been shown to characterize best the translation tuning of brainstem and cerebellar vestibular neurons (Bush et al., 1993; Angelaki and Dickman, 2000; Shaikh et al., 2005; Chen-Huang and Peterson, 2006). For the present analyses, only the fitted phase parameter of the STC model was used to separate each neural response into two half-cycles, as described below.

Our goal is to measure the sensitivity of neurons to changes in the direction of linear acceleration (i.e., heading). To do this, we need to compile a distribution of firing rates (across stimulus repetitions) for each distinct direction of translation. These distributions can then be subjected to Receiver Operating Characteristics (ROC) analysis to compute discriminability (Gu et al., 2007, 2008). However, if we compute the firing rate for each trial over the entire cycle of movement (0.5 s), positive and negative response modulations corresponding to opposite directions of motion would nearly cancel each other and give poor estimates of stimulus-driven responses. To overcome this obstacle, we separated each cycle of neuronal response into two half-cycles that correspond to the “excitatory” and “inhibitory” portions. Because response phase is generally non-zero (and varies as a function of stimulus direction) (Angelaki and Dickman, 2000; Dickman and Angelaki, 2002), we shifted the time of each zero-crossing of the stimulus according to the phase of the measured neural response for that particular direction of motion, using the phase estimated from the STC model fit described above. Recall that the STC model fits were effective at separating excitatory and inhibitory half-cycles of response, even for parts of the tuning curve that modulated little with the linear acceleration stimulus (Fig. 1C, left). Thus, for each cycle of motion (corresponding to a 0.5° change in heading direction), we compute two firing rates, each corresponding to one half-cycle of the neural response. Heading directions for these two half-cycles correspond to opposite stimulus directions, such that each stimulus cycle yields two firing rates corresponding to headings that differ by 180°.

Having transformed raw responses into firing rates for each direction of motion, we constructed direction tuning curves with fine resolution (Fig. 3A,B). Next, using ROC analysis (Britten et al., 1992; Prince et al., 2000; Uka and DeAngelis, 2003; Gu et al., 2007), we compute a neuronal direction discrimination threshold that quantifies the ability of an ideal observer to discriminate between nearby directions of motion based on the firing rates of a particular cell. To compute a neuronal threshold for a particular “reference” motion direction (e.g., 0°), we obtain firing rates for pairs of directions to the left and right of the reference direction (e.g., ±1°, ±2°, etc.) (Fig. 4B). For each pair of symmetrically spaced “comparison” directions, distributions of firing rates are compiled and an ROC metric (Green and Swets, 1966) is computed. The proportion of “rightward choices” (relative to the particular reference direction) obtained for a particular pair of comparison directions is taken as the area under the corresponding ROC curve (Newsome et al., 1989; Britten et al., 1992). The proportion of rightward choices of the ideal observer is then plotted against the angular separation between reference and comparison directions, yielding a neurometric function. The neurometric function is fit by a cumulative Gaussian function (Fig. 4C), and neuronal threshold is defined as the SD of the Gaussian, which corresponds to 84% correct performance. Note that it takes 1 s for translational motion direction to change by 1°. Thus, data from four sequential half-cycles (each lasting 0.25 s) were combined to compute neuronal thresholds to a resolution of 1°.

Figure 3.

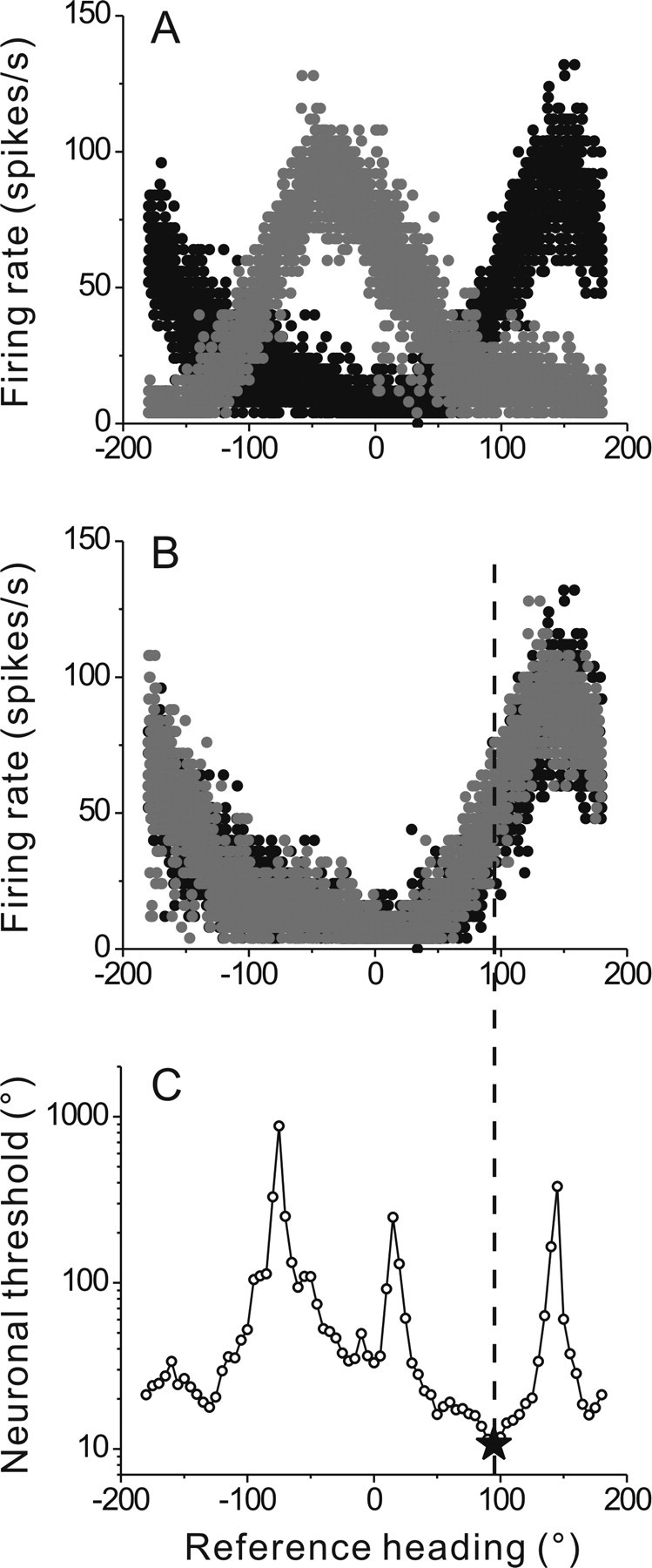
Firing rate as a function of heading direction for an example FN neuron. A, Data from the two half-cycles are shown by black and gray symbols, respectively (data pooled across 5 runs). B, Firing rate from the second half of each response cycle is shifted by 180° to overlap with data from the first half-cycle. C, Computed neuronal threshold plotted against reference heading direction. Data shown are from the same cell as in Figures 1 and 2. A vertical dashed line illustrates that the minimum discrimination threshold is observed away from the preferred direction, where tuning changes rapidly.

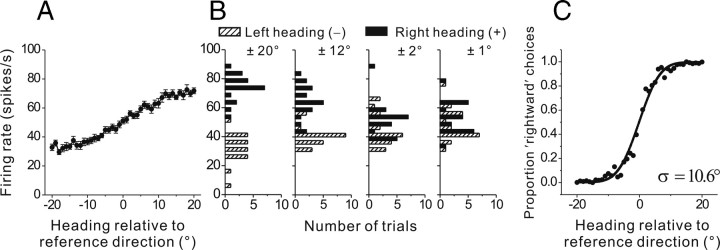
Figure 4.

Quantification of neuronal threshold for a single reference direction. A, Tuning curve, plotting firing rate (mean ± SE) as a function of heading direction in the range of ±20° around the reference heading. Positive angles indicate rightward directions; negative angles indicate leftward directions (relative to the reference). B, Firing rate distributions for four pairs of comparison headings, ±20° ±12°, ±2°, and ±1° relative to the reference. C, Example neurometric function showing proportion rightward decisions of an ideal observer as a function of heading direction. Each data point corresponds to an ROC value computed from a pair of firing rate distributions like those shown in B. Solid line shows a cumulative Gaussian fit to the neurometric function.

Although several full cycles of yaw rotation (runs) were collected for each neuron, isolation often deteriorated during this long experimental protocol (each run takes 6–9 min to complete). Thus, we instituted an off-line evaluation procedure to select runs for quantitative analysis. If single cell isolation is well maintained, the firing rate for the first half-cycle should be similar to that for the second half-cycle after 180° of yaw rotation. Thus, for each run, we calculated the correlation coefficient between firing rates obtained in the first half-cycle and the second half-cycle, after shifting the directions of motion corresponding to the second half-cycles by 180°. If neural response and tuning are stable, these two sets of firing rates should be well correlated. The median correlation coefficient was 0.53 across neurons. Only runs for which the correlation coefficient was larger than 0.5 have been included for further analysis. Because we required a minimum of two good runs to compute reliable neuronal thresholds, this criterion eliminated approximately one-third of the recorded neurons from further quantitative analysis. This exclusion criterion was important to ensure that neuronal thresholds were not overestimated due to less than ideal cell isolation.

The number of runs that met these criteria ranged from 2 to 9 across the population of neurons, with a mean of 4.1. Thus, the number of observations in each firing rate distribution for ROC analysis varied from 8 to 36. A potential concern is that discrimination thresholds might be overestimated for cells with smaller numbers of observations. The number of observations would be expected to determine the variance of the estimated threshold, but should not bias the estimate. To confirm this, we performed two additional analyses. First, using all neurons in our sample (n = 61), we found no correlation between minimum neuronal threshold and the number of runs used for analysis (p = 0.24, Spearman rank correlation). Second, for neurons tested with five or more runs (n = 20), we randomly subsampled (with replacement) smaller sets of trials that matched the smallest number of runs in the study (n = 2). For each cell, this subsampling procedure was repeated 5 times. We then compared, on a cell by cell basis, the minimum neuronal threshold computed from the whole dataset with the thresholds computed using the smaller subsample of runs, and we found no significant difference between the two (Wilcoxon signed-rank test, p = 0.23; type II regression slope = 1.02, 95% confidence interval = [0.94, 1.12]). Thus, the number of observations did not bias the outcome with respect to neuronal sensitivity.

Because of the continuous variation of yaw angle in a run, each dataset can be used for multiple (ROC) analyses, each corresponding to a different reference direction in the horizontal plane. Thus, we have computed heading discrimination thresholds for a wide range of reference headings, including 0°/180° (lateral motion) and ±90° (forward/backward motion), in steps of 5°. This allowed us to quantify the performance of each neuron for discriminating heading around different reference directions. Moreover, for each reference, the ROC analysis can be performed for pairs of directions that span different ranges; here, we have varied this range from ±5° (narrowest) to ±45° (widest). The values reported in the Results correspond to a range of comparison directions of ±20° (40°), which was found to produce near-optimal results.

It is important to emphasize that this analysis procedure is applicable to all cells, including those sensitive to yaw rotation, for multiple reasons. First, at the behavioral level, human linear acceleration thresholds are not influenced by simultaneous yaw rotation (Turner et al., 2008). Second, for a neuron with a typical gain of 1–2 spikes/s per degree per second, the rotation speed of 1°/s would evoke 1–2 spikes/s, which is typically 50–100 times (mean = 66.1) less than the peak-to-trough response to linear acceleration (Fig. 2). Finally, the constant yaw velocity of 1°/s is common to all linear acceleration cycles, thus at most resulting in a change in the mean firing rate of the cell. Because we are quantifying fine discrimination thresholds (i.e., how much firing rates vary for nearby cycles), a common response to the 1°/s yaw rotation stimulus will not affect the heading discrimination thresholds appreciably.

To determine whether a measured distribution was significantly different from uniform, we performed a resampling analysis (Takahashi et al., 2007). Briefly, the sum squared error (across bins) between the measured distribution and an ideal uniform distribution containing the same number of observations was first obtained. Next, a random distribution is generated by drawing the same number of data points from a uniform distribution and the sum squared error is again calculated between this random distribution and the ideal uniform distribution. This second step is repeated 1000 times to generate a distribution of sum squared error values that represent random deviations from an ideal uniform distribution. If the sum squared error for the experimentally measured distribution lay outside the 95% confidence interval of values from the randomized distributions, then the measured distribution is considered to be significantly different from uniform (p < 0.05).

Results

We present data from 41 rostral FN and 20 VN cells recorded in three monkeys. None of the cells responded to eye movements, but modulated during whole-body translation in the horizontal plane. Only runs from neurons during which single-unit isolation was maintained have been included in the quantitative analyses (see Materials and Methods). Figure 1 shows an example neuronal response during the main experimental protocol, which consists of a combination of 2 Hz translation and constant velocity (1°/s) yaw rotation. A convenient way to think of the stimulus is to consider it a 2 Hz sinusoidal translation whose direction changes very gradually in the horizontal plane (Fig. 1A), in steps of 0.5° (the duration of each cycle) (see Materials and Methods). Because it is difficult to visualize the 2 Hz sinusoidal modulation of firing rate when looking at a whole run (Fig. 1B), two five-cycle segments, one taken near the minimum response direction and the other near the maximum direction (Fig. 1B, marked with vertical dashed lines), are illustrated in Figure 1C. A clear 2 Hz modulation of IFR is visible in Figure 1C, right, but is absent in Figure 1C, left. Thus, the modulation amplitude in response to translation is smoothly modulated with the changing direction of the linear acceleration stimulus.

The amplitude and phase of the sinusoidal response modulation were characterized as a function of heading direction (resolution: 0.5°) by fitting a sinusoid to the neural response on a cycle-by-cycle basis (Fig. 2, symbols) (see also Materials and Methods). The dependence of amplitude and phase on heading direction was then quantified by fitting a spatiotemporal model to the data (Fig. 2, light gray lines) (Angelaki, 1991, 1992; Schor and Angelaki, 1992). Fitting was applied to the aggregate data from multiple experimental runs, each of which consists of >360° of constant velocity yaw rotation (see Materials and Methods). This cell had a preferred (i.e., maximum) response direction at 155° and a tuning ratio (i.e., minimum response/maximum response, see Materials and Methods) of 0.12. The fitted phase values as a function of heading direction were subsequently used to separate each response into two half-cycles.

Our goal is to characterize the cycle-by-cycle variability in firing rate in a parameter-free way that does not depend on how well a particular function fits the sinusoidal response modulation of a particular cell. For this reason, we did not make use of the fitted amplitude function from the previous analysis. Instead, we simply computed firing rates in response to each different direction of translation. However, because the linear acceleration stimulus was sinusoidal, each cycle of neural response was first split into two half-cycles. This was done by detecting the zero-crossing of the linear acceleration stimulus and shifting it according to the estimated phase of the neural response (from Fig. 2B, gray curve). Then we computed a firing rate (i.e., spike count divided by 0.25 s) for each half-cycle of translation.

Figure 3A illustrates how the firing rate for each of the two half-cycles depends on heading direction for the same example neuron as in Figure 2 (black dots: firing rate for the first half-cycle; gray dots: firing rate for the second half-cycle). The two tuning functions are, as expected, shifted by 180° because firing rate in the second half-cycle should be the same as that during the first half-cycle for the opposite stimulus direction. Thus, to increase the power of the ROC analysis, the two sets of responses were combined by shifting the gray dots by 180°, as illustrated in Figure 3B. This process was repeated for each cycle of yaw rotation, and the data from all runs were pooled for each neuron. Next we describe how ROC analysis was applied to these data to compute neuronal direction discrimination thresholds for different reference directions.

Computing neurometric functions and neuronal thresholds

We illustrate the ROC analysis procedure using a particular reference direction (95°) for the example neuron (this direction is recast as 0° heading in Fig. 4). For illustration, this reference heading was chosen to lie in a rapidly changing portion of the cell's tuning curve (Fig. 3B). We then group together all firing rates within each 1° heading bin, starting with the reference heading and extending outward ±20° from it. As expected from Figure 3B, the tuning curve of the cell over this narrow heading range around the reference direction is monotonic (Fig. 4A). This cell fires more strongly for rightward (positive) than leftward (negative) headings, relative to the reference heading.

The purpose of ROC analysis here is to quantify the sensitivity of the neuron to small changes in heading direction. For this purpose, one needs to quantify the overlap of two firing rate distributions, corresponding to a pair of heading directions symmetrically placed around the reference. Such pairs of distributions are illustrated for the example neuron in Figure 4B. When the two comparison headings are far apart (i.e., ±20° or ±12° relative to the reference), the firing rate distributions overlap little. As a result, an ideal observer would be able to distinguish whether a given firing rate came from the leftward or rightward distribution with a high degree of certainty. However, when the two comparison directions are closely spaced (i.e., ±1° or ±2° relative to the reference), the firing rate distributions overlap extensively, thus making the task of an ideal observer difficult.

This intuition is quantified using ROC analysis (Britten et al., 1992; Gu et al., 2007). For each pair of heading directions around the reference, an “ROC value” is computed which reflects the probability that an ideal observer could accurately report whether the heading was “rightward” or “leftward” (relative to the reference) based on a draw from the neuron's firing rate distribution. “Neurometric” functions can then be constructed by plotting ROC values for each pair of comparison directions (Fig. 4C). Quantification of this relationship captures the sensitivity of the neuron to directional signals in the same manner that psychometric functions capture perceptual sensitivity to directional signals in a 2AFC task (Britten et al., 1992; Purushothaman and Bradley, 2005; Gu et al., 2007). The neurometric function is summarized by fitting a cumulative Gaussian function to the data (Fig. 4C, smooth curve). From this fit, the neuronal threshold is defined as the SD of the underlying Gaussian (σ = 10.6° for the example of Fig. 4). Thus, for each reference heading selected, we obtain a neuronal discrimination threshold.

Summary of neuronal thresholds

For each cell, ROC analysis was applied across the full range of possible reference headings, in steps of 5°, as illustrated for the example cell in Figure 3C. The asterisk and vertical dashed line mark the minimum threshold, obtained for a reference heading of 95°, which for this cell occurred 60° away from the preferred response direction (155°, see above). Where the minimum threshold occurs depends both on the tuning curve slope (which determines the separation of the distribution means (Fig. 4B) and on the firing rate variability (which determines the width or variance of the firing rate distributions). Note also that the ROC analysis applied here does not make any a priori assumptions about the shape of the tuning curve or the firing rate distributions (Britten et al., 1992). Thus, estimation of neuronal thresholds using ROC analysis applies to both cosine-tuned and spatiotemporally tuned neurons (discussed further below).

Using this procedure, we could examine discrimination performance around different axes including 0°/180° (lateral motion) and ±90° (forward/backward motion). Minimum neuronal thresholds varied from 2.3° to 36.6° across the population of neurons studied (Fig. 5A) and distributions of minimum thresholds were similar for FN and VN cells (mean ± SE: 16.6° ± 1° for FN vs 15.3° ± 2.2° for VN; Wilcoxon rank test p = 0.3; ranges: 5.2–31.2° and 2.3–36.6°, respectively). Only 3 neurons had minimum thresholds <5°.

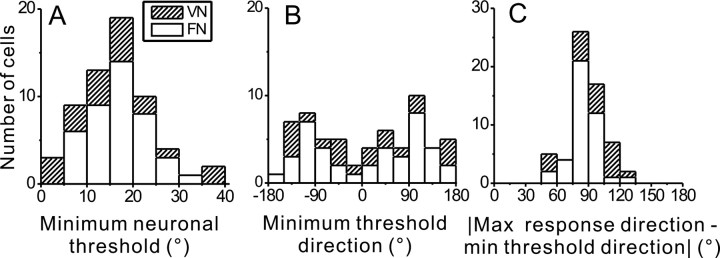
Figure 5.

Summary of neuronal thresholds. A, Distribution of minimum neuronal thresholds for 41 FN and 20 VN cells. B, Distribution of reference heading directions for which minimum neuronal thresholds were obtained. C, Distribution of the difference between minimum threshold direction and the maximum response direction. Open bars, FN cells; striped bars, VN cells.

The distribution of reference directions corresponding to minimum neuronal thresholds was not uniform for FN neurons (uniformity test p = 0.01). The majority of FN cells (25/41, 61%) had their minimum thresholds within ±30° of the forward/backward reference directions, whereas only 8/41 (19.5%) had their minimum thresholds within ±30° of the lateral axis (0°/180°, Fig. 5B). This distribution of minimum threshold directions is related to the fact that FN neurons tend to prefer lateral directions, as discussed further below (Shaikh et al., 2005).

In contrast to FN, the proportion of VN neurons with minimum thresholds near the fore-aft direction (5/20, 25%) was similar to the proportion (6/20, 30%) with minimum thresholds near the lateral (interaural) axis. Indeed, both the distribution of the minimum threshold directions and the distribution of preferred directions for VN neurons were not significantly different from uniform (uniformity test; p = 0.6, and p = 0.7, respectively). The absence of a biased distribution of direction preferences for VN might be due to the small sample size, as a preponderance of lateral-preferring neurons has been reported previously in a larger population of neurons (Angelaki and Dickman, 2000; Dickman and Angelaki, 2002; see Discussion).

What is the relationship between heading directions that elicit maximal firing rate and maximal discriminability (minimum threshold)? For the example cell of Figures 1–4, the minimum threshold and maximum response directions were 60° apart. As illustrated by the distribution in Figure 5C, the absolute value of the difference between minimum threshold and maximum response directions across the FN and VN cell populations ranged from 45° to 135°, with a mean value of 88.2 ± 2 (SE). For 33/41 (80.5%) FN cells and 8/20 (40%) VN cells, the difference between the minimum threshold direction and maximum response direction was within ±10° of 90°.

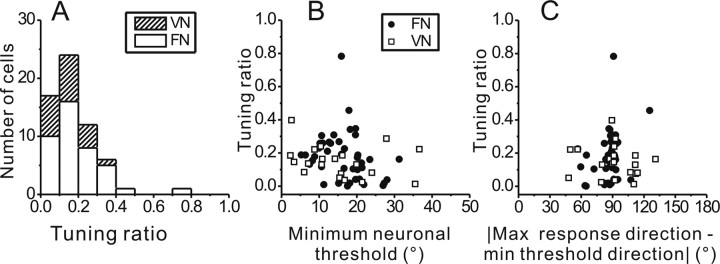
The relationship between minimum threshold and maximum response directions could depend on how much the spatiotemporal tuning of the cell departs from cosine tuning, a property that is captured by the tuning ratio (Bush et al., 1993; see Materials and Methods and Angelaki and Dickman, 2000). Figure 6A plots the distribution of tuning ratios for our sample of neurons. There was a weak, marginally significant correlation between tuning ratio and minimum neuronal threshold (r = −0.31, p = 0.017, Spearman rank correlation) (Fig. 6B), such that neurons with larger tuning ratios tended to have slightly smaller minimum thresholds.

Figure 6.

Relationship between minimum discrimination threshold and tuning ratio. A, Distribution of tuning ratio in VN (n = 20, striped bars) and FN (n = 41, open bars). B, Scatter plot of tuning ratio versus minimum discrimination threshold. C, Scatter plot of tuning ratio versus the absolute difference between minimum threshold direction and maximum response direction. Filled symbols, FN cells (n = 41); open symbols, VN cells (n = 20).

In Figure 6C we explore this relationship further by plotting the tuning ratio as a function of the absolute difference between minimum threshold and maximum response directions. If this relationship depended solely on tuning-curve slope, one would expect a “V-shaped” relationship; that is, cosine-tuned neurons (tuning ratio = 0) should have a direction difference of 90°, whereas spatiotemporal neurons with large tuning ratios should have a difference of 45–135°. A correlation analysis on data folded around the 90° direction difference (such that the expected relationship would be linear) revealed a very weak correlation that was opposite in sign to the expected relationship (r = 0.30, p = 0.019, Spearman rank correlation). These results are consistent with the expectation that the location of the minimum discrimination threshold depends considerably on the response variability of each neuron, and not solely on the tuning function.

It is of considerable interest to know whether neuronal discrimination thresholds depend on the reference direction relative to straight ahead. We directly compared neuronal thresholds for forward/backward versus lateral directions in the scatter plots of Figure 7 (see also Table 1). For FN cells, the geometric mean threshold (127.6°) for lateral directions was significantly larger than that (58.8°) for forward directions (Wilcoxon rank test, p < 0.001), and also larger than that (58.9°) for backward directions (Wilcoxon rank test, p < 0.001). For VN cells, the geometric mean threshold (77.9°) for lateral headings was not significantly different from that (72.3°) for forward headings (Wilcoxon rank test p = 0.8) and backward headings (55.6°) (Wilcoxon rank test p = 0.2). The ratio of lateral: forward heading thresholds averaged 2.2 ± 6.1 for FN neurons (geometric mean ± geometric SD) and 1.1 ± 4.4 for VN neurons (median values of 2.5 and 1.0, respectively). Thus, the distribution of heading preferences in the FN leads to greater discrimination capacity around forward directions than lateral directions.

Figure 7.

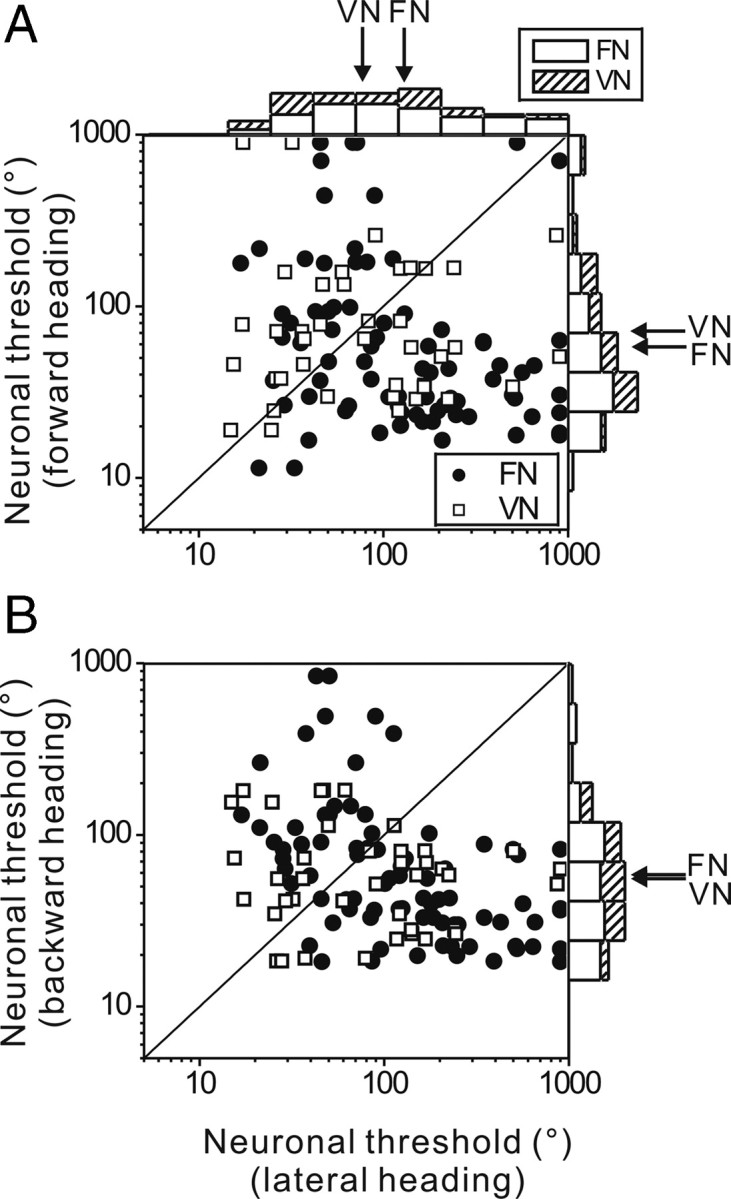
A, Comparison of neuronal thresholds for forward versus lateral reference headings. B, Analogous comparison for backward versus lateral reference headings. The histograms on top and right illustrate the corresponding distributions (capped at a threshold value of 900). Arrows illustrate geometric means (Table 1). Filled symbols, FN cells (n = 41); open symbols, VN cells (n = 20). Note that each cell is plotted twice, showing data for both rightward and leftward motion.

Table 1.

Threshold (geometric mean ± geometric SD), separately by animal and heading direction

	Minimum threshold	Forward	Backward	Lateral motion
FN/threshold (°)
Animal F (n = 24)	15.2 ± 1.5°	72.1 ± 3.7°	65.6 ± 2.5°	104.7 ± 3.1°
Animal N (n = 12)	13.3 ± 1.4°	30.4 ± 1.7°	40 ± 2°	206.4 ± 3.3°
Animal D (n = 5)	23 ± 1.2°	108.3 ± 2.3°	88 ± 2.6°	104.1 ± 1.7°
All monkeys	15.4 ± 1.5°	58.8 ± 3.2°	58.9 ± 2.4°	127.6 ± 3.1°
VN/threshold (°)
Animal F (n = 10)	14.7 ± 1.6°	64.6 ± 1.9°	48.7 ± 2°	74.6 ± 2.4°
Animal N (n = 10)	9.6 ± 2.5°	81 ± 3.4°	63.5 ± 2°	81.4 ± 3.4°
All monkeys	11.9 ± 2.2°	72.3 ± 2.7°	55.6 ± 2°	77.9 ± 2.9°

There are two parameters in our analysis that can affect the exact values of neuronal thresholds obtained for FN/VN cells. First, the calculations were based on firing rates computed during each half-cycle of motion (250 ms). Extracting firing rates from smaller time windows centered on the peak response might give more sensitive responses. As illustrated in Figure 8A, neuronal thresholds increased nearly exponentially when the time window for counting spikes was reduced below 50 ms (all intervals were centered on the middle of each half-cycle response). Thus, maximal discriminability required some integration time for estimating firing rates, and too short a time window had adverse effects on heading thresholds. However, this relationship asymptotes by ∼100 ms (Fig. 8A); counting spikes over longer time intervals does not substantially improve discrimination thresholds.

Figure 8.

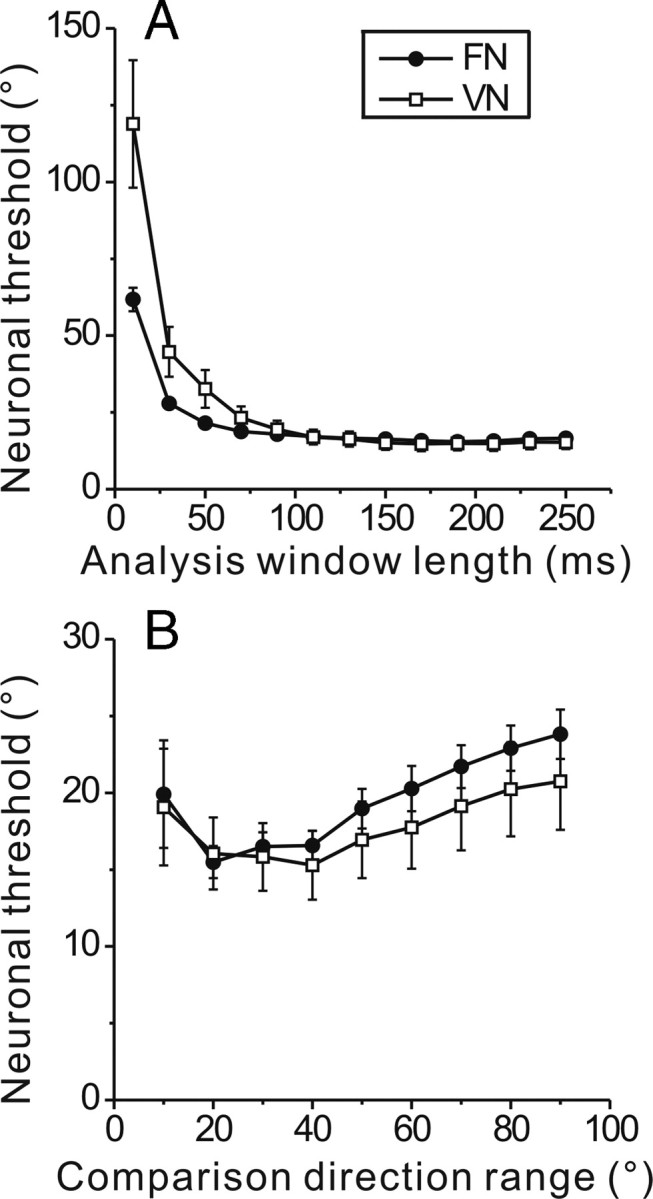
A, Dependence of neuronal thresholds on the length of the time window (centered on the middle of each response half-cycle) in which firing rates were computed. B, Dependence of thresholds on the range of comparison headings used to construct the neurometric function using ROC analysis. This dependence is illustrated for the reference heading that produced the minimum threshold for each neuron using a time interval of 250 ms and a 40° heading range. Filled symbols, FN cells (n = 41); open symbols, VN cells (n = 20). Data illustrate mean ± SE.

Second, the neurometric function for each reference heading was constructed by computing ROC values for symmetric pairs of headings that spanned a 40° range around the reference. However, choice of this range will affect the exact value of threshold. Small ranges are best for estimating thresholds around steep portions of the tuning curves (as in Fig. 4), and using too large a range will overestimate threshold by incorporating data from less steep portions of the tuning curve. In contrast, larger ranges are beneficial to reliably quantify thresholds for portions of the tuning curve that are relatively flat since a narrow range may produce ROC values that vary little. How average thresholds depend on the range of comparison directions is illustrated in Figure 8B. For this analysis, the reference heading was chosen as that which produced the minimum threshold, hence these data are obtained from the steep portion of each tuning curve. Thresholds were lowest for comparison heading ranges between 20° and 40°, but increased for smaller and larger ranges as expected from the considerations above. The comparisons in Figure 8 illustrate that the parameters used to compute neuronal thresholds in our standard analysis are near-optimal for maximizing neuronal sensitivity.

Discussion

We have used signal detection theory (ROC analysis) to measure, for the first time, how firing rate variability shapes the direction discriminability of subcortical vestibular neurons that code linear acceleration. This was done by characterizing firing rates during 2 Hz translation, as the direction of heading changed smoothly and gradually in the horizontal plane. This analysis quantifies how small changes in motion direction can be discriminated by neurons. The most sensitive neurons could discriminate among headings that differed by a few degrees, but most neurons were much less sensitive. The minimum threshold directions for FN neurons were not uniformly distributed, but tended to cluster around the forward/backward axis. As a result, heading discrimination thresholds were significantly lower for forward/backward than lateral directions.

Comparison with previous studies: parameters that determine direction discrimination thresholds

The only comparable study in which heading discrimination thresholds were measured during vestibular stimulation reported neuronal thresholds of 26.8° ± 2.9° and 14.6° ± 3.2° (geometric mean ± geometric SD for two different macaques) for discrimination around the forward direction in cortical area MSTd (Gu et al., 2007). MSTd thresholds are lower than FN/VN thresholds (Table 1; Wilcoxon rank test, p < 0.001). In both studies, stimuli were not tailored to the stimulus preferences of each neuron (as previously done to maximize neuronal sensitivity in visual cortex) (Britten et al., 1992; Celebrini and Newsome, 1994; Uka and DeAngelis, 2003, 2006). Because we recorded from every neuron sensitive to translation, these numbers represent a largely unbiased sampling of the vestibular-only cell population in the rostral FN and VN.

The difference in neuronal sensitivity between FN/VN and MSTd is interesting, as it might suggest an improvement in neuronal heading sensitivity from early vestibular areas to the cortex. Although neuronal processing cannot create new information, it is nevertheless possible for heading sensitivity to increase from FN/VN to MSTd. For example, the more sensitive neurons in FN/VN could project to MSTd, or the cortical circuits could effectively remove correlations among their vestibular inputs, thus increasing the fidelity of the explicit code in cortex. Note, however, that we cannot firmly conclude that MSTd neurons are more sensitive than FN/VN cells because the motion stimuli were different in the two studies. Here, we have used 2 Hz sinusoidal oscillations with peak accelerations of 0.3G, whereas Gu et al. (2007) used Gaussian velocity transients with peak accelerations of 0.1G. It would therefore be valuable to directly compare neuronal thresholds between cortical and subcortical neuronal populations using identical stimuli.

An important finding of the present study is that maximum direction discriminability is observed, on average, perpendicular to the preferred direction of FN/VN neurons (Fig. 5C). This observation is consistent with previous studies (Purushothaman and Bradley, 2005; Gu et al., 2007, 2008) and theoretical predictions based on Fisher information (Seung and Sompolinsky, 1993; Pouget et al., 1998), which show that maximum discriminability is observed for directions where firing rate changes steeply. In contrast, discriminability is expected to be very poor when a neuron is operating around directions that elicit near-maximal firing rates. More specifically, two response parameters influence direction discrimination thresholds: the slope of the tuning curve around the reference direction and the variability in firing rate. Thus, the overlap of the firing rate distributions in Figure 4B depends (1) on how far apart the means are, which is determined by tuning curve slope for a given pair of nearby headings, and (2) on the variance of the distributions, which measures response variability.

For cosine-tuned cells, the steepest slope of the tuning curve occurs for directions ∼90° away from the maximum response direction. In our data, however, the minimum threshold was observed to occur within a range of 45–135° relative to the maximum response direction (see example in Fig. 3 and distribution in Fig. 5C). Moreover, the distance between minimum threshold and maximum response directions was not strongly dependent on tuning ratio, which measures the departure from idealized cosine tuning. Thus, the location of minimum response threshold appears to depend substantially on both the tuning properties and response variability.

Previous recordings of FN responses have revealed a predominance of neurons that prefer lateral motion directions (Shaikh et al., 2005). Thus, the greater heading discriminability for forward/backward compared with lateral headings arises from the clustering of preferred directions along the lateral axis for FN neurons. Previous studies have also described a predominance of lateral-versus forward/backward-preferring neurons in the VN of awake macaques (Angelaki and Dickman, 2000; Dickman and Angelaki, 2002) and decerebrate cats and rats (Schor et al., 1984; Bush et al., 1993). However, such a preferential distribution was not observed here, perhaps due to the modest size of the VN sample.

Rostral VN and FN: projections and potential functions

The non-eye movement cell type in the rostral VN/FN that was targeted in the present experiments has been previously shown to participate in several important computations in the vestibular system (for review, see Angelaki and Cullen, 2008; Green and Angelaki, 2009). First, they reflect a population solution to a sensory ambiguity inherent in otolith afferents, which respond identically to translational motion (for example, running forward) and gravitational accelerations experienced as we reorient relative to gravity. In contrast, the VN/FN population activity encodes both inertial motion and orientation relative to gravity (Angelaki et al., 2004). Second, these same neurons carry information about vestibular “exafference,” i.e., they distinguish between rotations that are self-generated and those that are externally applied (McCrea et al., 1999; Roy and Cullen, 2001; Brooks and Cullen, 2009).

Vestibular neurons in the rostral VN and FN could project to multiple regions involved in vestibular processing. Both areas have strong projections to the upper cervical spinal cord (Asanuma et al., 1983; Boyle et al., 1996; Gdowski and McCrea, 1999). Neurons in the VN/FN are also heavily interconnected with each other (Noda et al., 1990; Homma et al., 1995), as well as with areas of the anterior and posterior vermis, including the nodulus/uvula of the vestibulo-cerebellum (Armstrong and Schild, 1978; Kotchabhakdi and Walberg, 1978; Noda et al., 1990; Wylie et al., 1994). Finally, both areas project to the ventral posterior thalamus (Lang et al., 1979; Meng et al., 2001, 2007), from which signals can be distributed to sensorimotor cortex (Huerta et al., 1986; Akbarian et al., 1992). However, it is not presently known which of the two areas contributes more to heading perception.

Relationship to heading perception

Unlike previous neural recordings in area MSTd, which were performed while trained animals performed a 2AFC heading discrimination task (Gu et al., 2007), we do not know the behavioral thresholds of the animals used in the present study. Thus, the present experiments do not allow a direct comparison between neural activity in FN/VN and perception, but some indirect comparisons are worth noting. First, heading direction discrimination thresholds around straight-forward in darkness have been reported to be in the range of 1–5° for both macaques and human subjects (Smith et al., 2002; Adeyemo et al., 2007; Gu et al., 2007; Fetsch et al., 2009). Given the much larger average neuronal thresholds reported here, additional processing beyond that already taking place in the vestibular and deep cerebellar nuclei may be needed to account for the precision of vestibular heading perception. Alternatively, behavior could depend on the activity of the most sensitive neurons, which have sensitivity that approaches behavioral thresholds (Fig. 5A). However, to account for behavior in this manner would require a highly selective decoding of the most sensitive neurons.

Second, behavioral studies in both macaques and human subjects have shown that perceptual heading discrimination thresholds increase with the eccentricity of the reference heading away from straight-forward (Smith et al., 2002; Adeyemo et al., 2007; Fetsch et al., 2009). In human subjects, we have observed that heading discrimination thresholds increase approximately twofold when the heading references changes from forward to lateral (Adeyemo et al., 2007). By comparison, the ratio of lateral over forward heading thresholds averaged 2.2 ± 6.1 (geometric mean ± geometric SD) and 1.1 ± 4.4 for FN and VN, respectively. Thus, at least for FN, the variation in neuronal thresholds with eccentricity is comparable to the twofold increase in human behavioral thresholds.

It would be valuable to quantify heading discriminability in the VN/FN while trained animals perform a heading discrimination task (as in Gu et al., 2007). Simultaneous neural and behavioral testing would allow comparison of neuronal and psychophysical thresholds under identical conditions, and would also allow one to examine correlations between responses of subcortical neurons and the monkey's perceptual choices (Britten et al., 1996; Gu et al., 2007, 2008). Whether trial-by-trial correlations between perception and neural firing rates exist for subcortical neurons is at present unknown. Such data could clarify the respective roles of VN versus FN in heading perception.