Kinetic Model for the ATP-Dependent Translocation of Saccharomyces cerevisiae RSC along Double-Stranded DNA

Abstract

The chromatin remodeling complex RSC from Saccharomyces cerevisiae is a DNA translocase that moves with directionality along double-stranded DNA in a reaction that is coupled to ATP hydrolysis. To better understand how this basic molecular motor functions, a novel method of analysis has been developed to study the kinetics of RSC translocation along double-stranded DNA. The data provided are consistent with RSC translocation occurring through a series of repeating uniform steps with an overall processivity of P = 0.949 ± 0.003; this processivity corresponds to an average translocation distance of 20 ± 1 base pairs (bp) before dissociation. Interestingly, a slow initiation process, following DNA binding, is required to make RSC competent for DNA translocation. These results are further discussed in the context of previously published studies of RSC and other DNA translocases.

Eukaryotic DNA is bound by basic proteins called histones and packaged into a hierarchically folded structure termed chromatin. The primary repeating unit of chromatin structure is the nucleosome, which consists of a central histone octamer (two molecules of each of the four core histones, H2A, H2B, H3, and H4) and the associated DNA (1, 2). In addition to providing a means of packaging the DNA within nuclei, this organization of DNA serves to regulate access of enzymes involved in its transcription, replication, and repair to their appropriate chromosomal target sites (3-6). As DNA replication, recombination, and repair require access to the duplex DNA itself, mechanisms by which chromatin structure can be regulated and modified are required. This regulation of chromatin structure is accomplished either through the covalent modification of the histone proteins (7, 8) or through an active mechanism of nucleosome remodeling carried out by a family of protein complexes, termed chromatin remodelers. Remodeler complexes each contain an ATPase subunit that harnesses the energy liberated by ATP binding and hydrolysis to drive conformational changes in chromatin structure (9-12). Specifically, these enzymes alter nucleosome structure by affecting histone–DNA interactions, thereby changing the location or conformation of the nucleosome.

All remodelers bear a related ATP-hydrolyzing subunit that has significant homology with those of the helicase family of proteins (13-15); these proteins are classified as members of the SF-II superfamily of helicases on the basis of amino acid sequence homology (16). DNA translocation is necessary, but not sufficient, for helicase activity, and the two properties can be uncoupled (17-20). Similarly, remodelers have been shown to lack helicase activity (21) but retain the ability to translocate along DNA in an ATP-dependent manner (22-25). This DNA translocation property plays a central role in certain models for ATP-dependent chromatin remodeling (13, 22, 23, 26-28). In one such model, the ATPase subunit of the remodeling enzyme translocates DNA around the nucleosome in an ATP-dependent manner (i.e., is the molecular motor), whereas additional subunits help anchor the complex to the histone octamer. Here, the translocating subunit pumps additional DNA from the internucleosomal linker onto the surface of the nucleosome, forming a loop or bulge that then propagates around the surface of the octamer (13, 22, 27, 29, 30).

To better understand the kinetics of DNA translocation, we have analyzed the ATPase time course of DNA translocation using the chromatin remodeling complex RSC. RSC is an essential and abundant SWI/SNF-family chromatin remodeling enzyme from the yeast Saccharomyces cerevisiae, which has previously been shown to be a DNA translocase (22, 24, 25, 31). Evidence of RSC's ability to translocate processively along DNA includes the ability of the enzyme to displace triple-helix strands (22), the difference in the stimulation of RSC's ATPase activity by linear and circular DNA (22), the ability of DNA gaps to reduce the accessibility of restriction enzymes to sites near the nucleosome dyad (27), and the ability of the enzyme to form DNA loops during nucleosome mobilization (25). Interestingly, the ATPase subunit of RSC, Sth1, is also a SF-II helicase and has been shown to be a monomeric DNA translocase (22). The results presented here both support the previous observation that monomeric RSC is capable of directionally biased translocation along double-stranded DNA and offer new insight into the kinetic mechanism for this translocation activity, including an estimate of its processivity.

A kinetic model (beyond Michaelis–Menten) has not yet been proposed to explain the double-stranded DNA translocation activity of RSC. The purpose of this study was to develop such a quantitative kinetic model and to subsequently use this model to obtain estimates of the kinetic parameters that are associated with the double-stranded DNA translocation activity of RSC.

RESULTS

Previous studies of RSC demonstrated that this enzyme translocates along double-stranded DNA with directional bias (22, 27). During its translocation along double-stranded DNA, RSC appears to commit to one of the two strands of the duplex as the tracking strand and to track along that strand in a 3′ to 5′ direction. Furthermore, RSC is incapable of traversing a gap of as little as 1 nucleotide (nt) in this tracking strand, but can traverse a gap of 5 nts in the nontracking strand. In previous work, the translocation activity of RSC was characterized using the Michaelis–Menten equation to determine both K_M and ATPase V_max [10 mM HEPES (pH 7.0), 5% glycerol, 20 mM potassium acetate, 1 mM ATP, 5 mM MgCl₂, 0.5 mM dithiothreitol, 0.1 mg/mL BSA at 30 °C] (22); these studies determined a value of K_M = 0.34 ± 0.02 μM (base pair) and demonstrated that V_max was dependent on DNA length. Recent single-molecule experiments have confirmed that the translocation of RSC along double-stranded DNA is directionally biased, as opposed to being a random walk, and have also provided an estimate of the macroscopic translocation rate of RSC along double-stranded DNA (24, 25); this rate was estimated to be ∼400 bp/s under buffer conditions (10 mM Hepes, pH 7.8, 50 mM KCl, 3 mM MgCl₂, 0.1 mM DTT, 60 μM BSA at room temperature) similar to those used in the bulk studies described above. However, other single-molecule measurements of DNA translocation rates with RSC on nucleosomes (also in similar buffer conditions) arrived at a very different rate of translocation (∼13 bp/s) (25), suggesting that either the substrate or the mode of measurement affects the apparent rate of translocation. Here we note that the V_max for ATPase is similar for both nucleosomes and for double-stranded DNA. Clearly, additional studies and models are required to resolve these issues.

RSC Is an ATP-Dependent Double-Stranded DNA Translocase

We studied the kinetics of RSC translocation along double-stranded DNA by analyzing the stimulation of RSC's ATPase activity in the presence of double-stranded DNA of various lengths. ATPase experiments were performed as described under Materials and Methods under solution conditions identical to those previously used to study the DNA translocation activity of RSC (22). We note that in this study we used a radioactivity-based assay for quantifying the ADP produced during translocation, whereas previous studies had relied upon a colorimetric assay for quantifying the inorganic phosphate produced during translocation (22); however, both assays have similar resolution of product formation from ATP hydrolysis.

The ATPase time courses observed for double-stranded DNA substrates ranging in length from 15 to 80 bp are shown in Figure 1. Previous work has shown that the minimal length of DNA required to stimulate RSC's ATPase activity is 15 bp (22), suggesting that this represents a minimal interaction or contact size of RSC with the DNA. Consistent with what has been reported previously (22), we observe that the ATPase rate of RSC increases with increasing DNA length (Figure 1). Because these experiments were conducted under conditions of excess DNA concentration, the binding of single complexes of RSC to the DNA is favored. Thus, these results are consistent with previously published data demonstrating that monomeric RSC is a double-stranded DNA translocase (22, 25, 27).

Figure 1.

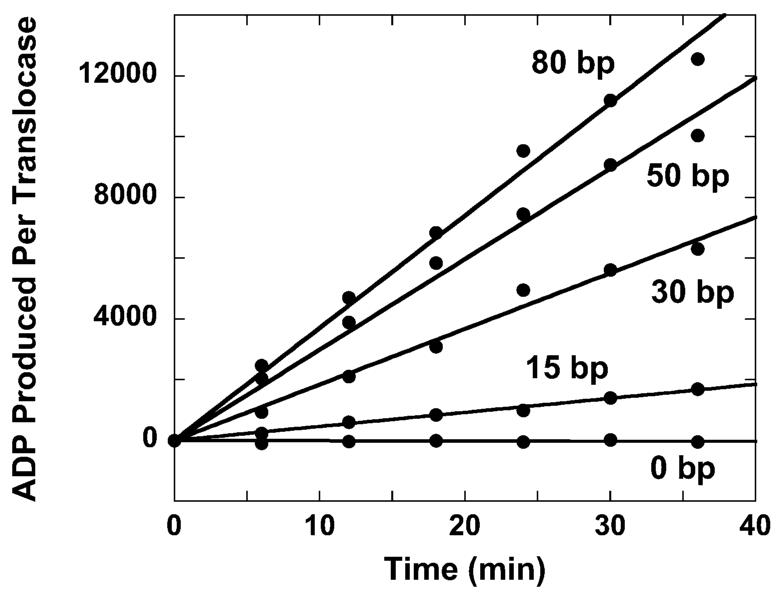
Time courses of ATP hydrolysis for RSC in the presence of a saturating concentration of double-stranded DNA of various lengths. The lengths of the DNA are 15, 30, 50, and 80 bp. A control experiment in which no DNA is included in the reaction is also shown.

Previous studies of the DNA translocation activity of bacterial helicases relied upon the analysis of pre-steady-state ATPase activity to determine the associated kinetic mechanism for translocation (19, 32-34). Interestingly, there is no indication of a pre-steady-state burst of ATPase activity in the time courses shown in Figure 1. To improve the resolution of these time courses we performed fluorescence stopped-flow studies of RSC translocation. In these experiments we measure ATP hydrolysis during RSC translocation as the production of inorganic phosphate (P_i), monitored by P_i binding to a fluorescently labeled Escherichia coli phosphate binding protein (PBP-MDCC) (34-37). The binding of P_i to PBP-MDCC is both rapid (the bimolecular rate constant for association is 1.36 × 10⁸ M⁻¹ s⁻¹) and tight (K_d = 0.1 μM) (35) so that phosphate binding by the PBP-MDCC is not rate-limiting in the overall reaction.

In these experiments RSC was initially incubated with the DNA substrate in a solution that also contained PBP-MDCC. The translocation reaction was subsequently initiated by rapid mixing in the stopped-flow spectrophotometer with a solution containing ATP. Representative time courses from these experiments are shown in Figure 2 and verify both that the double-stranded DNA stimulated ATPase activity of RSC is dependent upon the length of the double-stranded DNA and that there is no detectable pre-steady-state burst of ATPase activity in these time courses. Within the resolution of the instrument (∼100 pM Pi and 2 ms) only steady-state behavior is observed following ATP mixing.

Figure 2.

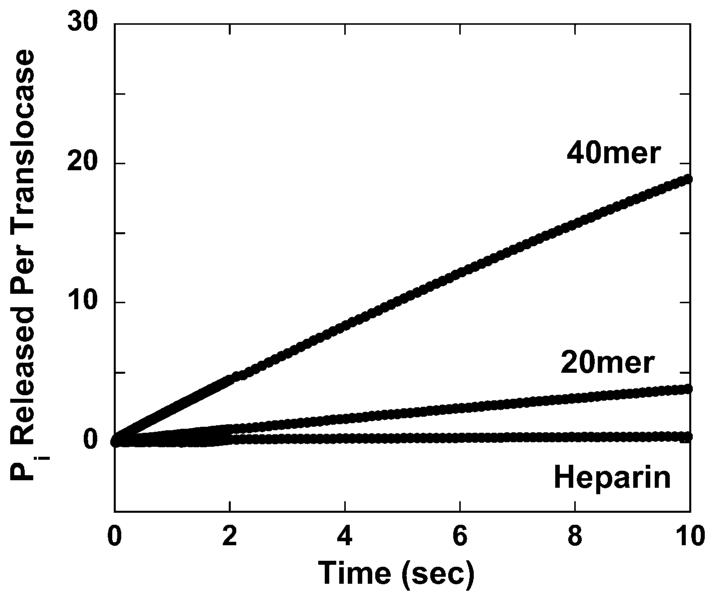
Time course of PBP-MDCC fluorescence (λ_ex = 430 nm, λ_em > 450 nm) measuring P_i production during double-stranded DNA translocation by RSC along 20 and 40 bp substrates. Also shown is the time course observed during experiments conducted in the presence of 40 bp DNA and 50 μg/mL heparin. Identical traces were obtained in experiments conducted in the presence of plasmid DNA and 50 μg/mL heparin. All curves presented are the average of four independent traces.

In a further attempt to monitor the pre-steady-state DNA translocation kinetics of RSC we performed single-round (with regard to DNA binding by RSC) fluorescence stopped-flow studies of RSC translocation. In these experiments we also included a protein trap, heparin, along with the ATP. Heparin is known to compete with DNA for protein binding (38, 39) and has been used in previous studies of single-stranded DNA translocation (19) and double-stranded DNA unwinding (40, 41) by helicases to ensure a single-round or “single-turnover” of enzyme activity with regard to DNA binding. The inclusion of heparin in our reactions thus ensures that the only ATPase activity that we observe is associated with the pre-steady-state DNA translocation of RSC complexes that were already bound to the DNA prior to the addition of ATP. Interestingly, the inclusion of heparin along with the ATP completely eliminates the DNA-stimulated ATPase activity of RSC (Figure 2). This result confirms that there is no detectable pre-steady-state ATPase activity associated with RSC translocation along double-stranded DNA.

Here, we emphasize that the experiments for which associated time courses are shown in Figures 1 and 2 were multiple-turnover with regard to DNA binding by RSC (in other words, in these experiments the RSC complex was allowed to continually rebind the DNA substrate following its dissociation). As such, one would expect the kinetics of the ATPase activity of the translocating RSC complexes to be dominated either by DNA binding or by DNA translocation, whichever is slower and thus rate-limiting for the overall reaction. Interestingly, neither of these scenarios is consistent with the data in Figures 1 and 2. Our reaction conditions included saturating (V_max) levels of DNA substrate, which would favor the formation of RSC–DNA complexes. If DNA binding were indeed rate-limiting, then we would expect to observe a pre-steady-state exponential or “burst” phase of ATPase activity, which is dominated by the translocation of RSC complexes that were already bound to the DNA upon the addition of ATP. This initial burst of ATPase activity would then be followed by a linear steady-state phase of constant ATPase activity once equilibrium between DNA binding, translocation, and dissociation has been established. An excellent example of this behavior is shown in the previously published ATPase-based studies of the translocation of the Bacillus stearothermophilus PcrA and E. coli UvrD helicases along single-stranded DNA (34, 36). If, on the other hand, the DNA translocation were rate-limiting, then one would expect no dependence of V_max on DNA length because the total population of bound protein is a simple function of the equilibrium association constant of DNA binding by RSC. Because these simulations and our experiments are performed under conditions of equal DNA concentration in terms of molar quantity of nucleotide (or equivalently binding sites), there would naturally always be the same fraction of bound protein, regardless of DNA length.

To verify this hypothesis we conducted a series of Monte Carlo computer simulations that monitored the ATPase activity of a DNA translocase. We generated a series of simulated ATPase time courses in which the rates of DNA binding, DNA dissociation, and DNA translocation were varied. The results of these simulations confirmed that V_max will be independent of the length of the DNA once DNA translocation becomes rate-limiting (see Figure 3A). The simulations that produced the time courses in Figure 3 assumed that the enzyme translocated along the DNA at a rate of 20 bp/s and a dissociation rate of 1 s⁻¹. The processivity of translocation in this simulation, P = 0.95, corresponds to what we determine for RSC translocation along double-stranded DNA (see below). For these simulations we also assumed that the hydrolysis of 1 ATP molecule was required for each 1 bp of translocation and that the pseudo-first-order rate constant for DNA binding was 100 s⁻¹. For the simulations in Figure 3B we also included an initial slow process with an associated rate constant of 0.01 s⁻¹ that preceeds processive DNA translocation.

Figure 3.

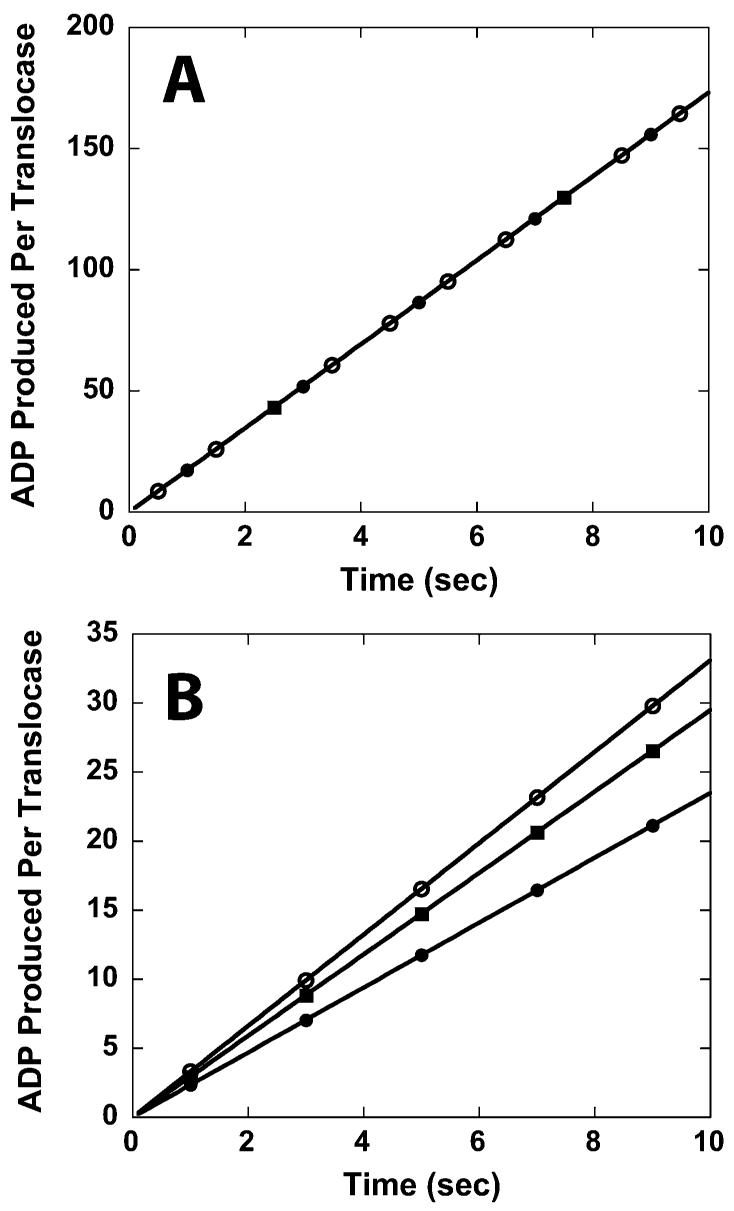
Time courses of ATP hydrolysis derived from Monte Carlo computer simulations. The time courses in (A) are obtained from simulations that do not include an initial slow step in the translocation mechanism. The time courses in (B) are obtained from simulations that do include an initial slow step in the translocation mechanism. For these simulations the enzyme was assumed to translocate along the DNA at a rate of 20 bp/s with an associated dissociation rate of 1 s⁻¹. The enzyme would hydrolyze one ATP molecule per bp translocated. The pseudo-first-order DNA binding rate constant was 100 s⁻¹. The simulations in (B) assumed an initial slow process with an associated rate of 0.01 s⁻¹. The lengths of the DNA used in the simulation are 20 bp (solid circles), 30 bp (solid squares), and 40 bp (open circles).

Because we observe a dependence of the steady-state ATPase rate on the length of the DNA, there must be an additional slow step that occurs either during translocation or at a step just preceding translocation of RSC. Indeed, we performed additional Monte Carlo computer simulations that revealed that a single slow process occurring only once during translocation generates ATPase time courses having associated steady-state rates that are dependent upon the length of DNA (see Figure 3B). Thus, our data are consistent with the occurrence of a single slow process (of unknown duration) occurring during the translocation of RSC along DNA. Furthermore, the ability of heparin to completely eliminate the DNA-stimulated ATPase activity of RSC also suggests that this slow process must occur before RSC becomes competent for processive DNA translocation and that heparin is able to actively displace RSC from the DNA while it is undergoing this process. Because the ability of heparin to actively dissociate proteins from DNA has previously been demonstrated in other systems (19, 38, 39, 42), it is likely that heparin is also capable of actively dissociating RSC from double-stranded DNA. In principle, this slow process might represent a conformation change that is required for a RSC–DNA complex to commit to DNA translocation.

Perhaps most significantly, this also means that the previously published kinetic models and associated mathematical equations for DNA translocation which assumed a single-turnover reaction (with regard to DNA binding) are not applicable here. An alternative derivation is required.

Kinetic Model for RSC Translocation along Double-Stranded DNA

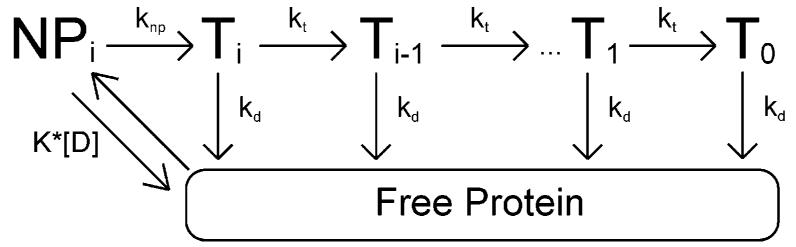
The simplest model consistent with the time courses in Figures 1 and 2 is shown in Scheme 1. This model is based upon models previously used to study the translocation of the E. coli UvrD helicase along single-stranded DNA (19, 32); although monomeric UvrD is not a functional helicase (19, 43, 44), it is capable of translocating along single-stranded DNA with a 3′ to 5′ directional bias (19). In this model, we assume that monomeric RSC binds randomly to one of its possible binding sites on the double-stranded DNA. Upon binding, the protein is i translocation steps away from the end of the DNA, but is unable to initiate translocation (it is in the NP_i state in Scheme 1). Upon the addition of ATP, the RSC complex undergoes a slow step, described by the rate constant k_np, before becoming competent for DNA translocation (the T_i state in Scheme 1). Upon subsequent repeating cycles of ATP binding, ATP hydrolysis, and release of ADP and inorganic phosphate, the RSC complex trans-locates along the double-stranded DNA with directional bias [tracking along one strand of the duplex from 3′ to 5′ as previously shown (22)] and finite processivity, P = k_t/(k_d + k_t). For this model we are thus defining processivity as the probability that at any instant during its translocation along the DNA the RSC will move forward an additional kinetic step along the DNA rather than dissociating from the DNA. This is the same definition of processivity that has been used for describing helicase translocation along single-stranded DNA (19, 32, 45).

Scheme 1.

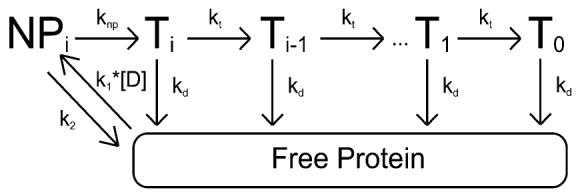
According to this model the translocation of RSC along the DNA occurs in discrete steps, of m nucleotides per step, with an associated rate-limiting translocation rate constant k_t. Because the kinetic step size m represents the average number of base pairs translocated by RSC between two repeating rate-limiting steps in the translocation reaction, it is possible that k_t may not reflect the actual rate constant for the forward motion of RSC along the DNA, but rather could reflect any step in the mechanism that is rate-limiting. The rate constant for dissociation during translocation is k_d. The maximum number of translocation steps, n, for a given reaction is related to the kinetic step size of translocation, m, and the length of the DNA, L, through the approximate relationship n = (L – m)/d, where d is the interaction site size of the protein (19, 32). Upon reaching the end of the DNA (the T₀ state in Scheme 1), the RSC complex can no longer translocate and so dissociates with rate constant k_d. The thermodynamic coupling efficiencies for the k_np and k_t rate constants are given by c_np and c, respectively; these scalars represent the number of ATP molecules that are hydrolyzed when RSC undergoes these steps. We further assume that because our experiments are performed under conditions of excess DNA concentration, there will be only one RSC complex bound per DNA, and thus we have ignored any potential protein–protein interactions. This assumption is further justified because monomeric RSC is the functional oligomeric state for nuclesome mobilization (27).

It is worth noting that in previous studies of DNA translocation by helicase proteins different rate constants were determined for dissociation from internal regions of the DNA and from the end of the DNA (19, 32, 36, 46); however, it is impossible to determine from our data if indeed these rate constants are different for RSC. Further experiments would be required for such a determination. Thus, for the sake of simplicity we have assumed that they are equal. We stress, however, that this assumption does not affect our calculation of the processivity of RSC translocation along double-stranded DNA. It is also important to note that we have neglected any contributions from the potential futile hydrolysis of ATP by RSC bound at the ends of the DNA. Such futile hydrolysis has been observed for helicase translocation along single-stranded DNA (34, 36), but we cannot determine if RSC is exhibiting similar behavior on the basis of our data. However, analysis of the single-turnover ATPase time courses in Figure 2 suggests that the rate of futile hydrolysis from proteins bound at the end of the DNA, if occurring at all, would be at least 1 order of magnitude smaller than the rate of hydrolysis associated with translocating protein for all lengths of DNA examined. Specifically, we estimate an upper limit of 0.04 ATP/s/complex for the rate of futile hydrolysis. Furthermore, the contribution of this futile hydrolysis would decrease with increasing DNA length (Fischer and Cairns, unpublished results), making its contribution to the dependence of the total observed steady-state ATPase rate on DNA length negligible.

All dissociated protein (and protein that was initially free in solution at the start of the reaction) will bind the DNA randomly at any of available binding sites. The second-order rate constant for RSC binding double-stranded DNA (and forming the complex NP_i) is k₁, and the corresponding dissociation rate constant from the NP_i state is k₂. It is worth noting that we assume the binding affinity is the same for all binding sites, and thus we ignore electrostatic end-effects. Furthermore, in our experiments the concentration of DNA is much larger than the concentration of protein, so we can treat the binding of RSC to DNA as a pseudo-first-order process with associated rate constant k₁[D], where [D] is the bp concentration of DNA in solution.

Interestingly, Monte Carlo simulations performed using Scheme 1 indicated that the rate constant k_np must be at least 2 orders of magnitude smaller than the rate constant k₂ for there to be no burst phase in the ATPase time courses (Fischer and Cairns, unpublished results). Because of this, we can use a modified version of Scheme 1 (Scheme 2), which assumes a rapid equilibrium of RSC binding and dissociation with regard to the subsequent k_np step; the initial binding and dissociation equilibrium can then be described by the equilibrium association constant K = k₁/k₂. This assumption of rapid equilibrium between protein binding and dissociation relative to the k_np step can also be justified in light of the fact that the addition of heparin to our reactions completely eliminates the double-stranded DNA stimulated ATPase activity of RSC. Heparin competes with the DNA for RSC binding and effectively lowers the equilibrium constant K to near zero either by reducing k₁ (because RSC can bind either heparin or DNA in this case) or by increasing k₂ (through active dissociation of RSC from the DNA) or by both mechanisms.

Scheme 2.

The differential equations describing the concentration of protein bound at each position (NP_i, T_i, and free protein) in Scheme 2 can be solved to obtain time-dependent equations for these protein concentrations that are functions of the maximum number of translocation steps (n) associated with a given DNA length; this is equivalent to finding expressions for these populations as a function of the length of the DNA and the kinetic step size of translocation (19, 32). These expressions can then be combined to form a time-dependent expression for the concentration of ATP hydrolyzed (or ADP or P_i produced) during the translocation of RSC along double-stranded DNA. The dominant term in this expression is linear with time and is shown in eq 1.

$$\left[\mathrm{ADP}\right]\left(t\right)=\left[\frac{c_{\mathrm{np}}K\left[\mathrm{D}\right]k_{\mathrm{d}}{k}_{\mathrm{np}}}{k_{\mathrm{d}}+K\left[\mathrm{D}\right](k_{\mathrm{d}}+k_{\mathrm{np}})}+\frac{c\left[\mathrm{D}\right]k_{\mathrm{t}}(k_{\mathrm{t}}(P^n-1)+k_{\mathrm{d}}n}{{k_{\mathrm{d}}}^2(1+n)K\left[\mathrm{D}\right]\left[k_{\mathrm{d}}(k_{\mathrm{d}}+k_{\mathrm{np}})(1+n)\right]}\right]t$$ (1)

Equation 1 can be rearranged into the more recognizable form of eq 2.

$$\left[\mathrm{ADP}\right]t=\left[\left({\mathit{ck}}_{\mathrm{t}}\left(\frac{n-\frac{P(1-P^n)}{1-P}}{n+1}\right)+c_{\mathrm{np}}{k}_{\mathrm{d}}\right)\left(\frac{k_{\mathrm{np}}}{k_{\mathrm{d}}+k_{\mathrm{np}}}\right)\times \frac{\left[\mathrm{D}\right]}{\frac{k_{\mathrm{d}}}{K(k_{\mathrm{d}}+k_{\mathrm{np}})}+\left[\mathrm{D}\right]}\right]t$$ (2)

Equation 2 is immediately recognized as the standard Michaelis-Menten equation with V_max and K_M defined in eqs 3 and 4, respectively.

$$V_{\max }=\left[{\mathit{ck}}_{\mathrm{t}}\left(\frac{n-\frac{P(1-P^n)}{1-P}}{n+1}\right)+c_{\mathrm{np}}{k}_{\mathrm{d}}\right]\left(\frac{k_{\mathrm{np}}}{k_{\mathrm{d}}+k_{\mathrm{np}}}\right)$$ (3)

$$K_{\mathrm{M}}=\frac{k_{\mathrm{d}}}{K(k_{\mathrm{d}}+k_{\mathrm{np}})}$$ (4)

It is worth noting again that previously published analysis of the double-stranded DNA translocation activity of RSC demonstrated that this activity was well characterized by the Michaelis–Menten equation (22). This provides further justification of the kinetic model we present in Scheme 2. Furthermore, it is interesting to note that this model (and corresponding eq 4) predicts that K_M is independent of the maximum number of steps or equivalently independent of the length of the DNA. This is consistent with measurements of the affinity (K_d) of RSC for DNA, which is independent of length when molecules of >20 bp are examine (ref 20 and Saha and Cairns, unpublished results).

In the limit of infinitely long DNA, eq 3 simplifies to eq 5 and under conditions of saturating DNA concentration, such as those used in the experiments depicted in Figures 1 and 2, eq 2 simplifies to eq 6.

$$V_{\max ,\infty }=({\mathit{ck}}_{\mathrm{t}}+c_{\mathrm{np}}{k}_{\mathrm{d}})\left(\frac{k_{\mathrm{np}}}{k_{\mathrm{d}}+k_{\mathrm{np}}}\right)$$ (5)

$$\left[\mathrm{ADP}\left(t\right)\right]=\left[\left(\frac{k_{\mathrm{np}}}{k_{\mathrm{d}}+k_{\mathrm{np}}}\right)\left({\mathit{ck}}_{\mathrm{t}}\left(\frac{n-\frac{P(1-P^n)}{1-P}}{n+1}\right)+c_{\mathrm{np}}{k}_{\mathrm{d}}\right)\right]t$$ (6)

Using eq 3 we analyzed the dependence of V_max on DNA length (Figure 4) using standard nonlinear least-squares (NLLS) techniques to determine an estimate of the processivity of translocation to be P = 0.96 ± 0.02. In this analysis we assumed that d = 15 bp, as RSC requires >15 bp both to bind DNA (determined by band shift assays) and to elicit ATPase activity both in prior bulk measurements and in the stopped-flow data described here (22, 27). We further assumed that m = 1 because previous studies of DNA translocation by RSC had shown that the enzyme was incapable of traversing a gap of as little as 1 nt in this tracking strand (27). This assumption for the kinetic step size thus implies that the rate-limiting step k_t in Schemes 1 and 2 corresponds to the physical motion of the enzyme along the DNA. Additional experiments are required to test the accuracy of this assumption; however, as discussed in more detail below, we can nevertheless use it to determine a macroscopic estimate of the processivity of translocation by RSC that is independent of a specific value of m. We were also able to determine estimates of additional combinations of the rate constants in Scheme 2 (see Table 1, second column), but are unable to resolve estimates of individual rate constants.

FIGURE 4.

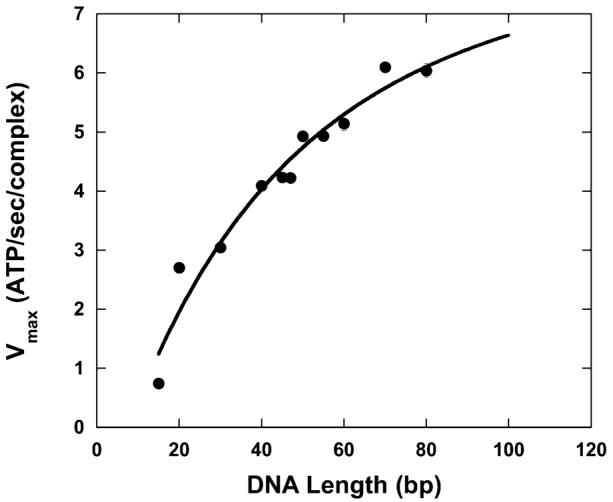
Dependence of V_max upon double-stranded DNA length. The solid line is a NLLS fit of the data to eq 3.

Table 1.

Estimates of Kinetic Parameters for RSC Translocation along Double-Stranded DNA According to Scheme 2 with k_np Assumed To Be ATP-Dependent

P	0.96 ± 0.02	0.951 ± 0.005
KM = kd/[K(kd + knp)]	0.34 ± 0.02 μMa
ckt[knp/(kd + knp)]	8 ± 2 ATP/s/complex	6.9 ± 0.3 ATP/s/complex
cnpkd[knp/(kd + knp)]	1.2 ± 0.3 ATP/s/complex	1.1 ± 0.3 ATP/s/complex
d	15 bp (fixed)	15 bp (fixed)
V max,∞	9 ± 2 ATP/s/complex	8.0 ± 0.1 ATP/s/complex (fixed)
variance	0.14421	0.13247

^aPreviously published results (22).

Translocation along Plasmid DNA

To obtain a better estimate of the kinetic parameters from our NLLS analysis of the data in Figure 4, we also measured the ATPase time course for the translocation of RSC along circular plasmid DNA. Circular DNA can effectively mimic infinitely long DNA, thus allowing for the application of eq 5 to analyze the associated time course. In these experiments we deliberately used very long DNA (∼4.4 kb) to minimize any potential complications arising from the curvature of the DNA (22).

The observed steady-state ATPase rate for RSC translocation along plasmid DNA, V_max,∞ was determined to be 8.0 ± 0.1 ATP/s/complex, which is in excellent agreement with the value of 9 ± 2 ATP/s/complex that we determined from our NLLS analysis of the data in Figure 4 using eq 3. Furthermore, we can now use this estimate of V_max,∞ as an additional constraint in our NLLS analysis of the data in Figure 4 using eq 3 to obtain better estimates of the errors of the associated kinetic parameters. The parameter estimates obtained from this fitting are shown in the third column of Table 1. Not surprisingly, the addition of this constraint in our fitting reduced both the variance of our fit and the errors associated with the various parameter estimates, but did not generate estimates for these parameters that differ significantly from those presented in the second column of Table 1.

DISCUSSION

Similar to other motor proteins, RSC is able to convert the chemical potential energy it derives from ATP binding and hydrolysis into mechanical work; its ability to translocate along DNA is essential for its nucleosome mobilization activity (22, 27, 47). In this paper, we present a novel kinetic model for the double-stranded DNA translocation activity of the RSC chromatin remodeling complex from S. cerevisiae. In addition, we present estimates of the kinetic parameters associated with double-stranded DNA translocation by RSC obtained from NLLS analysis of the double-stranded DNA stimulated ATPase activity of RSC using the differential equations derived from this model.

Model for DNA Translocation by RSC

Prior studies of the DNA translocation activity of several translocases have used sequential “n-step” mechanisms to characterize the kinetics of the DNA translocation activity of these enzymes (19, 32, 36, 46, 48). In these mechanisms several repeating cycles of ATP binding, hydrolysis, enzyme movement, and product release comprise the overall mechanism by which the enzyme moves along the DNA. Estimates of the rate constants associated with these various parameters have often proved to be difficult, with mathematically rigorous determination possible only for data collected from “pre-steady”-state experiments in which the binding of dissociated enzyme is prevented through the inclusion of a protein “trap” in the solution (19, 32). In this paper we present a model for DNA translocation that is suitable for the analysis of data collected in “multiple-turnover” experiments.

It is important to note, however, that the rate constant k_t in Schemes 1 and 2 does not necessarily correspond to the physical movement of the enzyme along the DNA, but rather reflects whatever step is rate-limiting in the repeating cycles of ATP binding, enzyme translocation, and product release. Because this rate-limiting step appears to be insensitive to the solution concentration of ATP, it is likely not the ATP-binding step; indeed, these experiments were performed at ATP concentrations (1 mM) well above the K_M for ATP (77μM) for RSC (31). Thus, protein translocation, product release, or any additional protein conformation changes that occur are likely rate-limiting for RSC translocation along double-stranded DNA under these solution conditions. In effect, we propose that there are at least two processes occurring in the double-stranded DNA translocation mechanism of RSC that are slower than ATP binding: an initial process required to make the enzyme competent for processive DNA translocation and a subsequent, repeating, process occurring during DNA translocation.

One might propose that these two slow processes are, in fact, the same. In other words, the slow initial process that we propose as an explanation for the lack of an initial exponential phase of ATPase activity might in fact simply be the first, slow cycle in the DNA translocation mechanism of RSC. This proposition is not supported by our computer simulations (Figure 3A), which indicated that such a mechanism predicts no dependence of the steady-state ATPase rate on DNA length; our data showed a clear dependence (see Figures 1 and 2). Thus, the time courses shown in Figures 1 and 2 require both a slow initiation process and a repeating, slow step in the “translocation” process.

ATP Dependence of the k_np Step

It is important to note that in Schemes 1 and 2 we have assumed that the k_np step is ATP-dependent. Alternatively, one could imagine that this step is not coupled to ATP hydrolysis, but rather that it is associated with a slow ATP-independent conformation change that follows the initial binding of RSC to the double-stranded DNA. Multiple-step DNA binding mechanisms have been previously observed for helicases (44, 46, 48-51) and polymerases (52), and thus their occurrence for chromatin remodeling proteins would not be unexpected. To test for an ATP-independent k_np process we set c_np = 0 in our NLLS analysis of the data in Figure 4 using eq 3; the results of this analysis are shown in the second column of Table 2. It should be noted that because the k_np process is no longer associated with the hydrolysis of ATP, we must also determine an estimate of d from our fitting, rather than simply taking it to be 15 bp. Not surprisingly, the estimate of the processivity of DNA translocation is independent of our assumption about the ATP dependence of the k_np step (compare the estimates of P in Tables 1 and 2). The third column in Table 2 records the parameter estimates obtained in fitting the data using the constraint V_max,∞ = 8.0 ± 0.1 ATP/s/complex that we determined from our analysis of the ATPase time courses observed in experiences monitoring the translocation of RSC along plasmid DNA. It is worth noting, however, that because the variance of the NLLS analysis of the data in Figure 4 is the same whether we assume k_np to be ATP-dependent or ATP-independent, we are not able to conclude which is the correct representation of the kinetic mechanism. Additional experiments will be required for such a determination.

Table 2.

Estimates of Kinetic Parameters for RSC Translocation along Double-Stranded DNA According to Scheme 2 with k_np Assumed To Be ATP-Independent

P	0.96 ± 0.02	0.947 ± 0.004
KM = kd/[K(kd + knp)]	0.34 ± 0.02 μMa
ckt[knp/(kd + knp)]	9 ± 2 ATP/s/complex	8.0 ± 0.1 ATP/s/complex (fixed)
cnpkd[knp/(kd + knp)]	0 (fixed)	0 (fixed)
d	8 ± 3 bp	9 ± 2 bp
V max,∞	9 ± 2 ATP/s/complex	8.0 ± 0.1 ATP/s/complex (fixed)
variance	0.14399	0.13375

^aPreviously published results (22).

Estimate of the Processivity of DNA Translocation and Comparison with Other DNA Translocation Studies with RSC

Our best estimate of the processivity of RSC translocation along double-stranded DNA, P = 0.949 ± 0.003, is determined from the average of the calculated values of P appearing in the third columns of Tables 1 and 2, in other words, calculated with the constraint that V_max,∞ = 8.0 ± 0.1 ATP/s/complex. This estimate of P implies that the average distance RSC translocates along double-stranded DNA before dissociation is 1/(1 − P) = 20 ± 1 bp.

It is important to emphasize that our assumption of a 1 bp kinetic step size for DNA translocation is based solely upon experiments measuring the ability of RSC to displace triple helix forming oligonucleotides (22, 27, 31); in these studies a 1 bp gap in the tracking strand of the duplex was sufficient to hinder triple helix displacement. These results suggest that the physical movement of the RSC complex along the duplex occurs in 1 bp increments (a 1 bp step size) and/or that in the process of tracking along a single strand of the duplex RSC requires an intact phosphodiester backbone at every position (a 1 bp tracking requirement). Regardless, it is not known whether this 1 bp movement is the rate-limiting process for DNA translocation. In other words, it is possible that additional processes might occur during the translocation of RSC along double-stranded DNA, such as protein conformational changes, which are slower than this 1 bp movement. Furthermore, these slow processes, if they exist, might well have a periodicity greater than 1 bp. An example of this is the single-stranded DNA translocation mechanism of the UvrD helicase (34). The single-stranded DNA translocation of monomeric UvrD occurs via a discontinuous stepping mechanism in which each repeated translocation cycle involves four rapid translocation steps in which one ATP is hydrolyzed per nucleotide translocated, followed by a slow step (or pause) that limits the overall rate of translocation.

The data and associated analyses presented here cannot resolve the kinetic step size of DNA translocation and, therefore, whether the 1 bp movement is truly rate-limiting. However, it is important to note that estimation of the average number of base pairs translocated by the RSC complex before its dissociation from the DNA is independent of our assumption of a 1 bp kinetic step size. This result is illustrated by the data presented in Table 3. These estimates of the kinetic parameters presented in Table 3 were calculated by NLLS analysis of the data in Figure 4 according to Scheme 2 with k_np assumed to be ATP-independent and V_max fixed to be 8.0 ± 0.1 ATP/s/complex. Qualitatively similar results are obtained if k_np is assumed to be ATP-dependent and/or if V_max is not fixed. As shown in Table 3, as the kinetic step size of translocation is increased, the associated processivity estimated from our NLLS analysis decreases. The corresponding estimate of how many steps RSC will translocate on average before dissociation also decreases with increasing kinetic step size, but the macroscopic measurement of the distance traveled (i.e., how many bp are translocated before dissociation) is independent of the kinetic step size. The smallest variance in the NLLS analysis of the data in Figure 4 was obtained with m = 1, although the increase in the variance with increasing m was not dramatic (see Table 3). The inability of our analysis to resolve the periodicity of the microscopic rate-limiting step of the DNA translocation mechanism for RSC results from the fact that we are analyzing multiple turn-over kinetic time courses for DNA translocation in which RSC is performing multiple cycles of translocation, dissociation, and rebinding.

Table 3.

Estimates of the Average Distance (Measured in Kinetic Steps or bp) Traveled by RSC before Dissociation

		av distance traveled
m (nt)	P	kinetic steps	bp	variance of fit
1	0.947 ± 0.004	19 ± 2	19 ± 2	0.13375
2	0.895 ± 0.008	9.6 ± 0.8	19 ± 2	0.134
3	0.85 ± 0.01	6.5 ± 0.5	19 ± 2	0.13425
4	0.80 ± 0.02	4.9 ± 0.4	20 ± 2	0.13453

Similarly, we cannot estimate the efficiency of the coupling of ATP binding and hydrolysis to DNA translocation by RSC on the basis of the analysis of the data presented in Figure 4. As shown by the data presented in Tables 1 and 2 the calculation of the thermodynamic coupling efficiency for DNA translocation, c, requires a determination of the rate constants k_np, k_t, and k_d and, implicitly, a direct determination of the kinetic step size. On the basis of recent studies of single-stranded DNA translocation by helicases (36, 45) it is tempting to speculate that c = 1 ATP/bp for double-stranded DNA translocation by RSC, but additional experiments are required to determine an explicit estimation of c for RSC.

Recently, Lia et al. (24) reported studies of the translocation of RSC along a stretched double-stranded DNA molecule in a single-molecule format. In these experiments, a nicked double-stranded DNA (∼ 3.6 kbp) has one end attached to a glass surface and the other end attached to a magnetic bead that can be manipulated in a magnetic field. In the presence of RSC, a decrease in the end-to-end length of the DNA molecule was detected by their instrument. This decrease was attributed to the formation of a DNA loop, which is formed as the RSC complex translocates along the DNA. Here, translocation initiates and then increases the length of a DNA loop, which is constrained between the translocase domain and a second (undefined) DNA-binding domain present in RSC. Interestingly, their results suggest that RSC is capable of looping an average of ∼420 bp of DNA before dissociation, indicating that the processivity of DNA translocation in these experiments is on the order of 0.998, far greater than the 0.949 ± 0.003 we determined from our analysis. The buffer conditions for the two sets of experiments are similar, so a trivial variation in solution chemistry is not likely the source of the difference. A subsequent study by Zhang et al. measured the ability of a single molecule of RSC to form and extend a DNA loop on the surface of a single nucleosome, using both optical and magnetic tweezers (25). Even under considerable tension (3–7 pN) RSC was shown to translocate DNA processively into the nucleosome at a velocity of ∼13 bp/s, with a mean processivity of ∼97 bp. Here, we note that RSC has a higher affinity for nucleosomes than for naked DNA and that the presence of ATP improves the affinity of RSC for the nucleosome, but not for DNA (27, 30). This property would be expected to increase RSC processivity and/or enable multiple rounds of translocation without dissociation. Indeed, this property may be one of the reasons why processivity appears higher on nucleosomes than our measurements here (see below).

Although these single-molecule studies provided important information about RSC translocation properties, it is important to note that this single-molecule format cannot detect loops of <25 bp (24). Thus, loops on the order of 1–20 bp, such as those that are expected to be generated according to our experiments, would not be observable in the single-molecule format. In light of this, it is tempting to postulate two separate modes of DNA translocation activity for RSC. The common, less processive mode gives rise to the behavior that we observe in our ensemble experiments, but is not readily observable in the single-molecule experiments reported by Lia et al. (24). The uncommon and highly processive mode gives rise to the behavior detected in their single-molecule experiments. However, because this second mode occurs infrequently, it does not significantly influence our ensemble results. This interpretation is also supported by the observation that the K_M for ATP in the highly processive translocation of RSC in the single-molecule experiments [>1 mM (24)] is larger than that which is observed in ensemble studies [77 μM (31)]. It is also worth noting that recent single-molecule studies of nucleosome mobilization by SWI/SNF suggesting that DNA loops of <28 bp serve as the primary intermediates in the reaction offer further justification of this hypothesis (53).

Interestingly, a similar discrepancy between the results of single-molecule and ensemble experiments has also been observed for the double-stranded DNA unwinding activity of the UvrD helicase from E. coli. Using a technique similar to that used by Lia et al. to study RSC translocation (24), Dessinges et al. (54) reported an unwinding rate ± 250 bp/s) and associated processivity ∼0.991) for UvrD catalyzed double-stranded DNA unwinding that were significantly larger than those measured in ensemble experiments [∼70 bp/s and ∼0.9, respectively (44, 55)]. In the paper by Dessinges et al. the authors noted this discrepancy, but did not offer an explanation for it. One possible explanation could be that double-stranded DNA unwinding by UvrD can proceed through multiple modes similar to how we are proposing to characterize double-stranded DNA translocation by RSC.

Another possible explanation for the discrepancy between the results would be if the physical conformation of RSC was affected by the length of the double-stranded DNA to which it was bound; our experiments focused on short DNA molecules, whereas the single-molecule studies used a much longer substrate. This explanation is not supported by our experiments with plasmid DNA, however, which gave results consistent with what we observe with shorter DNA molecules. Another possibility is that the tension in the DNA affects RSC binding and/or the processivity of DNA trans-location by RSC. Lia et al. demonstrated that loop size (and likely processivity) is affected by the applied stretching force, so this suggestion is at least partly supported by observation (24).

Comparison to Other DNA Translocases

Our estimate of the processivity of double-stranded DNA translocation by RSC is much lower than recently reported processivities of single-stranded DNA translocation by the UvrD helicase (P = 0.9996 ± 0.0001) (19) and the T7 DNA helicase (P ∼ 0.99996) (48). This suggests that RSC may possess a lower affinity for DNA than do these enzymes, which is not surprising because its primary function in the cell is to interact with DNA via nucleosomes, for which its binding affinity is higher (27, 30). As discussed above, recent single-molecule work suggests that RSC can display a higher processivity for double-stranded DNA translocation in the presence of nucleosomes (25). Of course, because processivity depends upon both k_t and k_d (Scheme 2), it is also possible that the rate-limiting process for forward translocation (k_t) is also slower for RSC than for other DNA translocases. Finally, we note that direct comparisons between various translocases are not necessarily justifiable because experimental studies of these enzymes were performed under different solution conditions.

Naturally, it would be very interesting to determine if the presence of this slow initiation step is unique to the double-stranded DNA translocation activity by RSC or if it also occurs during nucleosome mobilization by RSC. It is worth noting that recent kinetic studies of nucleosome mobilization by the ATP-dependent chromatin remodeling factor (ACF) also postulate a rapid-equilibrium nucleosome binding and dissociation prior to the subsequent slower steps in nucleosome centering (56). Similarly, it is important to now quantitatively characterize the kinetic mechanisms of double-stranded DNA translocation by other chromatin remodeling complexes to see if a mechanism similar to that presented in Scheme 1 or 2 is applicable.

Finally, it is worth noting that slow initiation steps have also been observed in both the single-stranded DNA trans-location and double-stranded DNA unwinding activities of bacterial helicases, and thus their introduction here is not unique. For example, the kinetic mechanism for single-stranded DNA translocation by B. stearothermophilus PcrA helicase includes an ATP-dependent conformational change that precedes processive translocation (36, 46), and the mechanism for single-stranded DNA translocation by the T7 DNA helicase includes an ATP-independent conformation change preceding DNA translocation (48). Also, the kinetic mechanism for double-stranded DNA unwinding by the E. coli RecBCD helicase also includes additional kinetic steps that are not associated with double-stranded DNA unwinding (40, 57), although for RecBCD it was not possible to determine where those additional steps occurred within the kinetic mechanism (40, 41, 57). Given the high degree of sequence homology between helicase proteins and chromatin remodeling proteins (13), these proteins are expected to share some similarities in their kinetic behavior, but may also display interesting differences that tailor them to their nucleosomal substrates and tasks.

MATERIALS AND METHODS

Buffers

Reaction buffer was prepared with reagent grade chemicals using twice-distilled water that was subsequently deionized with a Milli-Q purification system (Millipore Corp., Bedford, MA). All ATPase reactions were carried out in 10 mM HEPES (pH 7.0), 5% glycerol, 20 mM potassium acetate, 5 mM MgCl₂, 0.5 mM dithiothreitol, and 0.1 mg/mL BSA at 30 °C.

RSC Protein and DNA

RSC was purified from a yeast strain that expresses TAP-tagged Rsc2 from the chromosomal RSC2 locus. Cells were grown in 2 × YPD, and the soluble extract was used to purify RSC, essentially as described (47).

Oligonucleotides were purchased from Integrated DNA Technologies (Coralville, IA) or the University of Utah Core Facility and dialyzed extensively into Milli-Q water before use. Equal concentrations of complementary strands of DNA were mixed together in a buffer containing 20 mM Hepes (pH 7.0) and 40 mM KCl. This solution was then heated to 100 °C and allowed to cool slowly to room temperature over the course of 6–8 h. Plasmid pBR322 was purchased from Invitrogen (Carlsbad, CA) and was dialyzed extensively into Milli-Q water before use.

Radioactive ATPase Experiments

ATPase activity was determined by measuring the rate of conversion of ATP to ADP using [α-³²P]ATP. RSC and double-stranded DNA were incubated together on ice for 5 min prior to the addition of ATP. The final reaction conditions were as follows: 35 nM RSC, 100 μM nucleotide DNA, and 1 mM ATP. The solution was incubated at 30 °C during the entire experiment. Aliquots of this solution were removed every 6 min and quenched by adding an equal volume of 0.5 M EDTA. The extent of product formation at each time point was monitored by spotting 2 μL samples onto polyethyleneimine(PEI)-cellulose TLC plates (Merck KGaA, Darmstadt, Germany), which were developed using 0.6 M KPO₄ (pH 3.4) and quantitatively analyzed using a Bio-Rad Molecular Imager FX (BioRad, Hercules, CA). Spots corresponding to the radiolabeled ATP and ADP were quantitated using the Quantity One software supplied by the manufacturer.

The affinity for RSC binding to a 172 bp fragment of the Xenopus laevis 5S rNA gene in the absence of ATP was determined to be approximately 10⁻⁸ M⁻¹ with a 1:1 stoichiometry under similar solution conditions (30). On the basis of this result we can estimate an equilibrium association constant of approximately 5.8 × 10⁻⁸ M⁻¹ (base pair), assuming a simple single-step binding reaction between RSC and the DNA. Thus, under our experimental conditions, we estimate that >99% of the RSC will be bound at the start of the reaction.

Stopped-Flow ATPase Experiments

Single cysteine mutant (A197C) phosphate binding protein (PBP) was expressed in E. coli and purified as described previously (35, 37). It was then conjugated to the fluorophore N-[2-(1-maleimidyl)-ethyl]-7-diethylamino)coumarin-3-carboxamide (MDCC) in the presence of a coupled enzymatic phosphate mop composed of 0.2 unit/mL purine nucleoside phosphorylase (PNPase) with 200 μM 7-methylguanosine (MEG) and purified as described previously. The labeled protein (PBP-MDCC) after purification had a 280/430 nm absorbance ratio of 1.6, indicating the majority of the PBP was labeled. PBP-MDCC displayed an increase in fluorescence emission at 465 nm upon binding inorganic phosphate (P_i) by ∼ 6-fold.

Stopped-flow kinetic measurements of ATP hydrolysis were performed at room temperature in a buffer containing 20 mM Hepes (pH 7.3), 20 mM potassium acetate, 5 mM magnesium chloride, and 0.5 mM DTT. Phosphate released was monitored using a KinTek model SF-2001 stopped-flow apparatus with excitation at 425 nm through 4 nm slits. Emission was measured after a 450 nm cutoff long-wave pass filter (Corion, LL-450-F) (58). All solutions were cleaned of contaminating P_i using a phosphate mop, comprising 0.5 unit/mL PNPase and 500 μM MEG. The fluorescence signal of PBP-MDCC was calibrated using P_i standard on the stop-flow apparatus. RSC, DNA, and MDCC-PBP were mixed with ATP, and the change in fluorescence was measured and normalized using the P_i standard. Final concentrations after mixing were 0.1 μM RSC, 5 μM DNA, 3 μM PBP-MDCC, and 1 mM ATP. All curves presented are the average of four independent traces. The plasmid DNA used in these experiments was 3 kb phagemid Bluescript (Strategene, San Diego, CA).

Analysis of Kinetic Data

The ATPase rate for each length of double-stranded DNA was determined from a linear fit of the corresponding ATPase time courses. All NLLS analyses using eq 3 were performed using Conlin, kindly provided by Dr. Jeremy Williams. Fitting models and Monte Carlo simulation programs were written in the C++ computer language and compiled with the Microsoft C++ 6.0 compiler.