Oil/Water Transfer is Partly Driven by Molecular Shape, Not Just Size

Abstract

We present a new approach to computer modeling of solvation free energies of oil in water. In Semi-Explicit Assembly, we first precompute structural and thermal properties of TIP3P waters around different Lennard-Jones spheres. This tabulated information is then used to compute the nonpolar solvation properties of arbitrary solutes. By accumulating interactions from whole regions of the solute molecule, Semi-Explicit Assembly more properly accounts for effects of solute shape and solves problems that appear as nonadditivities in traditional γA approaches. Semi-Explicit Assembly involves little parameter fitting because the solute and water properties are taken from existing force fields. We tested the predictions on alkanes, alkynes, linear and planar polyaromatic hydrocarbons, and on a diverse set of 504 molecules previously explored by explicit solvent simulations. We found that not all hydrocarbons are the same. Hydrocarbons have ‘hot spots’, places where first-shell waters interact more strongly with the molecule than at other locations. For example, waters are more attracted to hover over hydrocarbon rings than at the edges. By accounting for these collective regional effects, Semi-Explicit Assembly approaches the physical accuracies of explicit solvent models in computing nonpolar solvation free energies, but because of the pre-computations and the regional additivities, it is nearly as fast to compute as γA methods.

Introduction

Various processes in nature – the folding of proteins, the self-assembly of lipid bilayer membranes and soap micelles, the chromatographic separations of materials, the binding of drugs to proteins, and the partitioning of environmental toxins into fish oils – are driven, at least in part, by the solvation or desolvation of oil-like molecules in water. Two approximations have been commonly used in modeling the molecular solvation of oil in water:

(1) The solute-solvent interface is assumed to be a miniature version of a macroscopic liquid interface

Key knowledge of hydrophobic interactions derives from bulk-phase experiments such as measurements of the interfacial tension γ between oil and water, where ΔG = γA is this nonpolar free energy of transfer; it increases in proportion to the interfacial area A. Microscopic solvation processes such as protein folding are often treated as sums of transfers of subcomponents, such as an oil moiety from water to oil. For example when a protein folds, its oil-like amino acids are transferred from a state of exposure to water to a state of burial in a nonpolar core. The free energies for such processes are often estimated by a quantity of the same form, γ_iA, where A is a microscopic property – the surface area of the oil molecule (which can be estimated in different ways), and γ_i is a parameter chosen for a particular type of chemical moiety i. This is the approach generally taken in “implicit” computer models of water.

(2) Solvation energies are approximated using group additivities

A main approach to computing solvation free energies for complex processes is to assume additivity and sum the free energies of component parts. Central to this enterprise are hydrophobicity scales, which are lists of free energies of transfer – typically between an oil or vapor phase and water – of model compounds that represent the component parts. There are more than 30 hydrophobicity scales for the amino acids alone^1–7 and many more for simple hydrocarbons and chemical groups.^{6, 8–10} This model-compound/hydrophobicity-scale approach rests on the underlying assumptions of additivity and transferability. Model-compound/hydrophobicity-scale studies would have little value if the component quantities measured in a simple oil/water experiment were not applicable to more complex media such as the interiors of lipid bilayers, protein cores, or nonpolar chromatographic stationary phases, extending to situations beyond just the direct measurements themselves. Such additivity approaches require the assumption that one methylene group or one amino acid somewhere in the molecule is equivalent to another methylene group or amino acid somewhere else. In this way, solvation free energies are assumed to only depend upon the numbers and types of substituents, and not their geometric arrangements.

Moreover, hydrophobicity scales depend on the premise of equivalence, namely that one type of oil is essentially the same as another type of oil. As Tanford and Nozaki noted in one of their first publication on such scales,¹ in order to have a ‘scale’ that spans from some extreme of maximum nonpolarity to the other extreme of maximum polarity requires a ‘gold standard’ of nonpolarity. Which type of oil best represents the essence of ‘nonpolarity’? If oils were all different, then it would be impossible to capture the spirit that somehow all protein cores or all lipid bilayers have the same property of being ‘hydrophobic’.

Some limitations of the γA approach

Some of the problems with these simple approaches to molecular solvation are known.

(1) Solute shape matters too, not just surface area

The γA model treats only the dependence of solvation free energy on solute surface area and not on solute shape. Yet, water adopts very different structures and thermal properties around highly curved or nonlinear solutes than around planar solutes or large (protein-sized) objects having the same surface area.^{6, 11–17} One result is that ΔG/A measured from interfacial tensions at planar surfaces is 75 cal mol⁻¹ Å⁻² from interfacial tension measurements, but only ΔG/A ≈ 30 cal mol⁻¹ Å⁻² for small-molecule hydrocarbon/water transfer¹² and 5 cal mol⁻¹ Å⁻² for air/water transfer, the value typically used in implicit models.^{18, 19}

(2) Dispersion interactions do not have the same form as cavity formation costs

Dissolving a solute in water entails: (1) opening a cavity in water, which involves unfavorable water ordering or unfavorable hydrogen-bond breaking in water, then (2) inserting the solute, which involves favorable dispersion interactions of the solute with the water. Both terms are treated in the scaled particle theory approach,^{20, 21} for example. Often, both terms are assumed to have the same mathematical form and are captured in a single γA quantity; in this approach both cavity formation and the attractive dispersion interactions are assumed linearly dependent on the solute surface area. However, Pitera and van Gunsteren showed that this simplification leads to underestimating the true attractive aspects of nonpolar solvation, a nearly 50 kcal/mol oversight for small proteins.²² A better accounting of dispersion interactions has been a driving force for new methods for treating nonpolar solvation.^23–26

(3) Different oil phases are different. Additivity sometimes doesn’t work

While Tanford and Nozaki did show that partitioning into water is not strongly dependent on the types of oil in some cases,^{1, 27} more recent studies have shown that partitioning can be substantially dependent on what oil is used for the oil phase,²⁸ indicating the limitations of this assumption. The atom arrangements, densities, and chemical character differ between different molecules. Solvation free energies can sometimes be non-additive because of these microscopic details.^{29, 30} Treating chemically distinct solute surfaces additively with a uniform γ parameter misses these effects.

The two standard routes to improved solvation modeling are: (1) to include additional parameters,^{25, 26, 31–34} or (2) to perform ‘explicit water’ computer simulations, but at considerably greater computational expense and loss of simplicity.^{35, 36}

Here, we present a third approach, which we call Semi-Explicit Assembly. We use parameters and water models that are taken directly from explicit-water forcefields, so our approach does not involve ‘learning’ or parameterization from databases. Semi-Explicit Assembly retains the simplicity of a type of additivity, but it is regional, collectively capturing results from multiple solute groups at the same time. In this way, it correctly captures effects that would be described as non-additivities in the simpler group-additivity approaches. Also, as a consequence of this additivity and of a pre-calculation step, this approach is computationally nearly as fast and simple as γA methods, and is much faster than explicit solvent simulations. Nevertheless, we find that the quality of the modeling is close to that of explicit solvent simulation modeling.

The Semi-Explicit Assembly approach to nonpolar solvation

Our aim in Semi-Explicit Assembly is to capture the parameters and much of the physics from explicit solvent modeling within a rapidly computable implicit framework. To do this, we use fully explicit solvent simulations to pre-compute the behaviors of waters around a series of nonpolar solute spheres having different radii and attractive dispersion interactions. After this one time precomputation, we probe the local interaction identity of an arbitrary solute molecule and assemble its nonpolar solvation free energy.

Pre-computations of Lennard-Jones spheres in explicit water

In computer modeling, molecules are usually represented as collections of bonded spheres. Steric repulsion and attractive dispersion interactions are most often handled using a standard Lennard-Jones (LJ) pair potential,

$$V_{\text{LJ}}(r_{ij})=\{\begin{array}{cc}4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]\hfill & r_{ij}\le r_c\hfill \\ 0\hfill & r_{ij}>r_c,\hfill \end{array}$$ (1)

where the size (σ) and well-depth (ε) parameters account for the steric and dispersive elements respectively,³⁷ r_ij is the distance between particles i and j, and r_c is an interaction cutoff distance. To gather the physics of solvation using LJ spheres, we start by performing explicit solvent free energy calculations to compute their nonpolar solvation free energy (ΔG) spanning a wide range of σ and ε values. These calculations are based on a constructing a thermodynamic cycle connecting simulations of the LJ sphere in two different media. We transfer the solute between vacuum and water, and obtain ΔG for this transfer process. This is similar to a combined scaled-particle theory approach,^{11, 20, 21} where cavity formation and interaction activation steps are carried out simultaneously. It should be noted that total solvation free energies include both a polar and nonpolar part. As indicated earlier, we are interested exclusively in the nonpolar part throughout this study, so atomic partial charges are always set to zero.

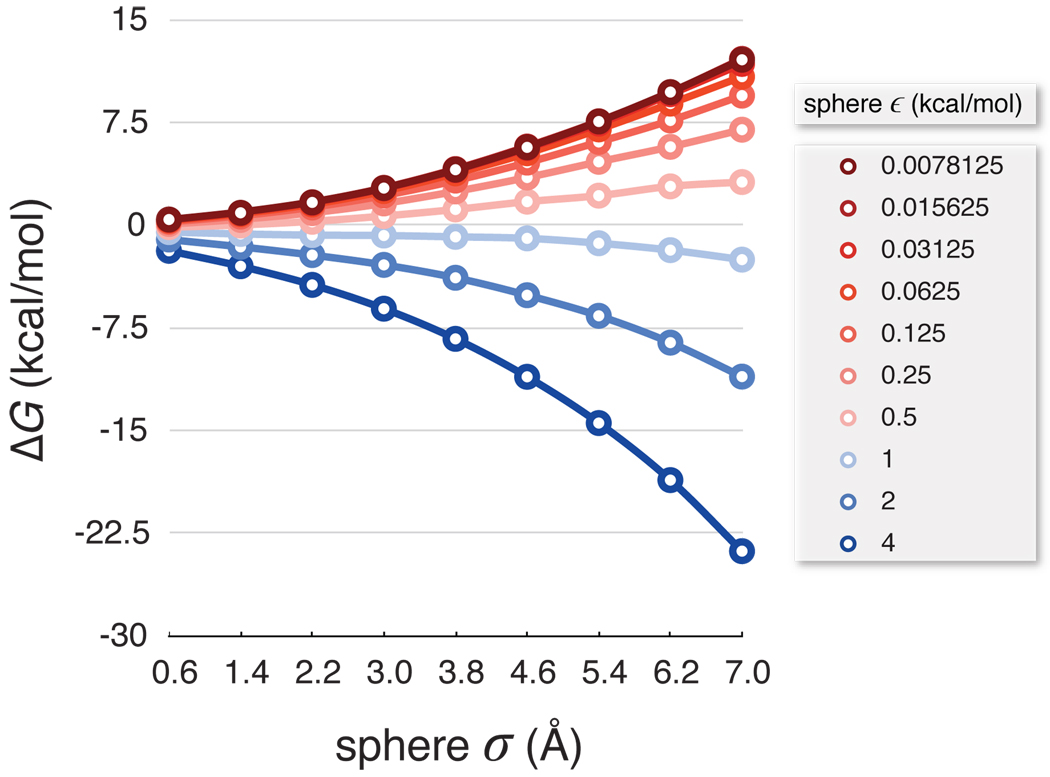
Figure 1 shows the pre-computed values of ΔG across a range of LJ spheres solvated in the TIP3P water model.³⁸ Increasing the LJ well-depth gives more favorable solvation free energies. As the well-depth decreases, the ΔG values converge toward the previously observed ΔG limit for purely hydrophobic hard spheres.^{15, 16, 39} A crossover from unfavorable to favorable solvation occurs around a well-depth value of ε = 0.75 kcal/mol. Individual atoms in molecular simulations rarely have dispersion attractions this strong, but we include these simulations because we find that collections of atoms can have attractive potentials of this magnitude.

Figure 1.

Nonpolar solvation free energy (ΔG) of single LJ spheres in TIP3P water at 300 K as a function of their σ and ε parameters. Unfavorable ΔG values are red. Favorable ΔG values are blue.

The pre-computation step that generates Figure 1 is computationally expensive, but it is only performed once for any given temperature, pressure, or solvent model. After the values in this plot are determined, they can be applied in much faster computations for any given solute.

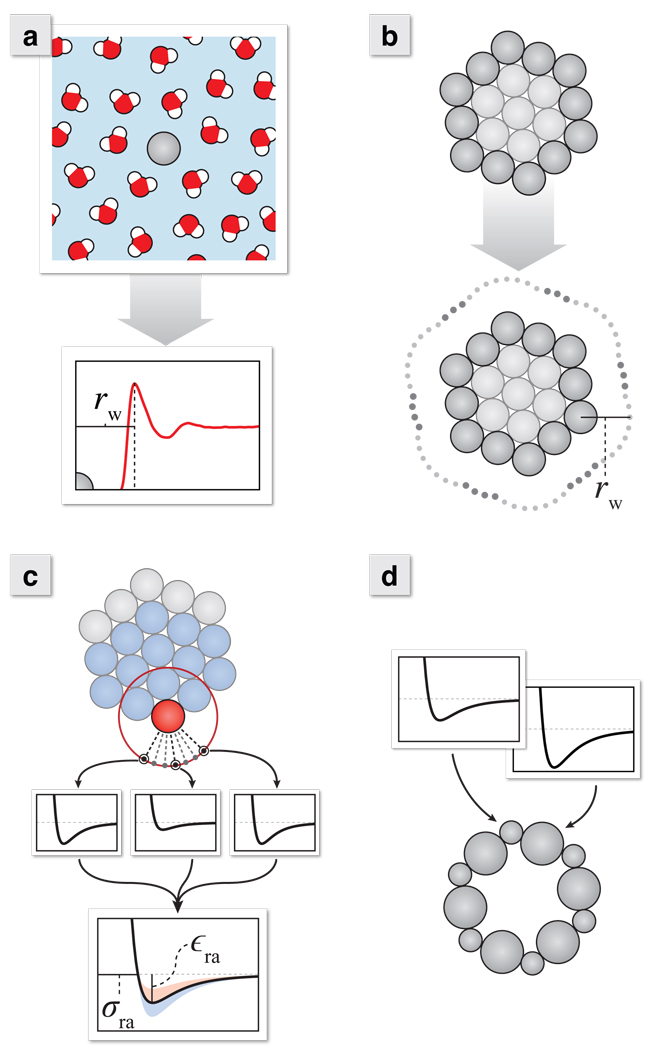
At the same time we compute ΔG values, we also construct a table of average separation distances between the solute and first-shell water. We collect these distances (r_w) from radial distribution functions of water oxygen atoms with respect to the centers of each type of LJ sphere; see Figure 2a. These distances are collected in a table as a function of σ and ε of the LJ spheres.

Figure 2.

The process for incorporating non-additive environmental effects on the solute surface atoms. (a) Sample LJ spheres in explicit water and build a map of water distances (r_w) as a function of σ and ε. (b) Construct the solvent accessible surface (SAS) using the distances from the explicit solvent map. (c) Probe the LJ potential of the solute along the line connecting each SAS dot to its surface atom. Average these potentials for each surface atom, and extract new “effective” LJ parameters (σ_ra and ε_ra) from this curve. (d) Use these effective potential parameters when calculating the solvation free energy. Note that edge atoms will have more attractive ε_ra values than corner atoms because of the greater number of atoms near to the probe particle.

Assembly of molecular solvation free energies

The explicit solvent pre-computations provide a detailed picture of how the chosen water model will solvate simple nonpolar spheres. To estimate the nonpolar solvation free energy of arbitrary solute molecules, the results from these representative atomic systems need to be brought to the unique solute surfaces. This assembly process is shown in Figures 2b, 2c, and 2d.

(1) Compute solvent-accessible surface (SAS) of the solute

For every atom of the solute molecule, with its given radii and LJ parameters, we look up (or interpolate) from the pre-computed table of r_w values, the average contact distance of the surrounding solvent. We form spherical accessibility boundary points around each solute atom from these interpolated r_w values and cull out points that are inaccessible due to other neighboring atoms. This generates an initial molecular SAS; (Figure 2b). This SAS differs from that of Lee and Richards⁴⁰ in two ways: (1) we do not use a hard sphere probe, so, in principle, our solvation boundary expands or contracts with pressure and temperature, and (2) the interactions governing solvent accessibility will not be with only a single nearest-neighbor solute atom (see below), hence we capture contributions from other nearby atoms.

(2) Compute a region-averaged dispersion-potential field

Now we construct local dispersion potential fields at different points in the solvation shell around the solute. First, we define a vector from a water dot point of the initial SAS to the center of the associated solute surface atom. In Figure 2c, the current surface atom is colored red. The dashed lines show vectors connecting this target solute atom to its SAS dot sites. Starting at the SAS dot sites, we probe the regional LJ potential field along these vectors. This regional field we use encompasses all solute atoms within the r_c of the target surface atom, the blue particles in Figure 2c. The gray particles are outside this cutoff and therefore ignored. By including more surrounding interactions, longer r_c values will result in a more accurate depiction of the total solute dispersion potential. Rather than use an infinitely long cutoff, we found that

$$r_c=2r_{\text{max}}+r_{\text{ww}},$$ (2)

gives results that were converged within the calculated error for the overall nonpolar free energy. Here, r_max is the maximum r_w found for the atoms making up the solute, and r_ww is the water–water packing distance extracted from a water–water radial distribution function (~2.7 Å).

In this probing process, the LJ interactions are accumulated between the solute atoms within the region described above and a probe particle along the dot site vector. The pairwise LJ potential (Equation 1) is dependent on both σ_p (the probe σ parameter) and atom σ parameters. So now σ_p becomes a parameter that is determined as discussed below. This probe particle is progressively stepped closer to the surface in order to construct a potential as a function of probe particle position, and this potential is stored for each surface dot. As shown in Figure 2c, the wells of potentials calculated for surface sites in closer proximity to more solute atoms (those nearer to solute edges rather than corners) will tend to be deeper. After constructing potentials for each surface dot about a solute surface atom, we average them together to generate a region-averaged dispersion potential (V_ra) which incorporates shape and the attractive interactions of nearby collections of solute atoms. We then extract region-averaged parameters for each surface atom (σ_ra and ε_ra) by fitting this curve to an LJ potential,

$$V_{\text{ra}}(r)\approx 4\sqrt{{\epsilon }_{\text{ra}}·{\epsilon }_{\mathrm{p}}}\left[{\left(\frac{({\sigma }_{\text{ra}}+{\sigma }_{\mathrm{p}})}{2r}\right)}^{12}-{\left(\frac{({\sigma }_{\text{ra}}+{\sigma }_{\mathrm{p}})}{2r}\right)}^6\right],$$ (3)

where r is the distance between the probe and the target surface atom. As V_ra is an average of collective atom dispersion potentials, fitting it to a single LJ potential is an approximation. It should be noted that the averaging procedure is technically unnecessary. We could retain a more detailed map of the dispersion potential based on these more numerous surface points rather than on an averaged, per atom basis. We have tested both routes, and they are equivalent for the nonpolar solvation of small molecules shown below, so we use the per atom averaging step for convenience.

(3) Reduce the region-averaged field to a single effective LJ interaction

Assign these newly derived σ_ra and ε_ra parameters to the associated surface atoms (Figure 2d). This procedure encodes information about the full solute structure and interactions into the solvent exposed regions of the molecule.

From the steps above, we obtain free energy component quantities of the solute that can be added to get the total nonpolar solvation free energy,

$$\mathrm{\Delta }G=p{V}_{\mathrm{v}}+{\displaystyle \sum _{i=1}^N{f}_i\mathrm{\Delta }{G}_i.}$$ (4)

Here, f_i is the fraction of the surfaced exposed for atom i, and ΔG_i is that atom’s free energy term extracted (via a linear interpolation) from the map pictured in Figure 1 using the region-averaged parameters as our σ and ε values. The pV_v “void” term is the cavity formation cost due to the buried particles within the molecule (the lightened atoms in Figure 2b).⁴¹ For small molecules, this void term is often zero because all the solute atoms also happen to be surface atoms. We found setting the pV_v term to zero for all the molecules studied within a good approximation. If one is interested in the absolute nonpolar solvation of macromolecular structures, optimization of this void term will become increasingly important.

As the SAS is a set of discretized points, the f_i will depend on the number of points remaining after the culling process in Step 1. Culling points near the intersection of nearby solvent-accessible surface shells will result in a slightly jagged edge. To arrive at converged estimates of the f_i values, we iterate over constructing the SAS and the calculation of ΔG in Equation 4. In these series of Step 1 surface constructions, the region-averaged LJ parameters are used to determine new r_w distances. In this way, this SAS used to determine the f_i values incorporates the collective structure of the solute molecule.

Optimization of the dispersion potential probe

In order to calculate a particular nonpolar solvation free energy, we must optimize the probe size (σ_p) for the Lennard-Jones field sampling procedure. This is necessary to insure that we pick up the surrounding dispersion interactions properly, and is similar to attractive probe optimization procedures in alternative techniques.^24–26 While one could optimize the probe size to a large set of target molecules, we decided to start with a single molecule, n-pentane - the middle sized molecule of our linear alkane series. After setting ε_p = 1 for convenience, we scanned σ_p values in 0.01 Å increments and sought to minimize the difference between the ΔG using our method and the explicit solvent ΔG for n-pentane. We tested different ε_p values and found that the choice of ε_p does not change the results. The optimized σ_p value of 0.82 Å turns out to be quite robust, and one can select values within a 0.1 Å window about this midpoint without significantly altering the results below. We attempted optimizing over a larger set of small molecules, but this did not significantly alter σ_p or lead to improvements in the solute ΔG estimations.

Algorithm performance and computational details

There is probably no simple and fair way to compare various methods for computational speed. However, the following provides a good rough estimate. Standard γA approaches are limited by the computational cost of constructing the solvent-accessible surface. These are currently the fastest available methods. Semi-Explicit Assembly, too, requires construction of the solvent-accessible surface. Additionally, there are the probing step described above which will optimally cost the same as construction of a solvent-accessible surface, and a reconstruction of the solvent-accessible surface with the region-averaged LJ parameters. Thus, in an optimized implementation, the maximum speed of Semi-Explicit Assembly would be about 3-fold slower than γA methods.

The free energy surface of LJ parameters pictured in Figure 1 was constructed using explicit solvent free energy calculations of individual spheres in cubic boxes of 1000 TIP3P water molecules at 300 K and 1 atm. The LJ σ values for solute particles in this map cover a range of 0.6 to 7.0 Å linearly in 0.8 Å steps. The LJ ε values range from ~0.008 to 4 kcal/mol, where each subsequent ε value is two times the previous value.

The free energy calculations were performed using thermodynamic integration with GROMACS 4.0.⁴² In thermodynamic integration, the LJ solute particles are reversibly transformed between a fully interacting and non-interacting state over a series of simulation windows, each with their own transformation parameter (λ). Integrating the change in the potential over the change in λ over the full range of λ values gives the free energy difference between these states. A detailed description of the theory behind such calculations can be found elsewhere.^43–45 Here, twenty one windows were used for the transformation process, and they spanned λ = 0 to 1 in even steps of 0.05 units. A soft-core potential was used to minimize integration error in the transformation process,⁴⁶ and the specifics of the actual simulations followed those outlined by Mobley et al.⁴⁷ One exception was that the interaction cutoff needed to be longer to accommodate the large particle sizes explored as part of this series. Thus, the LJ cutoff radius was smoothly switched off between 11 and 13 Å. Errors in the free energies were estimated by the limiting value of block averages.⁴⁸

For the polyaromatic hydrocarbon series, explicit solvent free energy calculations were performed on naphthacene, pentacene, hexacene, triphenylene, and perylene because literature values of ΔG were unavailable. The specifics of these calculations are identical to those described above for single LJ spheres, with the exception of larger numbers of water molecules in order to maintain hydration layers thicker than the specified cutoff lengths. The LJ parameters for these molecules were assigned using the general AMBER force field (GAFF).⁴⁹

The Semi-Explicit Assembly nonpolar solvation free energies were averaged values from 40 dot surfaces construction iterations, each using the same set of region-averaged LJ parameters calculated using the initial dot surface. For each of these dot surfaces, spheres of ~300 dots per atom were randomly rotated before culling overlapping points. The ΔG values for all the solutes come from single calculations about the dominant clustered conformation from the explicit solvent simulations. We attempted more detailed configuration analyses for several of the molecules that contained multiple rotatable bonds; however, this led to negligible changes in the final values, so we chose to simply take the dominant conformation as representative of the whole. With electrostatic effects being much stronger than dispersion, it is likely that the polar part of the free energy is much more sensitive to changes in internal conformations. Calculated error for Semi-Explicit Assembly over the 40 iterations was 0.05 kcal/mol, averaged over all molecules explored in this study. A post-calculation analysis indicated that a similar error can be obtained with fewer than 5 dot surfaces construction iterations.

Results

For testing our solvation approach, we assume the ‘gold standard’ right answer solvation free energies are given by experimental data where it exists, or otherwise by all-atom explicit solvent free energy calculations.³⁶ Here, we compare our predictions to these explicit solvent simulations, to experiments where possible, and to γA values. In supplementary material, we show that this semi-explicit method is also more accurate than other recent approaches.^{25, 26}

Linear hydrocarbons

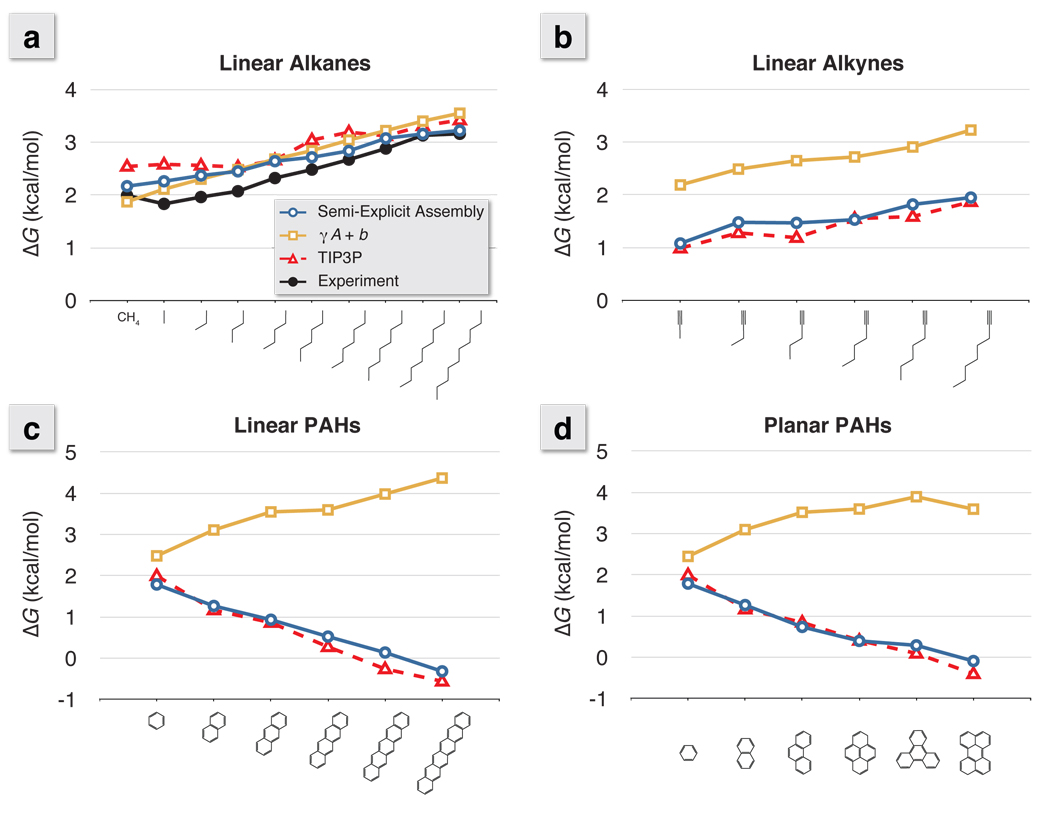
The standard first test of solvation models are the linear n-alkanes. Figure 3a confirms that the present model agrees with experiments, explicit-water simulations, and standard γA models for these molecules. Interestingly, because of its assumed linear dependence, typical γA methods give an erroneous prediction for the intercept, γA + b, where b = 0.92 kcal/mol corresponds to insertion of a solute of near zero size. In reality, the value should be much closer to zero for a solute of zero size. explicit solvent simulations with TIP3P water give a value of ~0.2 kcal/mol. Because our Semi-Explicit approach derives from explicit simulations, our values approximately equal the explicit values.

Figure 3.

The nonpolar solvation free energy for a series of a) linear alkanes, b) linear alkynes, c) polyaromatic hydrocarbons (PAHs) in a linear arrangement, and d) PAHs in a planar arrangement calculated using γA + b, Semi-Explicit Assembly, and explicit solvent. For γA + b, the traditional (0.00542 × SA_tot) + 0.92 was used,¹⁸ and the TIP3P results are those obtained through explicit free energy calculations.³⁶ Experimental comparisons to ΔG cannot be drawn with the linear alkynes or PAHs series, because they have a substantial polar term to the overall solvation.

Figure 3b shows solvation free energies for the linear alkynes, from the various models. Alkynes have a carbon-carbon triple bond at the end of the chain. In GAFF,⁴⁹ the dispersion interaction well-depth is twice that of carbon-carbon single bonds. Like the explicit simulations, but unlike γA, the Semi-Explicit approach captures the more favorable aqueous solvation of the alkynes relative to the alkanes. Figures 4a and 4c show that the extra attraction for water of the alkynes is localized near the triple bond.

Figure 4.

Maps of the collective dispersion attraction about the solvent accessible surface (SAS) of a) n-pentane, b) cyclopentane, c) pent-1-yne, d) benzene, and e) pyrene. The color of the surface indicates the LJ well-depth, with blue starting at 0 kcal/mol and red lowering to deeper than 5 kcal/mol. Note the red “hot spots” around the triple bond in pent-1-yne and in the center of the benzene and pyrene ring planes. These indicate a significant enhancement of dispersion attraction with the surroundings. As these regions grow with increasing molecule size, these collective dispersion attractions will offset the cost of cavity formation in surrounding solvent. With a simple γA, all these surfaces would be a uniform blue.

Hot spots: not all hydrocarbons are the same

Figures 4a and 4b show the LJ potential surfaces for n-pentane and cyclopentane. Seams between atom surfaces form favorable interaction “hot spot” regions, while methyl end-groups of the alkane chain are a deeper blue and less favorable. The surface area of cyclopentane is less than n-pentane, but this only accounts for a modest decrease of 0.2 kcal/mol in ΔG when using γA + b. This modest change is much less than the greater than 1 kcal/mol decrease seen experimentally.^{9, 50} Semi-Explicit Assembly includes the effects of these “hot spots” and lowers ΔG by an additional 0.4 kcal/mol. The remaining difference between the estimated and the experimental value likely comes from approximations in the Semi-Explicit Assembly approach, such as the void term discussed previously and the incomplete capturing of solvent-solvent interaction enhancement from optimal hydration cages.

Polyaromatic hydrocarbons: linear and non-linear topological effects

The solvation free energies of polyaromatic hydrocarbons (PAHs) provide a more stringent test. Aromatic rings have an important asymmetry. A water molecule at the lateral edge ‘sees’ one methylene-like group and its two lateral neighbors. But a water molecule centered above or below the plane sees 6 methylene-like groups; see Figures 4d and 4e. These combined attractions counter cavity formation costs, resulting in more favorable nonpolar solvation with larger arrangements of aromatic rings; see Figures 3c and 3d. The γA method errs by predicting that the nonpolar term of PAH molecule solvation should be less favorable with increasing size. Semi-Explicit Assembly correctly captures this non-additivity, and predicts that larger PAH molecules should be more readily hydrated than smaller ones because of the “hot spots” centered above and below the rings.

504 small solute molecules: a variety of molecular shapes

Here, we broaden our comparison to a large diverse test set of solutes. We have calculated ΔG values for the same extensive test set previously studied by Mobley et al.,³⁶ which is a subset of the molecules explored by Rizzo et al. using various implicit solvent methods.¹⁸ This is a diverse series of compounds that includes a variety of common functional groups in different arrangements.

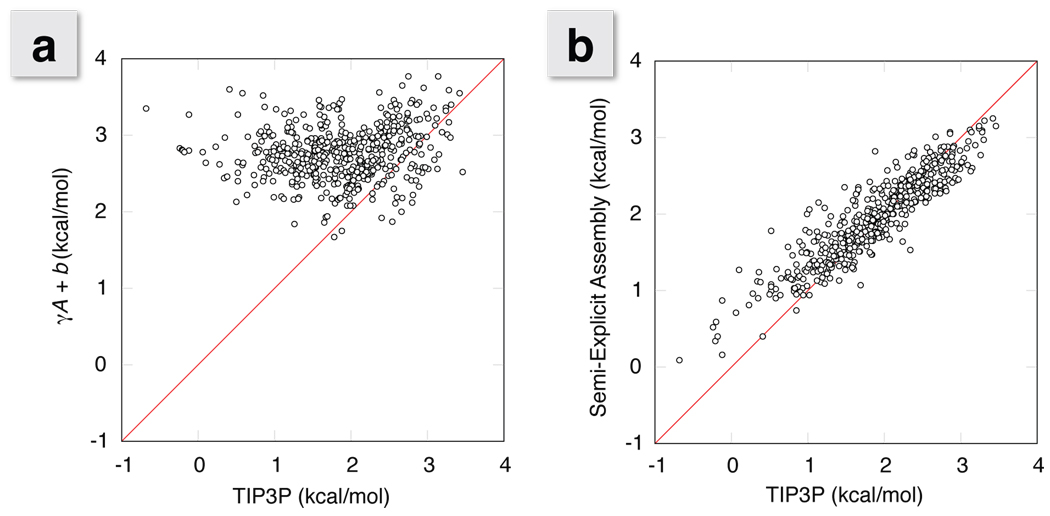
Figure 5a shows the finding of others^{18, 26, 36} that γA does not capture the nonpolar or cavity component of the solvation free energies from explicit solvent simulations. The correlation does not improve if a volume term replaces the area term.³⁶ Figure 5b shows that Semi-Explicit Assembly gives much better agreement with the atomically detailed simulations. The correlation coefficient for the latter is 0.91, as compared to 0.15 for the former. The key component in this improvement is accurate calculation of attractive interactions. This correctly lowers the ΔG values for solutes that contain strong attractive elements, like the example cases shown in Figure 3.

Figure 5.

Correlation plots of ΔG values comparing a) γA + b and b) our Semi-Explicit Assembly technique with the ΔG values from explicit solvent free energy calculations. A detailed incorporation of dispersion interactions takes what was originally a flat correlation and brings it much more in line with explicit solvent results. This results in a correlation coefficient improvement from 0.15 to 0.91 and an RMS deviation decrease from 1.2 kcal/mol down to 0.3 kcal/mol over the entire set.

Summary

We have described an approach to modeling the solvation free energies of nonpolar solutes in water. We call this approach Semi-Explicit Assembly since its parameters are taken without modification from explicit solvent simulations. The primary computational expense is a pre-computation step in which LJ spheres of various sizes are simulated in explicit water MD calculations. Here, we used the TIP3P water model at 300 K and 1 atm. However, this approach is general and is directly extensible to any explicit-water model, without modification, including to expensive polarizable models for example, and at other temperatures and pressures. These pre-computations intrinsically capture the various structural properties of the surrounding water that are needed to represent solvation free energies. This approach does not require parametrization to large databases of solvation free energies. It goes beyond simpler models in capturing solute shape effects, and not just dependences on solute size. It also goes beyond simpler models in capturing some of the important group non-additivities, but it retains a broader-scale “regional” additivity assumption, so it is nearly as fast to compute as γA methods. Comparisons with explicit solvent simulations of alkynes, branched alkanes, and planar and linear polyaromatic hydrocarbons show that a critical aspect missing from simpler additivity-based models is that some hydrocarbons have hot spots, i.e., regions where one water molecule comes into contact with many carbons at the same time, such as over the centers of aromatic rings. These are regions that contribute to very favorable solvation in water. The results presented show that it is not necessary to sacrifice computational efficiency in order to achieve physically accurate representations of solvation.