Summary
We measured the time course of sodium entry during action potentials of mouse central neurons at 37 °C to examine how efficiently sodium entry is coupled to depolarization. In cortical pyramidal neurons, sodium entry was nearly completely confined to the rising phase of the spike: only ~25% more sodium enters than the theoretical minimum necessary for spike depolarization. However, in fast-spiking GABAergic neurons (cerebellar Purkinje cells and cortical interneurons), twice as much sodium enters as the theoretical minimum. The extra entry occurs because sodium channel inactivation is incomplete during the falling phase of the spike. The efficiency of sodium entry in different cell types is primarily a function of action potential shape and not cell type-specific differences in sodium channel kinetics. The narrow spikes of fast-spiking GABAergic neurons result in incomplete inactivation of sodium channels; this reduces metabolic efficiency but likely enhances the ability to fire spikes at high frequency.
Introduction
Action potentials in mammalian neurons use the concentration gradients of sodium and potassium ions to encode and transmit information by a transient change in membrane voltage. In this process, the ionic gradients are partially dissipated and must be restored by the Na+/K+-ATPase pump, requiring metabolic energy. For an action potential in which the rising phase is generated by sodium entry and the falling phase by potassium efflux, there would be perfect metabolic efficiency if sodium entry were confined to the rising phase and potassium entry to the falling phase, each carrying the minimum charge needed to produce the voltage change during the action potential (CΔV, where C is the capacitance of the membrane and ΔV is the change in voltage during the spike). However, the extent to which this can be achieved depends on the gating kinetics of the underlying voltage-dependent channels. In practice, the time course of sodium channel inactivation is especially critical. In the classic analysis by Hodgkin and Huxley of the squid axon action potential, the predicted sodium entry is roughly four times the minimum needed for the change in voltage, primarily because sodium channels remain open to a significant extent during the falling phase of the action potential (Hodgkin and Huxley, 1952; Bezanilla et al., 1970).
Action potentials in mammalian central neurons are fundamentally similar to those in the squid axon in having a rising phase generated by sodium current and falling phase mediated by potassium current. However, many parameters likely to influence the kinetics of sodium entry and metabolic efficiency - including action potential shape, types and densities of sodium and potassium channels, channel kinetics, and temperature - are very different for mammalian neurons than the squid axon. A variety of data suggests that sodium entry may generally be more efficient in generating action potentials in mammalian neurons than in the squid axon. Direct measurements of sodium current kinetics during action potential waveforms in a variety of central neurons in rat and mouse brains show that there is generally far less sodium entry during the falling phase of the action potential than the rising phase (Raman and Bean, 1997; Raman et al., 2000; Taddese and Bean, 2002; Do and Bean, 2003; Jackson et al., 2004; Enomoto et al., 2007), in contrast to the squid axon action potential. However, an important limitation of these results is that all were obtained for action potentials and currents at room temperature. A recent examination of this issue for the action potentials in mossy fiber boutons of hippocampal granule neurons showed that even at 37 °C, sodium entry is much more confined to the rising phase than in the squid axon, with only ~30% "extra" sodium entry (Alle et al., 2009). However, given the high degree of variability in shapes of action potentials among different kinds of central neurons (Mountcastle, 1969; McCormick et al., 1985; reviewed by Bean, 2007), it is unclear how general this result is likely to be.
We set out to determine how efficiently sodium entry is used in the formation of action potentials in a variety of mammalian central neurons at physiological temperature. We find that the extent to which entry of sodium is limited to the rising phase - and thus the corresponding metabolic efficiency - varies considerably among cell types. Cortical pyramidal neurons operate with a high degree of ionic efficiency but cerebellar Purkinje neurons and cortical basket cell interneurons have much less efficient action potentials. Comparing the different neuronal types, we find that the efficiency of the sodium entry is primarily a function of action potential shape and is largely independent of cell type-specific differences in sodium channel kinetics. The lower metabolic efficiency of the action potential in fast-spiking neurons results from incomplete inactivation of sodium channels during the narrow action potential, which leads to unnecessary sodium influx but likely enhances the ability of the neurons to fire rapidly.
Results
Sodium entry is efficient in action potentials of cortical pyramidal neurons
To measure sodium entry during the action potential, we recorded the action potential in a neuron and then used it as the voltage command in voltage clamp, recording the elicited ionic current and using tetrodotoxin (TTX) to isolate the current entering through voltage-gated sodium channels. We used acutely dissociated neurons to enable accurate voltage clamp and ensure spatial uniformity of voltage. To achieve good voltage clamp control of the large and fast sodium currents flowing at 37 °C, we used a partially-blocking concentration of TTX to reduce the size of the currents, thereby reducing errors arising from imperfectly compensated series resistance of the pipette tip. Because TTX blocks channels in an all-or-none manner (Hille, 1966), we could then scale the recorded current to that expected in the absence of TTX, using a scaling factor experimentally determined (in each cell) from the degree of block by TTX. Figure 1 shows this procedure. An action potential recorded from a cortical pyramidal neuron at 37 °C (Figure 1A, top) was used as command waveform to elicit ionic current in the same cell (Figure 1A, bottom) either with sodium current present but reduced (in 90 nM TTX) or after complete block of sodium current (in 1 µM TTX). To determine the factor by which current was reduced by 90 nM TTX, the effect of TTX on current elicited by a step from −88 to +12 mV was measured in the same cell (Figure 1B). Then the action-potential-elicited sodium current expected in the absence of TTX (Figure 1C, red trace) was determined by scaling the sodium current recorded in partially-blocking TTX (after subtraction of traces recorded with full TTX block) by 3.9, the factor by which 90 nM TTX reduced step-evoked current. This sodium current is compared with the total net ionic current flowing during the action potential, which can be calculated from the action potential waveform as −C*dV/dt, where C is the cell capacitance and dV/dt is the time derivative of the voltage (Hodgkin et al., 1952; Fig. 1A, bottom, blue trace). The two currents are very similar in size during the rising phase of the action potential, which gives credence to the accuracy of the scaling procedure. The close temporal overlap in the rising phase also supports the accuracy of a correction for a time lag in the recorded membrane current relative to command voltage (see Methods).
Figure 1. Time-course of sodium current during the action potential of a cortical pyramidal neuron.
(A) The action potential recorded at 37°C in a dissociated cortical pyramidal neuron (top) was used as the command voltage to elicit current in voltage-clamp mode in the same neuron. Ionic current was recorded in the presence of partially-blocking (90 nm) TTX (black trace, bottom) and then in fully blocking (1 µM) TTX (red trace, bottom). The solutions used for voltage clamp additionally contained 10 mM TEA to reduce potassium current and improve the subtraction of currents with partially-blocking and fully-blocking TTX. (But the action potential was first recorded in control solution without either TTX or TEA.) To isolate ionic current in the voltage clamp recordings, recordings were made with compensation for both pipette and cell capacitance, and residual capacitative current (from imperfect compensation) was corrected off-line, using a signal-averaged step from −88 to −93 mV to define capacitative current, which was then scaled and subtracted from the digitized current in a point-by-point manner, treating each pair of digitized points as a step. (B) Determination of degree of block by 90 nM TTX (same cell as A). Current was elicited by a step from −88 mV to +12 mV as various concentrations of TTX were applied (with 10 mM TEA present in all solutions to reduce potassium current). Bottom: time-course of peak inward sodium current during application of 60 nM, 90 nM, and 1 µM TTX, followed by a return to 90 nM TTX. Peak inward sodium current was reduced by a factor of 3.9 between control and 90 nM TTX. (C) The time-course of TTX-sensitive sodium current during the action potential (red trace, bottom) was determined by subtracting current traces in 90 nM and 1 µM TTX (each signal-averaged from 12 traces). This current was scaled up by a factor of 3.9 to account for the blocking effect of 90 nM TTX determined in B. Total ionic current during the action potential was calculated from the action potential waveform as −C*dV/dt (blue trace, bottom), where C is cell capacitance (measured in voltage clamp using a step from −88 to −93 mV) and dV/dt is the time derivative of voltage. The "sodium entry ratio" was calculated as the ratio of total integrated sodium current during the action potential to CΔV, the minimum charge transfer necessary for the depolarization of the action potential, where ΔV is the change in voltage during the action potential (from spike threshold to peak of the action potential). (D) Collected data for the sodium entry ratio in 8 cortical pyramidal neurons. Filled symbols are calculations for individual neurons; the open symbol and error bars represent the mean ± standard deviation.
In this cortical pyramidal neuron, there was very little sodium current flowing after the peak of the action potential. We quantified the sodium entry during the action potential (sodium current integrated over the entire action potential) relative to the minimal necessary sodium entry (CΔV, where C is cell capacitance and ΔV is the change in voltage during the action potential). In this cell, the "sodium entry ratio" calculated in this way was 1.04. Figure 1D shows collected results from 8 cortical pyramidal neurons; the average sodium entry ratio was 1.24 ± 0.29 (mean ± standard deviation). The action potentials of these neurons reached a peak of +19 ± 8 mV and had an average width (measured at half-maximum amplitude) of 1.21 ± 0.29 msec, typical values for cortical pyramidal neurons (Connors et al., 1982; McCormick et al., 1985; Shu et al., 2007). Also typical of cortical pyramidal neurons, the maximum dV/dt in the upstroke is large compared to that of the downstroke (ratio of 6.5 ± 1.3), similar to previous measurements in cortical pyramidal neurons in guinea pig (McCormick et al., 1985).
Fast-spiking GABAergic neurons allow extra sodium entry
The shape of action potentials differs among various types of neurons in the mammalian brain. In general, GABAergic neurons have narrower spikes than glutamatergic neurons and often have a "fast-spiking" phenotype, with a capability of firing steadily at high frequencies during prolonged stimulation (McCormick et al., 1985; Connors and Gutnick, 1990; Kawaguchi, 1993; Nowak et al, 2003). Cerebellar Purkinje neurons are fast-spiking GABAergic neurons with narrow action potentials that can maintain steady firing rates of more than 200 Hz when stimulated (Llinás and Sugimori, 1980). Figure 2 shows an analysis of sodium entry during the action potential of a Purkinje neuron. In striking contrast to the cortical pyramidal neuron action potential, a substantial sodium influx was present during the falling phase of the Purkinje neuron action potential, as well as during the rising phase. In fact, more sodium entered during the falling phase of the action potential than during the rising phase. The sodium current during the upstroke reaches a maximum shortly before the peak of the action potential. At exactly the time of the peak, there is a dip in the sodium current reflecting the decreased driving force on sodium ions. This is followed by a second phase of sodium entry on the downstroke, presumably reflecting the increase in driving force during repolarization while at least some channels remain open. Largely because of the substantial "extra" sodium entry during the falling phase, the sodium entry ratio was 2.3. In collected results from 7 Purkinje neurons, the sodium entry ratio was 2.00 ± 0.61, which was significantly different from cortical neurons (p < 0.01, Mann-Whitney Rank-Sum test). The action potentials in these neurons had an average width of 0.23 ± 0.06 msec, peak of +13 ± 10 mV, and upstroke/downstroke ratio of 1.4 ± 0.4.
Figure 2. Time-course of sodium current during the action potential of a cerebellar Purkinje neuron.
(A) The action potential recorded at 37°C in a dissociated cerebellar Purkinje neuron (top) was used as a command in voltage-clamp in the same neuron. Sodium current (red trace, bottom) was isolated by TTX-subtraction using the same procedure as in Figure 1 and compared to the calculated net ionic current (blue trace, bottom). Current was recorded in 90 nM TTX and scaled by a factor of 10 (measured from the effect of TTX in reducing sodium current elicited by a step from −88 to −8 mV). The sodium entry ratio was calculated as in Figure 1. (B) Collected data for 7 cerebellar Purkinje neurons. Filled symbols are calculations for individual neurons; the open symbol and error bars represent the mean ± standard deviation.
To explore whether these differences in sodium entry are likely to be general between other types of fast-spiking versus non-fast-spiking neurons, we examined two other types of neurons. To examine another class of fast-spiking neurons, we isolated cortical interneurons from a transgenic mouse in which a subset of fast-spiking cortical GABAergic interneurons corresponding to parvalbumin-positive basket cells are labeled with enhanced GFP (Chattopadhyaya et al., 2004). Figure 3A shows an example of a recording from a labeled GABAergic interneuron. As expected, the action potential was narrow (width of 0.30 msec). There was substantial entry of sodium during the falling phase, and the sodium entry ratio in this cell was 1.5. This was typical; in collected results (Figure 3B), the sodium entry ratio was 1.98 ± 0.55 (n=5) for GABAergic interneurons, very similar to Purkinje neurons. These cells had an average spike width of 0.34 ± 0.08 msec, peak of 12 ± 7 mV, and upstroke/downstroke ratio of 1.6 ± 0.5, similar to previous measurements of fast-spiking cortical interneurons (McCormick et al., 1985; Kawaguchi, 1995), including parvalbumin-positive basket cells (Kawaguchi and Kubota, 1993).
Figure 3. Efficiency of sodium influx during the action potentials of cortical fast-spiking interneurons and CA1 pyramidal neurons.
(A) Analysis of sodium entry during the action potential of a cortical interneuron (identified by eGFP expression after isolation from cortex of GAD67-eGFP mouse line with specific labeling of parvalbumin-positive basket cell interneurons). Protocol as in Figure 1 and Figure 2. Sodium current was recorded in 90 nM TTX and scaled by a factor of 3.3. Black trace: action potential waveform. Red trace: sodium current. Blue trace: total ionic current calculated from −C*dV/dt. (B) Collected data for the sodium entry ratio in 5 cortical interneurons. Filled symbols are calculations for individual neurons; the open symbol and error bars represent the mean ± standard deviation. All recordings at 37°C. (C) Analysis of sodium entry during the action potential of a dissociated pyramidal neuron from the CA1 region of the hippocampus. Protocol as in Figure 1 and Figure 2. Sodium current was recorded in 90 nM TTX and scaled by a factor of 2.7. Black trace: action potential waveform. Red trace: sodium current. Blue trace: total ionic current calculated from −C*dV/dt. (D) Collected data for 8 CA1 pyramidal neurons. Filled symbols are calculations for individual neurons; the open symbol and error bars represent the mean ± standard deviation. All recordings at 37°C.
Figure 3C shows an analysis of sodium entry in a pyramidal neuron isolated from the CA1 region of the hippocampus. These neurons had action potential widths that varied from 0.41 to 1.4 msec (with a mean of 0.83 ± 0.33 msec) and had peaks of +18 ± 5 mV. For the cell in Figure 3C, the spike width was 1.4 msec and the sodium entry ratio was 1.3. In collected results (Figure 3D), the sodium entry ratio was 1.62 ± 0.67 for CA1 pyramidal neurons, less than either of the GABAergic cell types but more than cortical pyramidal neurons.
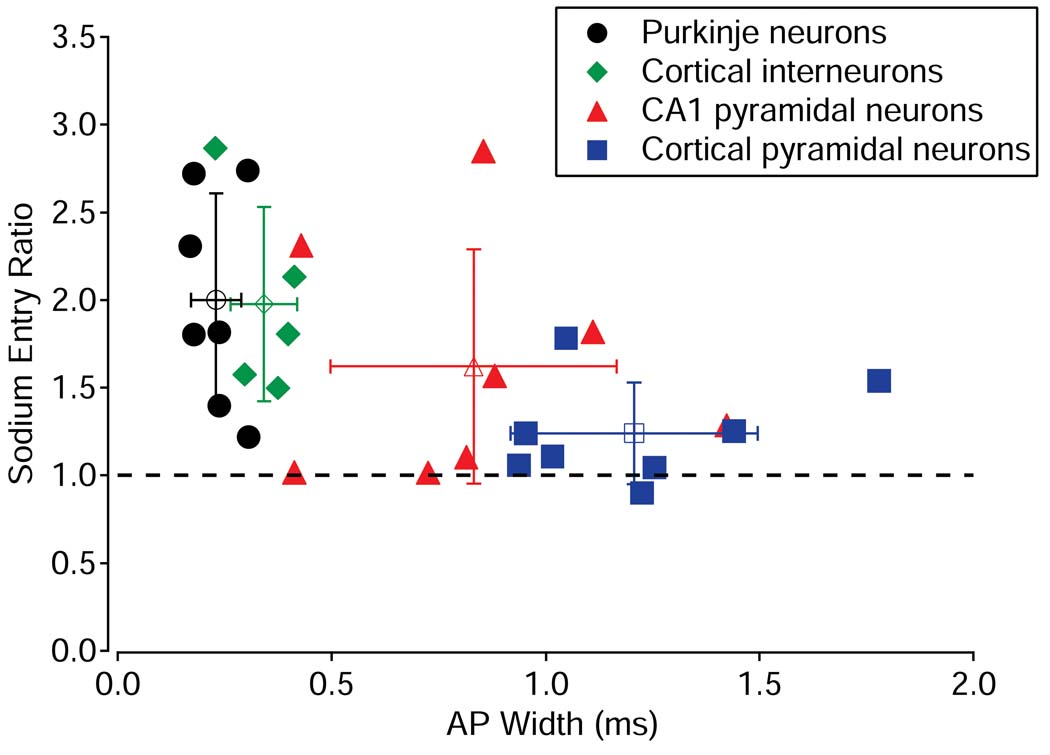
Figure 4 shows the collected results for sodium entry ratio for individual neurons for all four cell types. Systematic differences among the cell types are apparent, with Purkinje neurons and cortical interneurons having the largest amount of extra sodium entry and cortical pyramidal neurons the smallest. Moreover, comparing all cells, there was an inverse correlation of the sodium entry ratio with the width of the action potential (Spearman rank correlation coefficient =−0.48, p=0.012, n = 28). This correlation is consistent with the two fast-spiking cell types with narrow action potentials having the most extra sodium entry and cortical pyramidal neurons, with the widest action potentials, having the least.
Figure 4. Collected results for sodium efficiency in four neuronal types.
Sodium efficiency in all neurons tested, plotted as a function of action potential width. Filled symbols show measurements for individual neurons; open symbols and error bars represent the mean ± standard deviation for each cell type.
The sodium entry ratio gives a measure of how efficiently sodium entry is used for spike depolarization. We also used our data to calculate total sodium entry per action potential, which takes into account differences in action potential height. To do this calculation, we integrated sodium current during an action potential, converted it to moles of sodium ions, and normalized it to membrane area (measured from the cell capacitance, assuming 1 µF/cm2). The sodium influx per action potential was 0.82 ± 0.30 pmole/cm2 (n=8) for cortical pyramidal neurons, 1.54 ± 0.54 pmole/cm2 (n=7 for Purkinje neurons, 1.36 ± 0.27 pmole/cm2 (n=5) for cortical interneurons, and 1.27 ± 0.65 pmole/cm2 (n=8) for hippocampal CA1 pyramidal neurons. Thus, as expected from the sodium entry ratio, cortical pyramidal neurons had the least sodium entry and Purkinje neurons the most, with interneurons and CA1 pyramidal neurons intermediate. The sodium entry per spike in both Purkinje neurons and cortical interneurons was significantly greater than in cortical pyramidal neurons (p=0.018 and p=0.011 respectively, Mann-Whitney rank sum test).
Efficiency can be estimated by timing of sodium entry
In the recordings for each individual cell, it was clear that the amount by which the sodium entry ratio exceeds unity is mainly dependent on the extent of sodium entry during the falling phase of the action potential. Therefore, a simple way of estimating sodium efficiency is to compare total sodium entry during the entire action potential to the sodium entry during the rising phase (up to the peak of action potential). In principle, this measurement would underestimate the sodium entry ratio if there is substantial potassium current flowing before the peak of the action potential, in which case sodium entry even during the rising phase would have to exceed CΔV by the amount of overlapping charge carried by potassium efflux. In fact, however, estimating efficiency as the ratio of total sodium entry to rising phase sodium entry gave nearly identical results as measuring it by total sodium entry/CΔV. For example, the ratio of total sodium entry/rising phase sodium entry is 1.12 for the cortical pyramidal neuron in Fig 1C versus 1.04 calculated as total sodium entry/CΔV; the analogous values by the two methods were 2.29 versus 2.31 for the Purkinje neuron in Fig. 2A, 1.34 versus 1.57 for the cortical interneuron in Fig 3A, and 1.23 versus 1.29 for the CA1 pyramidal neuron in Fig 3C. The close correspondence of the two methods is expected if relatively little potassium current flows before the peak of the action potential. This appears to be case (for all the cell types) because the sodium current measured in voltage clamp superimposes well with total ionic current (−C*dV/dt) until just before the peak.
Basis of the variation in sodium efficiency among cell types
Differences in sodium channel kinetics have been found among various types of central neurons. For example, using identical recording conditions, differences in sodium channel kinetics have been seen comparing hippocampal CA1 pyramidal neurons with fast-spiking hippocampal interneurons (Martina and Jonas, 1997) and Purkinje neurons with hippocampal CA3 pyramidal neurons (Raman and Bean, 1997). Therefore, one explanation of the difference in action potential efficiency could be different sodium channel kinetics in the different cell types. Because the second method of estimating sodium efficiency is based simply on the timing of sodium entry during the action potential, it does not require using the cell's own action potential. We could therefore test whether the differences in efficiency among the different cell types are primarily due to differences in action potential shape or differences in sodium channel kinetics by measuring the time course of sodium entry in each cell type using pre-recorded action potentials from all four cell types (Figure 5). We found that efficiency of sodium influx depends primarily on action potential shape and not cell type-specific sodium channel kinetics. For example, using a Purkinje neuron action potential (Figure 5A, first column), all four cell types showed a large amount of sodium entry during the falling phase, while with an action potential from a cortical pyramidal neuron (Figure 5A, fourth column), sodium influx was nearly completely confined to the rising phase in all four cell types. Figure 5B summarizes collected data and illustrates that the sodium entry ratio depends on action potential shape, with little apparent influence of sodium channel differences among the cell types.
Figure 5. Sodium efficiency is determined by action potential shape rather than kinetic differences in sodium channels.
(A) Typical action potential waveforms from each of the four neuronal cell types (top, black traces) were selected and used as voltage commands for recordings of spike-elicited sodium current in the various types of neurons Sodium current in a given neuron was elicited by each of the four waveforms, using subtraction of current recorded in partially-blocking and fully-blocking TTX to define sodium current. Each row shows currents elicited in a single neuron of the indicated type. For each record, the sodium entry ratio was calculated as the ratio of total sodium influx to sodium influx during the rising phase (from threshold to the peak, shaded). The currents in each row are normalized according to the maximal dV/dt for each action potential waveform (largest for the Purkinje cell spike), which allows comparison of the magnitudes of the currents in a row as well as their time course. Time scale is the same for all records. (B) Collected results for the sodium entry ratio determined in each cell type by each waveform (mean ± standard deviation, n=5–15). Symbols are defined in (A).
Sodium channel availability remains after the action potential in fast-spiking neurons
The component of sodium entry occurring during the falling phase of the action potential in fast-spiking neurons must reflect channels that have not inactivated. The termination of this current could be due to either inactivation continuing as the falling phase progresses or to deactivation of channels that are still not inactivated. It is of interest to know whether inactivation becomes complete during the falling phase, since this will greatly influence the refractory period after the spike. To examine this, we performed an experiment to assay the time course of sodium channel availability during and after the action potential. The first part of the command consisted of an action potential waveform, which was followed by a test pulse to −8 mV to assay the degree of sodium channel availability. The test pulse was applied at various times during the falling phase of the action potential. The peak sodium current during each test pulse was compared to that elicited from a step to −8 mV from −88 mV, where availability was maximal. Figure 6A shows this protocol applied in a Purkinje neuron. It was clear from this experiment that sodium channel inactivation is never complete, even during the falling phase and immediately after the action potential. During the falling phase, the availability declined from about 0.32 early in the falling phase to a minimum of 0.17, reached when the action potential had repolarized to about −51 mV (Figure 6B). The lack of complete inactivation measured in this way is consistent with the substantial sodium current seen during the falling phase of Purkinje neuron action potentials. Interestingly, recovery from inactivation started near a voltage of −68 mV, even before the spike was over. The time course of sodium channel availability during the falling phase shows that the decay of sodium current during the falling phase of the spike is in part ongoing inactivation and in part deactivation. Figure 6C and 6D illustrate the same analysis for sodium channel inactivation during the action potential in a cortical pyramidal neuron. Here, inactivation becomes complete during the falling phase of the action potential, at a voltage of about −40 mV.
Figure 6. Incomplete inactivation of sodium channels during action potentials in a Purkinje neuron but not a cortical pyramidal neuron.
(A) Sodium currents in a Purkinje neuron (bottom traces) elicited in response to a step from −88 to −8 mV (left) and (right) in response to a pre-recorded Purkinje neuron action potential with a voltage step to −8 mV added at different times after the peak to assay sodium channel availability. (B) The time-course of sodium channel availability from the experiment in (A), plotted as time from the peak of the action potential. Availability was measured as the ratio of peak sodium current elicited by steps to −8 mV following partial action potential normalized to the peak current for step to −8 mV from −88 mV. (C,D) Same analysis for sodium channel availability during and after an action potential in a cortical pyramidal neuron.
Figure 7 shows collected results from this experimental protocol performed in all four cell types. In both Purkinje neurons and cortical interneurons, inactivation was never complete even when it was maximal immediately after the action potential; on average, the minimum availability was 0.15 ± 0.05 (n=15) for Purkinje neurons and 0.07 ± 0.04 (n=10) for cortical interneurons. In contrast, inactivation was essentially complete in cortical pyramidal neurons (minimum availability of 0.003 ± 0.007, n=5) and in hippocampal CA1 neurons (0.02 ± 0.02, n=7) by the end of the action potential. Thus, in the two fast-spiking cells but not the pyramidal neurons, there is a significant fraction of sodium channels available (non-inactivated) immediately after the spike.
Figure 7. Collected results for measurements of sodium channel availability during and after action potentials for all four cell types.
(A) The experimental protocol in Figure 6 was repeated in 20 Purkinje neurons, 12 cortical interneurons, 6 cortical pyramidal neurons, and 7 hippocampal CA1 pyramidal neurons. Data points indicate mean ± SD. (B) Collected results for the minimum sodium current availability using the different action potential waveforms applied to sodium currents in each cell type (the same waveforms used for the experiments in Figure 5). Symbols are the same as in Figure 5B representing mean ± standard deviation (n=5–15).
In addition to inactivation being incomplete in fast-spiking neurons, recovery from inactivation after a spike was also faster in fast-spiking neurons than in pyramidal neurons. At least in part, this is likely to be because more negative voltages are reached more quickly after the peak. In Purkinje neurons and cortical interneurons, availability returns to >75% within 2.5 ms, while in both types of pyramidal neurons, availability is still below 75% after 5 ms.
To test whether the differences in completeness of inactivation are a property of action potential shape or differences in sodium channel kinetics among the cell types, we did experiments using action potential waveforms from all four cell types applied to sodium currents in each cell type (Figure 7B). As for the sodium entry results in Figure 5, we found that the extent to which inactivation is complete after a spike depends primarily on action potential shape and much less on cell-specific sodium channel kinetics. There are small differences in channel kinetics among the cell types when tested with a given waveform; for example, the minimum availability following a Purkinje neuron spike waveform was greater for sodium currents in CA1 pyramidal neurons (0.26 ± 0.0.07, n=8) than for sodium currents in Purkinje neurons (0.15 ± 0.05, n=15). However, such cell type-specific differences were much smaller than the differences among the waveforms tested on the same cell type. When tested with a Purkinje neuron waveform, sodium currents in all four cell types had substantial availability (mean values > 0.15) while with either a CA1 pyramidal neuron waveform or a cortical pyramidal neuron waveform, inactivation was essentially complete (mean availability <0.02) for sodium currents in all four cell types.
Discussion
Our results show that the efficiency with which sodium entry is used for action potential formation varies considerably among different types of mouse central neurons, with sodium entry only ~25% more than the theoretical minimum in cortical pyramidal neurons but ~2-fold the minimum in cerebellar Purkinje neurons. In particular, the two types of fast-spiking GABAergic neurons we examined had substantially more "excess" sodium entry than cortical pyramidal neurons or most CA1 pyramidal neurons. The strong correlation of excess sodium entry with narrow action potentials suggests that the excess sodium entry associated with fast-spiking neurons is likely to be general, since there is a clear correlation between fast-spiking behavior and narrow action potentials (McCormick et al., 1985; Nowak et al, 2003; reviewed by Connors and Gutnick, 1990; Bean, 2007).
The experiments examining the pattern of sodium entry when cells are stimulated by the action potential waveforms of other cell types shows that the differences in sodium efficiency among different cell types is due primarily to the different shapes of action potentials, not to differences in sodium channel kinetics. Sodium channels do have different kinetics among different types of mammalian central neurons (e.g. Martina and Jonas, 1997; Raman and Bean, 1997), and differences in kinetics were apparent in the detailed time-course of sodium current elicited by a given spike shape applied to the four types of neurons (Figure 5). For example, the sodium current in Purkinje neurons decayed faster than the current in CA1 neurons for all waveforms, at least up to the action potential peak; the difference in time-course was especially clear for the narrow Purkinje neuron spike. Nevertheless, the total amount of sodium entry and resulting efficiency was not dramatically different among sodium currents in the different cells in response to any given waveform. In Purkinje neurons, sodium current elicited by step depolarizations inactivates with a biphasic time-course, and repolarization is accompanied by activation of "resurgent" current that is associated with the slower phase of inactivation (Raman and Bean, 1997; Raman and Bean, 2001). This mechanism may produce extra sodium entry late in the spike waveform that balances more rapid inactivation early in the waveform.
There was a strong correlation between sodium efficiency and action potential width, with narrower action potentials having less efficiency. The most obvious reason for the correlation is that sodium channel inactivation is less complete during the falling phase of narrower action potentials. In addition, the action potential peak was on average less positive in the fast-spiking cells with narrower action potentials, which has two consequences: first, the rate of inactivation is slower at less positive voltages and second, the voltage is further from the sodium equilibrium potential so that the driving force on sodium ions is greater.
Action potential width is mainly determined by the potassium channels expressed in the neuron. Fast-spiking neurons with narrow action potentials use fast-activating Kv3 channels to repolarize the membrane (Wang et al., 1998; Erisir et al., 1999; reviewed by Rudy and McBain, 2001). The presence of Kv3 channels not only produces narrow action potentials but also enables fast spiking (Lien and Jonas, 2003). Our results suggest that there are two related mechanisms underlying this effect. One is that sodium channel inactivation is incomplete (simply because the narrow spikes rise and fall so rapidly). The other is that recovery begins sooner and from more hyperpolarized voltages. Both effects speed recovery and thereby reduce the refractory period, and both effects result from the rapid repolarization of the action potential in fast-spiking neurons. However, this rapid repolarization leads to reduced metabolic efficiency because the incomplete sodium channel inactivation allows extra sodium influx during the falling phase. Thus the rapid repolarization produced by Kv3 channels has a functional benefit in allowing repetitive fast spiking but with an additional metabolic cost.
Our experiments focused on the efficiency of sodium entry during the action potential. There is also a metabolic cost associated with the efflux of potassium ions. We could not easily directly quantify total spike-evoked potassium current because there is no blocker equivalent to TTX that is effective against all the multiple components of potassium current with different kinetics. However, for an action potential composed only of sodium and potassium currents, the total potassium efflux should be equal to the total sodium influx (because net inward charge movement must be counteracted by the same net outward charge movement by the end of the action potential, ignoring the after-hyperpolarization). Therefore, the extra sodium entry in fast-spiking neurons must be associated with an equal amount of extra potassium efflux, effectively doubling its metabolic cost.
Cell bodies of mammalian central neurons also have voltage-dependent calcium channels that are activated during the action potential and carry inward current during the falling phase of the spike. This calcium entry is another metabolic cost associated with the action potential. Spike-evoked calcium current is typically only 20–25% of sodium current when the two have been recorded in the same neuron (Raman and Bean, 1999; Do and Bean, 2003; Jackson et al., 2004). Like sodium entry, calcium entry during the action potential must be countered by an equivalent amount of potassium efflux by the time the spike is over. Further work will be needed to quantify the extra metabolic cost associated with calcium entry (and associated potassium entry) during the action potential in various types of central neurons.
We analyzed sodium entry during somatic action potentials. It remains to be determined to what extent the efficiency of sodium entry might differ in a given cell type for somatic action potentials versus propagating axonal action potentials. Our measurements of sodium efficiency in the cell bodies of two glutamatergic cell types (sodium entry ratio of 1.2 ± 0.3 for cortical pyramidal neurons and 1.6 ± 0.7 for CA1 pyramidal neurons) are similar to the sodium entry ratio estimated for propagated action potentials measured in the en passant synaptic boutons of glutamatergic hippocampal mossy fibers (1.3; Alle et al., 2009). In at least some glutamatergic neurons, it has recently been found that both the action potential shape and the kinetic properties of voltage-dependent sodium channels can differ between the soma and the axon (Geiger and Jonas, 2000; Engel and Jonas, 2005; Kole et al.,2007; Shu et al., 2007). In particular, it is striking that the action potentials in hippocampal mossy fiber boutons are significantly narrower than in the parent cell bodies (Geiger and Jonas, 2000; Alle et al., 2009) and in fact are as narrow (0.25–0.38 msec at half-height; Geiger and Jonas, 2000; Alle et al., 2009 ) as the action potentials of many fast-spiking neurons. The fact that there is relatively little sodium current during the falling phase of the narrow action potential of mossy fiber boutons (Alle et al., 2009) - in contrast to the narrow action potentials of fast-spiking GABAergic neurons - apparently reflects the fact that the sodium channels in the mossy fiber boutons inactivate unusually rapidly, nearly two-fold faster than those in granule neuron cell bodies (Engel and Jonas, 2005). A comparison of how action potential shape or sodium channel kinetics might differ in the cell bodies and axons of fast-spiking neurons has not yet been made; it will be interesting to determine whether soma-axon differences are also present in these neurons.
Action potential shape can change with firing frequency, raising the possibility that sodium entry ratio and metabolic efficiency in a single neuronal type might be frequency-dependent. In preliminary experiments in Purkinje neurons, we found that although the action potential shape changes considerably in high-frequency firing stimulated by current injection (becoming smaller and broader), sodium entry during the falling phase was still present, and the sodium entry ratio changed very little at firing frequencies up to 300 Hz. By itself, action potential broadening might be expected to result in reduction in the sodium entry, but this is apparently counteracted by the reduction in action potential peak, which tends to reduce inactivation. It will be interesting to examine more systematically how the sodium entry ratio varies with frequency in different cell types.
Our results add to the recent results of Alle and colleagues (2009) in suggesting that action potentials in mammalian neurons have more efficient use of sodium entry than action potentials in the squid giant axon. In cortical pyramidal neurons, we measured a sodium entry of 0.84 ± 0.30 pmole/spike, about 4-fold less than in squid axon (~ 4 pmole/spike, Hodgkin and Huxley, 1952). It is striking that even in the least efficient examples we found, in Purkinje neurons, the sodium entry of 1.54 ± 0.54 pmole/spike is still much less than in the squid giant axon. It seems clear that the dramatic difference from the action potential in the squid giant axon is real and not because of different methods of estimation. The excess sodium entry in the squid axon action potential is because of a large sodium current during the falling phase, which was not only predicted from modeling (Hodgkin and Huxley, 1952) but also shown by direct experimental measurements of the time course of sodium and potassium conductance during action potential waveforms (Bezanilla et al., 1970). The predicted sodium entry from these electrophysiological measurements are also nicely consistent with experimental measurements of radiolabeled ion flux in squid axons (Keynes and Lewis,1951; Shaw, 1966; Atwater et al., 1970). Interestingly, both modeling and direct experiments using action potential waveforms also showed incomplete sodium channel inactivation and a large amount of sodium entry during the falling phase of action potentials in the node of Ranvier of the toad Xenopus laevis (Frankenhaeuser and Huxley, 1964; de Haas and Vogel, 1989), very similar to squid axon action potentials, suggesting that the more efficient use of sodium entry in mammalian central neurons compared to the squid axon is not general to all action potentials in vertebrate neurons.
Inefficiency of sodium entry in the action potential of the squid giant axon probably has very little overall metabolic cost to the animal. A single action potential fires during a startle-escape response (Otis and Gilly, 1990), and such responses are likely needed only occasionally. Therefore, the evolutionary pressure for the squid axon action potential may be primarily for velocity of spike propagation rather than metabolic efficiency.
In contrast, it has been suggested that the metabolic demands associated with action potential firing in mammalian cortex may be a limiting factor in determining the range of firing frequencies used during normal operation of the cortex and can help explain sparse coding in the cortex (Laughlin and Sejnowski, 2003; Lennie, 2003). Previous quantitative calculations of the metabolic cost of cortical action potentials have assumed a 4-fold excess of sodium entry, as in the squid axon (Atwell and Laughlin, 2001). Our results show that in fact, action potentials in cortical pyramidal neurons (which make up ~90% of all neurons in the cortex) are far more metabolically efficient than this, with only ~25% excess sodium entry. The impact of the lower metabolic efficiency of action potentials in cortical interneurons is difficult to evaluate; on one hand, there are fewer interneurons than pyramidal neurons and each one likely has less total membrane surface area, but on the other hand, cortical interneurons fire 5–6-fold more spikes/sec than pyramidal neurons during physiological activity (Simons, 1978; Contreras and Palmer, 2003).
Our results are quantitatively consistent with those of Alle and colleagues (2009) in the case of action potentials in glutamatergic neurons, suggesting very little extra sodium entry. However, the lower metabolic efficiency in the action potentials of cerebellar Purkinje neurons is quite striking, especially since these are large projection neurons. Indeed, the operation of Purkinje neurons could be viewed as a strong counter-example to the notion that metabolic efficiency is a particularly significant factor in the evolution of the nervous system. Not only is there substantial extra sodium entry in the Purkinje neuron spike, but these neurons fire spontaneously and continuously at average basal rates of ~40 Hz (Thach, 1968; Latham and Paul, 1971), even in the absence of synaptic stimulation (Hausser and Clark, 1997; Raman and Bean, 1997). This example suggests that whatever evolutionary pressure there may be to maximize metabolic efficiency can be balanced by functional benefits, conferred by mechanisms that also reduce metabolic efficiency. Specifically, our results suggest that in fast-spiking neurons, incomplete sodium channel inactivation during the action potential leads to an additional metabolic cost, but has a functional benefit by helping to enable high frequency firing.
Experimental Procedures
Preparation of cells
Experiments were performed with acutely dissociated mouse central neurons. Black Swiss mice (postnatal day 14–20) were used for isolation of CA1 pyramidal neurons, cortical pyramidal neurons, and cerebellar Purkinje neurons. Mice were anesthetized with isoflurane and the brain was quickly removed into ice-cold solution consisting of 110 mM NaCl, 2.5 mM KCl, 10 mM HEPES, 25 mM glucose, 75 mM sucrose, 7.5 mM MgCl2, pH adjusted to 7.4 with NaOH. For dissociation of CA1 pyramidal neurons, the hippocampus was removed and cut with a tissue chopper blade into 400 µm slices, and the CA1 region was dissected under a dissecting microscope. The tissue was treated for 10–20 minutes at room temperature with 3 mg/ml protease XXIII (Sigma Life Science) dissolved in a dissociation solution consisting of 82 mM Na2SO4, 30 mM K2SO4, 5 mM MgCl2, 10 mM glucose, and 10 mM HEPES, pH adjusted to 7.4 with NaOH. The protease solution was then replaced by ice-cold dissociation solution containing 1 mg/ml trypsin inhibitor and 1 mg/ml bovine serum albumin and the chunks were kept on ice in this solution until immediately before use. To release individual cells, the tissue was passed through Pasteur pipettes with fire-polished tips. A drop of the suspension was placed in the recording chamber and diluted with a large volume of Tyrode’s solution, consisting of 155 mM NaCl, 3.5 mM KCl, 1.5 mM CaCl2, 1 mM MgCl2, 10 mM glucose, 10 mM HEPES, pH adjusted to 7.4 with ~ 5mM NaOH. Cortical pyramidal neurons were prepared by the same procedure, but using chunks (~ 1 mm3) cut from the cortex. For both CA1 and cortical pyramidal neurons, neurons were identified by their size, pyramidal shape and presence of a thick apical dendrite stump at one end and thinner stumps of basal dendrites at the other end.
Cerebellar Purkinje neurons were prepared from chunks of cerebellar vermis (~ 1 mm3). The dissociation procedure was like that used for the hippocampal and cortical neurons. Purkinje cells could be recognized by their large size and a single large dendritic stump.
Cortical interneurons were prepared from a transgenic mouse line created by Chattopadhyaya et al. (2004), in which the GAD67 promoter drives expression of enhanced green fluorescent protein (EGFP) in parvalbumin-expressing basket cells, which are fast-spiking interneurons (obtained from Jackson Labs, strain CB6-Tg(Gad1-EGFP)G42Zjh/J). The cortical tissue was treated as for dissociation of cortical pyramidal neurons. All EGFP-expressing cells had the narrow action potentials and fast-spiking characteristics expected of cortical basket cells, firing at 220–350 Hz when stimulated with the largest current injections tested (450 pA, not saturating).
Recording
Electrodes were pulled from borosilicate glass (VWR 53432-921) using a Sutter Instruments P-97 puller. Electrode resistances were 1.5–3.0 MΩ when filled with the internal pipette solution, consisting of: 140 mM potassium methanesulfonate, 10 mM NaCl, 1.8 mM MgCl2, 10 mM HEPES, 1 mM EGTA, 0.2 mM CaCl2, 14 mM creatine phosphate (Tris salt), 4 mM MgATP, 0.3 mM Tris-GTP, pH adjusted to 7.36 with KOH. This solution has ~200 nM free calcium, calculated using Maxchelator (http://www.stanford.edu/~cpatton/maxc.html). Electrodes were wrapped with Parafilm (American National Can Company) from the shank to near the tip in order to reduce pipette capacitance (to levels ranging from 6.0–12.5 pF), allowing optimal series resistance compensation without oscillation. Reported membrane potentials are corrected for a liquid junction potential of −8 mV between the internal solution and the Tyrode's solution in which current was zeroed before sealing onto the cell, measured using a flowing 3 M KCl reference electrode as described by Neher (1992).
Solution exchange and temperature control
Cells were lifted while a gigaseal was forming and positioned in front of a series of quartz flow pipes (250 µM internal diameter, 350 µM external diameter, PolyMicro Technologies Inc.) attached with cyanoacrylate glue to a rectangular aluminum rod (cross section 1.5 cm × 0.5 cm) whose temperature is controlled using resistive heating elements and a feedback-controlled temperature controller (TC-344B, Warner Instruments). The flow pipes extend only ~1 mm from the aluminum rod, so the bulk solution near the ends of the flow pipes is quickly warmed by the large volume of the aluminum rod (which is electrically insulated with nail polish). Measured using a miniature thermocouple, the solution exiting from the flow pipes was found to be 37 °C when the temperature of the aluminum rod was set to 38°C. With this apparatus, each of the 8–10 flow pipes is heated identically and continuously, so rapid (<1 sec) solution changes can be made without fluctuations of temperature. All experiments were done at 37 °C (error of ~ 1 °C).
Electrophysiological methods
Recordings were made using a Multiclamp 700B amplifier (Molecular Devices Inc.) interfaced to a Digitdata 1322A A/D converter using pClamp 9.0 software (Molecular Devices Inc.). Data were filtered at 10 kHz with a 4-pole Bessel filter (Warner Instrument Corp.) and digitized at 200 kHz. Analysis was done using IGOR Pro (WaveMetrics Inc.) using DataAccess (Bruxton Software) to import pCLAMP files into IGOR Pro.
For the experiments in Figure 1–Figure 4, voltage clamp experiments were performed on the same cells in which the action potential waveform was first recorded in current clamp Current clamp recordings were performed with pipette capacity compensation (~70% of the measured pipette capacitance) and bridge-balance compensation. Most Purkinje neurons fired spontaneously, as did some neurons of the other cell types, in which case the action potential waveform was recorded during spontaneously firing; otherwise, it was elicited by just supra-threshold current injections (usually 10–40 pA). Of 7 Purkinje neurons, 5 fired spontaneously and two were stimulated (from resting potentials of −81 and −91 mV) with 20 pA current injections; of 8 CA1 pyramidal neurons, 1 fired spontaneously and 7 were stimulated (from an average resting potential of −81 ± 12 mV) with 36 ± 22 pA; of 8 cortical pyramidal neurons, 4 fired spontaneously and 4 were stimulated (from an average resting potential of −65 ± 5 mV) with an average of 25 ± 19 pA; of 5 cortical interneurons, 2 fired spontaneously and 3 were stimulated (from an average resting potential of −76 ± 8 mV) with an average of 23 ± 6 pA After recording the action potential in current clamp, the amplifier was switched to voltage clamp mode and tuned for optimal compensation for series resistance (typically, compensation for ~90% of a series resistance ranging from 2–10.5 MΩ). The capacity transients recorded before compensation could be fit very well by a single exponential decay (e.g. Figure 8A), consistent with the cell body and stumps of dendrites acting as a single compartment. After compensation for capacitative current and series resistance using the amplifier circuit, we recorded the ionic current elicited by the action potential waveform and isolated the component carried by sodium channels by subtracting currents before and after application of a saturating concentration of TTX (1 µM). In early experiments, we found that it was often difficult to obtain a cleanly-defined sodium current when recording the full ionic current because of series resistance errors. Even with optimal compensation for series resistance, the remaining uncompensated series resistance combined with the very large sodium currents during the action potential (often > 10 nA) produced an extra depolarization of 5–10 mV when the inward sodium current was present compared to when it wasn't (i.e. after TTX); the result was "extra" activation of outward potassium currents in the absence of TTX, so that the TTX-sensitive current defined by subtraction included an artifactual outward component during the falling phase of the action potential. We adopted two strategies to reduce this error. One was to do the subtraction (before and after TTX) using solutions in which 10 mM TEA was added to the normal Tyrode’s solution, which reduced the potassium currents during the falling phase of the action potential and reduced the error associated with extra activation of these currents from series resistance. The second strategy was to record the sodium current in the presence of a partially-blocking concentration of TTX, thus reducing the size of the sodium current and the resulting series resistance error, then scale up the measured current according to the known blocking potency of TTX, which was determined in each cell using sodium current elicited by voltage steps. Cells were moved between a series of solutions containing 30 nM, 60 nM, and 90 nM TTX and the lowest TTX concentration reducing sodium current to ~1–4 nA (assayed with a voltage step to −38 mV) was used for further recordings. The degree of block by TTX was assayed in each cell by voltage steps (to −38, −8, +12, or +22 mV). We tested the degree of block by a given concentration of TTX in each cell because it varied somewhat from cell to cell; on average, the sodium current in Purkinje neurons and cortical interneurons was somewhat more sensitive (block by 90 nM TTX to 14 ± 6 % (n=7) in Purkinje neurons, 15 ± 9% (n=5) in cortical interneurons, 26 ± 9 % (n=8) in cortical pyramidal neurons, 22 ± 9% (n=8) in CA1 pyramidal neurons). The current elicited by the action potential waveform was recorded in the partially-blocking concentration of TTX, and seconds later the cell was moved into a solution containing 1 µM TTX which completely blocked the sodium current. The action potential-evoked sodium current was obtained by subtraction of the records with partially-blocking and fully-blocking TTX (after signal-averaging 12 sweeps in each condition) and was then scaled up to that expected in the absence of TTX, using the scaling factor determined experimentally in that cell by the effect of the partially-blocking TTX on step-evoked sodium current. As shown in Figure 1–Figure 4, the scaling procedure resulted in a sodium current that superimposed well with the predicted current from −C*dV/dt during the initial rising phase of the action potential.
Figure 8. Tests for voltage control in dissociated Purkinje neurons under whole-cell voltage clamp at 37 °C.
(A) Cell membrane behaves as a single compartment. The decay of a capacity transient elicited by a step from −83 to −88 mV in a Purkinje neuron, before applying compensation for cell capacitance and series resistance (black, signal averaged from 3 traces), is fit well by a single exponential (red), consistent with a single compartment. Cell capacitance was 18 pF, input resistance was 1.0 GΩ, and series resistance was 4.2 MΩ. (B) Test of fidelity of voltage clamp using a second electrode to measure voltage. A Purkinje neuron was voltage clamped with an action potential waveform (Vcomm, previously recorded in a different Purkinje neuron). Current was first recorded in an external solution containing 90 nM TTX (red) and then with TTX increased to 1 µM TTX to completely block sodium current (blue). A second pipette in whole cell current clamp mode recorded voltage (V2). Current records were signal-averaged from 12 traces in each concentration of TTX (raw current records are shown, without correction for residual capacity current remaining after imperfect compensation for pipette and cell capacitance). Lower current trace shows sodium current as defined by subtracting the current in 1 µM TTX from that in 90 nM TTX. External solution contained 10 mM TEA to inhibit potassium current. Both electrodes (filled with the standard potassium methanesulfonate-based solution) had resistances of 2 MΩ. Current and voltage signals were both filtered with a 10 kHz (−3dB) 4-pole Bessel filter. The command voltage was applied to the amplifier without filtering but is shown after being passed through the same Bessel filter as the recorded voltage for comparison. In addition, the command voltage is plotted shifted 14 µs to the right in order to account for a lag in the recorded voltage and allow easier comparison on the waveforms.
To compare sodium entry using different action potentials applied to a particular cell, we used a method not requiring the cell's own action potential. This method was based on calculating the ratio of total sodium entry during the action potential (i.e. total integrated sodium current) to the entry occurring during the rising phase, integrated from threshold (defined as 1% of the maximal dV/dt) up to the peak of the action potential. This method gave nearly identical values of sodium entry ratio as the first method in cases where both were used.
Action potential width was measured at half the action potential height, measured as the difference in membrane potential from the peak to the most negative voltage reached after the spike.
Test of voltage clamp fidelity
Because the experiments used brief action potential commands, we did a series of control experiments to test the accuracy with which the command waveform was imposed on the cell membrane. In these experiments, we used a second pipette to record membrane potential while a Purkinje neuron was voltage clamped with an action potential command with the first electrode. Figure 8B shows an example. The command waveform was a typical action potential waveform with (amplitude 89 mV, width 245 µsec) previously recorded from a Purkinje neuron (at 37 °C). When this command was used to clamp the neuron with the first electrode in voltage clamp mode, the voltage waveform recorded with the second electrode in current clamp mode was found to have a nearly identical waveform, both in an initial external solution containing 90 nM TTX (red) and after application of saturating TTX (1 µm, blue trace). In this cell, the waveform recorded with the second electrode reached a peak that was 3 mV more depolarized than the command waveform. In collected results from 7 experiments, the average absolute deviation of peak voltage (which occurred in both directions in different cells) was 1.8 ± 1.4 mV, and the average difference in action potential width at half-maximum height was 14 ± 17 µS, corresponding to change of 5 ± 7%). The small differences seen were generally consistent with those expected from series resistance errors (extra depolarization when net inward currents were flowing in the pipette and extra hyperpolarization when net outward currents were flowing). Although the recorded waveform in Figure 8B was nearly identical in shape to the command waveform, it occurred with a small time lag relative to the command waveform, even after accounting for the time lag (40 µS) resulting from the 10 kHz 4-pole Bessel filter through which the recorded voltage was measured. For the cell whose records are shown in Figure 8B, the extra time lag was 14 µS; for clarity in comparing the time course of the waveforms, the command waveform is shown after passage through the same Bessel filter as the measured voltage and has been additionally shifted right by 14 µS so that the times of peaks match. In collected results the lag of the recorded voltage relative to command voltage (after accounting for the effect of the external filter) was 22 ± 11 µS (n=7). This lag presumably reflects a delay in charging the capacitance of the cell by passing current through the series resistance of the pipette; this charging is speeded by the amplifier circuitry for series resistance compensation, but such compensation is imperfect.
Time-lag correction
It was not practical to routinely record membrane voltage with a second electrode, and it was also not necessary, since these control experiments showed that the voltage waveform is faithfully imposed on the cell, albeit with a small time lag. We used two approaches to quantify the lag between command voltage waveform and recorded current in cells without an independent voltage recording. In the first, we used current through GABAA receptor channels in the cell membrane to report cell membrane voltage. GABAA currents were elicited by application of muscimol (5 µM) while repetitively applying (every second) a voltage sequence that included a voltage ramp and an action potential waveform. GABAA currents were obtained by subtraction of currents before and after muscimol application, using an external solution that minimized currents through voltage-dependent channels (with TEA fully replacing sodium and 1 µM TTX). The current voltage relation for muscimol-evoked current (reversing at the chloride equilibrium potential of −65 mV) was determined by using a slow ramp (15 mV/ms) from −98 to +52 mV; with this slow change in voltage, the effect of the time lag is negligible. Then, the muscimol-evoked current evoked by a fast action potential waveform was converted to a plot of membrane voltage versus time using the function derived from the slow ramp as a look-up table. The resulting plot of membrane voltage versus time closely matched the imposed command voltage, but with a time lag. Performing this procedure in different cells, we measured time lags ranging from 35 to 95 µsec (63 ± 20 µsec, n=6) after taking account of the lag of 40 µsec from the 10 kHz Bessel filter the current signal was treated with. In the second approach to measuring the time-lag of the total system, we recorded sodium current evoked by an action potential waveform in an external solution in which sodium was reduced to 32 mM. The reversal potential for current through sodium channels is near +20 mV with this solution, so that with action potential peaks near +30 mV, the action potential-evoked sodium current is transiently outward near the peak of the action potential. The time at which the current reverses during the action potential voltage command waveform (on both upstroke and downstroke) can be aligned with the time the command waveform crosses the reversal potential. Using this method, we recorded time lags ranging between 35 to 110 µsec (79 ± 29 µsec, n=5), very similar to the first method. The, time lags measured with both methods were strongly correlated with residual uncompensated series resistance (Spearman rank correlation coefficient = 0.73, p<0.02, n=11). In both these methods, the time lag is measured using the recorded membrane current, which takes into account the entire system, not only the delay in charging the cell membrane but also lags resulting from the current-measuring part of the voltage-clamp circuit. Having established the relationship of the lag with uncompensated series resistance by these methods, we used it to estimate time lags in cells in which it was not measured directly by one of the two methods.
Statistics and fitting
All descriptive statistics presented are mean ± standard deviation. The non-parametric Mann-Whitney rank-sum test was used to compare sodium efficiency between cortical and Purkinje neurons. The Spearman rank correlation coefficient was used to test for correlation between action potential width and sodium efficiency.
Acknowledgments
Thanks to Zayd Khaliq and Gary Yellen for helpful suggestions and to Guilan Yao for help with mouse breeding. Supported by the National Institutes of Health (R01-NS36855). BCC was supported by an NIH predoctoral fellowship (F31-NS064630).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alle H, Roth A, Geiger JR. Energy-efficient action potentials in hippocampal mossy fibers. Science. 2009;325:1405–1408. doi: 10.1126/science.1174331. [DOI] [PubMed] [Google Scholar]
- Atwater I, Bezanilla F, Rojas E. Time course of the sodium permeability change during a single membrane action potential. J Physiol. 1970;211:753–765. doi: 10.1113/jphysiol.1970.sp009302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D, Laughlin SB. An energy budget for signaling in the grey matter of the brain. J Cereb Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Bean BP. The action potential in mammalian central neurons. Nat Rev Neurosci. 2007;8:451–465. doi: 10.1038/nrn2148. [DOI] [PubMed] [Google Scholar]
- Bezanilla F, Rojas E, Taylor RE. Sodium and potassium conductance changes during a membrane action potential. J Physiol. 1970;211:729–751. doi: 10.1113/jphysiol.1970.sp009301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chattopadhyaya B, Di Cristo G, Higashiyama H, Knott GW, Kuhlman SJ, Welker E, Huang ZJ. Experience and activity-dependent maturation of perisomatic GABAergic innervation in primary visual cortex during a postnatal critical period. J Neurosci. 2004;24:9598–9611. doi: 10.1523/JNEUROSCI.1851-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ. Intrinsic firing patterns of diverse neocortical neurons. Trends Neurosci. 1990;13:99–104. doi: 10.1016/0166-2236(90)90185-d. [DOI] [PubMed] [Google Scholar]
- Connors BW, Gutnick MJ, Prince DA. Electrophysiological properties of neocortical neurons in vitro. J Neurophysiol. 1982;48:1302–1320. doi: 10.1152/jn.1982.48.6.1302. [DOI] [PubMed] [Google Scholar]
- Contreras D, Palmer L. Response to contrast of electrophysiologically defined cell classes in primary visual cortex. J Neurosci. 2003;23:6936–6945. doi: 10.1523/JNEUROSCI.23-17-06936.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Haas V, Vogel W. Sodium and potassium currents recorded during an action potential. Eur Biophys J. 1989;17:49–51. doi: 10.1007/BF00257145. [DOI] [PubMed] [Google Scholar]
- Do MT, Bean BP. Subthreshold sodium currents and pacemaking of subthalamic neurons: modulation by slow inactivation. Neuron. 2003;39:109–120. doi: 10.1016/s0896-6273(03)00360-x. [DOI] [PubMed] [Google Scholar]
- Engel D, Jonas P. Presynaptic action potential amplification by voltage-gated Na+ channels in hippocampal mossy fiber boutons. Neuron. 2005;45:405–417. doi: 10.1016/j.neuron.2004.12.048. [DOI] [PubMed] [Google Scholar]
- Enomoto A, Han JM, Hsiao CF, Chandler SH. Sodium currents in mesencephalic trigeminal neurons from Nav1.6 null mice. J Neurophysiol. 2007;98:710–719. doi: 10.1152/jn.00292.2007. [DOI] [PubMed] [Google Scholar]
- Erisir A, Lau D, Rudy B, Leonard CS. Function of specific K(+) channels in sustained high-frequency firing of fast-spiking neocortical interneurons. J Neurophysiol 23. 1999;82:2476–2489. doi: 10.1152/jn.1999.82.5.2476. [DOI] [PubMed] [Google Scholar]
- Frankenhaeuser B, Huxley AF. The Action Potential in the Myelinated Nerve Fiber of Xenopus Laevis as Computed on the Basis of Voltage Clamp Data. J Physiol. 1964;171:302–315. doi: 10.1113/jphysiol.1964.sp007378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiger JR, Jonas P. Dynamic control of presynaptic Ca(2+) inflow by fast-inactivating K(+) channels in hippocampal mossy fiber boutons. Neuron. 2000;28:927–939. doi: 10.1016/s0896-6273(00)00164-1. [DOI] [PubMed] [Google Scholar]
- Hausser M, Clark BA. Tonic synaptic inhibition modulates neuronal output pattern and spatiotemporal synaptic integration. Neuron. 1997;19:665–678. doi: 10.1016/s0896-6273(00)80379-7. [DOI] [PubMed] [Google Scholar]
- Hille B. Common mode of action of three agents that decrease the transient change in sodium permeability in nerves. Nature. 1966;210:1220–1222. doi: 10.1038/2101220a0. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF, Katz B. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J Physiol. 1952;116:424–448. doi: 10.1113/jphysiol.1952.sp004716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson AC, Yao GL, Bean BP. Mechanism of spontaneous firing in dorsomedial suprachiasmatic nucleus neurons. J Neurosci. 2004;24:7985–7998. doi: 10.1523/JNEUROSCI.2146-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi Y. Physiological, morphological, and histochemical characterization of three classes of interneurons in rat neostriatum. J Neurosci. 1993;13:4908–4923. doi: 10.1523/JNEUROSCI.13-11-04908.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi Y. Physiological subgroups of nonpyramidal cells with specific morphological characteristics in layer II/III of rat frontal cortex. J Neurosci. 1995;15:2638–2655. doi: 10.1523/JNEUROSCI.15-04-02638.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawaguchi Y, Kubota Y. Correlation of physiological subgroupings of nonpyramidal cells with parvalbumin- and calbindinD28k-immunoreactive neurons in layer V of rat frontal cortex. J Neurophysiol. 1993;70:387–396. doi: 10.1152/jn.1993.70.1.387. [DOI] [PubMed] [Google Scholar]
- Keynes RD, Lewis PR. The sodium and potassium content of cephalopod nerve fibers. J Physiol. 1951;114:151–182. doi: 10.1113/jphysiol.1951.sp004609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kole MH, Letzkus JJ, Stuart GJ. Axon initial segment Kv1 channels control axonal action potential waveform and synaptic efficacy. Neuron. 2007;55:633–647. doi: 10.1016/j.neuron.2007.07.031. [DOI] [PubMed] [Google Scholar]
- Latham A, Paul DH. Spontaneous activity of cerebellar Purkinje cells and their responses to impulses in climbing fibres. J Physiol. 1971;213:135–156. doi: 10.1113/jphysiol.1971.sp009373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laughlin SB, Sejnowski TJ. Communication in neuronal networks. Science. 2003;301:1870–1874. doi: 10.1126/science.1089662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lennie P. The cost of cortical computation. Curr Biol. 2003;13:493–497. doi: 10.1016/s0960-9822(03)00135-0. [DOI] [PubMed] [Google Scholar]
- Lien CC, Jonas P. Kv3 potassium conductance is necessary and kinetically optimized for high-frequency action potential generation in hippocampal interneurons. J Neurosci. 2003;23:2058–2068. doi: 10.1523/JNEUROSCI.23-06-02058.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llinas R, Sugimori M. Electrophysiological properties of in vitro Purkinje cell somata in mammalian cerebellar slices. J Physiol. 1980;305:171–195. doi: 10.1113/jphysiol.1980.sp013357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martina M, Jonas P. Functional differences in Na+ channel gating between fast-spiking interneurones and principal neurones of rat hippocampus. J Physiol. 1997;505(Pt 3):593–603. doi: 10.1111/j.1469-7793.1997.593ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Connors BW, Lighthall JW, Prince DA. Comparative electrophysiology of pyramidal and sparsely spiny stellate neurons of the neocortex. J Neurophysiol. 1985;54:782–806. doi: 10.1152/jn.1985.54.4.782. [DOI] [PubMed] [Google Scholar]
- Mountcastle VB, Talbot WH, Sakata H, Hyvarinen J. Cortical neuronal mechanisms in flutter-vibration studied in unanesthetized monkeys. Neuronal periodicity and frequency discrimination. J Neurophysiol. 1969;32:452–484. doi: 10.1152/jn.1969.32.3.452. [DOI] [PubMed] [Google Scholar]
- Neher E. Correction for liquid junction potentials in patch clamp experiments. Methods Enzymol. 1992;207:123–131. doi: 10.1016/0076-6879(92)07008-c. [DOI] [PubMed] [Google Scholar]
- Nowak LG, Azouz R, Sanchez-Vives MV, Gray CM, McCormick DA. Electrophysiological classes of cat primary visual cortical neurons in vivo as revealed by quantitative analyses. J Neurophysiol. 2003;89:1541–1566. doi: 10.1152/jn.00580.2002. [DOI] [PubMed] [Google Scholar]
- Otis TS, Gilly WF. Jet-propelled escape in the squid Loligo opalescens: concerted control by giant and non-giant motor axon pathways. Proc Natl Acad Sci U S A. 1990;87:2911–2915. doi: 10.1073/pnas.87.8.2911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Resurgent sodium current and action potential formation in dissociated cerebellar Purkinje neurons. J Neurosci. 1997;17:4517–4526. doi: 10.1523/JNEUROSCI.17-12-04517.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Ionic currents underlying spontaneous action potentials in isolated cerebellar Purkinje neurons. J Neurosci. 1999;19:1663–1674. doi: 10.1523/JNEUROSCI.19-05-01663.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Gustafson AE, Padgett D. Ionic currents and spontaneous firing in neurons isolated from the cerebellar nuclei. J Neurosci. 2000;20:9004–9016. doi: 10.1523/JNEUROSCI.20-24-09004.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman IM, Bean BP. Inactivation and recovery of sodium currents in cerebellar Purkinje neurons: evidence for two mechanisms. Biophys J. 2001;80:729–737. doi: 10.1016/S0006-3495(01)76052-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy B, McBain CJ. Kv3 channels: voltage-gated K+ channels designed for high-frequency repetitive firing. Trends Neurosci. 2001;24:517–526. doi: 10.1016/s0166-2236(00)01892-0. [DOI] [PubMed] [Google Scholar]
- Shaw TI. Cation movements in perfused giant axons. J Physiol. 1966;182:209–216. doi: 10.1113/jphysiol.1966.sp007819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y, Yu Y, Yang J, McCormick DA. Selective control of cortical axonal spikes by a slowly inactivating K+ current. Proc Natl Acad Sci U S A. 2007;104:11453–11458. doi: 10.1073/pnas.0702041104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons DJ. Response properties of vibrissa units in rat SI somatosensory neocortex. J Neurophysiol. 1978;41:798–820. doi: 10.1152/jn.1978.41.3.798. [DOI] [PubMed] [Google Scholar]; Enomoto A, Han JM, Hsiao CF, Wu N, Chandler SH. Participation of sodium currents in burst generation and control of membrane excitability in mesencephalic trigeminal neurons. J Neurosci. 2006;26:3412–3422. doi: 10.1523/JNEUROSCI.5274-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taddese A, Bean BP. Subthreshold sodium current from rapidly inactivating sodium channels drives spontaneous firing of tuberomammillary neurons. Neuron. 2002;33:587–600. doi: 10.1016/s0896-6273(02)00574-3. [DOI] [PubMed] [Google Scholar]
- Thach WT. Discharge of Purkinje and cerebellar nuclear neurons during rapidly alternating arm movements in the monkey. J Neurophysiol. 1968;31:785–797. doi: 10.1152/jn.1968.31.5.785. [DOI] [PubMed] [Google Scholar]
- Wang LY, Gan L, Forsythe ID, Kaczmarek LK. Contribution of the Kv3.1 potassium channel to high-frequency firing in mouse auditory neurones. J Physiol. 1998;509:183–194. doi: 10.1111/j.1469-7793.1998.183bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]