Abstract
When signaling molecules diffuse through the cytosol they encounter a wide variety of obstacles that hinder their mobility in space and time. Some of those factors include, but are not limited to, interactions with mobile and immobile targets or obstacles. Besides finding a crowded environment inside the cell, macromolecules assemble into molecular complexes that drive specific biological functions adding additional complexity to their diffusion. Thus, simple models of diffusion often fail to explain mobility through the cell interior and new approaches are needed. Here we used fluorescent correlation spectroscopy to measure diffusion of three molecules of similar size with different surface properties diffusing in actin gels. The fluorescent probes were a) quantum dots, b) yellow-green fluorescent spheres and c) the β isoform of Ca2+ calmodulin-dependent protein kinase II tagged with green fluorescent protein. We compared various models for fitting the autocorrelation function (ACF) including single component, two-component, and anomalous diffusion. The two-component and anomalous diffusion models were superior and were largely indistinguishable based on a goodness of fit criteria. To better resolve differences between these two models, we modified the ACF to observe temporal variations in diffusion. We found in both simulated and experimental data, a transient anomalous subdiffusion between two freely diffusing regimes produced by binding interactions of the diffusive tracers with actin gels.
Introduction
Macromolecules inside cells must navigate the complex physical and chemical interactions therein to perform their essential functions.1, 2 This complexity leads to difficulty in interpreting measurements of intracellular diffusion. One experimental design to address this problem is to attempt to mimic the physical conditions of the crowded cytoplasm using various carbohydrate polymers.3-7 In contrast, globular proteins have been the preferred molecules to mimic the crowded conditions found inside the cell because of the possibility of capturing additional interactions not reflected using carbohydrate polymers.8 However, this raises additional complexity that thus far is still unresolved. Another experimental design is to use biopolymers that exhibit similar interactions as those found in the interior of a cell such as actin gels.9-11 The latter are well characterized and is the approach used in this report to create a matrix to examine probe diffusion with the possibility of both non-specific and specific interactions.
The biophysical properties of actin, such as viscosity, rigidity, elasticity, among others have been widely studied either in its globular (G) or filamentous (F) form.12 These studies have led to the idea that the actin network probably forms one of the main elements that give a viscoelastic property to the cytosol.13-16 Actin is one of the most abundant proteins found inside cells with an estimate of ~4 mg/ml, half being in the polymerized state. Actin monomers polymerize to form long filaments of 8 nm in diameter and in the absence of capping proteins have a persistence length, in vitro, of 5-26 μm.17 Close to 60 different classes of actin-binding proteins exist. Actin binding proteins along with actin constitute more than 25% of proteins in non-muscle cells, whereas in muscles this number rises to more than 60%.18 One of the most recent studied actin binding proteins is the β isoform of the Ca2+/calmodulin-dependent protein kinase II (βCaMKII). βCaMKII is a dodecameric enzyme found in abundance in the brain,19 and recently has been found to regulate the actin cytoskeleton at synapses 20, 21 likely through interactions with both G- and F-actin.22
One of our motivations for the present work is to understand how molecules such as CaMKII can diffuse through complex molecular networks. We have used fluorescent correlation spectroscopy (FCS)23 to understand how diffusion of probes of similar sizes are affected by G-actin and F-actin cross-linked with filamin. In addition to an eGFP-tagged version of βCaMKII, we also used yellow-green fluorescent spheres and quantum dots. These have similar dimensions to those of βCaMKII but their surface properties are defined by their coating. Quantum dots are coated with PEG 5000 that makes them inert and non-interactive. 24 Yellow-Green spheres are coated with a sulfate functional group giving them a negative charge at neutral pH. We discovered that these probes show distinctly different signatures in their FCS curves when diffusing in actin. Thus, we compared the results from fitting the autocorrelation function (ACF) with the most common models: the single component, two-component, and anomalous diffusion model. The two-component and anomalous diffusion models were superior and were largely indistinguishable based on a goodness of fit criteria. In attempts to gain additional insights into distinctions between these models, we modified the ACF to extract the mean square displacement (MSD) and post processed it to find the temporal diffusion spectrum. First, we validated this approach by generating ‘perfect’ FCS data using various models of the ACF and applying this inversion methodology. Then, we used Monte Carlo simulations to generate more realistic FCS data with a temporal reaction that slows the diffusion of the molecules. By applying this new methodology, we observed that diffusion is not a constant over the entire time domain except for the case of a single population diffusing at a fixed rate. In the case of molecules transitioning between two diffusion coefficients at a low rate we observed a transient behavior between the two freely diffusing modes. We called this regime transient subdiffusion because the transition between states follows a power law of Dapp(t)∝tα−1, where α is the anomalous exponent. Experimentally, the diffusion values at the beginning and end of the transient anomalous regime agrees relatively well with the values obtained using the two-component model. Therefore, this method of analysis provides an interesting bridge between two-component fitting models and the anomalous diffusion model that should find application in diffusion analysis in other complex environments. In the present paper, we examine the case of non specific binding of YG spheres with actin as an opportunity to test the idea of observing a transient slowing of diffusion due to the interaction between the spheres as they encounter the actin obstacles. We compared this experimental result with the case of specific binding between βCaMKII and actin, and with solely steric interactions of QDots in similar conditions.
The theory and analysis of FCS
In this section, we consolidate and revise details of work described previously that capture the analysis of the experimental work presented. Thus, we look at the well-known fundamental 23, 25 and recent application of (two-photon) FCS work 26-29 from a slightly different perspective.
It is important to recognize that an analytical solution of ACF cannot be achieved without prior approximations. We review the major assumptions required for the different cases of single component, two components, anomalous diffusion, and molecules undergoing a transition on diffusion that can be thought of as an ‘isomerization’ reaction while diffusing. We are going to refer to the latter case as transitional diffusion.
Mathematically, the ACF of the photon counts collected by a given detector is
| (1) |
where variation in the photon counts δi are due to concentration fluctuations as a measure of underlying molecular dynamics. Of course, the exact fluctuations pattern also depends on the spatial distribution of the illumination source, as well as the molecular brightness Qk of each fluorescent species. This is calculated over a period time, Δt, by
| (2) |
with n = 1 or 2 for single and two photon excitation, respectively. The average collected photons are given by , where C‾i is the ensemble average of the concentration of the reagent i. Thus, the fluctuation of the local concentration of the labeled molecules over a well-defined observation volume would give rise to the ACF that can be calculated as
| (3) |
with the observation volume usually described by a 3D Gaussian in the form of , which in Fourier space the Gaussian illumination is written as .
To solve the ACF (Eq 3) first we need to calculate the local variations in the concentration , or where needs to satisfy the diffusion equation.
Near equilibrium, the diffusion equation including chemical reactions of the species j can be computed by
| (4) |
which can be solved by applying a Fourier transform. After the transformation the diffusion equation can be expressed as
| (5) |
where,
| (6) |
Thus, the solution of the diffusion equation can be expressed in terms of the eigenvalues λ(s) and the corresponding eigenvectors X(s) for the transfer matrix Mlk = Tlk - Dlq2δlk like
| (7) |
With the needed factors defined, the ACF Eq. 3 can be rewritten in a form that will be used to study special cases below
| (8) |
Single component diffusion
The case of single component diffusion has the transfer matrix of rank one, and has a single eigenvalue λ=−Dq2 and eigenvector X=1. Substituting in Eq. 8 we obtain
| (9) |
which yields the known solution of the ACF of
| (10) |
N‾ = C‾V is the average number of molecules in the excitation volume V. The average concentration of the tracer is C‾, and the 3D Gaussian volume is defined as . τD is the characteristic time of diffusion and is the ratio of the axial over the radial waist of the illumination volume. From the characteristic time of diffusion, the diffusion coefficient D can be extracted as (n=2 for two photon excitation).
Two-component diffusion
A two-component model of diffusion is incorporated by presenting the matrix Mjk as
| (11) |
from which the derived eigenvalues are λ(1) = −D1q2 and λ(2) = −D2q2, with the eigenvectors and . Eq. 8 can be solved as the sum of each population of molecules diffusing at two discrete diffusion coefficients as;
| (12) |
This equation can be easily expanded to a mixture of p independent molecular species 29, 30. However, for most experimental cases it is not realistically possible to differentiate more than two populations by pure diffusion, thus its significance and use is limited unless combined with other tools such as the maximum entropy method. 30, 31
Anomalous Diffusion
The implementation of anomalous diffusion into the ACF that is most commonly used is based on solving a modified diffusion equation, Eq 4, that now is written as
| (14) |
where is called the propagator, or in other words the solution to the diffusion equation if considering a particle diffusing out of a point source. Other sophisticated approaches have been proposed using the fractional diffusion equation as a way to describe anomalous diffusion 32, but they will not be considered further in this paper. For now, anomalous diffusion is only characterized by a power law in time regardless of the underlying nature giving rise to such behavior. With this constraint a propagator needs to be constructed that not only satisfies the diffusion equation but also describes D(t) as a power law function in time. For that purpose the following propagator for three-dimensional diffusion was introduced by Wu and Berland 33
| (15) |
In this case D(t) has been replaced by the instantaneous diffusion Dins(t) that has the form of
| (16a) |
| (16b) |
were Γ is the transport coefficient. Dins(t) is the time-dependent slope of the MSD versus time or . The propagator in Eq. 15 is very similar to the one introduced by Weiss et al 34, with the difference being that instead of using the apparent diffusion, the instantaneous diffusion is used. Moreover, the most common way to express the mean squared displacement in time-dependant diffusion is
| (17) |
This form of the MSD differs from the typical form by having a temporal diffusion coefficient. From here on we will be using the apparent diffusion rather than the instantaneous diffusion, but in either case, the propagator needs to satisfy the diffusion equation.
The extraction of the autocorrelation function becomes straight forward if we use the solution obtained for the case of single component as described above with the implementation of D→Dapp(t). Thus, the eigenvalue and eigenvector are λ(t)=−Dapp(t)q2, X=1 respectively. With such constraints the ACF becomes
| (18) |
where with n being 2 for two photon excitation.
One needs to keep in mind that anomalous diffusion is considered when the Central Limit Theorem (CLT) of a random walker breaks down 35. Deviations on the CLT might come from long term correlations in the jump probability density function. These correlations result in broadening the distribution of jump length and jump time. Hence, one can define anomalous diffusion mainly in three ways: time-dependent diffusion 33, 36, 37, length-dependent diffusion 38, 39 and fractional dynamics. 40-43 In the FCS literature, the most common implementation of anomalous diffusion uses time-dependent diffusion as described in Eq. 14, where pure anomalous diffusion is characterized by a power law dependence with respect to time, Eq. 16. In most cases the assumption is that anomalous diffusion is observed throughout the entire time spectra. Experimental and computational results44-46 have shown that anomalous diffusion is expected only at shorter timescales but that at longer timescales diffusion is normal. Therefore, a more accurate description is that anomalous diffusion occurs only over a certain section of the time spectrum.
Transitional diffusion
A simplified model on how diffusion can change over time is to consider a reaction such as
| (19) |
where the two states represent two diffusion values of the molecule that exchange at rates defined by kAB and kBA. This could happen by spatial or temporal constraints on the molecule. For the purpose of this paper we have ignored the mechanism of such reaction and focused our attention on the temporal domain of this reaction.
The solution to Eq. 8 then becomes challenging particularly because an analytical solution of the ACF can only be solved in special circumstances. For example, to solve for the ACF considering the reaction in Eq. 19, the transfer matrix can be constructed as follows
| (20) |
The two eigenvalues (λ(s)) for this matrix are
| (21) |
with R = kAB+kBA, and
The eigenvectors associated with the eigenvalues above are where
| (22) |
When DA≠DB an analytical solution for Eq. 8 can only be found when one assumes that the reaction kinetics happen at much shorter timescales than diffusion, . . The eigenvalues for this system simplify to λ(+) = −q2D(+) and λ(−) = −(q2D(−) + R), where and ; D(+) represents the weighted average of the diffusion coefficient.
We can then expand Eq. 21 in terms of the parameter α to first order and assume that all higher orders do not contribute to the solution.
| (23) |
with .
In our experiments we assume no change in molecular brightness QA=QB or Q’=1, then the second term vanishes and the only contribution to the correlation function is given by the first term with a τD that reflects the average diffusion. However, if the molecular brightness of the state B is null QB=0. Then the second term in Eq. 23 will have a significant contribution and in particular its effect will show an exponential decay with a value corresponding to the time frame of the reaction.
When the assumption is not valid, there is no analytical solution to the correlation function and higher orders on the expansion over the parameter α will contribute to the decay function. We refer to this case as a weak interaction of the tracer with the environment. However, as the reaction rate R→0 (for both the forward and backward reaction constants) the problem would approach the case of non-interacting species. The extreme case for this is represented by Eq. 12. This means that at the limit of weak interaction a model of two components can be recovered.
Analysis of ACF
The analysis of ACFs mostly relies on minimizing an error function like . However, the goodness of fit criterion does not often lead to a clear distinction in choosing one model over another in interpreting the data. The two most commonly used models for the ACF, two-component and anomalous diffusion, are known to give similar fits based on this criterion. 3,4 To allow for a safer and more objective way to determine not only the ‘best fit’, but also the ‘best model’, we propose a numerical solution to the autocorrelation function in which the apparent diffusion as a function of time is extracted.
Diffusion spectrum
An attractive methodology to extract additional information from the data is to solve the normalized autocorrelation function as a non-linear function of the ‘ensemble’ mean squared displacement (MSD). To do so, we need to rewrite Eq. 10 in terms of the MSD. Using some simple algebra replacing , n=2 in the case of two-photon excitation, we obtain
| (24) |
A similar approach has been used extensively for dynamic light scattering in which MSD has been extracted and further analyzed 47, 48. The MSD from Eq. 24 provides us with an ensemble average behavior of the molecules that move through the PSF. For the present discussion, we remove the linear dependence of the MSD with time to differentiate the various models of diffusion described above.
If the diffusion coefficient is constant a numerical solution of Eq. 24 in terms of D(τ) would lead to a diffusion spectra that is constant over time. However, if diffusion varies with time as in the case of Eq. 17 then anomalous diffusion would be evident as an apparent power law of Dapp(τ) with respect to time. To further evaluate the use of the numerical solution of Eq. 24, we generated data from various ACF and asked the question: In which cases D(τ) can be applied?. We identify how the various models show an apparent diffusion as a function of time with particular temporal characteristics.
Materials and Methodology
Actin purification and Polymerization
Actin was purified from frozen rabbit skeletal muscle following a modified version of the one presented in reference 49. This purification procedure depends on the differential salt solubility of actin and myosin that comprise most of the protein of the contractile apparatus. Tropomyosin was removed by treating the F-Actin with increasing salt concentration and polymerized actin was collected via ultracentrifugation followed by dialyses to achieve a concentration of ~5 mg/ml in Buffer A (5 mM Tris, 0.2 mM CaCl2, 0.2 mM ATP, and 0.5 mM DTT at pH 8.0). Fractions were kept at −80°C until use. The purity of the preparations was assessed by running samples on an SDS-PAGE (data not shown).
The day of the experiment actin was brought to room temperature and diluted as desired. Solutions of G-actin were kept in globular form by diluting in the same Buffer A. F-Actin was produced by adding a polymerization inducer having a final concentration of 2 mM MgCl2, 1 mM ATP and 50 mM KCl at pH 8.0. Polymerization was permitted to proceed in the presence of filamin for 45 minutes before data acquisition to help insure complete polymerization. F-actin was cross linked with filamin at a molar ratio of filamin to actin of 1:300. Transmission electron micrographs of these solutions were used as a way to determine the morphology of the solution (data not shown).
Filamin purification
Filamin was purified from smooth muscle obtained from chicken gizzards essentially as described in reference 50. Approximately 50 g of smooth muscle was minced and homogenized in 5 mM EDTA, pH 7.0 with 5 mM dithiothreitol at 4°C using a Polytron blender and the homogenate was centrifuged at 18,000 x g for 30 min at 4°C. The pellet was then resuspended in 50 mM KH2PO4, pH 7.5, 600 mM KCl, 1 mM EDTA and 1 mM dithiothreitol again using the Polytron and after stirring for 10 min the sample was centrifuged at 100,000 x g for 30 min at 4°C. After filtering the supernatant through glass wool, the sample was dialyzed overnight against 50 mM KH2PO4, pH 7.5, 100 mM KCl, 1 mM EDTA and 1 mM dithiothreitol. The precipitate that formed was removed the next day by centrifugation at 100,000 x g for 30 min at 4°C. The supernatant was then subjected to two rounds of ammonium sulfate precipitation (35% final each time) and the final pellet was dissolved in 20 mM KH2PO4, pH 7.5, 100 mM KCl, 1 mM EDTA and 0.5 mM dithiothreitol and dialyzed against the same buffer overnight at 4°C. Residual insoluble material was removed by centrifugation at 100,000 x g for 30 min and then aliquots of the filamin enriched samples were stored as aliquots at −80°C. When analyzed by SDS-PAGE and Coomassie blue staining, the preparations were found to be ~70% filamin at this stage, with the other predominant component being actin.
eGFP-β CaMKIIpurification
eGFP-βCaMKII was produced in the baculovirus system exactly as described previously.22 Purification of the enzyme was accomplished by binding the enzyme to a CaM-Sepharose affinity column, washing, and then eluting the bound material with EGTA as described.51 The peak fractions were >90% pure when analyzed by Coomassie stained SDS-PAGE and were dialyzed into 20 mM HEPES, pH 7.4, 0.5 M NaCl, and 10% glycerol before storage in aliquots at −80°C.
Before use, purified eGFP-βCaMKII was thawed on ice and spun at 4°C and 14,000 rpm for 10 min to remove aggregates. The supernatant was then diluted into solutions of actin or buffer for FCS measurements.
Qdots and Fluospheres
Non-targeted Quantum dots (Qtracker® 565; 17 nm diameter) were purchased through qdot.com now part of Invitrogen, Inc. These nanocrystals have a surface modified with PEG-5000. PEG is an inert hydrophilic biologically compatible polymer with low non-specific binding. Yellow green fluorescent spheres (20 nm in diameter) from Molecular probes (Invitrogen, Inc.) are sulfate coated to make them hydrophilic. Both, Qdots and YG spheres were diluted in buffer solution and sonicated for 20 min to reduce aggregation before making measurements either in buffer or in actin solutions.
TPFCS
Two photon fluorescent correlation spectroscopy was achieved by using a pulsed Ti:Sa (Mira 900) laser pumped by a 5W Verdi laser. The wavelength was set at 850 nm with a pulse width of ~8 nm (130 fs). The beam was coupled to an inverted microscope (Olympus IX-71) with adaptive optics so that the back aperture of a water immersion objective (Olympus UPlanApo/IR 60X/1.20W) was overfilled. Samples were prepared and poured into 25 μl Ibidi chips (Integrated BioDiagnostics, Germany) with flat plastic bottoms compatible with FCS measurements. The epifluorescence was detected using a fiber optic tip through the left side port, whose output was coupled into an avalanche photodiode. More details on the system can be found in Iyer et al. and Sanabria et al..52, 53
Data analysis and simulation
Data of twenty consecutive takes of ten seconds each was collected via an external correlator board (correlator.com, NJ) and further analyzed using an in-house fitting GUI developed in MATLAB (The MathWorks, MA). In some experiments, Mathematica 4.2 (Wolfram Research Inc., IL) was used off-line to numerically solve the autocorrelation function.
The waist of the point spread function, ωxy2 = 397 nm and the structure parameter κ = 3.2 was experimentally calibrated with a known dye, Alexa 546, and then fixed as described elsewhere.7 Laser powers were kept below 5 mW when eGFP-βCaMKII was the sample. Laser power was further decreased when Qdots and YG spheres were used due to the high quantum yield of these molecules. This also minimizes blinking of the Qdots.24 In addition, traces where spikes in intensity were seen -indicating aggregates of the fluorescent tracer that were not eliminated by sonication or formed during the experiment- were eliminated from the data.
Simulated FCS data was generated using the program SimFCS 2.0 (LFD, University of California at Irvine) and is available at (http://www.lfd.uci.edu/globals/). For details of its use, we direct the reader to tutorials found at the same URL. For our purposes, this platform was helpful in generating test data from the various autocorrelation functions described above and to simulate raw data where specific parameters (diffusion coefficients of single or multiple species and or changes in photophysical properties) could be evaluated. Typical simulations were for 65 sec and to test photophysical phenomena, 100 molecules were introduced into a volume with cyclic boundary conditions. The 100 molecules were divided into different species depending on the demands of the simulation with parameters bounded by the experimental results presented in this paper. Specifically, we were interested in synthetic data when the main diffusion coefficient was ~15 μm2/s. Triplet state kinetics and photobleaching were modeled using a transitional diffusion reaction, Eq. 19, with state A being the emitting state with a brightness of 10 kcpmps and B not emitting. The forward and backward rates R were 106 s−1 to 104 s−1, respectively (see supplementary data for the results of these simulations). Two-component diffusion was simulated with two molecular species at various ratios and with same molecular brightness (10 kcpmps). The diffusion coefficient for species A was 15 μm2/s and species B was 1 μm2/s. Other isomerization reactions were considered using two molecular species with the same brightness moving at 15 μm2/s and 1 μm2/s. The point spread function in the simulation was assumed to have the same dimensions as that in the experimental set-up mentioned above. We also included simulated background counts (200 cpmps) that were slightly higher than those determined for our experimental set-up. This was done to evaluate the impact of noisy data on the numerical solution of the ACF. The simulated data were then evaluated in the same way as the experimental data.
Results
Simulated data from various ACF
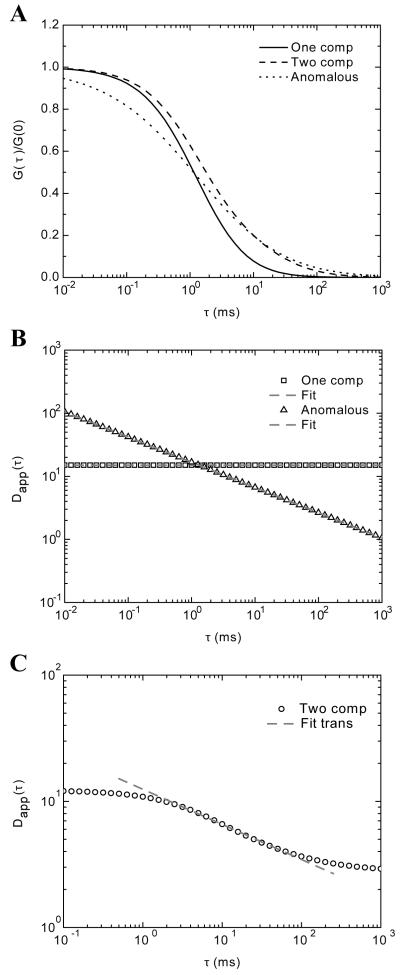
To test the implementation of the inversion methodology proposed in Eq. 24, we generated data using various models of the ACF. The goal was to determine the accuracy and reliability of the inversion process in ‘perfect’ conditions. We first modeled the case of single component diffusion with Eq. 10, anomalous diffusion with Eq. 18 and two-component diffusion with Eq. 12. In all cases, the experimental parameters for κ = 3.2, and ωxy = 397 nm were used. The diffusion for the single component was D1 = 15 μm2/s, and in the case of a second component the diffusion value was D2 = 1 μm2/s. For the anomalous diffusion α = 0.6. The differences in the autocorrelation data are as expected and are presented in panel A of Figure 1. With the generated data, we numerically inverted Eq. 24 to extract the MSD and then divided by 6τ to obtain the apparent diffusion over time, Dapp(τ). For the trivial case of single component diffusion, the expected return was a constant value, Dapp = 15 μm2/s, over the entire time spectra (Figure 1B). When the data generated using the anomalous ACF was inverted we obtained a linear decay function in the log-log plot. This represents a power law dependence with respect to time. We fitted the data with the model for and the extracted values were Γ = 6.33 μm2/sα and α = 0.6. These values were the ones used as the input to the simulation. We also fitted the single component diffusion data with the anomalous model and extracted an α=1 and Γ = 2.5 μm2/sα, which in turn give an apparent diffusion of Dapp = 15 μm2/s, as anticipated.
FIGURE 1.
Data generated from various ACF models. A) Single component, two component and anomalous diffusion autocorrelation data generated from Eq. 10, 12, and 18, respectively. B) The numerical inversion of Eq. 24 on the data generated from a one component ACF shows a flat temporal spectrum of the apparent diffusion (squares) that returns an apparent D of 15 μm2/s. The data generated from the anomalous diffusion ACF shows a power law dependence (triangles). The fitted values with a power law model are α= 0.6 and Γ = 6.33 μm2/sα. C) The result of numerical inversion for Dapp(t) for the case of data generated with the two-component model of the ACF Eq 12 is shown. This result shows a transition between two normal modes of diffusion. The transition region from x ms to x ms was fit with an anomalous diffusion model which returned an α = 0.72.
A not so obvious result is shown in Figure 1C. Here we use the ACF for two independent diffusion components and Dapp(τ) was extracted from Eq. 24. We observed two regions of normal diffusion one at shorter timescales, below 1 ms, and one at longer timescales, above 100 ms. However, the transition between them showed a power law dependence (fitted line in Figure 1C). When fitted with the same model for the anomalous diffusion, as done in the other two cases, α was 0.72, a value considered significant for anomalous subdiffusion. We have to keep in mind the artificial nature of these results. The ACF of Eq. 12 uses two single diffusion components with two different values of diffusion. The inversion methodology assumes only a single component whose diffusion is allowed to change over time.
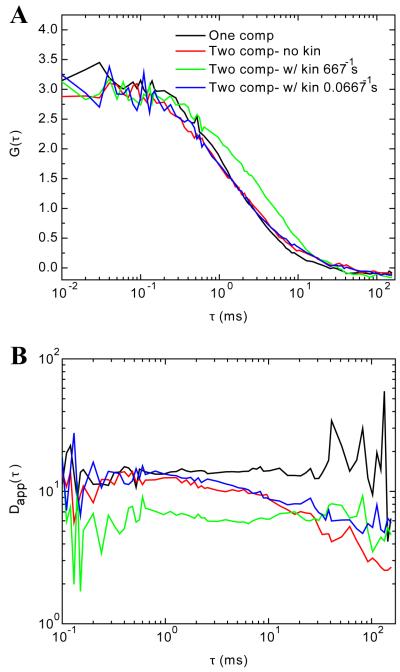
The interesting scenario would be if a single molecule would change its diffusion properties as a function of time. This case was tested using Monte Carlo simulations following the reaction described in Eq. 19. In which a transitional diffusion was achieved by allowing molecules to switch back and forth between two diffusion coefficients at a rate R. The goal of using Monte Carlo simulations is to realistically generate FCS data that would serve as anchor point for the experiments described in the following section. The simulated reactions consisted of 60 molecules in state A and 40 molecules in state B, except when only one population was simulated for which 100 molecules were considered. The chosen rates for simulation were at three particular cases: i) R = 0, ii) R1 = 667 s−1 and iii) R2 = 0.0667 s−1. R satisfies (DA-DB)/Rω2xy << 1 while R2 does not. Figure 2A shows the output FCS data of the single 65 s Monte Carlo simulations for all the cases mentioned above. The black curve shows one component FCS data, and the case of two populations of molecules diffusing at 15 μm2/s and 1 μm2/s is shown in red (Figure 2A). The FCS data where transitions between the two diffusing states is permitted for rates 667 and 0.0667 s−1 are shown in green and blue, respectively (Figure 2A). We purposely present noisy data from single simulation runs to show that even in those cases the extracted diffusion spectra show very different temporal characteristics. The Dapp(τ) spectra became smoother when 10 independent simulations were averaged together (data not shown). These trends are shown on panel B, where the Dapp(τ) for each of the autocorrelations shown on panel A was extracted. They are plotted using the same color code.
FIGURE 2.
FCS data generated with SimFCS. A) Shows the simulated data for either one diffusive component (black curve) and for the case of A↔B at three different conditions i) R = 0 (red curve), ii) R = 667 s−1 (green curve), and iii) R = 0.0667 s−1 (blue curve). Refer to the Methodology section for additional details concerning the simulations. Evaluating the ACF, the only significant difference is in the case of (ii) where the rate of transition of A↔B is on the same time scale as the transition time of the molecule through the focal volume. However, when Dapp(τ) is extracted there are clear differences in the spectra as shown in panel (B). The single component data (black trace) shows a flat line across the temporal spectrum as anticipated. With two component data (red trace) there is a period of normal diffusion at short timescales (<1 ms) which then shows a downward decay from 1-100 ms. When kinetics are added, where the rate of transition between two diffusing states is slow (0.0667 s−1; blue trace), we again see a region of normal diffusion that shows a downward trend up to ~100 ms. When the transition rate is fast (667 s−1; green trace), the curve is flat, as in the one component case (black curve) and the amplitude has decreased to reflect the average diffusion of the two components.
From the theory behind the reaction describing transitional diffusion, when (DA-DB)/Rω2xy << 1 and molecules keep their brightness, the ACF shows a constant weighted average of the Dapp(τ), this is observed in Figure 2B (green trace). When (DA-DB)/Rω2xy << 1 is not satisfied, Dapp is similar to the two components situation, compare the blue and red traces in Figure 2B. The two-component Monte Carlo simulation agrees well with the data generated for Figure 1. One difference, however, is that the software used to create the Monte Carlo simulations did not have the capacity to extend the length of the simulations to show the end of the Dapp spectrum, where Dapp appears constant again at times larger than 100 ms. As a conclusion, if there is a reaction where there is transient binding that slows the diffusion, the spectrum of Dapp(τ) will show a transition period between two regions of normal diffusion. This transition regime resembles the power law due to subdiffusion. For the moment it is worth noting that if this transition is long enough the power law can be fitted and an α value can be extracted. If one happens to choose the model of pure anomalous diffusion to fit the ACF (Eq 18), one is assuming anomalous diffusion over the entire time spectra, which is clearly not applicable in all cases. In conclusion, anomalous diffusion as measured by the slope in the log-log plot of D(τ) vs t is not constant over the entire spectrum independent of any variations on the specific value of the transport coefficient.
As hoped, extracting the diffusion spectrum reveals unique information in the time domain. The application of this inversion process would not be limited to cases of pure anomalous diffusion as shown in Figure 1B, but also to other deviations from normal diffusion, as generated with exchange reactions between two different diffusion values. In addition, one can also use this methodology to justify whether the use of the ACF with pure anomalous diffusion is appropriate, as they clearly show a distinct diffusion spectrum from one- or two-component diffusion.
Diffusion of Selected Fluorescent Tracers in Buffer
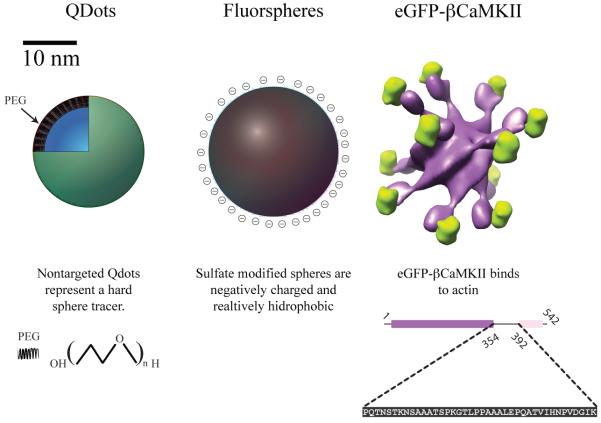
To establish experimental systems where diffusion with binding could be examined we took advantage of our previous experience with molecular diffusion in actin biopolymers.22 We used two non-biological tracers, Quantum Dots (Qdots) and Yellow Green (YG) fluorescent spheres, which are different in surface properties but are of similar size to each other (see Figure 3). Qdots are coated with PEG that provides an uncharged polar surface while the YG spheres are coated with a sulfate group making them negatively charged (see Figure 3). In addition, we used the β isoform of CaMKII which is a large protein complex made up of 12 identical subunits, each tagged with eGFP, known to interact with actin. A surface rendered model of eGFP-βCaMKII is shown in Figure 3. The linear amino acid sequence responsible for the actin binding for a single subunit 54 is highlighted below the surface rendered figure. eGFP-βCaMKII has been shown to bind up to 12 actin monomers. 22
FIGURE 3.
Cartoon representations of Quantum Dots, Yellow Green spheres and eGFP-βCaMKII and their respective surface properties. Quantum Dots from Invitrogen (Qtracker® 565) are coated with polyethylene glycol with a MW of 5000 Da. Fluorescent spheres are sulfate coated giving them an effective negative charge at neutral pH. A surface rendered model of eGFP-βCaMKII, (enhanced green fluorescent protein is shown in green, βCaMKII is shown in purple); below the structure, the linear sequence of amino acids, residues 354 to 392, of βCaMKII responsible for actin binding is shown 54. The individual molecules are shown scaled by the radius of gyration extracted from FCS (see Table 1).
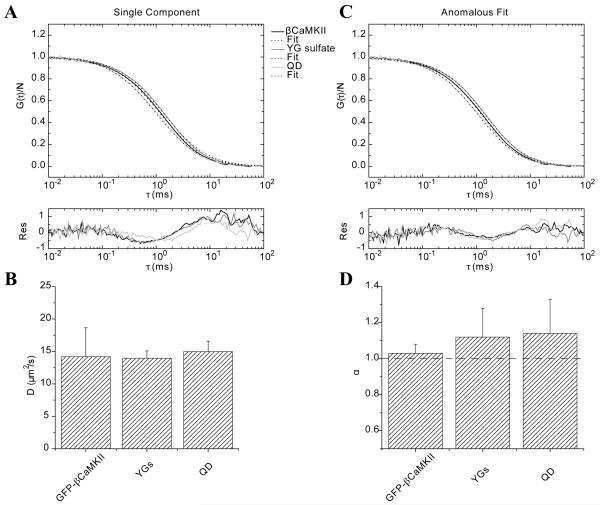
The first thing done experimentally was to characterize the diffusion of the fluorescent tracers in buffer and assure that triplet state, blinking or photobleaching were not apparent in the data at the power and wavelength settings used. FCS was accomplished with each sample in buffer. Each correlation consisted of ten consecutive 30 s takes that were averaged to reduce the choppy nature of experimental FCS data. All data were fit well with a single component model (Eq. 10) as expected, see Figure 4A. The residuals on the fits could be incrementally improved using the anomalous diffusion model (Eq. 18) as shown in Figure 4B for all three cases. The data in Table 1 show that the diffusion values recovered for each tracer obtained by the two fitting models is very similar. Panel 4C shows the diffusion at τ = τDa using the anomalous diffusion model averaged over three independent experiments accomplished on separate days. The anomalous exponent, averaged over three days, does not significantly change from the expected value of one (Figure 4D). The radius of gyration was computed using the experimentally determined D’s and the Stokes-Einstein relation (, where k is Boltzmann constant, and η is the viscosity). These values (Table 1) agree well with the expected size of the molecules and establish their diffusion characteristics in buffer that will serve as a baseline for comparison to diffusion in actin mixtures.
FIGURE 4.
Fluorescence correlation analysis of Quantum Dots (Qdots), YG spheres and eGFP-βCaMKII diffusing in buffer. A) Raw data and fits using a single component model and their residuals. B) Same data as that shown in panel A fitted with the anomalous diffusion model. Residuals show a slightly better fit than the single component model. C) The average diffusion at τDa coefficient of three independent experiments is plotted for each sample. The error bars represent the standard deviations. D) α exponent from the anomalous model fit for the same samples in buffer. A straight line at α=1 (normal diffusion) is shown as a reference.
Table 1.
Diffusion coefficients obtained by fitting FCS data with one-component and anomalous models for data presented in Figure 4A. The first column shows the diffusion values obtained from the single component fit and the second column corresponds to the calculated radii using Stokes-Einstein relationship. The diffusion at τDa, D(τDa), and the anomalous exponent for the same data is presented on the third and fourth columns of the table, respectively
| Sample | D (μm2/s) | Rh (nm) | D(τDa) (μm2/s) | α |
|---|---|---|---|---|
| Qdots | 19.5 | 12.5 | 18.6 | 1.05 |
| YGs | 14.1 | 17.3 | 13.7 | 1.07 |
| eGFP-βCaMKII | 16.3 | 15.0 | 16.0 | 1.01 |
Diffusion of Quantum Dots and Fluorescent Spheres through Actin Gels
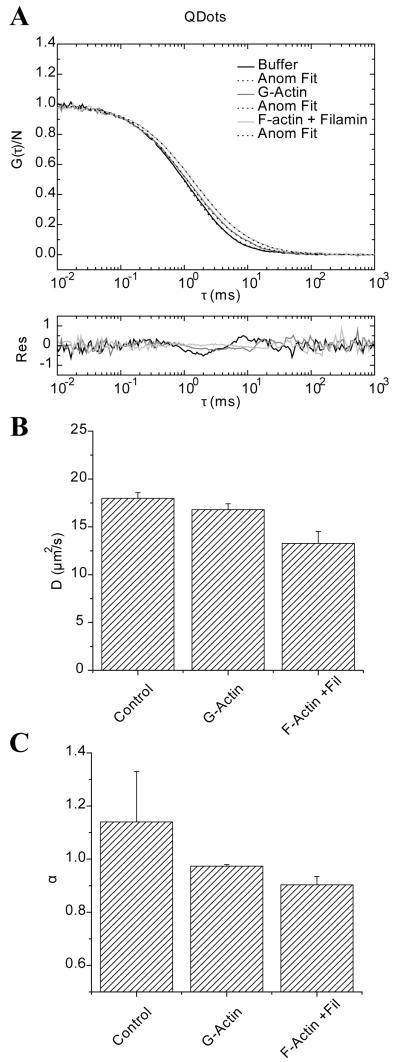
Qdots and YG spheres were used because of their similar radius of gyration but different surface characteristics. FCS was performed in G-actin (50 μM or ~ 2 mg/ml) or filamin cross-linked F-actin at a molar ratio of 1 filamin per 300 actin molecules (actin at 2 mg/ml). The actin meshwork size can be estimated using for a rod like polyelectrolyte 17, where CA is the actin concentration in mg/ml. For our particular polymerized solutions, ζ is on the order of ~ 200 nm without considering the filamin cross-linking agent, which would stabilize and most likely reduce the size of the pores in the actin meshwork 55. The raw data was fitted with both the anomalous diffusion model and the two-component model. In Figure 5A, we present the autocorrelation of Qdots in buffer, G-actin and the F-actin/filamin mix fit with the anomalous diffusion model. The residuals are shown below the plot. Qdots represent a non interacting tracer where in principle the diffusion coefficient at τ = τDa and the anomalous exponent would only be modestly affected by the obstacles presented by G-actin or F-actin. The autocorrelation shows a slight shift towards longer τ’s along with a subtle tilt of the decay function. For the particular data on panel A the diffusion at τ = τDa and anomalous exponent decrease from 16.4 μm2/s, α=1.14 in G-actin to 13.5 μm2/s, α=0.92 in the presence of cross-linked actin filaments. In panel B the mean value of the calculated diffusion coefficient (D; μm2/s) from three independent experiments are presented with the error bar representing the standard deviation. The same presentation is used for reporting the average of the anomalous exponent in panel C. It is important to note that the anomalous exponent is strongly related to the tilt of the fit to the autocorrelation observed in panel A.
FIGURE 5.
Fluorescence correlation spectroscopy of Quantum Dots in buffer, G-actin and F-actin cross linked with filamin. A) Raw data and fitting using the anomalous diffusion model. Residuals for each fit are shown below the plot. B) The average diffusion at τDa are presented and the error bars represent the standard deviation from three independent experiments. Panel C) shows the average and standard deviation of the anomalous exponent for the same samples.
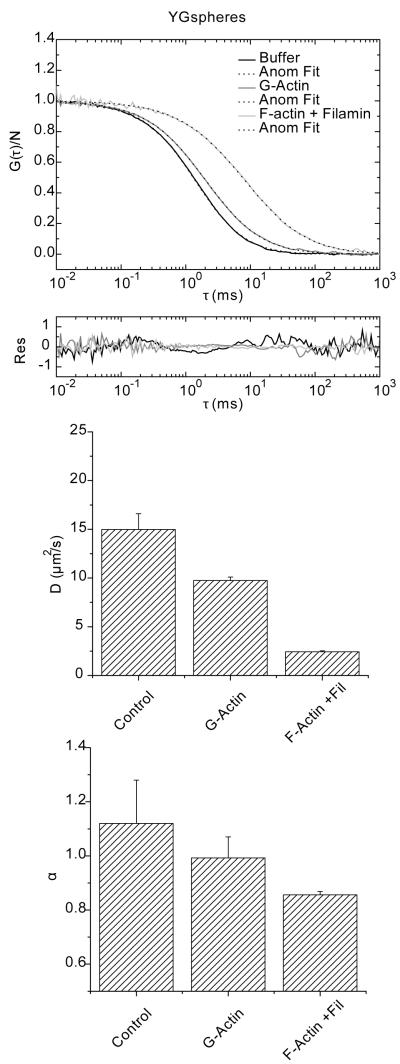
Figure 6A shows the autocorrelation plots of YG spheres in the same conditions as the Qdots. YG’s are negatively charged and they are expected to have electrostatic interactions with the actin matrix and thus a sub-diffusive behavior might be expected. This is evident by the strong right shift towards longer timescales on the autocorrelation, particularly for the case of F-actin/filamin. The residuals of the fit with the anomalous diffusion model are shown below the autocorrelation curves. The diffusion at τ = τDa shows that for the YG spheres the diffusion is the slowest with actin filaments cross-linked with filamin; rate of 2.4 μm2/s compared to 9.5 μm2/s in G-actin, with anomalous exponent of 0.85 and 0.94, respectively. The mean value of D for three independent measurements for the diffusion at τ = τDa and its standard deviation are shown in Figure 6B. In Figure 6C, the anomalous exponent shows a similar trend for both cases, with the lowest α value being found with the actin cross-linked with filamin.
FIGURE 6.
Fluorescence correlation spectroscopy of YG-spheres in buffer, G-actin and F-actin/filamin. A) Raw data and fitting with the anomalous diffusion model. Residuals for each fit are shown below the plot. B) The average diffusion at τDa are presented and the error bars represent the standard deviation from three independent experiments. Panel C) shows the average and standard deviation of the anomalous exponent for the same samples.
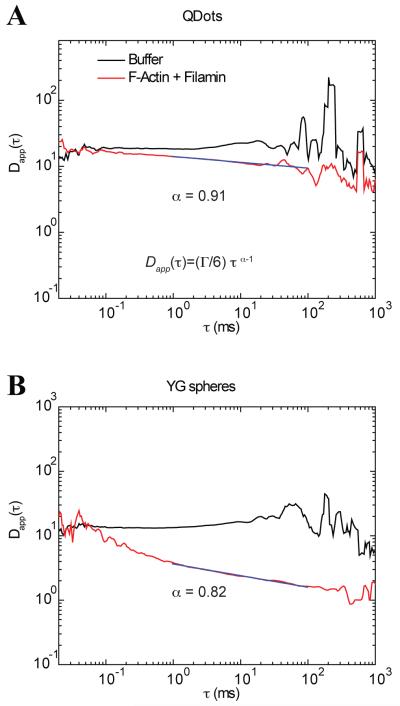
Next we used a different analytical approach to evaluate the temporal domain of diffusion. Using Eq. 24 we extracted the mean squared displacement as a function of time. For the presentation of the time dependence of diffusion, we divided the mean squared displacement of the time as . If the molecules diffuse freely, they will follow a linear relationship with respect to time and produce a flat line in plots of Dapp(τ) vs. τ as shown in Figure 1B. In Figure 7, we observe this behavior for both Qdots and YG spheres in buffer where the diffusion is flat from ~ 10 μs to 100 ms. The only regions at which they differ is at timescales larger than 100 ms, where fluctuations are observed that eventually show a slight decrease on the diffusion rate (Dapp(τ)). The noisy data from 50 ms and beyond is most likely due to the fewer points available to correlate at longer timescales. It is not immediately apparent what causes the slight downward trend in the plot beyond 200 ms. A different behavior is observed for the diffusion of Qdots and YG spheres in F-actin/filamin. For Qdots, fitting the ACF with the anomalous model returned an α=0.91. To examine which region of the spectrum obeyed this power law behavior, we identified the time domain which follows this power law by interactively expanding the time window while maintaining the α within 5% of its value (0.91 ± 0.045 in this case). The maximum temporal window which fit this criterion is shown by the solid line on top of the diffusion spectrum (Figure 7A). For Qdots the power law starts from values of Dapp(t) at ~15 μm2/s in buffer and reaches a lower limit of ~4 μm2/s in F-actin/filamin. If we compare the diffusion values using the two-component model, we find that the fastest component has a diffusion value of 18 μm2/s and the slowest component has a rate of 4 μm2/s (Table 2).
FIGURE 7.
Diffusion as a function of time of Qdots and YG spheres in buffer and in F-actin with filamin. A) Diffusion profile for Qdots in buffer shows a constant value for most of the time domain. For the case of Qdots in F-actin/filamin (red curve) there is a slight downward trend in the data. The fit of the same data to the anomalous model returned an α value of 0.91. This value was used to fit a line to the curve with extending end points until a deviation (> 0.05%) was detected and revealed that the spectral domain that fell within this criteria was from 1 to 100 ms (magenta line). B) Diffusion spectra of YG spheres under the same conditions as in panel A. In buffer, the profile is again flat for almost the entire time-domain. In F-actin/filamin the regime at which power law fit maintained an anomalous exponent of 0.82 ranges from 1-100 (magenta line).
Table 2.
Diffusion coefficients and percent population obtained by applying a two-component fitting model for data presented in panels A of Figures 5, 6 and 8.
| Sample | D1 (μm2/s) |
D2 (μm2/s) |
A1 (%) | A2 (%) |
|---|---|---|---|---|
| Qdots in F-actin/filamin | 18.1 | 4.0 | 79 | 21 |
| YGs in F-actin/filamin | 6.0 | 1.0 | 48 | 52 |
| eGFP-βCKII in G-actin | 21.6 | 0.8 | 65 | 35 |
| eGFP-βCKII F-actin/filamin | 30.2 | 6.0 | 52 | 48 |
A different temporal dependence is observed for the case of YG spheres in the F-Actin and filamin mix (Figure 7B). The diffusion at values < 0.1 ms fluctuates around a constant value similar to the one in buffer and then decays in what seems to be two components, one faster and one slower, to eventually fluctuate around a Dapp(τ) of 1 μm2/s. We called this transient subdiffusion, because the subdiffusive behavior covers only a fraction of the temporal spectrum. Using an analogous protocol to that described for Qdots, the time regime of 1 ms to 100 ms is the regime that the α value was maintained at 0.82. This timeframe is delimited by the black line on top of the red curve in Figure 7B. It is clear that the same power law will not hold at other timescales. In this particular example, the curved nature of the plot suggests that there is probably more than one mechanism that gives rise to subdiffusion of the YG spheres. These details would be missed simply by fitting the autocorrelation function with the anomalous diffusion model. It is clear that the main assumption of having a power law over the entire spectra when fitting the ACF with the anomalous model is not valid. Similarly, we can conclude that the two-component ACF does not fully represent this data. However, the two-component model seems to give the extremes of the diffusion values and the anomalous fit describes the power law behavior fitted between the two end points of the data. Importantly, the plots of Dapp(τ) vs. τ reveal at which timescales subdiffusion is observed and identifies transitions between normal and anomalous behavior.
Diffusion of eGFP-β CaMKII through Actin Gels
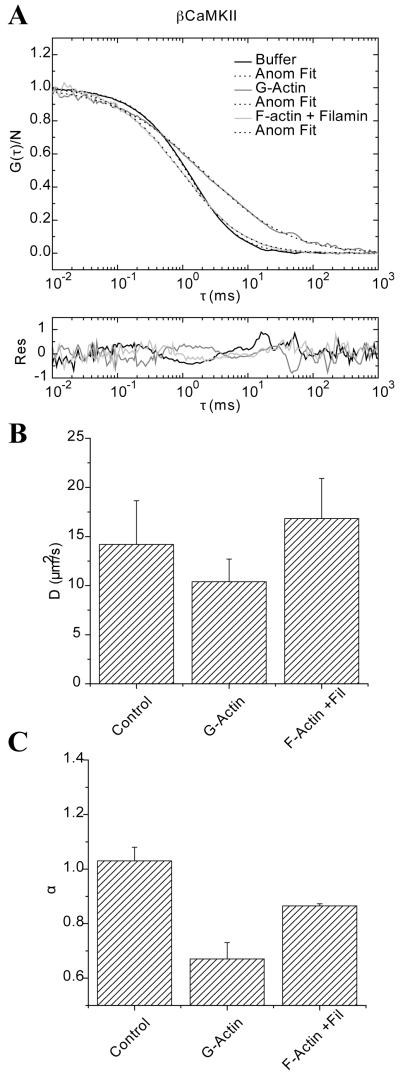
The third molecule that was studied was eGFP-βCaMKII. It was placed in similar solutions of G-actin and cross-linked actin filaments. The motivation to use this tracer is that it has a diffusion value in solution similar to the one found for the Qdots and the YG spheres. In addition, it is known that eGFP-βCaMKII binds to both G-actin and F-actin 22. These previous results identified that eGFP-βCaMKII can be fitted with a two-component model in the presence of actin. Thus, we wanted to compare how a specific interaction between the tracer and the media would affect the diffusion over time. In Figure 8A, we present the raw data and its fit with the anomalous model (Eq 18) for eGFP-βCaMKII diffusing in Buffer, in G-actin and in F-actin/filamin mix. The residuals are shown below the plot. It is clear that in the presence of G-actin the autocorrelation tails at longer τ’s as previously observed 22. This is not the case for eGFP-βCaMKII diffusing through the actin cross-linked with filamin. In this case, we see a change in the slope of the autocorrelation decay, but the apparent translational diffusion from the fits does not change significantly. As explained in an earlier publication 22, FCS is insensitive to the immobile pool of eGFP-βCaMKII that is tightly bound to F-actin/filamin. In Figure 8B the diffusion values are presented as calculated for Figures 4 and 5. The diffusion at τ = τDa value is slowed the most in the presence of G-actin (D(τDa) = 8.8 μm2/s, α=0.63), while in cross linked filaments diffuses at a rate of 13.9 μm2/s with an α = 0.87. The average α exponent in buffer is approximately 1, while the lowest value,0.67, is found in the presence of G-actin.
FIGURE 8.
Fluorescence correlation spectroscopy of eGFP-βCaMKII in buffer, G-actin and F-actin cross linked with filamin. A) Raw data and fitting using the anomalous diffusion model. Residuals for each fit are shown below the plot. B) The average apparent diffusion values in the same conditions are presented as bar plots. Day-to-day variations are shown as the error bars representing the standard deviation. Panel C) shows the average and standard deviation of the anomalous exponent for the same samples.
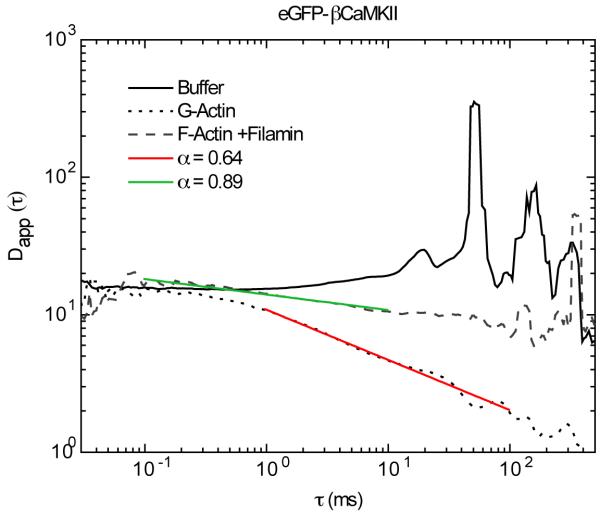
We then analyzed the same data by plotting Dapp(τ) vs. τ, as done in Figure 7 for the Qdots and YG spheres. Figure 9 shows the data for eGFP-βCaMKII in buffer, G-actin and F-actin/filamin. In buffer, eGFP-βCaMKII exhibits a constant diffusion value of ~16 μm2/s over most of the entire range of lag times (τ). Again, at timescales above 100 ms the noise increases in the data and a slight downward slope is evident as shown for the other tracers in buffer. In the presence of G-actin, the diffusion of eGFP-βCaMKII starts at values similar to the one in buffer up to lag times of ~1 ms. Then, there is a power law decay from a diffusion value of ~15 μm2/s to ~1 μm2/s. The transient power law between 1 ms to 100 ms is that which maintains an α value of 0.64 which was obtained using Eq 18 to fit the correlation functions. The diffusion spectra of eGFP-βCaMKII diffusing in F-Actin and filamin from lag times of 0.1 ms to 10 ms shows the α value that agrees with the anomalous model α=0.89. At longer timescales the fit gives values that are closer to one.
FIGURE 9.
Diffusion as a function of time of eGFP-βCaMKII in buffer, G-actin and in F-actin/filamin. The diffusion profile in buffer shows a constant value for most of the time domain but this does not hold true for diffusion in G-actin or F-actin/filamin. In G-actin the regime at which the power law fit maintained an anomalous exponent of 0.64 ranges from 1-100 ms (red line). The fit of βCaMKII in F-actin/filamin at which the power law fit maintained an anomalous exponent of 0.89 was over the time domain of 0.1 to 10 ms (purple line)
In summary our results indicate that the temporal diffusion of tracers with non-specific and specific interactions (Figures 7 and 9), show a transient subdiffusion that can be fitted with a power law between two freely diffusive modes. At shorter timescales, we find the fastest diffusion value of ~15 μm2/s while at longer timescales the diffusion decreases to the lower value obtained by the two-component fitting method. Specific and non-specific interactions lower the values for α, and slow the diffusion coefficient as observed with YG spheres and eGFP-βCaMKII while non-interacting tracers (Qdots) diffuse freely with just slight changes in the apparent diffusion and α value. The transition between these two modes of diffusion has been called in previous publications transient anomalous subdiffusion 46, 56.
Discussion
Impact of Specific, and Non-specific Interactions on Diffusion
We have measured the diffusion of three molecules of similar size with different surface properties diffusing in actin gels, and by comparing the various models for fitting the ACF we concluded that the two-component and anomalous diffusion models were superior and were largely indistinguishable based on a goodness of fit criteria. The two-component model is often preferred because of the viable physical interpretation of the identified components. For example, when there is specific binding it is easy to assign a second component to the bound fraction. However, the assumption made is that binding is strong such that the interaction lasts beyond the time that it takes for the complex to traverse the focal volume. In other cases, it is not as clear what the physical bases of the second component might be due to, because binding is not expected.7
To make a better decision on which model best describes the data, we proposed a modified version of the ACF to observe temporal variations in diffusion, Eq. 14. When we applied this inversion protocol to our data, we observed a transient anomalous subdiffusion between two freely diffusing regimes. First, we justified the use of this methodology by generating FCS data with known values and evaluated their diffusion spectra. Then, we used Monte Carlo simulations to generate FCS data using a simple, yet testable model for temporal variations of diffusion using an ‘isomerization’ like reaction for molecules exchanging diffusion rates at different timescales. In doing so, we observed that this model correctly captures the behavior observed experimentally, in particular for the case of slow reaction rates. Experimentally, this idea corresponds to a tracer that binds to actin filaments, or in other words when non-specific (electrostatic) interactions slow tracer diffusion, as the case of YG spheres in actin gels. Using Qdots we observed that steric interactions with the actin matrix did not produce this behavior as the Qdots diffused largely as they do when free in solution. Both cases show different characteristics on the diffusion spectra than the case of specific binding of βCaMKII and actin monomers.
One has to bear in mind that when dealing with specific (long-lived; slow dissociation rates) interactions, like that between βCaMKII and G-actin, the two-component fitting model should be valid. Thus, two independent diffusing components better describe the data rather than a time dependent diffusion spectra. We acknowledge that the simple transitional diffusion, where the diffusion of molecules switches from DA to DB, does not accurately describe the biochemistry in this example. This particular case is better depicted by a polynomial reaction of A+Bi→ABi 57, where actin (B) can bind with a stoichiometry of 12 monomers of actin to 1 holoenzyme of βCaMKII. 22 In spite of this, one can extract the diffusion spectrum to cases where binding interactions are poor and there is no analytical solution of the ACF for fitting. Thus, the extraction of Dapp(τ) still informs the decision making process relative to the validity of the chosen model.
Transient Anomalous Diffusion
To explain why we observed a transient subdiffusion in our data we note that, historically, three mechanisms have been identified which can produce anomalous diffusion: one is the presence of obstacles (above the percolation threshold), the second is the presence of binding interactions, and third is a system at non-equilibrium. 46, 56, 58. Saxton has additionally proposed that an infinite hierarchy of binding sites might generate pure anomalous diffusion. 46
The transient subdiffusion observed of YG spheres in actin gels is most likely due to transient binding instead of actin physically trapping the spheres, as has been recently proposed.59,56 This conclusion is based on the result that Qdots, which are approximately the same size as the spheres but have inert surface properties, do not show evidence of transient subdiffusion. Therefore, our results would tend to support the binding description of Saxton 46, and not hindrance within an immobile network as the cause of anomalous diffusion. However, the timescale at which we observe this transient behavior is shorter than predicted by Saxton. 46 Bronstein et al 60 used particle tracking of telomers in the nucleus and showed a transient anomalous subdiffusion up to 100 sec that agrees better with Saxton’s timescales. Other particle tracking and computational methods have observed this transition at longer timescales than the ones observed here.45, 46, 56, 58, 60, 61 We believe that the increased temporal resolution of FCS is an important factor in our ability to observe transient anomalous diffusion at shorter timescales than those found by particle tracking and imaging.45, 60, 62 However, one needs to keep in mind that FCS is a technique based on the temporal and ensemble averages of many more than one molecule, which restricts the ability to identify transient subdiffusion for each single molecule.
The transient subdiffusion observed for the case of the 12 subunit holoenzyme βCaMKII binding with a variable number of actin monomers could be an example of finite hierarchy of binding as proposed from the theoretical perspective by Saxton.46 In this case, the most plausible explanation for the normal diffusion at longer timescales, > 0.1 s, is that this corresponds to the motion of the saturated molecular complex formed between the G-actin and βCaMKII.
Moreover, it is striking that Eq. 18 is able to capture the subdiffusive behavior quite accurately in our experiments. Our data clearly shows that at timescales < 0.1 ms, molecules diffuse freely before interacting with targets or with obstacles. Upon interacting, from ~0.1 ms to ~100 ms, the molecules diffusive behavior decreases following a power law dependence which then relaxes again to normal diffusion on extended time scales. We propose that this phenomenology is likely a better description of what one would expect in measuring how molecules diffuse in complex solutions such as proteins inside cells.
Supplementary Material
Acknowledgement
We would like to thank Dr. Katrin Heinze for her suggestions on the theoretical FCS section. Also, we thank Dr. Yoshihisa Kubota for many insightful discussions on factors affecting diffusion. This work was supported by a grant from the NIH/NINDS R01 NS26086 (MNW). MNW also gratefully acknowledges an endowment from the William Wheless III Professorship. For a portion of this work, HS was supported by a training fellowship from the Keck Center Nanobiology Training Program of the Gulf Coast Consortia (NIH 2 R90 DK071054).
References
- 1.Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 2.Marsh BJ, Mastronarde DN, McIntosh JR, Howell KE. Structural evidence for multiple transport mechanisms through the Golgi in the pancreatic beta-cell line, HIT-T15. Biochem Soc Trans. 2001;29:461–467. doi: 10.1042/bst0290461. [DOI] [PubMed] [Google Scholar]
- 3.Dauty E, Verkman AS. Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: measurement by fluorescence correlation spectroscopy. J. Mol. Recognit. 2004;17:441–447. doi: 10.1002/jmr.709. [DOI] [PubMed] [Google Scholar]
- 4.Zhou YL, Liao JM, Chen J, Liang Y. Macromolecular crowding enhances the binding of superoxide dismutase to xanthine oxidase: implications for protein-protein interactions in intracellular environments. Int J Biochem Cell Biol. 2006;38:1986–1994. doi: 10.1016/j.biocel.2006.05.012. [DOI] [PubMed] [Google Scholar]
- 5.Banks DS, Fradin C. Anomalous diffusion of proteins due to molecular crowding. Biophys J. 2005;89:2960–2971. doi: 10.1529/biophysj.104.051078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lavalette D, Tetreau C, Tourbez M, Blouquit Y. Microscopic viscosity and rotational diffusion of proteins in a macromolecular environment. Biophys J. 1999;76:2744–2751. doi: 10.1016/S0006-3495(99)77427-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goins AB, Sanabria H, Waxham MN. Macromolecular Crowding and Size Effects on Probe Microviscosity. Biophys J. 2008;95:5362–5373. doi: 10.1529/biophysj.108.131250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zorrilla S, Hink MA, Visser AJ, Lillo MP. Translational and rotational motions of proteins in a protein crowded environment. Biophys Chem. 2006 doi: 10.1016/j.bpc.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 9.Hou L, Lanni F, Luby-Phelps K. Tracer diffusion in F-actin and Ficoll mixtures. Toward a model for cytoplasm. Biophys J. 1990;58:31–43. doi: 10.1016/S0006-3495(90)82351-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hou L, Luby-Phelps K, Lanni F. Brownian motion of inert tracer macromolecules in polymerized and spontaneously bundled mixtures of actin and filamin. J Cell Biol. 1990;110:1645–1654. doi: 10.1083/jcb.110.5.1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jones JD, Luby-Phelps K. Tracer diffusion through F-actin: effect of filament length and cross-linking. Biophys J. 1996;71:2742–2750. doi: 10.1016/S0006-3495(96)79467-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates Incorporated; 2001. [Google Scholar]
- 13.Janmey PA, Peetermans J, Zaner KS, Stossel TP, Tanaka T. Structure and mobility of actin filaments as measured by quasielastic light scattering, viscometry, and electron microscopy. J Biol Chem. 1986;261:8357–8362. [PubMed] [Google Scholar]
- 14.Palmer A, Mason TG, Xu J, Kuo SC, Wirtz D. Diffusing wave spectroscopy microrheology of actin filament networks. Biophys J. 1999;76:1063–1071. doi: 10.1016/S0006-3495(99)77271-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ruddies R, Goldmann WH, Isenberg G, Sackmann E. The viscoelasticity of entangled actin networks: the influence of defects and modulation by talin and vinculin. Eur Biophys J. 1993;22:309–321. doi: 10.1007/BF00213554. [DOI] [PubMed] [Google Scholar]
- 16.Ruddies R, Goldmann WH, Isenberg G, Sackmann E. The viscoelastic moduli of actin/filamin solutions: a micro-rheologic study. Biochem Soc Trans. 1993;21:37S. doi: 10.1042/bst021037s. [DOI] [PubMed] [Google Scholar]
- 17.Schmidt CF, Barmann M, Isenberg G, Sackmann E. Chain Dynamics, Mesh Size, and Diffusive Transport in Networks of Polymerized Actin. A Quasieleastic Light Scattering and Microfluorescence Study. Macromolecules. 1989;22:3638–3649. [Google Scholar]
- 18.Kreis T, Vale R. Guidebook to the cytoskeletal and motor proteins. Oxford University Press; Oxford; New York: 1999. p. xx.p. 551. [Google Scholar]
- 19.Erondu NE, Kennedy MB. Regional distribution of type II Ca2+/calmodulin-dependent protein kinase in rat brain. J Neurosci. 1985;5:3270–3277. doi: 10.1523/JNEUROSCI.05-12-03270.1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Okamoto K, Narayanan R, Lee SH, Murata K, Hayashi Y. The role of CaMKII as an F-actin-bundling protein crucial for maintenance of dendritic spine structure. Proc Natl Acad Sci U S A. 2007;104:6418–6423. doi: 10.1073/pnas.0701656104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Honkura N, Matsuzaki M, Noguchi J, Ellis-Davies GC, Kasai H. The subspine organization of actin fibers regulates the structure and plasticity of dendritic spines. Neuron. 2008;57:719–729. doi: 10.1016/j.neuron.2008.01.013. [DOI] [PubMed] [Google Scholar]
- 22.Sanabria H, Swulius MT, Kolodziej SJ, Liu J, Waxham MN. βCaMKII Regulates Actin Assembly and Structure. J Biol Chem. 2009;284:9770–9780. doi: 10.1074/jbc.M809518200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Magde D, Elson EL, Webb WW. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 1974;13:29–61. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 24.Michalet X, Pinaud FF, Bentolila LA, Tsay JM, Doose S, Li JJ, Sundaresan G, Wu AM, Gambhir SS, Weiss S. Quantum dots for live cells, in vivo imaging, and diagnostics. Science. 2005;307:538–544. doi: 10.1126/science.1104274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Elson EL, Magde D. Fluorescence correlation spectroscopy. I. Conceptual basis and theory. Biopolymers. 1974;13:1–27. doi: 10.1002/bip.1974.360130103. [DOI] [PubMed] [Google Scholar]
- 26.Schwille P, Heinze KG. Two-photon fluorescence cross-correlation spectroscopy. Chemphyschem. 2001;2:269–272. doi: 10.1002/1439-7641(20010518)2:5<269::AID-CPHC269>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 27.Berland KM, So PT, Gratton E. Two-photon fluorescence correlation spectroscopy: method and application to the intracellular environment. Biophys J. 1995;68:694–701. doi: 10.1016/S0006-3495(95)80230-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lamb DC, Schenk A, Rocker C, Scalfi-Happ C, Nienhaus GU. Sensitivity enhancement in fluorescence correlation spectroscopy of multiple species using time-gated detection. Biophys J. 2000;79:1129–1138. doi: 10.1016/S0006-3495(00)76366-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Krichevsky O, Bonnet G. Fluorescence correlation spectroscopy: the technique and its applications. Reports on Progress in Physics. 2002;65:251–298. [Google Scholar]
- 30.Sengupta P, Garai K, Balaji J, Periasamy N, Maiti S. Measuring size distribution in highly heterogeneous systems with fluorescence correlation spectroscopy. Biophys J. 2003;84:1977–1984. doi: 10.1016/S0006-3495(03)75006-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Modos K, Galantai R, Bardos-Nagy I, Wachsmuth M, Toth K, Fidy J, Langowski J. Maximum-entropy decomposition of fluorescence correlation spectroscopy data: application to liposome-human serum albumin association. Eur. Biophys. J. 2004;33:59–67. doi: 10.1007/s00249-003-0343-6. [DOI] [PubMed] [Google Scholar]
- 32.Lubelski A, Klafter J. Fluorescence correlation spectroscopy: the case of subdiffusion. Biophys J. 2009;96:2055–2063. doi: 10.1016/j.bpj.2008.10.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu J, Berland KM. Propagators and time-dependent diffusion coefficients for anomalous diffusion. Biophys J. 2008;95:2049–2052. doi: 10.1529/biophysj.107.121608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Weiss M, Elsner M, Kartberg F, Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bouchaud JP, Georges A. Anomalous diffusion in disordered media - statistical mechanisms, models and physical applications. Physics Rep. 1990;195:127–293. [Google Scholar]
- 36.Weiss M, Hashimoto H, Nilsson T. Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy. Biophys J. 2003;84:4043–4052. doi: 10.1016/S0006-3495(03)75130-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schwille P, Korlach J, Webb WW. Fluorescence correlation spectroscopy with single-molecule sensitivity on cell and model membranes. Cytometry. 1999;36:176–182. doi: 10.1002/(sici)1097-0320(19990701)36:3<176::aid-cyto5>3.0.co;2-f. [DOI] [PubMed] [Google Scholar]
- 38.Lacasta AM, Sancho JM, Romero AH, Sokolov IM, Lindenberg K. From subdiffusion to superdiffusion of particles on solid surfaces. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;70:051104. doi: 10.1103/PhysRevE.70.051104. [DOI] [PubMed] [Google Scholar]
- 39.Haugh JM. Analysis of reaction-diffusion systems with anomalous subdiffusion. Biophys J. 2009;97:435–442. doi: 10.1016/j.bpj.2009.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lubelski A, Klafter J. Temporal correlation functions of concentration fluctuations: an anomalous case. J Phys Chem B. 2008;112:12740–12747. doi: 10.1021/jp800242b. [DOI] [PubMed] [Google Scholar]
- 41.Metzler R, Klafter J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physics Rep. 2000;339:1–77. [Google Scholar]
- 42.Metzler R, Klafter J. Subdiffusive transport close to thermal equilibrium: from the langevin equation to fractional diffusion. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 2000;61:6308–6311. doi: 10.1103/physreve.61.6308. [DOI] [PubMed] [Google Scholar]
- 43.Kosztolowicz T, Dworecki K, Mrowczynski S. Measuring subdiffusion parameters. Phys Rev E Stat Nonlin Soft Matter Phys. 2005;71:041105. doi: 10.1103/PhysRevE.71.041105. [DOI] [PubMed] [Google Scholar]
- 44.Murase K, Fujiwara T, Umemura Y, Suzuki K, Iino R, Yamashita H, Saito M, Murakoshi H, Ritchie K, Kusumi A. Ultrafine membrane compartments for molecular diffusion as revealed by single molecule techniques. Biophys J. 2004;86:4075–4093. doi: 10.1529/biophysj.103.035717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Platani M, Goldberg I, Lamond AI, Swedlow JR. Cajal body dynamics and association with chromatin are ATP-dependent. Nat Cell Biol. 2002;4:502–508. doi: 10.1038/ncb809. [DOI] [PubMed] [Google Scholar]
- 46.Saxton MJ. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys J. 2007;92:1178–1191. doi: 10.1529/biophysj.106.092619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Berne BJ, Pecora R. Dynamic light scattering: with applications to chemistry, biology, and physics. Dover Pubns; 2000. [Google Scholar]
- 48.Pan W, Filobelo L, Pham ND, Galkin O, Uzunova VV, Vekilov PG. Viscoelasticity in homogeneous protein solutions. Phys Rev Lett. 2009;102:058101. doi: 10.1103/PhysRevLett.102.058101. [DOI] [PubMed] [Google Scholar]
- 49.Feuer G, Molnar F, Pettko E, Straub FB. Studies on the composition and polymerization of actin. Hung. Acta Physio. 1948;1:150–163. [PubMed] [Google Scholar]
- 50.Davies PJ, Shizuta Y, Pastan I. Purification and properties of avian and mammalian filamins. Methods Enzymol. 1982;85(Pt B):322–328. doi: 10.1016/0076-6879(82)85032-5. [DOI] [PubMed] [Google Scholar]
- 51.Putkey JA, Waxham MN. A peptide model for calmodulin trapping by calcium/calmodulin-dependent protein kinase II. J Biol Chem. 1996;271:29619–29623. doi: 10.1074/jbc.271.47.29619. [DOI] [PubMed] [Google Scholar]
- 52.Iyer V, Rossow M, Waxham MN. Peak two-photon molecular brightness of fluorophores is a robust measure of quantum efficiency and photostability. J. Opt. Soc. Am. B. 2006;23:1420–1433. [Google Scholar]
- 53.Sanabria H, Kubota Y, Waxham MN. Multiple diffusion mechanisms due to nanostructuring in crowded environments. Biophys J. 2007;92:313–322. doi: 10.1529/biophysj.106.090498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Swulius MT, Waxham MN. Ca(2+)/calmodulin-dependent protein kinases. Cell Mol Life Sci. 2008;65:2637–2657. doi: 10.1007/s00018-008-8086-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Stossel TP, Condeelis J, Cooley L, Hartwig JH, Noegel A, Schleicher M, Shapiro SS. Filamins as integrators of cell mechanics and signalling. Nat Rev Mol Cell Biol. 2001;2:138–145. doi: 10.1038/35052082. [DOI] [PubMed] [Google Scholar]
- 56.Saxton MJ. A biological interpretation of transient anomalous subdiffusion. II. Reaction kinetics. Biophys J. 2008;94:760–771. doi: 10.1529/biophysj.107.114074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kim SA, Heinze KG, Bacia K, Waxham MN, Schwille P. Two-photon cross-correlation analysis of intracellular reactions with variable stoichiometry. Biophys J. 2005;88:4319–4336. doi: 10.1529/biophysj.104.055319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Saxton MJ. Anomalous diffusion due to binding: a Monte Carlo study. Biophys J. 1996;70:1250–1262. doi: 10.1016/S0006-3495(96)79682-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Wedemeier A, Merlitz H, Wu CX, Langowski J. How proteins squeeze through polymer networks: a Cartesian lattice study. J Chem Phys. 2009;131:064905. doi: 10.1063/1.3205100. [DOI] [PubMed] [Google Scholar]
- 60.Bronstein I, Israel Y, Kepten E, Mai S, Shav-Tal Y, Barkai E, Garini Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys Rev Lett. 2009;103:018102. doi: 10.1103/PhysRevLett.103.018102. [DOI] [PubMed] [Google Scholar]
- 61.Saxton MJ. Anomalous subdiffusion in fluorescence photobleaching recovery: a Monte Carlo study. Biophys J. 2001;81:2226–2240. doi: 10.1016/S0006-3495(01)75870-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Martin DS, Forstner MB, Kas JA. Apparent subdiffusion inherent to single particle tracking. Biophys J. 2002;83:2109–2117. doi: 10.1016/S0006-3495(02)73971-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.