A Comprehensive Segmentation, Registration, and Cancer Detection Scheme on 3 Tesla In Vivo Prostate DCE MRI

Abstract

Recently, high resolution 3 Tesla (T) Dynamic Contrast-Enhanced MRI (DCE-MRI) of the prostate has emerged as a promising technique for detecting prostate cancer (CaP). Computer-aided diagnosis (CAD) schemes for DCE-MRI data have thus far been primarily developed for breast cancer and typically involve model fitting of dynamic intensity changes as a function of contrast agent uptake by the lesion, as done by schemes such as the 3 time point (TP) scheme. Non-linear dimensionality reduction schemes such as locally linear embedding (LLE) have been previously shown to be useful in faithfully embedding high dimensional biomedical data into a lower dimensional subspace while preserving the non-linear geometry of the data manifold. In this paper, we present a novel unsupervised detection scheme for CaP from 3T DCE-MRI that combines LLE and consensus clustering to discriminate between tissue classes at the image pixel level. The methodology comprises 3 distinct steps. First, a multi-attribute active shape model is used to automatically segment the prostate boundary from in vivo 3 T MR imagery. A robust multimodal registration scheme is then used to non-linearly align corresponding whole mount histological and DCE-MRI sections from prostatectomy specimens to determine the spatial extent of CaP. LLE followed by consensus clustering is finally used to identify distinct clusters. Quantitative evaluation on 21 histology-MRI slice pairs against registered CaP ground truth yielded a maximum CaP detection sensitivity of 60.72% and specificity of 83.24% while the popular 3TP scheme gave an accuracy of 38.22%.

1 Introduction

Prostatic adenocarcinoma (CaP) is the second leading cause of cancer related deaths among males in the United States, with an estimated 186,000 new cases in 2008 (Source: American Cancer Society). Recently, high resolution 3 Tesla (T) endorectal in vivo Dynamic Contrast-Enhanced MRI (DCE-MRI) has been shown to discriminate between normal and cancerous regions [1].

Most current efforts in computer-aided diagnosis of CaP from DCE-MRI via involve pharmacokinetic curve fitting based modeling approaches such as the 3 Time Point (3TP) scheme [2]. Based on the curve/model fits these schemes attempt to identify wash-in and wash-out points, i.e. time points at which the lesion begins to take up and flush out the contrast agent. Lesions are then identified as benign, malignant or indeterminate based on the rate of the dye uptake and wash out. The most recent work in this field is a supervised CAD scheme as demonstrated in Vos et al. [3] which analyzed only the peripheral zone of the prostate. Pharmacokinetic features derived from curve fitting [4] were used to train the model and coarse quantitative evaluation was performed based on a roughly registered spatial map of CaP on MRI. An accuracy of 0.83 was reported.

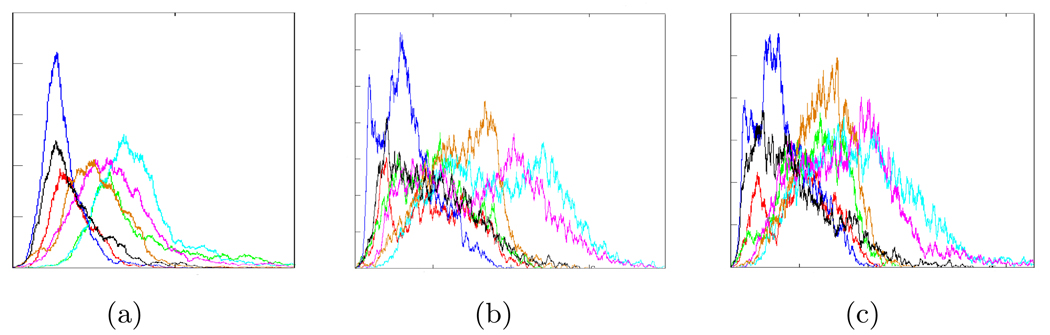
The 3TP and pharmacokinetic approaches are modeled on the dynamic MR image intensity profiles which we have previously shown suffers from intensity non-standardness [5] wherein MR image intensities do not have fixed tissue-specific meaning within the same imaging protocol, body region, and patient. Figures 1(a), (b), and (c) show the image intensity histograms for the non-lesion areas within 7 3T in vivo DCE-MRI prostate studies for timepoints t = 2, t = 4, and t = 6 respectively. Figures 1(a)–(c) show the intensity drift in the MR images and apparent mis-alignment of the intensity histograms. Non-linear dimensionality reduction methods such as locally linear embedding (LLE) [6] have been shown to faithfully preserve relative object relationships in biomedical data from the high- to the low-dimensional representation. Previously, Varini et al. [7] have performed a visual exploratory analysis based on applying different dimensionality reduction methods, including LLE on breast DCE-MRI data to differentiate between benign and malignant lesions. LLE was found to be relatively robust and accurate in this characterization as compared to results from application of linear methods such as Principal Component Analysis (PCA).

Fig. 1.

Image intensity histograms for non-cancerous regions in 7 in vivo 3 T DCE-MRI prostate studies at time points (a) t = 2, (b) t = 4, and (c) t = 6. A very obvious misalignment between the MR intensity histograms across the 7 DCE-MRI studies is apparent at multiple time points.

In this paper we present a comprehensive segmentation, registration detection scheme for CaP from 3T in vivo DCE-MRI imagery that has the following main features, (1) a multi-attribute active shape model [8] is used to automatically segment the prostate boundary, (2) a multimodal non-rigid registration scheme [9] to map CaP extent from whole mount histological sections onto corresponding DCE-MR imagery for radical prostatectomy studies, and (3) an unsupervised CaP detection scheme involving LLE on temporal intensity profiles at every pixel followed by consensus clustering [10] in the reduced dimensional space. Our proposed methodology is evaluated on a per-pixel basis against registered spatial maps of cancer on MRI. Additionally, we quantitatively compare our results with those obtained from the 3TP method for a total of 21 histology-MRI slice pairs.

2 Experimental Design

2.1 Data description and Notation

A total of 21 3 T in vivo endorectal MRI (T2-weighted and DCE protocols) images with corresponding whole mount histological sections (WMHS) following radical prostatectomy were obtained from 6 patient datasets from the Beth Israel Deaconess Medical Center. The DCE-MRI images were acquired during and after a bolus injection of 0.1 mmol/kg of body weight of gadopentetate dimeglumine using a 3-dimensional gradient echo sequence (3D-GE) with a temporal resolution of 1 min 35 sec. Following radical prostatectomy, the prostate was sectioned into whole-mount sections which were stained via Haemotoxylin and Eosin (H & E) and then examined by a trained pathologist to accurately delineate the presence and extent of CaP .

We define a 2D DCE-MRI image C^D,t = (C, f^D,t) where C is a set of spatial locations c ∈ C and t ∈ {1,…, 7}. f^D,t(c) represents the intensity value at location c ∈ C at timepoint t. We define a 2D T2-weighted (T2-w) MRI image as C^T2 = (C, f^T2) and the corresponding WMHS as C^H · G(C^H) is defined as the set of locations in the histology scene C^H that form the spatial extent of CaP (”gold standard”).

2.2 Automated prostate segmentation on in vivo MRI imagery

We have recently developed a multi-attribute, non-initializing, texture reconstruction based active shape model (MANTRA) [8]. Since MANTRA operates within a multi-resolution framework, only a rough initialization (such as a bounding-box) around the prostate is required to be able to segment the prostate accurately. The algorithm comprises the following main steps:

• Step 1: During the training step, a statistical shape model is generated by performing PCA on expert selected landmarks along the prostate border.

• Step 2: A patch of pixels is sampled from the area surrounding the prostate border formed by these landmark points for each training image. PCA is then performed across these patches to generate a statistical texture model for each landmark point.

• Step 3: To segment a new image, regions within are searched for the prostate border. Any potential location for the border has a patch of pixels sampled. The pixel intensity values within this patch are reconstructed from the texture model as best as possible, and mutual information is maximized between the reconstruction and the original patch to find the optimal border location. The shape model is fit to these border locations, and the process repeats until convergence of the active shape model algorithm (ASM).

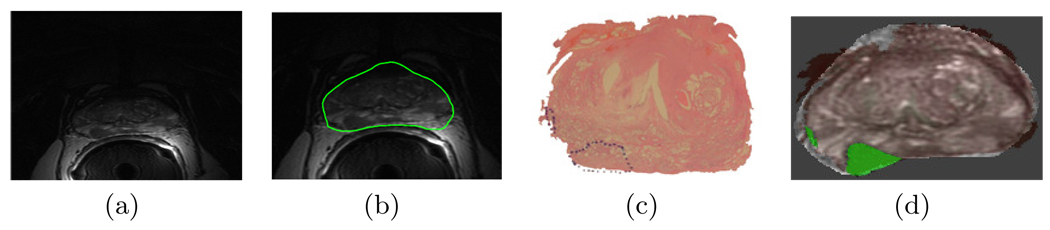
Unlike traditional ASMs MANTRA does not require model initialization and makes use of: (1) local texture model reconstruction to overcome limitations of image intensity, (2) multiple attributes with a combined mutual information metric. Figure 2(a) shows an original sample image C^T2. The final segmentation of the prostate boundary via MANTRA is seen in Figure 2(b). Similarly, MANTRA is applied to segment the prostate boundary for images C^D,t, t ∈ {1,…, 7}.

Fig. 2.

(a) Original 3 T in vivo endorectal T2-w prostate MR image C^T2, (b) prostate boundary segmentation via MANTRA in green, (c) corresponding WMHS C^H with CaP extent G(C^H) outlined in blue by a pathologist, (d) result of registration of C^H to C^T2 visualized by an overlay of C^H onto C^T2. The CaP extent on C^T2 (G^r(C^T2 )) is highlighted in green.

2.3 Establishment of Ground Truth on DCE-MRI via Elastic Multimodal Registration of Histology, T2-w, and DCE-MRI

To estimate the gold standard for spatial extent of CaP on DCE-MRI, we map the spatial extent of CaP determined from WMHS G(C^H) onto DCE-MRI via a multi-step elastic registration procedure which comprises the following steps:

1. Initial affine alignment of C^H to corresponding C^T2 using our previously presented registration technique, combined feature ensemble mutual information (COFEMI) [9], to incorporate multiple feature images for robustness to modality differences.

2. Elastic registration using thin plate splines (TPS) warping of C^H (Figure 2(c)) to correct for non-linear deformations from endorectal coil in C^T2 (Figure 2(b)) and histological processing. TPS warping is based on selected control points representing salient anatomical landmarks on both modalities.

3. Having put the underlying tissue represented by the pixels in C^T2 and C^H into spatial correspondence, mapping of histological cancer extent G(C^H) onto C^T2 to obtain G^r(C^T2 ) via the transformation r determined in (1) and (2).

4. Affine alignment of C^T2, on which CaP extent has now been mapped to C^D,0 using MI-based registration to correct for subtle misalignment and resolution mismatch between the MR protocols. It is known that C^D,t, t ∈ {1,…, 7} are in implicit registration, and therefore no alignment need be done between timepoints.

5. Mapping of histology-derived cancer ground truth G^r(C^T2 ) from registered C^T2 (Figure 2(d)) onto C^D,t to obtain G^R(C^D,t) via the transformation R determined in (3).

2.4 Classification of DCE data via LLE and Consensus Clustering

Locally Linear Embedding (LLE)

For each pixel c within each DCE-MRI image C^D,t, there is an associated intensity feature vector F(c_i) = [f^D,t(c_i)|t ∈ {1,…, 7}], c_i ∈ C, i ∈ {1,…, |C|} where |C| is the cardinality of C. The result of LLE [6] on the set F = {F(c₁) ,F(c₂) ,…, F(c_p)}, p = |C| of high-dimensional intensity feature vectors is the set of lower dimensional embedding vectors χ = {X_LLE (c₁) ,X_LLE (c₂) ,…,X_LLE (c_p)}. Let {c_ηi(1),…, c_ηi(m)} be the m nearest neighbors of c_i where η_i(m) is the index of the m^th neighbor of c_i in C. The feature vector F (c_i) and its m nearest neighbors (mNN), {F (c_ηi(1)) , F (c_ηi(2)) ,…, F (c_ηi(m))} are assumed to lie on a patch of the manifold that is local linearly, allowing us to use Euclidean distances between the neighbors. Each F (c_i) can then be approximated by a weighted sum of its mNN. The optimal reconstruction weights are given by the sparse matrix W_LLE (subject to the constraints W_LLE(i, j) = 0 if c_j does not belong to the mNN of c_i and ∑_j W_LLE(i, j) = 1) that minimizes

$${\mathit{\psi }}_1(W_{\mathit{\text{LLE}}})={{\displaystyle \sum _{i=1}^p\Vert \mathbf{F}(c_i)-{\displaystyle \sum _{j=1}^m{W}_{\mathit{\text{LLE}}}(i,{\mathit{\eta }}_i(j))\mathbf{F}(c_{\mathit{\eta }i(j)})}\Vert }}_2.$$ (1)

Having determined the weighting matrix W_LLE, the next step is to find a low-dimensional representation of the points points in F that preserves this weighting. Thus, for each F (c_i) approximated as the weighted combination of its mNN, its projection X_LLE (c_i) will be the weighted combination of the projections of these same mNN. The optimal χ_LLE in the least squares sense minimizes

$${\mathit{\psi }}_2({\chi }_{\mathit{\text{LLE}}})={\displaystyle \sum _{i=1}^p{\Vert X_{\mathit{\text{LLE}}}(c_i)-{\displaystyle \sum _{j=1}^p{W}_{\mathit{\text{LLE}}}(i,j)X_{\mathit{\text{LLE}}}(c_j)}\Vert }_2=\text{tr}({\mathit{\chi }}_{\mathit{\text{LLE}}}L{\mathit{\chi }}_{\mathit{\text{LLE}}}^{\mathrm{T}}),}$$ (2)

where tr is the trace operator, χ_LLE = [X_LLE (c₁) ,X_LLE (c₂) , …,X_LLE (c_p)],$L=(I-W_{\mathit{\text{LLE}}})(I-W_{\mathit{\text{LLE}}}^{\mathrm{T}})$ and I is the identity matrix. The minimization of (2) subject to the constraint ${\mathit{\chi }}_{\mathit{\text{LLE}}}{\mathit{\chi }}_{\mathit{\text{LLE}}}^{\mathrm{T}}=I$ (a normalization constraint that prevents the solution χ_LLE ≡ 0) is an Eigenvalue problem whose solutions are the Eigenvectors of the Laplacian matrix L.

Unsupervised classification via consensus k-means clustering

To overcome the instability associated with centroid based clustering algorithms, we generate N weak clusterings ${\tilde{V}}_n^1,{\tilde{V}}_n^2,\dots ,{\tilde{V}}_n^k,n\in \{0,\dots ,N\}$ by repeated application of k-means clustering for different values of k ∈ {3, …, 7} on the low dimensional manifold X_LLE(c), for all c ∈ C. As we do not know a priori the number of classes (clusters) to look for in the data, we vary k to determine upto 7 possible classes in the data. Based on accuracy values, we can then decide the correct number of classes that exist. As the number of elements in each cluster tends to change for each such iteration of k-means, we combine these clusters using the consensus clustering technique [10] via calculation of a co-association matrix H with the underlying assumption that pixels belonging to a natural cluster are very likely to be co-located in the same cluster for each iteration. H(i, j) thus represents the number of times c_i, c_j ∈ C were found in the same cluster over N iterations. If H(i, j) = N then there is a high probability that c_i, c_j do indeed belong to the same cluster. We apply MDS [11] to H followed by a final unsupervised classification via k-means to obtain the stable clusters $V_k^1,V_k^2,\dots ,V_k^q,q=k,k\in \{3,\dots ,7\}.$

3 Results

3.1 Qualitative Results

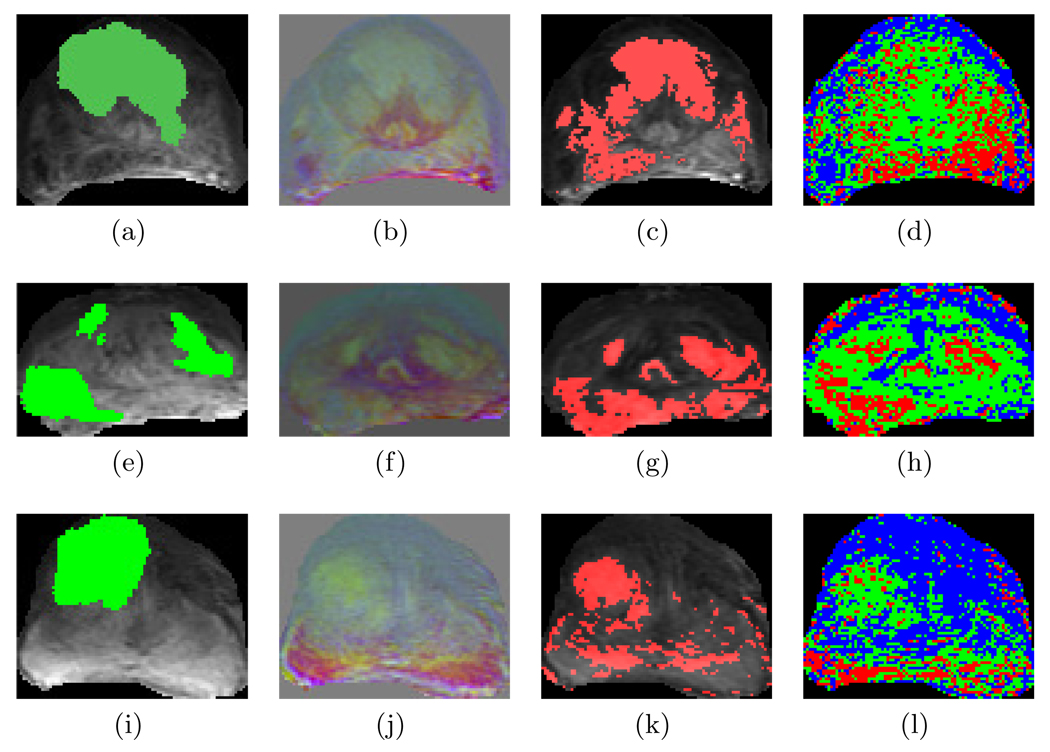
We have applied our scheme on 21 DCE-histology slice pairs. Representative results are shown in Figure 3 with each row corresponding to a different dataset. Corresponding histology sections (not shown) were registered to DCE-MRI data (C^D) to obtain the ground truth estimate G^R(C^D) shown in Figures 3(a), 3(e), and 3(i) highlighted in green. Figures 3(b), 3(f) and 3(j) show the RGB scaled values of X_LLE(c) at every c ∈ C. Hence similar colors in Figures 3(b), 3(f) and 3(j) represent pixels embedded close together in the LLE-reduced space. Each of the clusters $V_k^1,V_k^2,\dots ,V_k^q$ for each value of k ∈ {3,…, 7} are evaluated against G^R(C^D) and the cluster showing the most overlap is considered to be the cancer class. Figures 3(c), 3(g), and 3(k) show the result of plotting this label back onto the slice (in red). Additionally, the 3TP method was used to determine cancer extent on the same datasets. This method involves determination of inflection points within the intensity-time curves for each pixel which signify the wash-in and wash-out times of the contrast agent. Red, blue and green colors are then used to represent regions that are possibly cancerous, possibly benign and indeterminate respectively based on the ratio $w=\frac{\mathit{\text{Rate of wash}}–\mathit{\text{in}}}{\mathit{\text{Rate of wash}}–\mathit{\text{out}}}$of the contrast agent uptake. When w is close to 1, this implies the corresponding pixel is in a possibly cancerous area (red), when w is close to zero, this implies the pixel is in a possibly benign area (blue). For cases which do not fall under either of these, the pixel is said be in an indeterminate region (green). Results from the application of the 3TP scheme are shown in Figures 3(d), 3(h) and 3(l).

Fig. 3.

(a), (e), (i) showing the CaP extent G^R(C^D) on the DCE-MRI slice C^D high-lighted in green via registration with corresponding histology (not shown), (b), (f), (j) RGB visualization of the embedding coordinates from X_LLE onto the slice, (c), (g), (k) classification result from plotting the cluster in$V_k^1,V_k^2,\dots ,V_k^q$ that shows the highest overlap with the ground truth G^R(C^D) back onto the slice in red, (d), (h), (l) results from using the 3TP method on the DCE data. The improved correspondence of the regions labeled red in (c), (g), (k) with the ground truth regions shown in green in (a), (e), (i) over the red regions in the 3TP results in (d), (h), (l) can be seen.

3.2 Quantitative evaluation against registered CaP ground truth estimates on DCE

Within the consensus clustering framework, 5 separate classification results were achieved for k ∈ {3, 4, 5, 6, 7} (Table 1). For each of 21 slices, labels corresponding to the clusters $V_k^1,V_k^2,\dots ,V_k^q$ are each evaluated against the registered CaP extent on DCE-MRI (G^R(C^D)). The cluster label showing the largest overlap with the ground truth is then chosen as the cancer class. This class is used to calculate the sensitivity and specificity of our CAD system at a particular k value for the slice under consideration. The maximum sensitivity observed is 60.72% (k = 3) while the maximum specificity is 83.24% (k = 7). We see a reduction in sensitivity as k increases from 3 to 7, with a corresponding increase in specificity. Based on the change in sensitivity and specificity it is clear that k = 3 possible classes exist within the prostate MRI image. Using the 3TP technique (which assumes that only 3 classes can exist in the data), we achieve a sensitivity of 38.22%) and sensitivity of 69.12%. It can be seen that our proposed technique has an improved performance as compared to the existing 3TP method across k ∈ {3, 4, 5, 6, 7}.

Table 1.

CaP detection sensitivity and specificity at the pixel resolution averaged over 21 3 T DCE-MRI datasets. These are compared for different values of k within consensus clustering, as well as for the 3TP method.

	k=3	k=4	k=5	k=6	k=7	3TP
Sensitivity	60.72	51.14	48.55	42.50	42.78	38.22
Specificity	66.04	76.20	80.04	83.93	83.24	69.12

To put these results into context, Vos et al. [3] reported an accuracy of 0.83 in differentiation between non-malignant suspicious enhancing and malignant lesions in the peripheral zone of the prostate alone. Analyzing the reported values of sensitivity and specificity reveal that this sensitivity of 83% corresponds to a 58% specificity. These values have been achieved within a framework which utilized an approximation of the ground truth on MRI obtained by a rough registration of histology and MRI. Comparatively our metrics (60.72% sensitivity and 83.24% specificity) have been achieved when examining the whole of the prostate while utilizing a more rigorously registered CaP extent for evaluation. The difference in performance could be attributed to: (1) the larger region of interest (the whole of the prostate compared to the peripheral zone alone), (2) the more rigorous ground truth estimates obtained in this study via multimodal registration which were used for evaluation, and (3) the unsupervised approach to classification of the data.

4 Concluding Remarks

In this paper we have presented a novel integrated methodology for segmentation, registration, and detection of prostate cancer from 3 Tesla in vivo DCE prostate MR images. A multi-attribute multi-resolution active shape model-based segmentation scheme was used to automatically segment the prostate from in vivo DCE and T2-w images, following which a multimodal registration algorithm, COFEMI, is used to map spatial extent of CaP from corresponding whole mount histology to the DCE-MRI slices. Owing to the presence of MR image intensity non-standardness we utilized a non-linear DR scheme (LLE) coupled with consensus clustering to identify cancerous image pixels. An unsupervised approach was adopted owing to the lack of perfect slice correspondences between MRI and histology (due to different slice thicknesses). Our results, 60.72% CaP detection sensitivity and 83.24% specificity, compare very favourably with results obtained by Vos et al [3] as well as those obtained via the 3TP method. In comparison to Vos et al. [3] our methodology involves a larger region of interest (the whole of the prostate) for classification and a more rigorously determined ground truth estimate of CaP for evaluation. Future work will focus on validating our methodology on a much larger cohort of data.