Statistical Analysis of RNA Backbone

Abstract

Local conformation is an important determinant of RNA catalysis and binding. The analysis of RNA conformation is particularly difficult due to the large number of degrees of freedom (torsion angles) per residue. Proteins, by comparison, have many fewer degrees of freedom per residue. In this work, we use and extend classical tools from statistics and signal processing to search for clusters in RNA conformational space. Results are reported both for scalar analysis, where each torsion angle is separately studied, and for vectorial analysis, where several angles are simultaneously clustered. Adapting techniques from vector quantization and clustering to the RNA structure, we find torsion angle clusters and RNA conformational motifs. We validate the technique using well-known conformational motifs, showing that the simultaneous study of the total torsion angle space leads to results consistent with known motifs reported in the literature and also to the finding of new ones.

1 INTRODUCTION

Nucleic acid polymers play important roles in the storage and transmission of information. RNA can both encode genetic information and catalyze chemical reactions [9]. As the only biological macromolecule capable of such diverse activities, it has been proposed that RNA preceded DNA and protein in early evolution [2]. Over the past 15 years, the database of RNA conformation and interaction (the NDB [24]) has evolved rapidly or, to be more accurate, has exploded, in both size and complexity. The database has been transformed from tRNA and RNA oligonucleotides to moderately sized globular RNAs to massive complexes containing multiple large RNA molecules, many proteins, ions, water molecules, etc. These large complexes are a rich source of new information, but do not surrender to traditional methods of analysis. These complexes are of sufficient size that one can gather and analyze statistics that were not previously available. The development of techniques for discovering statistical rules governing RNA conformation and interaction will help answer fundamental biological and biochemical questions including those related to nonprotein enzymology and the origins of life. The goal here is to discover repetitive elements of interaction and conformation (motifs).

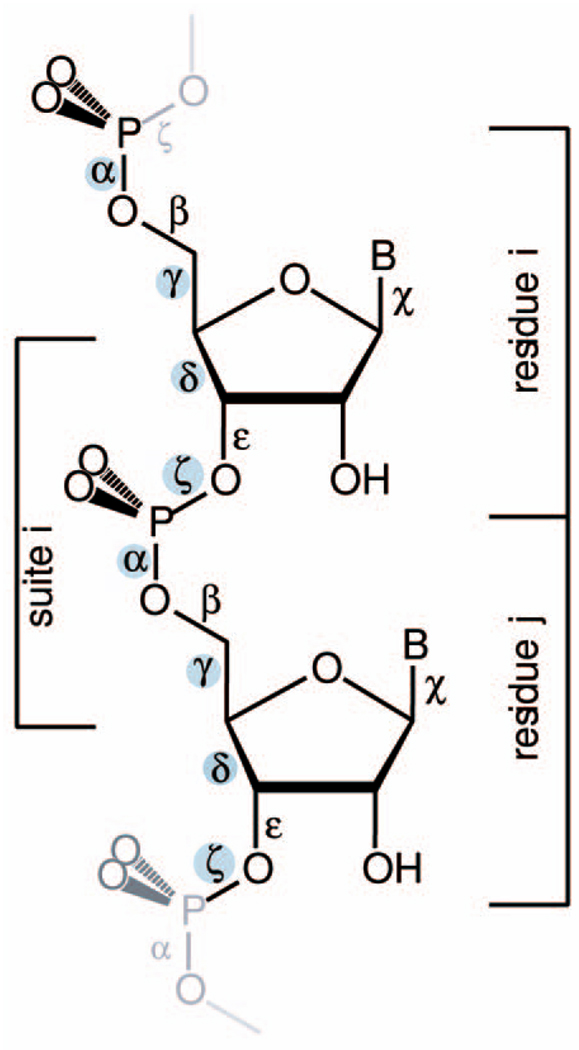
Murray et al. [20] noted the “rotameric” nature of RNA and articulated that RNA occupies an energy landscape governed largely by bond torsions. Torsion angles show clear frequency clustering, in one dimension. However, the analysis of RNA conformation presents particular problems. For protein backbones, for each amino acid residue, there are two torsional degrees of freedom: ϕ and ψ. Observed protein conformations are generally confined to limited regions of this two-dimensional space (Ramachandran plot) [26], [27]. For RNA, the dimensionality is much greater. For each nucleotide residue, there are seven independent torsion angles, see Fig. 1 and [29]. Each RNA residue has six backbone torsional angles and one angle χ that describes the rotation of the base relative to the sugar. The sugar has various puckering modes that are not independent of torsion angle δ. Differences in dimensionality are a distinguishing characteristic of RNA conformational analysis in comparison to protein conformational analysis.

Fig. 1.

RNA with six backbone and the glycosidic torsion angles labeled. The four identifier torsion angles are shaded. The two alternative ways of parsing out a repeat are indicated. A conventional nucleotide residue spans from phosphorous atom and 5’ oxygen atom, (changing residue number between 3’O and P), whereas an RNA suite is from sugar to sugar (or base to base).

To deal with the high dimensionality or RNA conformation, several approaches have been explored. A reduced set of two pseudotorsional angles per residue was proposed in [5]. This reduction in dimensionality from seven to two simplifies the analysis, but sacrifices information. Alternatively, work in [10], [20], [28] attempts to retain information from the full conformational space. The approach in [10] gives a structural alphabet based on the discretization of the conformation distribution function via binning the torsion angles taking one angle at a time. This method is called visual binning because it is based on visual inspection of torsion angle frequency distributions to define boundaries between conformational classes.

The approaches of [20], [28] decompose the seven-dimensional space into various subspaces of three dimensions. It is possible to locate centers of frequency clusters in torsional subspaces. The restriction to three-dimensional subspaces arises from requirements for manual (visual) detection of the frequency clusters. In addition, a filtering stage is described in [20] to remove conformations that are suspected to arise from measurement error. Finally, various elemental units can be parsed during conformational analysis of an RNA polymer. Murray et al. [20] suggest a base-to-base unit (a “suite”) instead of the chemically inspired, and more conventional, phosphate-to-phosphate unit (a residue); see Fig. 1.¹ The work of [28] utilizes a dinucleotide building block to attempt to include the correlations between neighboring residues.

The primary drawback of low-dimensional methods is that some clusters might avoid detection and defy description. Several distinct clusters at full dimensionality can be compressed into a single cluster at low-dimensionality. A limitation to three-dimensional subspaces is arbitrary and might inaccurately characterize some regions of RNA conformational space.

Here, all seven dimensions of RNA conformation are analyzed simultaneously with methods from classical signal processing. We use high-dimensional clustering, mainly vector quantization.² These methods have the potential to be automatic and parameter-free. Here, to avoid overclustering of high-frequency conformations, we impose known conformations, such as A-conformation, onto the clustering. A key contribution of this work is to show that one can successfully perform simultaneous analysis of the whole of RNA conformation space, leading not only to results in agreement with techniques based on significant human intervention, but also to the finding of new motifs. Vector quantization is also a natural extension to scalar work such as that reported in [10], although the framework presented here is not limited to the use of this particular clustering technique and others might be able to exploit intrinsic correlations between RNA torsion angles even further (see Section 6).

The work here continues the research line of [10] (see also [21], [22]), attempting to resolve some limitations there. Vector quantization gives well-defined distortion and quality metrics. It does not involve visual inspection and computes high-dimensional clusters. The VQ approach is validated and/or reinforced³ by comparison of the output with that of previously reported methods, as well as with the structural motifs library (SCOR) [14]. The VQ method allows us to describe potential motifs that were not found in [10].

We should note that we do not claim that the VQ approach described here based on torsion angle clustering is optimal in any sense, merely that it is a logical continuation of the clustering methods described in [10], which is easy to apply, and allows one to rediscover known motifs and to discover some possible new ones as well. Other methods based on sequence analysis or on other search methodologies (see, e.g., [12]) may be more appropriate in various circumstances and, ultimately, one would want to combine the different approaches. We regard the work in this paper as a first step in employing vector clustering techniques from statistics and signal processing to study an important problem in bioinformatics.

The remainder of this paper is organized as follows: In Section 2, we provide the basic background on vector quantization. In Section 3, we begin with a particular case of vector quantization, the scalar case, which permits us not only to introduce the basic concepts but also to show that the results reported in [10] are replicated and refined. In Section 4, we use the full power of vector quantization to analyze sets of four and seven torsion angles simultaneously, extending some of the results reported previously in such works as [10], [20]. We moreover present a modification of the basic vector quantization algorithm, namely, cluster merging, which is motivated by RNA properties and is needed to adapt this classical signal processing technique to the study of RNA structure. Section 5 presents the motifs that were found by our method and compares our findings with known structural motifs. Finally, in Section 6, we summarize our methods as well as describe some key research directions.⁴ In the Appendix, we summarize some of the key results of the visual binning method [10] for the convenience of the reader.

2 BACKGROUND ON SCALAR AND VECTOR QUANTIZATION

Vector quantization (VQ) is a clustering technique originally developed for lossy data compression [7], [8], [17]. In 1980, Linde et al. [17] proposed a practical VQ design algorithm based on a training sequence. The use of a training sequence bypasses the need for multidimensional integration, thereby making VQ a practical technique, implemented in many scientific computation packages such as Matlab (www.mathworks.com). This algorithm, of course, cannot guarantee convergence to the global minima of the optimization problem described below.

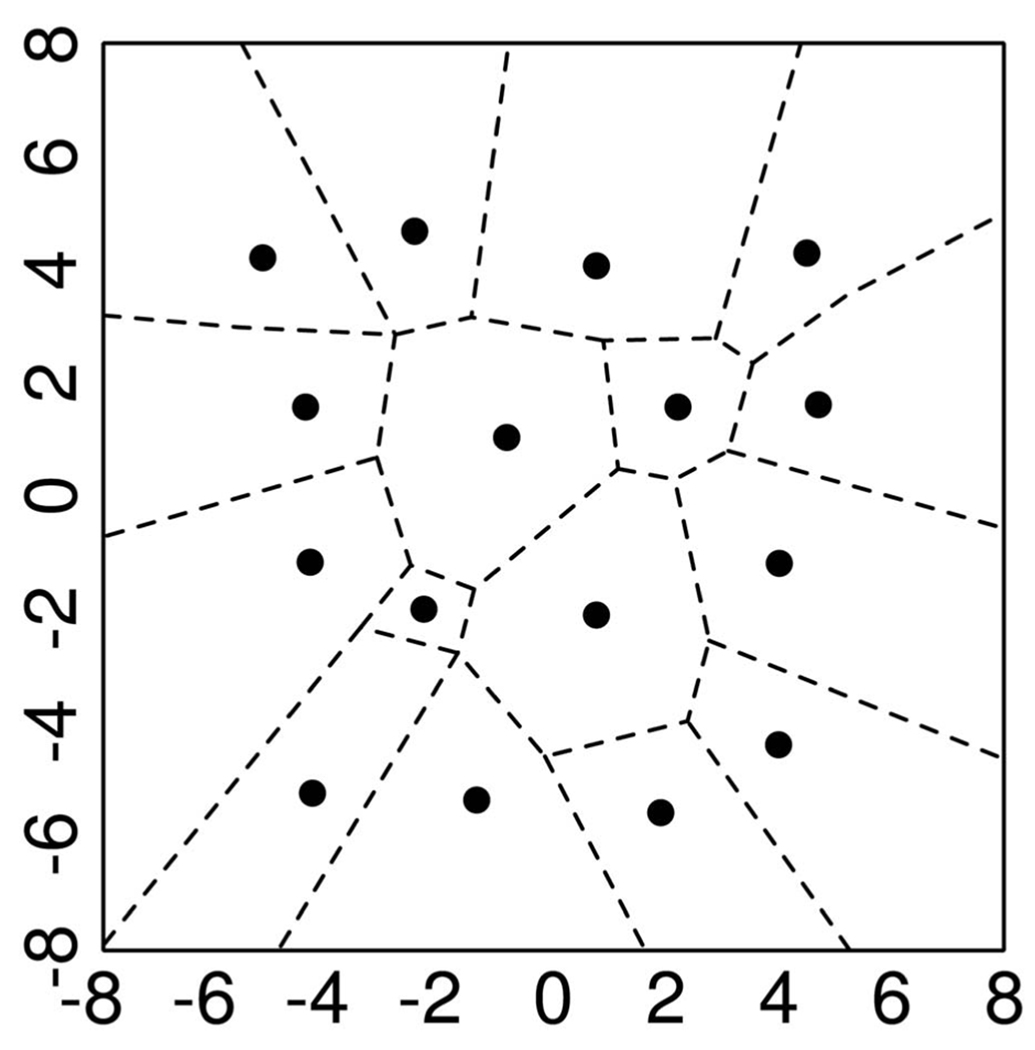
A VQ is analogous to an approximator. Fig. 2 presents a two-dimensional example of vector quantization. Here, every pair of numbers falling in a particular region is approximated by the marked “center” associated with that region (VQ is, of course, closely related to Voronoi diagrams).

Fig. 2.

Two-dimensional example of clustering via (vector) quantization. All the points in a given interval (in one dimension) or a given cell (two dimensions) are represented by the marked “center.”

The general VQ design problem can be stated as follows: Given a vector source with known statistical properties, a distortion measure, and number of desired codevectors, find a codebook (the set of all red stars) and a partition (the set of blue lines) that result in the smallest average distortion.

We assume that there is a training sequence (e.g., the measured torsion angles in RNA backbone) consisting of M source vectors of the form T = {x₁, x₂,…,x_M}. We assume that the source vectors are k-dimensional, e.g., x_m = {x_m,1, x_m,2,…,x_m,k}, for 1 ≤ m ≤ M. Let N be the number of desired codevectors and let C = {c₁, c₂,…,c_N} be the codebook, where each c_n, 1 ≤ n ≤ N, is, of course, k-dimensional as well. Let S_n be the cell associated with the codevector c_n and let P = {S₁, S₂,…,S_N} be the corresponding partition of the k-dimensional space. If the source vector x_m is in the encoding region S_n, then it is approximated by c_n, and let us denote by Q(x_m) = c_n (if x_m ∈ S_n) the corresponding map (each vector is simply associated to the closest center from C). Then, assuming, for example, a squared error distortion measure, the average distortion is given by

$$\begin{array}{c}D≔\frac{1}{M}{\displaystyle \sum _{m=1}^M{\Vert x_m-Q(x_m)\Vert }^2,}\hfill \\ \text{where}{\Vert e\Vert }^2≔e_1^2+e_2^2+\dots +e_k^2.\hfill \end{array}$$ (1)

The design problem then becomes the following: Given the training data set T⁵ and the number of desired codebooks (or clusters) N, find the cluster centers C and the space partition P such that the distortion D is minimized. This problem can be efficiently solved with the LBG algorithm [7], [17] and, as mentioned above, its implementation can be found in popular scientific computing programs. We should, of course, recall that convergence to the global minima is not guaranteed with this algorithm. Additional details on the technique can be found in [7], [8], as well as in the tutorial located at [4], from which we have prepared this summary. In future work, we plan to use more advanced techniques, such as those reported in [23].⁶

3 SCALAR QUANTIZATION: AUTOMATIC BINNING OF SINGLE TORSION ANGLES

To provide an accessible introduction to VQ, a brief discussion of scalar quantization (SQ) is provided here. SQ is a natural extension of our previous work and is extensible to VQ. With SQ, one can automate the previous binning method described in [10], where torsion angles are treated individually. In [10], conformational space is partitioned into boxes, each containing one conformational state, i.e., rotamer, or a subset of conformational states; see also [20]. The box boundaries were set by visual inspection, using minima of torsion angle frequency distributions as guides.

As was known from [25], [30], four torsional angles (α, γ, δ, ζ) (which we call the identifier angles) are, in general, sufficient for this classification. Here, the results of that work are reproduced with SQ. In the Appendix, more details are described from the work in [10], reproducing key tables for the convenience of the reader.

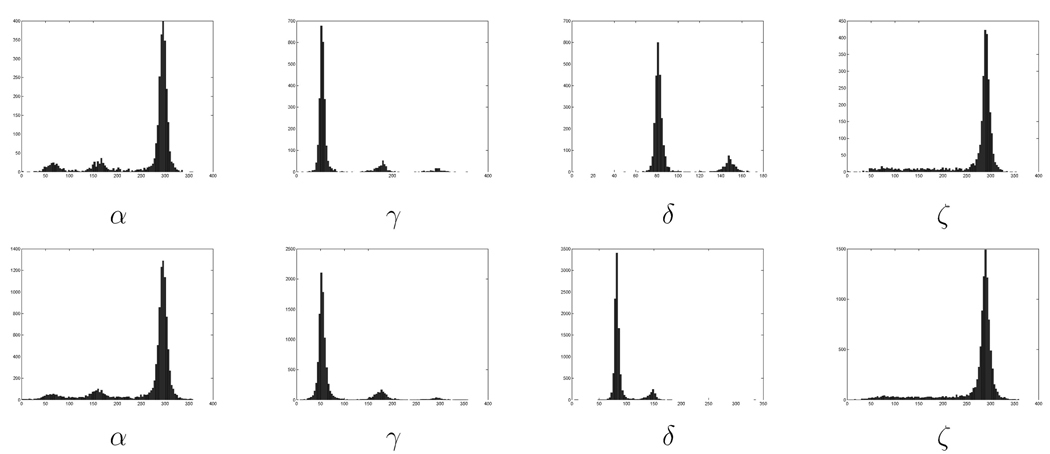
We argued in [10] that the frequency histograms of the four identifier torsion angles have a clear multipeak structure; see Fig. 3 and details below. Since the peak structure is the cornerstone for our proposed classification method, we describe here these results for a larger set of RNA structures than those reported in [10]. In particular, two data sets are used. One follows the work reported in [10] and is for a single RNA with 2,914 residues (HM LSU 23S rRNA, RR0033), while the second one follows work reported in [20], and is for a collection of 132 RNAs,⁷ giving a total of 10,463 residues (redundancies have not been eliminated). Here, as in the rest of this work, residues with undefined or unknown torsion angles were omitted. Coordinates were obtained from the Nucleic Acid Database [24]. We have not performed the filtering of [20]. That method may indeed improve the results. As mentioned above, in the SQ, we first limit the analysis to the torsion angles (α, γ, δ, ζ) (see Fig. 1) since the others are either dependent on these angles or have distributions which are almost unimodal [25], [30]. There is no intrinsic limitation which restricts one to this reduced set of angles and, indeed, being more automatic, the process can be easily applied to larger sets. As this is an unsupervised clustering technique, none of the residues were labeled. As we detail later on, clusters are merged if needed based on biochemical information and clusters proximity.

Fig. 3.

Distributions of the torsion angles α, γ, δ, and ζ for the single RNA (first row) and the collection of RNAs (second row). We observe the similitude among the distributions, marking the presence of “rotamers” not only for a given RNA but also across RNAs. We also observe clear modes, which are automatically detected by the proposed clustering technique. In addition, note that the ζ torsion angle has a large tail not present in the other distributions.

Fig. 3 shows the distributions for the four angles from the large and small data sets. The two data sets of histogram features have a strong resemblance, suggesting the generality of the cluster classification method for analysis of RNA conformation.

One potential problem with visually-based classification methods such as the binning in [10] and the technique presented in [20], in addition to being limited to ad hoc observations of three or less angles at a time (see more on this below), is that the resolution (and amount of data) may not be sufficiently fine, which may make it difficult to distinguish distinct features in the data, and clusters can be confused and merged.

This issue is demonstrated, for example, in the behavior of the torsional angle ζ. For ζ, the visually observed frequency distribution contains a single peak (centered about 290 degrees) in addition to a featureless plateau that extends over 200 torsional degrees. For visual binning [10], ζ was allocated to two bins. The first bin contains the 290 degree peak. The second bin, which does not correspond to a single conformational state, contains the extended plateau and, in visual binning [10], is called “other.” However, potential energy calculations predict that ζ should partition into three peaks [21], [22], [29]. The filtering method of Murray et al. carves ζ into the same three peaks. As demonstrated below, our approach retains these details without the need for filtering.

Understanding the peak shape of each cluster is crucial for probabilistic RNA design and for understanding local dynamics of folding. The peak shapes of the clusters contain important information on RNA dynamics, but might also be influenced by coordinate error. It appears that better fitting for the major clusters (see below for the limits of these clusters) is obtained using exponential distributions and not Gaussian distributions as argued, for example, in [10]. For the first data set, the kurtosis⁸ for the main peak is 5.3 for α and 4.6 for ζ, clearly indicating a significant deviation from Gaussian distributions (whose kurtosis is 3). The log-likelihood while fitting an exponential function improves by 24 percent with respect to fitting a Gaussian for the α torsion angle and by 23 percent for the ζ torsion angle. Similar behavior is observed for the other data set, although, in some cases, the improvement is more moderate (e.g., for the first mode of α in the first data set, the improvement is about 16 percent).

Using the clustering technique described in the previous section,⁹ and requesting the number N of codevectors following [10] (or just from visual inspection for now, this will be made automatic later), we found the codevectors or centers of the clusters C = {c₁,…,c_N} given in Table 1. Later on, for the classification, we enumerate the clusters in each coordinate by increasing values. For example, a residue whose torsional angles are in the third peak (center) in α, the first in γ and δ, and the third in ζ will be enumerated as 3113; see Table 1.

TABLE 1.

Cluster Centers Automatically Computed by Our Technique

	Dataset 1
α	68.3 (1), 169.7 (2), 294.3 (3)
γ	50.4 (1), 60.0 (1), 175.8 (2), 292.3 (3)
δ	81.7 (1), 147.8 (2)
ζ	118.0 (2), 286.7 (1)
	Dataset 2
α	68.6 (1), 167.8 (2), 294.0 (3)
γ	50.1 (1), 65.0 (1), 174.4 (2), 290.2 (3)
δ	82.7 (1), 144.4 (2)
ζ	116.4 (2), 286.0 (1)

Numbers in parentheses are used for cluster identification.

The results are similar for the two data sets. For γ, two of the centers are very close to each other and will be merged during clustering. This demonstrates a possible problem of overclustering by scalar quantization (or any other automatic clustering technique). In the next section, a simple merging algorithm is proposed to treat this difficulty. Once again, although the number of clusters is predefined, this could be accomplished as part of the automatic process; see Section 4.

Regarding ζ, if additional clusters are desired, e.g., three clusters for the first data set (see our discussion above), these clusters are automatically found at 1) 85.86, 2) 188.25, and 3) 289.27, thereby splitting the large tail (following the description in [20], but in an automatic fashion). These additional centers will also appear when considering torsion angles in vectorial form in the next section and will be used to search for motifs. Further increasing the number of clusters does not produce, in general, a significant change in the distortion D, an indication that the selected number of clusters is sufficient; see Section 4.

The clustering (binning) method that results from scalar quantization as described so far has one major difference fromh the one described in [10]. For scalar quantization, no bins are classified as “other.” In the scalar quantization case, every bin is populated. Every residue is associated with a specific set of four centroids (by simple proximity via the map Q defined in Section 2), each one corresponding to one of the four torsion angles (α, γ, δ, ζ). In Table 2, we give the corners of the boxes that define these bins. We could, of course, easily and automatically add the “other” class if so desired by simply forcing the torsion angles not to be “too far” from the center of the bin. This can be quantified for example by the standard deviation of each bin.

TABLE 2.

Enumeration of the Bins Obtained by Scalar Quantization and Their Boundaries

bin index	1	2	3
α	[0 – 115]	[115 – 220]	[220 – 360]
γ	[0 – 120]	[120 – 220]	[220 – 360]
δ	[50 – 118]	[118 – 170]
ζ	[10 – 130]	[130 – 220]	[220 – 360]

The scalar quantization method was used to automatically cluster the four identifier torsion angles. The fundamental difference between the binning method in [10] and the scalar quantization method is that bin boundaries were established manually by inspection of frequency histograms, while the clusters borders were automatically computed via a distortion minimization criterion. The four identified torsion angles of all the residues in RR0033 were classified by scalar quantization, with the three clusters in ζ described above.

In summary, the results of automatic classification by scalar quantization are very similar to the manual binning method of [10], except for an extra refinement (obtained automatically) in the ζ coordinate. As mentioned above, it can be shown that any increase in the number of clusters in the four coordinates will not reduce the distortion D. Indeed, it seems that any attempt to increase the refinement will only worsen the results.

4 VECTOR QUANTIZATION: AUTOMATIC AND SIMULTANEOUS BINNING OF MULTIPLE ANGLES

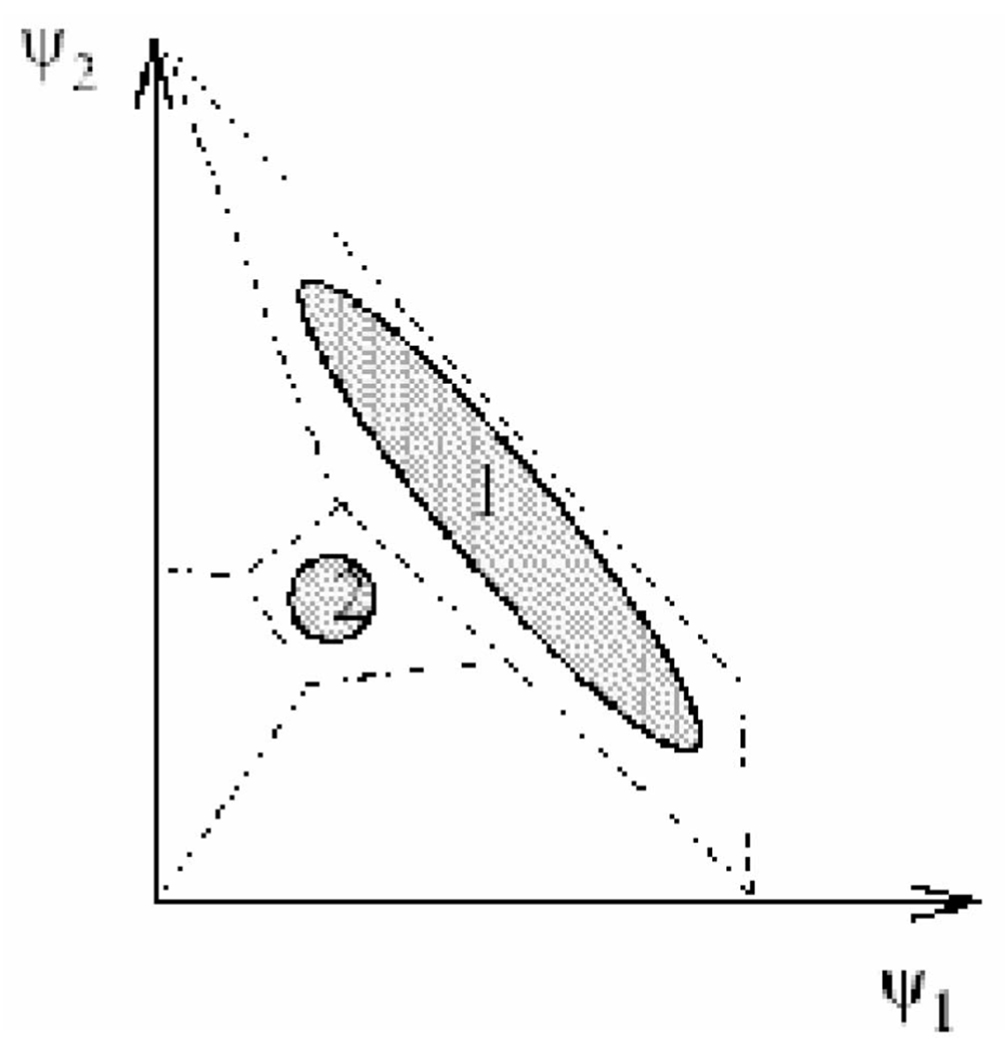
Important (biochemical) information in the torsion angles is lost in scalar quantization or any other analysis that considers single angles at a time. This loss occurs because each angle is considered in separation from the others. Scalar clustering is a one-dimensional projection that can merge clusters that are distinct in projections of higher dimension. For a schematic illustration of this problem, see Fig. 4.

Fig. 4.

Qualitative example showing the importance of vectorial investigation of torsion angles. In this example, the conformations space is projected onto two torsional angles, ψ₁ and ψ₂. There are clearly two population clusters, 1 and 2. The individual torsion angle histograms will give only one peak with a negligible tail and the two clusters cannot be identified when the analysis is purely scalar. There is a need, therefore, for vectorial analysis, as suggested in this work.

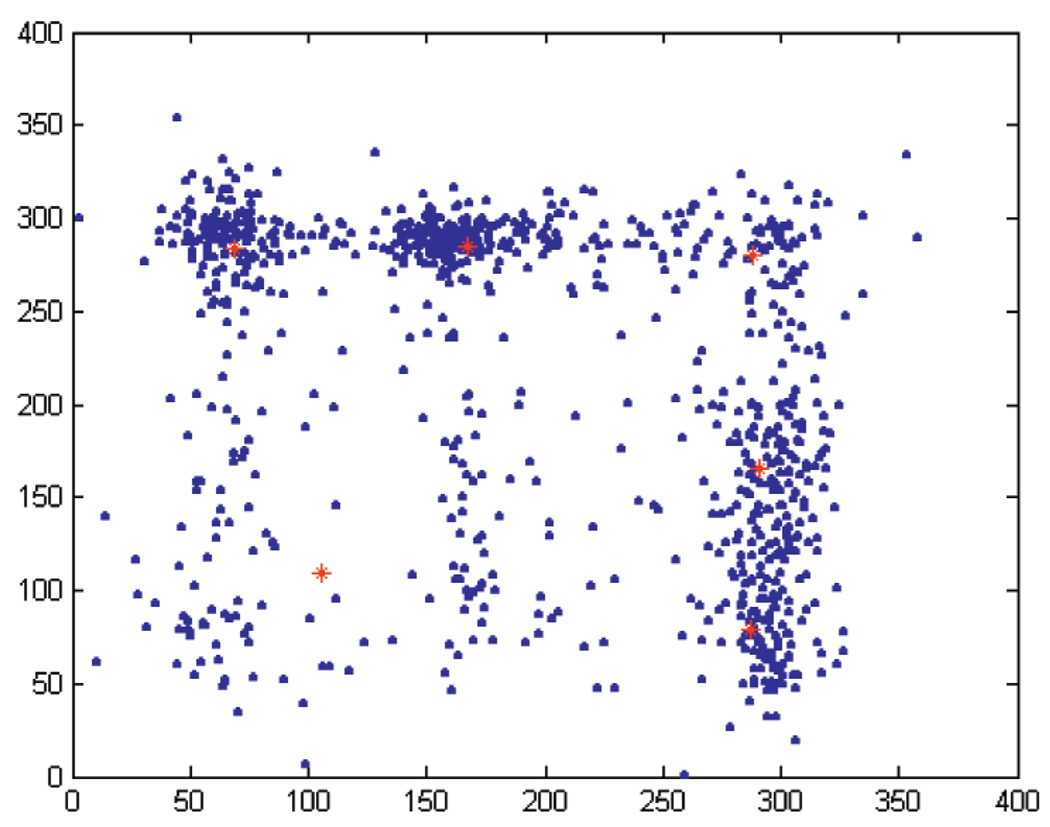
VQ analysis addresses this problem.¹⁰ For an illustration of the methodology, consider VQ analysis of two angles (with k = 2).¹¹ For example, requesting N = 6 clusters for the pair (α, ζ), we obtain the centers

$$\begin{array}{c}C=\{(69.1,284.2),(291.0,165.6),(287.4,79.0),\hfill \\ (167.6,284.6),(287.7,280.0),(105.3,109.8)\}.\hfill \end{array}$$

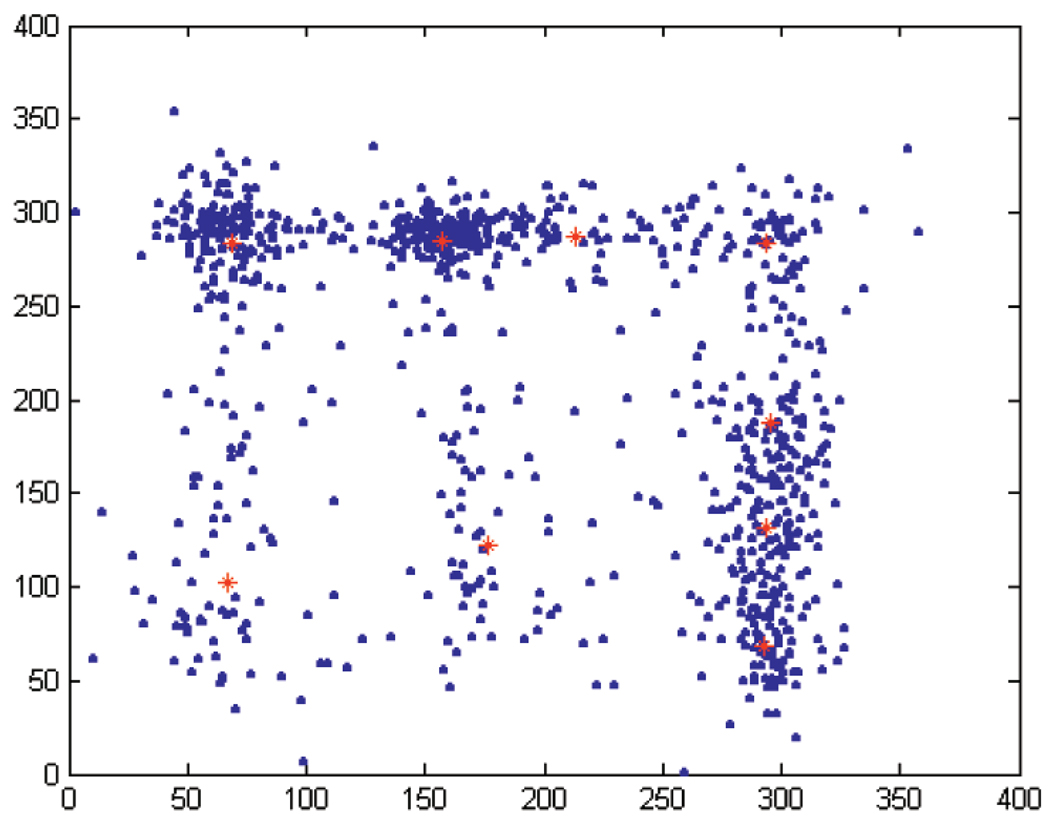
The α component of the automatically detected centers is as in the case of scalar quantization, while the ζ component includes terms that both appear when we request two and three bins for ζ in the scalar case. That is, VQ for k = 2 finds additional relevant clusters in ζ when considered as a vector in conjunction with α. In Fig. 5, the torsion angles are plotted (blue dots) together with the cluster centers (red stars). Repeating this exercise for N = 9 clusters for (α, ζ), gives the centers

$$\begin{array}{c}C=\{(292.2,68.3),(68.3,283.8),(176.5,122.6),\hfill \\ (157.5,284.9),(66.7,102.4),(213.1,287.0),\hfill \\ (293.4,284.0),(295.3,188.0),(293.5,132.0)\}.\hfill \end{array}$$

Fig. 5.

Torsion angles for the pair (α, ζ) (blue dots) together with the six cluster centers (red stars).

Fig. 6 contains plots of the torsion angles (blue dots) together with the cluster centers (red stars), showing that, while the main cluster centers are closely located to those when only six centers were considered, the three additional centers split the broad distributions (lower left region, where one center became two) as well as splitting the very popular conformations (e.g., additional center at the main α pick, right of the figure).

Fig. 6.

Torsion angles for the pair (α, ζ) (blue dots) together with the nine cluster centers (red stars).

It is clear from the illustrations above that high-dimensional clustering is necessary. All torsion angles should be considered simultaneously. The framework described in Section 2 permits that. Analysis of one dimension (one torsion angle at a time), four-dimensional (α, γ, δ, ζ), or the full seven-dimensional torsion angle space is of equal complexity with automatic VQ methods. Of course, due to the “curse of dimensionality,” more data is needed at higher dimensions. However, the work here is not limited by quantity of data. The dispersion within the clusters (i.e., the peak shape) might be used to infer energy potentials and dynamical processes.

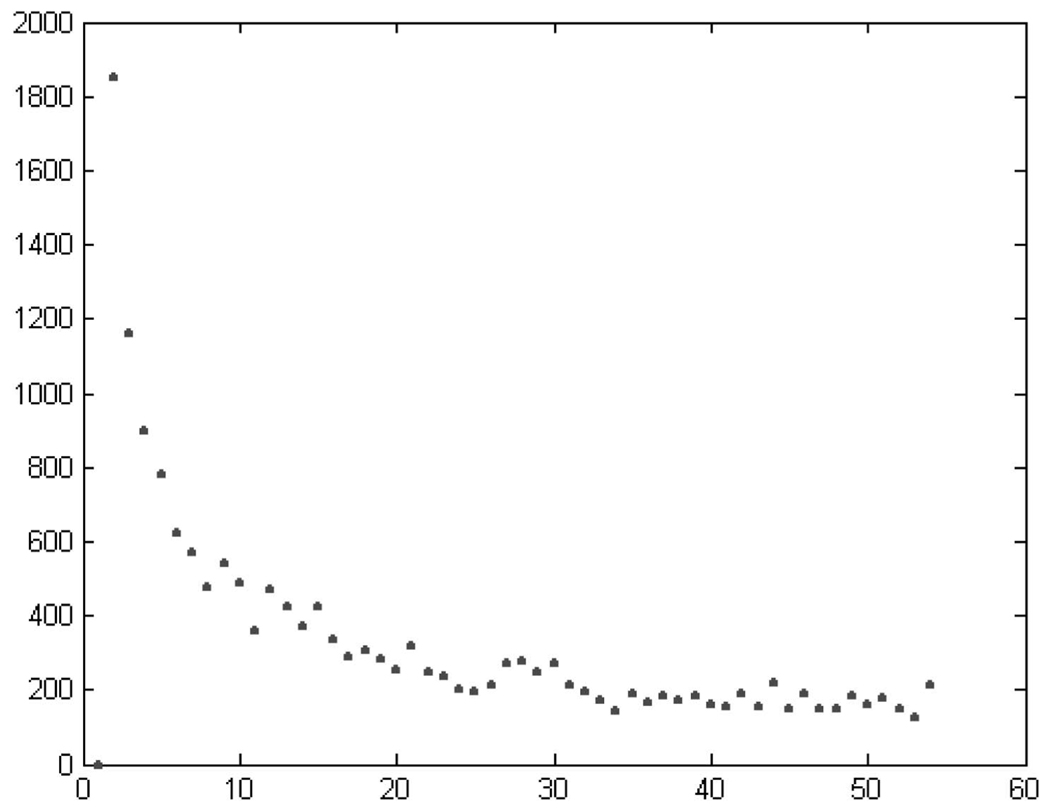
The first test of the vector quantization method used four dimensions (k = 4), the four identifier angles (α, γ, δ, ζ) of RR0033. To cluster these four angles, one must determine the optimum number of clusters (N). False clusters arise if N is too large (overpartitioning). Distinct clusters are merged if N is too small (underpartitioning). Several metrics are used here to optimize N. The relationship between the distortion, D, defined in Section 2, and the number of clusters N is useful for optimizing N. In addition, the observation of overlapping clusters indicates overpartitioning. The number of clusters N (see also Section 4.1 and Section 6) is also task dependent; analysis at different resolutions should require a different number of clusters and topics such as RNA dynamics might need a much more detailed partition than rough classification studies.

Fig. 7 shows a plot of D as a function of the number of clusters N. The distortion reaches a “plateau” value for N ≈ 50, meaning that the improvement is mild, compared to the initial value, when further increasing N. The oscillations observed in the graph are due to the convergence of the optimization algorithm to local and not global minima.¹² Vector quantization was performed for N = 40, 50, 60. N = 60 gave all the populated bins defined in [10]. All three cases, however, appear to be overpartitioned. This overpartitioning is especially pronounced in the A-conformation region. Most neighboring clusters in this region are overlapping. This overlap is not surprising since these clusters are so highly populated (over 60 percent of this RNA) that any distortion minimization approach will tend to invest a lot of resources (i.e., centers) there. This phenomenon emphasizes the need to impose structural definitions onto the clustering process, as described below.

Fig. 7.

Error as a function of the number of clusters for the vector (α, γ, δ, ζ).

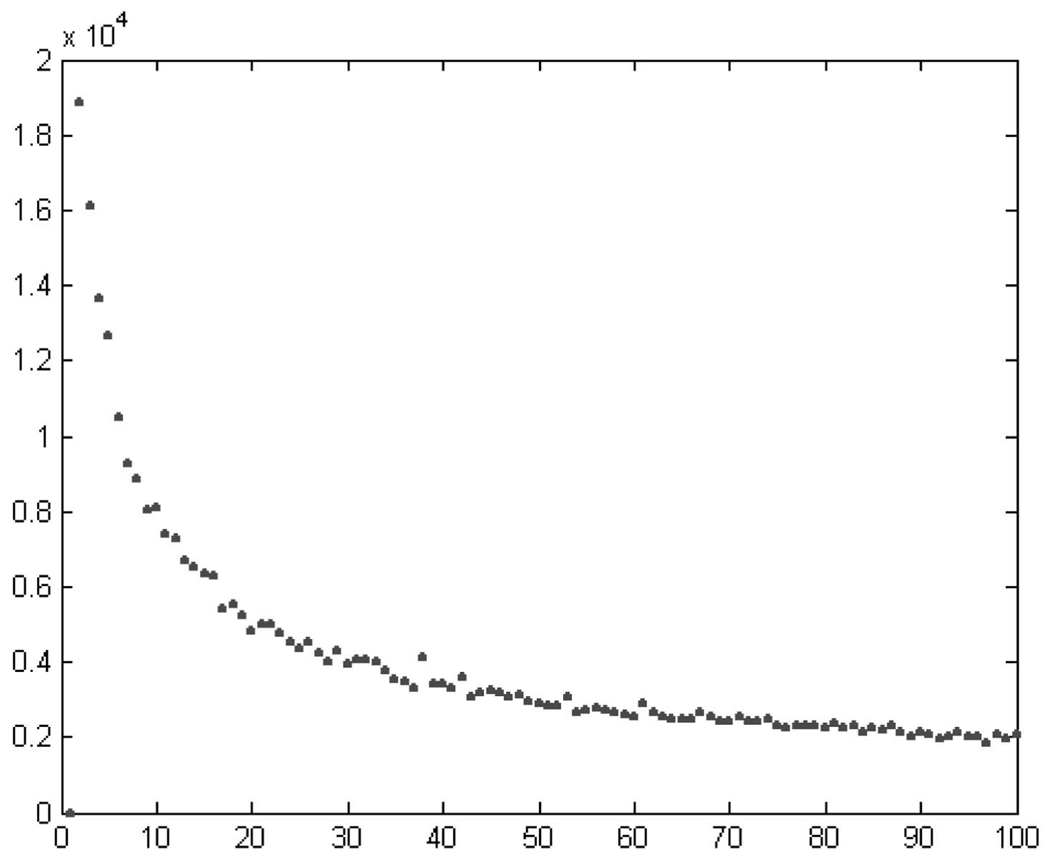
The full quantization of the conformation space, based on all seven torsional angles, was also performed. The algorithm is fast enough to perform a full quantization of the 2,800 residues of RR0033 to 60 classes in a few seconds. The distortion D virtually plateaus at about 60 classes; see Fig. 8 (recall once again that oscillations are due to local minima). N = 60 gives the representation of the most populated 15 bins from [10] and is in good correspondence to the results of the four-dimensional quantization. Additional partitioning of up to N = 100 reveals very sparsely populated new classes, see Section 6. Here, a “new class” is “far” from previously found classes. Classes are here considered “close” (or overlapping) when their centroids are in the same bin (as derived from the SQ, see Table 2) and “far” otherwise.

Fig. 8.

Error as a function of the number of clusters for the vector with all seven torsion angles.

4.1 Merging

“Closeness” is the first component of a merging criteria. Specifically, we require that two clusters with centroids that reside within the same bins are merged into a unique cluster, subject to conditions mentioned below.¹³

Note that binning, whether by observation, as in [10], or automatically done via SQ, as described above, gives a partition of the torsion angles space into multidimensional boxes. There is no a priori reason to believe that the basin of attraction of the specific energy minimum that defines a native conformer will have such a shape. Using vector quantization with merging can shift and change the basin and its boundaries. An additional advantage of this method is that, as mentioned before, vector quantization naturally partitions the entire torsion space.

In order to possibly discover new motifs, we added some natural conditions to the merging in the full dimensional case. First, we merge two clusters only if the angles (β, ε, χ) have the coordinates of their centroids within the same peak. These peaks may be quite small and very difficult to observe via simple histogramming.

The second additional merging condition is a structural one: We define a “tagged cluster” as a cluster that corresponds to a well-established conformation such as A-helical or tetraloop RNA. Tagged clusters are protected and are not merged with other clusters. Although there are relatively few of these clusters, they represent a large fraction of the RNA. Approximately 60 percent of globular RNA is found in the A-conformation.

The results of the proposed algorithm (VQ followed by merging of nontagged clusters or modified vector quantization) are presented in Table 3. Each row contains the ASCII code of the bin that matches the coding method of [10]¹⁴ (see Table 12 in the Appendix) and the enumeration of the peaks (numbers as obtained from the scalar quantization).

TABLE 3.

Results of the Modified VQ on Individual Residues, See Text for Details

Number	ASCII Code	Associated 4D Box	Remarks
1	a	3113	More than half of the cluster centroids are in this box
2	A	3113	β ∈ [125 – 155] Appears in mismatch motifs
3	e	3112	ε ∈ [170 – 240], ζ ∈ [180 – 230], Kink-turn motif.
4	J	3112
5	E	3111	Takes part in the E-loop motif.
6	U	3213	β = 94° Takes part in the E-loop
7	u	3213
8	o	2113	αcenter ∈ [140 – 180], χcenter = 160°
9	O	2113	αcenter ∈ [180 – 220], χcenter = 200°
			Takes part in the GNRA tetraloop
10	n	3213
11	r	3122	β ∈ [140 – 200],Hyper-Twist motif
12	q	3122	β ∈ [200 – 260]
13	R	3121	ζ ∈ [40 – 100], Kink-Turn motif
14	Q	3121	ζ ∈ [100 – 160]
15	h	3221
16	d	1322
17	z	3212
18	s	2121
19	t	1113	Starting conformation for an α stack
20	f	1112
21	v	3323	Starting conformation for an α stack
22	c	1123	Takes part in kink-turn motif
23	i	2213	Crank shaft of A-form RNA
24	g	2123
25	y	1312	Another crank shaft from A-form RNA
26	l	1213

TABLE 12.

ASCII Code Alphabet for the Binning Method from [10]

Number	ASCII Code	Associated 4D Box
1	a	3111
2	e	3112
3	r	3122
4	i	2211
5	o	2111
6	t	1111
7	n	3121
8	s	2122
9	l	1211
10	u	3211
11	c	1121
12	d	1322
13	p	4111
14	m	1122
15	h	3222
16	g	2121
17	b	4211
18	f	1112
19	y	1311
20	w	2222
21	k	4122
22	v	3311
23	x	4112
24	z	3213
25	j	2212
26	q	2112
27	1	3321
28	2	3322
29	3	1221
30	4	1321
31	5	3411
32	6	3131
33	7	4121
34	8	1212
35	9	2411
36	0	4311
37	+	3312
38	−	1222

In addition to being automatic and capable of handling all the torsion angles at once, a clear advantage of the VQ method as compared to manual binning is the smaller numbers of classes that are needed to classify the structure. Vectorial binning is based on 26 clusters versus 38 bins in the usual binning method [10]. The main reason for this reduction in the number of classes is that the clustering algorithm does not recognize the “transition states” bins or the bins classified as “other” from [10]. These are regions of conformation states that are very sparsely populated and which probably include energy bottlenecks between the low energy conformations. The result is that conformations that may be measurement error are included in the structural analysis [20].

5 AUTOMATICALLY FINDING MOTIFS: VALIDATION

Most motifs that are already known have highly conserved three-dimensional structures. Finding motifs with the modified vector quantization method proposed above can be used as a validity measure and this is the goal of the present section. In particular, we compare the sites of different known motifs with search algorithms based on: 1) manual binning following [10], 2) 4D vector quantization with the angles (α, γ, δ, ζ), and 3) 7D vector quantization with the whole torsion angles set.

5.1 Tetraloops

The tetraloop motif [1], [13], [18], [32] was used to compare various methods here to each other and to our previous visual binning method [10]. A tetraloop is a four residue element that caps an A-helix [1], [13], [18], [32]. The most abundant tetraloop sequence is GNRA, where N is the U-turn residue. Consensus molecular interactions of GNRA tetraloops are 1) “G” forms a non-Watson/Crick hydrogen bond with “A,” 2) the N1 of “G” forms a hydrogen bond with the O2P of “A,” and 3) the 2’ OH of “G” forms a hydrogen bond with the N7 of R. This motif has been found to be thermodynamically stable and ubiquitous in various RNAs. The high frequency of occurrence and conservation of molecular interactions makes this motif a very useful test case for our algorithms.

In previous work, we describe 25 tetraloops in RR0033 (23s rRNA), detected by visual binning. There we show that global and local RMS deviations of atomic positions of the tetraloops are related in a reasonable way to torsion angle deviations. RMSD space and torsional space have similar information content. Twenty-four of 25 tetraloops there are associated with the ASCII code aaoa in [10], while a single tetraloop is given by aaoe (see also Table 3). A minor adjustment of the visual binning structure converts the single outlier to the consensus, giving all 25 of the observed tetraloops as aaoa, shown in Table 4.

TABLE 4.

Results for the Tetraloop

First Residue	Sequence	Conventional Definition	Binning structure	4D VQ	7D VQ
149	GGAA		aeaa	aaoa	aaoA
252	CUCA	U-Turn	aaoa	aaoa	aaOa
313	UGGA	U-Turn	aaoa	aaoa	aaOa
468	UGUG	U-Turn	aaoa	aaoa	aaOa
505	CGAA		aaoa	aaoa	aaOa
624	UUUG	U-Turn	aaoa	aaoa	aaOa
690	GGAA	U-Turn	aaoa	aaoa	aaOa
804	CGAA	U-Turn	aaoa	aaoa	aaOa
1054	GGUA	U-Turn	aaoa	aaoa	aaOa
1197	GUAA	U-Turn	aaoa	aaoa	aaOa
1326	UGAA	U-Turn	aaoa	aaoa	aaOa
1388	UGAG	U-Turn	aaoa	aaoa	aaOa
1468	GCAA	U-Turn	aaoa	aaoa	aaOa
1499	UUAA	Octaloop	aaoa	aaoa	aaOA
1595	GUAA	Pentaloop	aaoa	aaoa	aaOa
1628	GGAA	U-Turn	aaoa	aaoa	aaOa
1706	GGCG	U-Turn	aaoa	aaoa	aaOa
1748	UUCG		aaoa	aaoa	aaOa
1793	CGGA	U-Turn	aaoa	aaoa	aaOa
1808	CGCA		aaoa	aaoa	aaOa
1862	CGCA	U-Turn	aaoa	aaoa	aaOa
1991	AUCA	U-Turn	aaoa	aaoa	aaOA
2248	CGGG	U-Turn	aaoa	aaoa	aaOa
2411	CGAA	U-Turn	aaoa	aaoa	aaOa
2629	CGUG	U-Turn	aaoa	aaoa	aaOa
2695	CGAG	U-Turn	aaoa	aaoa	aaOa

Our torsional definition (aaoa) is offset by one residue relative to the sequence-based definition (GNRA) such that the o of aaoa is the U-turn residue. The rationale for the offset of operational: In torsion space, aaoa appears to be a more accurate definition than aoaa. The word aaoa is much more frequent than the word aoaa. Note that “a” indicates the A-helical conformation and “o” indicates that the α torsional angle is rotated from g to transorientation to give the U-turn. Although our method searches in torsion space, not molecular interaction space, the consensus molecular interactions are well-conserved in the tetraloops of Table 4.

In Table 4, the first column gives the starting residue number, exactly as in our previous work [10]. The second column gives the sequence (in the aaoa frame, not in the GNRA). The conventional definition is provided in the third column. The fourth column gives the binning “word,” after adjustment of the visual binning structure, so that all 25 tetraloops, rather than 24 out of 25, are given by aaoa. The fifth and sixth columns show the new automatic results for the four and seven-dimensional vector quantization, respectively. For tetraloops, there is complete agreement between the visual binning and the SQ results. All of the SQ tetraloops are similarly classified as such by visual binning, with no false negative and no false positives. These results are an indication of the utility of the automatic clustering techniques.

In fact, we can find here a very good agreement among all of the methods. The table gives perfect agreement in 25 out of 26 cases with [10] (that is, all the methods agree) with just one false positive (the residue beginning at 149). This false positive replaces an e by an a and an a by an o. In both cases, the difference is in a single torsion angle and a different side of the cluster border was “selected.” This is an expected and tolerable error when working with high-dimensional data for “borderline” angles (recall that, as mentioned in the introduction and further discussed in Section 6, the proposed torsion clustering should be one component of the classification approach).

5.2 E-Motif

A second motif with conserved conformation is the E-Loop motif [16]. An E-loop is a double helical region with a G bulge and characteristic A-G, A-A, and trans-Hoogsteen U-A pairs. Visual binning identifies six E-Loops in RR0033 (23S rRNA), each with a + (with the G bulge) and − strand. In fact, there are two rotamers of the + strand that give the same global geometry. The − strand has a unique conformation. It has been proposed that this double-stranded motif has affinity for Mg²⁺ ions and arginine [16]. E-Loops are described as “looped with a dinucleotide platform in a triplet” by the SCOR library.

For E-Loops, there is full agreement between visual binning and 7D VQ (Table 5). A 4D VQ gives a single false positive. Inspection of conformation and interactions of the segment initiating at residue 1,069, identified by 4D VQ, reveals it is not an E-Loop.

TABLE 5.

Results for the E-Motif + Strand

First residue	Sequence	Conventional Definition	Binning Structure	4D VQ	7D VQ
172	UCAGUA	S-Turn	aeshaa	aEshaa	aEszAa
210	UUAGUA	S-Turn	aeshaa	aEshaa	aEszAa
355	CCAGUA	Loops with a dinucleotide platform in a triple	aesdaa	aEsdaa	aEsdAa
585	CCAGUA	Loops with a dinucleotide platform in a triple	aesdaa	aEsdaa	aEsdAa
1069	CAGGAC		aes-aa	aEsdaa	aEgdAa
1367	AUAGUA		aeshaa	aEshaa	aEszAa
2689	AUAGUA	Loops with a dinucleotide platform in a triple	aeshaa	aEshaa	aEszAa

The refinement of the ζ coordinate into three distinct regions is of utility here. The second residue of the E-loop + strand is in a conformation with ζ in the first peak (around 60°). A 7D VQ reveals that the fifth residue of the + strands (Table 5), which is invariably a U, is in the “A” cluster (as defined in the table) with a β coordinate centroid that deviates from (180°) (“a” cluster) to 140° (“A” cluster).

We did not merge this cluster with the “a” cluster. We also observe that “h” in the four-dimensional quantization and the visual binning is replaced by “z” in the seven-dimensional VQ.

The results for the − strand are shown in Table 6. This strand has an A-form stack with a kink at the second residue. Here, we can find full agreement between visual binning results and 4D VQ. The 7D VQ gives a bin “U” instead of “u.” The difference between the two in Table 6 is in the nonidentifier angle β = 94° that is outside the main envelope. Here, we have an example where a nonidentifier torsional angle gives extra information which is needed for correct definition of the conformation.

TABLE 6.

Results for E-Motif − Strand

First Residue	Sequence	Conventional Definition	Binning Structure	4D VQ	7D VQ
159	GAACU	S Turn	auaaa	auaaa	aUaaa
225	GAACG	S Turn	auaaa	auaaa	aUaaa
292	GACCG	Loops with a dinucleotide platform in a triple	auaaa	auaaa	aUaaa
568	GACCG	Loops with a dinucleotide platform in a triple	auaaa	auaaa	aUaaa
-	-	-	-	-	-
2053	GAACU		auaaa	auaaa	aUaaa
2701	GAACU	Loops with a dinucleotide platform in a triple	auaaa	auaaa	aUaaa

5.3 Kink-Turn Motif

This motif described in [19] also has the double-stranded structure. The kink-turn consists of a bulging + strand, which has a conserved structure, and a − strand, which has a more flexible structure. We will focus our attention here on the + strand only.

Referring to Table 7, we see some inconsistencies between the structures detected by the different methods. Two possible places for the ambiguity in the structure from the binning method are in the second place letter “e” and the fifth with the letter “r.” In both of these places, the ζ angle is out of the main peak, but the binning is not finely tuned enough to recognize the precise place; see also Table 2 and Table 3. With seven-dimensional vector quantization, it is obvious that one can find ζ in a second peak, which emphasizes an advantage of using the full dimensional quantization technique.

TABLE 7.

Results for the Kink-Turn Motif + Strand

First Residue	Sequence	Conventional Definition	Binning Structure	4D VQ	7D VQ
43	UGAUGA	Loops with multiple triples	aedcra	aadcRa	aedcrA
93	CGAAGA	Kink-turn	aedcra	aedcRa	aedcrA
260	CAAUGU	Kink-turn	aedcra	aadcra	aedcrA
1027	GUUUGA	Kink-turn	ae*1ra	aeuvRa	aeuvra
1147	CCUAGA	Kink-turn	aedcra	aadcra	aedcrA
1312	GAUGGA	Kink-turn	aedcra	aadcra	aedcra
1601	GCAGGA	Kink-turn	aercra	aaRcra	aahcra

5.4 Hyper-Twist Motif

The hyper-twist is another motif that is based on the double helix structure. Here, the double strand is twisted around a purine-purine mismatch. The mismatch is usually a G-A pair. This motif typically has a symmetric structure. There is a G-A pair and an A-G pair. In Table 8, we included both the + and the − strand.

TABLE 8.

Hyper-Twist Motif + and − Strands

First residue	Sequence	Binning Structure	4D VQ	7D VQ
20 – 27	GGUGGAUU	aaaaraaa	aaaaraaa	aaaarAaa
516 – 523	AUGAAAUC	aaraaaaa	aaraaaaa	aaraaaaa
365 – 370	GUGCGG	aaraaa	aaraaa	aaraaa
279 – 281, 285 – 287	CCU, AUC	iaaaaa	iaaaaa	iaaaaa
792 – 799	GAUGAAGC	aaaraaaa	aaaraaaa	aaaraaaa
814 – 822	GUGGAAGUC	aaaranzaa	aaaranHa	aaarAnHaa
1585 – 1592*	CGUGGAAG	aaaarara	aaaaraRu	aaaarARu
1602, 1605 – 1610	C,GAAGCG	eraaaaa	araaaaa	araaaaa
1881 – 1887	ACUGAAU	iaaraa	iaaraaa	iaaraaa
2015, 2016, 1771, 1847 – 1850	A,U,U,AGGU	aa7aaaa	aagaaaa	aagAaaa
2500 – 2505	CGCAAG	aaaraa	aaaraa	aaarAa
2515 – 2520*	CGACCG	aeaaaa	aeaaaa	aeaaaa

The SCOR description of these sites is mostly of “stacked paired non-Watson/Crick double strand” or “cross strand.” At*, the structure is considered to be a kink-turn motif. For the 7D VQ, there is a clear preference for the “r” conformation to be in one of the complexes (ζ = 130).

The entries marked with a * have a − strand with conformation “e” instead of “r.” There are some conformations which include a bulge. One of them coalesces with a kink-turn motif. It was found that all of the mismatch conformations that were marked by “r” belong to one specific cluster. We used this to unmerge this cluster from the other clusters that were merged with it before; see Table 3.

5.5 Mismatched GA-Motif

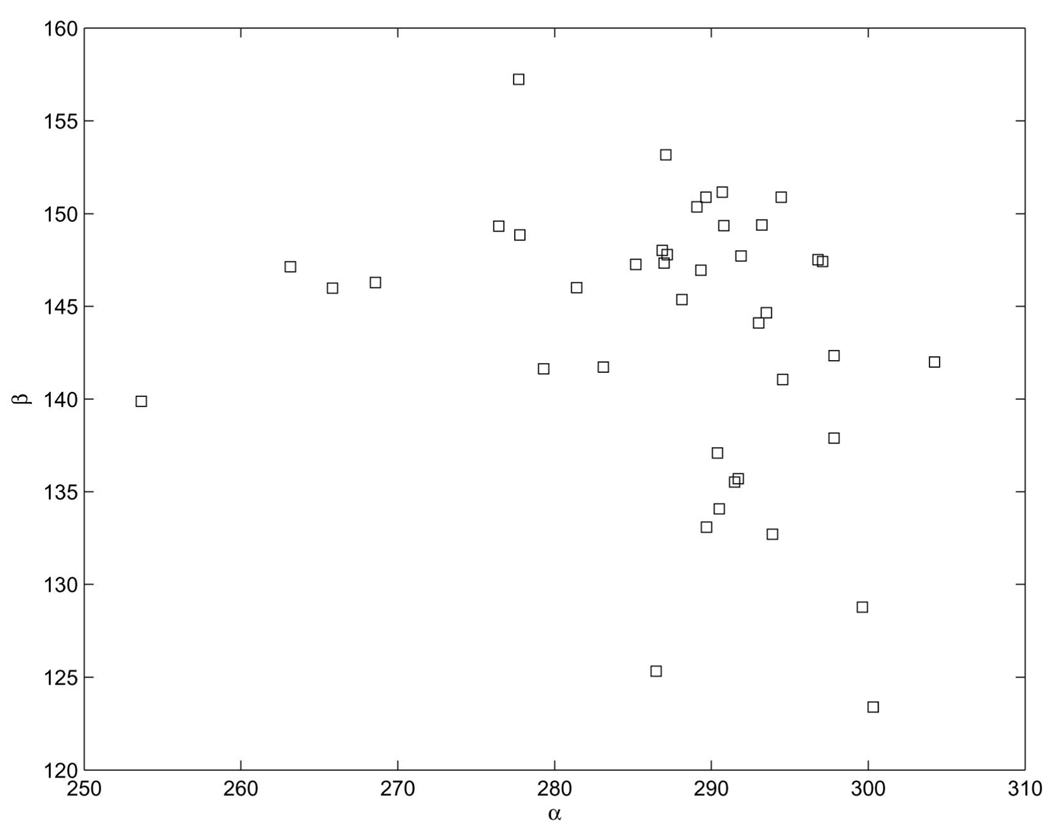
All of the above motifs are characterized by a double helix structure which may be twisted or bulged. The deformation is a result of a base pair mismatch. This is a secondary structural characteristic. We can find also a unique conformation in almost all of the above-mentioned cases. After a base pair mismatch, the residue acquires the conformation marked by “A.” This conformation is a single cluster. The identifier torsional angles of this conformation have the same values as that of the A-form helix. The only difference is that the β value is shifted to the shoulder of the main peak in the histogram of β. See also [28] for related results.

The α, β plot of this cluster is given in Fig. 9. The binning method (even with scalar quantization) as well as 4D VQ cannot recognize this cluster, while the full seven-dimensional VQ can. A similar cluster was found with the electron density technique in [28]. This conformation appears in the following locations:

1. Hyper-Twist: 25, 818, 1,590, 2,504.

2. Kink-Turn: 48, 98, 265, 1,152.

3. E-motif: 176, 214, 359,1,073, 1,371, 2,693.

Fig. 9.

The α, β torsional angles of the “A” cluster.

There is a generalization of the hyper-twist, that is a mismatched double strand that includes the “A” conformation in:

$$\begin{array}{c}721\in (716-726,702-712),\hfill \\ \mathrm{1,032}\in (\mathrm{1,031}-\mathrm{1,041},929-939),\hfill \\ \mathrm{1,742}\in (\mathrm{1,733}-\mathrm{1,744},\mathrm{2,035}-\mathrm{2,046}),\hfill \\ \mathrm{1,528}\in (\mathrm{1,527}-\mathrm{1,534},\mathrm{1,657}-\mathrm{1,664}),\hfill \\ \mathrm{2,827}\in (\mathrm{2,826}-\mathrm{2,830},\mathrm{2,910}-\mathrm{2,914}),\hfill \\ \mathrm{2,883}\in (\mathrm{2,880}-\mathrm{2,889},\mathrm{2,868}-\mathrm{2,877}).\hfill \end{array}$$

The conformation of this double strand is less conserved than the hypertwist.

Other “bulge motifs” with pair mismatches include 442, 465, 489, 593, 2,244, 2,427, 2,259, 2,906, as well as the short double helix with internal loop, 2,427. Some more complicated mismatch structures are

• 382, 489, 645, 1,528, 1,891, 1,973, 2,485, 2,675, 2,817, 2,904.

The conformation “A” appears in three places where it cannot be associated with mismatched structures.

5.6 Helix Initiation Knee

The helix initiation knee is a motif that has a bend at the beginning of a helix [28]. As its name implies, such a motif is associated with a “knee” between two adjacent helices. This occurs, for example, in the case of the “knee” between the T stem and the acceptor stem. We defined this motif to have the binning sequence “taaa”; see Table 9. We found this form to repeat 19 times in RR0033. Table 9 summarizes the search results for this motif.

TABLE 9.

Results for Double Helix Initiator Element

First Residue	Sequence	Conventional Definition	Binning Structure	4D VQ	7D VQ
116	GAGA	Double Helix	taaa	taaa	taaa
398	UCCC	Double Helix	taaa	taaa	taaa
636	GCCA	Double Helix	taaa	taaa	taaa
762	CCCG	Double Helix	taaa	taaa	taaa
826	UAGA	Double Helix	taaa	taaa	taaa
895	ACAG	Double Helix	taan	taaa	taae
961	ACCG		taaa	taaa	taaa
1089	GAUA	Double Helix	taaa	taaa	taaa
1138	GUCU	Double Helix	taaa	taaa	taaa
1177	AGCU		paaa	taaa	taaa
1703	GGCG	Double Helix	taaa	taaa	taaa
1986	GCCG	Double Helix	taaa	taaa	taaa
2023	GAGC	Double Helix	taaa	taaa	taaa
2059	UACA		taaa	taaa	taaa
2084	CACC	Double Helix	taaa	taaa	taaa
2284	GGGC		taaa	taaa	taaa
2444	UUGA	Double Helix	taaa	taaa	taaa
2566	AGAA		taaa	taaa	taaa
2738	GAGA	Double Helix	taaa	taaa	taaa
2750	GCCG	Double Helix	paaa	taaa	taaa
2840	AAGA		paaa	taaa	taaa

From the 21 structures that were found to be in the desired conformation (see Table 9), only six were not initiating a double helix and, also within these six cases, there are a large number of tertiary interactions with other parts of the LSU. The differences among the methods are minimal and are mostly confined to the case where t (1111) is changed with the transition state p in the binning method (4,111) (which includes the “other” region absent in the VQ method).

Another type of helix initiation motif has a typical conformation of “vaaa” in one of the strands. The “va” conformation was recognized in [28]. There were 13 such structures and they are summarized in Table 10.

TABLE 10.

Results for Double Helix Initiator “v” Element

First Residue	Sequence	Conventional Definition	Binning Structure	4D VQ	7D VQ
169	AUCU		1aaa	vaaa	vaaa
331	AGGG	3-Double Helix	vaaa	vaaa	vaaa
620	ACGU	Double Helix	vaaa	vaaa	vaaa
905	CCAA	Double Helix	vaaa	vaaa	vaaa
1239	GGGA	Double Helix	vaaa	vaaa	vaaa
1438	GCUG	3-Double Helix	1aaa	vaaa	vaae
1626	AGGG	2-Double Helix	vaaa	vaaa	vaaa
1634	GUGA	Double Helix	0aaa	vaaa	vaaa
1710	AAAG	3-Double Helix	1aaa	vaaa	vaaa
1919	ACAA		*aaa	vaaa	vaaa
1996	UAGC	bulged Double Helix	1aaa	vaaa	vaaa
2526	CUUG	3-Double Helix	*aaa	vaaa	vaaa
2638	GGUC	Double Helix	vaaa	vaaa	vaaa

There is full agreement between the 4D and the 7D VQs. Only seven of the above examples have the same binning structure. The three-double helix is a structure where the first residue in the “v” conformation is unpaired. It seems that, for this motif, the binning definition of the “v” conformation gives a more uniform motif. This will be addressed in more detail in Section 6 below.

6 DISCUSSION

RNA conformational motifs were characterized here with statistical techniques from classical signal processing. These automatic procedures do not use visual inspection or filtering. The overriding goal is to establish fast and easily applied yet rigorous methods for analysis of RNA conformation. The simplest method used here, scalar quantization, treats each dimension in isolation of the others. SQ successfully resolves the torsion angle ζ into the three distinct clusters (three rotamers) predicted by the potential energy surface. This resolution of ζ into three was not accomplished in [10] and was found by visual inspection in [20] only after application of quality filters. This is achieved following well-defined criteria, as well as the automatic analysis of multiple angles at once. As we have noted, we do not claim that clustering analysis in torsion angle space is the only or even best method for finding motifs, but simply a logical one which is very easy to use and can form part of more comprehensive criteria.

With VQ, populated clusters of RNA conformation are determined in simultaneous analysis of any dimensionality, up to the full seven-dimensional torsional space. We believe this work represents the first analysis of RNA torsional space at greater than three simultaneous dimensions (i.e., of more than three torsion angles). Although VQ was used in this work as the basis for our automatic analysis, other high-dimensional clustering techniques can be used as well. Here, four-dimensional VQ was applied first to the four angles (α, γ, δ, ζ) that have previously been termed “identifier angles” [10] because they appear to completely specify fundamental RNA conformations. The remaining three dimensions are considered to be dependent on the four identifier angles, although they are important for conformations search, see below. Based on the distortion measure from VQ, the number of four-dimensional clusters was experimentally found by 4D VQ to be about 60. This result suggests that there are about 60 fundamentally distinct nucleotide conformational states within globular RNA, although the subject of finding the exact number of conformational states (which can be resolution and task dependent) needs further investigation. The 4D VQ identified each of the populated bins reported in [10], which were obtained via manual classification. Agreement with SCOR was found as well.

We then added a merging stage to the VQ method, which is based both on cluster centroid proximity and on structural constraints, thereby adapting the generic VQ technique to the study of RNA torsion angles. For example, all clusters that meet the definition of A-helical RNA were merged into a single cluster. This initial overpopulation of A-helical RNA clusters was expected since, due to their popularity, VQ allocates to them a large number of resources (centroids) in order to minimize the distortion.¹⁵

We then used this modified VQ on the full set of seven torsion angles defined by a single nucleic acid residue. This study of the full seven-dimensional space led to new conformations that were not present at the one or four-dimensional studies. We validated the method by comparing it with known structural motifs, as well as the SCOR classification. The minor mismatches could be a result of a too coarse clustering (different motifs merged into a single cluster). We tested adding clusters (up to 100) and found small changes that are enough to fix these discrepancies (while requiring additional merging to eliminate the not-novel clusters).

It is important to note that neither SCOR nor our results are complete. The “true” definition of a given motif should involve the combination of a rotameric state (as is argued in this paper) and sequence information (which is the basis of SCOR). We believe that one of the contributions of our research is to start to develop a rotameric contribution to this definition.

We found a conformational signature for the existence of a mismatch motif, an umbrella motif that includes the bulging or twisted double-stranded cases. We found this conformation only when we used the modified 7D VQ, showing the importance of working with the whole conformational space and, thereby, the need for a formal analysis technique, such as the one described here, that go beyond ad hoc visualization-based approaches.

In the next step (in progress), we will seek the relationship between neighboring clusters using the method of mutual information. As has been done for secondary structures in protein research, e.g., [6], it is important to study the dispersion within clusters. It seems likely that information on shapes of potential energy surfaces and RNA dynamics is contained within the cluster shape. Finally, following work on proteins [6], we can also perform principal component analysis (PCA) on various clusters.

To conclude, in this paper, we have seen how some standard techniques from statistical signal processing are useful for the analysis of RNA structure. These techniques cover from the automatic finding of torsion angles clusters and their grouping into motifs, to the analysis of motif populations. These techniques can be augmented with novel clustering approaches being developed by the learning and signal processing communities and investigating those, together with the search for new motifs, is the subject of some of our current efforts.

Biographies

Eli Hershkovits received the BA degree in mathematics and physics in 1988 from the Hebrew University, the MSc degree in physics from the Weizmann institute of Science, Rehovot in 1991, and the PhD degree in physics from the Weizmann Institute of Science in 1997. He is presently a research scientist in the School of Electrical and Computer Engineering at the Georgia Institute of Technology, Atlanta. His research interests include bioinformatics, the study of RNA conformations, and stochastic perturbation methods in physical chemistry.

Guillermo Sapiro received the BSc (summa cum laude), MSc, and PhD degrees from the Department of Electrical Engineering at the Technion, Israel Institute of Technology, in 1989, 1991, and 1993, respectively. After post-doctoral research at the Massachusetts Institute of Technology, he became a member of the technical staff at the research facilities of HP Labs in Palo Alto, California. He is currently with the Department of Electrical and Computer Engineering at the University of Minnesota, where he holds the position of Distinguished McKnight University Professor. He works on differential geometry and geometric partial differential equations, both in theory and applications in computer vision, computer graphics, medical imaging, computational biology, and image analysis. He recently coedited a special issue of IEEE Image Processing on this topic and a second one in the Journal of Visual Communication and Image Representation. He has authored and coauthored numerous papers in this area and has written a book published by Cambridge University Press, January 2001. He was awarded the Gutwirth Scholarship for Special Excellence in Graduate Studies in 1991, the Ollendorff Fellowship for Excellence in Vision and Image Understanding Work in 1992, the Rothschild Fellowship for Post-Doctoral Studies in 1993, the US Office of Naval Research Young Investigator Award in 1998, the Presidential Early Career Awards for Scientist and Engineers (PECASE) in 1998, and the US National Science Foundation Career Award in 1999. He is a member of the IEEE and SIAM.

Allen Tannenbaum received the PhD degree in mathematics from Harvard in 1976. He has held faculty positions at the Weizmann Institute of Science, McGill University, ETH in Zurich, Technion, Ben-Gurion University of the Negev, and the University of Minnesota. He is presently the Julian Hightower Professor of Electrical and Biomedical Engineering at the Georgia Institute of Technology/Emory University. He has done research in image processing, medical imaging, computer vision, robust control, systems theory, robotics, semiconductor process control, operator theory, functional analysis, cryptography, algebraic geometry, and invariant theory.

Loren Dean Williams received the BSc degree in chemistry from the University of Washington in 1981, where he worked in the laboratory of Martin Gouterman. In 1985, he received the PhD degree in physical chemistry from Duke University, where he worked in the laboratory of Barbara Shaw. He was an American Cancer Society Postdoctoral Fellow, first at Duke University, then at Harvard University. From 1988 to 1992, he was an NIH Postdoctoral Fellow in the laboratory of Alex Rich in the Department of Biology at the Massachusetts Institute of Technology. He joined the School of Chemistry and Biochemistry at the Georgia Institute of Technology in 1992. He was promoted to associate professor in 1996 and to full professor in 2000. He received a US National Science Foundation CAREER Award in 1995 and the Sigma Xi Award for best paper from Georgia Tech in 1996. He is a member of the American Cancer Society Review Panel (Molecular Mechanisms in Cancer).

APPENDIX

BACKGROUND ON THE BINNING METHOD

In this appendix, for the convenience of the reader, we briefly review the main results reported in [10]. We introduce here some minor modifications in order just to elucidate the main ideas. We finally repeat some of the key tables from [10] for easy reference on the part of the reader.

Binning as formulated in [10] is a histogram-based method for describing RNA conformation and for identifying RNA tertiary structural motifs. The conformation of each bond can be described by a small number of discrete integers. Each residue can be assigned to a distinct configuration class. Further, some of the torsion angles are dependent or highly restrained. In summary, one can reduce the full multidimensional torsion angle space to a set of 38 configuration classes. An ASCII code can be assigned to each configuration class. Thus, the three-dimensional description of conformation is reduced to a single dimension.

More precisely, each torsion angle of a given residue is allocated to the appropriate bin. By definition, torsion angles with single-peak distributions cannot be readily separated into distinct bins because, essentially, all the angles are contained under a single envelope. Because of this, the angles β, ε, and χ are assumed not to contribute information to the conformational description and are ignored; see [10]. Because of their multipeaked nature, the remaining four torsion angles and P allow a straightforward separation into distinct configuration classes. However, δ and P are correlated, both by geometric definition and from analysis of the HM 23S rRNA data. Thus, to avoid redundancy, we eliminate P and consider only four torsion angles, α, γ, δ, and ζ. The reduction in parameters led us to a four digit structural representation of the conformation of a given residue. Each residue is assigned a sequence of four integers, n_α, n_γ, n_δ, n_ζ, where each digit denotes the envelope to which a torsion angle belongs.

Binning has several important advantages:

1. It allows one to exploit the large and sophisticated pattern recognition capabilities already developed for one-dimensional databases.

2. It allows one to combine sequence and conformational information in the same one-dimensional representation, for example, by interleaving the ASCII binning characters with sequence characters.

3. It allows one to represent conformational information along with base-pairing, tertiary interaction, etc., in simple two-dimensional representations.

4. It can be readily tuned to a given organism, class of RNA, etc.

5. It is relatively easy to implement, and may be automated in the manner indicated in this paper.

The results of the method in [10] are summarized in Table 11 and Table 12.

TABLE 11.

Enumeration and Borders of the Bins from [10]

bin index	1	2	3	4
α	[40 – 100]	[125 – 200]	[220 – 350]	others
γ	[10 – 110]	[140 – 210]	[230 – 350]	others
δ	[65 – 105]	[130 – 165]	others
ζ	[240 – 350]	others