Abstract
Physics-based simulation is needed to understand the function of biological structures and can be applied across a wide range of scales, from molecules to organisms. Simbios (the National Center for Physics-Based Simulation of Biological Structures, http://www.simbios.stanford.edu/) is one of seven NIH-supported National Centers for Biomedical Computation. This article provides an overview of the mission and achievements of Simbios, and describes its place within systems biology. Understanding the interactions between various parts of a biological system and integrating this information to understand how biological systems function is the goal of systems biology. Many important biological systems comprise complex structural systems whose components interact through the exchange of physical forces, and whose movement and function is dictated by those forces. In particular, systems that are made of multiple identifiable components that move relative to one another in a constrained manner are multibody systems. Simbios’ focus is creating methods for their simulation. Simbios is also investigating the biomechanical forces that govern fluid flow through deformable vessels, a central problem in cardiovascular dynamics. In this application, the system is governed by the interplay of classical forces, but the motion is distributed smoothly through the materials and fluids, requiring the use of continuum methods. In addition to the research aims, Simbios is working to disseminate information, software and other resources relevant to biological systems in motion.
Keywords: Biomedical computation, cardiovascular dynamics, dynamics, neuromuscular biomechanics, physics-based, protein folding, RNA folding, simulation
I. INTRODUCTION
In 1999, a panel of biomedical researchers was convened by the Director of the National Institutes of Health (NIH) to comment on the future of computation in biomedical research. The panel was chaired by a biologist, David Botstein, and a computer scientist, Larry Smarr, and made several important recommendations. In addition to goals for education, the panel stressed the need for NIH to create a set of centers for biomedical computing which would bring computation to biomedical research, in a way that it has been brought to virtually all other research agendas. The panel noted that for many reasons, biomedical research had not developed a strong cadre of researchers with a primary identification with computation as their niche, and with the ability to sit at the table of discussions among federal agencies about mission-critical computing needs. In addition, the panel noted that many areas of biomedical research were currently not taking sufficient advantage of computing to accelerate discovery and translation. In response to these recommendations, the NIH created a broad set of programs. One of the programs was the creation of several National Centers for Biomedical Computing (NCBCs) that would serve as focal points for research in strategic areas of biomedical computation. Each NCBC would be associated with independent, NIH-peer-reviewed biological projects that drive basic computer science and computational science research. The NCBCs were charged with acting as hubs for a nascent national network of biomedical computational capabilities, and had missions in primary research, software dissemination, education, and outreach. Seven National Centers for Biomedical Computing (NCBC) were funded under the NIH Roadmap for Bioinformatics and Computational Biology http://www.nihroadmap.nih.gov bioinformatics. The seven sites covered a broad array of biomedical research including systems biology, image processing, biophysical modeling, biomedical ontologies, information integration, and tools for gene-phenotype and disease analysis.
As part of their mission, the centers are expected to create innovative software tools that enable the biomedical community to integrate, analyze, model, simulate, and share data on human health and disease. Each Center has cores that are focused on (1) computational science, (2) biomedical computational science and (3) driving biological projects whose intent is to focus the interaction between computational and biomedical computational science.
The mission of Simbios, a center for physics-based simulation of biological structures, includes modeling and simulation of the dynamics of biological structures at several scales. In general, these are complex systems comprising physical parts that interact via the exchange of forces. In particular, systems that are made of separate, identifiable components that move relative to one another in a constrained manner are multibody systems, a paradigm that leads to useful models in several biological applications at many scales. Neuromuscular dynamics, which includes the study of movement arising from the coordinated excitation of many muscles, has been advanced by analyzing the musculoskeletal system as a multibody system, using rigid bodies for bones and treating muscles as force-generating elements, [1]. At a much smaller scale, the dynamics and structure of proteins and RNA can also be modeled with multibody methods. This includes the study of the mechanism of molecular folding as well as the study of the different conformations adopted along the folding pathways. One such example is the study of the RNA folding landscape, [2], [3]. Molecular motors or protein machines, such as myosins, are another example of molecular structures [4], which may be represented as multibody dynamic systems. The scope of Simbios is currently restricted to RNA and protein structures, but may extend in the future as we embrace new scientific challenges, perhaps involving DNA or lipid structure. In the limit, fluids and flexible structures could be considered multibody systems made of large numbers of individually indistinguishable molecules. However, the continuous distribution of matter, forces, and motion in these systems make continuum methods a better choice. In these cases, we use continuum models to represent fluid flow and fluid/structure coupling such as blood flow through deformable vessels, a central problem in cardiovascular dynamics. Taken together, these biological problems in neuromuscular dynamics, molecular simulation (currently RNA and protein), and cardiovascular fluid/structure dynamics form the basis for the algorithmic research and application software goals at Simbios.
There is tremendous excitement and potential associated with the emergence of systems biology in the last few years. Systems biology is defined in many ways, but usually includes quantitative approaches to integrated representations of biology. It differs, therefore, from traditional approaches to biology in its use of formal quantitative representations (including ordinary or partial differential equations and/or network representations of interacting biological entities), and in its goal of describing emergent biological phenomena (phenotypes) that are not easily studied in reduced systems. Furthermore, systems biology is often (but not exclusively) associated with approaches that use diffusion-reaction formalism to study the change in spatial and temporal activity of biological molecules over time. Physics-based simulation of biological structures can play an important role in systems biology. Simbios studies systems of physically linked and interacting subunits whose complex structural dynamics leads to phenotypes (functions) of importance. In neuromuscular dynamics, the interacting subunits are bones and muscles, controlled by neural signals from the brain and spinal cord to perform functions such as walking and running. In RNA dynamics, the interacting subunits are the RNA bases forming intricately linked double helices connected by single-stranded regions, controlled by the physical forces (e.g., electrostatics, van der Waals, etc…) that allow RNA to fold, bind and catalyze chemical reactions. In cardiovascular dynamics, the interacting subunits are the constituents of the blood as they interact with the complex topology of the vasculature, controlled by heart rate and vascular resistance to function in the delivery of oxygen and nutrients to tissues, and the transport of associated metabolic products. Thus, Simbios is focused on biological systems that are in motion, and both contain systems that may be described with diffusion-reaction formalisms and also are part of systems that may be described in that manner.
Of course, Simbios does not come to biological dynamics alone. The last thirty years have seen an expansion of modeling efforts throughout biology and medicine. These have included modeling and simulation efforts at widely differing time and length scales, including:
Small molecules. Organic and inorganic compounds can be modeled effectively with molecular mechanics codes, to understand their conformational repertoire and significant degrees of freedom. This information can be used, for example, to estimate the ability of a ligand to bind a target molecule, or to identify a pharmacophore that highlights the key properties required for a class of molecules that share some function, as described for example in [5], [6].
Biological macromolecules. RNA, DNA and Protein molecules can be modeled and simulated using the techniques of molecular dynamics. An extension of the physics required for small molecules, the key forces include electrostatics, van der Waals and covalent bond forces (constraining bond length, bond angle and dihedral angle), [7], [8]. In addition, the aqueous environment and its ionic characteristics are critical.
Biological macromolecular ensembles. Large ensembles of macromolecules can combine to form molecular machines on the nanometer scale. Recent high-resolution determination of some of these machines makes it clear that standard molecular dynamics techniques must be extended to handle these larger complexes, [9]. For example, models of the ribosome and RNA polymerase are now available at high resolution, but our ability to understand how the structures create the associated functions is still poor. Many other large ensembles, including the signal recognition particle, the spliceosome, and others will provide similar challenges.
Cellular models. The creation of physical models of the cell is in its infancy. Part of the reason for slow progress is that the cell represents a difficult modeling scale: the physics of individual molecules are still relevant, but there begins to be a need to aggregate forces, and introduce macroscopic notions of colloidal aggregation, friction, flow and gravity, [10], [11]. Thus, the models at the cellular level (length scales of 0.1 micron to 100 microns) are the most challenging. One of the goals of Simbios is to bring together technologies sufficient for building accurate cell-level models.
Biomechanical models. At length scales from millimeters to meters, there has been successful modeling of the cardiovascular system, respiratory system, skeletal geometry, neuromuscular control of gait, and other macroscopic physiological systems. These systems benefit from the availability of imaging techniques, which provide accurate, high-resolution information about anatomical structures. The tissue properties of these systems, however, are complex and yield a number of research challenges [12], [13].
Structural models have the capability to improve our understanding of a biomedical domain and our ability to create interventions for improved healthcare. In virtually all cases, a structural insight drives the understanding of function. Sometimes, a structural model immediately suggests the mechanism that produces function. Other times, the structural model defines the physical context in a way that defines more precisely how further investigations should proceed.
Limitations in biophysical modeling constrain our ability to capitalize on the explosion of experimental data. For example, functional genomics has been a major area of growth in molecular biology over the last decade. Much of the success of functional genomics can be traced to the successful sequencing of genomes, and the introduction of high throughput mRNA expression measurements with microarrays. Both of these activities are distinctly non-structural. The exciting contributions of these experimental technologies to our biological and medical knowledge base have been substantial. However, further progress may require more structural thinking. For example, the search for the complete set of human genes and the ‘code’ for determining which genes are transcribed (and when) may well require a more complex physical understanding of how DNA is packaged and packed into the nucleus, how it is selectively unpacked in the nucleolus, and what the physical constraints on the structures within the nucleus are.
Simulations are also needed to understand macroscopic system dynamics. Using experiments alone to understand movement dynamics has two fundamental limitations. First, important variables, including the forces that generate movement, are not measurable in experiments. Second, it is difficult to establish cause-effect relationships in complex dynamic systems from experimental data alone. As a result, elucidating the functions of muscles from experiments is not straightforward and no general principles that govern the coordination of voluntary movement have emerged.
A primary benefit of accurate modeling of biological and medical systems is the ability to cheaply (and safely) perform “what if” analyses. At the molecular level, an RNA or protein molecule can be mutated, and the effects of the mutation can be simulated. At the macroscopic level the accurate modeling and simulation of walking can predict the outcome and help in the choice of surgical intervention.
Computational modeling and simulation also allows access to phenomena that cannot currently be experimentally measured. Although simulations are often validated by their ability to correctly predict parameters that are experimentally measured, they also predict parameter values and detailed, time-resolved mechanisms of action that are very difficult to measure experimentally.
Although individual investigators have made elegant contributions to physics-based modeling in biomedicine, the field is fragmented. Modeling applications are typically limited to a single physical scale, and individual investigators frequently must create their own software. These conditions create a major barrier to advancing simulation capabilities. The fields of computational mechanics and biomechanics have produced a set of commercial codes that are broadly used to design and analyze complex dynamical systems, including SD/FAST (http://www.sdfast.com/), ADAMS (http://www.adams.com), and SIMM [14]. For soft-body simulations, many finite-element packages are available, varying from large commercial level codes (e.g., Abaqus, http://www.abaqus.com/) to smaller research-driven codes (e.g., NIKE3D, [15]). There is a large selection of molecular dynamics codes, which include CHARMM [16], Amber [17], Tinker [18]–[20] (http://www.dasher.wustl.edu/tinker/) and Gromacs [21], [22], to list just a few of the more commonly used ones. While these are fundamentally similar to one another in representation and functionality, they are quite different from packages used by those who simulate at other scales.
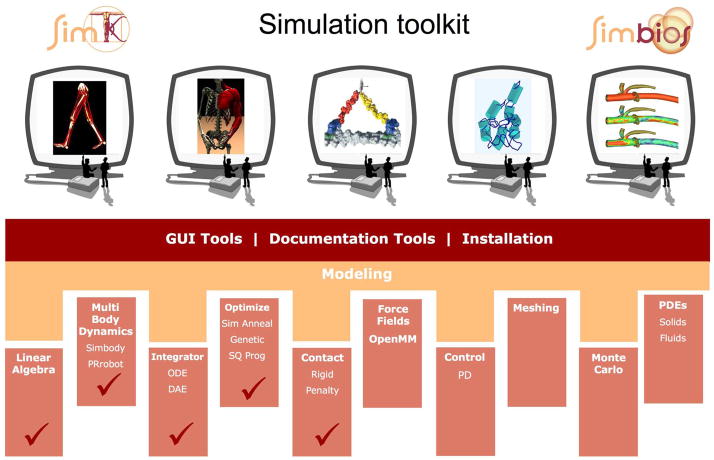
We have seen examples when the tools and techniques of one subdiscipline are needed to solve new problems that arise in another. These examples are particularly abundant at the interface of scales, between 0.1 μm and 0.1 mm (corresponding to 1000 to a million Angstroms), because some molecular forces may still be strong, but mechanical approaches are needed for management of complexity. For example, the motions of molecular motors, require molecular level detail for some analyses, but require mechanical analysis for others. Similarly, the analysis of ribosomal motions during translation can benefit from principles of biomechanical modeling. To facilitate this research we have committed to and are developing a toolkit for simulation: the SimTK Core toolkit (http://www.simtk.org), applicable at a very large range of scales. The creation of tools and their use outside of the research groups that create them is critical for the success of the program. Our tool development is driven by research needs, and their dissemination is enabling new research in the same or new biological applications. In the following section, we describe our open-source software that is needed for multibody systems biology, a multibody dynamics engine called Simbody. We then describe two application areas that are using Simbody for modeling. We then outline our initial efforts in addressing continuum methods for biological systems in motion. Finally, we describe our dissemination efforts to reach researchers from diverse disciplines.
II. SIMBODY: A SimTK CORE TOOLKIT COMPONENT FOR MULTIBODY DYNAMICS
A common feature of biological models at many scales is the presence of discrete, interconnected, near-rigid substructures undergoing substantial relative motion localized to specific hinge points. This description applies equally well to human skeletons as to macromolecules. It is also characteristic of most human-engineered mechanical systems such as vehicles and machinery. The need to model such systems in aerospace and robotics has resulted in an advanced mechanical engineering subdiscipline called multibody dynamics, which provides the ability to accurately simulate systems governed by Newton’s second law, F = ma, in any chosen set of coordinates. This difficult but important technology is ubiquitous in mechanical engineering, but is substantially underutilized in biosimulation. There are a few reasons for this. The techniques have evolved over many years in mechanical engineering and their adoption for biosimulation is challenging. Some of the major obstacles include the large number of degrees of freedom (e.g., the size of these systems), the difficulty of accurate computation of force fields under the multibody representation, and the large investment necessary to produce working software to address these challenges.
Currently multibody dynamics technology is available only to specialists and then usually through use of inflexible commercial software originally designed for use in mechanical engineering. The development of a new multibody code for biosimulation is an interdisciplinary project requiring mechanics, computer science, numerical methods as well as an understanding of the biological domains to which it will be applied. The result is an enabling technology useful in many disciplines, but not specific to any particular biomedical area. Simbody was conceived and developed at Simbios, but builds on classical multibody dynamics, robotics, biomechanics and molecular mechanics technology and open source software [23]–[25]. Simbody employs standard numerical integration techniques and a novel coordinate projection numerical integrator CPODES resulting from collaboration with the Lawrence Livermore National Laboratory’s Center for Applied Scientific Computing [26]–[28] (see: https://simtk.org/home/cpodes).
Simbody is a tool usable by biosimulation researchers for detailed internal coordinate modeling of molecules, for coarse-grained models based on larger atomic groupings, and for large-scale mechanical models, such as neuromuscular models of human gait. The goal is to enable biosimulation researchers to use robust, high-performance multibody dynamics technology in their work whenever appropriate.
A. Simbody Details
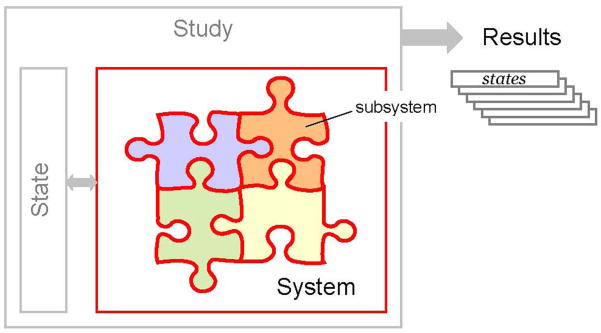
Simbody is an object-oriented, open source C++ programming library. It is not an end-user application program, but rather a toolset that enables biosimulation programmers to incorporate multibody simulation into their own domain-specific, end-user applications. To accomplish this without requiring these programmers to be multibody dynamics experts, Simbody supports a small number of meaningful abstractions that are sufficient for a programmer to use in describing the problem to be solved. Fig. 1 shows the overall structure of a Simbody simulation. The application programmer maps a domain-specific model (say a musculoskeletal system or coarse-grained model of RNA) onto a Simbody System, by using an extensible set of pre-defined Subsystems, or writing their own subsystems. A System is the computational embodiment of a mathematical model, and defines the objects of the model as well as their parameterization (for example, positions and velocities for bodies). However, a System does not contain any particular values for those parameters. Instead, all variation is captured in a separate object, called a State. Finally, there is a Study, which pairs a System and a State and then evolves the State according to specified rules, yielding a trajectory (set of states) as its result. For example, a dynamic study will evolve the system through time in accordance with Newton’s laws, while a Monte Carlo study will generate states that satisfy a prespecified statistical distribution.
Fig. 1.
The high-level structure of a Simbody simulation. The System, composed of independent but interacting subsystems, is the computational representation of a biological model, with specified parameterization. States contain a set of values for each of those parameters, such as the position and velocity of components within the System. A Study produces a trajectory of state values in accordance with some prescribed laws, such as the time evolution of the dynamical equations of motion, or adherence to a particular statistical distribution.
Simbody includes a “matter subsystem” that provides the multibody dynamics capability (independent of application domain) and an assortment of “force subsystems” that act on the matter to produce motion. Almost all of the domain-specific knowledge resides in the nature of the force subsystems, which are allowed to act on the bodies in the matter subsystem. Currently Simbody contains force subsystems useful for modeling gravity, contact, molecular forces, and general mechanical elements such as springs (harmonic restraints), dampers, motors and so on. We expect that biological researchers will extend the current set of subsystems to include domain-specific ones such as muscle models and knowledge-based RNA force fields, and that our user community will ultimately engage in active development and exchange of novel subsystems.
The Simbody matter subsystem encapsulates all the multibody dynamics technology. An application programmer interacts with that subsystem by specifying a model consisting of bodies and joints, where the bodies represent some aggregation of matter and the joints represent the mobility of that matter. Any model of matter and motion from a single rigid body, to bodies with selected internal coordinates, to thousands of individually mobile atoms can be accommodated within the same framework, with performance improving dramatically when the number of coordinates is reduced. Simbody provides all the tools needed to convert efficiently between the chosen set of generalized coordinates and the configuration and motion of the bodies in conventional Cartesian space. This permits the use of conventional Cartesian-space force models (Coulomb interactions or foot/ground interaction models, for example) with any coarse-grained multibody model. Additional details on Simbody are available at https://simtk.org/home/simbody.
We next discuss the use of Simbody in Neuromuscular Dynamics and RNA folding. It is worth noting that a researcher interested in one or the other of these two biological areas may be indifferent to the fact that the same code is also used in another very different biological application. There are however subtle advantages. Multibody dynamics has been used in the field of Neuromuscular Biomechanics for several years. Simbody will replace and enhance the capabilities of more mature codes, such as SD/FAST, and allow researchers to extend its capabilities. On the other hand, other application areas, such as molecular dynamics, will benefit from using a library that has been extensively tested in a previous application domain. Cross-fertilization of tools from one application area to another application area is something that national centers such as Simbios are well positioned to contribute.
III. USE OF MULTIBODY DYNAMICS IN BIOLOGICAL APPLICATIONS
Multibody dynamic modeling is an important component for the neuromuscular and molecular dynamics research efforts. The neuromuscular biomechanics research described in the next section has traditionally used a commercial multibody code to model skeletal mechanics. Because this code cannot be modified, some modeling tasks have been time consuming and awkward. For example, a one degree-of-freedom knee joint connecting three rigid bodies required eleven constraint equations, but can be modeled with Simbody through a custom knee joint with identical behavior and only a single equation. This has the potential for dramatic performance improvement for these models, which must be run repeatedly to develop patient-specific simulations. Dependence on commercial software is also problematic for distribution of the otherwise open source Simbios applications to other neuromuscular research groups. Our neuromuscular simulation platform, called OpenSim, has been converted to use Simbody. Our research in RNA folding seeks to understand RNA structure formation through coarse-grained modeling. Multibody methods have been shown effective for simulation of large biomolecules [26], but the methods and software used have not been available to other researchers. Simbody is specifically addressing this need and along with our open source application ToRNAdo (simtk.org/home/rna-viz-proto) for RNA modeling and simulation, is being investigated as an effective tool to extend the class of models, which can be studied with coarse-grained simulations. Other Simbios collaborations that can also take advantage of Simbody include Pengyu Ren at U.T. Austin, who is working on ellipsoidal nucleic acid models, which can be naturally modeled in a multibody framework [27].
A. Neuromuscular Biomechanics
Investigators in neuromuscular biomechanics bring together computational physics, neuroscience, and robotics to analyze muscle form and function, study human movement, design medical technologies, and guide surgery. Fundamental understanding of the mechanisms involved in the production of movement is essential and may lead to opportunities to improve treatments for individuals with impaired motion, such as patients with cerebral palsy. Computer simulations provide a powerful framework for investigating how the elements of the neuromusculoskeletal system interact to produce human movement. Neuromuscular simulations have now become widely used to study neural control, design surgical procedures and analyze biomedical devices.
Muscle-actuated simulations allow one to study how the elements of the neuromusculoskeletal system function together to generate movement. Although the value of simulation is broadly recognized and individual investigators have made elegant contributions, the field remains fragmented. Many laboratories develop their own custom simulation software, making it difficult for a simulation to be reproduced, evaluated, and used outside the laboratory where it was developed. In addition, since software tools are not freely accessible for assisting in the development and analysis of musculoskeletal simulations, researchers typically must spend a great deal of time implementing each new simulation and creating tools to analyze it. As a result, many laboratories cannot dedicate the resources needed to generate their own simulations. These conditions create a major barrier to advancing simulation technology and achieving the scientific potential of neuromuscular simulation.
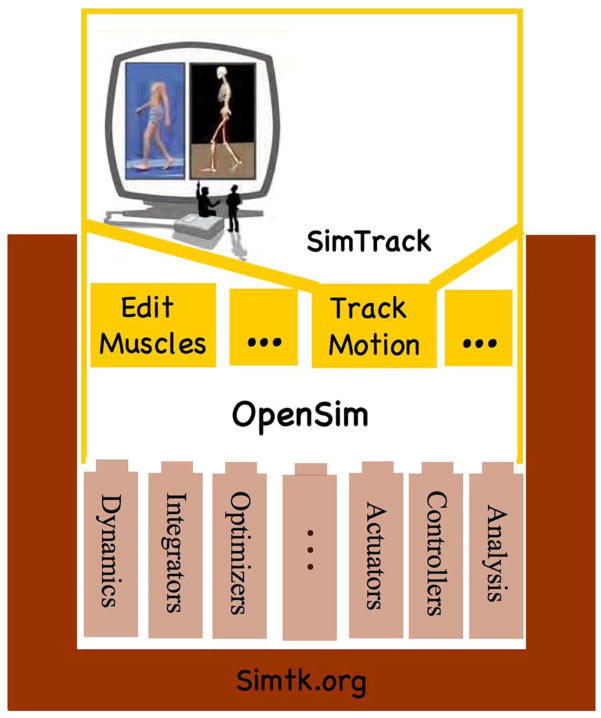
We have established a freely available open-source simulation platform, called OpenSim, to accelerate the development and sharing of simulation technology and to integrate dynamic simulations into the field of movement science. OpenSim is an object-oriented software platform written in C++ for modeling, simulating, and analyzing the musculoskeletal system (Fig. 2).
Fig. 2.
Schematic of OpenSim, an open source software system for modeling, simulating, and analyzing the neuromusculoskeletal system.
It is built on computational components that are part of SimTK core, such as Simbody, and that allow one to derive equations of motion for dynamical systems, perform numerical integration, and solve constrained non-linear optimization problems. Users can extend OpenSim by writing their own plug-ins for specialized controllers, analyses, actuators, and contact forces. A graphical user interface, written in Java, allows users to view models, edit muscles, and plot results. SIMM models [29] can be imported and analyzed. SimTrack, a set of tools in OpenSim, enables muscle-driven simulations to be generated that accurately represent the dynamics of individual subjects [30]. OpenSim is being developed and maintained on Simtk.org. All of the software is freely available. OpenSim provides a platform on which the biomechanics community can build a library of models and simulations that can be exchanged, tested, analyzed, and improved through multi-institutional collaboration.
The architecture of OpenSim encourages users to extend functionality by developing their own muscle models, contact models, controllers, and analyses. For example, over ten analysis plug-ins, authored by different users, are currently available in OpenSim. These analyses compute muscle moment arms and lengths, joint forces, muscle-induced accelerations, and other variables. Although these analyses were developed for different models, they have general applicability and can be used with any OpenSim model. The plug-in architecture of OpenSim thus provides a means of rapidly disseminating new functionality to the biomechanics community.
Historically, optimal control has been used to generate muscle-actuated simulations. Even with parallel computing, generating these solutions has been extremely costly (e.g., [31]). Recent advances have made it possible to generate simulations in minutes. With OpenSim, it is now practical to generate simulations on a per-subject basis. This opens up new possibilities for the use of simulation, including, for example, using simulation to assist in identifying the causes of a movement abnormality and evaluating potential treatments for an individual.
We believe the adoption of a community-owned open-source software platform for simulating and analyzing the musculoskeletal system will accelerate research. A common platform means that models can be evaluated and simulations can be reproduced. When a simulation is developed, it can be posted on Simtk.org, allowing anyone to download, evaluate, analyze, and extend it. Having access to the source code means that the mathematics underlying musculoskeletal models can be critically reviewed and improved. OpenSim has been seeded with an initial set of capabilities. Our hope is that the broader biomechanics community will not only use OpenSim, but also engage in its development by extending its functionality, building new models, and contributing new simulations.
OpenSim is used by a group of biomechanics researchers around the world. With the recent OpenSim 1.0 and subsequent 1.1 releases, we expect to engage an even larger group of users and developers.
B. RNA Dynamics
RNA is a unique biological polymer from both a functional and structural perspective. RNA’s ability to act as a messenger of genetic information (mRNA) and carry out complex chemical reactions in the cell distinguishes it from other biopolymers [32]–[34]. To carry out catalysis, RNA molecules adopt complex three-dimensional structures that define a highly specific active site. Our understanding of RNA folding is limited compared to protein folding [35]. The recent discovery of novel RNA regulatory elements in bacteria (known as riboswitches [36]) and the crystal structures of the 30S and 50S ribosomal subunits [37]–[39] emphasize the importance of improving our understanding of RNA folding. Our efforts in RNA dynamics aim at understanding and modeling the dynamic processes that allow a large, single-stranded RNA molecule to fold into an active conformation.
A notable characteristic of the RNA folding process is the presence of multiple, long-lived intermediates along the folding pathways. RNA folding is not a linear process, but occurs through multiple parallel pathways [3]. To address the specific challenges of the RNA folding problem computational tools are needed by the community.
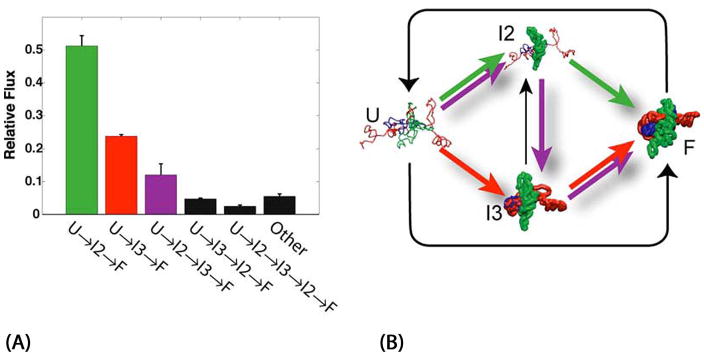
Simulating RNA folding dynamics from experimental data is difficult for a number of reasons. Chief among them are (1) we do not know the precise forces that act upon RNA during folding, and (2) there are many degrees of freedom in an RNA molecule, and so the search for the correct folding trajectories occurs in a very large search space. We are approaching the first of these challenges by augmenting physical theory with experimental measurements that enable us to measure some of the forces (either directly or indirectly) as we watch their effects on the structure. Towards this end, we are creating software for a number of challenges that arise. First, we are creating software to assist experimentalists in collecting and processing high-throughput data sets of RNA molecules as they fold [40]. Second, we are creating software to assist in the interpretation of these data and the creation of models of the interconversion between intermediate structures over time, thus building kinetic models of RNA folding, as shown in Fig. 3 and Fig. 4(A), [3]. Third, we are building tools to visualize structural models of the kinetic intermediates, and animations of their interconversion during folding (https://simtk.org/home/nast), Fig. 4(B). Fourth, we are developing fast codes for estimating the electrostatic forces around RNA molecules, since they are dominant in RNA stability and function.
Fig. 3.
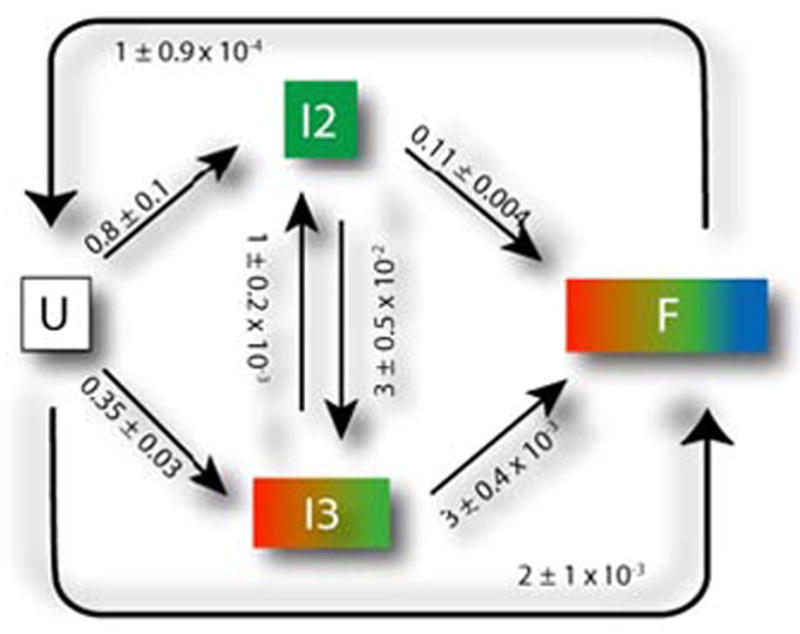
Kinetic model for folding of L-21 T. thermophila group I intron based on a KinFold [3] analysis. The rates and model topology are automatically determined based on experimental footprinting measurements. U is the unfolded RNA. F is the fully folded RNA. Time-resolved experimental measurements of the folding process are consistent with a model of two intermediates (I2 and I3) that can interconvert between one another, but which eventually should transition to the folded F conformation. Fig. 4 shows a statistical analysis of the most likely paths through this network, based on a discrete modeling.
Fig. 4.
(A) Analysis of the kinetic model determines the flux through the different pathways of the folding landscape. 50% of the molecules follow the major folding pathway, U → I2 → F (shown in green). The other 50% of molecules take an alternative path to the F state. (B) We modeled the intermediates shown in the right hand pane based on experimental data, which provides low-resolution structural information suitable for coarse-grain (one ball per RNA base) modeling.
The second challenge to RNA folding (a large number of degrees of freedom), can be approached using multibody dynamics and internal coordinates in the framework of Simbody. In particular, some parts of the RNA form relatively rigid units (most notably double helices) whose degrees of freedom are substantially reduced, and which can, to a first approximation, be modeled as rigid units. The subunits (individual RNA bases) that make up an RNA double helix have seven degrees of freedom each, and so a rigid double helix with two strands of 10 bases each removes 20 × 7 = 140 degrees of freedom from the system. RNA molecules may have 30–50% or more of their bases involved in double helices, and so there is a great simplification of the conformational search space by modeling RNA not as a collection of thousands of atoms with individual freedom in cartesian space, but as a set of linked subunits (some as helices, some as individual bases) with degrees of freedom added only where needed. This representation is precisely analogous to the representation of bones and muscles in neuromuscular dynamics, and so Simbody will allow us to perform conformational modeling and search in this markedly reduced search space. When coupled with the experimental and theoretical representation of the forces on these rigid bodies, we will be able to fully model the picture of RNA folding that emerges from the experimental data.
Simbody is intended to work for molecule models of up to approximately 2000 internal degrees of freedom. This corresponds to, for example, a molecule with 400 nucleotides and 30% of its bases in rigid helices. While the number of possible conformations for an RNA molecule with n degrees of freedom is exponential n, even if we assume that each degree of freedom yields only a constant number of possible states, the methods described here do not suggest exploring all possible states, but instead to follow a trajectory guided by physical forces. Determining the number of steps necessary to perform a simulation that yields meaningful results remains a challenge and will have to be addressed in each simulation.
Coarse graining, as described, should be possible in most cases to substantially reduce the number of coordinates. Fewer coordinates both reduce processing time and reduce the number of steps needed to produce a given result.
In order to map the RNA dynamics modeling problem to Simbody, we must create the following capabilities:
Determine the system of interest and the relevant properties of its environment.
Develop a model for each of the molecules of interest in which the atoms have been grouped into bodies whose relative motion is expected to contribute meaningfully to the results.
Determine the appropriate mobilities of the resulting bodies. This is typically specified for each body with respect to another body in the system called its “parent” body. For example, one may determine that a body moves only by rotation about an axis fixed in its parent, or by reorienting arbitrarily with respect to its parent, or by some combination of rotation and translation.
Map the mobilities into Simbody’s joints and constraints, so that the combination yields the desired mobility for the system as a whole.
Encapsulate desired forces into a Simbody force subsystem, which will have access to the bodies in the matter subsystem as needed for applying forces. Forces may be any combination of first-principles physical forces and empirically-derived knowledge based force fields.
Choose an appropriate numerical method for generating the desired trajectories. This may be forward dynamic simulation using a variety of numerical integration methods, or Monte Carlo sampling, or another method such as minimization or optimization.
C. Protein Folding
Current limitations of both simulation and experiment suggest that an ultimate understanding of protein folding will likely come from a coupled approach of detailed simulations validated and tested by experiment. This is particularly true if one seeks to understand the folding kinetics of proteins and protein-protein complexes. Simulations that can quantitatively mimic experimental kinetics remain a great theoretical challenge due to the long timescales involved and the difficulties and complexities of detailed, atomistic models. Molecular Dynamics approaches and associated software to simulate protein folding [17]–[22] have been developed and made available for many years. While the forces that act upon proteins during folding are somewhat well understood, two big challenges have yet to be addressed: 1) the ability to run simulations that are long enough for a protein to fold, 2) the ability to understand the folding process by simulating a multitude of trajectories and comparing results.
The challenge of obtaining simulations that result in a folded protein can, similarly to RNA, be approached using multibody dynamics and internal coordinates in the Simbody framework, which is one of the reasons this is an area of focus for Simbios. This is in fact the method most commonly used for computing protein structures from NMR data [23]. Protein domains also form relatively rigid units (such as helices) whose degrees of freedom are substantially reduced, when modeled as rigid units. The subunits (individual amino acids) have 2–6 internal degrees of freedom (depending on side chains and modeling choices), which are eliminated when modeling them within a rigid unit. Simbody will hence allows investigators to perform conformational modeling and search in this reduced search space for proteins as well. To account for water, which plays an essential role in protein folding, implicit solvent models will be used, [41].
In order to accurately model the folding kinetics of proteins (in addition to structure prediction), full atomic representations may be necessary. Here the basic methods are more clear, but performance is more problematic. The folding time of a typical protein can easily be 10 to 100 microseconds or more. Currently, even 10 microseconds of a full atomic simulation can take months of simulation time. Running longer simulations can be achieved through hardware acceleration, such as GPUs, [42], see also https://simtk.org/xml/protein-folding.xml. Producing hundreds of trajectories is possible through a distributed computing environment such as Folding@ home, [43]. Folding is a stochastic process, with an exponential distribution, hence there is a significant probability of trajectories that are shorter than the average folding time. Using Molecular Dynamics we have produced hundreds of trajectories (each longer than a single microsecond) of the 36 residue villin headpiece and have seen 35 simulations that have folded.
D. Cardiovascular Dynamics
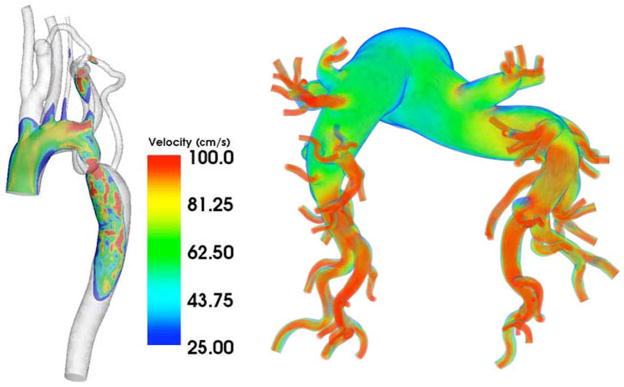
Cardiovascular dynamics are challenging because discrete rigid body representation of fluids is computationally not feasible. Thus, we must use continuum methods, and extend the SimTK Core toolkit for these kinds of modeling challenges. Here, we describe our advances in 3D, patient-specific modeling of blood flow and vessel wall motion for Cardiovascular Dynamics. Simulating blood flow and vessel dynamics, test hypotheses of disease formation under controlled conditions, and evaluate medical devices prior to implantation in humans are some of the goals of this biological program driving the development of our computational tools. In recent years, the emphasis has been on building computer models from three-dimensional medical imaging data including MRI and CT. The construction of subject-specific geometric models from medical imaging data has enabled an entirely new application of cardiovascular fluid mechanics, namely predicting changes in blood flow resulting from possible therapeutic interventions for individual patients. However, performing such patient-specific simulations requires special techniques to construct accurate patient models, generating finite element meshes for analysis, incorporating realistic models of human physiology and simulating blood flow and vessel motion on parallel supercomputing platforms. We have implemented techniques to model blood flow and vessel dynamics with unprecedented fidelity. Examples of the results of these simulations for patients with aortic coarctation and pulmonary hypertension are shown in Fig. 5. These computational methods have now been released in a software system for patient-specific cardiovascular simulation, SimVascular, available at https://simtk.org/home/simvascular. SimVascular is a unified framework that includes methods to construct complex, realistic patient-specific models, to generate finite element meshes, incorporate boundary condition data of vessels beyond the limits of imaging resolution, model blood flow and vessel wall dynamics on conventional desktop computers and massively parallel supercomputers, and visualize and interpret simulation results.
Fig. 5.
Patient-specific simulations of blood flow in patient with aortic coarctation (left) and pulmonary hypertension (right). Colors represent magnitude of blood velocity (blue—low velocity, red—high velocity).
E. Dissemination
The creation of tools and their use outside of the research groups that create them was a critical part of the NIH vision in supporting the National Centers. Our mission as a National Center includes performing research and building key toolkit components. However, we also serve the community by providing research infrastructure and dissemination opportunities. We have established a framework, Simtk.org, to distribute software tools, preliminary research results, and more generally to build a community of researchers from various disciplines, interested in physics-based simulation of biological structures. Simtk.org contains several separate components 1) the Simtk.org web site (facilities for users and facilities for developers) 2) SimTK Core software toolsets 3) SimTK applications.
Simtk.org is based on the open source project management facility GForge (http://gforge.org) and supports the Subversion source code version control system (http://subversion.tigris.org). The structure of Simtk.org allows members to contribute projects, which can be customized to reflect the nature of the project and encourages the use of images that identify them (Fig. 6). Project-by-project web statistics, available to project owners and outside observers, are a default feature for all projects, include a presentation in geographic form using personalized google maps (http://maps.google.com) and help gage the impact a project has on the biocomputation field, (as for example shown in https://simtk.org/stats/dbp_usagemap.php?topic_id=307). An additional useful feature is the ability for researchers to control the “degree of openness” of their project, which allows them to protect their precedence prior to publication. Hence, we have added infrastructure and policies to make Simtk.org a more attractive hosting environment with much finer control of privacy than GForge originally allowed. Users can start out using the Simtk.org infrastructure to host their code, while only making the project description public and later make all or only certain branches of code openly available. Simtk. org currently hosts several hundred projects and has well over a thousand members. Our work can be explored on the web at https://simtk.org, and the source code that operates our web site is available at https://simtk.org/home/website, see also http://www.sciencemag.org/content/vol312/issue5774.
Fig. 6.
The Simtk.org home page, with links to pages dedicated to the Driving Biological Problems. Simtk.org includes pages that instruct users how to contribute projects, which can be customized to reflect the nature of the project and encourage the use of images that personalize and identify projects.
Simtk.org also hosts the open source SimTK Core simulation toolkit. This tool kit contains state of the art tools needed for high quality, high performance, physics-based simulation software, which we have started to make available in a “turnkey” form, suitable for use by programmers in incorporating physics-based simulation into their biocomputation applications (Fig. 7). The SimTK Core comprises a group of interrelated Simtk.org projects, released together via the SimTKcore project (https://simtk.org/home/simtkcore). One of these components is Simbody (https://simtk.org/home/simbody), described in some detail earlier. Coding guidelines for our Core offerings can be found in the “resources” project at https://simtk.org/home/resources.
Fig. 7.
SimTK Core computational components currently in place.
To help build community amongst the highly varied audience of researchers interested in developing and utilizing biomedical computation, Simbios publishes the broadly scoped Biomedical Computation Review (BCR) magazine (http://biomedicalcomputationreview.org). BCR, edited by David Paik and Katharine Miller, employs eight professional science writers. BCR has published ten issues since its inception in Spring 2005, which are available both in print and on the web, (Fig. 8).
Fig. 8.

Covers of the first nine issues of Biomedical Computation Review.
IV. CONCLUSION
Over the last five years, NIH has made a substantial commitment to building an infrastructure for biomedical computation—both human and software resources. The National Centers for Biomedical Computing program is an important component of this effort, and has seeded seven centers to focus on critical elements of biomedical computation, and begin to form a national infrastructure to support research. Simbios is devoted to structural biological systems that are physically interacting and moving—responding to and creating forces as they execute biological functions. Many of these systems can be modeled using a multibody dynamics formalism. Others must be modeled with continuum methods, and this is a more recent focus of our center. To guarantee that the software tools we create are directly applicable to biology and human health, software development is tied tightly to specific biological research efforts. These biological systems occur at all scales from molecular to organismal, but share one critical feature—their function depends on structural motion created by the push and pull of classical forces as their parts interact.
Acknowledgments
This work was supported by the National Institutes of Health, through the NIH Roadmap for Medical Research Grant U54 GM072970.
Biographies
 Jeanette P. Schmidt received the B.Sc. degree in mathematics and statistics from the Hebrew University, Jerusalem, Israel. She received the M.S. degree in applied mathematics and the Ph.D. degree in computer science from the Weizmann Institute of Science, Rehovot, Israel, in 1981 and 1986, respectively.
Jeanette P. Schmidt received the B.Sc. degree in mathematics and statistics from the Hebrew University, Jerusalem, Israel. She received the M.S. degree in applied mathematics and the Ph.D. degree in computer science from the Weizmann Institute of Science, Rehovot, Israel, in 1981 and 1986, respectively.
She held Visiting Professor positions at Rutgers—The State University, New Brunswick, NJ, and the Courant Institute, New York University, New York. In 1989, she joined the Computer Science Department, Polytechnic University, Brooklyn, NY, where she was an Associate Professor. Her research has focused on computational biology, bioinformatics, and combinatorial algorithms. While on sabbatical from Polytechnic University, she spent a year with Stanford University, Stanford, CA, in the Department of Biochemistry and the Section for Medical Informatics, supported by a National Science Foundation grant for Visiting Professors. In 1997, she joined Incyte Genomics, eventually serving as Vice President of Bioinformatics Research and Development, leading bioinformatics research, operations, and product development. In 2004, she joined the newly funded National NIH Center for Physics-Based Simulation of Biological Structures (Simbios), Stanford University, as Executive Director.
 Scott L. Delp received the B.S. degree in mechanical engineering (summa cum laude) from Colorado State University, Fort Collins, in 1983 and the M.S. and Ph.D. degrees in mechanical engineering from Stanford University, Stanford, CA, in 1986 and 1990, respectively.
Scott L. Delp received the B.S. degree in mechanical engineering (summa cum laude) from Colorado State University, Fort Collins, in 1983 and the M.S. and Ph.D. degrees in mechanical engineering from Stanford University, Stanford, CA, in 1986 and 1990, respectively.
He was with Hewlett Packard’s graphics workstation group until 1985. After receiving the doctoral degree, he joined the Faculty of Northwestern University, Evanston, IL. He returned to Stanford in 1999, where he was Chairman of the Biomechanical Engineering Division, Mechanical Engineering Department. He became founding Chairman of Stanford’s Bioengineering Department in 2002. His work draws on computational mechanics, biomedical imaging, and neuromuscular biology to improve treatments for individuals with physical disabilities. He led the development of a software system that enables modeling and simulation of complex human and animal movements, now used at hundreds of research centers around the world. Computer models that he and his colleagues have developed have helped provide a scientific basis to better treat movement disorders resulting from osteoarthritis, cerebral palsy, and stroke. He is currently the Charles Lee Powell Professor of Bioengineering, Mechanical Engineering, and Orthopaedic Surgery at Stanford.
Prof. Delp has received numerous awards, including a National Young Investigator Award from the National Science Foundation, Faculty Fellowships from the Baxter Foundation and Powell Foundation, and a Technology Reinvestment Award for which he was honored at the White House with former President Clinton.
 Michael A. Sherman received the B.S. degree in electrical engineering and computer science from the University of California, Berkeley, in 1978.
Michael A. Sherman received the B.S. degree in electrical engineering and computer science from the University of California, Berkeley, in 1978.
He began his long professional software development career with Hewlett-Packard in Silicon Valley. He then joined supercomputer startup Elxsi in 1981, where he developed and then managed development of operating system software. Subsequently, he cofounded Symbolic Dynamics, serving as its President and Chief Software Architect for more than a decade, where he wrote and marketed the still widely used SD/FAST multibody simulation tool for mechanical, aerospace, robotics, and biomechanics applications. This software was acquired by Parametric Technology Corp. (PTC) in 1989, where he was a Consultant and Chief Software Architect for several PTC mechanical engineering simulation products. In 2000, he cofounded and was CEO of Protein Mechanics, a venture capital funded biotechnology startup, to apply multibody technology to the simulation of medically relevant biomolecules. After Protein Mechanics was sold to a pharmaceutical firm, he joined the Simbios center in 2004 as its Chief Software Architect, where he has been responsible for the design and development of the open-source SimTK Core biosimulation toolkit.
 Charles A. Taylor (Member, IEEE) received the B.S. and M.S. degrees in mechanical engineering and the M.S. degree in mathematics from Rensselaer Polytechnic Institute, Troy, NY, in 1987, 1991, and 1992, respectively. He received the Ph.D. degree from the Division of Applied Mechanics, Stanford University, Stanford, CA, in 1996.
Charles A. Taylor (Member, IEEE) received the B.S. and M.S. degrees in mechanical engineering and the M.S. degree in mathematics from Rensselaer Polytechnic Institute, Troy, NY, in 1987, 1991, and 1992, respectively. He received the Ph.D. degree from the Division of Applied Mechanics, Stanford University, Stanford, CA, in 1996.
His doctoral work focused on finite-element modeling of blood flow. He joined the Engineering Physics Laboratory, GE Research & Development Center, Schenectady, NY, in 1987. He joined the Faculty of Stanford University in 1997, where he is currently an Associate Professor in the Department of Bioengineering and has courtesy faculty appointments in the Departments of Mechanical Engineering and Radiology. He is internationally recognized for the development of computer modeling and imaging techniques for cardiovascular disease research, device design, and surgery planning.
Dr. Taylor is a Fellow of the American Institute for Medical and Biological Engineering.
 Vijay S. Pande received the B.A. degree in physics from Princeton University, Princeton, NJ, in 1992 and the Ph.D. degree in physics from the Massachusetts Institute of Technology, Cambridge, in 1995.
Vijay S. Pande received the B.A. degree in physics from Princeton University, Princeton, NJ, in 1992 and the Ph.D. degree in physics from the Massachusetts Institute of Technology, Cambridge, in 1995.
His doctoral work focused on the statistical mechanical models of protein. His current research centers on the development and application of novel grid computing simulation techniques to address problems in chemical biology. In particular, he has pioneered novel distributed computing methodology to break fundamental barriers in the simulation of kinetics and thermodynamics of molecules. As Director of the Folding@Home project, he has, for the first time, directly simulated protein folding dynamics with quantitative comparisons with experiment, often considered a holy grail of computational biology. His research also includes novel simulation methods for high-accuracy drug binding affinity calculations, protein misfolding, and related diseases such as Alzheimer’s. As a Miller Fellow working with Prof. Rokhsar at the University of California, Berkeley, he extended this methodology to atomistic protein models, laying the foundations for his later work. He is currently an Associate Professor of chemistry and structural biology (by courtesy) at Stanford University, Stanford, CA.
Prof. Pande has won numerous awards, including the Irving Sigal Young Investigator Award from the Protein Society (2006), the MIT Indus Global Technovator’s Award (2004), and a Henry and Camile Dreyfus Teacher-Scholar award (2003). He was named to MIT’s TR100 and a Frederick E. Terman Fellow in 2002.
 Russ B. Altman received the A.B. degree from Harvard College, Cambridge, MA, in 1983, the Ph.D. degree in medical information sciences from Stanford University, Stanford, CA, in 1989 and the M.D. degree from Stanford Medical School, Stanford, in 1990.
Russ B. Altman received the A.B. degree from Harvard College, Cambridge, MA, in 1983, the Ph.D. degree in medical information sciences from Stanford University, Stanford, CA, in 1989 and the M.D. degree from Stanford Medical School, Stanford, in 1990.
He is a Professor of bioengineering, genetics, and medicine (and of computer science by courtesy) and chairman of the Bioengineering Department, Stanford University. His primary research interests are in the application of computing technology to basic molecular biological problems of relevance to medicine. He is currently developing techniques for collaborative scientific computation over the Internet, including novel user interfaces to biological data, particularly for pharmacogenomics. His other work focuses on the analysis of functional microenvironments within macromolecules and the application of algorithms for determining the structure, dynamics, and function of biological macromolecule. He is a Past-President and founding Board Member of the International Society for Computational Biology and an organizer of the annual Pacific Symposium on Biocomputing.
Prof. Altman is a Fellow of the American College of Physicians, the American College of Medical Informatics, and the American Institute for Medical and Biological Engineering. He received the U.S. Presidential Early Career Award for Scientists and Engineers and a National Science Foundation CAREER Award. He received the Stanford Medical School Graduate Teaching Award in 2000.
Contributor Information
Jeanette P. Schmidt, Email: Jeanette.Schmidt@stanford.edu, Departments of Bioengineering, Stanford University, MC-5448, Stanford, CA 94305-5448 USA
Scott L. Delp, Email: Delp@stanford.edu, Departments of Bioengineering, Mechanical Engineering, and Orthopaedic Surgery, MC-5444, Stanford University, Stanford, CA 94305-5444 USA
Michael A. Sherman, Email: Msherman@stanford.edu, Departments of Bioengineering, Stanford University, MC-5448, Stanford, CA 94305-5448 USA
Charles A. Taylor, Email: Taylorca@stanford.edu, Departments of Bioengineering, Mechanical Engineering and Radiology, MC-5431 Stanford University, Stanford, CA 94305-5431 USA.
Vijay S. Pande, Email: Pande@stanford.edu, Departments of Chemistry and Structural Biology, Stanford University, MC-5080, Stanford, CA 94305-5080 USA
Russ B. Altman, Email: Russ.Altman@stanford.edu, Departments of Bioengineering, Genetics, Medicine and Computer Science, MC-5444, Stanford University, Stanford, CA 94305-5444 USA
References
- 1.Zajac FE. Muscle coordination of movement: A perspective. J Biomechanics. 1993;26:109–124. doi: 10.1016/0021-9290(93)90083-q. [DOI] [PubMed] [Google Scholar]
- 2.Russell R, Herschlag D. Probing the folding landscape of the tetrahymena ribozyme: Commitment to form the native conformation is late in the folding pathway. J Mol Biol. 2001;308(5):839–851. doi: 10.1006/jmbi.2001.4751. [DOI] [PubMed] [Google Scholar]
- 3.Laederach A, Shcherbakova LI, Liang M, Brenowitz M, Altman RB. Local kinetic measures of macromolecular structure reveal partitioning among multiple parallel pathways from the earliest steps in the folding of a large RNA molecule. J Mol Biol. 2006 May;358(4):1179–1190. doi: 10.1016/j.jmb.2006.02.075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Houdusse A, Szent-Gyorgyi AG, Cohen C. Three conformational states of scallop myosin S1. Proc Natl Acad Sci USA. 2000;97:11238–11243. doi: 10.1073/pnas.200376897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shoichet BK, McGovern SL, Wei B, Irwin JJ. Lead discovery using molecular docking. Current Opinion in Chemical Biology. 2002;6:439–446. doi: 10.1016/s1367-5931(02)00339-3. [DOI] [PubMed] [Google Scholar]
- 6.Clark DE. Rapid caclulation of polar molecular surface area and its application to the prediction of transport phenomena. J Pharmaceutical Sciences. 2000;88:807–814. doi: 10.1021/js9804011. [DOI] [PubMed] [Google Scholar]
- 7.Hansson T, Oostenbrink C, van Gunsteren WF. Molecular dynamics simulations. Current Opinion in Structural Biology. 2002;12:190–196. doi: 10.1016/s0959-440x(02)00308-1. [DOI] [PubMed] [Google Scholar]
- 8.Snow CD, Nguyen H, Pande VS, Gruebele M. Absolute comparison of simulated and experimental protein-folding dynamics. Nature. 2002;420:102–106. doi: 10.1038/nature01160. [DOI] [PubMed] [Google Scholar]
- 9.Karplus M, McCammon A. Molecular dynamics simulations of biomolecules. Nature Structural Biology. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 10.Tomita M. Whole-cell simulation: A grand challenge of the 21st century. Trends in Biotechnology. 2001;19(6):205–210. doi: 10.1016/s0167-7799(01)01636-5. [DOI] [PubMed] [Google Scholar]
- 11.Kwon RY, Lew AJ, Jacobs CR. A microstructurally informed model for the mechanical response of three-dimensional actin networks. Computer Methods in Biomechanics and Biomedical Engineering. doi: 10.1080/10255840801888686. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Thelen DG, Anderson FC, Delp SL. Generating forward dynamic simulations of movement using computed muscle control. J Biomech. 2003;36:321–328. doi: 10.1016/s0021-9290(02)00432-3. [DOI] [PubMed] [Google Scholar]
- 13.Taylor CA, Draney MT. Experimental and computational methods in cardiovascular fluid mechanics. Annual Review of Fluid Mechanics. 2004;36:197–231. [Google Scholar]
- 14.Delp S, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Computer in Biology and Medicine. 1995;25(1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- 15.Puso MA, Maker BN, Ferencz RM, Hallquist JO. Nike3d: A Nonlinear, Implicit, Three-Dimensional Finite Element Code for Solid and Structural Mechanics. Lawrence Livermore National Lab Technical Report 2002 [Google Scholar]
- 16.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy minimization and dynamics. J Comp Chem. 1983;4:187–217. [Google Scholar]
- 17.Keasar C, Rosenfeld R. Empirical modifications to the Amber/OPLS potential for predicting the solution conformations of cyclic peptides by vacuum calculations. Fold Des. 1998;3(5):379–88. doi: 10.1016/S1359-0278(98)00051-0. [DOI] [PubMed] [Google Scholar]
- 18.Ren P, Ponder JW. Polarizable Atomic Multipole Water Model for Molecular Mechanics Simulation. J Phys Chem B. 2003;107:5933–5947. [Google Scholar]
- 19.Pappu RV, Hart RK, Ponder JW. Analysis and application of potential energy smoothing for global optimization. J Phys Chem B. 1998;102:9725–9742. [Google Scholar]
- 20.Kong Y, Ponder JW. Reaction field methods for off-center multipoles. J Chem Phys. 1997;107:481–492. [Google Scholar]
- 21.Berendsen HJC, van der Spoel D, van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comp Phys Comm. 1995;91:43–56. [Google Scholar]
- 22.Lindahl E, Hess B, van der Spoel D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J Mol Mod. 2001;7:306–317. [Google Scholar]
- 23.Schwieters CD, Clore GM. Internal coordinates for molecular dynamics and minimization in structure determination and refinement. J Mag Res. 2001;152(2):288–302. doi: 10.1006/jmre.2001.2413. [DOI] [PubMed] [Google Scholar]
- 24.Chang KS, Khatib O. Efficient algorithm for extended operational space inertia matrix. Proc. 1999 IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems; 1999. [Google Scholar]
- 25.Jain A, Vaidehi N, Rodriguez GA. Fast recursive algorithm for molecular dynamics simulation. J Comput Phys. 1993;106(2):258–268. [Google Scholar]
- 26.Vaidehi N, Jain A, Goddard WA. Constant temperature constrained molecular dynamics: The newton-euler inverse mass operator method. J Phys Chem. 1996;100(25):10508–10517. [Google Scholar]
- 27.Golubkov PA, Ren P. Generalized coarse-grained model based on point multipole and Gay-Berne potentials. J Chem Phys. 2006;125:064103. doi: 10.1063/1.2244553. [DOI] [PubMed] [Google Scholar]
- 28.Cohen SD, Hindmarsh AC. CVODE, a stiff/nonstiff ODE solver in C. Computers in Physics. 1996;10(2):138–143. [Google Scholar]
- 29.Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans Biomedical Engineering. 1990;37(8):757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- 30.Delp SL, Anderson FC, Arnold AS, Loan JP, Habib A, John C, Guendelman E, Thelen DG. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomedical Engineering. 2007;54(11):1940–1950. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- 31.Anderson FC, Pandy MG. Dynamic optimization of human walking. J Biomech Eng. 2001;123(5):381–390. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- 32.Cech TR. Self-splicing of group I introns. Annu Rev Biochem. 1990;59:543–568. doi: 10.1146/annurev.bi.59.070190.002551. [DOI] [PubMed] [Google Scholar]
- 33.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Kundrot CE, Cech TR, Doudna JA. Crystal structure of a group I ribozyme domain: Principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 34.Golden BL, Gooding AR, Podell ER, Cech TR. A preorganized active site in the crystal structure of the Tetrahymena ribozyme. Science. 1998;282:259–264. doi: 10.1126/science.282.5387.259. [DOI] [PubMed] [Google Scholar]
- 35.Thirumalai D, Hyeon C. RNA and protein folding: Common themes and variations. Biochemistry. 2005;44:4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 36.Tucker BJ, Breaker RR. Riboswitches as versatile gene control elements. Curr Opin Struct Biol. 2005;15:342–348. doi: 10.1016/j.sbi.2005.05.003. [DOI] [PubMed] [Google Scholar]
- 37.Ban N, Nissen P, Hansen J, Moore PB, Steitz TA. The complete atomic structure of the large ribosomal subunit at 2.4 A resolution. Science. 2000;289(5481):878–879. doi: 10.1126/science.289.5481.905. [DOI] [PubMed] [Google Scholar]
- 38.Wimberly BT, Brodersen DE, Clemons WM, Jr, Morgan-Warren RJ, Carter AP, Vonrhein C, Hartsch T, Ramakrishnan V. Structure of the 30S ribosomal subunit. Nature. 2000;407:327–339. doi: 10.1038/35030006. [DOI] [PubMed] [Google Scholar]
- 39.Yusupov MM, Yusupova GZ, Baucom A, Lieberman K, Earnest TN, Cate JH, Noller HF. Crystal structure of the ribosome at 5.5 A resolution. Science. 2001;292:883–896. doi: 10.1126/science.1060089. [DOI] [PubMed] [Google Scholar]
- 40.Das R, Laederach A, Pearlman SM, Herschlag D, Altman RB. SAFA: Semi-automated footprinting analysis software for high-throughput quantification of nucleic acid footprinting experiments. RNA. 2005;11:344–354. doi: 10.1261/rna.7214405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cramer CJ, Truhlar DG. Implicit solvation models: Equilibria, structure, spectra, dynamics. Chem Rev. 1999:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 42.Elsen E, Houston M, Vishal V, Darve E, Hanrahan P, Pande VS. N-Body simulation on GPUs. Proc. 2006 ACM/IEEE Conf. on Supercomputing; 2006. p. 188. [Google Scholar]
- 43.Shirts MR, Pande VS. Screen savers of the world, unite! Science. 2000;290:1903–1904. doi: 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]