Large-Scale Modeling of Wordform Learning and Representation

Abstract

The forms of words as they appear in text and speech are central to theories and models of lexical processing. Nonetheless, current methods for simulating their learning and representation fail to approach the scale and heterogeneity of real wordform lexicons. A connectionist architecture termed the sequence encoder is used to learn nearly 75,000 wordform representations through exposure to strings of stress-marked phonemes or letters. First, the mechanisms and efficacy of the sequence encoder are demonstrated and shown to overcome problems with traditional slot-based codes. Then, two large-scale simulations are reported that learned to represent lexicons of either phonological or orthographic word-forms. In doing so, the models learned the statistics of their lexicons as shown by better processing of well-formed pseudowords as opposed to ill-formed (scrambled) pseudowords, and by accounting for variance in well-formedness ratings. It is discussed how the sequence encoder may be integrated into broader models of lexical processing.

1. Introduction

Wordforms are strings of phonemes or letters that denote the words of a language as they appear in speech or text. Wordforms are essential parts of all theories of lexical processing, and they are typically represented in computational models as conjunctive codes (e.g., Coltheart, Rastle, Perry, Langdon, & Ziegler, 2001; Harm & Seidenberg, 1999; McClelland & Rumelhart, 1981; Perry, Ziegler, & Zorzi, 2007; Plaut, McClelland, Seidenberg, & Patterson, 1996). The conjunctions in these models are between phonemes or letters and their positions. For instance, the wordform CAT might be coded by activating one representational unit that stands for C in conjunction with the first position, another for A in the second position, and another for T in the third position.

Conjunctive coding has proven useful for model building and theory testing in the domain of lexical processing, but it has three important limitations. First, conjunctive codes have thus far been built into models of lexical processing, and so these models do not explain how tens of thousands of wordforms are learned during language acquisition. Second, conjunctive codes do not inherently capture the statistical relations among the phonemes or letters of a language. For instance, consonants and vowels in English are often found in clusters (such as STR, NG, EA, IE, etc.). These phonotactics and graphotactics determine the well-formedness of wordforms relative to a given language (Bailey & Hahn, 2001), and effects of well-formedness are evident in measures of lexical processing (Baron & Thurston, 1973; Reicher, 1969; Vitevitch & Luce, 1999). Conjunctive codes cannot be used to explain these effects without building phonotactics or graphotactics directly into the codes.

The third limitation of conjunctive coding is that elements bind phonemes or letters with their positions. This binding makes it difficult to generalize knowledge about phonemes or letters across positions (i.e., the dispersion problem; Plaut et al., 1996; Whitney, 2001). It is also difficult to align positions across wordforms of differing lengths (i.e., the alignment problem; see Davis & Bowers, 2004). To illustrate, all of the commonalities between CAT, SCAT, CATS, and SCATS cannot be captured by traditional conjunctive codes. Various techniques have been developed to help alleviate these problems (Daugherty & Seidenberg, 1992; Plaut et al., 1996; Seidenberg & McClelland, 1989), but they all break down as the variability in word lengths increases. This problem has, in part, limited the scale of current models to monosyllabic wordforms (but see Ans, Carbonnel, & Valdois, 1998).

In the current study, we present the sequence encoder as a connectionist architecture that overcomes the limitations of traditional conjunctive codes, and in doing so may facilitate the development of lexical processing models that accommodate tens of thousands of wordforms, both mono- and multisyllabic. The architecture also stands as an example of how connectionist models can encompass the scale of real language structures, despite arguments to the contrary (G. F. Marcus, 2001).

The sequence encoder is an extension of the simple recurrent network (SRN; Elman, 1990; Jordan, 1986) that learns to (a) take as input a variable-length sequence of phonemes or letters, (b) code the sequence as a fixed-width pattern, and (c) use that pattern to reproduce the input sequence as an output sequence. It is by virtue of this auto-encoding task that the fixed-width patterns serve as wordform representations that are shaped by statistical relations among phonemes or letters (see Bishop, 1995).

There are two previously developed models that are similar to the sequence encoder and are relevant to the present work. One is the recursive auto-associative memory (RAAM; Pollack, 1990) that learns to encode and decode variable-length sequences using an explicitly assigned hierarchical structure—that is, the modeler must assign an N-ary (typically binary) tree structure to each sequence that is learned. The RAAM is then trained to learn a representation at each node of the tree for each sequence in the corpus. Each representation is learned by recursively auto-encoding the concatenation of subordinate node representations. A RAAM could be used to create wordform representations, but it would impose a fixed hierarchical structure, specified by the modeler, onto all wordform representations. By contrast, the structures of real wordforms vary from one to the next (Andrews, 1989).

The other relevant model was presented by Botvinick and Plaut (2006). They used SRNs to simulate serial recall performance. These networks learned to reproduce variable-length input sequences, like the RAAM, but without imposing hierarchical structures. However, as reported later, we found Botvinick and Plaut's model to be incapable of learning wordform representations on the scale of real wordform lexicons. The problem is that feedback (i.e., error signals) from the decoding stage of processing is not integrated in its effect (via backpropagation) on the encoding stage of processing. Thus, in learning to encode input sequences, there is implicit but no explicit mechanism for learning representations of all sequence elements in order. Also, their model uses “teacher forcing,” where information about the correct sequence elements is given to the model online (i.e., as it decodes the sequence). Such online information is not provided by the environment when learning and processing wordforms.

Unlike Botvinick and Plaut's (2006) model, the sequence encoder does not use teacher forcing, and its training procedure integrates the feedback from decoding in order to learn wordform representations. A small-scale simulation is presented next in order to demonstrate the sequence encoder's mechanisms and properties of learning and representation.

2. Simulation 1

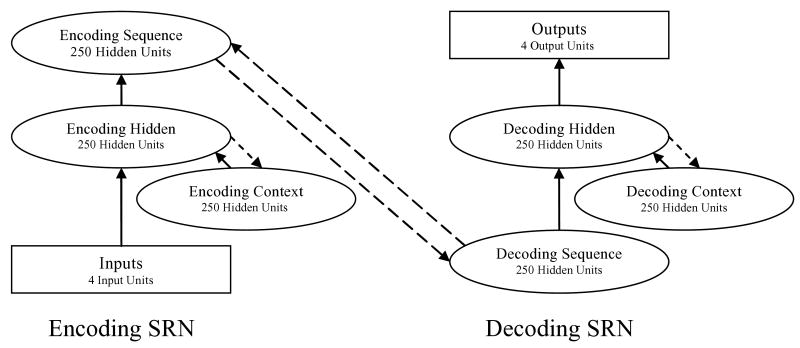
The sequence encoder architecture is shown in Fig. 1. It consists of one SRN that encodes sequences of inputs into wordform representations, and a second SRN that decodes wordform representations as output sequences. Each SRN consists of four groups of processing units. For groups connected by learned connections, weights were randomized at the beginning of training to values in the range [−0.1, 0.1]. For groups connected by copy connections, output values of the sending units were simply copied to their corresponding receiving units.

Fig. 1.

Diagram of the sequence encoder architecture, with numbers of units used in Simulation 1 shown for each group. Note: These numbers were determined by trial and error to be sufficient to support near asymptotic performance on the training sequences. Solid arrows denote full connectivity and learned weights, and dashed arrows denote one-to-one copy connections. Rectangular groupings denote external (prescribed) representations coded over localist units, and oval groupings denote internal (learned) representations distributed over hidden units. SRN = simple recurrent network.

2.1. Alphabet and wordform lexicon

Simulation 1 used an artificial alphabet of three arbitrary letters {A,B,C}, plus a fourth “end-wordform” letter {#} that was appended to the end of each wordform. Each letter was represented by one input unit and one output unit. The corpus consisted of wordforms from five to nine letters long (excluding the end-wordform letter), and training examples were sampled as follows: Of all 243 possible sequences of length five, about one half (121) were chosen at random to be added to the training corpus. For sequences of length six to nine, the number sampled was double that of the next shorter length—that is, 242, 484, 968, and 1,936, respectively. This sampling procedure ensured that longer sequences were adequately sampled without vastly out-numbering the shorter sequences. The training corpus totaled 3,751 wordforms (13% of a possible 29,403) from five to nine letters long, and the remaining 25,652 untrained wordforms were used to test generalization.

2.2. Training procedure

The processing of each training sequence proceeded in three stages: S1, S2, and S3. For time steps S1₀ to S1_n (where n is the number of letters including the end-wordform letter), the activation values a_i of input units corresponding to each letter in the sequence were set to 1 in order, from first to last letter (values for non-activated units were set to 0). Activation was propagated forward on each time step up to the encoding sequence units. This was done by first calculating net inputs $I_j^{[t]}$ at each time step t, for each input hidden and encoding sequence unit as

$$I_j^{[t]}=\sum _i{w}_{ij}{a}_i^{[t]},$$ (1)

where w_ij was the connection weight from sending unit i to receiving unit j. Each unit activation a_j was then calculated as

$$a_j^{[t]}=\text{tanh}(I_j^{[t]}),$$ (2)

which is a sigmoidal function with asymptotes at −1 and 1. For the input context units, activations at time t were copied from the input hidden units at time t− 1 (context unit activations were initialized to 0 for the first time step). On the final time step S1_n, the encoding sequence activations were copied to the decoding sequence units.

For time steps S2₀ to S2_n, the decoding sequence units' activations were held constant and repeatedly propagated forward to the output units. The decoding hidden and decoding context units were activated as in S1. Output unit activations a_j were each computed using the normalized exponential (see Luce, 1959; Nosofsky, 1990):

$$a_j^{[t]}=e^{I_j^{[t]}}/\sum _i{e}^{I_j^{[t]}},$$ (3)

where i spanned the four output units. On each time step the Kullback–Leibler divergence error (Rumelhart, Durbin, Golden, & Chauvin, 1995) was computed as

$$E_p^{[t]}=-\text{log}(a_T^{[t]}),$$ (4)

where $a_T^{[t]}$ is the activation of the target output unit. These errors were back-propagated to the decoding sequence units (Rumelhart, Hinton, & Williams, 1986), where error derivatives were accumulated on each unit over the S2 time steps. On the last time step, the accumulated derivatives were copied back to the encoding sequence units. For time steps S3₀ to S3_n, the encoding sequence derivatives were back-propagated through time to the input units by reinstating the activation vectors from time step S1_n to S1₀ in reverse order.

As errors were back-propagated during both S2 and S3, weight derivatives ∂E_p/∂w_ij were calculated and accumulated for each weight. Training sequences were sampled randomly from the training corpus, and weight derivatives were accumulated over every 50 training sequences. After every 50 sequences, weights were updated according to

$$\Delta w_{ij}=\mathit{\eta }\sum \partial E_p/\partial w_{ij},$$ (5)

where η was a learning rate set to 1 × 10⁻⁶ for the encoding SRN and 0.0005 for the decoding SRN in order to compensate for larger unit derivatives for the decoding SRN. The reduction in error was judged to asymptote after 20,000 training sequences, at which point training was halted.

2.3. Sequence encoder performance

To test model performance, each wordform was processed through stages S1 and S2 as during training, except that error and weight derivatives were not computed; and for S2, activation was propagated forward for 20 time steps or until the end-wordform output unit was most active, whichever came first. The resulting sequence of most active output letters was recorded as the decoded wordform. Wordforms were processed correctly if, and only if, every input was reproduced in the proper order.

The model correctly encoded and decoded 100% of the trained wordforms, and it correctly generalized to 98% of the untrained wordforms five to nine letters long. However, there was virtually no generalization to wordforms outside of the trained lengths. This lack of generalization occurred because the sequence encoder learned that the end-wordform letter only appeared in the 6th through 10th positions of training sequences. The model's computational resources were, therefore, dedicated to wordforms five to nine letters long. In Simulations 2a and 2b, this “greedy” use of computational resources is shown to restrict generalization to wordforms that are well-formed with respect to statistical dependencies in the training corpus. In an experiment reported thereafter, this selective generalization is shown to account for participant ratings of well-formedness for English orthographic wordforms.

2.4. Wordform representations

Performance results demonstrate that the sequence encoder learned to encode and decode variable-length sequences via fixed-width, distributed wordform representations. The analysis reported here shows that the sequence encoder's coding scheme can be construed as learning a set of conjunction patterns. Each pattern spans the entire wordform representation (i.e., all 250 units in Simulation 1) and corresponds to the conjunction of one letter with its position in a wordform of a given length. Wordform representations are composed by linearly combining their constituent conjunction patterns.

To illustrate, the wordform ABACA# is composed of six conjunctions: A in the first position of a five-letter wordform, B in the second position of a five-letter wordform, and so on. A single pattern is learned for each conjunction and used in the composition of all wordforms that contain the conjunction. The encoding SRN generates a wordform representation of ABACA# that is a linear combination of its six constituent patterns, and the decoding SRN unpacks this combination to reproduce the wordform as a sequence of outputs.

To show that wordform representations can be construed in this way, principal components analysis (PCA) was used to extract the hypothesized conjunction patterns from wordform representations. To begin with, the learned wordform representations were grouped by shared conjunctions. For instance, one group contained all learned representations of five-letter wordforms that have an A in the first position. PCA was conducted separately on each group in order to derive the eigenvector corresponding to the first principal component of the set of activation vectors. The first principal component corresponds to the axis of maximally shared variance that projects through the activation vectors. Variation along this axis was used as the conjunction pattern corresponding to its respective group (e.g., A in the first position of a 5-letter word).

If wordform representations are composed of linearly combined conjunction patterns, then we should be able to use the patterns to synthesize new, untrained wordform representations. We tested this prediction by building multivariate linear regression models from the conjunction patterns and then using the models to synthesize wordform representations. Five regression models were built, one for each wordform length. Each model was built to predict each activation value of every untrained wordform representation in its corresponding wordform space (e.g., all possible 5-letter combinations). Each model took the form of

$$y_{ij}={\mathit{\beta }}_0+\sum _{k=1}^l{\mathit{\beta }}_k{x}_{kj}+\mathit{\epsilon },$$ (6)

where y_ij was the activation produced by unit j of representation i, l is the length of the string, and x_kj was the jth value of conjunction pattern for the letter in position k. The regression models accounted for 96.5%, 96.1%, 95.7%, 89.4%, and 95.7% of the variance in untrained wordform representations of lengths five, six, seven, eight, and nine, respectively. The success of these regression models confirms that wordform representations can be construed as linear combinations of their constituent conjunction patterns.

2.5. Dispersion and alignment problems

As mentioned earlier, using traditional conjunctive codes for wordform representations is problematic because it is difficult to generalize knowledge that is dispersed across positions, and difficult to align positions across wordforms of differing lengths. Sequence encoder representations do not engender the alignment problem because conjunction patterns are created for length-specific positions (e.g., the last position in a 5-letter word). Length-specific conjunctions could also be coded using localist units, as is traditionally done, but then the knowledge would be dispersed across lengths as well as positions. The sequence encoder alleviates this dispersion problem by learning distributed conjunction patterns.

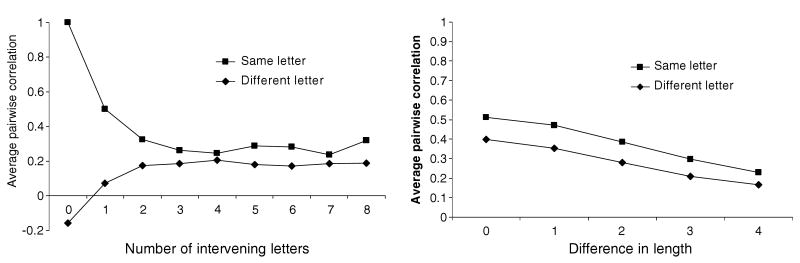
The distributed nature of conjunction patterns also means that they have varying degrees of similarity with each other. This property is important because learning for one conjunction pattern will naturally generalize to other conjunctions with similar patterns (Hinton, McClelland, & Rumelhart, 1986). The analysis reported here shows that the sequence encoder learned conjunction patterns that were more similar to the extent that they coded the same letter. Moreover, conjunction patterns were even more similar if the shared letter was in similar positions or in wordforms of similar lengths. Pattern similarity was measured in terms of pairwise correlations, and correlation coefficients were averaged across all pairs as a function of intervening letters and difference in wordform length (see Fig. 2).

Fig. 2.

Average pairwise correlations between conjunction patterns, plotted as a function of intervening letters (left) or difference in wordform length (right). Note: For intervening letters, the effect of wordform length was partialled out before correlations were computed.

Both graphs in Fig. 2 show that patterns for same-letter conjunctions were more correlated than those for different-letter conjunctions. The graphs also show that the contrast between same- and different-letter patterns was greater for nearby conjunctions, and for conjunctions from wordforms of similar lengths. It was these graded similarities among conjunction patterns that enabled the sequence encoder to overcome the dispersion and alignment problems, and hence capture the commonalities between wordforms like CAT, SCAT, CATS, and SCATS.

3. Simulations 2a and 2b

In Simulations 2a and 2b, two sequence encoder models learned wordform representations on the scale of real wordform lexicons. One model was trained to encode and decode nearly 75,000 phonological wordforms of English, and the other model was trained on a comparable number of orthographic wordforms. These wordforms were different from the sequences used in Simulation 1, not only in terms of scale, but also because real wordforms have statistical dependencies among their phonemes or letters. Sequences in Simulation 1 had no significant dependencies (except for position of the end-wordform letter) because they were drawn at random. Simulations 2a and 2b therefore served to test whether learning wordform representations entails the learning of statistical dependencies among wordform elements. If so, then learning should generalize only to untrained wordforms that conform to the trained dependencies (i.e., only to well-formed English pseudowords).

The importance of well-formedness has been demonstrated in a number of empirical studies. In wordform processing tasks, readers have been found to identify letters faster when they are embedded in well-formed pseudowords as opposed to random letter strings (Aderman & Smith, 1971; Baron & Thurston, 1973), and same–different judgments for pairs of spoken pseudowords have been shown to be quicker and more accurate when pairs are relatively well-formed (Vitevitch & Luce, 1999). More directly, readers have been shown to judge pseudowords as better formed (more word-like) to the extent that they conform with the phonotactics and graphotactics of their native language (Bailey & Hahn, 2001). Even attentional preferences in infants (Jusczyk, Friederici, Wessels, & Svenkerud, 1993) and evoked response potentials in adults (Bonte, Mitterer, Zellagui, Poelmans, & Blomert, 2005) have been shown to be sensitive to the phonotactics of pseudowords. Collectively these findings make clear that wordform representations need to be sensitive to well-formedness.

3.1. Alphabets and wordform lexicons

Phonological and orthographic wordforms were taken from the Carenegie Mellon University Pronouncing Dictionary (http://www.speech.cs.cmu.edu/cgi-bin/cmudict). Wordforms not in the Wall Street Journal corpus (M. Marcus, Santorini, & Marcinkiewicz, 1993) were discarded, yielding 74,265 unique pairs of orthographic and phonological wordforms. Phonological wordforms were comprised of strings of stress-marked phonemes (14 vowels, 25 consonants, and one end-wordform element), where consonants were marked as no-stress and vowels were marked as having primary, secondary, or tertiary stress (the end-wordform element was unmarked). One set of localist units was used to code phonemes, and a second set coded for lexical stress. A given phoneme was coded by activating one phoneme unit and one stress unit. Orthographic wordforms were also coded using two sets of localist units—one for letters (5 vowels, 19 consonants, and 1 end-wordform element) and the other to mark each letter as a consonant or vowel (letters do not explicitly code lexical stress). Consonants and vowels were marked to parallel the phonological wordforms.

3.2. Training procedure

Each of the two models was built and trained as in Simulation 1, except that the number of hidden units per group was doubled to 500, and the learning rates were set to 1 × 10⁻⁸ for the encoding SRN and 5 × 10⁻⁵ for the decoding SRN. Learning rates were reduced compared with Simulation 1 in response to the large increase in lexicon size. The reduction in error for both models was judged to asymptote after 250,000 training sequences.

3.3. Sequence encoder performance

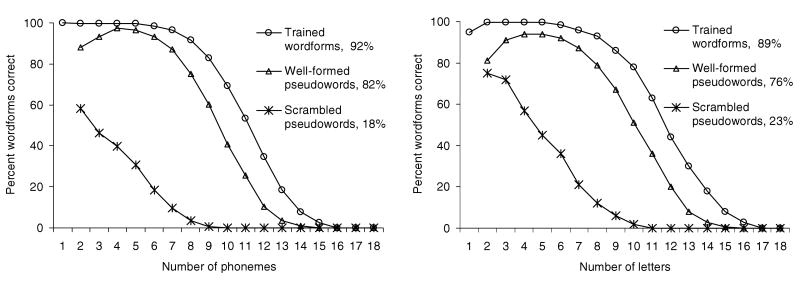
Performance was assessed in the same way as in Simulation 1, except that a wordform was encoded and decoded correctly if, and only if, all elements and markings were reproduced in the proper order. Performance was assessed for three types of wordforms. One type was comprised of all trained wordforms, and two other types were derived from the training sets: Scrambled pseudowords were created by scrambling the orders of elements in trained wordforms, and well-formed pseudowords were created by replacing one element of each trained wordform with a new one such that the resulting wordform was untrained yet possible given its respective lexicon. For instance, the wordform SPORTY could be changed into the well-formed pseudoword SPARTY because the substring SPART appears in the trained wordform SPARTAN (up to 3 elements to either side of the replacement position were considered in determining whether a replacement was possible).

Overall percent correct for each model and each wordform type is shown in Fig. 3, with percent correct graphed as a function of wordform length and type for each model. The figure shows that performance for well-formed pseudowords was nearly as accurate as for trained wordforms, but much poorer for scrambled pseudowords. The figure also shows that performance deteriorated as wordform length increased beyond eight elements. This deterioration occurs because more information must be coded for longer sequence representations, and error signals must be back-propagated over more time steps. The slight deterioration for very short wordforms was due to their low probability of occurrence relative to longer wordforms.

Fig. 3.

Correct percentages for Simulations 2a and 2b, plotted as a function of wordform length and type.

To test whether Botvinick and Plaut's (2006) model can learn to represent large-scale lexicons, we attempted to train it on the current lexicons. We used their online training procedure, and examples were sorted by length and alphabetically within length. Separate models were trained to match either the numbers of hidden units per group (500) used in Simulations 2a and 2b, or the total number connection weights (slightly over 1 million). We explored a wide range of learning rates (between .001 and 10), and found that learning never converged (no more than 1% of the trained wordforms were processed correctly for any given learning rate). Learning rates outside this range would not have worked either because .001 was too small to preserve error signals across back-propagation, and 10 was too large to maintain stable learning. This failure does not invalidate the Botvinick and Plaut model as a way to simulate short-term memory in serial recall tasks, but it does show that the model cannot be used to learn wordform representations.

4. Well-formedness experiment

Simulations 2a and 2b showed that the sequence encoder can learn to encode and decode large-scale lexicons of both phonological and orthographic wordforms, from mono- to multisyllabic. The basic effect of well-formedness indicated that, over the course of learning, computational resources become dedicated to combinations of conjunctions that occur (and occur more often) in the trained wordforms. To test this effect empirically, we collected ratings of well-formedness from skilled readers for a set of 600 orthographic pseudowords. Ratings were predicted to be correlated with sequence encoder performance, and only relatively well-formed pseudowords were used (i.e., a restricted range) in order to provide a more stringent test than the coarse distinction of well-formed versus scrambled that was demonstrated in Simulations 2a and 2b.

4.1. Participants, stimuli, and procedures

Nine men and six women were each paid $10 to participate in the experiment. They were all native English speakers and U.S. college graduates. Six hundred wordforms were sampled at random from the lexicon used in Simulation 2b, 150 from each of the four most common wordform lengths (i.e., 5–8 letters long). A pseudoword was created from each wordform using the same procedure for creating well-formed pseudowords as in Simulation 2b, except that letters were replaced five times instead of just once. Multiple replacements helped to create a range of well-formedness that mostly excluded illegal wordforms. Each participant was given the entire list of pseudowords in random order and instructed to rate the well-formedness (“wordlikeness”) of each one on a scale ranging from 1 to 5.

4.2. Results

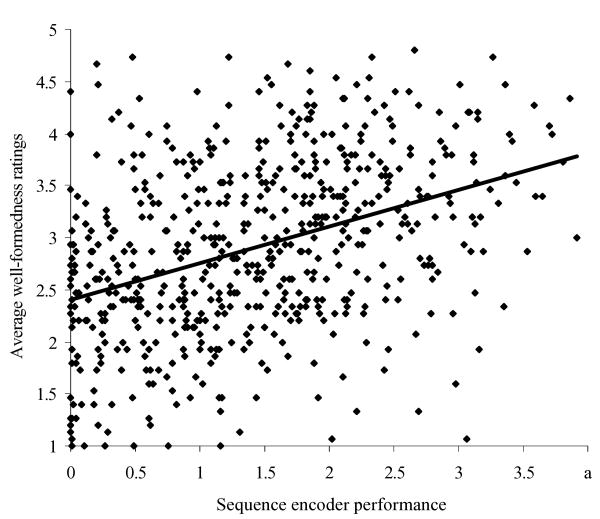
Ratings were averaged across participants for each wordform, and sequence encoder performance was assessed by treating output activations as probabilities of individual letter responses. Probabilities were treated as independent and combined accordingly to derive a measure of the probability of a correct response, specifically

$$P(w)=-\text{log}\left(1-\prod _{t=S{2}_0}^{S{2}_n}{a}_T^{[t]}\right).$$ (7)

In Fig. 4, average ratings are plotted against this probabilistic measure of performance. The sequence encoder accounted for 15.4% of the variance in average ratings: R² = .154; F(1, 598) = 108.4, p < .001. Some of this variance can be attributed to the participants and the sequence encoder both being sensitive to single letter and bigram frequencies; but even when the single letter and bigram frequencies were partialled out of the performance measure, the sequence encoder still accounted for 12.3% of the variance in ratings: R² = .123; F(1, 598) = 83.78, p < .001. Thus, there were higher order statistical dependencies to which participants and the sequence encoder were both sensitive. This R² value may seem relatively low, but one must bear in mind that pseudowords were restricted to be relatively well-formed in order to provide a more stringent test of the model. The R² value would have been substantially higher if ill-formed (e.g., scrambled) wordforms were included.

Fig. 4.

Scatter plot of average well-formedness ratings against sequence encoder performance.

5. Conclusion

The sequence encoder was shown to learn wordform representations for large-scale English lexicons. Its ability to scale is due, in part, to overcoming the alignment and dispersion problems that have plagued traditional means of wordform representation. The sequence encoder learns wordform representations as linear combinations of distributed conjunction patterns. By virtue of learning such representations, performance generalized to well-formed pseudowords, but much less so to ill-formed (scrambled) pseudowords. A graded measure of performance was shown to be correlated with the degree of well-formedness as determined by participant ratings.

The sequence encoder is a model of lexical performance in its own right, as demonstrated by its ability to account for data on readers' sensitivity to graphotactics. But more generally, it paves the way toward developing large-scale models of written and spoken word processing. An auto-encoding task was used in the current study, but the sequence encoder can learn mappings between any set of variable-length input–output pairs. In the context of word naming, the input sequences can be orthographic wordforms, and the output sequences can be their phonological counterparts. Thus, the sequence encoder could be used to scale-up the models presented by Seidenberg and McClelland (1989) and Plaut et al. (1996) to handle large-scale lexicons of mono- and multisyllabic words. More generally, the wordform representations learned herein are not restricted to any particular architecture of the lexical system; they may be incorporated into any model of lexical development and processing that can interface with distributed representations.

It has been argued that connectionist models are fundamentally limited in their ability to account for realistic language phenomena (G. F. Marcus, 2001). The biggest problem in this regard is the limited ability of many connectionist models to generalize much beyond the items on which they are trained (Berent, 2001; G. F. Marcus, 2001; Berent, Marcus, Shimron, & Gafos, 2002). Our simulation results show that generalization can be quite robust when connectionist models are trained on sufficiently large sets of items (i.e., sets that approximate the full scale of the language phenomena in question). Thus, instead of scale being a liability for connectionist models, it may actually be an important factor in how they explain language phenomena.