Fluctuations and stimulus-induced changes in blood flow observed in individual capillaries in layers 2 through 4 of rat neocortex

Abstract

Cortical blood flow at the level of individual capillaries and the coupling of neuronal activity to flow in capillaries are fundamental aspects of homeostasis in the normal and the diseased brain. To probe the dynamics of blood flow at this level, we used two-photon laser scanning microscopy to image the motion of red blood cells (RBCs) in individual capillaries that lie as far as 600 μm below the pia mater of primary somatosensory cortex in rat; this depth encompassed the cortical layers with the highest density of neurons and capillaries. We observed that the flow was quite variable and exhibited temporal fluctuations around 0.1 Hz, as well as prolonged stalls and occasional reversals of direction. On average, the speed and flux (cells per unit time) of RBCs covaried linearly at low values of flux, with a linear density of ≈70 cells per mm, followed by a tendency for the speed to plateau at high values of flux. Thus, both the average velocity and density of RBCs are greater at high values of flux than at low values. Time-locked changes in flow, localized to the appropriate anatomical region of somatosensory cortex, were observed in response to stimulation of either multiple vibrissae or the hindlimb. Although we were able to detect stimulus-induced changes in the flux and speed of RBCs in some single trials, the amplitude of the stimulus-evoked changes in flow were largely masked by basal fluctuations. On average, the flux and the speed of RBCs increased transiently on stimulation, although the linear density of RBCs decreased slightly. These findings are consistent with a stimulus-induced decrease in capillary resistance to flow.

Brain homeostasis depends on adequate levels of blood flow to ensure the delivery of nutrients and to facilitate the removal of metabolites and excess heat. The exchange of material between constituents in the blood and neurons and glia occurs at the level of individual capillaries (vessels that are 5–8 μm in caliber). Furthermore, sensory stimulation or even ideation may lead to an increase in the electrical activity within populations of neurons that subsequently results in a shift in blood flow between activated and quiescent regions (1). These shifts are of sufficient duration and magnitude to form the basis of imaging techniques in which neuronal activity is inferred from changes in blood flow and blood oxygenation (2). Although capillaries throughout the middle layers of cortex, particularly layer 4, are expected to play a predominant role in the coupling of neuronal activity to blood flow (1, 3), little is known about this coupling at the spatial scale of these vessels.

The flow of blood through individual capillaries in cortex has been investigated extensively at the level of the pia mater (4, 5), a region in which capillaries form largely planar networks (6), and in the upper layers of cortex (7). Yet our knowledge on the nature of the flow that occurs deep to the cortical surface, where the capillaries from a tortuous plexus of loops and junctions (8), has been limited so far by the inability to image blood flow much below the pia.

Here we introduce the use of two-photon laser scanning microscopy to image blood flow in cortical microvasculature that lies deep below the pia. In this technique, molecular excitation is achieved with infrared light with the result of increased depth penetration and reduced photodamage as compared with single-photon optical sectioning with visible light (9, 10). Furthermore, with two-photon laser scanning microscopy, even fluorescently emitted light scattered by brain tissue can be collected (11).

We ask (i) To what depth below the pia can we resolve capillary blood flow? In particular, can we resolve blood flow at the level of layer 4, whose superficial boundary lies 500 μm below the pia? This layer is the primary locus of afferent input and, consistent with a high density of presynaptic terminals, contains the highest density of vasculature throughout the neocortex (6). (ii) What is the nature of red blood cell (RBC) flow in capillaries and across junctions between capillaries in the absence of external stimuli? (iii) What is the nature of the change in RBC flow in response to natural stimuli?

METHODS

Preparation.

Eight male Sprague–Dawley rats, 210–240 g in weight, served as our subjects. In brief, animals were anesthetized with urethane [0.12% (wt/wt) i.p., supplemented at 0.02% (wt/wt) as needed], received a prophylactic dose of atropine (0.1 mg s.c. every 2 hr), and were supplemented with 5% (wt/vol) glucose in saline (2 ml s.c. every 2 hr) (12, 13). Body temperature was maintained near 36.5°C. A craniotomy was prepared above the parietal cortex, and a field electrode was placed near the boundary of the primary and secondary vibrissa areas (14) with a reference in occipital cortex for electrocorticogram (ECoG) verification of vibrissa stimulation. A metal frame surrounding the craniotomy was fixed to the skull as a means to hold the head of the animal rigidly and, unless noted, the dura was removed.

Animals were maintained under urethane anesthesia for all measurements. The somatotopic representation of vibrissa and other areas was mapped via measurements of evoked surface potentials with a ball electrode (15). On completion of the map, the cortical surface was sealed by a chamber composed of the metal frame and a cover glass (16), with the interior of the chamber filled with 2% (wt/vol) agarose in an artificial cerebrospinal fluid (12). Blood serum was labeled through a tail-vein injection of 0.5-ml boluses of 5% (wt/vol) fluorescein isothiocyanate-labeled dextran (10 kDa) in physiological saline; the initial concentration of dye in the serum was estimated to be 150 μM. These injections were repeated at intervals of 2–3 hr.

Measurements.

We imaged the fluorescent serum with a laser scanner and an upright microscope as described (13). The excitation wavelength was 830 nm. The objective, unless noted otherwise, was a ×40 water-immersion lens (0.7 numerical aperture; Zeiss), for which the focus region is estimated to be <1 μm in lateral extent (full width at half-maximal excitation) and <3 μm in axial extent. The total average power delivered to the cortex ranged from 30 to 300 mW; higher values were required to image at greater depths in the brain to compensate for the scattering of incident. The total average power delivered to the focus was <10 mW.

The three-dimensional anatomy of the vasculature in a region of interest was reconstructed from two-dimensional (planar) scans of the fluorescent intensity obtained at successive depths in the cortex. These scans form an array of intensities F(x, y, z), where x and y refer to in-plane coordinates and z is the depth relative to the pia. We corrected for the attenuation of the signal along the z-direction through multiplication of each planar image by the factor Ae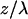, where the constant A is proportional to the incident power and the constant λ was determined empirically from plots of the mode of the intensity distribution for each planar image as a function of depth (see Results). Projections of the labeled vasculature in the x–y, y–z, and z–x planes were constructed by selecting the maximum value of Ae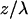F(x, y, z) along the direction normal to the plane of interest.

The motion of RBCs was inferred from line-scan measurements, i.e., repetitive scans of the laser along the central axis of a capillary. We electromechanically oriented the direction of the scan and typically scanned a distance of 38 μm with a spatial resolution of 0.7 μm per pixel, a temporal resolution of 2 msec per scan, and a record length of 128 sec. Multiple records were taken from the same vessel. The ECoG and the electrocardiogram were recorded with all flow measurements.

Stimuli.

For vibrissa stimulation, we used a galvanometer to jog a group of ≈15 vibrissa encompassing the straddlers and rostral vibrissae of rows B–E. Sinusoidal motion, typically 2° in amplitude, was delivered at 10 Hz—close to the natural frequency of exploratory whisking (17, 18)—for a period of 1 sec. For cutaneous stimulation, the body area was stroked with a blunt needle at 1–2 Hz for a period of 5 sec. In some control measurements, moderate shock was delivered to the tail in the form of a 1-sec train of 3-msec wide bipolar pulses repeated at 20 Hz.

RESULTS

Penetration Depth.

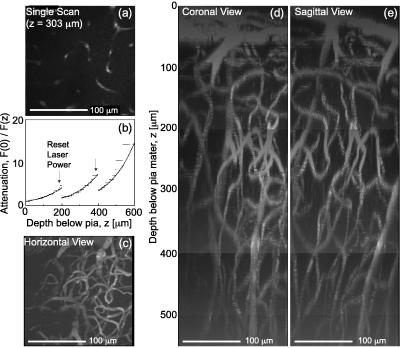
A single, planar image appears to contain fragments of individual blood vessels (Fig. 1a). A series of such images, acquired at successive depths through the cortex, was used to infer the attenuation of the detected fluorescent light as a function of depth below the pia and to reconstruct the three-dimensional angioarchitecture.

Figure 1.

Reconstruction of labeled vessels in primary vibrissa cortex. (a) A 170 μm × 170 μm single planar scan at a depth of 303 μm below the pia. The dark stripes in vessels correspond to the location of unlabeled RBCs at the time of the scan. (b) Attenuation of the measured fluorescent intensity as a function of depth. We acquired planar scans as in a at successive 1-μm intervals below the pia, and determined the mode of the distribution of measured amplitudes for each image. We plot the inverse of the intensity at the mode at each depth. The jumps in the data (↓) correspond to a manual increase in the incident laser power. The solid line is a fit to the data, with F(0)/F(z) = exp{z/λ} and a constant attenuation length (λ = 140 μm). (c) Horizontal view (x–y projection) of the microvasculature in three dimensions reconstructed from the set of planar scans used in a and b. We corrected each scan for attenuation with depth (see Methods) and calculated the maximum intensity in the x–y plane for sections 50–550 μm below the pia. (d and e) Coronal and sagittal views (x–z and y–z projections, respectively) of the microvasculature reconstructed from the set of planar scans as in a. We corrected each scan for the attenuation with depth and calculated the maximum intensity in the x–z and y–z planes for sections 0–550 μm below the pia.

Our estimate of the penetration depth depends on the assumption that the fluorescent yield of the labeled serum is independent of depth, z. We calculated the distribution of fluorescent amplitudes at each depth, from which we determined the mode of each distribution, denoted F(z). The attenuation of the measured intensity, which depends mainly on the scattering of incident light (11), was found by plotting F(0)/F(z) versus depth. For the data in Fig. 1a, we observed that the intensity was attenuated by a factor of ≈70 between the pia and a depth of 600 μm. The attenuation is well described by an exponential with an attenuation length of λ = 140 μm (Fig. 1b). In general (15 depth series), we found that the attenuation length varies between λ = 120 and 220 μm.

We constructed orthogonal projections of the vasculature for the data set of Fig. 1 a and b (see Methods). To visualize the small vessels in the horizontal view (Fig. 1c), we included only sections below the uppermost 50 μm of cortex. The large surface vessels in these layers, which would otherwise dominate the horizontal view, are seen in coronal and sagittal views (Fig. 1 d and e), along with the web of smaller vessels that course beneath them.

We consistently resolved vessels within the upper 400–450 μm of cortex, and in some preparations we could resolve vessels as far as 600 μm below the pia. The vasculature could even be resolved with the dura intact (data not shown), although this precluded accurate electrical mapping of cortical somatotopy. Last, we could resolve vessels at depths down to 1000 μm, albeit with a concomitant loss in spatial resolution, with the use of a lower power (×20) objective (data not shown).

Determination of Flow Parameters.

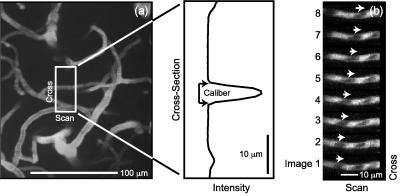
We readily imaged single microvessels (Fig. 2a) whose caliber was determined from the measured cross section in a planar image ( Fig. 2a Inset). Successive, rapidly acquired planar images of such microvessels revealed a succession of dark objects that moved across a sea of fluorescently labeled serum (Fig. 2b). The dark spots are RBCs, which exclude the dye and therefore are not fluorescent (7). The change in position of the spots between successive images is proportional to the velocity (Fig. 2b).

Figure 2.

Illustration of individual capillaries and RBC flow in a capillary. (a) Horizontal view in the vicinity of a capillary reconstructed from a set of 100 planar scans acquired every 1 μm between 310 and 410 μm. The Inset shows the intensity profile along the cross section for the scan that passed through the central axis of the capillary in question (z = 360 μm). The caliber is estimated from the number of pixels with intensity above the background level, as noted. (b) Successive planar images through a small vessel, acquired every 16 msec. The change in position of a particular unstained object, interpreted as a RBC, is indicated by the series of arrows (→); the velocity of the RBC is +0.11 mm/sec. Depth = 450 μm.

In general, we had insufficient temporal resolution to characterize the motion of RBCs from planar images of the entire vessel. Thus, we acquired repetitive scans along the central axis of a capillary (7), i.e., line scans. In this mode, the data comprise a matrix with one spatial (x) and one temporal (t) dimension. The motion of RBCs leads to dark bands in the data set (Fig. 3 a–c). The time between bands at a fixed position (Δt) is inversely proportional to the flux, the distance between bands at a fixed time (Δx) is inversely proportional to the linear density of RBCs, and the slope of the band (Δt/Δx) is inversely proportional to the velocity of the RBCs (Fig. 3a Inset). These three quantities are related by

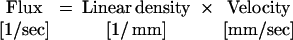1

The average velocity of RBCs in 0.1-sec intervals was determined by using an automatic procedure§. The average flux of RBCs was determined by manually counting the number of bands in successive 0.5-sec intervals.

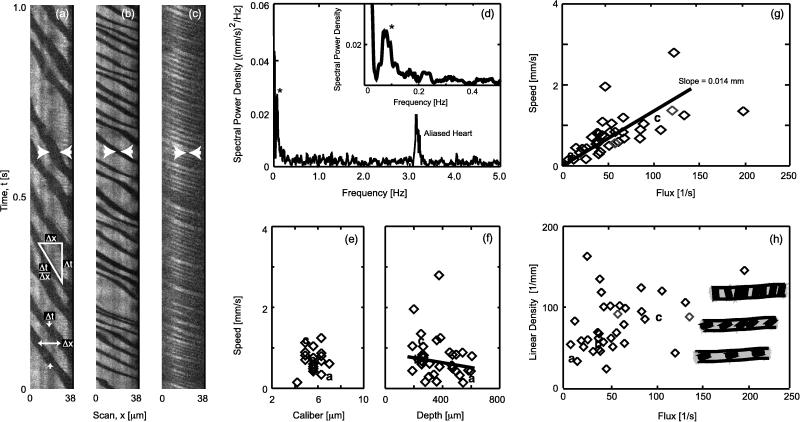
Figure 3.

Characterization of the basal motion of RBCs in capillaries. The vessels were scanned at 2 msec per line, except for one vessel with very fast flow that was scanned at 1 msec per line. (a–c) Selected 1-sec segments of the line-scan data for flow in three different vessels. Note the increase in speed and flux in the progression from a to c. The width of the dark bands (distance between arrows) is seen to decrease with increasing flux; this implies that the profile of the RBCs relative to the central axis of the capillary decreases in the progression a to c. The Inset in a is a characterization of RBC flow. The instantaneous velocity is Δx/Δt, the flux is 1/Δt, and the linear density is 1/Δx. (d) Representative plot of the spectral power density in a 128-sec record of speed versus time; we used multitaper estimation techniques (36) with a half-bandwidth of 0.02 Hz. Note the peak near 0.1 Hz (∗); the peak at 3.2 Hz is aliased heart rate (6.8 Hz aliased to 3.2 Hz by the T = 100-msec window of the velocity calculation). (e) Plot of speed versus caliber for 21 vessels. The speed was determined from 20-sec intervals that included no sensory stimuli. a, b, and c refer to data for the line-scans in a, b, and c, respectively. (f) Plot of speed versus depth below the pia for flow in all 38 vessels. The solid line is a fit to the data, excluding the two points with exceptionally high speed, with slope 0.007 ± 0.0004 (mm/sec)/μm (mean ± SEM). (g) Plot of speed versus flux. The solid line is a best fit to all points in the data set. (h) Plot of linear density (Eq. 1) versus flux. The drawings illustrate the change in packing that was hypothesized to occur as the RBCs shift their orientation from planar at low density to axial at high density.

Basal Flow.

We examined 38 vessels at depths between 200 and 600 μm below the pia; in 21 of these vessels we also measured the caliber (Fig. 2a). In the majority of vessels, the passage of RBCs appeared to occur at irregular intervals (e.g., Fig. 3 a–c). The spectral composition of this variability was not uniform; in essentially all cases, the fluctuations in speed (magnitude of the velocity) exhibited a spectral peak between 0.1 and 0.2 Hz (Fig. 3d).

The properties of the blood flow through each vessel were examined first in terms of the values of the speed and flux averaged over a 20-sec interval. We observed that the speed and flux vary over a range of values mainly between 0 and 1 mm/sec, and 0 and 100 sec⁻¹, respectively. The speed was independent of the caliber of the vessels we studied, whose diameters, with one exception, ranged between 5 and 7 μm (Fig. 3e). The speed exhibited a weak but significant dependence on depth, with blood flow in deeper vessels tending to be slower (Fig. 3f).

The speed and flux track each other linearly at low values of flux (Fig. 3g). The value of the slope, Δ(speed)/Δ(flux) = 14 ± 2 μm, corresponds to the mean spacing between RBCs. At high values of flux, the speed has a tendency to plateau (Fig. 3g). The deviation of the speed and flux from a solely linear relation (Eq. 1) implies that the linear density of the RBCs is not a constant. To highlight this issue, we plotted the linear density versus flux (Fig. 3h). Although there is considerable scatter in the relation between these quantities, there is a significant trend for the density to increase with increasing flux¶. One clue to the cause of this increase comes from an examination of the line scan data at different values of flux. At low values, the spatial extent of the dark band is relatively broad, whereas at high flux the extent narrows; cf. the gap defined by the horizontal arrowheads in Fig. 3a versus Fig. 3c. This implies that the profile of the RBC is greater at low levels than at high levels of flux. A scenario consistent with this observation is that the average orientation of the RBCs changes from planar (face perpendicular to the direction of flow) at low density to axial (face along the direction of flow) at high density, so that the RBCs tend to move as a “stack” at high values of flux (Fig. 3h Inset).

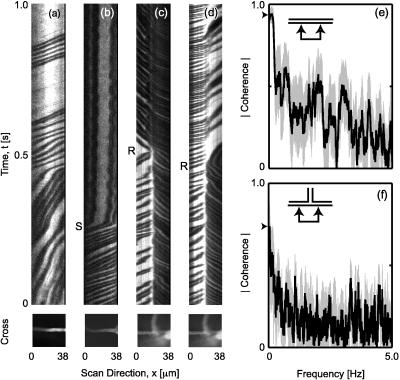
In the course of these studies, we observed instances of highly irregular flow in which the speed and flux changed suddenly (Fig. 4a) or in which individual RBCs stalled for extended periods of time (Fig. 4b) as reported previously for the upper layers of cortex (20). The most extensive irregularities occurred at the confluence of three vessels that formed a T junction, a commonly found configuration in cortex (21). We simultaneously scanned the two collinear arms and often observed stalls in one arm as well as sustained reversals in the direction of flow in one or both arms (Fig. 4 c and d). These data suggest that capillary flow is shunted in loops, consistent with the plexuses of microvessels (21) and sphincters (8) in neocortex.

Figure 4.

Examples of highly variable flow. (a) A 1-sec segment of the line-scan data through a straight section of a capillary in which the speed changes from relatively slow (large slope) to fast (small slope). The image below the line-scan record is the average of 100 planar scans that include the axis of the capillary. Depth = 240 μm. (b) A 1-sec segment of data at the onset of a transient stall in flow (S). Note that the RBCs remain stuck in the vessel. Depth = 260 μm. (c) A 1-sec segment of data that shows the flow in two collinear arms of a junction. Note the reversal in the direction of flow in the arm on the left (R). Depth = 260 μm. (d) Segment of flow in the same capillary junction as in c acquired approximately 200 sec later. Multiple reversals in the direction of flow in the right arm were seen, one of which is shown (R). (e) Trial-averaged (n = 8) spectral coherence between two ≈10-μm segments in a straight vessel separated by a center-to-center distance of 25 μm. The thick line is the magnitude of the mean coherence and the gray band indicates one SD in the trial average (n = 8). The arrow indicates the coherence at zero frequency. We used multitaper spectral estimation techniques (36) with a half-bandwidth of 0.04 Hz; the SD is a jackknife estimate (37). (f) Trial-averaged (n = 4) spectral coherence between the velocity in right versus left arms of the junction shown in c and d.

Last, we consider the bandwidth of coherent fluctuations in velocity across separate sections of a vessel. For the case of an unbranched capillary, the magnitude of the spectral coherence between regions separated by ≈25 μm approached 1 at the lowest frequencies‖ and then decayed toward 0 over a band of nearly 5 Hz (Fig. 4e). In contrast, for the case of a junction, the magnitude of the coherence between collinear arms was significantly less than 1 at the lowest frequencies and decayed to 0 within a band of ≈0.5 Hz (Fig. 5f). These data imply that the velocity of capillary flow is essentially incoherent on length scales that include one or more junctions except at frequencies near or below 0.1 Hz.

Figure 5.

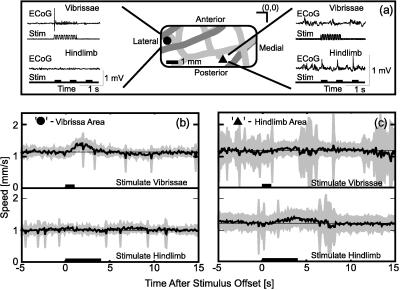
The regional specificity of stimulus-induced changes in the speed of RBCs. (a) Example of the procedure for mapping the somatotopy of parietal cortex. A ball electrode was placed at various locations on the cortical surface that were noted by reference to the surface vasculature [Inset; (0,0) indicates the Bregma point]. For each location, we show the ECoG for stimulation of the vibrissa and for stimulation of the hindlimb (see Methods). The lateral location is seen to respond solely to stimulation of the contralateral vibrissae, and the medial-posterior region responds solely to strokes on the contralateral hindlimb. (b) Trial-averaged speed for a capillary in the vibrissa area (• in a) in response to vibrissa (Upper) or hindlimb (Lower) stimulation. The dark line is the average over 12 trials, and the gray band is the SD of the trial average. The spikes in the SD are caused by the many trials containing a brief stall. Depth = 255 μm. (c) Trial-averaged speed for a capillary in the hindlimb (• in a) in response to vibrissa (Upper) or hindlimb (Lower) stimulation. Twenty-four trials were averaged for each stimulus. Depth = 260 μm.

Stimulus-Dependent Changes in Blood Flow.

We first consider the regional localization of changes in blood flow in response to external stimuli. The somatotopy of parietal cortex was mapped via the surface ECoG to locate the areas most sensitive to stimulation of vibrissae and to stimulation of the hindlimb, respectively (see Methods). Rhythmic motion of the vibrissae led to a punctate ECoG response followed by a sustained phasic response at a lateral location (Fig. 5a) that was centered near the canonical location for the representation of vibrissae in primary somatosensory cortex (15). No electrical response was seen on stimulation of the hindlimb or other body structures. In contrast, we observed a punctate ECoG that was time-locked to strokes of the hindlimb, but no response on vibrissa stimulation, at a medial region (Fig. 5a) centered near the known location for hindlimb representation (15).

With the somatotopic map as a guide, we measured the trial-averaged speed of RBCs within the finest-caliber vessels in the vibrissa and hindlimb areas to determine the amplitude of stimulus-induced changes in capillary blood flow. In the vibrissa area, we observed a significant increase in speed in response to stimulation of the vibrissae (5 of 14 capillaries across five animals). The case with the largest change (≈20% of the baseline value) is shown in Fig. 5b; the solid line is the mean and the gray band is one standard deviation in the average over all trials. No significant change in the speed of the RBCs was observed in a subset of these capillaries in response to hindlimb stimulation (Fig. 5b) (six capillaries across three of the five animals). In the hindlimb area of cortex, we observed a smaller but nonetheless significant change in the speed of the RBCs on stimulation of the hindlimb (three of nine capillaries across three animals). The example with the largest change (≈15% of the baseline value) is shown in Fig. 5c. No significant change in the speed of the RBCs was observed in any of these capillaries in response to vibrissae stimulation (Fig. 5c). These data confirm that stimulus-induced changes in capillary blood flow are localized on the scale of gross somatotopic representation, and further show that the value of the stimulus-induced change in speed is on the order of the trial-to-trial variability (standard deviation) in speed**.

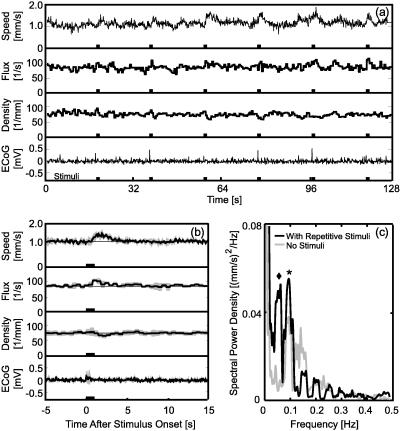
To further explore the issue of single-trial variability and to examine the effect of stimulation on the flux and linear density of the RBCs, we considered the analysis of records that were free of stalls or other large irregularities over the entire 128-sec period of acquisition (n = 4). For the example of Fig. 6a, we observed considerable trial-to-trial variability in the value of the stimulus-induced change in the speed of RBCs and the change in flux (Fig. 6a), as well as in the ratio of these quantities (Eq. 1), i.e., the linear density (Fig. 6a). Furthermore, the variations in the blood flow parameters did not necessarily track the variations in the ECoG (Fig. 6a). An examination of the average quantities for these trials revealed that the flux, as well as the speed, transiently increase on stimulation (Fig. 6b) but that the values of these increases were such that there was a small but significant decrease in the linear density after stimulation. Similar levels of variability, along with transient decreases in density, were observed in all of these records.

Figure 6.

The nature of the single-trial response of RBC flow to vibrissa stimulation. We recorded from the equivalent of the area denoted • in Fig. 5a. (a) A complete 128-sec record with six separate stimuli, spaced 20 sec apart. Shown are the speed, the flux, the linear density [computed as flux/speed (Eq. 1)], and the ECoG (recorded from a site ≈2 mm lateral to the optical measurement). Depth = 255 μm. (b) Trial average of the quantities shown in a. The dark line is the average over all six trials; the gray band is the SD of the trial average, and the thin straight line is drawn through the prestimulus portion of the data. Depth = 255 μm. (c) Spectral power for the speed shown in a (black line) along with the power for a record taken immediately after but without simulation (gray line). The ⧫ corresponds to variation in the speed at the 0.05-Hz repetition frequency of the stimulation and the ∗ corresponds to a peak at 0.1 Hz associated with vasomotor oscillations. The half-bandwidth of the spectral estimation was 0.016 Hz.

A final point concerns the relative amplitude of the stimulus-induced response. For the data of Fig. 6a, the spectral composition of the speed indicates that the magnitude of the peak at the repetition rate of the stimulus (0.05 Hz; ♦ in Fig. 6c) is similar to the magnitude for peak that corresponds to low-frequency oscillations (0.1 Hz; ∗ in Fig. 6c). The latter peak is present independent of stimulation (Figs. 3d and 6c). A similar ratio of magnitudes is observed in all cases (n = 4). This analysis suggests that the trial-to-trial variability in the response of blood flow to stimulation is caused largely by low-frequency oscillations.

DISCUSSION

We have demonstrated that two-photon laser scanning microscopy provides a means to image vasculature (Figs. 1 and 2) and to probe dynamic aspects blood flow (Figs. 2–6) at depths to 600 μm below the pia. The latter range encompasses layer 2–3 of neocortex and the superficial part of layer 4 (the level of the dominant thalamic input to neocortex). The further optimization of laser parameters may allow two-photon laser scanning microscopy to be used to probe blood flow at even greater depths without a loss in resolution. However, significant increases in peak laser powers may induce large background signals—and possibly photodamage—through the absorption of out-of-focus laser light in the upper layers of cortex.

Other investigators, using whole-field imaging (22), have reported on the speed of RBCs in individual vessels only as deep as the pia (refs. 5, 23–26; Table 1). To visualize capillary blood flow throughout the upper 250 μm of cortex, which encompasses layer 1 and superficial aspects of layer 2–3, Dirnagl and Villringer (7) pioneered the use of confocal-laser scanning microscopy to follow the motion of RBCs in individual capillaries. They report both the speed and flux of RBCs (ref. 20; Table 1). Our measurements of the basal flow (Fig. 3f) are within the ranges of these studies (Table 1), although there is considerable variability between the results of different studies. Whereas spatially localized increases in flow through capillary networks in response to sustained sensory stimulation have been inferred (27, 28), there appear to be no previous reports on the effect of sensory stimulation on blood flow (Figs. 5 and 6) at the level of individual capillaries.

Table 1.

Distribution of basal RBC flow parameters in neocortical capillaries in rat

Depth, μm	Speed, mm/sec	Flux, sec−1	Ref.
0 (pia mater)	0.75  ±  0.60	—	23
	0.79  ±  0.30	—	24
	1.60  ±  0.70	—	25
	0.98  ±  0.27	—	26
	0.68  ±  0.20	—	5
0 to 250	0.50  ±  0.44	36  ±  28	20
200 to 600	0.77  ±  0.51	56  ±  39	This study

Values given are mean ± SD. 

We observe low-frequency fluctuations in the speed of RBC flow (Figs. 3d and 6c) that appear to be correlated across junctions separating neighboring capillaries (Fig. 4f). The frequency of these oscillations is similar to that reported for the speed of RBCs imaged in capillaries close to the cortical surface by wide-field techniques (26) and inferred from laser–Doppler measurements (29). Furthermore, oscillations with a similar spectral character are observed with intrinsic optical imaging of cortical function in rat (30) and result in a change in the blood-related signal that is coherent over distances of 1 mm or more across cortex (D.K. and P.P.M., unpublished observations). These oscillations are generally termed vasomotion and consistent with their spatially extended correlations are believed to result from oscillations in the arterial supply (31). From the perspective of functional imaging of nervous activity, these oscillations constitute a physiological noise source that is likely to limit the sensitivity of optical or MRI techniques (30, 32), in which the contrast mechanism is related to changes in blood flow (33).

We observed that natural sensory stimulation leads to a transient increase in the flux of RBCs in some individual capillaries (Fig. 6). Such an increase is consistent with either an increase in the pressure head to the vessel or a drop in the impedance of the vessel to the motion of RBCs. Concomitant with the change in flux (Eq. 1) was an increase in velocity and a relatively small decrease in the density of RBCs (Fig. 6). Both of these changes are consistent with a decrease in the impedance to the motion of RBCs. A scenario discussed by Woolsey, Rovainen, and coworkers (1, 28) and consistent with the present findings is that sensory stimulation leads predominantly to a decrease in the impedance of a capillary or a network of capillaries. This implies that sensory stimulation shifts the available pool of blood from nonactivated regions to activated regions, consistent with global measures of blood flow (34). It further implies that the linear density of RBCs depends on the speed on the driving force (presumably the speed of the blood serum); the relation of the speed of RBCs in capillaries to that of the serum is an open experimental and theoretical issue (35).

ABBREVIATIONS

ECoG

electrocorticogram

RBC

red blood cell.