Experimentally determined chaotic phase synchronization in a neuronal system

Abstract

Mathematical analysis of the subthreshold oscillatory properties of inferior olivary neurons in vitro indicates that the oscillation is nonlinear and supports low dimensional chaotic dynamics. This property leads to the generation of complex functional states that can be attained rapidly via phase coherence that conform to the category of “generalized synchronization.” Functionally, this translates into neuronal ensemble properties that can support maximum functional permissiveness and that rapidly can transform into robustly determined multicellular coherence.

Subthreshold oscillations are a salient feature of the biophysical membrane dynamics in the inferior olivary (IO) neurons (1). These oscillations have been proposed to be one of the main determinants of the spike generation and collective behavior properties in the olivo-cerebellar system (2). Determining the dynamic character of the subthreshold membrane potential oscillation in IO neurons and its relation to the integrative dynamics of electrically coupled neuronal ensembles (3) is the central goal of this paper. However, not much is known about the linear or nonlinear nature of this rhythmic behavior: e.g., whether single cell (most probably coupled with other cells) oscillation displays nonlinear dynamic properties and, if so, its role, if any, in the rhythmic synchronization of electrically coupled neurons. This issue is significant because different mechanisms will produce different perturbation sensitivities and different characteristic synchronization times and eventually will lead to different neuronal ensemble dynamics. Here, we analyze the oscillation properties of single IO neurons and extend the analysis to the synchronization of the oscillation properties of electrically coupled IO neuronal pairs recorded simultaneously.

MATERIALS AND METHODS

The experimental procedures used are the same as those used in previous in vitro slice recording in the IO nucleus (1). Intracellular recordings were obtained by using bridge amplifiers, which allow single or dual intracellular recordings by using two independent head stages (Fig. 1 A and B).§ Extracellular stimulation was accomplished via the exposed tips of a twisted pair of teflon-coated stainless-steel wires positioned on the surface of the slice. The data used for analysis were digitized at 5 kHz, and 25–30 × 10³ continuous data points were analyzed, at 1 kHz, for the time series calculation (125 to 150 oscillatory cycles).

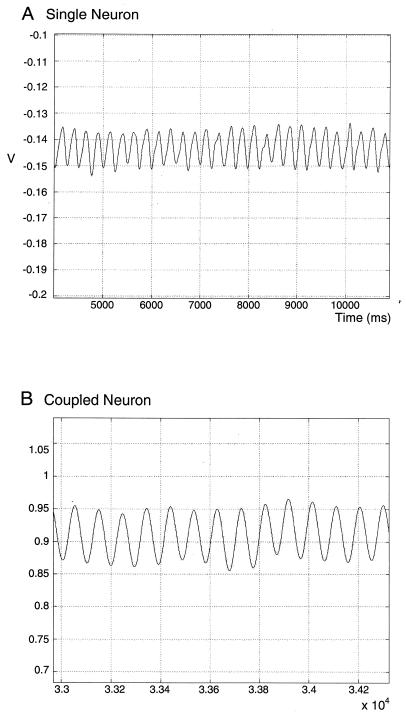
Figure 1.

(A) Subthreshold membrane potential oscillation recorded intracellularly in an IO neuron. (B) Similar traces recorded from one of a pair of coupled IO neurons.

The study implemented the following paradigms: (i) the nonlinear analysis of transmembrane voltage oscillatory behavior in single and in pairs of coupled IO neurons recorded intracellularly, (ii) analysis of the phase difference between oscillations in coupled neurons, and (iii) computer modeling of nonlinear dynamics oscillators resembling properties of the experimental data.

Nonlinear Analysis.

Individual subthreshold oscillations, and related ensemble dynamics, were addressed by using a recently developed nonlinear dynamics methodology (4) that allows quantitative analysis of all major time series characteristics in nonlinear systems. This approach requires a number of implementation steps: (i) calculation of the spectral analysis, (ii) determination of the average mutual information (AMI), (iii) determination of the global and local embedding dimensions, and, finally, (iv) calculation of the Lyapunov spectra. The set of steps in the analysis is stipulated, in our case, by the nonlinear nature of the neuronal subthreshold oscillation and by the irregularity of its dynamics. Thus, a linear approach cannot define the dominant dynamics of this neuronal activity (5).

Because the intracellular data available was of sufficient duration to satisfy the requirements for this analysis (i.e., the time series analysis must be based on a number of data points, n, where n ≥ 10^D, and D is the dimensionality of the system), the computational steps were followed. The results indicated that IO oscillations can be described as a low-dimensional nonlinear system, with no more than four independent variables. After the demonstration of feasibility, the next step attempted to construct an attractor to determine whether an appropriate time delay (τ) for the chaotic process could be extracted. In most cases, a good guess for the value of τ can be obtained from deriving the value of the first minimum of AMI, a value related to the Kolmogorov–Sinai invariant (6). The first minimum determines the “forgetting speed” for the previous trajectory: i.e., the value of τ for each component of the vector

1

constructed from the initial time series V_n to become independent, d, is a dimension of the phase space that contains the attractor.

We also have studied the synchronization between pairs of subthreshold membrane potential oscillations as a nonlinear property. This approach addressed the synchronization characteristic of this system, which, given its dynamic character, could not be derived from linear systems analysis. Indeed, in the last few years, theoretical and experimental research in nonlinear systems analysis has established that chaotic dynamic systems, previously regarded as not able to synchronize (given their chaotic mode of dynamics), can, in fact, do so. Moreover, it has been shown that such synchronicity demonstrates important new properties (7–9), such as threshold synchronization, phase locking, and dynamic mode switching from chaos to periodic oscillation. The implementation of computer modeling of the neuronal dynamics observed experimentally provided further support for the conclusions obtained from the analysis of experimental data.

AMI.

Given two sets of measurements, A and B, mutual information between point ai from the set A and point bj from the set B is defined as the amount of information that the measurements ai and bj have with respect to each other.

If the measurements are independent, then the mutual information is zero. Averaging over all measurements:

Replacing ai and bj with s(n) and s(n + T), respectively, determines when the AMI reaches its first minimum: i.e., the time interval required to regard the processes as independent from each other.

False Nearest Neighbors (FNNs).

The FNN method is based on the estimation of the Euclidean distance R² between nearest points in dimension d and then in dimension d+1 and comparing the difference with respect to some threshold value, ɛ, which is defined as a quantitative criterion of neighborhood:

In general terms, the value of threshold is an empirical parameter that must be adjusted to the size and form of the attractor.

Computer Model.

To verify that the results suggest that well characterized nonlinear interactions are present in experimental data, we repeated the computational analysis by using a Rossler oscillator (10). The model is simple enough but captures many important features, such as periodicity, low dimensional chaos, and the ability to synchronize. This model represents single neuronal dynamics by three main components—membrane potential, fast currents (associated with potassium and sodium ion channels), and slow current: x(t), y(t), and z(t), respectively. The oscillators are mutually coupled electrically:

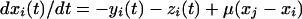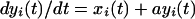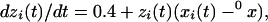where a, μ, and ⁰x are constants. The μ coefficient determines the strength of the coupling, a = 0.148, ⁰x = 8.5. By using this system, it has been demonstrated that, when signals are large, chaotic synchronization will occur when the subsystems signals are identical (8). The fourth order Runge-Kutta-Merson method (11), with accuracy control, was used in integrating these equations.

Analysis of Electrophysiological Data.

Subthreshold oscillations from single neurons. Use of the AMI method, as specified above, gives us an experimental time delay of τ ≈ 4 msec (Fig. 2A). The attractor reconstructed in three-dimensional phase space with coordinates [x(n), x(n + τ), x(n + 2τ)] using the aforementioned delay showed clear structural features (Fig. 2B).

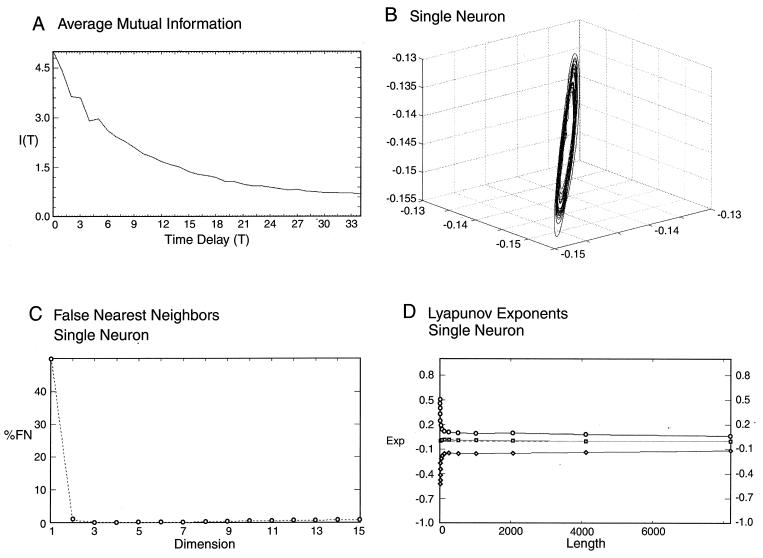
Figure 2.

AMI for a single neuron. First minimum happens at a value of 4 (A). Taking slightly different values—i.e., 8—does not influence the structure of the attractor. The attractor was reconstructed from a time series for a single neuron with a four-time delay (B). The attractor has a structure close to a limit cycle with regular periodic trajectory. (C) FNNs for a single neuron. The minimum is reached at value of 3, and undetectable growth is observed at higher values, indicating a low noise system. Lyapunov exponents show negative, zero, and positive values (D), indicating that the system displays low-dimensional chaotic dynamics.

Our next step was that of determining the number of coordinates required to unfold the attractor of the subthreshold oscillations, i.e., the dimension d_E, to be used in the reconstruction of vector X_n from observed time series so that no overlapping of orbits because of projection from a higher dimension would occur. Here we used the FNN method. The method allows the determination of the segment of the nearest neighbors for each data point provided by the projection from higher dimensions. That is, if the dimension is chosen correctly, then no further decrease in the number of the neighboring data point will occur with increased dimensionality. The percentage of the false neighbors reaches nearly zero at d_E = 3 and remains as such for higher dimensions (Fig. 2C) This indicates the presence of a low-dimensional nonlinear system and demonstrates that a consistent description of IO dynamics requires only a three-dimensional phase space. The results further demonstrate that, regardless of the number of biological variables at play in the generation of subthreshold oscillation in this in vitro system, such variables are not independent from each other or, in other words, that, mathematically, three independent variables are sufficient to incorporate the variables expressing in the oscillatory property of this system.

At this point, we examined the possibility of chaotic behavior in the time series of the experimental subthreshold oscillations by determining the Lyapunov exponents, which characterize the stability of the orbits on the attractor. Chaotic behavior is associated with at least one positive Lyapunov exponent. Our data shows one negative and one positive exponent and one at zero (Fig. 2D). The values of the exponents define the Lyapunov dimension of the system, which is ≈2.85.

The above analysis indicated that we were dealing with a chaotic signal generated by a low-dimensional nonlinear system. Although chaotic properties of single cell dynamics have been demonstrated in the past (12, 13, 14), no generalization to neuronal ensemble properties were derivable because of the ad hoc properties of the dynamics of the single cell behavior.

Subthreshold oscillations of coupled neurons.

The dynamic properties of coupled neurons were determined from pairs of electrotonically coupled IO neurons. The corresponding time series from each neuron is shown in Fig. 3 A and B. The analysis of coupled oscillators used a similar methodology to that used in the calculation of the single neuron times series. The results from this analysis are illustrated in Fig. 3C. Unexpectedly, little change, if any, was found in the characteristics of the signal. The difference resulting from the comparison preserved the structural properties of the attractor, and all characteristics closely coinciding with that of the individual neuron. Note that, because we are dealing with two oscillatory signals between coupled neurons, we could assume close synchronization between them. This problem can be addressed easily in nonchaotic signals; however, it turns out to be quite complicated when addressing chaotic systems. A fruitful approach to dealing with identical as well as with nonidentical chaotic oscillators has been developed recently (8, 9), and that approach was implemented in this study, with some changes dictated by the specifics of our experimental data. Basically, the simplest case of chaotic synchronization occurs when coupled systems produce identical chaotic signals. In such a case, the difference must be nonchaotic: i.e., the difference signal must be a fixed state. Geometrically, it implies the existence of a hyperplane at which corresponding variables are identical.

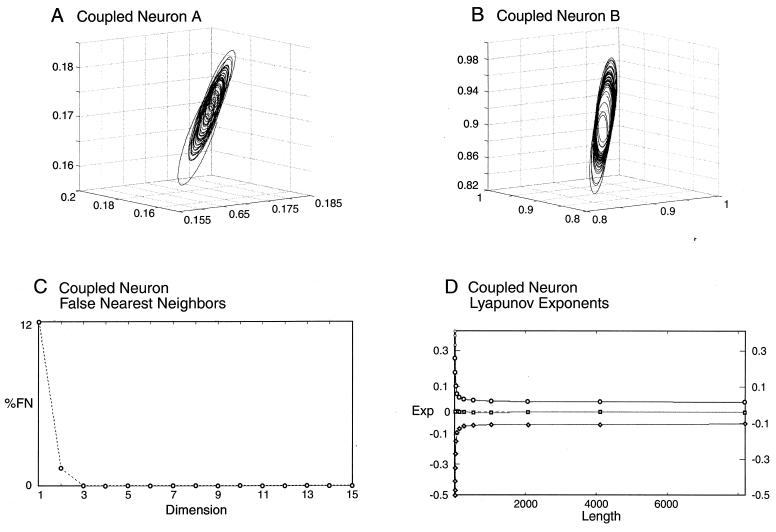
Figure 3.

Times series analysis for the coupled neurons. Attractors reconstructed by using the time delay six have the same space structure as that of the single neuron (A and B). The FNN graph (C) demonstrates that the system is uninfluenced practically by noise because the FNN reaches the zero value at close to the same value as for a single neuron. The graph for Lyapunov exponents (D), which have almost the same values as for a single cell, shows appreciable stable, indicating that coupling plays a stabilizing role in the neural dynamics.

In search of the appropriate measure for synchronization between systems with attractor topology similar to that obtained in this study, a definition was offered in a recent paper (9). In that study, the authors tackled the problem by determining the phases for such systems and then determining if the phase difference—φ_i − φ_j, φ_k = arctan(y_k/x_k), where x_k and y_k, correspondingly, are coordinates of a system—grows with time or remains bounded, demonstrating, in the latter case, phase locking.

The experimental results demonstrated that the difference between the two signals was not constant or regularly periodic (Fig. 4A) and that the phase difference remained bounded and small (Fig. 4B). This regime is also present in our computer model based on Rossler model oscillators, which also demonstrates a phase difference for the simulated membrane potentials under chaotic phase synchronization (Fig. 4 C and D). Our results demonstrated similar properties to those described for a lattice of nonidentical oscillators (9).

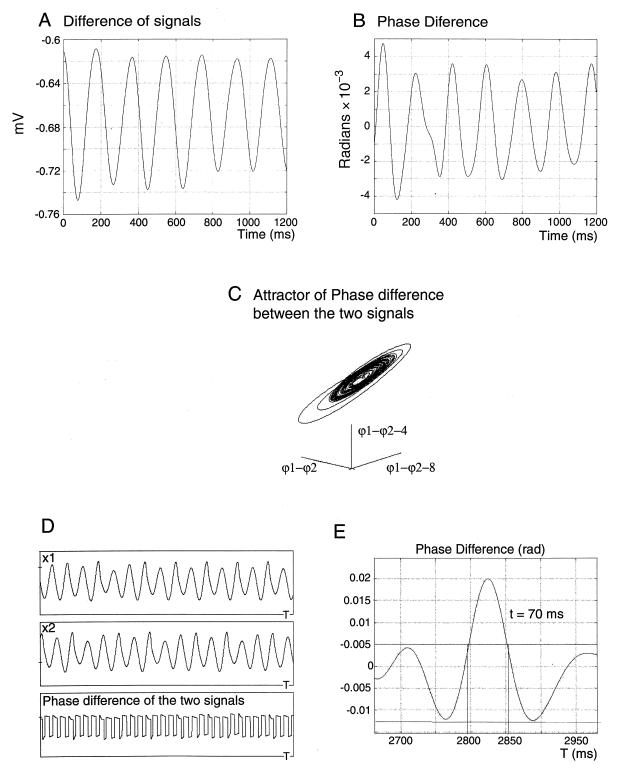
Figure 4.

Difference between the signals of two coupled neurons. The lack of a fixed frequency or amplitude demonstrates that the signals are not identical (A). Phase difference between the signals stays small through the observed time series, indicating chaotic phase synchronization between the two coupled neurons (B). (C) The attractor, reconstructed for the phase difference by using the same time delay. (D) Numerically computed traces for the model systems 1 and 2. The systems stay phase-locked with periodically changing phase difference (E). For large values of coupling coefficient, full chaotic synchronization happens when systems produce identical signals. Shown is the time of return after perturbation of the coupled neuron by external current. The time (70 ms) is less than half of the averaged period of oscillations of the neuron. The exponential dependence on the initial conditions can work as an amplifier that detects the discordance between the systems and therefore accelerates appropriate orbital selection.

These results demonstrate that subthreshold membrane potential oscillations in IO neurons, while being chaotic and generally having nonidentical oscillation properties, are, nevertheless, synchronized through phase locking. The periodicity of change of the phase difference (e.g., that at different parts of the attractor a point along a trajectory may move at a different speed) most probably lies in the biophysics of the membrane potential dynamics engendered by the individual kinetics of the different ionic currents. The model also showed that, with high coupling coefficients (larger than some critical value), full chaotic synchronization will occur, leading to identity of the two signals.

DISCUSSION

That neuronal systems demonstrate nonlinear dynamic properties capable of supporting chaotic behavior as an operational mode may be considered a biological quirk of little functional significance [the work of Abarbanel et al. (14) on the properties of general systems notwithstanding]. The present set of results argues the opposite view. Indeed, our results indicate that the nonlinear chaotic behavior of the subthreshold oscillations in the IO neurons and the synchronization between them support a fundamental and absolutely necessary property in neuronal ensembles. That is, the nonlinear dynamic properties support a system having maximum functional permissiveness, which can transform rapidly into robustly determined functional multicellular coherence (15).

Assuming that the hypothesis that subthreshold oscillations support a clock-like role in IO function (2) is correct, one runs into the problem that, as a rule, such “clocks” must be synchronized locally in some particular domains and that the domains must easily be desynchronized to adapt to changes in synaptic input. In addition to their intrinsic oscillatory properties, one of the remarkable organizational features of the IO neurons is their electrical coupling (1, 3), which allows continuous and very rapid communication between them. This fact carries a functional limitation in the case of periodic oscillators: namely, the lack of a coupling threshold below which synchronization does not happen. With periodic oscillators, all that can be controlled is the time required for synchronization to occur. On the other hand, chaotic oscillators are characterized by having certain coupling values required for the onset of synchronization. Because the synchronization in the IO system has been experimentally shown to be sensitive to changes in the strength of coupling (16) with respect to synchronization, this finding represents a further argument for a chaotic phase synchronization: in this case, in an in vivo condition. In addition, a chaotic system can be brought into a fixed state by a strong perturbation whereas the transition from synchronization to desynchronization and vice versa is modulated by the electrotonic coupling strength. In IO, this property is regulated by the inhibitory feedback onto the electrical junctions (3, 15) and is probably responsible for the reset of both phase and frequency observed in the periodic oscillation of the membrane potential (1).

The fact that the IO neurons are able to phase-synchronize their subthreshold oscillations does not prevent them from keeping the rhythm but, rather, allows for individual variability. This is not surprising for a biological system. This particular form of synchronization was defined in mathematical physics as “generalized synchronization” (8). It is also important to note that the time necessary for synchronization in a chaotic system is much shorter, under appropriate values of coupling, than for the regular periodic system. Thus, the exponential dependence on initial conditions serves as an amplifier to correct an error of discordance of oscillatory phases between neurons, forcing them to rapidly sort out among the orbits of the attractor along which they move until the satisfactory one is found. We have determined, by estimating the return time to the range of usual phase difference between signals, that the resynchronization time after an external stimulation is comparable with the average oscillatory period (Fig. 4E).

It has been shown experimentally that the IO generates action potentials, which form rapidly occurring and highly correlated spatiotemporally functional groupings during the organization of motor activity pattern and which lead to complex spike activation of Purkinje cells (16, 17). Furthermore, a single-compartment two-variable model of IO neuronal oscillation corroborates the fact that such patterns of activity would be quite difficult, if not impossible, to generate without coupled subthreshold oscillation (18).

From the above, we conclude that there are two types of synchronies in the IO system: one “closed” (subthreshold), in the sense that it is not relayed directly to the other brain structures, and a second “open,” which is used to relay synchronous action potentials to the Purkinje cells. The former is a “loose,” generalized synchronization, allowing for some neuronal individuality. The latter is quite “rigid,” and is responsible for the stereotyped and highly secured signals represented by the climbing fiber activation of the Purkinje cells. The closed synchronization properties, while not directly observable outside the IO, provide, nevertheless, the mechanism for the temporal binding that ultimately results in the coordination of motoneuron activity required for properly timed motor execution. We further suggest that this mechanism is operant in many other brain structures in which subthreshold oscillations are found (19).

In short, we have established that (i) subthreshold oscillations of the membrane potential of IO neurons, produced by dynamic ionic mechanisms (3), support low dimensional chaotic dynamics, (ii) the electrotonic coupling in these neurons leads to the generation, via phase-coupled coherence, of complex functional states that can be generated rapidly without increasing the dimensionality of the system, and (iii) synchronization of the individual neurons conforms to the category of generalized synchronization. This allows a less rigorous condition for neuronal synchronization without the loss of the ability to control the temporal pattern in each of its independent functional compartments, the main advantage of synchronized systems.

ABBREVIATIONS

IO

inferior olivary

FNN

false nearest neighbor

AMI

average mutual information