Abstract
Direction finding of more sources than sensors is appealing in situations with small sensor arrays. Potential applications include surveillance, teleconferencing, and auditory scene analysis for hearing aids. A new technique for time-frequency-sparse sources, such as speech and vehicle sounds, uses a coherence test to identify low-rank time-frequency bins. These low-rank bins are processed in one of two ways: (1) narrowband spatial spectrum estimation at each bin followed by summation of directional spectra across time and frequency or (2) clustering low-rank covariance matrices, averaging covariance matrices within clusters, and narrowband spatial spectrum estimation of each cluster. Experimental results with omnidirectional microphones and colocated directional microphones demonstrate the algorithm’s ability to localize 3–5 simultaneous speech sources over 4 s with 2–3 microphones to less than 1 degree of error, and the ability to localize simultaneously two moving military vehicles and small arms gunfire.
INTRODUCTION
Acoustic localization or direction finding with arrays of only a few microphones finds applications in areas such as surveillance, auditory scene analysis for hearing aids, and many other applications. For instance, localization of the source of a gunshot in a crowded battlefield environment may be useful in military applications. Similarly, localization of multiple talkers in a crowded restaurant or social event might be useful for a hearing aid. In many applications such as hearing aids, only a small array is practical. In many situations with such arrays, the number of sources often exceeds the number of sensors, and most localization algorithms cannot deal with this case. In general, with stationary Gaussian sources, only fewer sources than the number of sensors can be localized (Schmidt, 1986). However, if there are fewer sources than sensors in disjoint frequency bands, then by localizing in each band, overall localization of more sources than sensors is possible. Taking advantage of such sparseness is crucial to localize more sources than sensors.
Previous methods for localizing more sources than sensors implicitly assume such sparse time-frequency structures. Pham and Sadler (1996) use an incoherent wideband MUSIC (Schmidt, 1986) approach where they assume that “a single frequency bin is occupied by a single source only” and sum the individual MUSIC spectra across all time-frequency bins. However, their method makes no provision for cases when this is not the case, and thus can be expected to fail for multiple sources that are similar or are not extremely sparse, e.g., a cocktail-party scene with multiple human speakers. The method presented in this paper overcomes this limitation. Using the same assumption, Rickard and Dietrich (2000) estimate the source locations at each time-frequency (TF) bin using a ratio-based technique followed by a histogram-like clustering of all the estimates across time and frequency. Two other methods use parametric models for the sources’ temporal behavior. Su and Morf (1983) model the sources as rational processes. Assuming that the number of sources sharing a pole is less than the number of sensors, they apply MUSIC to the data at the estimated poles and combine the directional spectra across poles. The TF-MUSIC method of Zhang et al. (2001) uses a quadratic TF representation. Assuming frequency-modulated sources, they are able to identify time-frequency bins that correspond to a certain source and average the covariance matrices from those bins. The averaged covariance matrix has a higher signal-to-noise ratio (SNR) and thus leads to a better directional spectrum.
The previous methods exploit the nonstationarity of the sources through prior knowledge of the source’s time-frequency structure or through assumptions on the reduced-rank nature of the data. When dealing with mixtures of more nonstationary sources than sensors, such as four speech signals and two microphones, an approach requiring no knowledge of the source’s spectra to identify time-frequency bins where the data is low rank or contains fewer active sources than the number of sensors would be attractive. Conventional methods of spectral estimation can be applied to low-rank data. But as different low-rank data are available across time and frequency, the issue of coherently combining or incoherently combining the data is investigated. Specifically, creating directional spectra at each low-rank bin and incoherently combining those or coherently combining the low-rank data in some manner and then creating a directional spectrum is compared.
Although the time-frequency sparsity of the sources is key to localizing more sources than sensors, the response of the array itself plays an important role. Most direction-finding techniques use an array of spaced omnidirectional sensors, each with an isotropic spatial response. These techniques exploit the time delays between the sensors that vary as a function of direction (Johnson and Dudgeon, 1993). Directional sensors have a spatial response that is preferential to certain directions. Gradient, cardioid, and hypercardioid microphones are examples of different spatial responses. An array of two or three colocated directional sensors that are oriented in orthogonal directions form a vector sensor, providing an amplitude difference between the sensors that varies as a function of direction. Single-source localization with a vector sensor using the minimum variance or Capon spectrum has been described by Nehorai and Paldi (1994) and Hawkes and Nehorai (1998). Multisource localization with a vector sensor using an ESPRIT-based method was presented by Wong and Zoltowski (1997) and Tichavsky et al. (2001). In these methods, the authors assume the sources are sinusoidal and disjoint in the frequency domain, noting that “it is necessary that no two sources have the same frequency” as only one source can be localized in each frequency bin (Tichavsky et al., 2001). They also mention that their algorithm could be “adapted to handle frequency-hopped signals of unknown hop sequences” (Tichavsky et al., 2001). To deal with signals with time-varying overlapping frequency content, identifying low-rank time-frequency bins is a key element of our algorithm. Last, an important practical advantage of a vector-sensor is that it can be designed to occupy a very small space or volume (Miles et al., 2001).
In the following sections, an algorithm is presented that can localize more acoustic sources than the number of microphones employed for common types of nonstationary wideband sources. The algorithm’s ability to localize (1) simultaneous speech sources and (2) gunshot sounds simultaneous with military vehicles using different microphone arrays of omnidirectional and gradient microphones is demonstrated. To our knowledge, this is the first time that high-resolution multisource localization has been practically demonstrated with aeroacoustic gradient microphones.
SIGNAL MODEL
We briefly establish the signal model and notation here before describing the localization algorithm.
-
(1)
All text in bold denotes vector quantities or vector operations.
-
(2)
(⋅)H denotes Hermitian transpose.
-
(3)
(⋅)* denotes the complex conjugate.
-
(4)
Let be the temporal waveforms of the sources, where L is the number of sources. We assume that the sources are bandlimited to B Hz.
-
(5)
Let si(n) be samples at times t=nT of the ith source signal, where the sampling interval T⩽1∕2B satisfies the Nyquist requirement.
-
(6)
We assume that the sources are independent and block stationary; i.e., the are essentially stationary over several adjacent N-sample intervals and .
-
(7)
Let M be the number of sensors in the array.
-
(8)Let x(n) be the discrete-time signal at the array output after sampling at or above the Nyquist frequency of 2B Hz. We assume that the system is linear and time invariant so that the received signal is a convolutive mixture of the sources:
(1) -
(9)
h(n,θi) is an M×1 impulse response vector that is a function of θi, the direction-of-arrival (DOA) of the ith source.
-
(10)
⋆ denotes discrete-time convolution.
Section 3 explains the localization algorithm. Section 4 describes the results of testing the algorithm on microphone arrays with acoustic sources. Section 5 contains the conclusions.
MULTISOURCE LOCALIZATION ALGORITHM
The algorithm uses four main steps to localize simultaneous nonstationary wideband sources when the number of sources may be greater than the number of sensors. First, the discrete-time data from the microphone array is transformed into an overlapped short-time Fourier transform (STFT) representation. Second, a coherence test is used to find time-frequency bins with fewer active sources than the number of sensors. After that step, there are two variants of the algorithm. In variant 1, a directional spectrum is computed from the covariance matrix at each low-rank bin. The directional spectra from all low-rank bins are summed to yield a final directional spectrum, which is used to estimate the DOAs of the sources. In variant 2, the covariance matrices from low-rank bins are clustered across time into groups based on Frobenius norm. The goal is for each cluster to contain low-rank data corresponding to a particular source. As the steering vector is frequency dependent, a separate clustering must be performed (across time) at each frequency bin. Next, the low-rank covariance matrices within each cluster are averaged and the averaged matrix is used to compute a directional spectrum. The directional spectra from all clusters are summed to yield a final directional spectrum, which is used to estimate the directions of arrival of the sources. Figure 1 contains a block diagram of the localization algorithm.
Figure 1.
Block diagram of the localization algorithm with variants 1 and 2.
Transformation to time-frequency
The first step in the algorithm is to transform the time-domain data into an overlapped STFT representation (Hlawatsch and Boudreaux-Bartels, 1992). The STFT of a signal s(n) is defined as
| (2) |
where w(n) is an N-point window, F is the offset between successive time blocks in samples, m is the time-block index, and ωk is the frequency-bin index (ωk=2πk∕N,k=0,…,N−1). X(m,ωk) is the STFT of the x(n) and is a linear combination of the source STFTs:
| (3) |
where h(ωk,θ) is the M×1 frequency-domain steering vector (i.e., location-to-microphones channel response) that is parametrized by a source’s location.
Coherence test
Next, time-frequency bins with low-rank data are identified by applying a coherence test to the estimated covariance (or power spectral density) matrix at each time-frequency bin. The true (unknown) M×M time-varying frequency-domain covariance matrix is R(m,ωk), a linear combination of rank-1 outer products of the source steering vectors weighted by the source powers:
| (4) |
| (5) |
where ) is the power (and variance) of the ith source over the (m,ωk)th time-frequency bin. A causal sample covariance matrix is used to estimate the covariance matrix at time-frequency bin (m,ωk):
| (6) |
where C is the number of time-blocks averaged to obtain the short-time estimate. Due to the time-frequency uncertainty principle (Hlawatsch and Boudreaux-Bartels, 1992), a specific short-time Fourier transform value represents signal content over a region of time and frequency (loosely referred to as a “time-frequency bin”) around that frequency and time. As the estimation of a covariance matrix requires averaging, the averaging across time blocks in Eq. 6 increases the temporal spread of this bin accordingly above the minimum required by the time-frequency uncertainty principle.
At any time-frequency bin, for many common nonstationary wideband sources such as speech and transient sounds like gunfire and passing vehicles, some source powers will be large, whereas other source powers will be negligible. A source that contributes a significant fraction of power (e.g., more than 10%) to the covariance matrix is an active source at that time-frequency bin. Equation 5 shows that time-frequency bins with the number of active sources greater than or equal to the number of sensors will have effective full rank, whereas time-frequency bins with fewer active sources than the number of sensors will have low effective rank or be poorly conditioned.
Identification of a low-rank bin is usually done by performing an eigendecomposition of the covariance matrix and examining its eigenvalues (Schmidt, 1986). The following algorithm can be applied to all low-rank time-frequency bins, defined as any time-frequency interval with a short-time-frequency correlation matrix with a maximum-to-minimum eigenvalue ratio greater than a selected threshold. However, a particularly simple statistical test arises if the search for low-rank bins is restricted to finding rank-1 bins, or time-frequency bins with only one active source.
A simple test for a rank-1 time-frequency bin involves the pairwise magnitude-squared coherences or the elements of the covariance matrix. Let be the MSC between sensors i and j (Carter, 1987):
| (7) |
Theorem1: Necessary and sufficient conditions for an M×M covariance matrix to be rank-1 are that the M(M−1)∕2 pairwise MSCs are equal to 1, and that for M>2, the phases of the off-diagonal components of the matrix satisfy ∠(Rij)−∠(Rik)+∠(Rjk)=0 ∀i<j<k, where ∠(Rij) is the phase of the ijth element of the covariance matrix. Proof: See the Appendix0.
Thus, the coherence test for identifying a rank-1 time-frequency bin involves computing the MSCs at that bin, checking if they are above a threshold (such as 0.90) and checking if the phases of the covariance matrix satisfy certain constraints.
If we were dealing with stationary sources, estimating the covariance matrix at different times would provide no new information. With nonstationary sources, the covariance matrix at each frequency bin is time varying, providing “new looks” at the statistics of different sources as time evolves. The coherence test (and any test aimed at finding low-rank bins) implicitly exploits the sparse time-frequency structure of the sources to find low-rank bins.
Time-frequency clustering and∕or combining
At this point, all rank-1 time-frequency bins have been identified, but the number and location of sources, and which source is associated with each rank-1 bin, remains to be determined. In variant 1 of the algorithm, a narrowband spectral estimator is computed at each low-rank time-frequency bin. The directional spectra are then combined incoherently across time and frequency, yielding a final directional spectrum. The peaks of this final spectrum are used to estimate the source DOAs (Mohan et al., 2003a,b). This approach is similar to the incoherent combining of Pham and Sadler (1996), but through the coherence test avoids the degradation they report by discarding low-SNR or higher-rank bins containing corrupt spatial-spectral estimates. Whereas Pham and Sadler require most time-frequency bins to be sparse for good performance, this method requires only a few nonoverlapped bins from each source to produce accurate, high-resolution localization of all sources.
In variant 2 of the algorithm, the normalized rank-1 covariance matrices at each frequency-bin are clustered across time into groups. The goal is to create groups containing rank-1 covariance matrices corresponding to the same active source. Thus, after the clustering, each frequency-bin ωk contains Q groups, each corresponding to one of the Q distinct sources detected, such as {R(m1,1,ωk),…,R(m1,P1,ωk)},…,{R(mQ,1,ωk),…,R(mQ,PQ,ωk)},…, where Pi is the number of rank-1 time-frequency bins at that frequency associated with the ith source. The covariance matrices in a group cluster together because they have the same structure (up to a scaling which is removed by the normalization); i.e., R(m1,ωk)=σ(m1,ωk)2h(ωk,θ1)h(ωk,θ1)H, R(mP,ωk)=σ(mP,ωk)2h(ωk,θ1)h(ωk,θ1)H. As the steering vector h(ωk,θ) varies as a function of ωk, a separate clustering must be performed at each frequency bin. Next, the covariance matrices within each group are averaged and a directional spectrum is computed from each averaged matrix. The directional spectra from each frequency bin are summed across frequency to yield a final spectrum from which the source DOAs are estimated.
MATLAB’s clusterdata command was used to cluster low-rank matrices by pairwise distance; the matrices were normalized to unit Frobenius norm prior to clustering. This algorithm forms a hierarchical tree linking the elements by pairwise distance and then prunes this tree to automatically determine the optimal number of distinct clusters (and hence sources) as well as the cluster assignments. After clustering, the normalization was removed before averaging matrices within a group because a covariance matrix with a higher norm usually indicates a higher instantaneous SNR for that active source; the averaging of unnormalized covariance matrices can reduce the effects of low-rank bins with bad SNR.
Variant 2 of the algorithm aims to exploit the assumption of spatial stationarity of the sources (which implies that their steering vectors are not changing as a function of time and can therefore be clustered) to improve the accuracy of the localization. Variant 1 of the algorithm would likely be more useful for tracking moving sources.
Directional spectrum estimation
The well-known MUSIC spectral estimator was used to compute a directional spectrum. The MUSIC estimator requires R(m,ωk) to have low rank so that a basis, UN(m,ωk), for the noise-subspace exists (Schmidt, 1986). The MUSIC estimator is then defined as
| (8) |
What separates variants 1 and 2 of the algorithm is the covariance matrix that is used to implement the above spectral estimators. Variant 1 can be described as incoherent combining of directional information as in Pham and Sadler (1996) (but only of coherent bins) because the data at each time-frequency bin is first transformed nonlinearly to a directional representation before combining across time and frequency. Variant 2 first combines the data at a low level by averaging covariance matrices within clusters and can be described as coherent combining of correlation data prior to nonlinear transformation to a directional representation.
Having described all the aspects of the localization algorithm in detail, in the next section, we test our algorithm with speech sources and microphone arrays.
EXPERIMENTAL RESULTS
An experimental study of the localization algorithm was performed using a microphone array intended for hearing-aid research. The Hearing-Aid-6 (HA6) microphone array contains three omnidirectional microphones and three gradient microphones mounted on a single behind-the-ear hearing-aid shell. The three gradient microphones are orthogonally oriented. One or two HA6 arrays were mounted on the ears of a Knowles Electronic Mannekin for Acoustical Research (KEMAR). This array was chosen both because of interest in hearing-aid applications and because it represents an extreme test case including a small number of microphones, very small aperture requiring super-resolution, and HRTF distortions. Free-field experiments with this array yielded even better performance, so are not reported here.
The HA6 array allows for various choices of microphone processing. The five different array configurations tested were:
-
1.
OOm: two omnidirectional microphones of the same HA6 array on the right ear of a KEMAR, 8 mm separation between microphones;
-
2.
OOOm: three omnidirectional microphones of the same HA6 array on the right ear of a KEMAR, 8 mm separation between microphones;
-
3.
GGm: two colocated gradient microphones of the same HA6 array on the right ear of a KEMAR;
-
4.
OOb: two omnidirectional microphones, one each from an HA6 array on the right and left ears of a KEMAR, 15 cm separation between microphones; and
-
5.
OOOb: three omnidirectional microphones, two from an HA6 array on the right ear of a KEMAR with 8 mm separation and one from an HA6 array on the left ear of a KEMAR, separated 15 cm from the other two microphones.
The subscripts m and b refer to monaural and binaural. Using the OOm, OOOm, and GGm arrays leads to monaural processing because the microphones are all on one side of the head, whereas use of the OOb and OOOb arrays leads to binaural processing because microphones are located on both sides of the head.
Comparisons between the OOm and OOOm evaluate the benefit of three microphones versus two microphones with the same microphone spacing. Arrays OOm and GGm compare using two omnidirectional microphones versus two gradient microphones. Differences between arrays OOm and OOb reflect the effect of aperture (specifically, 8 mm versus 15 cm). Array OOOb tests the addition of both an extra microphone and more aperture with respect to array OOm.
A second test of the localization algorithm was performed using two elements of a four-microphone free-field acoustic-vector-sensor array, the XYZO array, with acoustic data recorded at the DARPA Spesutie Island Field Trials at the Aberdeen Proving Ground in August 2003. The XYZO array consists of three gradient microphones and one omnidirectional microphone. The gradient microphones are mutually orthogonally oriented, creating a vector sensor. Only two of the gradient microphones were used to localize military vehicles and gunfire in azimuth. This test was intended to demonstrate the algorithm’s ability to localize acoustic sources other than speech sources and to localize in a free-field situation rather than in a room environment.
Vector gradient arrays of hydrophones have been used in the past for underwater direction-finding by Nickles et al. (1992) and Tichavsky et al. (2001). However, the successful application of aeroacoustic vector gradient arrays for high-resolution direction-finding has not been reported to our knowledge, except in our initial studies (Mohan et al., 2003a,b).
Steering vector of the microphone arrays
In array signal processing, the steering vector h(ωk,θ) describes the response of an array as a function of frequency and DOA. Arrays of spaced omnidirectional sensors have been well studied; These arrays are characterized by a time delay between the microphones that varies with the DOA of a source (Johnson and Dudgeon, 1993). For an array of two omnidirectional microphones in a free-field anechoic environment, the steering vector of a source with a DOA of θ degrees azimuth is
| (9) |
where ωk=frequency bin, d=spacing between the microphones, and c=speed of sound.
Arrays of directional microphones, especially colocated arrays, have been studied to a lesser extent. Directional microphones respond preferentially to certain directions. Various types of directional responses such as gradient, cardioid and hypercardioid can be constructed (McConnell, 2003). The HA6 and XYZO arrays contain colocated gradient microphones that are oriented in mutually orthogonal directions, causing an amplitude-difference to exist between the microphones that varies with the DOA of a source (Nehorai and Paldi, 1994). The steering vector of two colocated orthogonally oriented microphones for a source with a DOA of θ degrees azimuth is
| (10) |
Although the steering vector described previously is ideally frequency independent, real gradient microphones possess a low-frequency rolloff due to the large wavelength at lower frequencies.
When omnidirectional or gradient microphones are placed on the head of a KEMAR, the steering vectors (the responses of the array as a function of the source DOAs) are distorted by the head shadow of the KEMAR (Gardner and Martin, 1995). The head-shadow effect reduces the amplitude of a microphone’s response to directions from the side of the head opposite to where the microphone is placed.
Steering vector estimation and calibration
Impulse responses are often used in acoustical studies to capture the response of a microphone array in a room; these methods can also be applied to measurements from a free-field environment. The steering vectors for arrays on or near objects, such as the hearing-aid arrays in the experiments reported later in this section, are strongly altered and must be measured as a function of direction before the algorithm can be applied. The frequency-domain steering vector is obtained from the Fourier transforms of the impulse responses. One method for calculating an impulse response involves maximum-length sequences (MLS) (Gardner and Martin, 1995). Impulse responses were measured as a function of azimuth (with 15° resolution) around each microphone array by playing MLS from loudspeakers and recording the response from the microphones. As the frequency response of the MLS signal is known, the frequency-domain steering vector was calculated by frequency-domain deconvolution. The inverse discrete Fourier transform of the steering vector is the vector of room impulse responses. These impulse responses and their corresponding Fourier transforms are referred to as the measured impulse responses and the measured steering vector. More details on this method of calculating impulse responses are described by Lockwood et al. (1999, 2004). For the first experimental study, recordings were performed using the HA6 array and a KEMAR in a modestly sound-treated room (T60≈0.25 sec reverberation time) in the Beckman Institute; further physical and acoustical details of the room were described by Lockwood et al. (1999, 2004). Similar recordings were conducted using the XYZO array at the Aberdeen Proving Ground.
In order to increase the azimuthal resolution of the steering vector, the measured steering vector was interpolated from 15° resolution to 1° resolution using a Fourier-series technique. The coefficients of the Fourier-series expansion that best fit the data were found by least-squares solution to an overdetermined system of equations where the knowns consisted of the frequency-domain steering vector at 24 measured angles (15° azimuthal resolution) and the coefficients of the system were complex exponentials in azimuth evaluated at the 24 measured angles.
For an nth-order Fourier series fit for microphone i of an array, the least squares solution to the following equation is found:
| (11) |
| (12) |
| (13) |
| (14) |
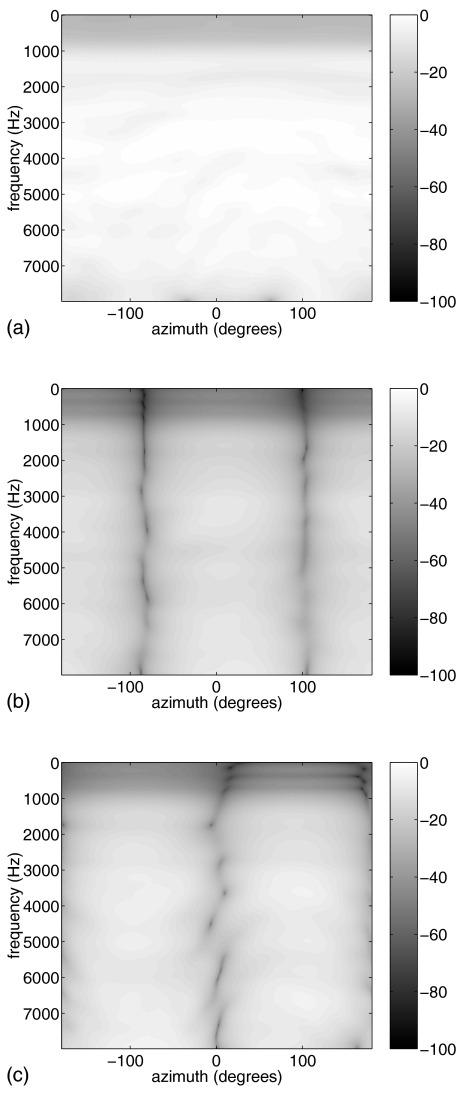
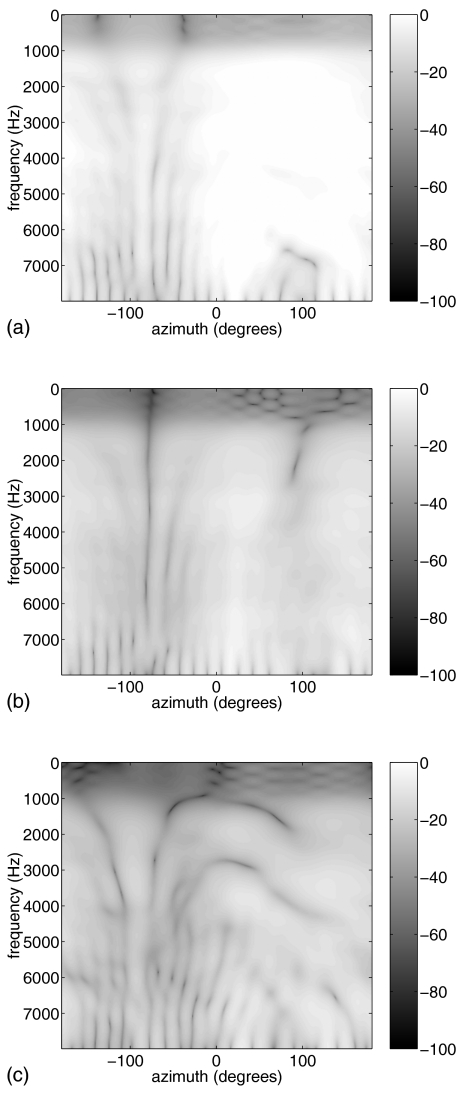
After solving for c(ωk), the coefficients of the Fourier expansion, the expansion was computed at 1° resolution in azimuth to produce the interpolated steering vector. A twelfth-order (full-order) Fourier-series fit was used for most of the localization tests. One localization test used a fourth-order fit to determine if similar localization results could be obtained with a lower-order interpolation. A separate fit was computed for each microphone in an array. Figures 23 show the magnitudes (in decibels) of the interpolated microphone responses using a full-order fit as a function of frequency and azimuth for one of the omni microphones and two of the orthogonally oriented gradient microphones from the HA6 array both in free-field and on the left ear of KEMAR. The nulls of the gradient microphones, the dark lines in Figs. 2b, 2c, are clearly seen in the free-field situation. Distortion of the nulls caused by the head shadow of KEMAR is seen in Fig. 3.
Figure 2.
Decibel magnitudes of the responses from the HA6 array in free-field (a) omnidirectional microphone and (b) and (c) two orthogonal gradient microphones.
Figure 3.
Decibel magnitudes of the responses from the HA6 array on the left ear of a KEMAR (a) omnidirectional microphone and (b) and (c) two orthogonal gradient microphones.
Results
The localization algorithm was implemented in MATLAB and tested with the microphone subsets of the HA6 array described in the five arrays OOm, OOOm, GGm, OOb, and OOOb. Acoustic scenes were created by convolving 4 s of speech signals sampled at 16 kHz from the TIMIT database with the measured impulse responses corresponding to each source’s DOA (Garofolo et al., 1993). The power of each speech signal was equalized by scaling the signal appropriately. The number of sources was varied from 3 to 5. For each number of sources, 50 acoustic scenes were constructed by choosing the speech signals randomly from the TIMIT database. The short-time processing parameters used by both variants 1 and 2 of the localization algorithm were 16 ms rectangular windows with 4 ms overlap, 256-pt fast Fourier transform and 120 ms (30 adjacent frames) averaging for each covariance matrix estimate. In variant 2 of the algorithm, the clustering described in Sec. 3C was performed using MATLAB’s clusterdata command. The covariance matrices were normalized to unit norm prior to clustering. The number and location of sources is determined automatically by finding all local maxima in the composite directional spectrum and counting all above an empirically determined threshhold.
Tables 1, 2 show the bias and standard deviation of the DOA estimates from the 50 trials, respectively. Tables 3, 4, respectively, show the average number of sources localized per trial and the number of trials that did not localize all sources. Some entries in Tables 1, 2 are exactly zero, indicating no error or bias. This is an artifact of the processing; direction was discretized to one-degree increments in these experiments, so zero standard deviation and bias actually indicates that in all 50 trials, the error never exceeded half a degree, which merely indicates that the biases and standard deviations are a great deal less than half a degree under these conditions.
Table 1.
Bias of the DOA estimates using the MUSIC spectrum.
| Variant 1 | Variant 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| True DOA (deg) | OOm (deg) | OOOm (deg) | GGm (deg) | OOb (deg) | OOOb (deg) | OOm (deg) | OOOm (deg) | GGm (deg) | OOb (deg) | OOOb (deg) |
| Three talkers | ||||||||||
| 0 | 0 | 0 | 0.02 | 0 | 0 | 0.02 | 0 | 0.22 | 0 | 0 |
| 30 | 0 | 0.02 | 0.3 | 0 | 0 | −0.02 | 0.08 | 0.45 | 0 | 0 |
| 45 | 0 | 0 | −0.04 | 0 | 0 | 0 | 0 | −0.2 | 0 | 0 |
| Four talkers | ||||||||||
| −60 | 0.17 | 0.08 | 0.16 | 0.06 | 0 | 0.48 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0.22 | 0.17 | 0.02 | 0.02 | 0.06 | 0.02 | 0 | 0 | 0 |
| 30 | 0.23 | 0.02 | 0.22 | 0.04 | 0.27 | 0.18 | −0.04 | −0.16 | 0 | 0 |
| 45 | 0.15 | −0.3 | −0.29 | 0.15 | −0.04 | 0.19 | 0.04 | −0.10 | 0 | 0.15 |
| Five talkers | ||||||||||
| −75 | 0.05 | 0 | 0.03 | 0.05 | 0 | 0.29 | 0.04 | 0.32 | 0.42 | 0 |
| −60 | 0 | 0 | 0 | 0 | 0 | −0.02 | 0 | −0.02 | 0.17 | 0.02 |
| 0 | 0.1 | 0.06 | 0 | 0.1 | 0.06 | 0.04 | 0 | −0.08 | 0 | 0 |
| 30 | −0.1 | 0.03 | 1.0 | −0.1 | 0.03 | 0.04 | 0.02 | 0 | 0 | 0 |
| 45 | 0.08 | −0.08 | 0.3 | 0.08 | −0.08 | 0.11 | −0.08 | 0.33 | 0 | 0.04 |
Table 2.
Standard deviation of the DOA estimates using the MUSIC spectrum.
| Variant 1 | Variant 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| True DOA (deg) | OOm (deg) | OOOm (deg) | GGm (deg) | OOb (deg) | OOOb (deg) | OOm (deg) | OOOm (deg) | GGm (deg) | OOb (deg) | OOOb (deg) |
| Three talkers | ||||||||||
| 0 | 0 | 0 | 0.14 | 0 | 0 | 0.15 | 0 | 0.42 | 0 | 0 |
| 30 | 0 | 0.14 | 0.61 | 0 | 0 | 0.26 | 0.34 | 0.5 | 0 | 0 |
| 45 | 0 | 0 | 0.20 | 0 | 0 | 0 | 0 | .64 | 0 | 0 |
| Four talkers | ||||||||||
| −60 | 0.38 | 0.28 | 0.37 | 0.24 | 0 | 0.51 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0.42 | 0.38 | 0.15 | 0.14 | 0.24 | 0.14 | 0 | 0 | 0 |
| 30 | 0.79 | 0.25 | 0.88 | 0.51 | 0.41 | 0.39 | 0.20 | 0.44 | 0 | 0 |
| 45 | 0.66 | 0.58 | 0.75 | 0.35 | 0.29 | 0.38 | 0.28 | 0.66 | 0 | 0.02 |
| Five talkers | ||||||||||
| −75 | 0.21 | 0 | 0.16 | 0.21 | 0 | 0.73 | 0.3 | 0.54 | 0.08 | 0 |
| −60 | 0 | 0 | 0.35 | 0 | 0 | 0.40 | 0 | 0.35 | −0.03 | 0.15 |
| 0 | 0.31 | 0.25 | 0.45 | 0.31 | 0.25 | 0.20 | 0 | 0.49 | 0 | 0 |
| 30 | 0.33 | 0.16 | 0 | 0.33 | 0.16 | 0.55 | 0.15 | 0 | 0 | 0 |
| 45 | 0.28 | 0.35 | 0.58 | 0.28 | 0.35 | 0.52 | 0.35 | 0.58 | 0 | 0.2 |
Table 3.
Average number sources localized per trial using the MUSIC spectrum.
| Variant 1 | Variant 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of talkers | OOm | OOOm | GGm | OOb | OOOb | OOm | OOOm | GGm | OOb | OOOb |
| 3 | 3 | 3 | 3 | 3 | 3 | 2.9 | 2.98 | 2.98 | 2.95 | 3 |
| 4 | 3.98 | 4 | 3.50 | 3.28 | 4 | 3.7 | 3.95 | 3.6 | 3.83 | 3.71 |
| 5 | 2.7 | 4.3 | 2.1 | 2.7 | 4.32 | 2.9 | 4.4 | 2.2 | 4.0 | 3.8 |
Table 4.
Percent of trials that did not localize all sources using the MUSIC spectrum.
| Variant 1 | Variant 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of talkers | OOm | OOOm | GGm | OOb | OOOb | OOm | OOOm | GGm | OOb | OOOb |
| 3 | 0 | 0 | 0 | 0 | 0 | 10 | 2 | 2 | 4 | 0 |
| 4 | 2 | 0 | 42 | 56 | 0 | 80 | 2 | 26 | 14 | 22 |
| 5 | 98 | 56 | 100 | 98 | 56 | 84 | 40 | 84 | 61 | 66 |
Tables 1, 2 show that when a source is localized, it is localized very accurately or near its true DOA. The binaural arrays performed better than the monaural arrays, indicating that the addition of aperture improves the performance more than the addition of an extra microphone at smaller aperture. Also, the gradient microphones performed worse than the omnidirectionals both in terms of accuracy and the average number of sources localized. In all the arrays, the localization of more speech sources than microphones seemed to break down at five speech sources; on average, only two to three out of the five total sources were localized. This occurs because the speech sources have overlapping time-frequency spectra, and the undetected sources overlap others in all or almost all time-frequency bins over the test interval. This gives some indication of the fundamental effective sparseness of active speech; sparser types of sources would allow more sources to be localized, as would real conversations in which speakers sometimes stop talking. However, it does appear that the three-microphone arrays on average localize somewhat more sources than the two-element arrays, so there is some dependence on the number of microphones as well. With more microphones the energy from multiple weaker sources of noise is likely spread across more small eigenvalues, thus increasing the probability of a successful rank-1 coherence result and providing more bins with which to localize. When the power of some sources is weaker than others, the probability of detecting these sources decreases, but the directional accuracy when detected is similar.
The accuracy of variant 2 of the algorithm was similar to variant 1, but in most of the arrays, variant 2 did not localize as many sources on average as variant 1. The results seem to show that variant 2 is susceptible to errors in clustering, which can account for fewer sources being localized. If a source exhibits only a few low-rank covariance matrices which are improperly clustered at a particular frequency-bin, the contribution of these matrices vanishes in the averaging within a cluster. This is a weakness of variant 2. Similarly, a weakness of variant 1 is that a source with fewer low-rank data contributes fewer spectra peaked at that source’s DOA; sources with more low-rank data can dominate the final directional spectrum. One goal of the experiment was to study the tradeoffs in the two approaches, and variant 1 seems to be better at capturing more sources.
Table 5 shows the performance of the algorithm (variant 1) with a two-element free-field 15 cm array with three speech sources at directions −45°, −10°, and 20° with additional additive white Gaussian noise on each channel at SNRs ranging from 15 to 30 dB. In all cases, the biases and standard deviations are all well less than a degree, demonstrating that the method offers considerable robustness to additive noise. The method performs well with substantial additive noise both because the coherence test rejects low-SNR bins rather than allowing them to degrade the directional estimates and because the errors introduced are uncorrelated from bin to bin and tend to average away in either the clustering or the averaging that produces the composite directional spectrum. Excessive additive noise eventually causes the coherence test to reject most bins, however, so the technique will eventually fail at very low SNRs. A thorough study of the performance in reverberant conditions is beyond the scope of this work, but preliminary simulations show tolerance to reflections of the order expected in typical rooms.
Table 5.
Mean locations and standard deviations of location estimates with uncorrelated additive noise.
| SNR (dB) | Mean locations (deg) | Standard deviations (deg) | ||||
|---|---|---|---|---|---|---|
| 15 | −44.72, | −9.65, | 20.08 | 0.13, | 0.61, | 0.14 |
| 20 | −44.54, | −9.94, | 20.13 | 0.09, | 0.26, | 0.09 |
| 25 | −44.50, | −9.83, | 20.10 | 0.06, | 0.13, | 0.07 |
| 30 | −44.54, | −9.63, | 19.95 | 0.05, | 0.07, | 0.06 |
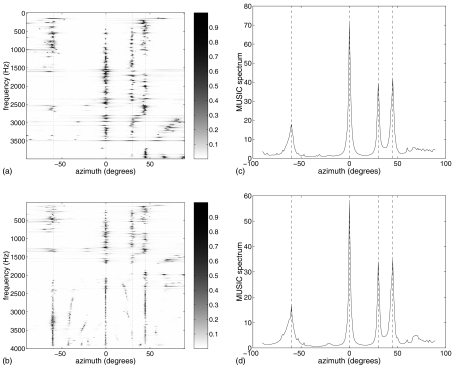
Figures 4a, 4b are the composite MUSIC spatial spectra at each frequency taken from an acoustic scene with the OOb array and four speech sources, using steering vectors estimated from HRTF measurements on the KEMAR head as in Sec. 4B. Darker areas in the plots indicate higher values in the MUSIC spectra. The dashed lines in Figs. 4a, 4b indicate the true DOAs of the sources. Figures 4a, 4b demonstrate that multiple sources are being localized at many frequency bins. In this example, with variant 1, three sources at −60°, 30°, and 45° are localized at 1 kHz while two sources at 0° and 30° are localized at 1.5 kHz. Figures 4c, 4d show the final MUSIC spectra after summing across frequency.
Figure 4.
MUSIC spectra from 4 s of four simultaneous speech sources using the measured responses of the OOb array on the KEMAR head. Dashed lines show the sources’ true DOAs (−60°, 0°, 30°, and 45°). (a) and (b) MUSIC spectra as a function of frequency and azimuth using variants 1 and 2 and (c) and (d) final MUSIC spectra using variants 1 and 2.
As more than 4 s of data are accumulated, if more low-rank time-frequency bins are available, then the localization performance may improve. However, an inherent property of the algorithm is better localization of sources that exhibit more low-rank time-frequency bins. Thus, peaks due to other sources may disappear when summing across time and frequency. An alternate approach is to observe how the algorithm tracks different sources’ DOAs as a function of time for longer time periods. Figures 5a, 5b show the MUSIC spectra computed every 100 and 500 ms with the short-time-frequency covariance matrix estimates averaged over the corresponding intervals, respectively, as a function of time and azimuth for an acoustic scene with the OOb array on the KEMAR and 10 s of four simultaneous speech sources. The sources’ sparseness in the time domain is clearly observed; peaks for the four sources appear and disappear depending on the availability of low-rank time-frequency bins.
Figure 5.
MUSIC spectra as a function of time and azimuth for 10 s of four simultaneous speech sources using the measured responses of the OOb array on a KEMAR. MUSIC spectra were computed every, (a) 100 and (b) 500 ms. Dashed lines show the sources’ true DOAs (−60°, 0°, 30°, and 45°).
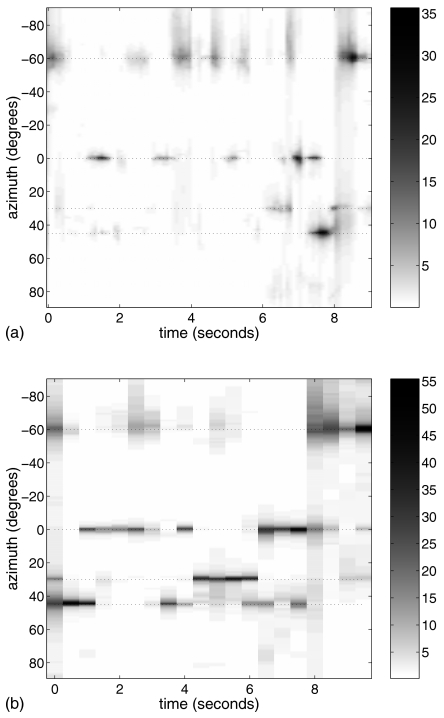
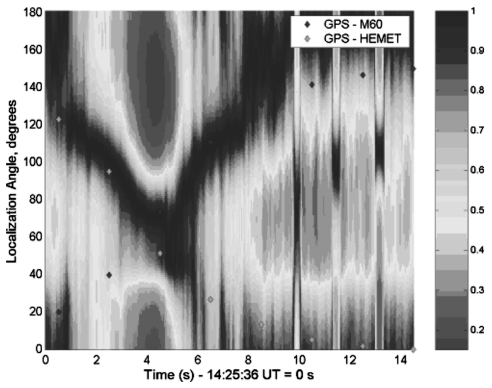
In recordings from the Spesutie Island field trials, military vehicles moved around a track, and the microphone array was located 27 meters away from the edge of the track. A composite recording was constructed containing a moving M60 tank, a moving HEMET vehicle, and small arms fire about 30–40 m away from the XYZO array. Figure 6 shows the MUSIC spectrum as a function of time and azimuth, in which the two vehicles were localized in azimuth to within their physical spans and the small arms fire was sharply localized in azimuth. Three gunshots were localized, occurring at 10, 11.5, and 13 s, at azimuths of 90°, 98°, and 105°. The azimuths were obtained by looking at the first onset of the peak in the MUSIC spectrum, which is at 90° for the first shot (not readily apparent in the plot, but visible with some magnification). These shots were recorded as the shooter fired his weapon at three locations on the track, separated by approximately 4 m. As the distance to the track was 27 m, an expected change in angle was calculated to be approximately 8.4° between shots, which correlates very well with the localization results.
Figure 6.
MUSIC spectrum as a function of time for an acoustic scene consisting of an M60, a HEMET, and small arms fire.
CONCLUSION
The successful localization of multiple speech sources was experimentally demonstrated using different subsets of omnidirectional and gradient microphones from the HA6 array located on a KEMAR dummy. Localization of military vehicles and gunfire in a free-field environment using gradient microphones from an acoustic-vector-sensor array was also experimentally demonstrated. To our knowledge, this study contains the first demonstration of high-resolution localization using an aeroacoustic vector sensor.
The two variants of the algorithm localize more speech sources than sensors by exploiting the sparse time-frequency structure and spatial stationarity of the speech sources. First, the coherence test provides a simple means to identify low-rank time-frequency bins, specifically those containing one active source. The data at these low-rank bins can be used in two ways: Variant 1 of the algorithm can be used to perform incoherent combining of directional information across time and frequency, or variant 2 can be used to perform coherent combining of data (by clustering low-rank covariance matrices and averaging within each cluster) followed by transformation to a directional representation. The source direction of arrivals are estimated from the composite directional spectrum regardless of which variant of the algorithm was used.
When speech sources were localized, they were localized accurately, since the bias and standard deviation of the DOA estimates were both less than 1° among all various arrays tested. The average number of sources localized dropped significantly across all microphone arrays tested with 4 s of speech when changing from four speech sources to five speech sources. The upper limit appears largely to be a function of the inherent time-frequency sparsity of the sources, and can be expected to be higher or lower depending on the source sparseness characteristics. Both variants of the algorithm performed similarly in bias and standard deviation, whereas variant 1 typically localized more sources on average than variant 2. The performance of the binaural arrays was also usually better than the monaural arrays, probably due to the increase in aperture, which leads to a greater diversity in the steering vectors as a function of azimuth.
The algorithm complexity is of the same order but generally less than that of Pham and Sadler (1996), with the primary complexity in the computation of the individual bin-by-bin MUSIC directional spectra. By restricting the computation only to rank-1 bins, the coherence test becomes simple and inexpensive, and the degradation in performance observed by Pham and Sadler with some source overlap is avoided. In addition, the number of relatively expensive MUSIC directional spectra computations are reduced. The complexity depends on the required resolution, but it should be possible to implement at least variant 1 in real time on a modern DSP microprocessor.
ACKNOWLEDGMENTS
This work was supported by U.S. Army Research Laboratory Contract No. DAAD17-00-0149, National Institute on Deafness and Other Communication Disorders R01 DC005762-02, and NSF CCR 03-12432 ITR. Portions of this work were reported in Mohan et al. (2003a,b).
APPENDIX: COHERENCE TEST
TWO-SENSOR COHERENCE TEST
Claim: A necessary and sufficient condition for a 2×2 covariance matrix R to be rank 1 is that the pairwise MSC is equal to 1.
Proof: Let the 2×2 covariance matrix be
| (A1) |
Now, let R be rank 1; then
| (A2) |
where h=[ab]T for some a,b∊C.
Then, the covariance matrix is
| (A3) |
The pairwise MSC is
| (A4) |
Now, assume that the pairwise MSC is equal to 1 and show that R is rank-1. As the pairwise MSC is equal to 1, then
| (A5) |
| (A6) |
| (A7) |
So, we can express the covariance matrix as
| (A8) |
and we see that
| (A9) |
So, R is rank-1 (regardless of the phase ϕ12).
M-SENSOR COHERENCE TEST
Claim: A necessary and sufficient condition for an M×M covariance matrix to be rank 1 is that its pairwise MSCs are equal to 1 and the phases of the its off-diagonal components satisfy ∠(Rij)−∠(Rik)+∠(Rjk)=0 ∀i<j<k where ∠(Rij) is the phase of the ijth element of the covariance matrix.
Proof: Let R be rank 1.
| (A10) |
| (A11) |
Then, the ijth component of R is
| (A12) |
The pairwise MSCs are all equal to 1.
| (A13) |
The phase constraint, ∠(Rij)−∠(Rik)+∠(Rjk)=0 ∀i<j<k, is also satisfied.
| (A14) |
| (A15) |
| (A16) |
| (A17) |
Now, assume that the pairwise MSCs are equal to 1 and the phase constraint is satisfied. We can then show that R is rank-1.
| (A18) |
We obtain the following relationships between the columns of the covariance matrix.
| (A19) |
| (A20) |
Thus, only a single linearly independent column exists in R, or R is rank-1.
References
- Carter, G. C. (1987). “Coherence and time delay estimation,” Proc. IEEE 75, 236–255. [Google Scholar]
- Gardner, W., and Martin, K. (1995). “HRTF measurements of a KEMAR,” J. Acoust. Soc. Am. 10.1121/1.412407 97, 3907–3908. [DOI] [Google Scholar]
- Garofolo, J. S., Lamel, L. F., Fisher, W. M., Fiscus, J. G., Pallett, D. S., and Dahlgren, N. L. (1993). “DARPA TIMIT acoustic-phonetic continuous speech corpus,” US National Institute of Standards and Technology,CD-ROM.
- Hawkes, M., and Nehorai, A. (1998). “Acoustic vector-sensor beamforming and Capon direction estimation,” IEEE Trans. Signal Process. 10.1109/78.709509 46, 2291–2304. [DOI] [Google Scholar]
- Hlawatsch, F., and Boudreaux-Bartels, G. F. (1992). “Linear and quadratic time-frequency signal representations,” IEEE Signal Process. Mag. 10.1109/79.127284 9, 21–67. [DOI] [Google Scholar]
- Johnson, D., and Dudgeon, D. (1993). Array Signal Processing: Concepts and Techniques (Prentice Hall, Englewood Cliffs, NJ). [Google Scholar]
- Lockwood, M., Jones, D., Bilger, R., Lansing, C., O’Brien, W., Wheeler, B., and Feng, A. (2004). “Performance of time- and frequency-domain binaural beamformers based on recorded signals from real rooms,” J. Acoust. Soc. Am. 10.1121/1.1624064 115, 379–391. [DOI] [PubMed] [Google Scholar]
- Lockwood, M., Jones, D., Elledge, M., Bilger, R., Goueygou, M., Lansing, C., Liu, C., O’Brien, W., and Wheeler, B. (1999). “A minimum variance frequency-domain algorithm for binaural hearing aid processing,” J. Acoust. Soc. Am. 10.1121/1.427790 106, 2278 (Abstract). [DOI] [Google Scholar]
- McConnell, J. (2003). “Highly directional receivers using various combinations of scalar, vector, and dyadic sensors,” J. Acoust. Soc. Am. 114, 2427 (Abstract). [Google Scholar]
- Miles, R., Gibbons, C., Gao, J., Yoo, K., Su, Q., and Cui, W. (2001). “A silicon nitride microphone diaphragm inspired by the ears of the parasitoid fly Ormia ochracea,” J. Acoust. Soc. Am. 110, 2645 (Abstract). [Google Scholar]
- Mohan, S., Kramer, M., Wheeler, B., and Jones, D. (2003a). “Localization of nonstationary sources using a coherence test,” 2003 IEEE Workshop on Statistical Signal Processing, pp. 470–473.
- Mohan, S., Lockwood, M., Jones, D., Su, Q., and Miles, R. (2003b). “Sound source localization with a gradient array using a coherence test,” J. Acoust. Soc. Am. 114, 2451 (Abstract). [Google Scholar]
- Nehorai, A., and Paldi, E. (1994). “Acoustic vector-sensor array processing,” IEEE Trans. Signal Process. 10.1109/78.317869 42, 2481–2491. [DOI] [Google Scholar]
- Nickles, J. C., Edmonds, G., Harriss, R., Fisher, F., Hodgkiss, W. S., Giles, J., and D’Spain, G. (1992). “A vertical array of directional acoustic sensors,” IEEE Oceans Conference 1, 340–345. [Google Scholar]
- Pham, T., and Sadler, B. (1996). “Adaptive wideband aeroacoustic array processing,” in 8th IEEE Signal Processing Workshop on Statistical Signal and Array Processing, pp. 295–298.
- Rickard, S., and Dietrich, F. (2000). “DOA estimation of many W-disjoint orthogonal sources from two mixtures using DUET,” Proceedings of the Tenth IEEE Workshop on Statistical Signal and Array Processing, pp. 311–314.
- Schmidt, R. (1986). “Multiple emitter location and signal parameter estimation,” IEEE Trans. Antennas Propag. 10.1109/TAP.1986.1143830 AP-34, 276–280. [DOI] [Google Scholar]
- Su, G., and Morf, M. (1983). “The signal subspace approach for multiple wide-band emitter location,” IEEE Trans. Acoust., Speech, Signal Process. ASSP-31, 1502–1522. [Google Scholar]
- Tichavsky, P., Wong, K., and Zoltowski, M. (2001). “Near-field/far-field azimuth and elevation angle estimation using a single vector hydrophone,” IEEE Trans. Signal Process. 10.1109/78.960397 49, 2498–2510. [DOI] [Google Scholar]
- Wong, K., and Zoltowski, M. (1997). “Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation,” IEEE Trans. Antennas Propag. 10.1109/8.633852 45, 1467–1474. [DOI] [Google Scholar]
- Zhang, Y., Mu, W., and Amin, M. (2001). “Subspace analysis of spatial time-frequency distribution matrices,” IEEE Trans. Signal Process. 10.1109/78.912919 49, 747–759. [DOI] [Google Scholar]