Automated detection of microcalcification clusters for digital breast tomosynthesis using projection data only: A preliminary study

Abstract

Digital breast tomosynthesis (DBT) is a promising modality for breast imaging in which an anisotropic volume image of the breast is obtained. We present an algorithm for computerized detection of microcalcification clusters (MCCs) for DBT. This algorithm operates on the projection views only. Therefore it does not depend on reconstruction, and is computationally efficient. The algorithm was developed using a database of 30 image sets with microcalcifications, and a control group of 30 image sets without visible findings. The patient data were acquired on the first DBT prototype at Massachusetts General Hospital. Algorithm sensitivity was estimated to be 0.86 at 1.3 false positive clusters, which is below that of current MCC detection algorithms for full-field digital mammography. Because of the small number of patient cases, algorithm parameters were not optimized and one linear classifier was used. An actual limitation of our approach may be that the signal-to-noise ratio in the projection images is too low for microcalcification detection. Furthermore, the database consisted of predominantly small MCC. This may be related to the image quality obtained with this first prototype.

INTRODUCTION

Digital breast tomosynthesis (DBT) is a promising modality for early breast cancer detection.¹ DBT addresses the main limitation of mass detection in conventional mammography, the overlaying tissue problem: In projection mammography, overlaying tissue structures can obscure masses or mimic the appearance of a lesion. In DBT, the three-dimensional (3D) breast structure is resolved, removing “visual clutter.”² DBT has the potential to improve lesion conspicuity, in particular for mass lesions.^{3, 4}

DBT can be interpreted as limited-angle cone-beam computed tomography. Currently, several DBT prototypes have been built.^{5, 6, 7, 8, 9} Typically, 11–25 projections are taken over an angular range of 15–60°. The total dose delivered to the patient is equal or below that of a mammographic exam, i.e., two screen-film mammograms.

Microcalcification clusters (MCCs) are an important early indicator for breast cancer.¹⁰ Microcalcification (MC) detection in conventional mammography is time consuming and requires the careful search of the entire mammogram at high resolution, often with the use of a magnifying device. In DBT, this search would have to be extended over many slices. A typical DBT image consists of 40–70 slices, depending on breast thickness. For MCC search, a “slab-view” has been suggested.¹¹ In this view mode, maximum-intensity projections (MIPs)¹² of 5–10 slices are presented, improving MCC conspicuity by collecting the entire cluster into one plane, rather than having individual MC spread over several slices.

Computer-aided detection (CADe) for conventional mammography has been approved for clinical use since 1998. Freer and colleagues¹³ found that the CADe system’s ability to detect MCC was largely responsible for the increase in cancer detection performance observed in that study. Recent work on MCC CADe for full-field digital mammography reached a cluster-based sensitivity of 80% at 0.69 false positive clusters per image.¹⁴ In that work, two classification stages (non-linear for individual MC features, linear for MCC features) were used to reduce false positive detections.

In this work, we explore an algorithm to automatically detect MC clusters in the DBT data using the projection views only. Such an approach is independent of reconstruction algorithms, which are still being developed and optimized. Further, this approach is computationally efficient, since 11 projections need to be analyzed for each breast, rather than 40 to 70 slices. We previously investigated such an approach for computerized mass detection.¹⁵ Initial performance estimates based on a small data set were comparable to that of current mass CADe for conventional mammography. This result may not apply to MC detection because the mechanisms that govern mass or MC detection are fundamentally different: Burgess and co-workers¹⁶ demonstrated that mass detection in conventional mammography is limited by anatomic structure noise. In DBT, in-depth resolution is sufficient to considerably reduce structure noise and is thereby expected to improve mass detectability. However, MC detectability in projection mammography is primarily limited by signal-to-noise ratio (SNR).¹⁷

There are several reasons for the SNR of MCC to be reduced in DBT. In DBT, the exposure is typically distributed equally over all projections, increasing the quantum noise in the individual projections. Further, at low exposures, the electronic noise of the detector is a higher fraction of the total noise, and it can be significant. In several DBT prototypes, no scatter grid is used, increasing the exposure to the detector but also decreasing SNR due to the scattered radiation. Several systems operate the x-ray source in continuous mode,^{6, 7, 8} which increases blur in the projections. Furthermore, for geometries with stationary detector,^{5, 7} the MTF decreases as the source angle increases.^{18, 19} The effect of these physical factors on MC detectability has not been investigated, either for human detection or for CADe.

Image quality has been explored in DBT in order to characterize reconstruction algorithms.²⁰ So far, quantitative experiments exploring detection performance in DBT have focused on larger lesions²¹ or on lung nodule detection in chest tomosynthesis,²² but not on MC detection. A qualitative study to investigate MC detection in DBT has been conducted by Smith and co-workers.²³ It was observed that MC detectability in DBT was not reduced compared to full-field digital mammography (FFDM). In their experiments, a phantom containing MCC was imaged on top of cadaverous breast tissue. The MCC clusters were not embedded in the tissue and were therefore separated from breast tissue in the DBT image. It is not clear whether the same result would be obtained for MCC embedded within breast tissue, in particular for subtle MCC within glandular tissue.

In this work we have implemented an algorithm for automated MCC detection. In the following sections, the patient database as well as the DBT prototype unit used to acquire the projection data will be described. The three steps of the CADe algorithm, namely MC detection in projection images, point backprojection, feature analysis, and clustering will be described. Algorithm performance results will be presented, followed by a discussion of the limitations of the algorithm.

MATERIALS

Database

Patient images were acquired at the Massachusetts General Hospital under IRB protocol. Patients who participated in this study were recalled from screening mammography and received a tomosynthesis scan before undergoing biopsy. All patient images from this study were provided by Massachusetts General Hospital, along with pathology. The corresponding screen-film mammograms were not available. Each image data set consisted of both the projection views as well as the reconstructed breast volume.

The DBT images in this pool were reviewed by either an expert mammographer (D.B.K.), or by a research technician (A.V.E.) with 10+years of experience in mammography. There was no double reading, the two readers simply shared the work load. For all images, truth was established when a lesion found in the DBT image corresponded to the pathology findings. This was true for all images read by D.B.K. Images in which no lesion corresponding to pathology findings could be found by A.V.E. were reviewed by an experienced mammographer (R.A.S.). Cases for which MCCs were not visible on DBT were not included in the database. By this procedure, one potential MCC case was excluded: Pathology indicated DCIS, but no MCC could be located in the DBT image. All other malignant calcification clusters imaged during the study were included in the database, except one case with segmental calcifications. Benign MCC were kept if more than three individual calcifications could be marked. Five benign cases were excluded from the dataset because at most three microcalcifications could be marked. Three microcalcification clusters were associated with masses.

All patient cases (see Table 1) included in this study (n=56) were selected from a cohort of women who underwent tomosynthesis imaging after being recalled from screening mammography. For each patient case, tomosynthesis images of one or both breasts were available. Within this cohort, 30 tomosynthesis images (9 benign, 21 malignant) contained 44 microcalcification clusters. A control group of 30 tomosynthesis images was selected from contralateral breasts without visible findings (n=27), as well as from normal unilateral images (n=3). Normal unilateral images were those where an architectural distortion was seen in the mammogram, which was then identified as overlaying tissue in the corresponding tomosynthesis image.

Table 1.

Breakdown of patient cases and image sets included in this study

Description	Number
Total number of patients	56
Number of Unilateral cases	23
Number of Bilateral cases	33
Number of image sets	89
Number of images w∕o visible findings	30
Number of selected image sets w∕o visible findings	30
Number of image sets with findings	59
Number of image sets with MCC	30
Number of benign image sets	9
Number of malignant image sets	21

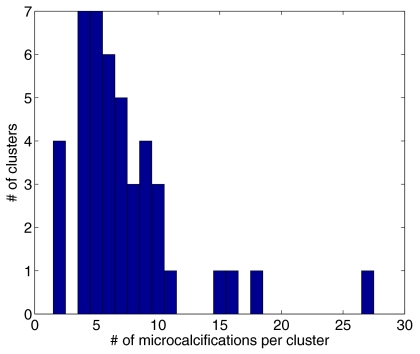
Truth was marked in the 3D tomosynthesis breast volume, which was reconstructed using iterative maximum likelihood expectation maximization (ML-EM). This was the only instance at which the reconstructed images were used. The detection algorithm used only the projection data as input. Figure 1 shows a histogram of the number of marked MC per cluster in our database.

Figure 1.

Distribution of number of microcalcifications per cluster in the database. The mean number of microcalcifications per cluster is 7.3.

DBT images were viewed at full resolution on 5 megapixel monochrome LCD monitors (Totoku ME511L∕C). Display software was ImageJ.²⁴

Tomosynthesis image acquisition system

The projection data were acquired at Massachusetts General Hospital on the first GE DBT prototype.²⁰ The x-ray source covered an arc of 50° while acquiring 11 images in step-and-shoot mode. The source-to-detector distance was 66 cm, and the source pivoting point was located at 21.7 cm above the breast support. The detector was an amorphous silicon flat-panel detector with a pixel size of 100 μm. The characteristics of this detector are described in Ref. 25. No anti-scatter grid was used during DBT projection data acquisition.

METHOD

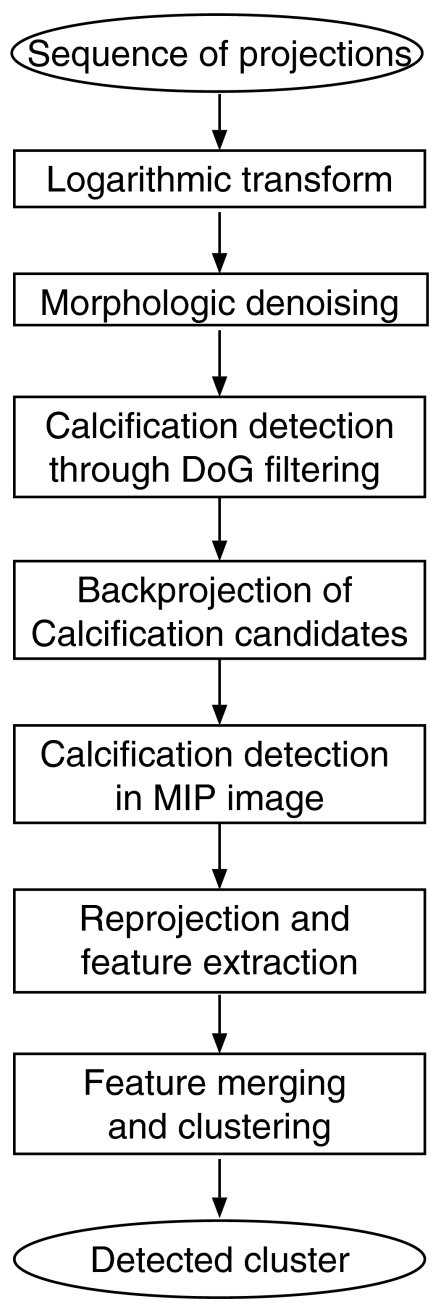
A flow chart of the proposed MCC detection scheme is shown in Fig. 2.

Figure 2.

Flow chart of the proposed MCC detection scheme.

Within this detection scheme, each projection image is treated as a separate mammogram and analyzed individually. An binary image is created for each projection with sites corresponding to microcalcification candidates set to one. All binary images are backprojected into the breast volume. In this volume, high intensity regions indicate an increased likelihood for the presence of a microcalcification.

Preprocessing

Each projection image undergoes two preprocessing steps prior to microcalcification detection. First, projection images are contrast enhanced using a logarithmic transform.¹⁴ Second, morphologic denoising is applied to each image.

Morphologic denoising

The goal of the morphologic denoising is to remove single and double pixel noise peaks and troughs from an image I(x,y), while maintaining structures larger than three pixels. This is achieved as follows. Let H be the set of all structuring elements containing three eight-connected elements. There are a total of 60 structuring elements in this set. A maximum erosion image E(x,y) and the minimum dilation image D(x,y) are created through

$$\mathcal{E}(x,y)=\max \left\{I(x,y)\ominus \mathcal{H}\right\},$$ (1)

$$\mathcal{D}(x,y)=\min \{I(x,y)\oplus \mathcal{H}\},$$ (2)

where ⊖ and ⊕ are gray scale erosion and dilation, respectively. The noise filtered image is then obtained through

$$G(x,y)=\{\begin{array}{ll}E(x,y),& \text{if}|I(x,y)-E(x,y)|⩾|I(x,y)-D(x,y)|\\ D(x,y),& \text{if}|I(x,y)-E(x,y)|<|I(x,y)-D(x,y)|\end{array}\phantom{\}}.$$ (3)

In this denoised image G(x,y), single and double pixel peaks or troughs are removed, leaving regions three pixels and larger intact. An example MCC in the ML-EM reconstructed slice, as well as in the denoised log-projection images, is shown in Fig. 3. The effect of denoising is shown in Fig. 4.

Figure 3.

Microcalcification cluster in the ML-EM reconstructed slice (top left), and in the denoised log projections.

Figure 4.

(a): Log-projection image of a MCC. (b): Denoised log-projection image of the same cluster. This MCC is the same as the 25° projection in Fig. 3.

Microcalcification detection and point backprojection

Individual microcalcifications were detected by thresholding a Mexican hat²⁶ filtered image. This method has been used for detecting MCC both in screen-film mammography (SFM)^{27, 28, 29} as well as FFDM.¹⁴ A brief description of the method is given here: A 9×9 pixel Mexican hat filter is used to enhance individual microcalcifications. The effect of this filter is to enhance small structures of the order of three pixels in diameter, while suppressing larger scale variations. A threshold t_g is applied to the histogram of this difference image, selecting the fraction t_g of highest pixel values in order to identify microcalcification candidates.

Subsequently, the neighborhood of each microcalcification candidate is analyzed by computing the standard deviation σ_n of all pixels within a 51×51 pixel neighborhood centered on the candidate, excluding all pixels above threshold. The microcalcification candidate is rejected if its pixel value is below t_l⋅σ_n. The thresholds t_g and t_l used for detecting microcalcifications in projection images are listed in Table 2. The minimum size of a valid detection was three pixels. The thresholds t_g and t_l were chosen to allow for high sensitivity, i.e., t_g was set higher than in our previous experience to allow for detection of subtle signals, while t_l was set relatively low to account for higher noise in the projections (which causes an increase in σ_n). The threshold values were varied and true positive fraction as well as false positive rates for individual MC detection was computed. The values in Table 2 were selected because for a false positive rate comparable to that observed in SFM, they resulted in the highest sensitivity.

Table 2.

Parameter settings and algorithm performance for the two first detection steps. The true positive rate is computed for individual microcalcification detection and does not include clustering. Performance was estimated through self-consistency.

Image	tg	tl	TPF	FP
Projection	5.0	3.0	0.67	4700 (per projection image)
Point-back projection MIP	0.05	7.0	0.61	104 (per volume)

For each projection image, a binary image is created with pixels in valid detected regions set to “1,” while all other pixels are set to “0.” The sequence of binary images is then backprojected into the breast volume, creating a 3D feature volume. In this volume, microcalcification candidates that were detected in several projections are enhanced, whereas detections that resulted from noise tend to be suppressed.

Calcification candidates are identified in this feature volume by analyzing the maximum-intensity projection (MIP). An example of a MIP image for a clinical case is shown in Fig. 5b. The MIP image is analyzed using Mexican hat filtering and neighborhood processing as described above. The thresholds t_g and t_l used at this stage are listed in Table 2. They were chosen to achieve high sensitivity. However, at this stage, the microcalcification candidates are very conspicuous, allowing for a small t_g threshold. On the other hand, the noise relative to the MC candidates is low, therefore the high value of t_l. Threshold values were varied and true positive fraction for the detection of at least two individual MCs was computed, as well as the false positive rate for individual MC. The values in Table 2 represent the thresholds that resulted in the highest true positive fraction.

Figure 5.

Example of (a) a slice of the point backprojection volume containing the MCC, and (b) the corresponding MIP image.

The (x,y,z) coordinates of each microcalcification candidate in the feature volume are identified by finding the slice with a pixel value equal to that in the MIP image.

Reprojection and feature extraction

For each detection, segmentation and feature analysis is performed in the denoised, contrast-enhanced projection images. Each detection is identified by its (x,y,z) coordinate in the breast volume. The corresponding locations (x_p,y_p), p=1,2;..11, in the sequence of projections are computed for each x-ray source position p.

For segmentation of individual MC, a 1 cm² region of interest (ROI) centered on (x_p,y_p) is extracted and a two-dimensional second order polynomial background trend correction is applied. The MC region L is identified through L(x,y)⩾0.5∗max(ROI) and (x_p,y_p)∊L, where L is a 4-connected region. This is the first step in a segmentation method used.³⁰ Because DBT projection images are noisy, we did not implement a more sophisticated MC segmentation. Furthermore, only intensity-based features were used, which are less dependent on the actual segmentation.

From the segmented region, three features were computed, namely the mean pixel value within the segmented region $\mathcal{L}\left({\overline{x}}_L\right)$, contrast (c), and attenuation (μ). Features were computed based on pixel values in the denoised log-projection image. The advantage of using the log-projection image is that the attenuation coefficient is independent on scatter:

$$c={\overline{x}}_L-{\overline{x}}_{\mathit{BG}},$$ (4)

$$\mu =\frac{c}{\sqrt{A}},$$ (5)

where A is the pixel sum in L, ${\overline{x}}_L$ is the mean pixel value within L and ${\overline{x}}_{BG}$ is the mean pixel value within the ROI outside of L.

Feature merging and clustering

Since feature extraction was performed in the projection images, the feature data f is an (n_fea×n_proj) array where n_fea is the number of features, and n_proj is the number of projection images (n_proj=11 for this database).

Two different approaches of merging features and combining the information from all projection images were explored. In both cases, features were merged using linear-discriminant analysis (LDA), and round robin³¹ was used for classifier training∕testing.

The first approach was to compute the median of each feature i over all projections, F_i=median([f_i,1,…,f_i,11]). The resulting features F_i were then merged using LDA. In the second approach, features f_i were merged for each projection image individually, resulting in a 1×11 vector of linear discriminant distances, d_LD. To be counted as a computer-detected microcalcification, a number of elements of d_LD were required to exceed a threshold; Results for requiring 8(11) and 10(11) linear discriminant distances above threshold will be shown. Following feature merging, each testing case in the round-robin scheme underwent clustering. Clustering was done in 3D. First, individual detections that were within a distance of d_w=30 mm were assembled into clusters, with a cluster containing at least two detections. Whenever cluster borders were within a distance d_b=70 mm, the two clusters were merged. In order to be scored a true cluster, a detected cluster centroid was required to be located within 1 cm of a true cluster centroid. True microcalcifications were clustered based on the rules above, using the same parameters d_w and d_b. All distances were measured in 3D.

RESULTS

The detection rate for individual microcalcification detection is listed in Table 2, along with the global and local threshold settings (t_g,t_l). Those parameters were set such that detection rate for individual MC was maximized, regardless of false positive rate. The false positive rate for MC detection in the projection images was 4700 FP∕image, which is comparable to what was observed for screen-film mammography (SFM). On the other hand, the true positive fraction (TPF) for individual MC detection was 0.67, which is higher than that observed in SFM (typically 0.4 in our previous research).

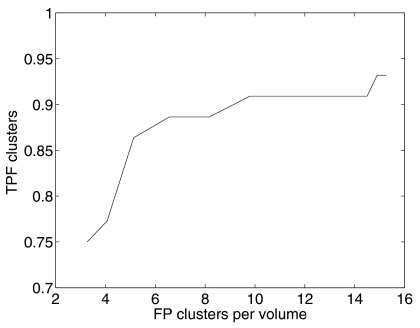
The false positive rate was reduced to 104 individual MC per volume through point backprojection. The TPF for individual MC detection dropped slightly to 0.61. At this stage, it is also useful to inspect the true cluster detection fraction. The free-response operating characteristic (FROC) curve shown in Fig. 6 was generated by varying the local threshold t_l. Further analysis was carried out for t_g=0.05 and t_l=5, which corresponds to a TPF of 0.91 at 11.1 FP clusters.

Figure 6.

FROC curve after point backprojection: True-positive-cluster fraction as a function of the average number of false-positive clusters per volume. Performance was estimated through self-consistency.

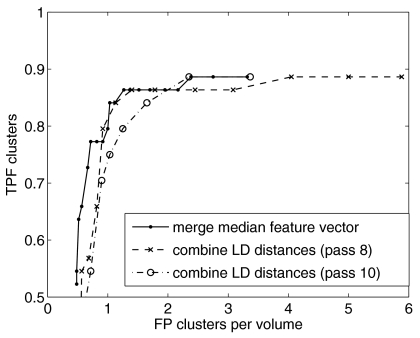
Algorithms performance after feature analysis and clustering is shown in Fig. 7. The FROC curve was obtained by varying the linear discriminant distance threshold. Performance was estimated using a round-robin training and testing scheme. Three features $({\overline{x}}_L,c,\mu )$ were combined. This feature set was selected manually based on performance for the entire database. This procedure introduces a positive bias in the selected feature set.³² On the other hand, it fixes the feature set, so that the performance we report here is for one particular CADe scheme, not for an aggregate of schemes all with potentially different feature sets. The graphs show that the two schemes of combining features and projections, described in Sec. 3D, achieve similar performance if outliers are tolerated. In the first scheme, the value of a given feature is approximated through the median of the values in the individual projections. The median value was chosen because it is less sensitive to outliers. Likewise, in the second scheme, 8 (out of 11) linear discriminant distances were required to exceed a threshold in order to be counted as a detection. The more stringent requirement of 10 out of 11 reduces TPF from 0.81 to 0.75, at about 1 FP cluster per volume.

Figure 7.

Algorithm performance including feature analysis and clustering stages, estimated using round-robin analysis.

DISCUSSION

The FROC curves shown in Fig. 7 present a subset of methods to combine and merge the feature set obtained when extracting features in the projection image. There are other ways of combining features, such as mean, standard deviation, max, or min. Including those would effectively increase the size of the feature set. Optimization of the feature set is currently not possible because of the small number of patient cases available. We point out that the median feature value in all projection images represents an approximation to the voxel value in the breast volume (as obtained through backprojection). Further, these parameters were not optimized and therefore results are not definitive.

We did not have access to the corresponding screen-film mammograms. This limits our ability to compare CADe performance on DBT and screen-film mammography. Because of the lack of screen-film mammograms, it may be possible that there were clustered calcifications visible in the film mammogram, but invisible, even in retrospect, in the DBT images. Selecting lesions visually is consistent with the way we select cases when developing computer-aided detection (CADe) for other modalities—we do not include occult lesions. The goal of CADe is to alert radiologists to lesions that they have overlooked. Therefore, only lesions visible in the image need to be detected. However, it is possible that there were very subtle calcifications present in the DBT images that we were unable to identify. If this occurred, then our dataset would be biased by the omission of these very subtle calcifications.

Lesion detectability in DBT, compared to lesion detectability in projection mammography, has not yet been fully investigated, in particular not for MC. Ultimately, a comparison of MC detection performance between DBT and FFDM needs to be performed in a clinical study. However, at this stage, DBT is at a disadvantage since image quality has not been optimized yet. In addition, the data used in this study were acquired on the first tomosynthesis prototype based on the GE Senographe 2000D.³³ The current GE DBT prototype is based on the GE Essential digital mammography unit, with improved detector performance.³⁴ Also, several other manufacturers have built prototypes using different detector technologies as well as different acquisition configurations, which may affect microcalcification detectability.³

This algorithm may be a useful approach to MCC detection in DBT, despite the low performance. Current work on MCC CADe for FFDM^{14, 35} reaches higher performance. Some of the earlier work on CADe for SFM showed comparable performance.³⁶

We did verify whether algorithm sensitivity could be improved by analyzing the point-backprojection volume, rather than its maximum-intensity projection. Upon inspection of missed clusters, we found that clusters that were missed in the MIP were also not visible or not conspicuous in the volume. Therefore we concluded that the information relevant to MC detection was retained in the MIP image. This also underscores that in the point backprojection, the conspicuity of MC is dramatically increased, to the point that MC becomes visible in the MIP. In contrast, in our experience, most MC is not visible in a MIP of the reconstructed breast volume.

We are investigating several possible causes for this low algorithm performance: First, from an algorithm point of view, the proposed algorithm is not fully optimized: Only intensity-based features were extracted from the projection images, no texture or shape features. A linear discriminant analysis was used to merge features, rather than a non-linear classifier as in Ref. 14. Furthermore, no cluster features were extracted. The optimization of feature and classifier selection requires more patient cases than what is currently available. In the clustering stage of our algorithm, the minimum cluster size was set to “two,” i.e., a pair of two MC within d_w was counted as a valid cluster. In other works, clusters are required to consist of three²⁸ or four¹⁴ individual MC, which reduces false positive clusters that occur through the detection of radiologically insignificant scattered MC.

Second, the projection data used in this study were acquired on the first DBT prototype. The x-ray source on this prototype was operated in step-and-shoot mode, which could have introduced mechanical vibrations³⁷ and thereby caused motion artifacts in the DBT projections. As a result, the spatial correlation is destroyed, which affects point backprojection as well as the actual reconstruction. Also, there may have been patient motion. Last, the DQE of the detector being used in the current GE prototype is substantially increased, which should improve MC detection.

This issue of image quality relates to another observation. The database on which this algorithm was developed consisted primarily of small clusters, i.e., small number of MC per cluster. Those may indeed be subtle microcalcification clusters. On the other hand, the clusters were marked in the DBT images, where MC may have been undetectable because of DBT system limitations. This impacts algorithm performance at the clustering stage: Despite relatively high detection rates for individual MC (above 50%, see Table 2), which are higher than the 40% that we have observed in SFM, only 2 MC per cluster are detected for a large fraction of clusters in the database. Note that we also had to set the minimum cluster size to “two” when clustering the true clusters in order to be able to obtain actual clusters for all malignant cases. Increasing the minimum cluster size to 3 or 4, which is more typical for projection mammography, would reduce algorithm sensitivity. If minimum cluster size were increased to 3, another 11% of the 44 MCC would be missed.

Third, MC signal-to-noise ratio in the projection images may be too low for the detection of subtle MC. If this is the case, then there may be an advantage in analyzing the reconstructed DBT volume, rather than the projection images, as a subtle MC signal may be recovered during reconstruction. We would like to point out, that in our algorithm, a MC does not need to be detected in each projection image in order to be detected in the point backprojection. In our experience, a MC that was detected in eight projection images (amounting to about 75%) becomes conspicuous in the point-backprojected image.

We anticipate that this proposed algorithm will depend on the DBT configuration, in particular, on the number of projection views acquired. For a fixed overall exposure, the absolute amount of quantum noise in the projections decreases with number of projections, although the SNR decreases. However, the electronic noise component is independent of x-ray exposure and therefore electronic noise can become the dominant noise source. When increasing the number of projections, it has to be ensured that quantum noise is the dominant noise source in the projection image.

CONCLUSION

We presented a method for automated detection of clustered microcalcifications. The CADe algorithm uses the projection data as input. Initial MC detection is performed in the projection data. False positive detections are reduced effectively through point backprojection, where binary images of lesion candidate regions are backprojected into the breast volume. Overall the algorithm suffers from low cluster-based sensitivity. Detection efficiency for individual microcalcifications is higher than what was observed in screen-film mammography. The database predominantly contained clusters consisting of few MC, which made it difficult to reduce false positive clusters during the clustering stage.

This work raises several questions that can only be answered through a more detailed and quantitative investigation of MC detectability in DBT.