Abstract
Semi-mechanistic pharmacodynamic (PD) models that capture tumor responses to anticancer agents with fidelity can provide valuable insights that could aid in the optimization of dosing regimens and the development of drug delivery strategies. This study evaluated the utility and potential interchangeability of two transduction-type PD models: a cell distribution model (CDM) and a signal distribution model (SDM). The evaluation was performed by simulating dense and sparse tumor response data with one model and analyzing it using the other. Performance was scored by visual inspection and precision of parameter estimation. Capture of tumor response data was also evaluated for a liposomal formulation of paclitaxel in the paclitaxel-resistant murine Colon-26 model. A suitable PK model was developed by simultaneous fitting of literature data for paclitaxel formulations in mice. Analysis of the simulated tumor response data revealed that the SDM was more flexible in describing delayed drug effects upon tumor volume progression. Dense and sparse data simulated using the CDM were fit very well by the SDM, but under some conditions, data simulated using the SDM were fitted poorly by the CDM. Although both models described the dose-dependent therapeutic responses of Colon-26 tumors, the fit by the SDM contained less bias. The CDM and SDM are both useful transduction models that recapitulate, with fidelity, delayed drug effects upon tumor growth. However, they are mechanistically distinct and not interchangeable. Both fit some types of tumor growth data well, but the SDM appeared more robust, particularly where experimental data are sparse.
Key words: cancer, drug delivery, paclitaxel, pharmacodynamics, pharmacokinetics, transduction models
INTRODUCTION
For cancer chemotherapeutic agents, a delay is often observed between the time course of drug concentration [pharmacokinetics (PK)] and effect [pharmacodynamics (PD)]. A quantitative and predictive understanding of the PK/PD relationships for anticancer drugs could contribute to the design of improved therapies. Two broad types of models frequently have been used to describe a temporal dissociation of PK and PD: “biophase” models (1) and “indirect response” models (2). In the biophase model, the drug concentration profile at a hypothetical effect site is determined by plasma PK and the distribution parameter keo, and it assumes that equilibration of the drug between plasma and effect site is relatively slow. This approach has been successful for some cardiovascular and CNS drugs (1,3). A key characteristic of the biophase model is that the time of peak effect is dose independent and largely constrained by plasma PK; that is, the onset of effect cannot occur days or weeks after drug is eliminated from body. The biophase model rarely is used to model PD responses to cancer chemotherapy, where complex pharmacological events can result in effects being observed long after clearance of the drug from the effect site.
Indirect response models represent a second approach to account for temporal dissociation of PK and PD. They are based on the turnover concept [reviewed in (4)], in which drug acts upon the rate constants for production (kin) or elimination (kout) of one or more PD response biomarkers. Signature features of indirect response models include an initial change in the magnitude of effect that progresses from baseline to a peak (or nadir), followed by a return to baseline as drug is eliminated from the body. In contrast to the biophase model, the time to peak effect is dose dependent; a larger dose results in a later peak effect because of the increased time that drug concentrations exceed the half-maximal effect concentration (EC50) (5).
An alternative approach based upon transduction processes has evolved to address mechanistic features of pharmacological systems that are not well-suited to biophase or basic indirect response models. In these “transit compartment” models, observed responses can lag behind the plasma PK as a result of rate-limited pharmacological effect cascades and, therefore, accommodate situations in which signal transduction processes are involved in response generation (6,7). Conceptually, the events intervening between drug/receptor interaction and the observed PD effects are responsible for temporal dissociation of the drug concentration/effect curves. Standard PD models characterize such delays poorly. Because the intervening steps in transduction cascades often cannot be measured readily, transit compartment models make two important assumptions: (1) Pharmacokinetic effects within the cells or tissues do not affect the drug signal transduction rate; (2) drug signal transduction through unknown intervening transit compartments proceeds with a common mean transit time.
Here, we compared the properties of two promising transduction models that were developed to describe the PD of anticancer agents. The issue of model interchangeability was evaluated using data simulated by the models themselves. The utility and fidelity of the models in capturing in vivo antitumor responses to chemotherapeutic agents was investigated by applying the models to compare their performance in the analysis of PD effects of a drug-resistant murine tumor to paclitaxel in a liposomal formulation. In order to accommodate the biodistributional characteristics of paclitaxel formulations, a suitable PK model was developed from literature data obtained from mice.
THEORY
Two PK/PD models potentially suitable for modeling delayed anticancer drug effects upon tumor volume were identified in the literature (8,9). The strength of both is that they incorporate a combination of empirical and mechanism-based elements that are well-justified based on known mechanisms of anticancer drug action and would be extensible as additional mechanistic information or empirical data are obtained. This extensibility is an advantage given broad interest in relating highly detailed mechanistic information at a molecular/cellular level to the effects of chemotherapeutic agents on a systems pharmacological level.
The cell distribution model (CDM) (8,10) is based on a system of simple transit compartments that link dosing regime (PK) to tumor growth response (PD). The mass of the untreated tumor increases as cells traverse the cell cycle according to a growth model. Conceptually, the effect of drug is not to eliminate tumor cells directly; rather, drug acts via a second-order cell-kill rate constant (k), which, in conjunction with plasma drug concentrations (Cp), governs the proportion of cells that are shunted into a transduction cascade that ultimately progresses to cell death and removal (Fig. 1a). The measured tumor volume therefore consists of the proliferating cell mass plus the terminally committed cells within the transduction cascade that are not yet eliminated. Differential equations and initial conditions of the CDM are as follows:
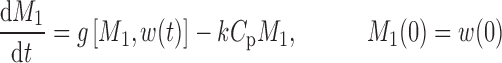 |
1 |
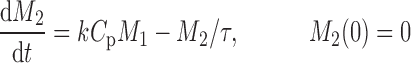 |
2 |
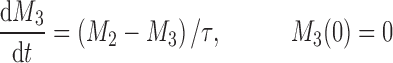 |
3 |
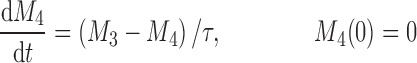 |
4 |
where M1 represents cycling cells, g[M1, w(t)] is the growth function of cycling cells, Cp is plasma concentration of drug, τ is the mean transit time, k is the second-order killing constant, w(0) is the initial tumor size or number of proliferating cells, and M2–M4 refer to the terminally committed cell compartments; their initial value is zero. Tumor size, w(t), is the sum of all the compartments; 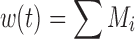 .
.
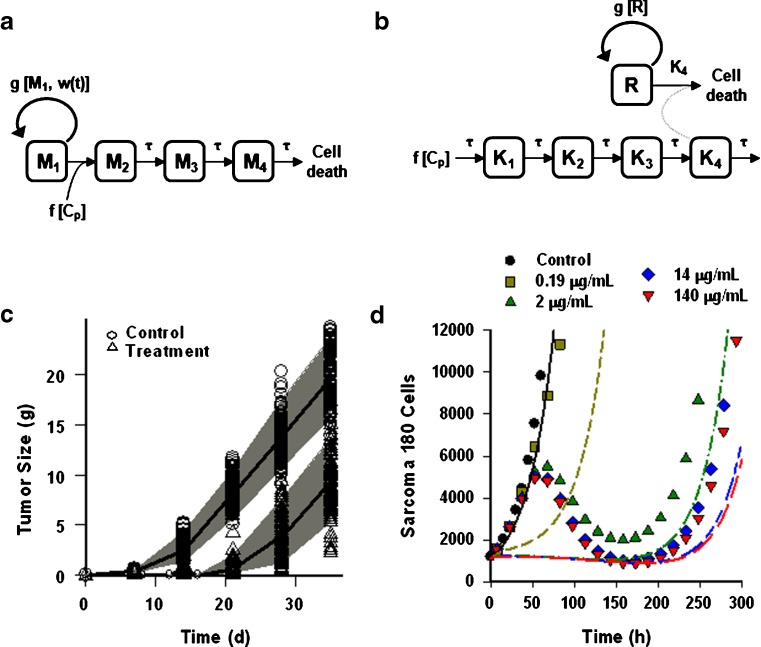
Fig. 1.
Two transduction-type pharmacodynamic models to capture chemotherapeutic drug effects upon tumor cell volume. a Cell distribution model (CDM) described in (8); the action of drug is to transition a fraction of cycling cells into a transduction cascade that progresses to cell death and removal. b Signal distribution model (SDM) described in (9); drug interaction with a receptor initiates transduction of a pharmacological signal that propagates through a cascade, and the drug bio-signal ultimately results in the death of a fraction of the cycling cell population. a, b Symbols and abbreviations are defined in “THEORY”. c PD profile of the SDM fitted to a sparse data set (6 points) simulated with error and parameter variability by the CDM, using the original parameters reported (8) for fitting in vivo A2780 human ovarian tumor growth in animals that were untreated (“control”) or treated with 30 mg/kg Cre-pac (“treatment”). NONMEM was used for the fitting. Symbols represent simulated data points and lines represent mean predicted profiles. Shaded area shows the 95% confidence interval based on a 1,000-point Monte Carlo simulation. d PD profile of the CDM applied to a dense (1,000 points) data set simulated by the SDM without error or variability using the original parameters reported (9) for fitting the in vitro response of Sarcoma 180 cells to various concentrations of MTX over a 20-day period. Symbols represent simulated data points and lines represent the model fit: control, black solid line; 0.19 μg/mL, brown dash; 2 μg/mL, green dash-dot; 14 μg/mL, blue long-short-short dash; 140 μg/mL, red long-short dash. For clarity, symbols mark only one of every 50 data points
A signal distribution model (SDM) (9) was originally developed simply to describe the growth rate of tumor cells in vitro as a function of time after exposure to varying concentrations of methotrexate (MTX) (9). A schematic is shown in Fig. 1b. In the SDM, drug acts upon a receptor, which initiates an effect signal that is transduced through a cascade of transit compartments. The magnitude of the initial response is related to drug concentration, and the temporal profile of the response changes as it propagates through the intermediate compartments (6,7). At the end of the transduction cascade, the drug bio-signal results in the death of a fraction of the cycling cell population. Thus, in the SDM, the killing effect is exerted through the transduction cascade rather than directly upon the cycling cells. In this subtle but significant respect, the SDM differs from the CDM.
The differential equations and initial conditions for the SDM are as follows:
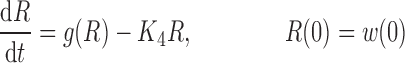 |
5 |
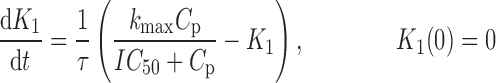 |
6 |
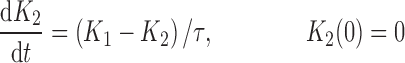 |
7 |
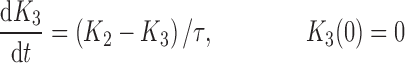 |
8 |
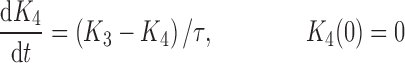 |
9 |
where R represents the population of cycling cells, g(R) is their growth function, kmax is the maximum cell kill rate, and IC50 is the plasma drug concentration producing 50% of kmax. The killing effect can also be modeled as a linear function (kCp) that is dependent upon the nature of the drug effect. The initial condition for R is the initial tumor size and for K1–K4 is 0. In the SDM, the tumor volume consists only of cycling cells, i.e., w(t) = R.
Tumor growth functions
Tumor cell growth under unperturbed conditions has been described using numerous relationships. Three were examined here: (1) exponential growth (first-order), (2) first-order growth with a logistic function that constrains the maximum tumor size, and (3) the unperturbed growth model of (8). Simple exponential growth is defined as:
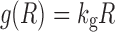 |
10 |
where kg is the first-order rate constant of net growth (equivalent to a first-order growth rate constant minus a first-order death rate constant). This expression can be modified using the logistic function that describes a maximum tumor volume (Rss):
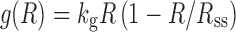 |
11 |
when R is very small, the ratio of R/Rss approximates to zero and the growth approaches first-order. When R approaches Rss, the ratio of R/Rss approximates 1, and the net growth approaches zero. The logistic function is applicable when a plateau in tumor volume is observed.
The equation for the unperturbed growth model (8) is:
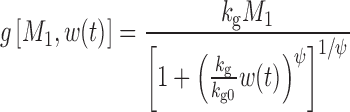 |
12 |
where kg0 is a zero-order growth rate constant. In the original publication, ψ was fixed to a large value (i.e., 20) to allow the system to transition sharply from first-order to zero-order kinetics. When w(t) is small, 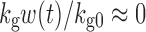 and
and 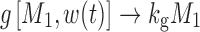 ; thus, growth resembles a first-order model (Eq. 10). When w(t) approaches a certain value,
; thus, growth resembles a first-order model (Eq. 10). When w(t) approaches a certain value, 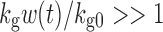 , 1 is negligible in the denominator of Eq. 12, so g[M1, w(t)]→kg0 and the function tends toward zero-order. The unperturbed model often is used when the growth rate switches from first-order to zero-order upon reaching an inflection point.
, 1 is negligible in the denominator of Eq. 12, so g[M1, w(t)]→kg0 and the function tends toward zero-order. The unperturbed model often is used when the growth rate switches from first-order to zero-order upon reaching an inflection point.
MATERIALS AND METHODS
Evaluation of PD Model Interchangeability
Simulations
We employed an approach similar to previous work (11) that evaluated the interchangeability of several empirical models of pharmacological tolerance. Dense (36 points) and sparse (6 points) data were simulated with and without error according to the original data and descriptions of both cancer PD models (8,9) using a nonlinear mixed effects approach implemented in NONMEM (Version 6, ICON, Columbia, MD). Simulations using the CDM were based upon data for A2780 human ovarian tumor growth in athymic mice treated with 30 mg/kg paclitaxel every 4 days for 3 weeks (8). In that study, paclitaxel was administered in the standard clinical formulation, which contains Cremophor EL/ethanol (Cre-pac). The PK/PD structural model and parameters used here were taken from the original publication (8). Simulations using the SDM were based upon the data and PD analysis for Sarcoma 180 cells exposed in vitro for 24 h to different concentrations of MTX and monitored for up to 20 days (9). The PD parameters used for the CDM and SDM simulations are listed in Table I.
Table I.
Parameters Used for Simulations by the CDM and SDM
| Parameters | Value (CDM) | Value (SDM) |
|---|---|---|
| τ (day) | 1.03 | 1.25 |
| k (10-4 mL ng−1 day−1) | 6.29 | N/A |
| k g (1/day) | 0.273 | 0.84 |
| k g0 (g/day) | 0.814 | N/A |
| w(0) (g) | 0.055 | N/A |
| k max (1/h) | N/A | 0.34 |
| IC50 (µg/mL) | N/A | 0.32 |
| R(0)a | N/A | 1,200 |
N/A not applicable, CDM cell distribution model, SDM signal distribution model
aNumber of cells
In each simulation, a 10% CV on all PD parameters was assigned in an exponential manner: θpopexp(ηi), where individual parameters are given by the population value (θpop) and intersubject variability (ηi). Residual error (10%) was also incorporated into each simulation using a proportional error model, and each simulation contained 500 subjects.
Analysis of the Simulated Data
PD profiles simulated by one model were analyzed by the alternate model using NONMEM. Inter-individual variability was described by an exponential model, and the residual error model was defined by a combination of proportional and additive errors: 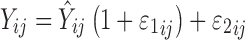 . The first-order conditional estimation method was used to estimate population means and variances of the parameters. The criteria for evaluating model performance was based on changes in the NONMEM objective function value, goodness of fit plots, including simulated vs. individual or population predicted observations, as well as weighted residual plots. Monte Carlo simulations using final parameter estimates were conducted (n = 1,000) to perform a visual predictive check of the final model. To increase model flexibility and allow for the best fitting of the data, three tumor growth functions (Eq. 10, 11, and 12) were evaluated.
. The first-order conditional estimation method was used to estimate population means and variances of the parameters. The criteria for evaluating model performance was based on changes in the NONMEM objective function value, goodness of fit plots, including simulated vs. individual or population predicted observations, as well as weighted residual plots. Monte Carlo simulations using final parameter estimates were conducted (n = 1,000) to perform a visual predictive check of the final model. To increase model flexibility and allow for the best fitting of the data, three tumor growth functions (Eq. 10, 11, and 12) were evaluated.
Comparison of PD Model Behavior in the Analysis of Tumor Therapeutic Responses
Pharmacokinetic Model for Paclitaxel
A PK model is necessary as a driver for the PD models under investigation. Because paclitaxel is poorly soluble in water, the clinical formulation (e.g., Taxol®) contains Cremophor EL and ethanol. Cremophor EL can cause acute, severe anaphylactoid responses in humans (12,13), and a variety of alternative formulations have been developed, including microparticulate phospholipid-based (liposomal) formulations (L-pac) (14–16). In both animal models and humans, the toxicity of L-pac is significantly lower than that of Cre-pac (15,17,18), and therefore, analysis of PD data for L-pac was a motivating interest for this work.
PK data for L-pac in the specific tumor model employed were not available, and it was necessary to develop a PK model that captures key characteristics of the formulations. Cre-pac exists as a microemulsion at the time of administration (19), from which drug is released to plasma. Liposomes similarly represent a circulating reservoir from which drug may be released (20). Therefore, the PK model included an additional compartment (A1) to represent drug incorporated in the circulating carrier (Fig. 2a). A key assumption is that after release of paclitaxel from either vehicle in the blood, the free drug binds rapidly to plasma proteins (20–22), and the subsequent pharmacokinetic processes affecting released drug are identical for both formulations. This is consistent with a previous mechanism-based analysis of Cre-pac PK (23).
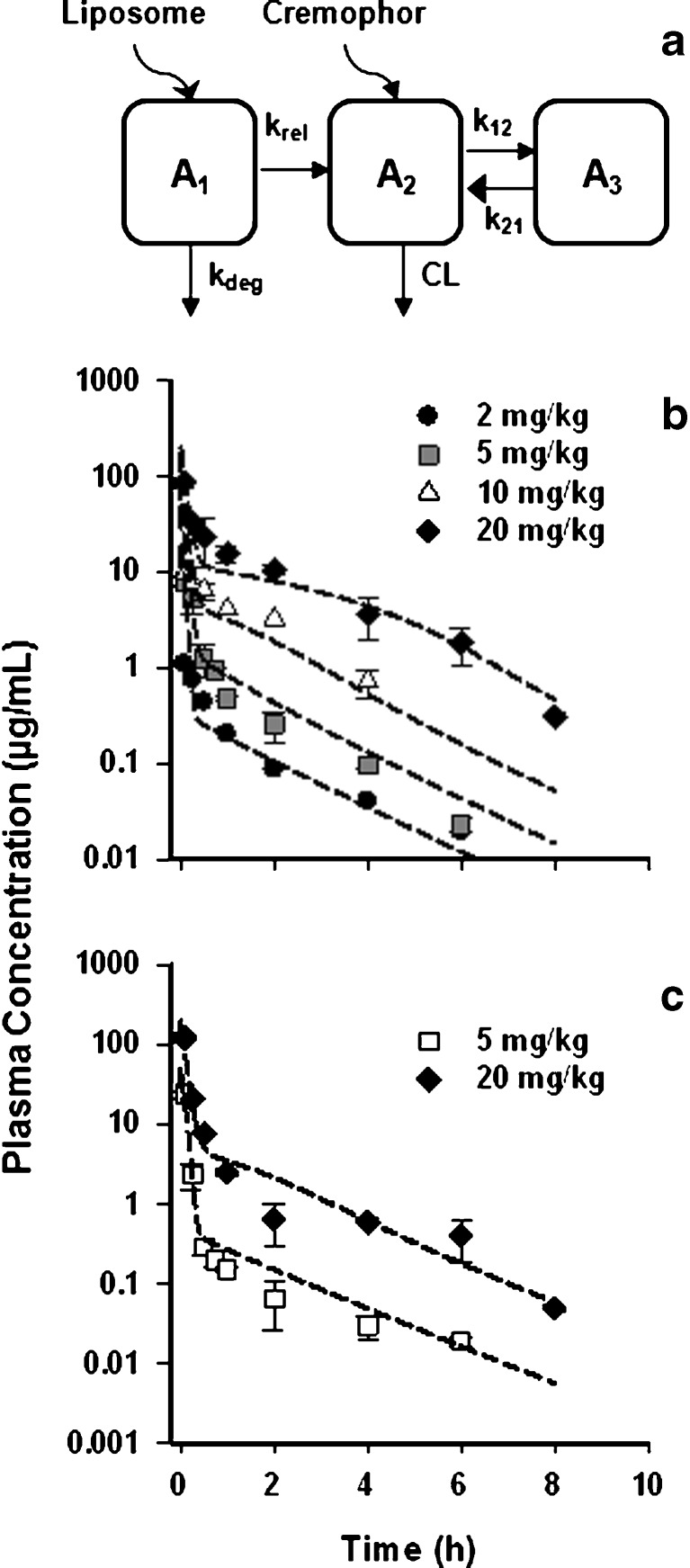
Fig. 2.
Pharmacokinetics of paclitaxel in Cremophor- or liposome-based formulations in mice. a Schematic of the pharmacokinetic model developed to fit data for the Cre-pac and L-pac formulations simultaneously. To accommodate the delayed release of drug from the liposome vehicle and clearance of the carrier by the RES before drug release, an additional compartment (A 1) was added. It was not necessary to include a drug release term for Cre-pac to obtain satisfactory model fits (RESULTS). b Plasma concentration profiles of Cre-pac and c L-pac formulations administered i.v. to mice. Symbols represent the data points digitized from the original publications (16,24,25). Lines represent the simultaneous fit of the PK model to data for both formulations
The differential equations describing the PK model are as follows:
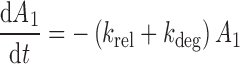 |
13 |
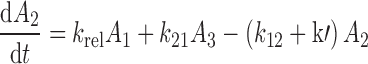 |
14 |
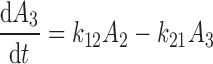 |
15 |
where A1 and A2 represent the amount of drug associated with the carrier or released into the central compartment, respectively. A3 is a peripheral distribution compartment, and Vc is the central volume. First-order rate constants k12 and k21 describe drug transfer between the central and peripheral compartments. The krel term accounts for drug released from the carrier, and kdeg represents drug remaining in the carrier that is cleared/degraded by the reticuloendothelial system (RES). Both are assumed to be first order. In the final model, Cre-pac is dosed directly into the central compartment (A2) because inclusion of the drug-release term did not improve model fits (RESULTS). Drug concentrations are equated as A2/Vc; A1, krel and kdeg are fixed to zero. For L-pac, the observed concentration (i.e., total drug in blood or plasma) is the sum of liposome-associated drug and released drug, that is, (A1 + A2)/Vc. It is important to emphasize that released drug in blood consists of both free (unbound) and protein-bound forms. Elimination from the central compartment (k′) was modeled using either the nonlinear Michaelis–Menten equation:
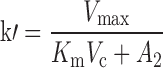 |
16 |
or linear disposition (k10).
PK data for L-pac and Cre-pac in mice were taken from the literature (16,24,25). For application to the therapeutic data analyzed here (15), it was necessary to assume that paclitaxel PK is independent of the mouse strain and that the tumor does not alter paclitaxel blood PK appreciably. The available plasma data included i.v. doses of 2, 5, 10, and 20 mg/kg Cre-pac and 5 and 20 mg/kg L-pac. Numerical values were digitized from published figures using Graph Digitizer (v2.16).
Pharmacodynamic Models
Tumor responses to multiple doses of both Cre-pac and L-pac were reported for the highly paclitaxel-resistant murine Colon-26 tumor model (15). Treatment was initiated when tumors were well-established (day 8). Drug was administered i.v. on three successive days, and treatment was repeated weekly for 3 weeks. Cre-pac was therapeutically ineffective at any dose, and the data are not included in this analysis. L-pac was administered at 10, 40, and 60 mg/kg and was effective at arresting tumor volume progression at the two higher doses. Tumor volumes were determined by caliper measurement.
Both the CDM (Fig. 1a) and SDM (Fig. 1b) were applied to these treatment/response data. The PK appropriate for L-pac was fixed as a driving function for the PD models. Three tumor growth models (Eq. 10, 11, and 12) were tested to allow the greatest flexibility and best fitting for each model.
Data Analysis
The PK/PD analysis strategy was based on a naive pooled approach. The variance models were defined as follows:
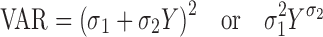 |
17a,b |
where σ1 and σ2 are the variance parameters. Y represents the model-predicted value of drug concentration (PK) or tumor volume/cell number (PD).
Goodness of fit was assessed by model convergence, visual inspection, precision of the parameter estimates, Akaike information criteria (AIC), Schwarz criteria (SC), and examination of residuals. The maximum likelihood method was applied for parameter estimation using ADAPT II (26).
RESULTS
The CDM has been shown to describe tumor growth kinetics well for numerous tumor models, treatment regimens, and chemotherapeutic agents (8). The SDM, however, has only been applied to in vitro data for tumor cell growth inhibition by MTX. Therefore, the performance of both models for fitting other types of data was evaluated.
Simulation Studies
Data Simulated by CDM and Fit by SDM
In order to create simulated data sets for model comparison that resemble authentic tumor responses to chemotherapy, the CDM was used to simulate tumor growth based on the response of A2780 human ovarian tumors in athymic mice to 30 mg/kg Cre-pac, using data and parameters from the original publication (8). The tumor response to drug (Fig. 1c) is typical of observations in many systems in that there is a period of slow growth of varying duration, followed by a phase of rapid tumor growth. Both dense and sparse data sets were simulated, with and without error, based on data from untreated- and Cre-pac-treated animals. The SDM was then used to fit these data sets. Three different tumor growth functions were tested, and the SDM incorporating the unperturbed growth model of (8) best fit the tumor progression data [Eq. 12, with M1 and w(t) set to R, substituted for g(R) in Eq. 5].
The sparse data set (6 points) simulated by the CDM was very well described by the SDM (Fig. 1c), which characterized tumor growth kinetics satisfactorily for treated and untreated animals. PD parameters were estimated with good precision (Table II). The unperturbed growth function parameters (kg, kg0) estimated by fitting are similar to the values used for simulation (Table II). A similarly good fit with similar final parameter estimates was also obtained for the dense data set (not shown).
Table II.
Parameter Estimates Obtained from Model Fitting of CDM and SDM Data Sets Using the Alternate Structural Model
| Parameters | CDM data no error (SDM fit) | CDM data with error (SDM fit) | SDM data no error (CDM fit) | |||
|---|---|---|---|---|---|---|
| Estimate | CV% | Estimate | CV% | Estimate | CV% | |
| τ (day) | 0.096 | 1.8 | 0.102 | 22.6 | 3.51 | –a |
| k max (1/day) | 0.301 | 0.3 | 0.298 | 18.3 | N/A | N/A |
| k (mL µg−1 h−1) | N/A | N/A | N/A | N/A | 0.002 | –a |
| k g (1/day) | 0.273 | 0.0 | 0.270 | 11.8 | 0.031 | –a |
| k g0 (g/day) | 0.813 | 0.1 | 0.805 | 14.1 | N/A | N/A |
| IC 50 (µg/mL) | 0.012 | 3.0 | 0.011 | –c | N/A | N/A |
| R(0) | 0.055 | 0.1 | 0.056 | 10.3 | 1,100 | –a |
| ε 1 b | 0 | –c | 0 | –c | 0.272 | –a |
| ε 2 b | 0.013 | 1.6 | 0.011 | 15.9 | 1.05 | –a |
N/A not applicable, CDM cell distribution model, SDM signal distribution model
aCV% values were not obtained owing to poor precision of parameter estimates
bResidual error model defined by a combination of proportional (ε 1) and additive (ε 2) terms (see METHODS)
cFixed value
Data Simulated by SDM and Fit by CDM
Sparse and dense data sets simulated with or without error by the SDM (9) were fit by the CDM using NONMEM. The original data set captured in vitro tumor cell growth rates in response to varying concentrations of MTX (Fig. 1d). The lowest concentration of drug resulted in a cell growth response similar to the in vivo responses of the A2780 tumor to Cre-pac (Fig. 1c). However, the higher, more effective concentrations of drug showed a pronounced delay in onset of effect (approximately 48 h), which resulted in a decrease in cell number that is analogous to a reduction in tumor volume by treatment. Eventually, cells exhibited a phase of recovery and then expansion (symbols in Fig. 1d).
Neither dense nor sparse sets of these data could be described well by the CDM, and all NONMEM runs failed to converge acceptably. In order to evaluate model performance, the CDM was fit to a very rich data set (1,000 data points per dose level), simulated without error or variability in PD parameter values, using ADAPT. Figure 1d shows the simulated cell counts. For clarity, only approximately 20 of the 1,000 points/dose level are marked with symbols. Despite the rich sampling scheme, parameter estimates were unreliable (Table II), and fitting of the data was poor. Notably, the model failed to recapture the duration of the initial growth delay and time of peak effect (Fig. 1d). None of the three tumor growth functions tested improved the final fits of the CDM to these data (not shown). In addition, initial parameter estimates were varied 10- and 100-fold to determine whether the choice of initial values unfairly biased model fitting. However, these efforts also failed to improve model fitting criteria.
Pharmacokinetics of Paclitaxel
A data set consisting of Colon-26 tumors treated with a liposomal formulation of paclitaxel was used in an additional evaluation of both models. However, the PK data necessary to drive the PD models were not available. Therefore, a suitable PK model was developed based on data from the literature. The model incorporates key characteristics of carrier-based drug formulations (Fig. 2a): Drug resides within the vehicle at the time of injection and comprises a compartment from which drug is released into the plasma. Cre-pac exists as a circulating micellar compartment (19), whereas drug in L-pac initially is embedded in the liposome membrane (27). Drug release was assigned a first-order rate (krel). Sequestration or degradation by the RES system represents a second clearance mechanism for particulate carriers and was also assigned a first-order rate (kdeg).
Data for blood concentrations of Cre-pac (Fig. 2b) and L-pac (Fig. 2c) in mice (16,24,25) were fit simultaneously by the PK model developed. A two-compartment non-linear model provided the best simultaneous fit for plasma concentrations, and the estimated PK parameters are summarized in Table III. Subsequent to the distribution phase, the blood PK profiles were essentially identical for L-pac and Cre-pac (Fig. 2b, c), fulfilling a key assumption of the modeling strategy.
Table III.
Pharmacokinetic Parameters of Paclitaxel
| Parameters | ||
|---|---|---|
| Estimate | CV% | |
| Vmax (µg kg−1 h−1) | 3,044 | 14.80 |
| k 12 (1/h) | 7.36 | 12.59 |
| k 21 (1/h) | 0.72 | 13.37 |
| V c (mL/kg) | 139.7 | 26.31 |
| K m (µg/mL) | 1.08 | 31.28 |
| k 10 (1/h) | N/A | N/A |
| k rel (1/h) | 7.17 | 39.38 |
| k deg (1/h) | 7.71 | 32.23 |
| σ 1 b | 0 | –a |
| σ 2 b | 0.946 | 12.2 |
The rate of paclitaxel release from the circulating carrier (krel) may represent a key mechanism by which the formulation differs pharmacodynamically in animal models and humans. Release from liposomes was estimated successfully (7.17 h−1), corresponding to a release half-life of approximately 6 min in mice. The inclusion of a drug release term was investigated for Cre-pac but did not appreciably improve fitting of the available data. The estimations suggested that drug release from Cre-pac micelles in the circulation was much more rapid than from L-pac (data not shown).
Mechanism-based analysis of Cre-pac PK shows that the kinetics of drug released from the carrier are linear (23) and that accounting for (1) direct proportional binding to Cremophor, (2) linear and nonlinear binding to plasma proteins, and (3) linear and nonlinear binding to blood cells can account completely for nonlinearities in drug exposure (25,28). Our goal was to derive the simplest pharmacokinetic model that described adequately the L-pac concentration-time profiles, in order to provide the appropriate input to the PD analyses. The simplified model derived (Fig. 2a) appeared adequate for that purpose.
Pharmacodynamic Analysis of Colon-26 Tumor Growth
Using the developed PK model as a driving function, the CDM and SDM were applied to analyze the therapeutic effects of L-pac in a drug-resistant murine colon cancer model (15). In this model, as in humans, L-pac was significantly less toxic than Cre-pac, and doses of Cre-pac at or above the maximum tolerated dose were ineffective in delaying tumor volume progression (not shown). Notably, Cre-pac dosed repetitively at 30 mg/kg per injection (270 mg/kg cumulative dose) was uniformly lethal over a 3-week regimen and had no discernable antitumor effect. In contrast, L-pac dosed at 9 × 40 mg/kg per injection (360 mg/kg cumulative dose) was uniformly survived (n = 10 mice) and showed arrest of tumor volume progression (Fig. 3). L-pac dosed at 60 mg/kg per injection also arrested tumor growth but was uniformly lethal after administration of only six doses (360 mg/kg cumulative).
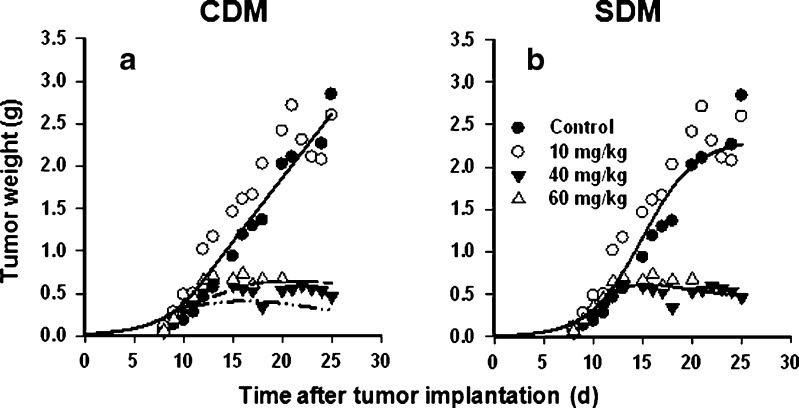
Fig. 3.
Model predictions of paclitaxel effects on colon tumor volume progression in mice. Data comparing the therapeutic efficacy of multiple i.v. doses of L-pac on s.c. Colon-26 tumors in mice were taken from the literature (15) and fit using the CDM and the SDM. Controls were treated with vehicle only. Symbols represent the data points, and lines represent the model fits to the data. Doses are as indicated in the figures. a CDM analysis of the data. b SDM analysis of the data
Data for the higher doses of L-pac were analyzed using both the CDM and SDM. Because 10 mg/kg per injection L-pac had no statistically significant effect, that data were modeled in the simultaneous fitting as equivalent to control animals administered vehicle alone.
The CDM described the Colon-26 tumor growth reasonably well overall, and the original unperturbed growth model (8) appeared to provide the best fit to these data. However, the therapeutic response to the highest dose of L-pac (60 mg/kg per injection) was overestimated (Fig. 3a); the model suggested an increased reduction of tumor volume with increased dose, which is inconsistent with the data. The parameter estimation is presented in Table IV. The τ (mean transit time) parameter was initially estimated as 4.5 days, and the CV was large. Therefore, τ was fixed to 4.5 days to obtain the best and final fit.
Table IV.
Parameter Estimates Obtained by Fitting Colon Cancer Tumor Growth Data in Mice Using the CDM and SDM Models
| Parameters | CDM fit | SDM fit | ||
|---|---|---|---|---|
| Estimate | CV% | Estimate | CV% | |
| τ (day) | 4.5 | –a | 1.21 | 15.2 |
| k (10−3 mL µg−1 day−1) | 0.981 | 15.7 | N/A | N/A |
| k max (1/day) | N/A | N/A | 0.32 | 9.6 |
| k g (1/day) | 0.288 | 17.2 | 0.370 | 5.6 |
| k g0 (g/day) | 0.151 | 4.3 | N/A | N/A |
| R ss (g) | N/A | N/A | 2.3 | 3.9 |
| R(0) (g) | 0.021 | 50.3 | 0.009 | 23.3 |
| IC50 (µg/mL) | N/A | N/A | 0.08 | –b |
| σ 1 c | 0.047 | 13.7 | 0.42 | 13.9 |
| σ 2 c | 0.825 | 20.6 | 1.34 | 11.9 |
The SDM achieved a relatively better fit of the same data (Fig. 3b, Table IV). Notably, the response curve for the highest dose of L-pac (60 mg/kg per injection) was captured well, and the model accurately predicted efficacy to be no greater than observed for the lower effective dose (40 mg/kg per injection). The logistic growth function (Eq. 11) provided a better fit of the data than did a simple first-order growth model (Eq. 10), and the parameter estimation is presented in Table IV. The IC50 was fixed to 0.08 µg/mL, which was obtained from in vitro experiments with Colon-26 cells (29). τ was estimated with good precision (CV = 15.2%) as 1.21 days. Based on visual inspection, the SDM achieved better fitting for Colon-26 tumor growth than did the CDM. The SDM also resulted in lower values of the AIC (−59.4 for SDM vs. −32.3 for CDM) and the SC (−40.2 for SDM vs. −15.8 for CDM).
DISCUSSION
A temporal delay between peak drug concentrations and therapeutic effects such as tumor growth inhibition is commonly observed for cancer chemotherapeutic agents. Capturing this delay in mechanistically based PD models can provide insight into system-level pharmacological effects and assist in the development of new therapies (30). The objective of the present research was to investigate the behavior of two PD models of anticancer drug action. Both models incorporate the concept of transduction processes as a mechanism underlying the concentration/effect temporal displacement. One key assumption that they share is that the transit compartments are homogeneous, and pharmacokinetic processes do not affect the time of signal propagation. This assumption allows the transduction cascade to be simplified to a varying number of steps (compartments) having a mean transit time (τ) between steps. The strength of such models is that when the PD response is rate-limiting, rather than PK, peak drug effects can lag behind plasma concentrations. Accommodating this lag in PK/PD models has been an enduring challenge in the field of quantitative pharmacology. The models investigated here are able to capture faithfully the experimentally observed characteristics of drug onset and recovery.
An advantage common to both models is the integral concept of an IC50 (which is stated explicitly in the SDM) or effective threshold drug concentration (derivable mathematically from the kg/k ratio in the CDM). Threshold concentrations estimated by application of the CDM to preclinical data correlated with typical therapeutic doses for select chemotherapeutic agents (31), emphasizing the clinical translational potential of this approach. Here, we observed that the SDM provided excellent fits of in vivo tumor responses based upon in vitro IC50 data for the Colon-26 cell line. Because the IC50 usually is available for anticancer drugs and tumor models, this feature permits the further constraint of the model by empirical data.
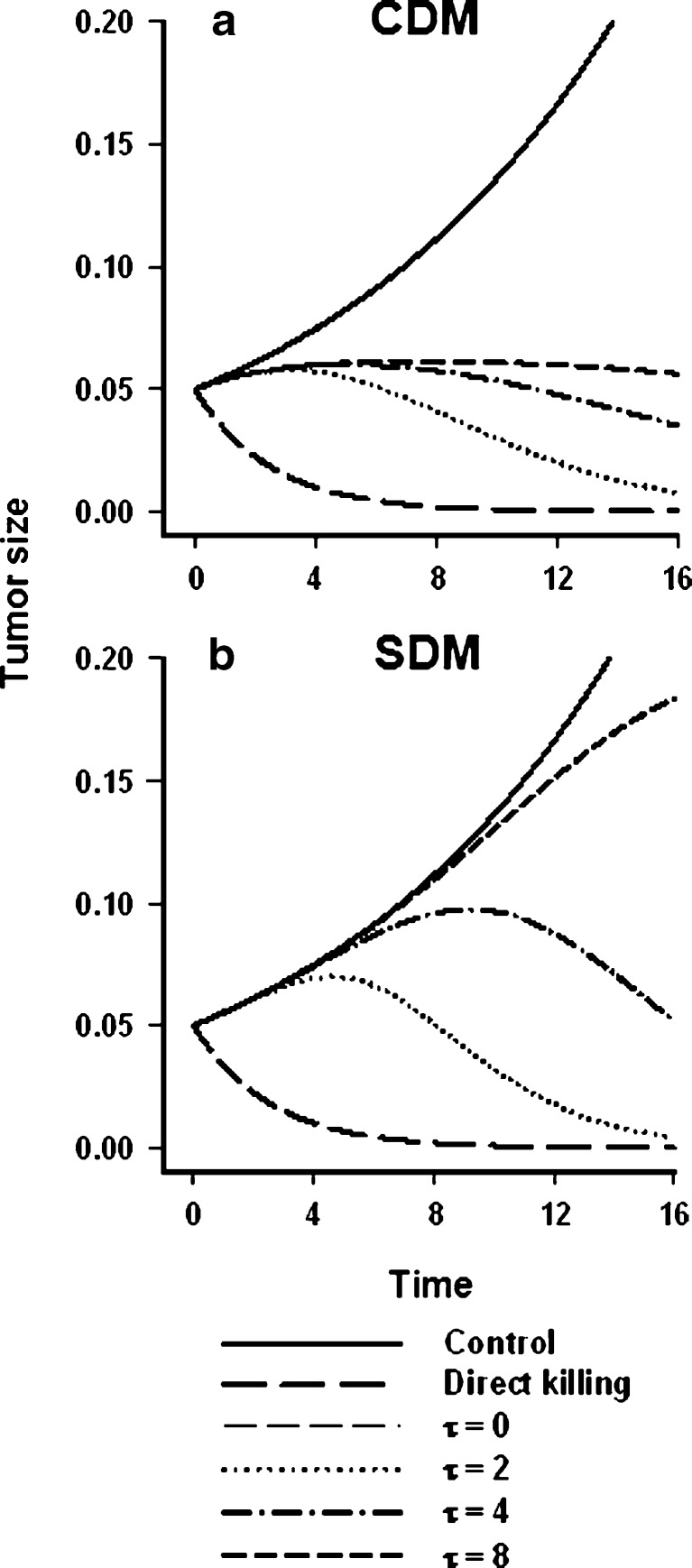
Despite similarities between the models, they are distinct in several respects. The mechanism of tumor volume reduction differs: Whereas the CDM models the delay in tumor response to drug as the duration over which cell death occurs, the SDM attributes the delay to signal transduction processes intervening between drug/receptor interaction and the killing event. Both models employ homogenous transit compartments connected in series, which translates into an Erlang probability density function (10). It is likely that both the cell-kill signal and the proportion of cells committed to cell death are defined by such distribution functions. This emphasizes the challenge in selecting model components for PD systems analysis, which necessitates elucidation of the processes that are more dominant for a given drug, its mechanism of action, and the observed time course of tumor growth kinetics. For example, because the irreversible killing effect in the CDM is acting directly upon the proliferating cell pool (Fig. 1a), the model’s flexibility to capture prolonged delays in the onset of effect is somewhat limited. This point was identified by performing simulations examining the effect of mean transit time (τ) on tumor growth. The CDM failed to mimic a long delay in onset of effect (Fig. 4a), even with a larger value of τ, whereas the SDM had sufficient flexibility to capture the delay (Fig. 4b).
Fig. 4.
Simulation of the effect of the mean transit time parameter upon tumor growth. The effect of the signal transit time (τ) upon tumor volume progression in the presence of a fixed concentration of drug was examined for the two models by simulation. A first-order unperturbed growth model (Eq. 10) was employed for both the CDM and SDM, and the Hill equation in the SDM (Eq. 6) was reduced to a simple linear function (kC p). The values of the model parameters were fixed for both models: k = 0.5, k g = 0.1, w o = 0.05, C p = 1 unit. Importantly, the drug concentration (C p) was 5-fold greater than the effective threshold concentration, i.e., the k g/k ratio in the CDM. Ordinate represents magnitude of effect (arbitrary units). a Behavior of the cell distribution model; b behavior of the signal distribution model
An additional difference between the models is the effect of dataset density. The SDM showed better performance with simulated data sets that were sparse, which is notable in that experimental data on tumor volume progression often are sparse. Nonetheless, experimental and computational approaches are available to support the application of either model to sparse data sets. For example, where infrequent sampling appears to affect identifiability of the mean transit time through the transit compartments in the CDM, in vitro cell growth inhibition studies might be used to estimate delays in onset of drug effect, from which mean transit time could be approximated. Such approximations can be optimized further using a MAP Bayesian algorithm for model fitting (32). Finally, staggered sampling designs, coupled with nonlinear mixed effects modeling, can also improve the ability to estimate model parameters accurately.
Within the scope of the present study, it was not possible to map comprehensibly the domains of concordance and discordance of the two PD models under discussion. More extensive approaches for sensitivity analysis of PK/PD models have been described (33). Extensive simulations of scaled (or non-dimensionalized) models have also been used to evaluate and compare models and to assess the validity of model assumptions (34). In addition, simulation of a greater range of drug input profiles could yield insight into the types of data for which the models are most appropriate. Nonetheless, the data sets that were simulated or taken from the literature permitted the identification of important differences in the behavior of these two useful tumor PD modeling approaches. Selection of any model for specific data will be guided by an understanding of the degree to which the model structure appears to match known mechanisms underlying drug response, as well as by the evaluation of objective criteria, as performed in these studies.
Insights gained from the application of these models are directly relevant to the development of paclitaxel-based therapeutics. As with most nonlinear systems, testing a suitable range of drug concentrations is required to ascertain specific system properties, such as the capacity of the pharmacological response. The overlap observed in the Colon-26 tumor growth curves for the two highest dose levels of L-pac (40 and 60 mg/kg; Fig. 3b) suggests a capacity-limited response, which was described reasonably by incorporating a saturable PD function (Eq. 6). Thus, the PD analyses captured formulation-dependent therapeutic responses in a quantitative, systems framework, and richer data sets could investigate dosing schemes with L-pac that are efficacious but non-saturating in terms of antitumor effect.
CONCLUSION
The CDM and SDM are both useful models for the analysis of tumor responses to chemotherapeutic agents. Both capture known mechanisms of anticancer drug responses, but they are not interchangeable. The application of these models to therapeutic data for a liposomal formulation, which is less toxic than Cre-pac in animals and humans, yielded novel insights, such as the possible existence of a capacity-limited response of this highly drug-resistant tumor to paclitaxel therapy. Given that the SDM and CDM represent similar but mechanistically distinct approaches to describing anticancer drug action, a future evolution of these models could incorporate features from both. However, such a detailed pharmacological system model would require experimental data that capture the key processes driving both model mechanisms, in order to provide adequate identification of model parameters.
Acknowledgements
Support for the studies that provided the data analyzed in this publication was obtained from various sources, including grants R01-CA55251 and R01-CA107570 from the National Cancer Inst., National Institutes of Health, to RMS. JY was supported by unrestricted postdoctoral fellowship funds provided to the University at Buffalo (SUNY) through the UB/Pfizer Strategic Alliance.
References
- 1.Sheiner LB, Stanski DR, Vozeh S, Miller RD, Ham J. Simultaneous modeling of pharmacokinetics and pharmacodynamics: application to d-tubocurarine. Clin Pharmacol Ther. 1979;25:358–71. doi: 10.1002/cpt1979253358. [DOI] [PubMed] [Google Scholar]
- 2.Dayneka NL, Garg V, Jusko WJ. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993;21:457–78. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.van Steeg TJ, Freijer J, Danhof M, de Lange EC. Pharmacokinetic-pharmacodynamic modelling of S(−)-atenolol in rats: reduction of isoprenaline-induced tachycardia as a continuous pharmacodynamic endpoint. Br J Pharmacol. 2007;151:356–66. doi: 10.1038/sj.bjp.0707234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mager DE, Wyska E, Jusko WJ. Diversity of mechanism-based pharmacodynamic models. Drug Metab Dispos. 2003;31:510–8. doi: 10.1124/dmd.31.5.510. [DOI] [PubMed] [Google Scholar]
- 5.Gobburu JV, Jusko WJ. Role of dosage regimen in controlling indirect pharmacodynamic responses. Adv Drug Deliv Rev. 1998;33:221–33. doi: 10.1016/S0169-409X(98)00030-1. [DOI] [PubMed] [Google Scholar]
- 6.Sun YN, Jusko WJ. Transit compartments versus gamma distribution function to model signal transduction processes in pharmacodynamics. J Pharm Sci. 1998;87:732–7. doi: 10.1021/js970414z. [DOI] [PubMed] [Google Scholar]
- 7.Mager DE, Jusko WJ. Pharmacodynamic modeling of time-dependent transduction systems. Clin Pharmacol Ther. 2001;70:210–6. doi: 10.1067/mcp.2001.118244. [DOI] [PubMed] [Google Scholar]
- 8.Simeoni M, Magni P, Cammia C, De Nicolao G, Croci V, Pesenti E, et al. Predictive pharmacokinetic-pharmacodynamic modeling of tumor growth kinetics in xenograft models after administration of anticancer agents. Cancer Res. 2004;64:1094–101. doi: 10.1158/0008-5472.CAN-03-2524. [DOI] [PubMed] [Google Scholar]
- 9.Lobo ED, Balthasar JP. Pharmacodynamic modeling of chemotherapeutic effects: application of a transit compartment model to characterize methotrexate effects in vitro. AAPS PharmSci. 2002;4:E42. doi: 10.1208/ps040442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Magni P, Simeoni M, Poggesi I, Rocchetti M, De Nicolao G. A mathematical model to study the effects of drugs administration on tumor growth dynamics. Math Biosci. 2006;200:127–51. doi: 10.1016/j.mbs.2005.12.028. [DOI] [PubMed] [Google Scholar]
- 11.Gardmark M, Brynne L, Hammarlund-Udenaes M, Karlsson MO. Interchangeability and predictive performance of empirical tolerance models. Clin Pharmacokinet. 1999;36:145–67. doi: 10.2165/00003088-199936020-00005. [DOI] [PubMed] [Google Scholar]
- 12.Lorenz W, Riemann HJ, Schmal A, Schult H, Lang S, Ohmann C, et al. Histamine release in dogs by Cremophor EL and its derivatives: oxyethylated oleic acid is the most effective constituent. Agents Actions. 1977;7:63–7. doi: 10.1007/BF01964882. [DOI] [PubMed] [Google Scholar]
- 13.Grem JL, Tutsch KD, Simon KJ, Alberti DB, Willson JVK, Tormey DC, et al. Phase I study of taxol administered as a short iv infusion daily for 5 days. Cancer Treat Rep. 1987;71:1179–84. [PubMed] [Google Scholar]
- 14.Riondel J, Jacrot M, Fessi H, Puisieux F, Poiter P. Effects of free and liposome-encapsulated taxol on two brain tumors xenografted into nude mice. In Vivo. 1992;6:23–8. [PubMed] [Google Scholar]
- 15.Sharma A, Mayhew E, Straubinger RM. Antitumor effect of taxol-containing liposomes in a taxol-resistant murine tumor model. Cancer Res. 1993;53:5877–81. [PubMed] [Google Scholar]
- 16.Cabanes A, Briggs KE, Gokhale PC, Treat JA, Rahman A. Comparative in vivo studies with paclitaxel and liposome-encapsulated paclitaxel. Int J Oncol. 1998;12:1035–40. doi: 10.3892/ijo.12.5.1035. [DOI] [PubMed] [Google Scholar]
- 17.Sparreboom A, Scripture CD, Trieu V, Williams PJ, De T, Yang A, et al. Comparative preclinical and clinical pharmacokinetics of a cremophor-free, nanoparticle albumin-bound paclitaxel (ABI-007) and paclitaxel formulated in Cremophor (Taxol) Clin Cancer Res. 2005;11:4136–43. doi: 10.1158/1078-0432.CCR-04-2291. [DOI] [PubMed] [Google Scholar]
- 18.Fetterly GJ, Grasela TH, Sherman JW, Dul JL, Grahn A, Lecomte D, et al. Pharmacokinetic/pharmacodynamic modeling and simulation of neutropenia during Phase I development of liposome entrapped paclitaxel. Clin Cancer Res. 2008;14:5856–63. doi: 10.1158/1078-0432.CCR-08-1046. [DOI] [PubMed] [Google Scholar]
- 19.Sparreboom A, van Zuylen L, Brouwer E, Loos WJ, de Bruijn P, Gelderblom H, et al. Cremophor EL-mediated alteration of paclitaxel distribution in human blood: clinical pharmacokinetic implications. Cancer Res. 1999;59:1454–7. [PubMed] [Google Scholar]
- 20.Fetterly GJ, Straubinger RM. Pharmacokinetics of paclitaxel-containing liposomes in rats. AAPS PharmSci. 2003;5:E32. doi: 10.1208/ps050432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kumar GN, Walle UK, Bhalla KN, Walle T. Binding of taxol to human plasma, albumin, and a1-acid glycoprotein. Res Comm Chem Pathol Pharmacol. 1993;80:337–44. [PubMed] [Google Scholar]
- 22.Longnecker SM, Donehower RC, Cates AE, Chen T-L, Brundrett RB, Grochow LB, et al. High-performance liquid chromatographic assay for taxol in human plasma and urine and pharmacokinetics in a Phase I trial. Cancer Treatm Rep. 1987;71:53–9. [PubMed] [Google Scholar]
- 23.Gelderblom H, Mross K, ten Tije AJ, Behringer D, Mielke S, van Zomeren DM, et al. Comparative pharmacokinetics of unbound paclitaxel during 1- and 3-hour infusions. J Clin Oncol. 2002;20:574–81. doi: 10.1200/JCO.20.2.574. [DOI] [PubMed] [Google Scholar]
- 24.Bardelmeijer HA, Beijnen JH, Brouwer KR, Rosing H, Nooijen WJ, Schellens JH, et al. Increased oral bioavailability of paclitaxel by GF120918 in mice through selective modulation of P-glycoprotein. Clin Cancer Res. 2000;6:4416–21. [PubMed] [Google Scholar]
- 25.Sparreboom A, van Tellingen O, Nooijen WJ, Beijnen JH. Nonlinear pharmacokinetics of paclitaxel in mice results from the pharmaceutical vehicle Cremophor EL. Cancer Res. 1996;56:2112–5. [PubMed] [Google Scholar]
- 26.D'Argenio DZ, Schumitzky A. ADAPT II user's guide: pharmacokinetic/pharmacodynamic systems analysis software. Los Angeles: Biomedical Simulations Resource; 1997. [Google Scholar]
- 27.Balasubramanian SV, Straubinger RM. Taxol-lipid interactions: taxol-dependent effects on the physical properties of model membranes. Biochemistry. 1994;33:8941–7. doi: 10.1021/bi00196a011. [DOI] [PubMed] [Google Scholar]
- 28.Henningsson A, Karlsson MO, Vigano L, Gianni L, Verweij J, Sparreboom A. Mechanism-based pharmacokinetic model for paclitaxel. J Clin Oncol. 2001;19:4065–73. doi: 10.1200/JCO.2001.19.20.4065. [DOI] [PubMed] [Google Scholar]
- 29.Sharma A, Straubinger RM. Novel taxol formulations: preparation and characterization of taxol-containing liposomes. Pharm Res. 1994;11:889–96. doi: 10.1023/A:1018994111594. [DOI] [PubMed] [Google Scholar]
- 30.Mager DE, Jusko WJ. Development of translational pharmacokinetic-pharmacodynamic models. Clin Pharmacol Ther. 2008;83:909–12. doi: 10.1038/clpt.2008.52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rocchetti M, Poggesi I, Germani M, Fiorentini F, Pellizzoni C, Zugnoni P, et al. A pharmacokinetic-pharmacodynamic model for predicting tumour growth inhibition in mice: a useful tool in oncology drug development. Basic Clin Pharmacol Toxicol. 2005;96:265–8. doi: 10.1111/j.1742-7843.2005.pto960325.x. [DOI] [PubMed] [Google Scholar]
- 32.Xu L, Eiseman JL, Egorin MJ, D'Argenio DZ. Physiologically-based pharmacokinetics and molecular pharmacodynamics of 17-(allylamino)-17-demethoxygeldanamycin and its active metabolite in tumor-bearing mice. J Pharmacokinet Pharmacodyn. 2003;30:185–219. doi: 10.1023/A:1025542026488. [DOI] [PubMed] [Google Scholar]
- 33.Nestorov IA. Sensitivity analysis of pharmacokinetic and pharmacodynamic systems: I. A structural approach to sensitivity analysis of physiologically based pharmacokinetic models. J Pharmacokinet Biopharm. 1999;27:577–96. doi: 10.1023/A:1020926525495. [DOI] [PubMed] [Google Scholar]
- 34.Marathe A, Krzyzanski W, Mager DE. Numerical validation and properties of a rapid binding approximation of a target-mediated drug disposition pharmacokinetic model. J Pharmacokinet Pharmacodyn. 2009;36:199–219. doi: 10.1007/s10928-009-9118-8. [DOI] [PubMed] [Google Scholar]