Maximum-Likelihood Methods for Processing Signals From Gamma-Ray Detectors

Abstract

In any gamma-ray detector, each event produces electrical signals on one or more circuit elements. From these signals, we may wish to determine the presence of an interaction; whether multiple interactions occurred; the spatial coordinates in two or three dimensions of at least the primary interaction; or the total energy deposited in that interaction. We may also want to compute listmode probabilities for tomographic reconstruction. Maximum-likelihood methods provide a rigorous and in some senses optimal approach to extracting this information, and the associated Fisher information matrix provides a way of quantifying and optimizing the information conveyed by the detector. This paper will review the principles of likelihood methods as applied to gamma-ray detectors and illustrate their power with recent results from the Center for Gamma-ray Imaging.

I. Introduction

In imaging applications, gamma-ray detectors are usually based on scintillators or semiconductor materials. Scintillation detectors are often some variant of an Anger camera in which each event produces signals in an array of photomultipliers (PMTs) or other optical detectors. These signals are conventionally used in a simple centroid algorithm to produce estimates of the two-dimensional (2D) coordinates of the interaction position and the energy deposited in the material by the interaction.

Semiconductor detectors are often pixellated arrays where the interaction produces electrical signals directly on pixel electrodes. In these devices, the 2D location of the pixel that produces the maximum signal is usually taken as the estimate of the interaction location, and the magnitude of that signal is taken as the estimate of the energy. A similar approach is usually taken in crossed-strip semiconductor devices, merely defining the pixel by the overlap area of two orthogonal strip electrodes on opposite sides of a slab of semiconductor.

In thick detectors, there is also considerable interest in the third coordinate of the interaction, often referred to as depth of interaction or DoI. Numerous clever methods have been devised for estimating the DoI from either PMT signals in an Anger-like scintillation camera or waveforms produced in semiconductor arrays.

For application in positron emission tomography, an important additional parameter to estimate is the time of occurrence of the interaction event. Considerable effort has been expended on sophisticated analog electronics for this application.

The signal-processing algorithms for all of these estimation tasks are usually chosen for ease of electronic implementation and rapid execution, but there is no reason to believe that they are optimal in any sense. They do not incorporate any model for the statistical properties of the signals, and they usually make simplifying assumptions about the average or deterministic properties as well. Moreover, they do not incorporate prior knowledge of the parameters being estimated.

It is the premise of this paper that methods from statistical estimation theory, and in particular maximum-likelihood estimation (MLE), can be advantageously applied to signal processing for gamma-ray detectors. Moreover, ML theory provides a rigorous approach to design of the detectors themselves because the well-known Fisher information matrix, to be defined in Section II, provides a quantitative measure of the information conveyed by the detector signals. MLE methods provide a way of extracting that information, and they are readily modified to incorporate prior information.

MLE also provides a way of approaching entirely new parameter estimation problems in gamma-ray detection. For example, a single incident gamma ray can deposit energy at multiple sites in a thick crystal by Compton scattering one or more times before being photoelectrically absorbed or escaping. MLE methods can be devised for estimating the number of interaction sites associated with each gamma ray and the position and deposited energy for each.

Another example of a new estimation problem, which we shall discuss in this paper, is determination of time of occurrence and energy of an event from sampled waveforms, rather than by analog signal processing. As we shall see, timing resolution substantially better than the sampling interval can be obtained.

In addition, MLE provides new ways of rejecting scattered events or other data that are inconsistent with the statistical model used.

Finally, there is considerable current interest in listmode image reconstruction, especially in PET, and the relevant event likelihoods for this problem are greatly simplified, as we shall see, if the list entries are ML estimates.

The application of statistical estimation methods to gamma-ray detectors originated with the seminal work of Gray and Macovski [1], who considered the 2D position-estimation problem with and without prior information. Further embellishments and practical implementations of this concept were developed at both the University of Arizona [2]–[4] and the University of Michigan [5]. ML estimation of depth of interaction was suggested by Gagnon [6]. It was demonstrated by Marks [7], [8] in semiconductor arrays and recently by Hunter [9], [10] and Moore [11] in scintillation cameras for PET. A likelihood window for scatter rejection was described by Milster [4] and Chen [12], [13], and ML estimation of time of occurrence was demonstrated by Furenlid [14].

This paper begins in Section II with a short review of ML estimation theory, in the context of gamma-ray detectors. Section III then discusses specific likelihood models of relevance to gamma-ray detectors, and Section IV discusses ways of estimating the free parameters in these models. Section V surveys some applications of ML methods and recent results from the Center for Gamma-ray Imaging. A summary and conclusions are found in Section VI.

Because of page limitations and the scope of the methods surveyed, many details are left out. For mathematical background and implementation details, see [15] and [16].

II. Fundamentals of MLE Theory

A. Data Sets and Parameter Vectors

For parameter-estimation tasks, a likelihood is a probability (or probability density function if appropriate) of the form pr(g|θ), where θ is an N × 1 vector with components given by the N parameters to be estimated and g is an M × 1 data vector.

As a simple example, consider an Anger camera with 37 photomultipliers in a hexagonal array, and suppose that we wish to estimate the lateral coordinates x and y, the DoI z and the energy $\mathcal{E}$ of each event. Because there are four parameters to be estimated, N = 4, and $\theta ={(x,y,z,\mathcal{E})}^t$, where the superscript t denotes transpose. If all 37 PMT signals are used in the estimation, then M = 37 and component g_m of the vector g is the peak signal from the m^th PMT (m = 1, ... , 37). It is common, however, to use only the data from the PMT that produces the largest signals (the “hottest tube”) and from some subset of PMTs in the neighborhood. If the six nearest neighbors are used along with the hottest tube, then M = 7 and the seven components of g are these seven peak signals.

A less familiar example is afforded by the task of estimating the time of occurrence and energy of a gamma-ray interaction in a single-element (non-imaging) detector such as one element in a PET system consisting of independent scintillation crystals, each with its own photodetector. The data vector in this case might consist of M samples of the waveform produced by a single gamma-ray interaction, rather than just its peak value. If the detector elements are designed so that the average amount of light reaching the photodetector is independent of position of the interaction, then there are just two parameters to estimate: the time of occurrence τ and the energy $\mathcal{E}$.

We shall refer to the data format for these two examples as super listmode, to distinguish it from the usual meaning of the term listmode, where the list entries are position and energy estimates. To be precise, if we estimate x, y, z and $\mathcal{E}$, by whatever means, for the j^th event, then the estimate of ${\theta }_j={(x_j,y_j,z_j,{\mathcal{E}}_j)}^t$ is denoted as ${\widehat{\theta }}_j={({\widehat{x}}_j,{\widehat{y}}_j,{\widehat{z}}_j,{\widehat{\mathcal{E}}}_j)}^t$. It is this ${\widehat{\theta }}_j$ that is an entry in a conventional listmode data set to be used for tomographic reconstruction. A super-listmode entry, on the other hand, is the original g_j, composed of raw PMT or electrode signals.

If we wish to perform an image reconstruction from listmode data (in the conventional sense), for example by the listmode maximum-likelihood expectation-maximization (LMMLEM) algorithm [17]–[19], we require a different likelihood from what we have been discussing. We need to know $\mathrm{pr}(\left\{{\widehat{\theta }}_j\right\}\mid \mathbf{f})$, where f is some discrete representation of the object that produced the listmode data and $\left\{{\widehat{\theta }}_j\right\}$ is the set of estimates for all events, j = 1, . . . j. A super-listmode reconstruction, which is also possible in principle [20], [21], requires pr({g_j}|f).

On the other hand, not all gamma-ray detectors produce the raw data vector for each event directly. Some detectors operate in an integrating mode, periodically reading out frames of data which may contain signals from multiple gamma-ray events. An example is the Arizona Hybrid [22], a pixellated cadmium zinc telluride (CZT)detector with a 64 × 64 array of electrodes bonded to an integrated circuit that integrates the current from each electrode for 1 msec and then reads it out, regardless of how many events have occurred in this period. Because of charge spreading by Coulomb repulsion and diffusion as well as hole trapping, each event that occurs during the 1 msec integration time produces signals on some cluster of detector pixels. If the number of events in a frame is large, these clusters overlap and we have an integrating detector as in digital radiography. If the number of events per frame is small enough, however, cluster overlap may be rare, and it may be possible to identify the pixels associated with an individual event. In that case we can construct a raw data vector g_j for each event, and the integrating detector functions in a photon-counting mode.

Scintillation detectors based on CCDs (charge-coupled devices) are another example of integrating detectors that can function in a photon-counting mode [23] if the number of events per frame is small enough and the cluster size is small enough in comparison to the size of the CCD. Several authors [23]–[25] have shown that electron-multiplying CCDs with low readout noise can be used in this way, and more recently microchannel-plate intensifiers in close proximity to the scintillation material have been used [26]. Miller has also shown how ML estimation can be applied beneficially to estimate the 3D position and energy of each scintillation event from the cluster of signals it produces.

We refer to the preprocessing step of identifying and separating the clusters as frame parsing. Conditions under which unambiguous frame parsing is possible with minimal overlap have been discussed by Furenlid et al. [27].

B. ML and MAP Estimation

An estimation rule, also called an estimator, is a function that maps a data vector g to an estimate θ(g), or simply θ for short. One possible estimation rule is to choose the value of θ that maximizes the likelihood. Formally,

$${\widehat{\theta }}_{ML}\equiv \underset{\theta }{\text{arg max}}\left\{\mathrm{pr}(\mathbf{g}\mid \theta )\right\},$$ (1)

where the argmax operator returns the value of the θ argument that maximizes the quantity in brackets for the observed value of g. Thus the ML estimate of a parameter is the value that maximizes the probability of the observed data with the specified parametric probability model.

An equivalent rule is to maximize the logarithm of the likelihood:

$${\widehat{\theta }}_{ML}=\underset{\theta }{\text{arg max}}\left\{\ln \left[\mathrm{pr}(\mathbf{g}\mid \theta )\right]\right\}.$$ (2)

If we treat θ as a random vector about which we have some prior knowledge, we can make use of this information by forming the maximum a posteriori or MAP estimator, given by

$${\widehat{\theta }}_{MAP}=\underset{\theta }{\text{arg max}}\left\{\mathrm{pr}(\theta \mid \mathbf{g})\right\}=\underset{\theta }{\text{arg max}}\left\{\mathrm{pr}(\mathbf{g}\mid \theta )\mathrm{pr}\left(\theta \right)\right\}.$$ (3)

The equality of these two expressions follows from Bayes’ rule and the fact that pr(g) is independent of θ.

The MAP estimator in (3) has the same form as the ML estimator in (1) except that the likelihood is weighted by the prior. If all values of θ are equally probable a priori, then pr(θ) is a constant and MAP estimation reduces to ML.

An example of a useful prior for MAP estimation in gamma-ray detector is Beer's law; if we want to estimate DoI z for a detector used with a parallel-hole collimator, for example, we know a priori that pr(z) ∝ exp(–μz), where μ is the attenuation coefficient for the gamma rays.

C. Basic Properties of ML Estimators

In classical estimation theory, the performance of an estimator is specified by its bias and variance. For a vector parameter, the bias is defined by

$$\mathbf{b}\left(\theta \right)\equiv {\langle \widehat{\theta }\rangle }_{\mathbf{g}\mid \theta }-\theta ,$$ (4)

where the angle brackets denote statistical averaging over many realizations of the data for a given true value of the parameter θ. In general, the bias will depend on this true value. An unbiased estimator is one for which the bias equals zero for all true values.

The variance of the estimate of the n^th component of θ is defined by

$$\text{Var}\left({\widehat{\theta }}_n\right)\equiv {\langle {\left[{\widehat{\theta }}_n-\langle {\widehat{\theta }}_n\rangle \right]}^2\rangle }_{\mathbf{g}\mid \theta }.$$ (5)

The variances can also be regarded as the diagonal elements of the covariance matrix for the estimates. This matrix is denoted as ${\mathbf{K}}_{\widehat{\theta }}$, and its elements are given by

$${\left[{\mathbf{K}}_{\widehat{\theta }}\right]}_{n{n}^{\prime }}\equiv {\langle \left[{\widehat{\theta }}_n-\langle {\widehat{\theta }}_n\rangle \right]\left[{\widehat{\theta }}_{n^{\prime }}-\langle {\widehat{\theta }}_{n^{\prime }}\rangle \right]\rangle }_{\mathbf{g}\mid \theta }.$$ (6)

If the components of θ include coordinates of gamma-ray interactions in an imaging detector, then the bias of the estimates of these components can be interpreted as spatial distortion and the variance relates to the spatial resolution.

There is a fundamental lower limit on the variance, called the Cramér-Rao bound. To explain this concept, we must first introduce the Fisher information matrix [28], [29], which will be denoted F. The elements of this matrix are given by

$${\left[\mathbf{F}\right]}_{n{n}^{\prime }}\equiv {\langle \left[\frac{\partial }{\partial {\theta }_n}\ln \mathrm{pr}(\mathbf{g}\mid \theta )\right]\left[\frac{\partial }{\partial {\theta }_{n^{\prime }}}\ln \mathrm{pr}(\mathbf{g}\mid \theta )\right]\rangle }_{\mathbf{g}\mid \theta }.$$ (7)

If a general estimator $\widehat{\theta }\left(\mathbf{g}\right)$ is unbiased, its variance must satisfy the Cramér-Rao inequality,

$$\text{Var}\left({\widehat{\theta }}_n\right)\ge {\left[{\mathbf{F}}^{-1}\right]}_{nn}.$$ (8)

There is a slightly more complicated version, which we will not give here, for biased estimators. An unbiased estimator that achieves the bound is called efficient.

An efficient estimator does not exist for every estimation problem, but when an efficient estimator does exist, the ML estimator is efficient. Moreover, The ML estimator is always asymptotically efficient as more independent replications of a measurement, all with the same true θ, are acquired. This limit may seem to be irrelevant for event estimation with gamma-ray detectors, where we get only one data g vector for each event, but each event produces multiple secondary particles (optical photons in a scintillator or electron-hole pairs in a semiconductor); to the extent that these secondaries are independent (a point to be discussed further below), the asymptotic properties of ML estimators hold in the limit of a large number of secondaries.

An ML estimator is not only unbiased and efficient in this asymptotic limit, but it is also normally distributed, and the covariance matrix of the estimates is asymptotically equal to the inverse of Fisher information matrix: ${\mathbf{K}}_{\widehat{\theta }}\to {\mathbf{F}}^{-1}$. Thus the probability density function (PDF) of the estimates, conditional on the true values, becomes

$$\mathrm{pr}(\widehat{\theta }\mid \theta )\to \frac{\sqrt{\text{det}\left(\mathbf{F}\right)}}{{\left(2\pi \right)}^{N∕2}}\text{exp}\left[-\frac{1}{2}{(\widehat{\theta }-\theta )}^t\mathbf{F}(\widehat{\theta }-\theta )\right],$$ (9)

where N is the number of parameters being estimated, det(·) denotes determinant, and we have used the fact that det(F^–1) = 1/det(F). We shall make use of (9) in Section III-H.

III. Likelihood Models

An accurate likelihood function, pr(g|θ), should account for all random effects that influence the data when the parameter of interest is held constant.

In a scintillation camera, the random effects include:

• The random number of optical photons in each event;

• Random propagation of light to PMT photocathodes;

• The random number of photoelectrons produced;

• Random gain in the PMTs;

• Electronic noise.

For semiconductors, the random effects are:

• The random number of electron-hole pairs per event:

• Random trapping and recombination;

• Electronic noise.

In addition, in both kinds of detector, the deposition of energy by a gamma ray is a complicated random process.

A. Gamma-Ray Interactions

The first random effect to consider is the location of the initial interaction of the gamma ray with the detector material. If we wish to estimate the 3D coordinates of the interaction, these coordinates are not treated as random because the likelihood is conditioned on them, but if we wish to estimate only the two lateral coordinates, the DoI is a random variable.

Even given the coordinates, the initial interaction is random because it can be either Compton or photoelectric. If it is Compton, the resulting scattered gamma ray can be reabsorbed or rescattered at a random location or it can escape. Similarly, if the initial interaction is photoelectric absorption in a K shell of the detector material, the K vacancy can be filled randomly either by production of a K x-ray photon, which can be reabsorbed at a random site or can escape, or by production of an Auger electron which is usually absorbed relatively close to the original interaction site. In both cases, the initial electrons (photoelectrons, Auger electrons or Compton electrons) dissipate their energy along random tracks.

One way to simplify the modeling of the complicated events following an initial interaction is to distinguish between local and nonlocal energy deposition. For a 140 keV gamma ray, for example, the range of the photoelectron in a typical scintillator or semiconductor material is around 50 μm, and the range of Auger or Compton electrons is somewhat less. The range of the K x rays is around 50–100 μm, but a Compton-scattered photon can go substantially farther. At this gamma-ray energy, therefore, all energy-deposition processes except Compton reabsorption are local to a spherical region about 100 μm in diameter, and all photoelectric events deposit the full photon energy within this sphere. The size of this region increases with gamma-ray energy, but to the extent that it remains small compared to the spatial resolution of the detector, the local-deposition model should be adequate.

B. Poisson-Based Models for Scintillation Cameras

The energy deposited in the local region defined above produces optical photons in a scintillation material. If the scintillator responds linearly to the deposited energy $\mathcal{E}$, then the mean number of optical photons is given by

$${\stackrel{‒}{N}}_{opt}\left(\mathcal{E}\right)=Q_{sc}\mathcal{E},$$ (10)

where Q_sc is the scintillator efficiency expressed in optical photons per unit deposited energy. A common assumption for scintillators is that the actual number of optical photons is a Poisson random variable with this mean, but many scintillators, notably NaI(Tl), respond nonlinearly to the deposited energy [30]–[33]. In this case we can regard the mean ${\stackrel{‒}{N}}_{opt}$ as itself being a random variable, because of the randomness in the complicated physical process discussed above. If the nonlinearity is significant, ${\stackrel{‒}{N}}_{opt}\left(\mathcal{E}\right)$ must be replaced by ${\overline{\stackrel{‒}{N}}}_{opt}\left(\mathcal{E}\right)$, where the second overbar indicates an average over the details of how the energy is deposited in the local region. The actual number of optical photons, N_opt, is then referred to as a doubly stochastic Poisson random variable, a topic discussed in detail in [16]. One key point is that the variance of N_opt is greater than its overall mean in the doubly stochastic case.

If N_opt is a Poisson random variable, it follows at once that the number of photoelectrons produced in each PMT is also a Poisson random variable. If the 3D vector R = (x, y, z) denotes the location of the initial gamma-ray interaction, on average a fraction f_m(R) of the optical photons will reach the m^th PMT, and on average a fraction η_m of these will produce photoelectrons (where η_m is the quantum efficiency of the photocathode). Each of these processes is a binomial selection: each emitted photon will either make it to the PMT or not, and once there it will either produce a photoelectron or not. A fundamental theorem [16] states that a binomial selection of a Poisson random variable is also a Poisson random variable, and the same holds true for two successive binomial selections. For a linear scintillator and a specified R and $\mathcal{E}$, the number of photoelectrons produced by the m^th photocathode, denoted n_m, is a Poisson random variable with mean

$${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})={\eta }_m{f}_m\left(\mathbf{R}\right)Q_{sc}\mathcal{E},$$ (11)

and the probability of observing photoelectrons is

$$\mathrm{pr}(n_m\mid \mathbf{R},\mathcal{E})=\frac{{\left[{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})\right]}^{n_m}}{n_m!}\text{exp}[-{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})].$$ (12)

Moreover, Poisson random variables are inherently independent [16], so the multivariate probability of the set of photoelectron numbers, {n_m, m = 1, . . . , M} in all M PMTs is given by

$$\mathrm{pr}(\left\{n_m\right\}\mid \mathbf{R},\mathcal{E})=\prod _{m=1}^M\frac{{\left[{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})\right]}^{n_m}}{n_m!}\text{exp}[-{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})].$$ (13)

In scintillators with significant nonlinearity, N_opt is not a Poisson random variable, but nevertheless the Poisson law for the photoelectrons is an excellent approximation in practice. One way of deriving the Poisson law—indeed, the one used by Poisson himself—is to to consider a binomial process with a small probability of success but a large number of trials. In our context, this refers to the limit where ${\overline{\stackrel{‒}{N}}}_{opt}$ is large but η_mf_m (R) is small; in other words, many optical photons are produced but only a small fraction of them produce photoelectrons in a single PMT, and the resulting distribution of photoelectrons in approximately Poisson. Colloquially, rarity begets Poissonicity [16].

A simple and effective way of making use of (12) and (13) is to neglect gain noise in the PMT and subsequent electronic noise (see below). In that case, we can accurately determine the number of photoelectrons produced by a given event in a given PMT just by correcting for the PMT gain. The raw data needed for ML estimation of position and energy are given by

$$g_m=\mathrm{NINT}\left(\frac{V_m}{G_m}\right),$$ (14)

where V_m is the voltage produced by the m^th PMT and its associated electronics, G_m is the gain in volts per photoelectron, and the operator NINT(·) returns the nearest integer to its argument. With this definition of the data, the requisite likelihood is given by [cf. (13)]

$$\mathrm{pr}(\mathbf{g}\mid \mathbf{R},\mathcal{E})=\prod _{m=1}^M\frac{{\left[{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})\right]}^{g_m}}{g_m!}\text{exp}[-{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})].$$ (15)

We refer to this expression as the scaled-Poisson model.

If ${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})$ is greater than about 4 or 5, we can go a step further and approximate the univariate Poissons in (15) by univariate Gaussians with mean and variance both given by ${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})$.

C. Gain Noise

Many gamma-ray detectors include elements with internal gain, such as PMTs or APDs (avalanche photodiodes). These elements inevitably introduce another source of randomness, not accounted for in the scaled-Poisson model. This section briefly discusses the effect of this noisy gain. For more details see [16] and [15].

The first key point is that the excess noise from different gain elements is statistically independent. Thus, for a scintillation camera with M PMTs, we can write the PDF for the set of output signals as

$$\mathrm{pr}(\left\{V_m\right\}\mid \mathbf{R},\mathcal{E})=\prod _{m=1}^M\mathrm{pr}(V_m\mid \mathbf{R},\mathcal{E}).$$ (16)

In the absence of electronic noise, the voltage signal V_m is related to the number of electrons K_m produced on the PMT anode in response to one gamma-ray interaction by

$$V_m=G_m^{\left(elec\right)}{K}_m=G_m^{\left(elec\right)}{G}_m^{\left(PMT\right)}{n}_m,$$ (17)

where $G_m^{\left(elec\right)}$ is the gain of the electronics associated with the m^th PMT in units of volts per output electron and $G_m^{\left(PMT\right)}$ is the random gain (output electrons per input photoelectron) of the PMT itself.

A lot of effort has gone into devising expressions for the PDF of the random gain, but for application to gamma-ray detectors a great simplification results from the reasonable assumption that different photoelectrons produced on the PMT photocathode are amplified independently. The total signal V_m is then the sum of statistically independent signals from a large number of individual photoelectrons. It follows from the central-limit theorem, discussed in [16] and many other texts, that V_m is well represented as a Gaussian random variable. To specify the PDF of this univariate Gaussian, all we need is its mean and variance.

The mean of V_m, conditional on the interaction location and energy, is

$${\stackrel{‒}{V}}_m(\mathbf{R},\mathcal{E})=G_m^{\left(elec\right)}{\stackrel{‒}{G}}_m^{\left(PMT\right)}{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})={\stackrel{‒}{G}}_m{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E}),$$ (18)

where ${\stackrel{‒}{G}}_m^{\left(PMT\right)}$ is the mean PMT gain and ${\stackrel{‒}{G}}_m$ is the mean overall gain; note that the electronic gain in not random.

The conditional variance of K_m is given by the Burgess variance theorem [16] as

$$\begin{array}{cc}\hfill & \text{Var}(K_m\mid \mathbf{R},\mathcal{E})\hfill \\ \hfill & =\text{Var}\left(G_m^{\left(PMT\right)}\right){\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})+{\left({\stackrel{‒}{G}}_m^{\left(PMT\right)}\right)}^2\text{Var}(n_m\mid \mathbf{R},\mathcal{E})\hfill \\ \hfill & =\left[\text{Var}\left(G_m^{\left(PMT\right)}\right)+{\left({\stackrel{‒}{G}}_m^{\left(PMT\right)}\right)}^2\right]{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E}),\hfill \end{array}$$ (19)

where the latter form holds if, as we argued above, n_m is well approximated by a Poisson random variable.

The variance of V_m is larger than the variance of K_m by a factor of ${\left(G_m^{\left(elec\right)}\right)}^2$ so

$$\begin{array}{cc}\hfill & \text{Var}(V_m\mid \mathbf{R},\mathcal{E})\hfill \\ \hfill & =\left[{\left(G_m^{\left(elec\right)}\right)}^2\text{Var}\left(G_m^{\left(PMT\right)}\right)+{\left({\stackrel{‒}{G}}_m\right)}^2\right]{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E}).\hfill \end{array}$$ (20)

Note that the variance of V_m is proportional to the mean but not equal to it; it could not be because V_m has units of volts and its variance has units of volts².

We can use the PMT signals directly as the data from which to estimate R and $\mathcal{E}$, or we can choose to divide by the mean gain to once again get the data values into units of photoelectrons. In the former case, g_m = V_m and $\mathrm{pr}(g_m\mid \mathbf{R},\mathcal{E})$ is a univariate Gaussian with mean and variance given by (18) and (20), respectively; the multivariate likelihood $\mathrm{pr}(\mathbf{g}\mid \mathbf{R},\mathcal{E})$ is a simple product as in(16). If the PMT gain noise is negligible, so that $\text{Var}\left[G_m^{\left(PMT\right)}\right]\ll {\left[{\stackrel{‒}{G}}_m^{\left(PMT\right)}\right]}^2$, this likelihood is equivalent to a Gaussian approximation to the scaled-Poisson likelihood of (15).

D. Electronic Noise

Electronic noise is usually well described by a zero-mean Gaussian random process. Moreover, noise in different electronic channels is statistically independent. Thus the product form of (16) is still valid, and if we use univariate Gaussians for the factors in that expression, we can account for electronic noise by replacing the variance of V_m in (20) by

$$\text{Var}(V_m\mid \mathbf{R},\mathcal{E})={\alpha }_m{\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})+{\sigma }_m^2,$$ (21)

where αm is the expression in square brackets in (20) and ${\sigma }_m^2$ is the variance of the electronic noise for the m^th PMT. The actual value of ${\sigma }_m^2$ depends on the shaping time constants and other details of the analog electronics and on how the analog waveform is sampled to get the digital data used for estimation.

E. Gaussian Models for Semiconductor Detectors

There are several important differences between semiconductor and scintillation detectors which affect the likelihood calculations. The first is that semiconductors are much more efficient than scintillators in converting gamma-ray energy to measurable signals. With available photocathodes, it takes about 100 eV to produce an observable photoelectron in a PMT with a NaI(Tl) detector, but it takes only about 3 eV to produce an electron-hole pair in germanium or silicon. On the other hand, the availability of PMTs with high gain makes electronic noise much less important in scintillation cameras than in semiconductors. Finally, optical photons do not create a measurable signal until they reach the PMTs or other optical sensors, but trapped electrons and holes in a semiconductor can still induce signals on distant electrodes.

The minimum energy required to generate an electron-hole pair is the bandgap energy ${\mathcal{E}}_g$, so a high-energy photoelectron of kinetic energy ${\mathcal{E}}_{kin}$ could in principle produce ${\mathcal{E}}_{kin}∕{\mathcal{E}}_g$ pairs. Because of competing processes such as phonon generation, however, a smaller number will be produced on average. We define the mean energy expended per electron-hole pair, ${\mathcal{E}}_{eh}$, such that the mean number of pairs is ${\stackrel{‒}{N}}_{eh}={\mathcal{E}}_{kin}∕{\mathcal{E}}_{eh}$.

If there were no competing processes, conservation of energy would require that $N_{eh}={\mathcal{E}}_{kin}∕{\mathcal{E}}_g$, which is not a random number at all. At the opposite extreme, if only a small fraction of the electron energy goes into creation of electron-hole pairs, the pairs would be generated independently, and N_eh would be a Poisson. Thus $0=\text{Var}\left\{N_{eh}\right\}\le {\stackrel{‒}{N}}_{eh}$. To describe this range, we define the Fano factor F_eh as

$$F_{eh}=\frac{\text{Var}\left(N_{eh}\right)}{{\stackrel{‒}{N}}_{eh}}.$$ (22)

A value of F_eh < 1 implies sub-Poisson behavior. In Si and Ge, F_eh ≈ 0.07 to 0.15.

New sources of electronic noise must be considered in semiconductor detectors. Flicker or 1/f noise is often dominant, and in integrating detectors there is an effect called kTC noise [16].

In many semiconductor detector material, charge transport is poor, and there is a high probability that charge carriers, especially holes, will be trapped before they reach the electrodes. Modeling of these effects requires knowledge of the mobility and lifetime of the charge carriers as well as the weighting potentials, which specify the effect of a charge at a given location on the output signals.

The only practical way of dealing analytically with all of these effects is to use a multivariate Gaussian model, where all we need is the mean vector and covariance matrix, both conditioned on the parameters we wish to estimate. If M signals are used to perform the estimation, the mean vector is M × 1 and the covariance matrix is M × M.

The mean vector and covariance matrix depend on the mean number of electron-hole pairs produced, the Fano factor, the mobility-lifetime products for both holes and electrons, the details of the electronics and the electronic noise. For integrating detectors such as the Arizona Hybrid, they depend also on the PDF of the trapped charge at the end of the integration period.

Explicit expressions for the mean vector and covariance matrix for estimation of R and $\mathcal{E}$ in integrating detectors may be found in Barrett and Myers [16]

F. Nuisance Parameters

So far we have implicitly assumed that the PDF on the detector signals is fully determined by the parameters being estimated, but this is not always the case. Often there are nuisance parameters, defined as quantities that we have no interest in estimating but which do influence the data.

As an example, for a scintillation camera used with a parallel-bore collimator, the z coordinate of the interaction (where the z axis is parallel to the bores) is of no interest because it has no effect on the image in the x – y plane. If the detector is thin and designed so that z does not significantly influence the mean PMT signals, we can ignore it altogether, but if it does influence the signals, we must regard z as a nuisance parameter.

As a second example, when we write $\mathrm{pr}(\mathbf{g}\mid \mathbf{R},\mathcal{E})$, we are assuming that this PDF depends on just the 3D coordinates and energy of a single interaction and on no other unknown parameters. For a thick detector used at high energy, however, the gamma-ray photon might interact initially by Compton scattering and the scattered photon might be absorbed or rescattered at a second location. In that case we would need a total of eight parameters to specify the PDF: three coordinates and an energy at each of two interaction sites. If the detector is used in a Compton camera, all eight parameters are of interest and should be estimated. For a PET or SPECT application, however, the coordinates of the second interaction convey no information about the object being imaged, but they do influence the data, so they have to be considered nuisance parameters.

There are several possible ways to deal with nuisance parameters, depending on how much we know about an estimation problem [16], [34]. The simplest approach, and the one most used in practice, is just to ignore the nuisance parameters and use an inaccurate likelihood. This approach will produce an unpredictable bias and generally suboptimal variance of the estimate.

The second approach is to estimate the nuisance parameters and discard the result. This approach is feasible if the number of nuisance parameters is small, but it rapidly leads to a large computational burden if there are many nuisance parameters. For the case of a scintillation camera used with a parallel-bore collimator, for example, we can estimate the z coordinate of the interaction even if we have no interest in it, thereby avoiding bias in the estimate of x and y.

Another approach, which is optimal in a sense discussed in Sec. 13.3.8 of Barrett and Myers [16], is to compute the likelihood for the parameters of interest by integrating out (“marginalizing”) the nuisance parameters. In the example of a scintillation camera with parallel-bore collimator, we would write

$$\mathrm{pr}(\mathbf{g}\mid x,y,\mathcal{E})={\int }_0^{L_z}dz\mathrm{pr}(\mathbf{g}\mid x,y,z,\mathcal{E})\mathrm{pr}\left(z\right),$$ (23)

where L_z is the thickness of the detector and, by Beer's law, pr(z) = μ exp(–μz)/[1 – exp(–μL_z). If we use the scaled-Poisson model from (15), we get

$$\begin{array}{cc}\hfill & \mathrm{pr}(\mathbf{g}\mid x,y,\mathcal{E})=\frac{\mu }{1-\text{exp}(-\mu L_z)}{\int }_0^{L_z}dz\prod _{m=1}^M{\left[{\stackrel{‒}{n}}_m(x,y,z,\mathcal{E})\right]}^{\frac{g_m}{g_m!}}\hfill \\ \hfill & \times \text{exp}[-{\stackrel{‒}{n}}_m(x,y,z,\mathcal{E})]\text{exp}(-\mu z).\hfill \end{array}$$ (24)

After the marginalization, the likelihood is no longer a simple product of univariate PDFs. If we wish to use a Gaussian approximation, it must be multivariate and we must determine the covariance matrix.

G. Likelihood Windowing

Another way to deal with nuisance parameters is to use hypothesis testing to reject events that are not consistent with the assumptions built into the likelihood model.

A simple but useful example is the likelihood window suggested by Milster [4]. Consider the hypothesis that the initial interaction is photoelectric, that the K x ray is absorbed locally and that there has been no scatter in the patient's body. In that case the energy deposited locally in the detector material is the full original energy of the gamma ray, denoted ${\mathcal{E}}_0$. The unknown parameters for the interaction under this hypothesis are just its 3D coordinates contained in R, and the appropriate likelihood is $\mathrm{pr}(\mathbf{g}\mid \mathbf{R},{\mathcal{E}}_0)$. The ML estimate of the location is found by searching over R with energy fixed:

$${\widehat{\mathbf{R}}}_{ML}=\underset{\mathbf{R}}{\text{arg max}}\left\{\mathrm{pr}(\mathbf{g}\mid \mathbf{R},{\mathcal{E}}_0)\right\}.$$ (25)

After finding ${\widehat{\mathbf{R}}}_{ML}$, we then accept the event only if the resulting maximized likelihood, $\mathrm{pr}(\mathbf{g}\mid {\widehat{\mathbf{R}}}_{ML},{\mathcal{E}}_0)$, exceeds some threshold. A smaller threshold allows acceptance of more photons that do not satisfy the hypothesis (false positives), as well as more that do (true positives). A plot of true-positive fraction vs. false-positive fraction as the threshold is varied yields a photon ROC curve [12], [13], analogous to the receiver operating characteristic curves used in signal detection. The area under the photon ROC curve is a measure of the ability of the detector to reject photons that are Compton-scattered either in the patient's body or in the detector.

Similar methods can be used to discriminate against multiple interactions. We can use any of the forms given above for $\mathrm{pr}(\mathbf{g}\mid \mathbf{R},\mathcal{E})$ and maximize over both R and $\mathcal{E}$. Comparison of the maximized likelihood to a threshold is an effective way of discriminating against events that deposit energy at multiple sites, while retaining both photoelectric events and Compton interactions followed by escape of the scattered photon.

H. Event Likelihoods for Listmode Reconstruction

As noted in Section II-A, image reconstruction from listmode data requires knowledge of the PDF of the list entries conditional on an object f. Suppose now that the list entries are ML estimates of interaction locations and that likelihood windowing has been used to reject scattered radiation and multiple interactions in the detector. If j events are observed, the data set for listmode reconstruction is $\{{\widehat{\mathbf{R}}}_j,j=1,\dots ,J\}$.

The events are statistically independent, so

$$\mathrm{pr}\left(\left\{{\widehat{\mathbf{R}}}_j\right\}\mid \mathbf{f}\right)=\prod _{j=1}^J\mathrm{pr}({\widehat{\mathbf{R}}}_j\mid \mathbf{f}),$$ (26)

and the log-likelihood can be written as

$$\ln \left[\mathrm{pr}\left(\left\{{\widehat{\mathbf{R}}}_j\right\}\mid \mathbf{f}\right)\right]=\sum _{j=1}^J\ln \int d^3{R}_j\mathrm{pr}({\widehat{\mathbf{R}}}_j\mid {\mathbf{R}}_j)\mathrm{pr}({\mathbf{R}}_j\mid \mathbf{f}),$$ (27)

where R_j is the true location of the j^th event.

In practice both f and R_j will be discretized, so pr(R_j|f) will be realized as a matrix-vector multiplication as in any reconstruction algorithm. The integral over R_j can be implemented efficiently as a sum over a small number of values of R_j in the neighborhood of ${\widehat{\mathbf{R}}}_j$.

All that remains is to obtain the factor $\mathrm{pr}({\widehat{\mathbf{R}}}_j\mid {\mathbf{R}}_j)$, which describes the detector blur (in 3D in general). This step is actually quite difficult for most position-estimation algorithms used in gamma-ray detectors, but it is straightforward for ML algorithms. We have already seen in (9) that the ML estimates asymptotically obey a multivariate normal distribution with mean given by the true value and covariance matrix approaching the inverse of the Fisher information matrix. The asymptotic limit holds when the number of photoelectrons or electron-hole pairs produced by a gamma-ray event is large, which is usually an excellent assumption. The Fisher information matrix can be computed by taking numerical derivatives of the MDRF.

In short, an accurate model for detector blur is readily incorporated in a listmode reconstruction algorithm provided the list entries are specifically ML estimates of the photon interaction positions.

IV. Calibration Methods

All of the likelihood functions presented above include some free parameters that are characteristic of individual detectors. For the scaled-Poisson model of (15), for example, we need know the mean number of photoelectrons produced by each PMT, ${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})$, as well as the gains G_m. When PMT gain noise is considered, we need also to measure the excess noise factor seen in (20). When the signals are correlated, as when we perform 2D position estimation and ignore DoI [see (24)], we also need a covariance matrix on the signals.

A. 2D Mean Detector Response Function

Consider a scintillation camera with a thin scintillation crystal so that DoI effects are negligible, and ignore scintillator nonlinearities for now. Then ${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})$ is independent of z and (11) can be rewritten as

$${\stackrel{‒}{n}}_m(x,y,\mathcal{E})=MDR{F}_m(x,y\mid {\mathcal{E}}_0)\frac{\mathcal{E}}{{\mathcal{E}}_0},$$ (28)

where $MDR{F}_m(x,y\mid {\mathcal{E}}_0)$ is called the mean detector response function for a specific energy ${\mathcal{E}}_0$. It accounts for the effects of scintillator efficiency, propagation of light from the interaction site to the m^th PMT, and the quantum efficiency of that tube.

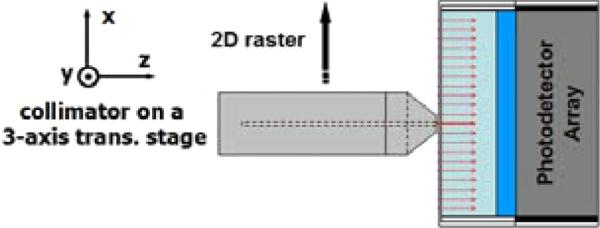
This MDRF can be measured with the apparatus shown in Fig. 1 [36]. A radioisotope such as Tc-99m is used to produce a collimated beam of gamma rays which can be raster-scanned over the face of a scintillation camera. At each position a spectrum is acquired, and the mean response is estimated from the photopeak position. In practice, the MDRF can be measured on a coarse grid of points and interpolated to a finer grid [36], [39].

Fig. 1.

Apparatus for measuring the MDRF of a scintillation camera.

The resulting MDRF for a modular scintillation camera with a monolithic (not segmented) NaI(Tl) crystal of dimensions 12.5 cm × 12.5 cm × 5 mm and a 3 × 3 array of PMTs is shown in Fig. 2. Each of the nine images is the MDRF for one of the nine PMTs, and the grey level in the image depicts the MDRF for that tube as a function of the x – y location.

Fig. 2.

Measured MDRF for a scintillation camera with a 3 × 3 array of PMTs.

B. 3D Mean Detector Response Function

For thick detectors as used at higher photon energies, a 2D MDRF is not adequate. We can still collect data with an apparatus similar to the one in Fig. 1, but we cannot control the DoI so ${\stackrel{‒}{n}}_m(x,y,z,\mathcal{E})$ cannot be measured directly. Instead, we must represent this 3D function in a parametric form and estimate the parameters. The parameters can be coefficients in some linear expansion of the 3D function, or they can be parameters such as reflectivities and surface roughnesses associated with a model for optical propagation. The data used to perform the parameter estimation can include spectra obtained with multiple gamma-ray energies or with scanned beams at other than normal incidence. For more details, see [10], [37], [38].

V. Applications and Recent Results

A. 2D Position Estimation in Scintillation Cameras

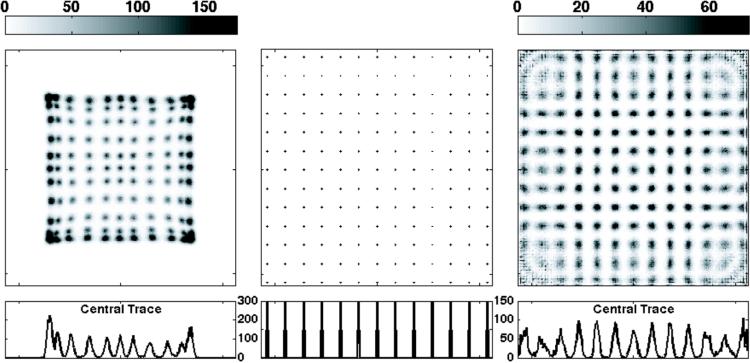
As an example of the effectiveness of MLE of interaction locations in 2D, Fig. 3 shows some experimental images from the modular scintillation camera whose MDRF is shown in Fig. 2. The raw data were generated by stepping the collimated ^99mTc source shown in Fig. 1 over a 13 × 13 array of positions separated by 9 mm. The central image in Fig. 3 illustrates this pattern of points. Approximately 5,000 events were collected at each location in super-listmode format (recording all nine PMT signals for each event).

Fig. 3.

Center: Object imaged by a scintillation camera. Left: Image obtained with standard Anger arithmetic. Right: Image with ML position estimates.

The x and y coordinates of each event were estimated by maximizing the scaled-Poisson likelihood of (15) with the MDRF functions, ${\stackrel{‒}{n}}_m(\mathbf{R},\mathcal{E})$, being those shown in Fig. 2. The energy used in this likelihood model was 140 keV, corresponding to photopeak events, and a likelihood window was used with the threshold set to accept approximately 85% of all events. The resulting ML image is shown on the right in Fig. 3, and the trace below the image runs through the central horizontal row of points.

For comparison, the same super-listmode data were also processed with standard Anger arithmetic, with position estimates given by

$$\widehat{x}=\frac{\sum _{m=1}^9{V}_m{x}_m}{\sum _{m=1}^9{V}_m},\widehat{y}=\frac{\sum _{m=1}^9{V}_m{y}_m}{\sum _{m=1}^9{V}_m},$$

where x_m and y_m are the coordinates of PMT m. The resulting image is shown on the left in Fig. 3.

In Fig. 3, a 13 × 13 array of points was imaged, and all points are well resolved in the ML image except in the corners of the camera. In the Anger image, however, only an 11 × 11 array of points is seen; the points in the top and bottom two rows and the left and right two columns are completely unresolved. In addition the Anger image is distorted, indicating that the position estimates are biased, but the ML point images are centered on the correct grid locations, so the ML estimates are unbiased as expected from the discussion in Section II-C.

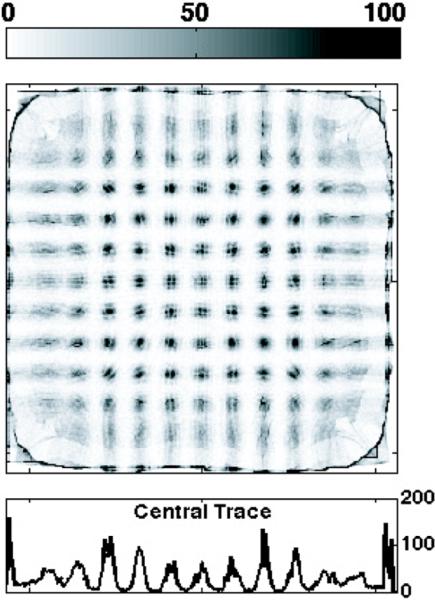
To provide a more direct comparison, we attempted to remove the bias in the Anger image by geometrical remapping, with the result shown in Fig. 4. Though the distortion was removed in the center of the image, no improvement in resolution on the outer rows or columns was seen.

Fig. 4.

Anger image from Fig. 3 after geometrical distortion correction.

To provide a more quantitative resolution comparison, we computed the full width at half maximum (FWHM) of representative point images in the original ML image and in the remapped Anger image. No points near the camera edge were included because the Anger method gave no measurable resolution there, but we included the nine points centered under the PMTs (referred to as center points) and the four in the interstices between PMTs (interstitial points). The numbers reported in Table I are the FWHMs in the x direction, in the y direction and the geometric mean of these two.

TABLE I.

Resolutions (FWHM), mm

Method	Location	FWHMx	FWHMy	Geom. mean
Anger	centered	4.12	3.89	4.01
MLE	centered	3.41	3.60	3.50
Anger	interstitial	3.64	3.41	3.52
MLE	interstitial	2.82	2.66	2.73

To summarize, this comparison indicates the superior resolution of ML position estimation, especially at the edges of the camera, and it shows that good spatial linearity is obtained with no need for distortion correction. The resolution is a measure of the variance of a position estimator and the linearity is a measure of bias, so the results are in accord with the theorems that state that the ML estimator is efficient (minimum variance and unbiased) if an efficient estimator exists, and that it is asymptotically efficient in any case.

B. Likelihood Windowing

One advantage of likelihood windowing with this same modular scintillation camera is shown in Fig. 5, from the work of Hesterman [39]. By varying the value of the likelihood threshold with position, excellent spatial uniformity can be obtained.

Fig. 5.

Illustration of flood images without (a) and with (b) position-dependent likelihood windowing.

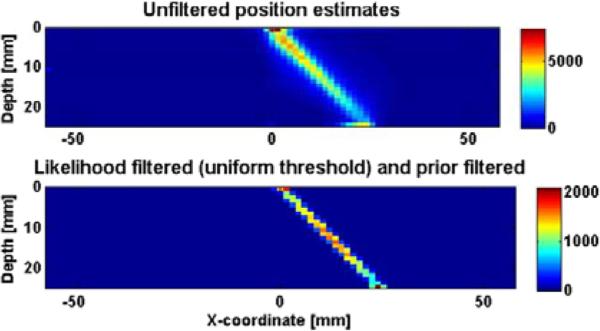
C. ML Estimation of Depth of Interaction

The recent work of Hunter [9], [10], illustrated in Fig. 6, affords an illustration of how well 3D ML position estimation performs when the 3D MDRF is known. The simulated detector was a scintillation camera with a 12.5 cm × 12.5 cm × 2.5 cm monolithic NaI(Tl) crystal and a 3 × 3 array of PMTs. The sides and entrance face of the crystal were assumed to be covered with retroreflectors to increase the light reaching the PMTs, though the same results would be obtained by assuming a more efficient scintillator.

Fig. 6.

Simulation study of 3D position estimation in a monolithic PET camera. Top: Without likelihood windowing. Bottom: With likelihood windowing.

The simulated input to the camera was a thin beam of 511 keV photons incident at 45 degrees to the entrance face of the scintillator. Nearly isotropic spatial resolution around 1–2 mm is observed.

Experimental confirmation of 3D position estimation in a monolithic PET detector is provided by the work of Moore [11], shown in Fig. 7, which shows experimental images of a 511 KeV beam about 1 mm in diameter, incident at 60 degrees from the surface normal of the crystal. The scintillation camera had the same 3 × 3 arrangement of PMTs as discussed above, but all faces of the crystal except the one in contact with the PMTs were painted black to minimize reflections. With this configuration the 3D MDRF could be calculated fairly accurately from the solid angles subtended by the PMTs at the interaction site, with experimental correction for the spatial variation of the total light collected.

Fig. 7.

Experimental demonstration of 3D imaging of a slanted beam of 511 keV photons with a modular scintillation camera. Projections of the 3D estimates onto three orthogonal faces of the camera are shown.

D. Time-of-Arrival Estimation From Waveforms

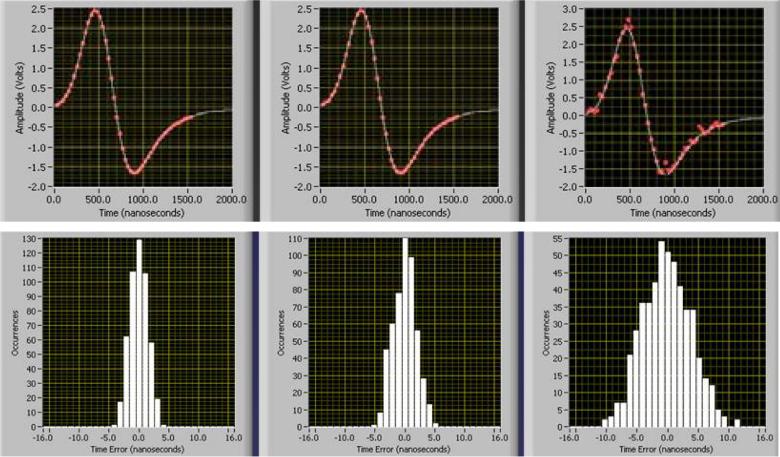
A simulation study of ML estimation of time of arrival in a single-element (nonimaging) scintillation detector for PET was performed by Furenlid [14]. Two random processes were considered: a Poisson random process describing the emission of optical photons from an NaI(Tl) crystal, and a Gaussian random process describing noise in the PMT and subsequent electronics. The Poisson random process was amplified by the PMT and passed through a filter with a bipolar impulse response. The filter output was sampled at 32 nsec intervals and Gaussian noise of varying levels was added, providing the data for MLE of pulse amplitude and time of arrival.

The results of the study are shown in Fig. 8. Although the scintillation decay time was taken as 270 nsec and the sample interval was 32 nsec, timing resolution better than 4 nsec FWHM was found for realistic levels of electronic noise (left column in the figure). Increasing the level of this noise degraded the performance as shown in the center and right columns.

Fig. 8.

Results of a simulation study of ML timing estimation with varying degrees of electronic noise. Top: Sample noisy waveforms. Bottom: Histogram of the estimates of time of arrival. Left to right: Increasing levels of electronic noise

VI. Summary and Conclusions

Estimation of position, energy, timing and other parameters of a gamma-ray interaction in a detector is fundamentally a statistical problem, and the data analysis should make use of the statistics of the detector signals. Maximum-likelihood and Bayesian statistical estimators can be used if accurate models of the likelihood for parameter estimation from these signals are known.

The photoelectrons produced in the PMT photocathodes in a scintillation camera are well described by Poisson statistics, but the signals at the PMT outputs have an increased variance because of PMT gain noise. Conditional on the 3D location of the interaction, signals from different PMTs are statistically independent, but correlations may be introduced if the random depth of interaction is ignored. In semiconductor detectors, the number of hole-electron pairs produced may be sub-Poisson, but signal induction by trapped charges leads to a multivariate normal model.

In any kind of gamma-ray detector, MLE is advantageous and practical. The ML estimator is efficient (unbiased and best possible variance) if an efficient estimator exists, and it is asymptotically unbiased as the number of photoelectrons or electron-hole pairs gets large. For position estimation, that means that MLE yields low spatial distortion and optimal spatial resolution. ML estimates are also asymptotically normally distributed, with a covariance matrix equal to the inverse of the Fisher information matrix. This observation greatly simplifies the formulation of listmode likelihoods for image reconstruction.

Examples were presented showing the usefulness of MLE for 2D and 3D position and for estimation of time of arrival of a gamma-ray photon. The likelihood window for rejecting scattered photons or other events not compatible with the likelihood model was also discussed and illustrated.

We have not discussed computational issues here, but many efficient hardware implementations exist [15], [34]. For example, we have recently demonstrated that 2D position estimation with a 9-PMT modular scintillation camera can be performed at a rate exceeding 10⁶ events per second on a Sony PlayStation3 gaming console.