A cross-validation procedure for general pedigrees and matched odds ratio fitness metric implemented for the multifactor dimensionality reduction pedigree disequilibrium test

Abstract

As genetic epidemiology looks beyond mapping single disease susceptibility loci, interest in detecting epistatic interactions between genes has grown. The dimensionality and comparisons required to search the epistatic space and the inference for a significant result pose challenges for testing epistatic disease models. The Multifactor Dimensionality Reduction Pedigree Disequilibrium Test (MDR-PDT) was developed to test for multilocus models in pedigree data. In the present study we rigorously tested MDR-PDT with new cross-validation (CV) (both 5- and 10-fold) and omnibus model selection algorithms by simulating a range of heritabilities, odds ratios, minor allele frequencies, sample sizes, and numbers of interacting loci. Power was evaluated using 100, 500, and 1000 families, with minor allele frequencies 0.2 and 0.4 and broad-sense heritabilities of 0.005, 0.01, 0.03, 0.05, and 0.1 for 2 and 3-locus purely epistatic penetrance models. We also compared the prediction error measure of effect with a predicted matched odds ratio for final model selection and testing. We report that the CV procedure is valid with the permutation test, MDR-PDT performs similarly with 5 and 10- fold CV, and that the matched odds ratio is more powerful than prediction error as the fitness metric for MDR-PDT.

INTRODUCTION

From a methods development perspective, the difficulties encountered when searching for replicable statistical epistasis in human populations are essentially three-fold. The first difficulty encountered is multiple comparisons, due to the extremely large space that must be searched to exhaustively catalog all possible interactions for a set of variables. Commensurate with these large searches is the problem of over-fitting a model to a particular sample, which does not generalize well in other samples from the same population [Chatfield 1995]. The third difficulty is the curse of dimensionality [Bellman 1961], and essentially refers to the loss of sampling precision due to excessive data subdivision.

Over-fitting is a major concern where large searches have been performed in limited data to find a best model [Feng et al., 2004]. This issue is usually managed either by an internal validation method, such as bootstrapping, splitting samples, or cross-validation, or an external method, such as collecting an independent sample [Coffey et al., 2004a]. While the gold standard for model validation is independent sampling, internal methods can also provide some protection against over-fitting. These methods are relatively efficient and should be employed when samples are difficult or expensive to collect [Hastie et al., 2001].

The Multifactor Dimensionality Reduction – Pedigree Disequilibrium Test (MDR-PDT)[Martin et al., 2006] is an approach that uses a modified pedigree disequilibrium test (PDT) statistic [Martin et al., 2003] within the multifactor dimensionality reduction (MDR) algorithm [Ritchie et al., 2001]. The MDR-PDT was designed to perform exhaustive searches for epistasis in pedigree data. The initial debut of MDR-PDT did not feature cross validation (CV) or a means to perform a search or hypothesis test from among several orders of model with different numbers of loci, two features of the standard MDR algorithm. MDR uses CV to perform omnibus searches for multiple orders of SNP models, where order refers to the number of SNPs in a given model, and also uses CV in permutation testing to conduct a valid hypothesis test on a single best model from among all orders considered. Currently, MDR-PDT is restricted to searches and tests within a single order of model, and so several tests must be performed to evaluate multiple orders of models (e.g. 2-locus, 3-locus, etc.) sacrificing statistical efficiency for multiple testing, and leading to confusion when models share several SNPs.

Cross validation finds consistent signals in the data, protects against over-fitting, and helps select a single best model from among orders of model [Coffey et al., 2004b]. With this extension, MDR and MDR-PDT use K-fold cross-validation, in which the data are split into K approximately equal sized subsamples. One of the subsamples is used for testing the model from the pooled K-1 subsamples, which is the training set. This provides an estimate of how well a model should predict outcomes in unseen samples. The process is repeated K times, using each subsample as the testing set. The estimates of prediction can be averaged across test sets to produce a single estimate, and each observation is used one time for model testing.

This procedure has been shown to be effective in simulation studies at multiple levels of CV for MDR [Motsinger et al., 2006]. Here we present an algorithm to perform CV for MDR-PDT in family data and select a best model from among models of various numbers of loci. We also present an improved fitness metric for comparing final models, the matched odds ratio. This measure is an epidemiological statistic for estimating effect sizes from matched data [Mantel et al., 1959].

METHODS

The MDR-PDT is a within-family measure of association between genotype and disease. As described previously [Martin et al., 2006], the PDT statistic [Martin et al., 2003] functions within the framework of the MDR algorithm [Ritchie et al., 2001]. All possible discordant sib pairs (DSPs) and genotypes transmitted to affected offspring and untransmitted (T/UT pairs) are taken for all sibships and pooled. For an extended sibship with several affected and unaffected offspring, several DSPs and T/UT pairs would be available. These pairs contribute to the statistic only if at least one parent of a T/UT pair is heterozygous, or if DSP members have different genotypes. This determines which genotypes are high and low risk by comparing the genoPDT statistic to a threshold of 0, where positive statistics indicate evidence for association at that genotype. The MDR-PDT statistic is then calculated for the pooled high-risk genotypes for each set of loci. The models are ordered and evaluated by the MDR-PDT statistic. A permutation test is applied to estimate the significance of the result, the significance of which is inherently adjusted for the size of the search performed.

A notable difference between MDR and MDR-PDT is the ability of MDR to choose a single best model when several orders of model, for instance 2-locus and 3-locus, have been considered. In practice this is a very important capability since it allows much larger searches to be performed under a single hypothesis test, thus removing the need for multiple testing corrections for tests of each order of model. This capability of MDR is based on the cross-validation (CV) procedure.

Cross-Validation Procedure

To implement CV in MDR-PDT, a method to split the data evenly must be developed. MDR is typically used to analyze case-control data, with each individual representing an independent observation and proportion of the data available. In MDR, the data are binned into equal-size bins prior to analysis based on counts of cases and controls, with no regard for missing data, so some bins may be unequal splits for some loci. For MDR-PDT the data may be from independent pedigrees of various structures and sizes, each contributing different amounts of information to the dataset. The individual units of information used by MDR-PDT are transmissions from informative parental matings to DSPs and T/UT pairs. Quantification of the number of observations available to PDT from each family is necessary to evenly bin the pedigree data and perform CV as in MDR.

Consider a dataset consisting of pedigrees containing extended sibships of arbitrary size. Let x_ij be the number of possible DSPs and T/UT pairs from a pedigree consisting of sibships sharing both parents with complete genotypes, where i indexes sibships i = (1,2, …, n) in a pedigree j, j = (1,2, …, m). The variable s_i will be calculated for a sibship within a pedigree sharing genotyped parents by ((#affected sibs × #unaffected sibs) + #affected sibs). Without genotyped parents, s_i is (#affected sibs × #unaffected sibs). Let x_j = Σ_is_i for full sibships within the jth pedigree. This gives the maximum information available to the statistic for that pedigree.

To perform CV, randomly split the data by randomly putting intact families into k bins, with the value of k specified by the user. Let X_b = Σ_jx_j, b = (1,2, …, k), over the j pedigrees in a bin. Set a variance threshold V_x for the variance V of X_b over bins, where the variance will not exceed V_x. Compare V_x to V. If V_x < V, reject the split and repeat the procedure up to 30 times. Continue until V_x ≥ V. If no split provides a satisfactory binning of the data, relax V_x or change the number of bins.

Model Selection Statistic

Once the data are split into equal parts, an extension allowing best model selection for MDR-PDT is possible. Each CV interval is used as a test set, as in MDR, to develop a measure of how well a model will predict disease status in independent samples. Across the k folds of the data, evidence accumulates to support a model if it is the best model from several training sets. This provides a measure of cross-validation consistency (CVC) for each best model found in the training sets, which indicates whether a few outliers might be responsible for a signal. Unlike MDR, the MDR-PDT statistic for the best model at a given level is not comparable across orders of models. As a result, this statistic cannot be used to determine which level of model produces the strongest signal. To overcome this challenge in selecting the best overall model, we evaluated the sensitivity and power of two fitness metrics, prediction error (PE) and the predicted matched odds ratio (MOR). The prediction error is defined as the average classification error from test sets during the CV procedure. The matched odds ratio is calculated by pooling the DSPs or T/UT pairs from test set pedigrees and plotting them in a 2×2 table relating the high/low risk variable to status. The ratio of DSPs and T/UT pairs that are correctly classified to those that are incorrectly classified is a matched odds ratio [Mantel et al., 1959]. The average predicted MOR is calculated using DSPs and T/UT pairs from test sets across CV intervals.

The modified MDR-PDT omnibus procedure for evaluating multiple orders of multilocus models with a single test follows and is illustrated in Supplementary Figure 1:

1. Data are split into k approximately equal parts

2. All possible DSPs and T/UT pairs are generated within each sibship (affected times unaffected) and pooled within k-1/k of the data. This is a training set.

3. Each genotype is determined to be high or low risk by comparing the genoPDT statistic [Martin et al., 2003] from the pooled DSPs and T/UT pairs to a threshold τ, such as τ = 0, which indicates positive or negative association with affected status.

4. Statistics for high-risk genotypes are calculated using the MDR-PDT statistic [Martin et al., 2006].

5. The procedure repeats for every combination of loci within the order range specified, calculating an MDR-PDT statistic for each, choosing the largest MDR-PDT statistic from each order as the best model at that level.

6. MOR or PE is calculated from the testing set for the best model of each order using the high-low risk levels established during training.

7. Steps 1–6 are repeated in the other splits of the data, so that each CV interval is used as a test set. Where the same model is observed in multiple training sets, a measure of cross-validation consistency (CVC) is observed. To select the best from among all models found in training, CVC is considered first, and if necessary the average PE or MOR from test sets can serve as a tiebreaker.

A permutation test is performed using at least 1000 permutations to estimate the distribution of the null hypothesis of no association. The result from step 7 is compared to this distribution for significance assessment.

Data Simulations

GenomeSIMLA [Edwards et al., 2008a] software has been developed by merging the software packages of genomeSIM [Dudek et al., 2006] and SIMLA [Bass et al., 2004; Schmidt et al., 2005] to simulate pedigree data with purely epistatic penetrance. To estimate the Type I error rate for MDR-PDT with CV following an MDR-PDT search, each of the 1000 null datasets with 500 DSP families each were permuted 100 times to determine whether the best model from the original null dataset exceeded the 1^st or 5^th largest value from the 100 permutations, corresponding to an alpha of 0.01 or 0.05. One-hundred permutations were used due to processing time constraints. Where a null dataset yielded a statistic that equaled or exceeded the 1^st or 5^th largest permutation, a type I error occurred and was scored. Type I error was estimated in this way for 2-locus models with 5 and 10-fold CV and omnibus searches for 2 and 3-locus models using either the PE or MOR fitness metrics with either 5 or 10-fold CV.

Purely epistatic models with marginal relative risks < 1.001 were simulated with a genetic algorithm, modified from [Moore et al., 2004], for 2 and 3 loci, minor allele frequency (MAF) of 0.2 or 0.4, and broad-sense heritability of 0.005, 0.01 0.03, 0.05 or 0.1 There were a total of 20 genetic models, each of which were simulated as 100 20-locus datasets with independent model loci and 100, 500, and 1000 pedigrees (Supplementary Table 2). These models were evaluated for the sensitivity of MDR-PDT to detect the correct model loci with and without permutation testing and with and without the CV algorithm and subsequent omnibus model selection. For experiments with permutation testing, only models with broad-sense heritability of 0.03 or larger were used.

All loci in the simulations were independent to provide conservative estimates of power due to increased data noise. Due to the larger number of effectively independent variables (M_eff) without LD it is expected that the critical values from the permutation test would be larger than if there were correlations among variables in the data. This is because the search space is M_eff choose 2 instead of #SNPs choose 2, where M_eff < #SNPs with LD, and M_eff = #SNPs without LD. This is analogous to the principles underlying the multiple testing correction method SNPSpD [Nyholt 2004].

RESULTS

Type I Error

Estimates of the type I error rate for the MDR-PDT with CV after a 2-locus search using the T-statistic was 0.011 and 0.052 when set to an alpha rate of 0.01 and 0.05, respectively for 5-fold cross validation (Table 1). The error rates for PE were 0.012 and 0.051, and the error rates for MOR were 0.012 and 0.054 for 5-fold CV. The error rates for a 2-locus search with 10-fold CV were 0.013 and 0.052. For an omnibus search investigating 2 and 3-locus models using the PE fitness metric with 10-fold CV, the error rates were 0.012 and 0.049. For an omnibus search for 2 and 3-locus models with 10-fold CV using the MOR fitness metric, the error rates were 0.010 and 0.053.

Table 1.

Type I error rates for MDR-PDT with CV

	CV5			CV10
Alpha	2-locus	PE	MOR	2-locus	PE	MOR
0.01	0.011	0.012	0.012	0.013	0.012	0.010
0.05	0.052	0.051	0.054	0.052	0.049	0.053

Sensitivity and Power

The raw sensitivity without permutation testing for the N-locus (e.g. only 2-locus or only 3-locus) search method was compared to the omnibus (e.g. 2 and 3-locus) strategy employing CV. These results show that for a variety of models the CV procedure and omnibus model selection criteria function well (Supplementary Figures 2a–e). The models are epistatic with very subtle main effects, with marginal relative risks less than 1.001. The sensitivity of five and ten-fold CV is very similar across all the simulated scenarios. Also, the sensitivity of the PE and MOR metrics were very similar. Compared to the n-locus search, where only interactions of the order present in the simulated model were sought, the N-locus with CV performed almost as well as or better than N-locus searches without CV. The omnibus search, where two and three-locus models were examined, tended to lose some sensitivity; however, this can be explained by the larger number of comparisons performed for those searches.

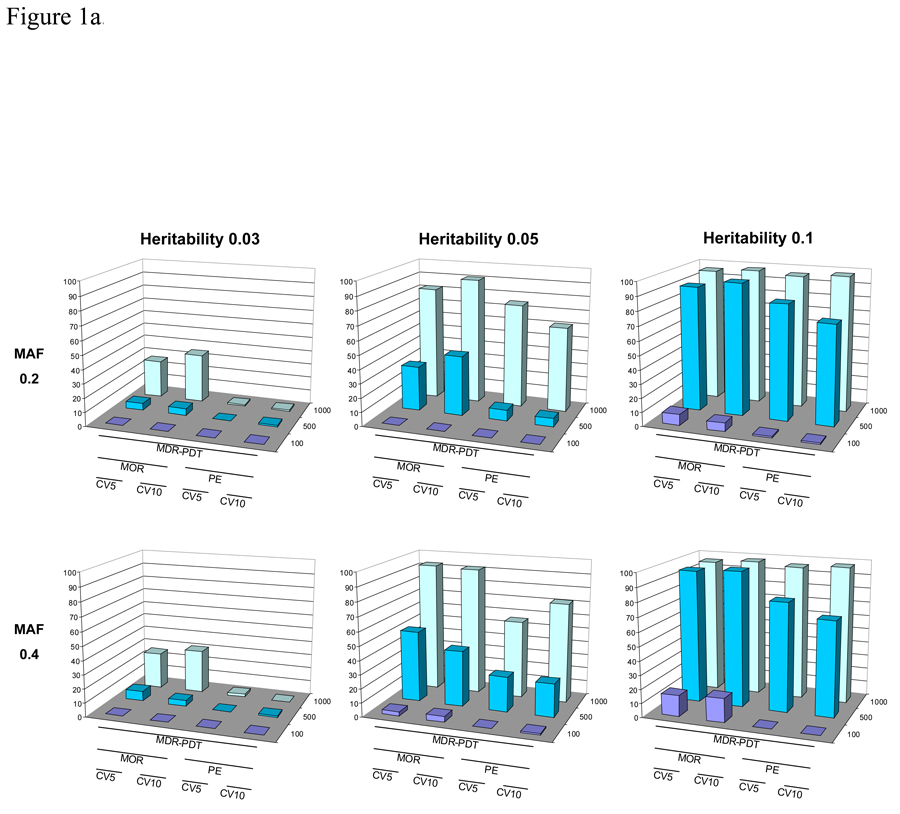
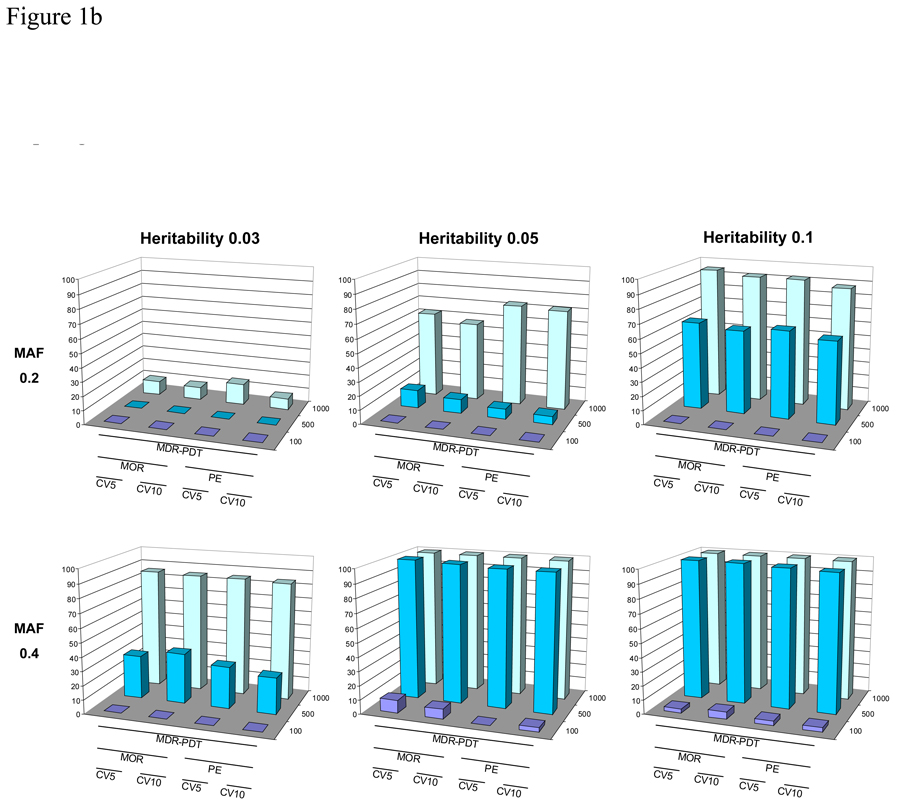
The power after permutation testing for MDR-PDT with 5 and 10-fold CV, with the PE and MOR fitness metrics, for 100, 500, and 1000 discordant sib-pair families is presented in Figures 1a and 1b. In these results, the MOR metric consistently provided more power to reject the null hypothesis for the correct 2-locus epistatic model. For 3-locus models, the power for MOR vs. PE was very similar. There was not much variability in power at 5 versus 10-fold CV in these simulations. We also observed that MDR-PDT with CV was sensitive to broad-sense heritability and allele frequency, which is consistent with previous work in MDR [Bush et al., 2008; Motsinger et al., 2006; Ritchie et al., 2003; Velez et al., 2008].

Figure 1.

Figure 1a. The power of MDR-PDT to reject the null hypothesis after permutation testing with five and 10-fold CV, with either PE or MOR as the fitness metric for six 2-locus models with allele frequency 0.2 or 0.4 and broad-sense heritability of 0.03, 0.05, and 0.1. Power is on the Y-axis, the type of analysis is labeled on the X-axis, and the number of pedigrees is on the Z-axis.

Figure 1b. The power of MDR-PDT to reject the null hypothesis after permutation testing with five and 10-fold CV, with either PE or MOR as the fitness metric for six 3-locus models with allele frequency 0.2 or 0.4 and broad-sense heritability of 0.03, 0.05, and 0.1. Power is on the Y-axis, the type of analysis is labeled on the X-axis, and the number of pedigrees is on the Z-axis.

DISCUSSION

We developed a new algorithm for splitting pedigree data into CV intervals, and a new way to select best models from among several orders of model. This approach is philosophically identical to the original MDR algorithm, and further develops the MDR-PDT for use in current searches for epistasis. This extension provides some protection against over-fitting, since higher-order models would not be penalized under the previous algorithm, and also decreases the number of hypothesis tests for a search. With this extension, MDR and MDR-PDT results can be compared between data sets without the uncertainty of which significant model from MDR-PDT best captured the relationship between the outcome and genotypes. Previous applications of MDR-PDT to real data had resulted in multiple significant models driven by a strong main effect, such as APOE in Alzheimer’s disease [Edwards et al., 2008b; Martin et al., 2006]. There was no means of determining which model might represent the best evidence of epistasis, and so interpretation of results was difficult. Here we provide a means to select a single best model for further evaluation and hypothesis testing.

The results of this study are consistent with the previous study on reduction of cross-validation intervals [Motsinger et al., 2006]. In that study, it was demonstrated that reducing cross-validation intervals from 10 to 5 did not have a strong effect on the ability of MDR to find the loci from simulated multilocus models. Here, we observe similar behavior for the MDR-PDT when varying the number of cross-validation intervals. However, the time to completion for MDR-PDT with 5-fold CV is approximately half that of 10-fold CV.

The MOR statistic outperformed the PE measure of model effect for 2-locus models after permutation testing. This is possibly due to the wider range of possible values for MOR, since PE is bounded at 0 and 1, similar models might have very similar PE values. Also, as an epidemiological measure of effect size, MOR is likely a more relevant way to compare models. Superior performance for alternate model fitness functions has been observed for MDR [Bush et al., 2008], and here we provide a superior measure than PE for MDR-PDT permutation testing. More fitness functions will be evaluated in future work.

These developments make MDR-PDT a more useful and ultimately a more powerful tool for detecting interactions in pedigree data. Under permutation testing, the threshold for significance for the omnibus test would be α, and the threshold for the several N-locus tests would be α/j, where j is the number of n-locus searches performed. For instance, for an omnibus search of all 2, 3, and 4-locus models the threshold for significance might be set to 0.05, but for the 3 N-locus searches, the threshold would be set to 0.05/3. This algorithm allows a single hypothesis test to be performed for a range of model sizes, facilitating interpretation and reducing tests. Additionally, the CV procedure provides some protection from over-fitting, which was a potential problem for MDR-PDT without CV. Here we show with our power results that MDR-PDT will find the correct model and reject the null if the sample size and effect size are sufficient. Previous versions of MDR-PDT suffered from multiple significant models of various numbers of loci from an analysis, some of which might be nested within larger significant models, and driving significance. These extensions remedy those problems and facilitate more meaningful analysis of pedigree data for interactions.