Computational exploration of the network of sequence flow between protein structures

Abstract

We investigate small sequence adjustments (of one or a few amino acids) that induce large conformational transitions between distinct and stable folds of proteins. Such transitions are intriguing from evolutionary and protein-design perspectives. They make it possible to search for ancient protein structures or to design protein switches that flip between folds and functions. A network of sequence flow between protein folds is computed for representative structures of the Protein Data Bank. The computed network is dense, on the average each structure is connected to tens of other folds. Proteins with a higher-than-expected number of neighboring folds are more likely to be enzymes and alpha/beta fold. The large number of connections between folds may reflect the need of enzymes to adjust their structures for alternative substrates. The network of the Cro family is discussed and we speculate that capacity is an important factor (but not the only one) that determines protein evolution. The experimentally observed flip from all alpha to alpha+beta fold is examined by the network tools. A kinetic model for the transition of sequences between the folds (with only protein stability in mind) is proposed.

Introduction

The most accurate approach to model protein structures is homology ¹. In homology we seek an evolutionary related protein (template) for a target sequence with an unknown fold. The template has an experimentally determined structure. Based on the three-dimensional shape of the template, a model is built for the target sequence. The modeling is frequently based on the assumption that if the sequences of the template and the target are similar then they share the same fold. Experimentally, however, a few exceptions are known ^2–5. Foldable sequences can be found in which a minor modification in the sequence results in a dramatic change in the three-dimensional structures of the proteins. An intriguing example ⁵ compares structures of two sequences with 88 percent sequence identity; one sequence folds to a three-helix bundle and another to an alpha+beta protein. A second, and more recent example⁴, is that of biological sequences from the Cro family with 40% sequence identity. In the biologically related sequences an alpha helix is converted to a beta sheet. Another famous and related example is of prions⁶ in which mutations change alpha helical segments into beta sheets causing aggregation.

Empirically the number of exceptions is much smaller than the number of sequences that belong to the same fold, raising the concern that they are not significant. However, even rare transitions can be frequent on the evolutionary time scale. We illustrate in this paper (based on detailed calculations and a kinetic graph-based model) that large changes in the population of protein folds can be found if the transient sequences are taken into account. The existence of sequences at the interface between folds poses a number of intriguing questions on the applied side (of protein design) and on the evolutionary side (the origin of fold space as we see it today).

From the perspective of protein design an intriguing new possibility is the exploitation of transitional sequences. If one or a few amino acid changes can induce dramatic structural flips ⁵, it is plausible that an environmental change will be able to create a similar effect. This observation raises the possibility of creating a protein switch between two distinct folds (that may be different in their functions and their structures) responding to environmental changes. This type of tertiary transitions is different from quaternary changes common in biochemical allostery in which packing of tertiary subunits is adjusted.

From the perspective of evolutionary processes, these transient sequences may have played an important role in increasing the diversity of protein folds, following the pioneering ideas of Maynard on pathways in sequence space⁷. In evolution, one may adopt two pictures of the relationship between sequences and folds. The first is that protein folds are isolated islands in sequence space. A sequence that folds to a particular structure either remains in that particular conformation upon point mutation or loses its stability, and unfolds. The alternative possibility that we examine in the present manuscript is that folds are not exactly isolated islands, but only approximately so. There are some small “channels” in sequence space that allow flips between structures. These flips make it possible to induce dramatic modifications to a protein fold with a series of mutations in which all sequences fold into unique structures.

Considerable computational work was done on protein design in which the overall fold is fixed and sequences that adopt this structure are optimized and (or) enumerated. Shakhnovich has done pioneering work on estimating the number of sequences that fold into a particular structure⁸. Others have made important contributions to the theory and to numerical simulations of sequence design^9–14. A biologically interesting application of capacity was noted by reference ¹⁵. In their study they correlate the rate of protein mutations with an approximate measure of capacity. Protein folds with higher capacity evolve faster. Here we compute the capacity directly, providing a more straightforward measure for biological applications. Ultimately, the goal should be the design of atomically detailed models that can be tested in the laboratory; a few impressive successes have been recorded^16,17. While we also consider the sequence capacity of folds the present study is different by considering the possibility of fold switches and sequence flow between folds globally. Pathways in sequence space that connect folds upon point mutations are elusive and are significantly less probable than observing a sequence in a particular structure. Here we explore computationally a sequence space and the fold space of the complete Protein Data Bank (PDB¹⁸).

We compute a network of sequence flow with the constraint of a single chain in aqueous solution. We use coarse-grained energy functions that represent an amino acid by a single point. Given the scope of our exploration of sequence and fold space (about 1,000 folds and at least 10 million sequences for each of the folds), this coarse grained picture is a reasonable place to start. The present study is an extension and further validation of the concept of the network presented in reference ¹⁹. Perhaps the most striking result of our study as discussed below is the discovery of a dense network of sequence flow between protein folds.

Considerable work has been done recently on linking evolutionary processes with protein structure (in particular with sequence capacity^15,20,21) and with models of population genetics and evolution. While of considerable insight and interest, certain assumptions are made and it is desirable to test the hypotheses by experiments or simulations. For example, the transition of sequences between folds that were discussed above are not considered.

In addition to the transient sequences, the present paper re-visits the sequence capacity of a fold– the number of sequences that fold into a particular structure. As we illustrate for the Cro family, it is expected that protein folds with a larger capacity will be more stable for mutations and will be better attractors for sequences from other folds. That is, it is more likely that sequences of other folds will end up in a structure with higher sequence capacity.

We are using accurate and efficient sampling procedures and three well-tested energy models to calculate sequence capacities that are discussed at lengths later in the manuscript. Nevertheless, the computational costs are significant and are making it difficult for us (for example) to sample transient sequences efficiently. While we presently explore computational statistics methods to sample rare sequences that flip between protein structures, this manuscript focuses on more straightforward uniform sampling. Estimating the capacity and the existence of network edges for one node in the set takes between 14 and 45 CPU hours on a single Intel core of 2.33 GHz. The simulations of the complete network use about 1,000 cores for a period of about a week.

The calculations are conducted for a representative set of folds from the PDB. The numerical results can be used to examine analytical models of the capacity. For example, the calculations illustrate that the computed capacity is weakly correlated with the contact density -- CD (the number of contacts between amino acids of a fold divided by the protein length). The contact density was proposed as a measure of sequence capacity in other studies^15,20,22. The search for a simple global descriptor of capacity consistent with direct simulations on experimentally determined protein structures is therefore still open. Of course the simulations provide numerical estimates of the capacity and the transient sequences that can be used “as is” in evolutionary models. Indeed, in the present manuscript we use the raw flow data to propose a kinetic model of sequence evolution based on fold stability.

Yet another (technical) reason why the network of sequence flow is of interest emerges from computational modeling of protein structures. For protein design and for zero-order evolutionary models it is useful to consider protein stability. Computationally, protein stability is measured by energy or free energy values, measures that in our design are not perfect. It is therefore useful to consider more than the lowest energy for a target sequence. Fold candidates that are connected to the prime structure with a few mutations may reflect uncertainties in the energy and suggest alternatives to a target fold in a protein design study.

Finally, and for convenience, we list common abbreviations used in this manuscript: CD (contact density), IE (incoming edges), OE (outgoing edges), MP (Mathematical Programming), SP (Statistical Potentials), PDB (Protein Data Bank)

Definitions of network parameters

The components of the computational model are described below. First we consider the subset of structures from PDB¹⁸ that is used in the calculations. Second, the potential energies to score the sampled sequences in the different folds are discussed, and finally the explicit calculation of the network parameters is explained. We start however with the following network descriptors, which are defined below: N_k(E_0k), C_k(E_0k), f_k (E_0k), r_kj (E_0k)

The energy of the native sequence of fold k is E_0k (native sequence and fold are input and are determined experimentally; they are extracted from the PDB). The energy, E, is a function of the sequence, S_k, and the fold X_k -- E ≡ E (S_k, X_k) The number of sequences of fold k that have energy lower than E is denoted by N_k(E). The fraction of sequences that are rejected during sampling of fold k since they are above a threshold energy of E₀ is Δ_k(E₀). It is also given by 1 − N_k(E₀)/20^L where L is the protein length. The fraction of sequences that have energy lower than E in fold k and do not have better (lower) energy in other folds is f_k(E). The function f_k(E) is also called the retention function and is a measure of how well a structure keeps its sequences against the competition of other folds. The fraction of sequences that are originated in fold k (see section Calculations of the network(s)) with energy below E that have their lowest energy in another fold j is r_jk (E). These functions form the edges in the network and create a directed and weighted graph. The edge function r_jk(E) describes a flow of sequences from node k to node j. One of the transitions described by r_jk(E) is to the unfolded state. The total number of sequences that remain in fold k, taking into account the competition of other folds, is C_k(E_k) = f_k (E_k)N_k (E_k) Another useful relation is $1-f_k(E)={\displaystyle \sum _j}{r}_{jk}(E)$. Finally we also define the function $\omega =\frac{1}{L}log\left[\frac{N(E)}{{20}^L}\right]$ and $\theta =\frac{1}{L}log\left[\frac{C(E)}{{20}^L}\right]$ in an attempt to understand length-independent features of the capacity.

Dataset

The folds that make the nodes of the network of sequence flow are 874 protein structures. The complete list is provided in supplementary material. This is a smaller number of structures compared to what we have used in an earlier study of the network ¹⁹. However, the current set is filtered more rigorously than before and better reflects the distribution of isolated protein chains in aqueous solution. Our list started with the complete PDB (37,138 structures) as of 06/13/2006 and was filtered to (i) remove redundancies in sequences and structures, (ii) take out membrane proteins, (iii) exclude folds with native sequences that are not the most stable in their native structures (when threaded through all the folds in the database), and to (iv) eliminate proteins that are not globular. Proteins that deviate significantly from a globular shape are likely to participate in other interactions (e.g. forming complexes) and are not appropriate for our study that focuses on stability of isolated chains. We also removed membrane proteins since the coarse-grained energy functions that we use cannot adequately describe the stability of proteins in both membranes and aqueous solutions. Another subset that was removed is of protein folds with native sequences that do not have their lowest energy in their own folds.

The filtering of the initial list was done as follows. First, we consider only pairs of sequences with lower than 70% sequence identity. This set is available from the PDB http://www.pdb.org and was simply downloaded. It contains 12,689 structures. Second, structural similarities between all the pairs of the remaining proteins are examined with the TM score. The TM program was developed by Zhang and Skolnick²³. It provides a local structural alignment between two protein chains and a measure of similarity -- TM score. The TM score varies from 0 (absolutely no similarity) to 1 (the two structures are identical). To avoid structural degeneracy one structure from any pair of proteins with a TM score greater than 0.65 was removed. The choice of structure to eliminate was random.

This left us with 1849 protein folds. Of these proteins, 148 were removed because their sequence lengths were shorter than 50. Next membrane proteins were removed. We created a union of all the membrane proteins with 3-D structures annotated in both Mptopo²⁴ and PDBTM²⁵. The two databases are well maintained and up-to-date; in PDBTM all annotated membrane proteins have experimentally solved 3-D structures while in Mptopo there are additional membrane protein sequences with unknown folds. The number of proteins that were removed in this step is 31. In the next filtering step (271 proteins) we excluded proteins with some atom missing and (or) median energies (in all three energy functions) higher than their native energy. Such poor energies are typical to open non-compact structures that are likely to be involved in complexes. Another stricter compactness criterion removed non-globular proteins. We use the formula²⁶ R_g = 0.395L^⅗+ 7.257 for the expected radius of gyration for a globular protein with amino acid sequence length L. If the predicted radius of gyration deviates by more than 15 percent from the actual radius of gyration, the structure is removed from the list. The number of structures that were removed in this final step was 447. Finally we screen the proteins by the energies of their native folds and sequences. We checked that the energy of the native sequence embedded in its own native structure is lower that the energy of embedding the same sequence in any other fold of our set. We have made this comparison using the two most accurate coarse-grained energy functions in our disposal: BT and FREADY²⁷. Seventy-eight proteins did not pass that test.

To further evaluate the accuracy of the energy functions we consider the ranks of the 78 rejected proteins. The average ranks of the 78 protein sequences in their own folds are 18, 23 and 40 for BT, THOM2 and TSLE energies, so even the misses are ranked quite high. Nevertheless, the accuracy of the potentials is clearly a weakness of the present study. Despite our significant effort and experience in energy optimization and the use of three different scoring functions, we cannot exclude significant impact of the quality of the energy models on the results. The observation that misses are detected already at the level of native sequences is evidence to that effect.

We did not use the potential FREADY mentioned above in our network calculations (we only used BT, THOM2 and TSLE) since FREADY includes a hard core that makes it more difficult to model mutations with a fixed backbone. For a detailed description of the energy functions used in the present study see section Potentials.

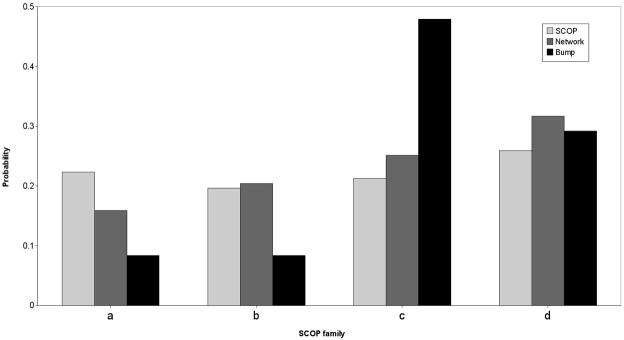
The five filtering criteria lead to a final set of 874 folds (873 for TSLE energy) that was used in the follow up calculations. Figure 1 illustrates that the distribution of folds in our data set resemble the distribution of folds in the SCOP data base²⁸ at least at the top of the hierarchy.

Figure 1.

A distribution of folds included in our study according to the coarser description available in SCOP. Four families are considered: (a) alpha proteins, (b) pure beta proteins, (c) alpha/beta proteins (d) alpha+beta proteins. The light gray bars are the distributions in the Protein Data Bank according to the SCOP classification. The darker gray bars are the selected representative folds that are the nodes in the network. The black bars is the distribution of folds selected from the “bump” of the distribution of incoming edges of the consensus network as explained in figure 8. These “bump” folds are enriched with respect to “scale-free” network. They are more likely to be of alpha+beta type and to be an enzyme. See text for more details. Note that the green bars are quite similar to the brown bars.

Alignment

The matching of sequence to structure is done without allowing for gaps in the sequence. If the sequence is shorter than the structure it attempts to adopt, then gapless threading is used. We “slide” the sequence through the structure, evaluating the energy for sequences with various steps. The sequence of length L is placed in a fold of length M starting at positions j=1,Δ+ 1,2·Δ +1,… (with a step size Δ= 40), and its energy is evaluated. The number of steps is then 1+(M−Δ)/L if M is longer than L and 1+(L−Δ)/M otherwise (the fraction is rounded down). If the sequence is longer than the structure then gapless threading is applied as before and the excess sequence is removed. There is no explicit penalty for amino acid deletion due to a too-short structure. However, implicit penalty takes place. Contacts reduce the mean threading energies and a smaller number of amino acids and contacts mean higher and worse energies on the average.

The gapless threading that we use is clearly a compromise and ideally a more extensive model that includes deletions and insertions in the middle of the sequence and structure is desired. However these models are considerably more complex and require the addition and evaluation of new parameters. We prefer to keep our model simple to begin with. Moreover, an efficient algorithm to align sequences into structure with pair potentials (see next paragraph) is not known. Finally, our computed network (as discussed below) is dense with many connections between different folds. This is perhaps the most striking observation of our study. A better alignment model is likely to increase even further the flow of sequences between the folds since the alignment will improve the energy of a sequence match into a non-native structure. Hence the refinement of the calculations along these lines is unlikely to change the most striking observation of the present study.

Potentials

The energy is a function E(S_j, X_k) that scores a match of a sequence S_j to a structure X_k. In the present calculations the structures are fixed (they are selected from the PDB as described in the Dataset section). The fitness of a sequence to a structure is measured by a “raw” energy score and also with a measure of the significance of the “raw” score.

It is possible that for a particular sequence a large number of structures provide the same or very similar energies. In this case it is not meaningful to pick a “winner” fold since many structures may share this sequence with significant probability. Having the same sequence shared by many folds suggests that there is no unique structure that this sequence adopts with high probability and that this protein folds poorly. We therefore add the condition of a stability gap. We require that the energy of the most stable fold is better than the average energy of that sequence by at least n times the standard deviation δ. The average and the standard deviation are computed from the energy distribution of the sequence under consideration in alternative folds. If the stability condition is not satisfied, the protein is considered unfolded and is not made part of the sequence pool of the prime or of the competing folds. Samples of these unfolded sequences are given in the supplementary material.

In our set some of the energies are very high which pushes the average to high values, making the stability condition too weak. We therefore consider only the tail of the distribution and compute the mean energy and the variance of the folds with the lowest energies. Assignment of the sequence j to a structure k (with the minimal energy) is accepted if E(S_j, X_k) ≤ E_mean+ n·δ where n is an integer, otherwise the sequence is rejected. The mean values and the standard deviations were determined from the 200 structures that are lowest in energy. If all structures are used then conformations with exceptionally high energies dominate the averages and make this test less useful. In the present manuscript we examined the cases n= 0 and n= 3. Stability criteria, similar in spirit, were discussed extensively in the literature^29,30.

To enhance efficiency we pre-compute geometrical factors. The structures are kept as a list of contacts. A contact between two amino acids is assumed when the distance between the geometric centers of their side chains is equal or less than 6.5Å. We do not change the contact data upon amino acid mutations, a common practice in residue-based assessments of protein templates³¹. We prepare lookup tables that list all possible energy values for each of the contacts. As a result, a modification of an amino acid (a mutation) requires a table access but no geometrical calculations. We did not use more elaborate distance dependent potentials since they are too sensitive for our purpose.

We generate and examine between ten to one hundred million (10⁷–10⁸) sequences for a single protein fold. Using state-of-the-art algorithms^32,33, these calculations allow us to obtain statistically converged results for a wide range of network parameters. However, it is not possible to statistically converge the network parameters using atomically detailed models or other refined energy functions. The requirements to build side chains for every mutation (with or without explicit solvent), and to optimize the backbone structure to refine side chain packing are too costly to perform in the present investigation. To increase confidence in the results that are derived using reduced models of proteins we repeat the calculation with different residue-based energies and seek properties that are consistent in the networks generated with different potentials. We tried the distance-dependent potential FREADY²⁷. However, since we are fixing in the network calculations the backbone of the protein the distance-dependent energy varies widely upon mutations. In most cases mild relaxation of the backbone is sufficient to avoid the energy fluctuations and the overall fold remains the same. However, backbone relaxations are too expensive to compute in the present study. Therefore only coarser energy functions (residue based, square well potentials) are found suitable.

We used three coarse-grained potentials that differ in their functional forms and in the way in which they were derived. We call these energies THOM2³⁴, BT³⁵ and TSLE³⁶. The THOM2 energy, E_THOM2 was learned with the mathematical programming approach (MP) and is based on a single body interaction term. It is defined as a sum over contact energies u_in. It is $E_{\mathit{THOM}2}={\displaystyle \sum _i}{\displaystyle \sum _{n=1,\dots ,N}}{u}_{in}({\alpha }_i,m_n)H(r_{in}-r_{\mathit{cut}})$. The summation over the index i is over the structural sites of the fold (also called the prime structural sites, see figure 2). The second summation (n) is over the contacts of amino acid type αof site i. The single contact energy u_in depends on the type of the amino acid αof site i. It also depends on the number of neighbors m of the n–th site in contact with site i. Computationally u_in is a look up table. The function H(x) is a heavy side function. It is zero if x>0 and one if x≤0. Since in our calculation the structures are fixed, the heavy side functions that we need are pre-prepared before the simulations start for all proteins in the set and are used ever after.

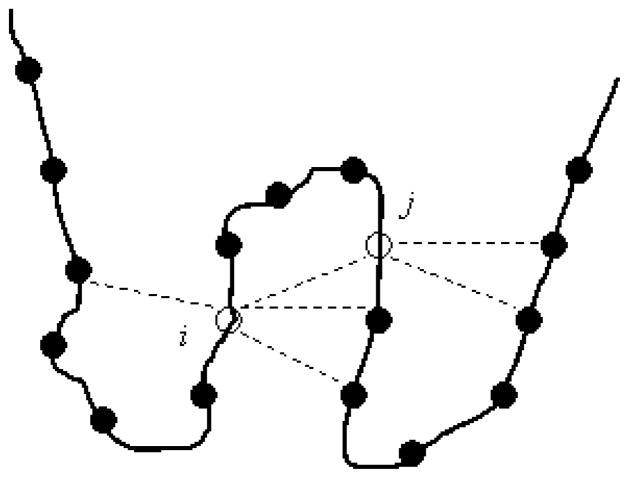
Figure 2.

An illustration of the definition of a contact in the THOM2 energy function. The total energy of a protein is a sum over the energies of individual contacts. A contact is defined by distance between the geometric centers of two side chains which is less than 6.4 Å. The energy of a contact (i, j) is computed according to the identity of the amino acid at the prime site (site i) and the number of neighbors to the secondary site (site j). Making the energy of a contact depend on one amino acid is helpful in application to bioinformatics (use of Dynamic Programming is possible) and in the calculations of the sequence capacity. The last calculation can be shown of polynomial complexity for the THOM2 energy (see text and reference ³³ for more details).

Hence in contrast to the popular contact potentials, which we discuss next, in THOM2 we do not determine the energy of a contact from the identity of two amino acids. THOM2 functional form uses the type of amino acid only in the prime structural sites and characterizes the other end of the contact with a structural feature of that site (number of contacts). The expectation is that sites with a large number of neighbors prefer hydrophobic residues, etc.; so the use of structural features implies certain types of amino acids.

The THOM2 energy was introduced for applications in bioinformatics because its functional form allows for efficient alignments (with dynamics programming)³⁷. It was also found to provide rigorous statistical bounds for the errors in the calculations of sequence capacities(N(E)) of individual folds³³. In brief, it was shown that the space of sequences of a single fold is well mixed (ergodic). A Markov chain in sequence space with a step of one amino acid change at a time samples the correct distribution after a polynomial number of steps in the sequence length. We do not have a similar convergence proof for other energy functions that we considered. The attractive features of THOM2 come with a cost. Empirically we demonstrated that the THOM2 energy is less accurate than the popular contact potential. The lower accuracy was illustrated by having a smaller number of correct folds recognized with the same number of potential parameters. Optimal parameters were determined with Mathematical Programming (MP)³¹.

The other two potentials that we consider are of a form that is used broadly: pairwise contact energies. They are defined as $E_{\mathit{contact}}={\displaystyle \sum _{i>j}}{u}_{ij}({\alpha }_i,{\beta }_j)H(r_{ij}-r_{\mathit{cut}})$. The energy of a contact, u_ij, depends on the identity of the two amino acids in contact. The contact potentials were introduced into practice in the pioneering work of Miyazawa and Jernigan^38,39. Miyazawa and Jernigan showed how the 210 parameters of the contact potentials could be learned from the distribution of contacts that one finds in the PDB. They introduced to the field the concept of Statistical Potentials (SP). Their statistical analysis opens the way for many applications and refinements (e.g. by Hinds and Levitt⁴⁰, Godzik and Skolnick⁴¹, Betancourt and Thirumalai³⁵ and others). In the present study we are using the potential of Betancourt and Thirumalai (BT) which is based on the original Miyazawa and Jernigan potential with an alternative reference state. We also use the potential developed by Tobi et al.³⁶ which was derived with the MP approach. MP is conceptually different from SP since it considers explicitly false matches. Use of potentials derived with MP and SP allows us to probe alternative solutions in parameter space for the same functional form. MP learning of parameters of folding potentials was introduced first by Maiorov and Crippen ⁴², was further exploited by Vendruscolo and Domany⁴³, and by Tobi et al.³⁶. One of the main differences between SP and MP is that SP learns only positive examples (correct matches) of sequences to structures. The MP approach learns the parameters from positive and false matches. In reference ³⁶ detailed analysis of potentials concluded that the different classes of learning yield similar results. Nevertheless, important differences remain as was shown in the past and is also illustrated in the present manuscript.

Calculation of the Network(s)

The network of sequence flow between protein folds is presented by a directed and weighted graph, characterized by the functions (see the beginning of section Definitions of network Parameters) N_k(E_0k), C_k(E_0k), f_k(E_0k), Δ_k(E_0k), r_jk(E_0k), ω_k (E_0k), and θ (E_0k). We estimate these functions with the help of a Markov chain in sequence space and telescoping ratios as was briefly described in reference ¹⁹ and for completeness also discussed below.

The energy ladder

The calculations are based on an algorithm to estimate the sequence capacity of a fold k without competition N(E_0k). Other functions of the network are computed with a similar algorithm to the one that was used to generate N(E_0k). The expectation is that the capacity is growing exponentially with the sequence length, L, i.e. N(E) ∞c^L where c is a constant. Since the average length of a protein is about 200 amino acids, it is not practical to estimate the capacity by exhaustive enumeration and more indirect computational methods are needed. It is convenient to write N(E₀) as a ratio of capacities that multiply a single function, N(E_ref) that we can calculate directly (which is also called below “an anchor” or the capacity of a reference energy)

$$N(E_0)=N(E_{\mathit{ref}})\frac{N(E_m)}{N(E_{\mathit{ref}})}\frac{N(E_{m-1})}{N(E_m)}\dots \frac{N(E_0)}{N(E_1)}$$

Formally, the anchor N(E_ref) can be cancelled by N(E_ref) of the first ratio. Similarly, N(E_m), which is the numerator of the first ratio, is cancelled with the denominator of the second ratio, and so on. The sequence of cancellations gives the (trivial) identity N(E₀) = N(E₀). The computational advantage of writing this expression, which is reduced to an obvious result, is that we are able to compute efficiently both components: the anchor capacity, and each of the ratios (that are also called telescoping ratios in the literature⁴⁴)

A ratio N(E_i)/N(E_i+1) can be computed efficiently provided that E_i is sufficiently close to E_i+1 so the ratio N(E_i)/N(E_i+1)is of order O(1) (in the present study it is typically not smaller than 0.08). This is why we use multiple ratios, each of the ratios is not very different from one, but their multiplications (multiplications of positive numbers smaller than one) can be different from one by a large number. To complete the calculation it is necessary to compute efficiently the absolute value of N(E) at a specific anchor energy E_ref. In reference³² we used for E_ref the lowest energy as a function of the sequence. The rationale for this choice was that at low energies the number of sequences is small and therefore countable directly. Unfortunately, even if countable, the low energy sequences are not necessarily easy to find. Determination of the lowest energy sequence can be done exactly and efficiently only for the THOM2 energy using a search through a bipartite graph, (Meyerguz Leonid, PhD thesis). However, finding optimal sequences for pairwise interaction energies is a NP complete process in terms of computational complexity. These sequences are therefore difficult to determine. For the present investigation they are not even necessary since determining the capacity at the native energy can be done with an energy ladder from above (the median or mean energies). We therefore changed E_ref in later studies from the lowest to the average and then to the median energy.

Determination of the reference energy

In reference ¹⁹ we used the average energy and in the present paper the median energy, which is a conceptually similar choice. Both the average and the median energies are relatively easy to estimate by direct sampling of random sequences. For each fold, for the purpose of determining the reference energy (or the anchor), we generate a million sequences of the correct length sampled uniformly and at random from the twenty amino acids at each site. The distribution of amino acid types in native proteins is not uniform (e.g. tryptophan is rare). It is determined by many factors such a stability, codon biases, active site residues, etc. In the present study we wish to determine the impact of stability (only) on the frequencies of amino acid types. Therefore we cannot use the empirical distribution, even if it will be more efficient to use, since we do not know the contribution that stability already made to it. The energies of the sampled sequences are averaged (to estimate the average energy). Similarly, the value of the median energy in which half of the sequence energies are above it and half are below (per definition) is estimated quite accurately from a sample of a million random sequences. The law of large numbers⁴⁵ states that uncorrelated sampling from bound distributions converges to well determined averages with error bars inversely proportional to the square root of the number of data points independent of the system dimensionality. This convergence rate is easy to verify. Since the total number of sequences is 20^L where L is the protein length, the number of sequences below the median energy is simply (1/2)20^L, i.e., N(E_median) = (1/2)20^L making it possible to “seed” the telescoping ratio.

We use the median energy as a reference or anchor for all 3 energy functions. However, to examine the impact on the results of the initial anchor energy we computed the network for the BT energy twice; once using for a reference the median energy and a second time with the average energy. The capacity of the average energy is estimated as q·20^L, where q is the fraction of sequences that are sampled uniformly from the set of 20^L possible sequences and are below the average energy. The maximum difference in capacities at the native energies computed with median or mean energies as anchors is 1.37% and is typically much smaller. The mean difference is 0.013%. The variations depend on protein length; for example a short protein (1UXC, 50 amino acids) shows a difference of 0.2% and for a long protein (1EA0, 1452 amino acids) the difference is 0.04%.

Estimating ratios of capacities

Each ratio of the type N(E_i)/N(E_i+1) E_i+1 >E_i is estimated in a separate (Markov chain) calculation. We first discuss the initiation of the Markov chain and then the sampling.

Initiation

We start a Markov chain in sequence space for a fixed fold X_k and a sequence S_0. The fold and the sequence are of the same length. The energy of the initial sequence is such that E(S₀, X_k)<E_i+1. Finding an initial sequence that satisfies the previous condition can be difficult if E_i+1 is low. Therefore the initial sequence for the calculation of one ratio N(E_i)/N(E_i+1)is picked from the Markov chain sampling of the previous step of the energy ladder N(E_i+2)/N(E_i+1) E_i+2> E_i+1 Some sequences of the previous step indeed satisfy the condition E(S₀, X_k)< E_i+1making possible the selection of a starting sequence for the next step. For the first step in the ladder (the median energy) we do not have a previous run and we need another approach to determine a starting sequence. This is easy to do from the sample that was used to estimate the median energy. The first sequence of the energy ladder is one of the half of the sequences that were found below the median energy during the initial sampling.

Sampling the Markov Chain

Let S_t≡a₁a₂ …a_N be the sequence of the protein that we thread into a structure of the same length uniformly X_k = x₁x₂,…, x_N. We select a site j and at random from the N structural sites and mutate the amino acid at site j (uniformly and at random again) to one of the other nineteen amino acids. If the energy E(S_t+1, X_k) of the new mutant sequence S_t+1is lower than the energy E_i+1 the mutation is accepted. If it is not, the sequence (step) is rejected. The Markov chain is terminated after a fixed number of accepted mutations, which is typically a million sequences at each of the steps of the energy ladder.

The fraction of number of accepted sequences from the trial moves of the Markov chain is typically a few tenths and is higher for the shorter sequences. For example, for a protein of 56 amino acids the acceptance probability was 0.80. To decide on the length of the Markov chain we check empirically the convergence of the capacity of sequences. Million sequences at the native energy are more than we need for the short proteins and appropriate for the longest proteins. The actual dependence of the convergence on the protein length is complex and we choose a fixed number of accepted moves (a million at the native energy) rather than guess the length dependence in our large-scale automated calculations. While the space of sequences is growing exponentially with the sequence length, the size of sample that is required for accurate estimate of the capacity is not. Polynomial convergence in the sequence length for THOM2 was demonstrated mathematically³³. In the same reference we also illustrated empirically efficient convergence for pairwise interaction potentials.

A concern in optimizing sequences for a fixed structure is the sampling of homo-polymers. Sampling of homo-polymers can be a problem, since knowledge-based energy functions have low energy sequences of the same hydrophobic residue (e.g. poly-cysteine). These sequences have energies much lower than the native energies³² on which we focus. However, they do not have a unique structure since many compact structures have similar (degenerate) energies. The use of the energy gap reduces their importance (homopolymers tend to have similar energies in different compact structures which makes the gap smaller between the energy of the best scoring structure and the average energy). Moreover, homopolymers are statistically insignificant in the estimate of the capacity since their number is exponentially smaller than that of hetero-sequences (permutations between sites with the same amino acid do not produce a new sequence). Hence, for network and capacity calculations, homo-polymer sampling does not pose a difficulty.

We return to the computational estimate of N_k(E_i)/N_k(E_i+1) for a fold k. Our procedure follows the ideas outlined in ⁴⁴ and is similar in spirit to umbrella sampling and calculations of free energy differences⁴⁶. Let the total length of the Markov chain in sequence space, which is bound to energies below E_i+1be l(E_i+1). Some of the sequences of the same Markov chain are below E_i and the number of times that the chain samples sequences below E_i is l(E_i). The ratio l(E_i)/l(E_i+1)is an approximation to the desired ratio of N(E_i)/N(E_i+1). The approximation is an estimator with guaranteed error bars for the energy THOM2³⁷. The sampling would be from the correct distribution (ergodic) in a polynomial number of mutation steps in the fold length. For other energy functions the errors are not known a-priori and are tested empirically by (for example) changing the length of the Markov chain or the first (seed) sequence.

The above procedure was used in our earlier studies to determine the sequence capacity without competition for fold k --N_k(E)³². It was enhanced in reference ¹⁹ for the calculation of a network, a study that is further extended here. In contrast to the capacity calculations without competition that considers one fold at a time, in the network calculation we consider all folds every step of the Markov chain. If the energy of a newly generated sequence for fold k is below the current threshold, the move is accepted and we increase N_k(E) by one. If the energy of the accepted move is the lowest compared to the energies of the same sequence embedded in all other folds of the set, then the number of sequences that remain in fold k, C_k(E)is increased by one. If the energy of another fold j is the lowest for the sequence just sampled in fold k, then the number of sequences that migrate from k to j, R_kj(E)is increased by one (r_kj(E)= R_kj(E)/N_k(E)). If the sequence and structure are not of the same length then a gapless alignment as described in section Alignment is employed. A sequence may be rejected if it does not satisfy an energy gap criterion (as discussed in the next paragraph).

Results and discussions

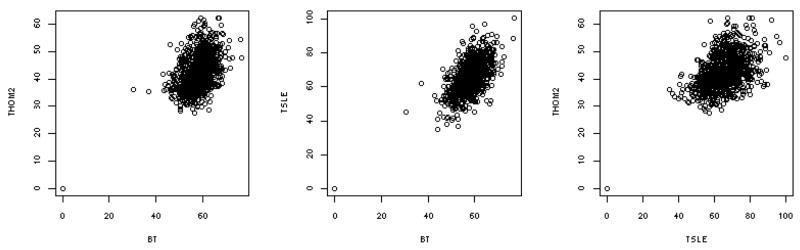
In figures 3–5 we present correlation plots of the three energy functions that we used in our study. The native energies (figure 3) are highly correlated. To obtain such high correlation the absolute value of the three native energies must depend in a similar way on protein length, composition of amino acids, number of contacts, etc. Energies that were learned on positive examples, and energies that were learned on positive and negative examples are showing remarkable similarity in ranking the correct matches with respect to each other. However the similarity of the absolute energies of the native folds is only a part of the story. The stability energy is determined from the difference of the energy of the folded state and energy(ies) of misfolded structures.

Figure 3.

Correlation plots of the three energy functions that we used in this study: THOM2³⁷, BT⁵³, and TSLE³⁶. Each of the native sequences is embedded in its own structures and its energy is computed according to the above three energies. Three panels are shown in which we compare pairs of energy function (each of the axes corresponds to one energy and a total of three comparisons are made). The left panel compares BT and THOM2, the second TSLE and THOM2 and the third TSLE and BT. Note that while the absolute energy values differ appreciably the correlation is obvious and high.

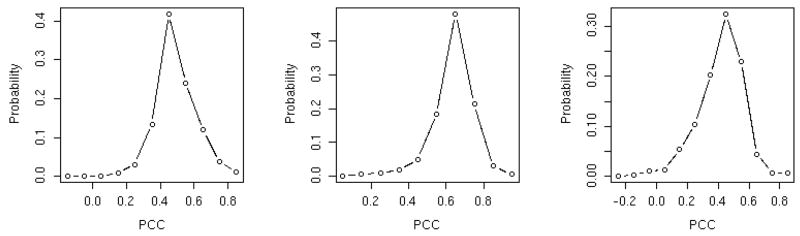
Figure 5.

A histogram of the Pearson correlation coefficients comparing energies of native sequence in non-native structures. For every incorrect match of a sequence to a protein structure (both from the PDB) we compute the energy of the match three times (for the energies THOM2, BT and TSLE) and record it. For 874 proteins we have 381,501 false matches. To simplify the presentation of the data the Pearson correlation coefficients of the energies of misfolded proteins are computed and binned. The histogram plot is a summary of the correlations. The left panel is the distribution of correlation coefficients of false matches of THOM2 and BT. The central panel compares BT and TSLE and the right panel THOM2 and TSLE. Note the relatively low level of correlation between the false matches (peaked around 0.5) compared to the very high correlations of the native energies. This implies that the energy functions are very similar in the neighborhood of the native structures but are significantly different for misfolded conformations.

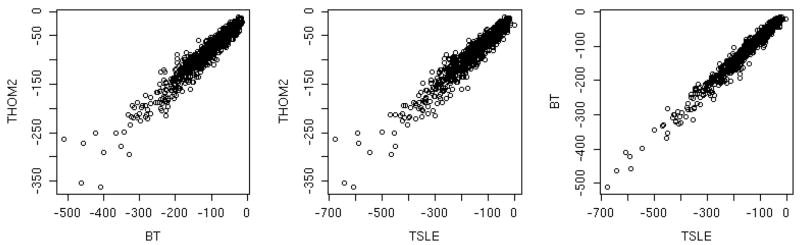
We model the energies of unfolded structures by threading a native sequence without gaps into PDB folds that are wrong for that sequence. Every native sequence has 873 false structures to try. Plotting the data for all native sequences in all false structural matches produces very crowded plots. We therefore plot the correlation between different energy scores of the false matches for only one of the sequences (1QV0) (figure 4). The correlation by inspection is significantly poorer than what we saw for the native energies and is similar to other protein sequences in our set. To have a global measure of the correlations we compute the Pearson correlation coefficient between the energies of the unfolded structures for the different energy functions. The Pearson coefficient for the energy correlation is

Figure 4.

The same as in figure 3 except that this time the graph is for non-native matches. A non native match is defined as a sequence of one protein of our set which is embedded in a structure of another (different) protein which is also in our set. Since the number of non-native matches is large (for 874 proteins we have 381,501) we show energies of the false matches to structures of only one sequence (1QV0). In the left panel we compare the BT and THOM2 energies, the panel in the center BT and TSLE and in the right panel TSLE and THOM2. The correlation is considerable poorer to what we have seen for the native matches (figure 3).

$$r_j(k,k\text{'})=\frac{1}{N-1}\sum _{i=1,i\ne j}^N\frac{(E_i^j(k)-\langle E^j(k)\rangle )(E_i^j(k\text{'})-\langle E^j(k\text{'})\rangle )}{{\sigma }_{E^j}(k)·{\sigma }_{E^j}(k\text{'})}$$

Where j is the index of a native sequence, i is an index of the fold and k and k ′ are the indices of two energy functions we compare. The brackets 〈…〉 denote average over folds and σ the corresponding standard deviation. The values of the Pearson correlation coefficients were computed for all sequences j. The coefficients were binned and their distribution is shown in figure 5. The distributions (when comparing the three energy functions) are peaked at around 0.6 for BT and TSLE, 0.5 for THOM2 and TSLE, and near 0.4 for THOM2 and BT. The similarity (which is weak) is consistent with previous results in which TSLE was more similar to BT than to THOM2. The variations for unfolded structures between the different energy functions suggest that repeats of the network calculations with the different energy functions are likely to provide new information not available with network calculations based on only one energy function.

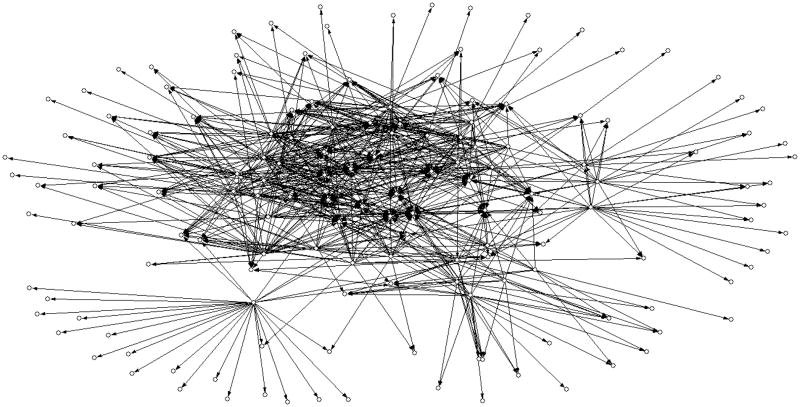
In figure 6 we show a coarse picture of the network with an energy gap of 3σthat includes only edges shared by the networks of the three energies. For clarity we kept only edges with transition probabilities (r_ij) greater than 0.008. It is clear that the network has a significant number of hubs and sinks and that the number of edges is high.

Figure 6.

A schematic drawing of the network. Only edges with at least minimal sequence flow from one fold (node) to another, and that are shared by the three potentials are shown. The minimal (out going) flow is 0.008 of the total number of sequences sampled at the native energy. Nodes without edges are not shown. The chart was created with the program Pajek⁵⁴ for analysis and display of networks.

In table 1 we provide a coarser view of the network (but more quantitative) by reporting the average number of edges per node (the total number of edges divided by the total number of nodes of the network) generated with the three energy functions. In the table an edge between nodes k and j is created if the number of sequences going out from node k to its neighbor j is larger than 0.0025 of the total number of accepted sequences in the Markov chain of fold k. The comparison is repeated with and without energy gaps and we differentiate between incoming edges (IE) and outgoing edges (OE). Nodes that do not have IEs are not included in the corresponding average. While the presence of the energy gap reduces the connectivity, the trend of the networks computed with the three energies (number of edges greatest for THOM2 and smallest for BT) remains.

Table 1.

The average number of incoming and outgoing edges in the networks computed with the three potentials THOM2, BT and TSLE. Calculations without energy gap (n=0), and with an energy gap (n=3) were conducted. See text for more detail.

	n=0		n=3
	Out	In	Out	In
THOM2	95	118	83	105
BT	64	113	61	108
TSLE	80	143	79	142

In table 2 we compare the networks and report the absolute number of edges that are shared between any pair of the three networks and by all three. It is evident (and we will see the same phenomenon using other measures) that the THOM2 energy is quite different from BT and TSLE while the last two are quite similar. Perhaps at variance with the usual intuition about connectivity between protein folds, the network is dense allowing for a large number of transitions between different folds (however, the probability of a sequence to be in an edge is much lower than remaining in the same fold). The observation that many edges are shared in networks computed with two and even three different energy functions increases confidence in the robustness of the calculations. The same shared-edge list is used to create the network view in figure 6.

Table 2.

The number of shared edges found in the networks computed with the three potentials with and without energy gap. We provide the number of shared edges between any pair of the three energies and for the intersection of edges of the three potentials

		BT	TSLE	All
n=0	THOM2	19037	24511	17728
	BT		51681
n=3	THOM2	16254	20722	15075
	BT		48655

To illustrate the tools of the network on concrete experimental observations we examine two cases of sequence flow between folds. The experimental results were reported earlier^3,5 and are based on experiments (our data is based on computations). In the first example we consider the transition of synthetic sequences from an alpha+beta fold to pure alpha fold (PDB structures 1PGA and 2FS1)⁵. There are six sequence pairs that were shown to flip between the two structures and are denoted GA30, GB30, GA77, GB77, GA88, and GB88 respectively. The statistics of this small set of sequences for network calculations is obviously limited. However, we can test the assignment of the sequences into the correct folds according to our network protocol and energy functions. For example, the correct fold of a particular sequence should have the lowest energy compared to all other folds. If we consider as accurate only the assignments for which there is a consensus between the three energy functions then the network is undecided about two pairs (GA77 and GA88, BT provides the correct assignment but THOM2 and TSLE do not). For the rest of the sequence pairs all the energies agree on the correct fold.

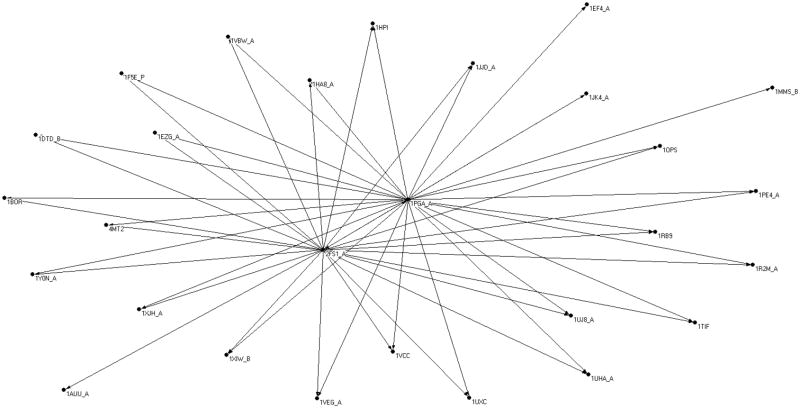
A more complete view from a computational perspective is provided in figure 7. We show the sub-network that includes the folds 1PGA and 2FS1 at the core. Structures are added to the network if they have an edge from the core, and if their length does not deviate by more than 50% of 2FS1 or 1PGA. There are 34 (labeled) structures in the set. The interesting observations of this sub-network are two fold: First, our network model performs reasonably well when compared to experimental observations. Second, the sub-network may be expanded (by 32 proteins) beyond the two folds at the core. Samples of transitional sequences are provided in supplementary material.

Figure 7.

A view of a sub-network of sequence flow with the two folds 2FS1 (alpha protein) and 1PGA (alpha+beta protein) at the core. The two folds at the core were investigated experimentally⁵ and a number of sequences were found that “flip” between the two structures following a small number of mutations. The experimental results were used to test the network calculations, and the network calculations expand the initial network to include the addition of 32 proteins with their PDB codes given in the graph. See text for more details.

The second example is of fold evolution in the Cro family. The oldest fold in the group of four structures we considered is 1RZS (PDB id)^4,47,48. It is followed by 3BD1, 2PIJ and 5CRO in sequence. To correlate the observed “evolutionary age” with the network we compute the sequence capacity (with competition) for each of these folds. Note that the last two proteins form dimers and our capacity calculations must be modified to account for this state. The space of sequences for the dimers was the same as the monomers (a mutation at one monomer “creates” an identically mutated second monomer). The energy calculation was however different, since contacts between the monomers were taken into account during the modeling of the dimers. The sequence capacities for each of the folds with competition are very similar for the three energies, and we therefore provide below only the average capacity. We sort the logarithm of their capacities (log[C(E)], which is given in the square brackets) to have 1RZS [177.69], 3BD1 [187.58], 2PIJ [336.87], 5CRO [355.55]. Hence the younger is the protein the larger is its sequence capacity. This observation suggests the intriguing speculation that proteins evolve to structures with higher sequence capacity. Hence, the speculation is that the entropy in sequence space plays a useful role in directing structural changes (in the same way that elementary physical chemistry tells us that gas flows to larger volumes). Obviously entropy is not the only factor. However when correlate the average energies of the folds (average over sequence space), with their ages we found correlations weaker than with capacities. For example the BT average energies are 1RSZ [−24.1], 3BD1 [−27.86], 2PIJ [−48.31] 5CRO [−40.14] and are not monotonic with age.

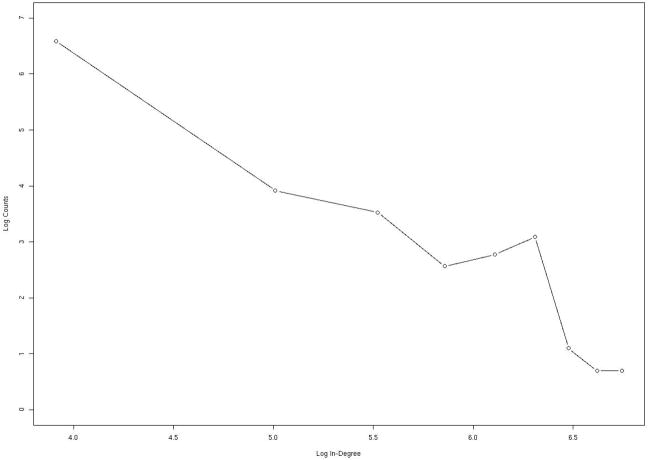
In figures 8–9 we examine the distribution of edges per node using a log-log plot attempt to fit the number of nodes (NoN) that were found with a specific number of in (n_IE) and out (n_OE) edges. In other words we plot the number of folds linked via sequence flow with a given number of structures. If the plot of log(NoN) versus log(n_IE) or log(n_OE) is linear (the distribution is a power law) we say that the network is “scale-free”. Power law or scale free networks are timely concepts in social sciences⁴⁹ and have migrated also to biology⁵⁰. In figure 8, which is derived from the consensus network, there is a “bump” (local maximum) near 500 in edges (IEs). The peak is present in the three calculations of the network (with different energy functions) and it cannot be fitted by power law or exponential distributions. This is because the last two functions are monotonous and do not have maxima. To gain structural insight to the proteins that make that peak, we examine the distribution of the folds in the neighborhood of the peak and compare the distribution to SCOP families of structures and to the rest of the folds in our database (figure 1). We find that folds that belong to the bump are enriched with α/βproteins. We have also noticed that 61% of the proteins that are assigned to the bump are enzymes (the identification that a protein is an enzyme is based on PDBsum⁵¹). This is in comparison to a total of 33.3% enzyme proteins in the total network. We note that the group of alpha/beta proteins is already enriched in enzymes compared to the general network. Proteins that belong to the alpha/beta group are 53% enzymes. We cannot separate the causes for enzyme selection (secondary structure or in-edges). However, the contribution of the network to the selection of enzymes is more significant than the contribution of the SCOP class. We may speculate that enzymes need the structural neighbors to allow for more flexibility in binding and processing alternative ligands.

Figure 8.

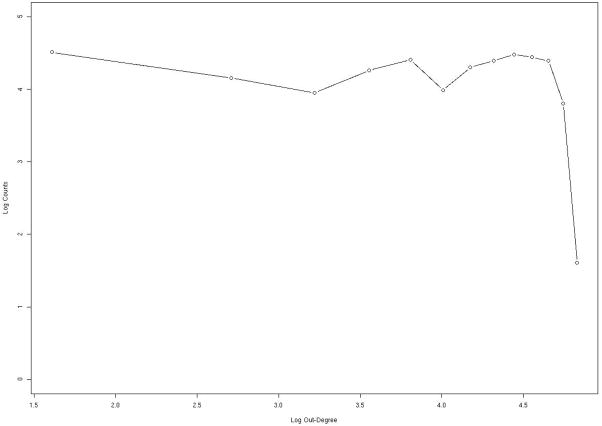
Statistical properties of network connectivity analyzed for the consensus network. For each node (protein structure) we count the number of other structures that are connected to it (the number of edges). We then count the number of nodes that have a specific number of edges. In this figure we consider the in-edges; in-edges represent sequences that fold into one structure which is the node we consider now, but originate from a mutation of a sequence that folds to another structure. The log of the number of in-edges log(IE) is plotted as a function of log of the number of nodes with that number of in-edges log(n_IE). If the log-log plot is linear (power law) then the network is called “scale free”. The figure deviates significantly from power law behavior only in the neighborhood of 500 in-edges, suggesting specific and potentially interesting features. Further examinations of the proteins that deviate from the scale-free characteristics indicate that they are more likely to be of the alpha/beta type and enzymes. See text for more details.

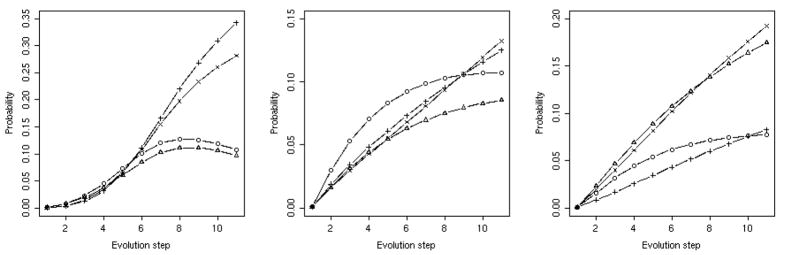
Figure 9.

The same as in figure 8 except that the out-edges are considered. Out edges represent sequence flow from the node of current interest (a protein structure) to other nodes. In other words, sequences that fold into the current node and upon mutation fold to other structures form out-edges. We plot log[n_OE] as a function of log[OE] for the consensus network. The plot is relatively flat (the distribution is almost independent of the number of out-edges per node) up to around 150 in which it drops rapidly. Note the very different behavior of the out-edges and the in-edge. No-scaling behavior is observed for the out-edges.

The decay in the number of nodes is not fast. The number of in-degree edges varies from zero (most populated -- 2⁸= 64 nodes) to the least populated 2⁰=1 with about 800 IE edges. The high end of the edge distribution is staggering given the small size of the network (874 folds). There are two folds with more than 860 incoming edges, which means that most proteins contribute sequences to these extreme folds (1A9X_A and 1EA0_A PDB entries). These strong attractors are assisted by their large size. In our model many short protein sequences can easily migrate to (fragments) of longer proteins that share comparable or more compact partial folds. We do not penalize gaps and deletions at the beginning and the end of the sequence when fitting a short sequence in a larger structure. The interesting observation that short sequences of proteins fit fragments of larger proteins is consistent with domain swaps of multi-domain proteins⁵². While we do not simulate domain swaps (the basic step is a flip of one amino acid at a time), we do observe domain-matching indirectly by successful fitting short sequences to fragments of large folds.

Also of considerable interest is the behavior of outgoing edges (figure 9). The number of outgoing edges per node has significantly narrower distribution compared to the in-edges. Rather than extending to 800 in-edges (per node) the distribution of out edges terminates at less than 150 and is relatively flat.

In table 3 we examine the correlation between nodes that have a large number of in-edges and nodes that have a large number of out-edges. It is not surprising that the correlation is negative (nodes that accept sequences from many proteins are less likely to lose sequences to other proteins). Perhaps more surprising is how weak is the correlation which is consistently lower than 0.5. The introduction of the energy gap reduces the correlation further.

Table 3.

The correlation coefficient of the number of in-edges and the number of out-edges of a node in the network. The negative correlation is expected. A fold with a lot of sequences going out (a large number of out edges) is unlikely to have a large number of sequences coming in. The correlation coefficient is reported for the three energy functions and for two values of the gap. Note the relatively small value of the correlation coefficient (i.e. the correlation is weak).

	n=0	n=3
THOM2	−0.41	−0.35
BT	−0.41	−0.39
TSLE	−0.45	−0.45

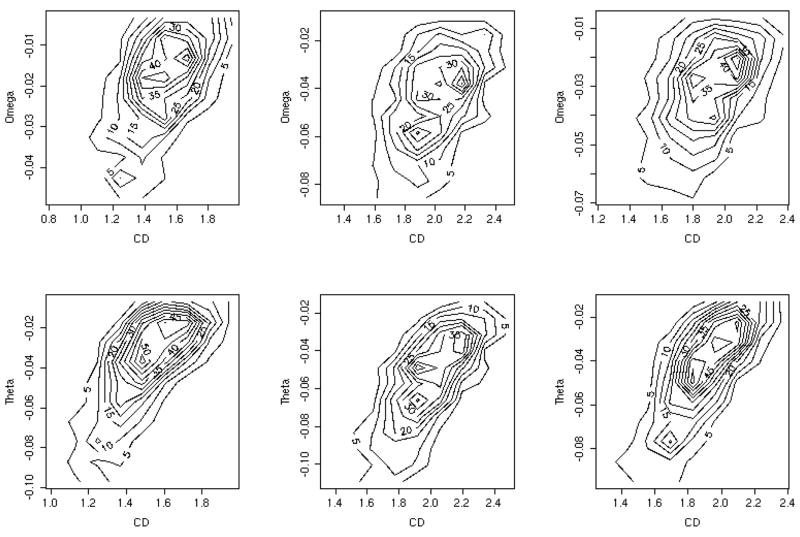
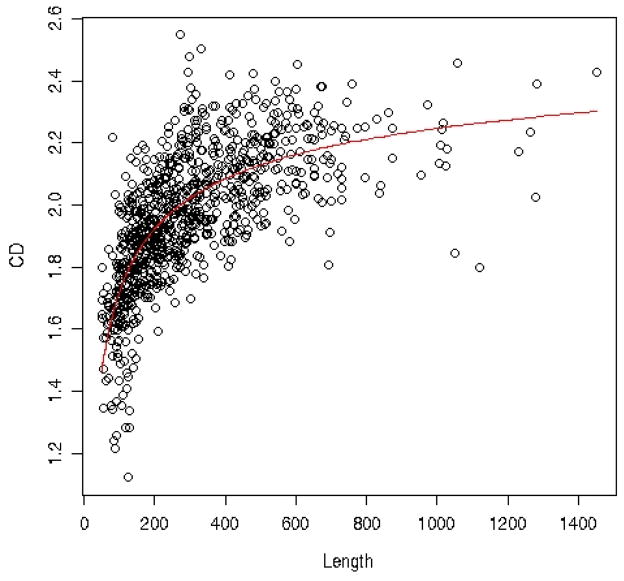
We defined the normalized capacities -- $\omega =\frac{1}{L}log\left[N(E)/{20}^L\right]$ and $\theta =\frac{1}{L}log\left[C(E)/{20}^L\right]$ and present them in figure 10 as a function of the contact density. A related plot (for a different data set and for the THOM2 energy only) was presented in ¹⁹. The contact density of a protein is defined as number of contacts between residues divided by the protein length. Theoretical studies in the past correlate the capacity with protein symmetry²², or with the contact density^15,20. In our hands the correlation of CD with the normalized capacities ω (table 4) is rather weak. Even the capacities with competition of other folds, θ, improves the correlation only slightly. Both capacities are only marginally better correlated with the contact density than with the trivial measure of protein length. Interestingly the contact density is not independent of the protein length as is illustrated in figure 11. The red line is a fit to a simple theory that explains the length dependence of the contact density and is discussed below.

Figure 10.

Comparing sequence capacities (the number of sequences that fold into particular structure) and contact densities (the number of contacts between all amino acids in a protein divided by the protein length): Upper three panels: A contour plot of the logarithm of the sequence capacity without competition of other folds -- $\omega (E_0)=\frac{1}{L}log\left(\frac{N(E_0)}{{20}^L}\right)$ as a function of the contact density (CD) for the three energies from left to right, BT, THOM2 and TSLE. The lower three panels: the same as the top three except that the logarithm of the normalized capacity with competition -- $\theta (E_0)=\frac{1}{L}log\left(\frac{C(E_0)}{{20}^L}\right)$ is shown instead of ω(E₀).

Table 4.

Table 4.a. The Pearson correlation between ω, the log of the normalized capacity without competition with other folds, the length, L, and the contact density (CD) of proteins. The correlation are given for the three energy functions.
	L vs ω	CD vs ω
THOM2	0.38	0.39
BT	0.44	0.44
TSLE	0.39	0.35

Table 4.b. The Pearson correlation between θ, the log of the normalized density with competition, and the length and CD of proteins under two gaps
	n=0	n=3	n=0	n=3
	L vs θ	L vs θ	CD vs θ	CD vs θ
THOM2	0.62	0.61	0.67	0.66
BT	0.62	0.62	0.70	0.70
TSLE	0.63	0.63	0.67	0.67

Figure 11.

A plot of the contact density (CD), the total number of contacts between pairs of amino acids in the protein divided by the protein length, as a function of the protein length L for all protein folds that are included in the network calculations. The analytical fit (thin red line) accounts quite well for the length dependence of the contact density. See text for more details.

Assume a protein with an internal volume V and exposed surface area to the solvent S. We consider the surface to have thickness of one amino acid so the surface has the same unit as volume. The number of residues of the protein is equal to the protein length L. The probability of finding a residue at the surface is q = S/(S+V) = (S/V)/[1+(S/V)]. The probability of finding the amino acid in the internal volume is p = V/(V+S) = 1/(1+(S/V)), A typical size measure of the protein is approximately R ≈ αL^⅓, Hence we can write S/V ≈ αL^−⅓. We now assume β contacts for an internal amino acid and β/2 contacts for an amino acid on the surface. The contact density (CD) is therefore $CD=\beta \left[\frac{1}{2}\frac{\alpha L^{-1/3}}{1+\alpha L^{-1/3}}+\frac{1}{1+\alpha L^{-1/3}}\right]$. The term αL^−⅓ is smaller than one for a typical protein and an expansion can be attempted. We have CD = β[1/2 · αL^−⅓(1− αL^−⅓)+1 − αL^−⅓] to the first order in αL^−⅓ we have CD ≈ β(1 − α/2 · L^−⅓

The above argument means that correlations between contact density and sequence capacity may be at least partially related to the length dependence of the capacity and not to an intrinsic protein property. In fact it is not hard to imagine why the contact density may fail to correlate with capacity. Consider two extreme cases, one in which every site in the protein has the same number of contacts and a second case of a fold with a few sites with a large number of contacts and the rest of the sites with a small number of contacts. Sites with a small number of contacts have in general higher capacity since the energy of the amino acids without contacts varies more slowly. Therefore proteins, with a few sites with a large number of contacts will have higher capacity. England and Shakhnovich recognized this observation²⁰ and formulated the measure of capacity more generally, based on the contact matrix and its moments. However, the general calculation is more complex, and in follow up studies the contact density was used as an order parameter to measure capacity.

Evolutionary kinetics

A stability-motivated model of protein evolution is proposed following the directed graph discussed earlier. This model is clearly incomplete since many biological factors (such as kinetic selection according to single mutation of DNA codons, the presence of protein-protein interactions, and protein active sites) are not included. However, it is likely to suggest a basis for the development of more complex and detailed description of protein evolution.

Network dynamics is computed with a transition matrix T_ij(E₀) -- the transition probability from state i to state j. The off diagonal elements are r_ij(E₀) and the diagonal elements are f_i(E₀)/(1 + Δ_i(E₀)). The last term includes the loss of sequences due to unacceptable mutations -- Δ_i(E₀) with energy above E_0k. As a result the population of folded sequences decreases in every step. We therefore renormalize the probability vector p(t) every step by multiplying every element by a normalizing constant p(t)←c·p_old(t) such that ${\displaystyle \sum _i}{p}_i(t)=1$. The model is therefore of a constant population size but with variable weights of different protein members. A more sophisticated model of the time evolution of the population is discussed in reference ²¹. However that model was not based on detailed sampling of sequences in their corresponding structures.

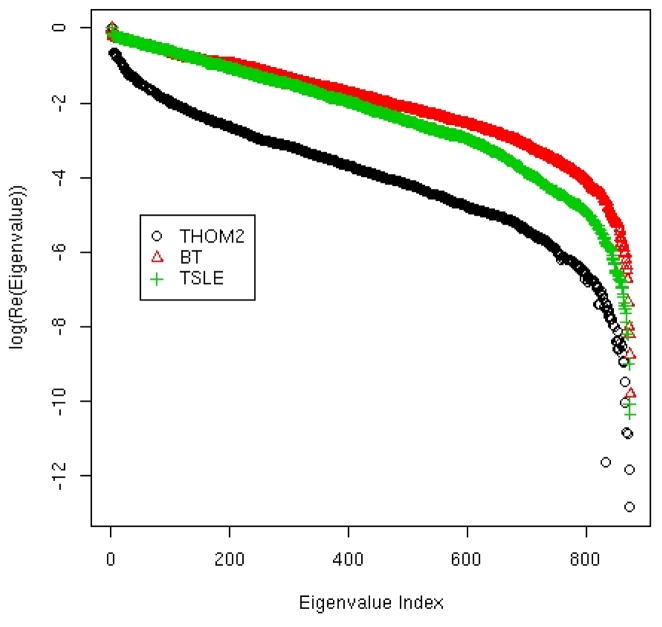
The initial probability of being at each of the nodes is p_i(t = 0) and the probability vector is propagated in time using the transition matrix p(n · Δt)=Tⁿ · p(0). Each Monte Carlo step corresponds to 10⁶ accepted mutations that either stay in the current fold or flip to alternative three-dimensional structures. The real parts of the eigenvalues of the transition matrix determine the rate of stability-driven evolution. The values of the real components are between zero and one. If it is exactly one then it is an equilibrium vector, if it is zero its amplitude disappears in one step. An eigenvector with an eigenvalue close to one that is separated from other eigenvectors (eigenvalue gap) is a starting point to establish well-separated clusters. The log of the real components of the eigenvalues is plotted in figure 12 sorted by magnitude. Only the network generated with the THOM2 energy has well-separated eigenvalues near the value of one. Such separation suggests useful clustering. In contrast the eigenvalue spectra of the BT and TSLE networks are linear. Hence the real parts of the eigenvalues are distributed uniformly along an exponential curve without clear clusters to form.

Figure 12.

The eigenvalues of the transition matrix Tij for the three potentials. The transition matrix was constructed to model transitions between folds as induced by sequence mutation. The element Tij is the probability that the sequence that folds into structure i will fold into structures j after one million mutation steps. The matrix was diagnonalized to extract relevant time scale and to search for clusters. No meaningful clustering for the set at hand was observed. See text for more details.

In figure 13 we show the evolution of fold populations in different networks. In all networks we observe significant deviations from the starting uniform distribution and the creation of a small number of preferred folds. If the time unit is the time to generate an acceptable mutation of one amino acid, it takes only a few millions of acceptable mutations to generate substantial change in the observed population. The stability pressure on the populations is highly significant and includes a number of sinks. To avoid collapse of the diverse space of protein folds to a few attractors as suggested by the stability model it is necessary to add to the model additional biological drives besides structure stability that will increase fold diversity.

Figure 13.

Time evolution of folds. A kinetic equation was solved using the kinetic matrix Tij created in this work that represent the probability of flipping from fold i to fold j in unit time. A unit time corresponds to one million acceptable mutations. We only show proteins that by the end of the simulation have more than 5 percent of total probability. For THOM2 (left panel) we kept the proteins: 1TQW:A (circle) 1K32:A (triangle) 1N35:A (plus) 3BTA:A (cross). For BT (center panel) 1WX1:A (circle) 1R6V:A (triangle) 1A9X:A (plus) 1EA0:A (cross). For TSLE (right panel) 1R6V:A (circle) 1A9X:A (triangle) 1T3T:A (plus) 1EA0:A (cross).

Concluding remarks

We present a model of a network in which the nodes are experimentally determined protein folds and the edges are estimated by a simulated sequence flow (a Markov chain in sequence space). The direction of the flow between the nodes is determined by protein stability. Such a network is of interest in protein design of switches and in providing zero order models for protein evolution. To enhance the reliability of the computational model we considered three different coarse-grained energy functions and searched for shared observations. The following observations are shared by the different energy functions: (1) the network is dense, (2) the distribution of incoming edges includes a “bump” of proteins enriched by α/β proteins, and (3) longer proteins tend to be sinks. The fraction of migrating sequences is at least 5 orders of magnitudes smaller than the number of sequences that belong to a particular fold. Interestingly the introduction of an energy gap as a requirement for stability did not change the network significantly. The pairwise energy functions, which were derived with different algorithms, generate similar networks, supporting the stability of the general properties of the network. Even the vastly different energy function THOM2 generates a network of similar qualitative properties to the two other cases.

The networks so computed can be tested “as is” in the field of protein design. Perhaps direct application of the present simulation is in studies of protein design searching for protein switches that can be turned on and off by small environmental changes that may induce drastic structural changes.

From an evolutionary perspective they are clearly incomplete since many biological factors such as protein-protein interactions, active site requirements and more were not included in our study. Connecting the network to the evolution of a population is also very intriguing. A recent stimulating work that builds on protein structure stability is described in reference ²¹ and is likely to attract other investigators. The present paper may help add to the last interesting theory a more detailed view of protein structures and their relationship to sequence evolution.