Abstract
Diffusion Tensor MRI (DT-MRI) can provide important in vivo information for the detection of brain abnormalities in diseases characterized by compromised neural connectivity. To quantify diffusion tensor abnormalities based on voxel-based statistical analysis, spatial normalization is required to minimize the anatomical variability between studied brain structures. In this article, we used a multiple input channel registration algorithm based on a demons algorithm and evaluated the spatial normalization of diffusion tensor image in terms of the input information used for registration. Registration was performed on 16 DT-MRI data sets using different combinations of the channels, including a channel of T2-weighted intensity, a channel of the fractional anisotropy, a channel of the difference of the first and second eigenvalues, two channels of the fractional anisotropy and the trace of tensor, three channels of the eigenvalues of the tensor, and the six channel tensor components. To evaluate the registration of tensor data, we defined two similarity measures, i.e., the endpoint divergence and the mean square error, which we applied to the fiber bundles of target images and registered images at the same seed points in white matter segmentation. We also evaluated the tensor registration by examining the voxel-by-voxel alignment of tensors in a sample of 15 normalized DT-MRIs. In all evaluations, nonlinear warping using six independent tensor components as input channels showed the best performance in effectively normalizing the tract morphology and tensor orientation. We also present a nonlinear method for creating a group diffusion tensor atlas using the average tensor field and the average deformation field, which we believe is a better approach than a strict linear one for representing both tensor distribution and morphological distribution of the population.
Keywords: Diffusion tensor, Spatial normalization, Tractography
Introduction
Diffusion tensor magnetic resonance imaging (DT-MRI), initially proposed by Basser and colleagues (Basser et al., 1994), is a rapidly evolving technique that can be used to investigate the diffusion of water in brain tissue. It is particularly useful for evaluating white matter abnormalities in the brain, because the measurement of water diffusion in brain tissue is based on the movement of water molecules, which is restricted in white matter. Specifically, in pure liquids, such as water, the motion of individual water molecules is random, with equal probability in all directions. However, within white matter, which is comprised of myelinated fibers, the movement of water molecules is substantially restricted and that restriction, when compared with pure water, is present along all directions, but particularly perpendicular to the fiber axis. Consequently, in white matter fiber tracts, the major axis of the diffusion tensor ellipsoid is much larger than the other two axes, and it coincides with the direction of the fibers. Thus, linking the major diffusion axes in white matter makes possible the visualization and appreciation of white matter tracts within the brain. Such fiber-tracing schemes, also called DT-MRI tractography (Basser, 1998; Conturo, et al. 1999; Jones et al., 1999; Mori et al., 1999; Westin et al., 1999, 2002; Basser et al., 2000; Poupon et al., 2000; Gossl et al., 2002; Mori et al., 2002), where fiber tracts follow the major eigenvector of the diffusion tensor, provide important information about the connectivity between brain regions.
The quantification of diffusion tensor data for investigating white matter abnormalities is generally approached using one of two methods: (1) region-of-interest-(ROI) based methods or (2) voxel-based methods. Most researchers have used ROI methods that begin by identifying anatomical brain regions and by comparing the anisotropy or the extent of the region having thresholded high anisotropy (Peled et al., 1998; Kubicki et al., 2002; McGraw et al., 2002). For studies where the region of interest (ROI) of potential abnormality is difficult to define precisely, voxel-based methods tend to be used (Eriksson et al., 2001; Rugg-Gunn et al., 2001). A voxel-based strategy is more exploratory and is suitable for identifying unanticipated or unpredicted/unhypothesized areas of abnormal white matter morphology. Voxel-based quantification of diffusion tensor, however, requires more sophisticated spatial normalization in order to remove anatomical confounds, such as the extent of white matter, misalignment of fiber tracts, and slight variations in fiber bundle thickness.
Spatial normalization involves the registration of images and the generation of a stereotaxic atlas that represents the statistical distribution of the group at each voxel (Friston et al., 1995; Mazziotta et al., 1995; Thompson and Toga, 1997; Grenander and Miller, 1998; Guimond et al., 2000). The registration of diffusion tensor images has generally been performed in a similar way to the registration of T1-weighted or SPGR MR images. That is, T2-weighted MR or fractional anisotropy (FA) images, which are scalar data, have been used to estimate deformation fields or transformation functions to minimize the intensity difference between the template and the normalized image. With the estimated deformation field or transformation function, the morphology of the diffusion tensor is deformed to fit a stereotaxic space. This transformation function can be either an affine transformation or a nonlinear elastic warping. For the accurate registration of diffusion tensor images, however, an additional step is required to adjust the orientation of the tensor according to the transformation. As was proposed by Alexander and colleagues (Alexander and Gee, 2000; Alexander et al., 2001), the rotational component of linear transformation, or the local rotational component of deformation field, can be applied in order to reorient tensors in the whole tensor field.
As mentioned above, an appropriate atlas for diffusion tensors is also required in order to represent a population of diffusion tensors. Jones and colleagues (Jones et al., 2002) created a diffusion tensor average brain by normalizing tensors with a linear transformation derived from the individual fractional anisotropy images. Their work demonstrates the feasibility and the importance of an atlas template derived from the studied population.
As a registration method for the diffusion tensor, Alexander and coworkers (Alexander and Gee, 2000) have proposed a multiresolution elastic matching algorithm using similarity measures of the tensor in order to manage tensor data instead of scalar data. Our group has proposed diffusion tensor registration methods using tensor similarity (Ruiz-Alzola et al., 2000, 2002) and multiple channel information (Guimond et al., 2002). Ruiz-Alzola and colleagues (Ruiz-Alzola et al., 2000, 2002) extended the general concept of intensity-based similarity in registration to the tensor case and also proposed an interpolation method by means of the Kriging estimator. Their work is based on template matching by locally optimized similarity function. Of further note, Guimond and colleagues (2002) have noted the importance of channel information used for registration and they introduced multiple channel registration for tensor images by, for example, using all components of the tensor simultaneously in the registration process with successively updating tensor orientation.
The performance of spatial registration is worth evaluating in terms of the input information used for registration, i.e., either a univariate scalar data (for instance, FA or T2) or multivariate tensor data, because most neuroimaging groups are familiar with a univariate registration due to its easy access to the registration algorithms, such as SPM (Ashburner and Friston, 1999) or AIR (Woods et al., 1998). When evaluating the spatial registration of diffusion tensor data, it is important to define the concept of anatomical correspondence between data sets that are to be spatially registered. Because the anatomical correspondence is determined by the intensity distribution of channels (i.e., types of information) used for registration, appropriate channels should be used to achieve the definition of anatomical correspondence in the registration process. In this article, we define anatomical correspondence between white matters in terms of both spatial location of the fibers and their local tensor orientation, and we evaluate the registration performance to determine an optimal set of information types to meet these criteria.
To evaluate the registration performance, we have proposed an evaluation method based on tractography, where we compare the similarity/dissimilarity of pairs of fiber bundle maps, i.e., the results of the fiber tractography, derived from both the registered diffusion images and the target (template) diffusion images. The assumption here is that small local registration errors will accumulate and become visible in the tractography results. Such a method will also be simultaneously sensitive for both spatial errors in the registration as well as geometrical tensor alignment errors. The better the images are registered, the more similar the fiber bundle maps will be. We have also evaluated the registration performance with voxel-based measures by examining the dispersion of tensors at each voxel after registration. The evaluation of registration performance in terms of the type of similarity function and the type of matching process specific to registration algorithms are not covered in the article. Additionally we have proposed a method for creating a group diffusion tensor atlas utilizing the average brain morphology as well as the average tensors derived from the registration using the whole tensor information.
Materials and methods
Subjects and data acquisition
Sixteen normal healthy subjects, with a mean age of 42 (range = 30–51), were recruited from the general community at the VA Boston Healthcare System, Brockton, MA. This research was approved by the local Institutional Review Board of the VA Boston Healthcare System, and all subjects signed written informed consent prior to participation. Subjects were scanned using Line Scan Diffusion Imaging (LSDI) (Gudbjartsson et al., 1996; Maier et al., 1998; Mamata et al., 2002), which is comprised of a series of parallel columns lying in the image plane. The sequential collection of these line data in independent acquisitions makes the sequence largely insensitive to bulk motion artifact because no phase encoding is used and shot-to-shot phase variations are fully removed by calculating the magnitude of the signal.
A quadrature head coil was used on a 1.5-T GE Echospeed system (General Electric Medical Systems, Milwaukee, WI), which permits maximum gradient amplitudes of 40 mT/m. For each slice, six images with high diffusion-weighting (1000 s/mm2) along six noncollinear and non-coplanar directions were collected. Two base line images with low diffusion weighting (5 s/mm2) were also collected and averaged. Scan parameters were as follows: rectangular FOV (field of view) 220 × 165 mm; 128 × 128 scan matrix (256 × 256 image matrix); slice thickness 4 mm; interslice distance 1 mm; receiver bandwidth ± 4kHz; TE (echo time) 64 ms; effective TR (repetition time) 2592 ms; scan time 60 s/slice section. A total of 31–35 coronal slices covering the entire brain were acquired, depending on brain size.
Multiple-channel spatial registration
Spatial registration was used to determine anatomical correspondences between source and target (template) images or, in statistical terms, to remove anatomical confounds. We used a multiple-channel demons algorithm for estimating deformation fields in the spatial normalization (Guimond et al., 2002). This algorithm finds the displacement v(x) for each voxel, x, of a target image, T, to match the corresponding location in a source image, S. The optimal solution can be found by using the iterative scheme as follows:
| (1) |
where S̃cn = Sc ○hn(x), ○ denotes the composition with the local tensor reorientation, and the transformation h(x) is the sum of current position and its deformation, i.e., h(x) = x + v(x). C is the number of channels in the images. Gσ is a Gaussian filter with a variance of σ2; * denotes the convolution. A more detailed formulation of this model, and its association with other registration methods, such as the minimization of the sum of squared difference criterion, optical flow and the demons algorithm, can be found in Guimond and Roche (1999).
The Gaussian filter used to smooth the displacement has a progressively decreasing standard deviation σ. This progressive method constrains deformation strongly in the beginning of the registration procedure to correct for gross displacements, whereas later it applies weaker constraints near the end of the procedure for finer displacements. The multiresolution process of the registration was performed at four resolution levels to accelerate convergence. A trilinear interpolation was used for the resampling process. When the full tensor field was used during the registration, the tensor orientations were adjusted iteratively according to deformation field using the Preservation of Principal Direction algorithm, as described by Alexander et al. (2001).
The advantage of the demon's algorithm compared with several low dimensional registration algorithms is the high dimensional warping which renders local registration. Additional advantages of this modified demons algorithm include multiple channel registration and its iterative adjustment of tensor orientation during tensor registration.
Because the demons algorithm matches voxel values between the source and target images, the resulting transformation is determined by the type of information contained in these voxels. Below we compare the registration performance by combining into these voxels information obtained from various channels.
Evaluation of fiber bundle registration
Evaluation data
The registration schemes were evaluated using both artificially deformed DT-MRI data and real DT-MRI data from different subjects.
Registration of artificially deformed DT-MRI data to its original DT-MRI data
The artificially deformed diffusion tensor data were created by applying nonlinear transformations to 10 DT-MRI data sets. To avoid bias to any of our registration schemes, and for the easy control of the deformation for generating the test data, we chose to apply a low-order (in this study, using 7 × 8 × 7 basis functions) nonlinear registration method from SPM99 (Ashburner and Friston, 1999). For each subject, the nonlinear transformation g was generated using SPM99 by registering the subject's T2-weighted image of diffusion tensor image (Vs) to the T2-weighted image of a target diffusion tensor image (Vt) arbitrary chosen from the extra DT-MRI data. A registered diffusion tensor image, Vr, was created by applying the transformation g to the original tensor image, Vs, followed by the regional adjustment of tensor orientation, using the Preservation of Principal Direction method (Alexander et al., 2001). In this case, the registered image, Vr, keeps the same topology but changed morphology of the original diffusion tensor, Vs.
The performance of fiber tract registration according to the channel information was evaluated by inversely transforming the registered image, Vr, to the source image, Vs. For the inverse registration, we applied the demons algorithm with the following six different combinations of information: (1) T2-weighted image (T2); (2) fractional anisotropy (FA), i.e.,
| (2) |
where λ1, λ2, λ3 are eigenvalues of the tensor from bigger to lower values, respectively: (3) difference of the first and second eigenvalues (DE), i.e., λ1 − λ2; (4) fractional anisotropy and trace of tensor (AT), i.e., FA and λ1 + λ2 + λ3; (5) three channel eigenvalues (EV), i.e., λ1, λ2, λ3; and (6) six channel tensor components (TC), i.e., Dxx, Dxy, Dxz, Dyy, Dyz, and Dzz components of tensors. FA, DE, AT, and EV are scalar indices without directional information of the tensor, whereas the TC comprises both direction and magnitude of the diffusivity. Figure 1 shows the types of intensity information used for registration. T2, FA, and mean ADC (i.e., trace) images are displayed in the first row and λ1, λ2, λ3 images, i.e., the three channels of EV, are displayed in the second row. DE image, i.e., λ1 − λ2, is displayed in the right side of the third row and all tensor images of TC, i.e., Dxx, Dxy, Dxz, Dyy, Dyz, and Dzz, are shown with absolute values of diffusion in the left bottom three rows.
Fig. 1.
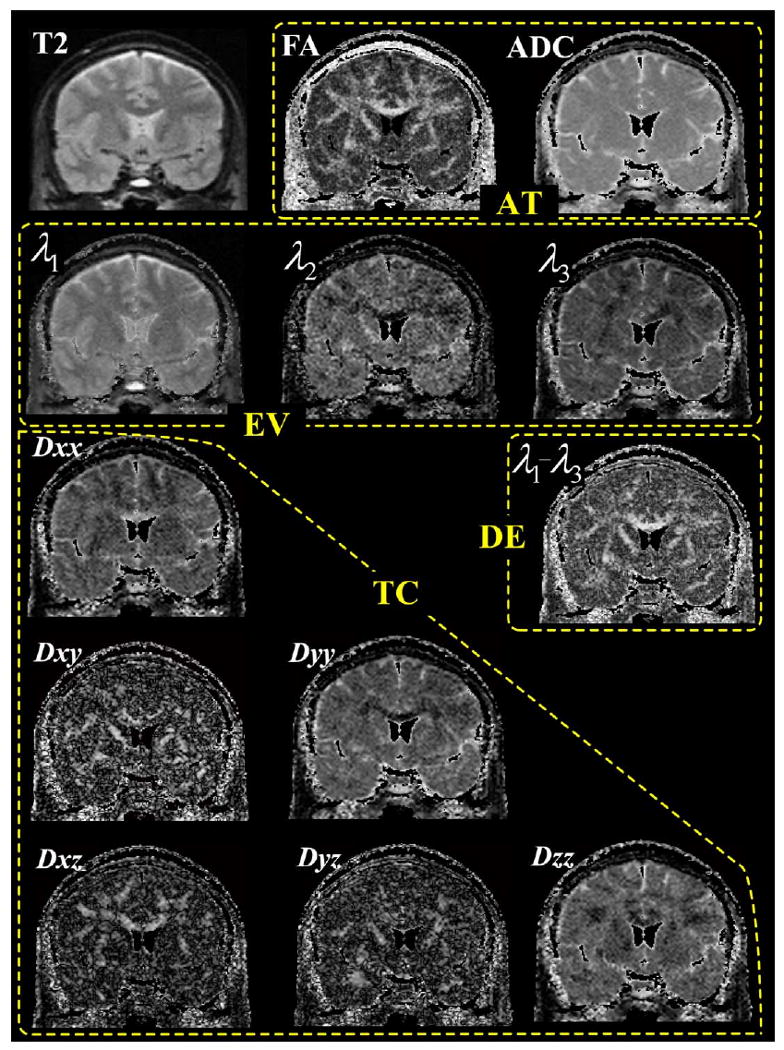
Types of intensity information used for registration. T2, FA (fractional anisotropy), and mean ADC (apparent diffusion coefficient, the trace of tensor) images in the first row, DE (difference of the first and second eigenvalues, i.e., λ1 − λ2) in the right side of the third row are used as a single channel registration respectively. AT contains two channels information, i.e., fractional anisotropy and trace of tensor (mean ADC). Three channels of information in EV (eigenvalues, i.e., λ1, λ2, and λ3 images) are displayed in the second row. Absolute intensity of each channel of TC (tensor components, i.e., Dxx, Dxy, Dxz, Dyy, Dyz, and Dzz gradient images) is seen in the last three rows. Areas with very low signal (surrounding air) or with mean apparent diffusion coefficient (ADC) values higher than 2.0 μs/mm2 (cerebrospinal fluid) were excluded.
In order to bias the registration to the brain region, i.e., to gray and white matter, we multiplied all channels by the brain mask of the T2-weighted image derived from SPM99. Thus, we derived deformation fields, fX (i.e., fT2, fFA, fDE, fAT, fEV, and fTC), according to the type of information used for registration (T2, FA, DE, AT, EV, and TC), respectively. We created inversely transformed tensor images, VsX (i.e., VsT2, VsFA, VsDE, VsAT, VsEV, and VsTC), by applying respective deformation fields, fx, to the registered tensor image, Vr. The procedure can be summarized as follows:
| (3) |
We compared the tensor field, Vs, with each of the inversely transformed tensor images, VsT2, VsFA, VsDE, VsAT, VsEV, and VsTC, using dissimilarity measures of fiber tracts and a voxel-based overlap measure, which are described below under “Performance index of fiber bundle registration” and “Voxel-based evaluation of registration performance.”
Registration of DT-MRI data from different subjects
For the evaluation of the registration of DT-MRI data from different subjects, we normalized 15 diffusion tensor images, Vs, to one target diffusion image, Vt, using multiple channel information, using the above procedure. The registration performance was evaluated by comparing the target image, Vt, and the registered images, VrX (i.e., VrT2, VrFA, VrDE, VrAT, VrEV, and VrTC), derived from the various types of channel information. Here, the tensor fields, VrX, may have differences in topology compared with target image, Vt. This procedure can be summarized as follows:
| (4) |
The above evaluation processes are shown in Fig. 2. We compared the original images and the reverted images, which were registered to a target image and then inversely registered to the original images (bottom left side in the figure). We also compared the target image and the registered images of original images that were registered to the target image (bottom right side in the figure) using different intensity information: T2, FA, DE, AT, EV, and TC.
Fig. 2.
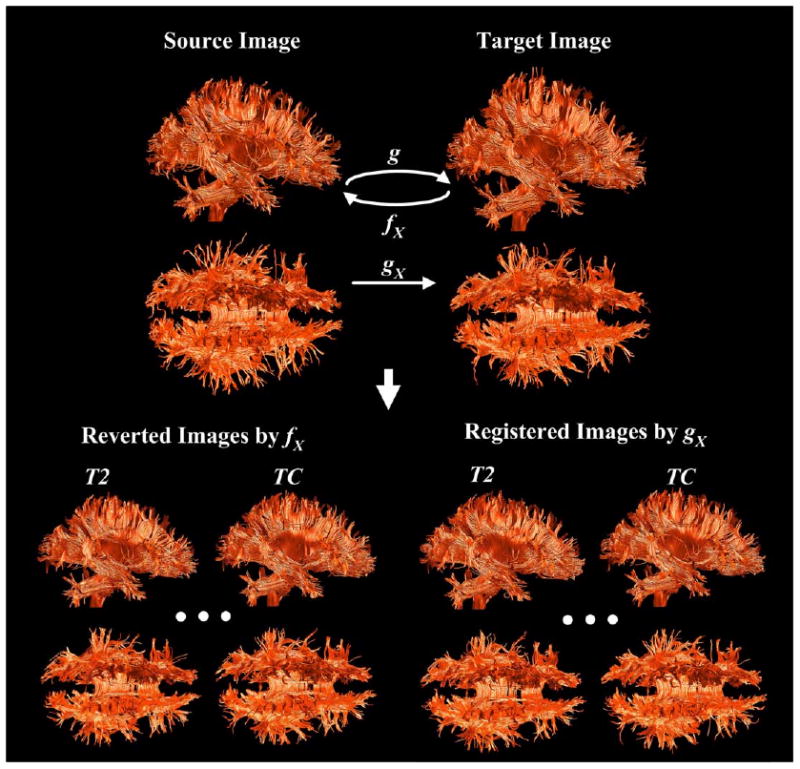
Evaluation of registration with artificially deformed DT-MRI. For evaluation on the registration of artificially deformed data, images registered to a target image were inversely transformed to source images using different intensity information: T2, FA, DE, AT, EV, and TC (reverted images, bottom left). Evaluation of the registration to different subject was conducted on the registered images on a arbitrary chosen subject image (registered images, bottom right). The dissimilarity between two comparing tensor images was evaluated using fiber bundle map that was derived using regularized Runge–Kutta fourth-order integration method. Regularization was incorporated to render fiber tracking at the region of crossing fibers. Streamtubes were used for the tract visualization.
Generation of fiber bundle maps
In order to evaluate the registration performance in terms of minimization of tensor field distortion, we used a traditional eigenvector tracking method. In the tract calculation, we used a fourth-order Runge–Kutta method for the integration solver (Press et al., 1992; Basser et al., 2000; Tench et al., 2002). This gains both speed due to a larger step length and stability compared with a direct Euler method. A trilinear interpolation method was used for obtaining subvoxel estimation with a 1-mm step size.
A straightforward implementation of the eigenvector tracking method is highly dependent on the major eigenvector and will have problems following fibers at locations where other fibers are crossings and the anisotropy is low. To reduce the impact of this problem, we adopted the regularization scheme proposed by Bjornemo and colleagues (Bjornemo et al., 2002) and added a small bias toward the previous tracking direction to the current tensor as follows:
| (5) |
where D is the current tensor at xt and ẋt is the direction vector from the current point xt, i.e., major eigenvector of D, denoted as ê1 (D). α controls the regularization strength and a larger value of α will smooth the proposed fiber paths to a greater extent. α was adaptively applied according to the fractional anisotropy, as in Eq. (6), so that at the high anisotropy tensor fields, no regularization was applied:
| (6) |
where α(v) and FA(v) are alpha value and fractional anisotropy at a voxel v with a global constraint αg, a lower bound threshold of FA, THR_FAlow and a higher bound threshold THR_FAhigh αg, THR_FAlow, and THR_FAhigh were determined manually according to the tensor images case by case. Fiber tracts were visualized by the stream tube method (Schroeder et al., 1991), as used for example by Zhang et al. (2000).
A probability map of white matter derived from T2-weighted image was created as a seed mask for tractography using the SPM99 segmentation algorithm (Ashburner and Friston, 2000). The voxels that had a higher value than 0.9 in the white matter probability map were used as initial seeds for the fiber tracking. As stopping criteria for the fiber tracking, we used the criteria of low FA (0.2) and a rapid change of direction (30° per 1 mm), as well as white matter mask.
Performance index of fiber bundle registration
The accuracy of the deformation was evaluated by calculating the dissimilarity between fiber tracts derived from the tensor images at all the seed points within white matter segmentation. We calculated mean dissimilarity between the tracts in the original tensor field, Vs, and tracts in the inversely transformed tensor fields, VsX (i.e., VsT2, VsFA, VsDE, VsAT, VsEV, and VsTC). We also measured the dissimilarity between tracts in the target field, Vt, and tracts in the normalized tensor fields, VrX (i.e., VrT2, VrFA, VrDE, VrAT, VrEV, and VrTC).
Mean dissimilarity was defined by the following equation:
| (7) |
where trS (x, Vs) indicates a tract in the original tensor field, Vs, with a seed point x and trX (x, VsX) indicates a tract in the inversely transformed tensor field, VsX, with the same seed point x. We calculated the dissimilarity function, dX, of fiber bundles at all the seed points of the white matter segmentation, S, with the total number of seed points, n(S), in the original tensor field, Vs. In the calculation, we ruled out those seed points that had both fibers in comparison shorter than 5 cm in length. The dissimilarity function between fiber bundles was defined by the two following methods:
Mean square error (MSE)
We defined the mean square error between tracts as the mean distance normalized by the tract length in the following equation:
| (8) |
where trS (t|x, Vs) indicates spatial position on trace line trS at the offset t from the starting point. ‖ · ‖ denotes the square error between trace lines trS and trX. |trS| and |trX| indicate the lengths of the trace lines and T is equal to |trS|. The tract trX was resampled to have the same number of tracking points with trS with the resampling ratio of λ.
Endpoint divergence (EDIV)
We defined the end point divergence as the distance between end points of both tracts normalized by mean tract length, T, seeded from a same point x.
| (9) |
where T is equal to |trS|, length of fiber tract trS, and tT is the location of the end point of trS, whereas λtT is the location of the end point of trX. Because fiber tracking was performed bidirectionally from the seed point, we calculated the end point divergence in both directions and chose maximum divergence.
Note that we did not transform the points of the original fiber bundle maps to a stereotaxic space as was done by Xu et al. (2002), instead we performed tractography in the transformed diffusion fields.
Voxel-based evaluation of registration performance
We also applied a voxel-based measure of tensor overlap between the source images and the registered images.
Overlap (OVL)
Overlap of eigenvalue-eigenvector pairs between tensors was defined by Basser and Pajevic (2000) by the following equation:
| (10) |
| (11) |
where λi, εi and , are eigenvalue–eigenvector pairs of the x-th tensors in the tensor fields V and V′ respectively. S is the white matter segmentation of the original tensor field, Vs, with a total number of tensors, n(S). The minimum value 0 indicates no overlap and maximum value 1 indicates complete overlap of the principal axes of the diffusion tensor between voxels.
The alignment of tensors in the samples of normalized images can be a measure of registration performance. As a measure of alignment, we calculated the mean dispersion index of normalized tensor images inside the white matters and the mean fractional anisotropy of the white matters in the average image:
Mean dispersion index (MDI)
Dispersion index indicating the alignment of principal eigenvectors was also proposed by Basser and Pajevic (2000) and was defined as follows:
| (12) |
| (13) |
where β1 (largest), β2, and β3 are eigenvalues of the mean dyadic tensor 〈ε1ε1T〉 derived from the eigenvectors associated with the largest eigenvalue (ε1) of the tensors, for the N subjects, in the voxel, x, that belongs to the white matter segmentation, S, of the average tensor field with a total number of tensors, n(S). The mean dyadic tensor 〈ε1ε1T〉 can be written as the following equation:
| (12) |
where is the ith component of the principal eigenvector in the voxel for the jth subject. The minimum dispersion index of 0 indicates that there is no scatter about the mean eigenvector and a maximum of 1 when the eigenvectors are uniformly distributed about the sphere.
Mean fractional anisotropy (MFA)
Fractional anisotropy of the average tensor image can be a measure of the alignment of the tensor, an alignment of eigenvectors associated with not only the largest eigenvalue but also of all eigenvalues and eigenvectors. This index is based on the fact that the average of anisotropic tensors stays anisotropic if they are aligned and that the average of a set of nonaligned anisotropic tensors will become more isotropic and thus the FA will decrease. We calculated the mean fractional anisotropy inside the white matter of the average image.
Diffusion tensor atlas as an average of tensors and deformation fields
We created average maps of the diffusion tensor according to normalization schemes by combining mean intensities of all the normalized images and the mean of the deformation fields (Guimond et al., 2000, 2002). A diffusion tensor image among the group was chosen as a temporary atlas and all other images were registered to the temporary atlas with an adjustment of tensor orientation. The average of the registered diffusion tensor images was resampled with the inverse of the average deformation field in order to achieve morphological (shape) mean as well as the intensity (tensor) mean. The average map was again used for the target atlas of the next iteration. Four iterations were used to create an average diffusion tensor map. The following equations explain how the average of the intensity and the average of the deformation field were incorporated into the generation of the target atlas:
| (13) |
where is the deformation field of subject j from the source image of the subject Sj-to the target image Ti−1, i.e., the average atlas created from the previous iteration i−1. Initially, T0 is an arbitrary image chosen from the group of diffusion images. is the rotational component of deformation derived from the deformation field and the operator ⊗ indicates adjustment of the tensor orientation with . Note that the selection of a first target image does not affect the creation of the average template with this method (Guimond et al., 2000, 2002).
For averaging tensors at each voxel from the normalized diffusion images, we used both the mean and median of the tensors, as suggested by Jones et al. (2002). The mean and the median of a sample of tensors are derived from the definition of Frechet (1948), where the central location is defined to minimize the sum of distances in the domain of the samples. As a measure of the distance between two tensors A and B, the following metric d (A,B) is used:
| (14) |
where Aij and Bij indicate the components of tensors.
To calculate the median, X, of N tensors, Di (i = 1 … N), the gradient descent of the absolute distance function is solved with the mean of a sample of tensors, i.e., used as initial value. Due to the time complexity, the median averaging method was used only at the final iteration. In our atlas generation, both mean and median tensor images are resampled with the inverse mean deformation field.
From the normalized diffusion images registered using T2, FA, DE, AT, EV, and TC, we created average maps by calculating the mean of the tensors and by calculating the median of the tensors. In order to compare linear registration and nonlinear registration, we created average images, using the mean and median from the normalized images linearly registered using all TC channels. We compared these average images in terms of the mean dispersion index (MDI) and the mean fractional anisotropy (MFA).
Results
The performance of registration according to channel information was evaluated using both the dissimilarity of fiber bundles [i.e., mean square error (MSE) and divergence (DIV) index] and the voxel-based overlap measure (OVL).
We applied a nonparametric sign test to evaluate the difference between registration using TC and registration using other methods. The results of this evaluation are displayed in Fig. 3 and summarized in Table 1. When performing registration of artificially deformed data sets, TC showed significantly increased performance in EDIV, MSE, and OVL (P < 0.005) over T2, FA, and DE, but did not show significantly increased performance over AT and EV. Only improvement of TC in OVL was found over that of AT (P < 0.05) for this simulated deformation. In the registration of different subjects, TC showed significantly increased performance (P < 0.005) over any other type of channel information in terms of MSE, EDIV, and OVL.
Fig. 3.
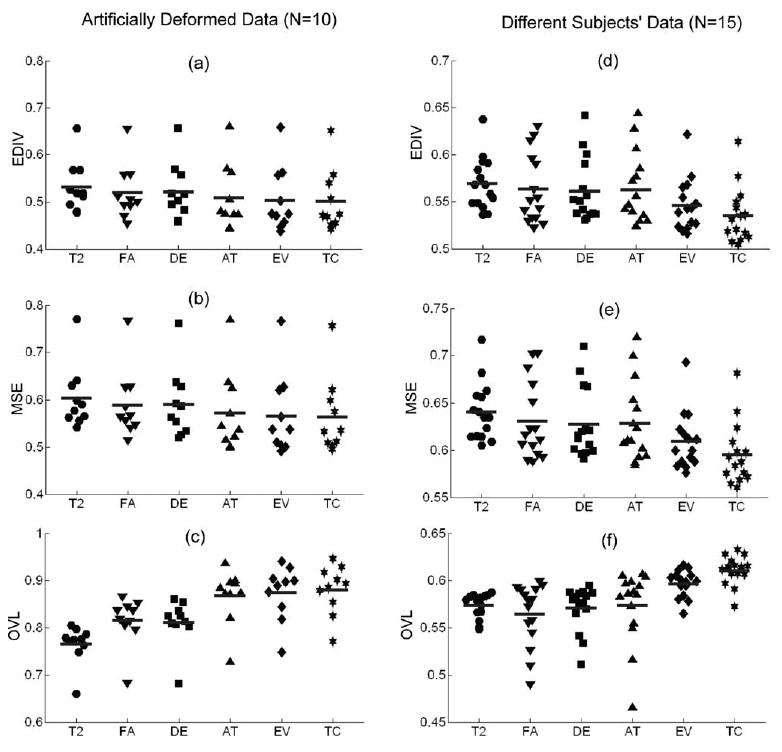
Scattergram of registration performance. The evaluation results of both registration of artificially deformed data and registration of different subjects are displayed in scattergram. The midline indicates the mean. EDIV (end point divergence), MSE (mean square error), and OVL (overlap of tensors) were calculated according to the input channel type used for registration, i.e., T2 (T2-weighted), FA (fractional anisotropy), DE (difference of eigenvalues), AT (fractional anisotropy and trace), EV (three eigenvalues), and TC (total six tensor components). Ten images were used for evaluation on artificially deformed data and 15 images were used for evaluation on different subjects.
Table 1.
Performance of diffusion tensor registration according to intensity information
| Measure | T2 | FA | DE | AT | EV | TC | |
|---|---|---|---|---|---|---|---|
| Simulated Deformation | EDIV | 0.528 (0.056)* | 0.516 (0.060)* | 0.518 (0.062)* | 0.503 (0.070) | 0.498 (0.070) | 0.495 (0.066) |
| MSE | 0.599 (0.069)* | 0.585 (0.075)* | 0.586 (0.075)* | 0.566 (0.087) | 0.559 (0.087) | 0.557 (0.082) | |
| OVL | 0.767 (0.043)* | 0.818 (0.054)* | 0.812 (0.053)* | 0.873 (0.058)† | 0.881 (0.057) | 0.887 (0.053) | |
| Different Subjects | EDIV | 0.569 (0.028)* | 0.563 (0.037)* | 0.561 (0.034)* | 0.563 (0.038)* | 0.546 (0.028)* | 0.535 (0.030) |
| MSE | 0.641 (0.031)* | 0.631 (0.041)* | 0.627 (0.037)* | 0.629 (0.042)* | 0.610 (0.030)* | 0.595 (0.033) | |
| OVL | 0.574 (0.013)† | 0.565 (0.034)† | 0.571 (0.024)* | 0.574 (0.039)* | 0.597 (0.014)* | 0.611 (0.015) |
Note. The values are mean (standard deviation). Abbreviations: EDIV, Endpoint Divergence; MSE, Mean Square Error; OVL, Overlap; T2, T2-weighted; FA, fractional anisotropy; DE, λ1 − λ2; AT, two channels of FA and trace of the tensor; EV, three eigenvalues (λ1, λ2, λ3); and TC, six tensor components (Dxx, Dxy, Dxz, Dyy, Dyz, Dzz). Lower values of EDIV and MSE imply better performance, whereas higher values of OVL imply better performance.
indicates significant difference in registration performance (p < 0.005) compared with registration using TC when nonparametric sign test was applied.
indicates significant difference in registration performance (p < 0.05) compared with registration using TC when nonparametric sign test was applied.
The average diffusion tensor brain was created using TC by four iterations of averaging the intensity and deformation fields. T2, FA, and 2D visualization of TC of a single brain used as the initial atlas are displayed in the upper row of Fig. 4, and corresponding images of the average brain are displayed in the lower row of the same figure. The average brain shows higher signal to noise ratio due to the averaging scheme employed to build this image.
Fig. 4.
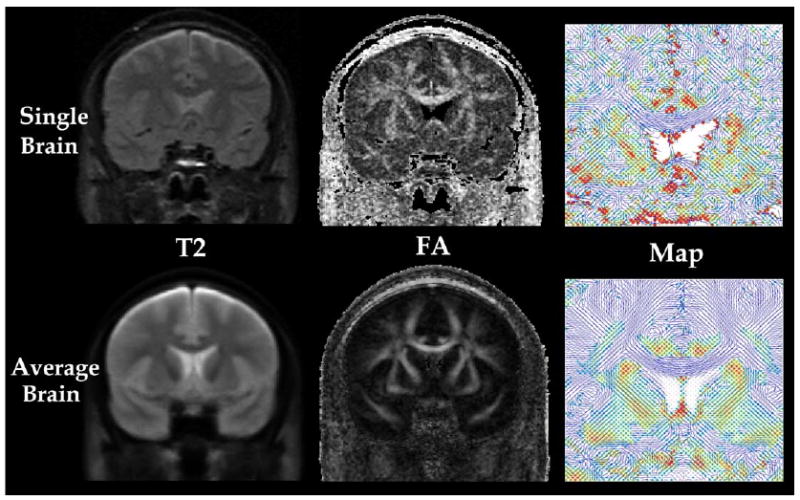
DT-MRI of single brain and a group averaged brain (n = 15). T2-weighted image (T2, first column) and fractional anisotropy image (FA, second column) are displayed for a single brain DT-MRI (top row) and a group average DT-MRI (bottom row). Major eigenvectors of all tensor components (TC, third column) around the corpus callosum of single brain and average brain are also visualized in 2D space by line and colors. The color level indicates the strength of the component of major eigenvector perpendicular to the slice from blue (lowest) to red (highest).
The fiber bundle maps of the average brains and a comparative single brain are displayed in Fig. 5. Fiber bundle maps of the average brains show much smoother tracts than a fiber bundle map of a single brain. As was noted in Jones et al. (2002), most of the short fibers in the peripheral region of brain, such as the arcuate fibers, do not appear in the average brains due to smoothing effects caused by registration errors, intersubject variability, or both.
Fig. 5.
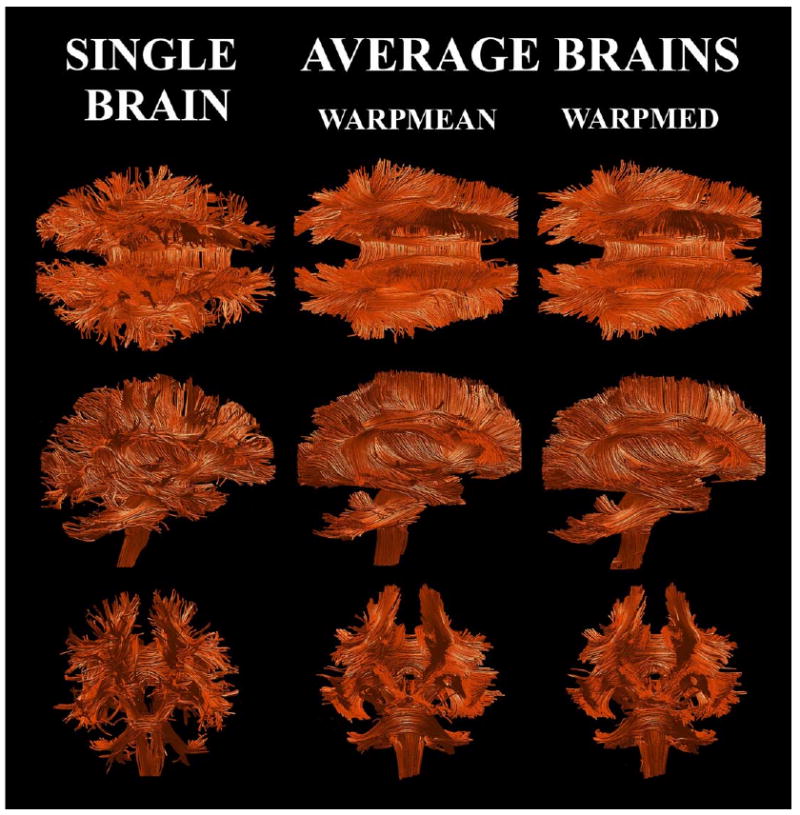
Fiber bundle maps of averaged DT-MRIs. Averages of 15 DT-MRIs (n = 15) are created by calculating the mean and the median of nonlinearly transformed images (WARPMEAN and WARPMED respectively). A comparative fiber bundle map of a single brain is also displayed.
The registration performance in terms of the mean of the dispersion index (MDI) of normalized images using different methods and the mean of fractional anisotropy (MFA) of different type of average atlas is summarized in Table 2. We calculated the mean dispersion index (MDI) on two types of normalized tensor images, registered to a single subject and to a group atlas as a target image.
Table 2.
Performance of registration in creating average brain of the group
| Meas | T2 | FA | DE | AT | EV | TC | LIN + TC | |
|---|---|---|---|---|---|---|---|---|
| To a subject | MDI | 0.39 (0.15) | 0.41 (0.16) | 0.40 (0.16) | 0.39 (0.16) | 0.36 (0.16) | 0.35 (0.16) | |
| To an Atlas | MDI | 0.44 (0.15) | 0.40 (0.18) | 0.39 (0.17) | 0.39 (0.17) | 0.38 (0.17) | 0.34 (0.17) | 0.41 (0.16) |
| MEAN | MFA | 278.9 (118.4) | 266.2 (144.0) | 287.5 (141.2) | 290.5 (137.9) | 296.1 (138.7) | 323.6 (136) | 305.8 (124.2) |
| MED | MFA | 284.4 (121.7) | 271.7 (146.2) | 293.3 (144.1) | 293.4 (140.0) | 298.9 (140.9) | 325.9 (137.6) | 308.3 (127.6) |
Note. The values are mean (standard deviation) values of voxels inside the white matter, not a mean (standard deviation) of a group sample. Abbreviations: MDI, mean dispersion index, MFA of MEAN, mean fractional anisotropy of the mean averaging method, MFA of MED, mean fractional anisotropy of the median averaging method. All means are evaluated within white matters. LIN + TC, linear normalization using six tensor components. Except for LIN + TC, nonlinear normalization was used for all evaluations.
Results demonstrate that the mean of the dispersion index of nonlinear normalization using TC (0.34) is lower than the linear normalization using TC (0.41). This result indicates a higher alignment of the eigenvectors associated with the largest eigenvalue at each voxel in the nonlinear normalization. MDI of the nonlinear normalization using TC is lowest in both registration to a single brain and to an atlas. MFA was highest in the atlases generated by both the mean and median methods when the nonlinear normalization using TC was used. These results imply that the best registration was done with the nonlinear registration using all the tensor components. These two indices support previous findings of similarity of fiber bundle maps and overlap of tensors between different subjects, suggesting that nonlinear registration using all the tensor information is optimal for normalization. The mean fractional anisotropy of the median average inside white matter was higher than that of the mean image in our evaluation.
Maps of the dispersion index from linearly normalized diffusion images and those from nonlinearly normalized diffusion images using TC are displayed in Fig. 6a and histograms of MDI according to channel information are displayed in Fig. 6b. In Fig. 6a, the gray level colors indicate the dispersion index. The black color indicates the lowest dispersion, indicating complete coherence of the principal direction between tensors of the group, whereas the white color indicates the highest dispersion, indicating random distribution of the principal tensor direction. Dispersion index maps of nonlinear registration show clear and wider black areas than linear registration, which indicates better performance of nonlinear registration in the alignment of the principal direction of tensors. From Fig. 6b, we can see that the dispersion index histogram of nonlinear registration using TC demonstrates a shift toward zero, compared with both nonlinear registration using T2, FA, DE, AT, and EV and linear registration using TC (linTC). This closeness to zero implies the better performance of nonlinear registration using TC.
Fig. 6.
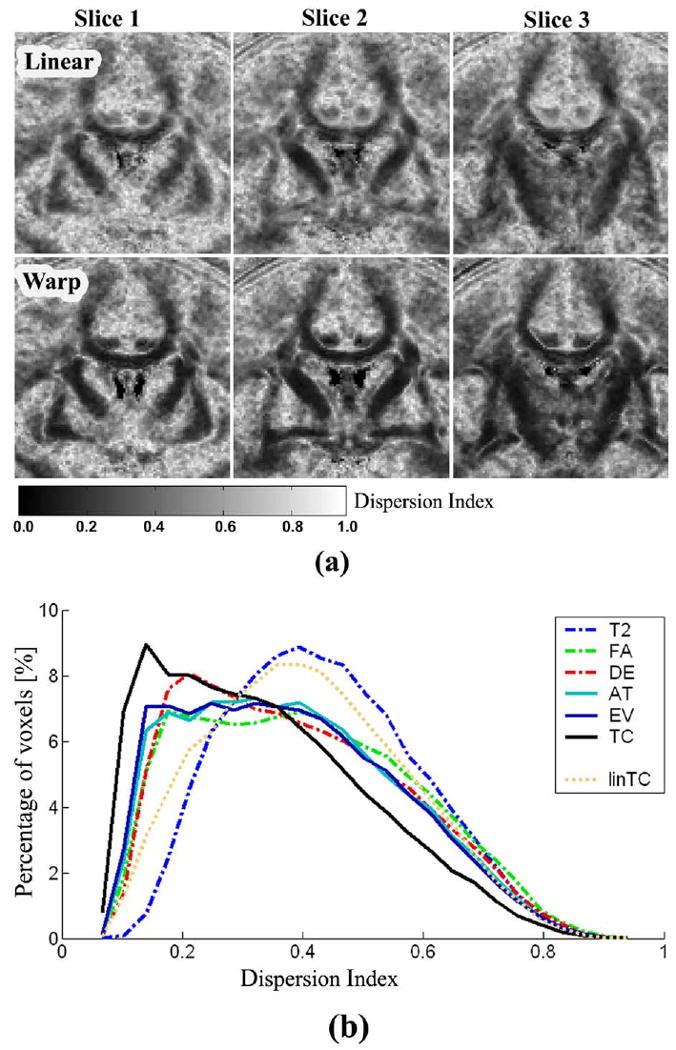
Maps and histograms of dispersion index for linear registration and nonlinear registration. Dispersion maps at three different coronal slices derived from linear registration (Linear) using TC are displayed in the upper row of (a) and those of nonlinear registration (Warp) using TC are displayed in the lower row of (a). Gray level color shows the dispersion index. Black indicates the lowest dispersion meaning complete coherence of the direction of tensors of the group, whereas white indicates the high dispersion indicating random distribution of tensor directions. Dispersion index maps of nonlinear registration shows more dark black areas than linear registration, indicating better performance of nonlinear registration in the alignment of principal direction of tensors. The dispersion index histogram (b) of nonlinear registration using TC (black line) shows shifted toward zero compared with nonlinear registration using T2 (blue dash-dot line), FA (green dash-dot line), DE (red dash-dot line), AT (cyan line), EV (blue line), and linear registration using TC (linTC, ochre dotted line). This closeness to zero implies the better performance of registration. This histogram was calculated inside the white matter.
Discussion
Evaluation of spatial normalization of white matter
In contrast to traditional MRI where both gray and white matter are relatively homogeneous, the information contained in the diffusion tensor components is much more complex. Therefore, we need precise spatial normalization and interpretation focusing on the properties of tensors. The registration method for tensors should be able to match the spatial location of white matter structures, i.e., fiber bundles, and to match the orientation of tensors. Accordingly, the evaluation of the registration should include the detection of anatomical correspondence defined in terms of the spatial structures of the diffusion tensor fields. In this article, we proposed a new evaluation method using fiber tractography in combination with voxel-based correspondence metrics. The advantage of using fiber tractography is that it imposes a stronger model of what we would like to register, the white matter fibers.
We evaluated both the registration of artificially deformed data to its original data and registration between DT-MRI from different subjects. In the first evaluation, the tensor fields are topologically the same, whereas in the second, the tensor fields may include topological variation. Our evaluations using tractography and voxel-based tensor metrics showed similar results, i.e., a nonlinear registration using TC has better performance in most evaluations and is more robust to the difference between source and target images, thus strengthening our belief that our tractography-based evaluation is useful to measure the performance of the registration of DT-MRI data. The assumption here is that the better the images are aligned, the more similar the fiber bundle maps and the more overlap of the tensor orientation.
With respect to limitations of our study, we acknowledge that errors in fiber tracking affect the evaluation of the registration. The inherent errors arise from the limitation of the current technique of diffusion tensor tractography due to noise effects and the intrinsic limitations of DT-MRI, known as partial volume effects. Anisotropic voxel units of 1.72 × 1.72 × 4 mm, used in the study, may add to the errors in fiber tracking even though we used an interpolation scheme to continuously estimate tensors. However, the evaluation was done systematically to all tensor images and we expect that such errors were evenly distributed for all comparison procedures. Additionally, to ensure that there was no bias introduced by the choice of target image, a smaller number of source images (five) with a different target were evaluated. No significant changes in our results could be found.
Using multiple channels for registration
Because the anatomical correspondence is determined relative to the anatomical landmarks or local intensity distribution that the matching algorithm utilizes, the type of input information can determine the registration process of tensor images. Previous registration methods have utilized mostly scalar images such as FA or T2 image or T1-weighted image coregistered to TC. However, the anatomical correspondence derived from FA or T2 may have different meanings, that is, the white matter of T2 does not correspond exactly to that of FA.
We therefore questioned which information is optimal in terms of registering fiber tracts. T2-weighted data can delineate the gray and white matter as well as the CSF relatively well. However, white matter in T2 is relatively homogeneous throughout the brain and contains little information concerning the location and orientation of fiber bundles. FA is a widely used index for the anisotropy of a tensor, which is related to the fiber density, coherence, and myelination, and thus it shows the location of fiber bundles very well. DE was chosen as a non-normalized index for anisotropy. Because FA is a normalized anisotropic index which is insensitive to the magnitude of diffusivity, adding the trace of the tensor (AT) is thought to provide complementary information on the registration. EV contains all the magnitude information of the tensor due to multiple channels of eigenvalues. However, it does not guarantee that corresponding points are in the same fiber tracts or not, because the tensors of different fiber tracts showing different orientation may have similar eigenvalues. The peculiarity of TC is that TC contains the directional information of tensors, including the tensor anisotropy. Using TC, the optimization algorithm can search corresponding tensors of target images for the same anisotropy, magnitude of diffusivity and direction with source images.
In terms of the overall performance of registration, using TC showed the best performance, especially in the registration of images from different subjects, and in the registration to a group atlas. The robustness of using TC may be due to utilization of tensor orientation information in the registration process. In the artificially deformed registration, that two channels of the fractional anisotropy and the trace of the tensor combination (AT), three channels of eigenvalues (EV) and six channels of tensor components (TC) showed more or less similar performance and these three methods showed significantly increased performance over a channel of T2-weighted image (T2), a channel fractional anisotropy (FA), or a channel of major eigenvalues difference (DE). We conjecture that information contained in all the tensor components contain is redundant and is not necessarily required in this registration, because the deformation we artificially applied contains relatively low spatial-frequency-ranged deformation field. This conjecture is supported by the fact that the registration of the artificially deformed data showed better performance than registration between different subjects. A low-dimensional warping of SPM99 has a highly smoothed deformation field and therefore the high dimensional warping could approximate the deformation field successfully with a larger size of Gaussian smoothing kernel. In this situation, the effect of the input channel may not be too noticeable in the estimation as long as it contains the basic information to register. But in the registration of the real brain between different subjects, more precise matching using anisotropy, magnitude of diffusivity and orientation information is required with a lower Gaussian smoothing kernel size. Mean dispersion index of normalized images, in Table 2, registered both to a single subject and to a group atlas also suggests that registration using the whole tensor information is more robust than other methods.
The computational time grows proportional to the number of channels used for registration. In an explorative study, the accuracy is more important than the complexity and the time requirement is not essential as long as it stays within a reasonable range. In this study, the calculation time of one 2.0 GHz Pentium 4 processor is about 5 min for one channel and for TC calculation it takes about 30 min, which is quite acceptable.
Considering the time complexity, the registration using three eigenvalues showed a comparable performance to that using all the tensor components. Therefore, we may choose to use three channels of eigenvalues in the registration with acceptable confidence and reduced time complexity.
In general, registration algorithms are controlled by a similarity function as well as the input information type, i.e., type of channels. For the registration of the tensor, various similarity measures between tensors of source and target images can be defined. The demons algorithm does not use a specific tensor similarity measure during registration, but, instead, it simply utilizes the difference of the intensity of each channel from source and target images. Incorporating a precise tensor similarity measure and optimizing the weight of each channel might increase the registration performance. Data reduction using a principal component method can potentially be used to efficiently reduce the number of channels and thus decrease the computational burden without compromising the registration error. Though these topics are of interest to further research, in this study, we restricted our evaluation to only optimal choices of input channels in the tensor matching process.
Creation of a group atlas of diffusion tensor brain
For creating the group average diffusion atlas, we used an iterative scheme similar to the one presented by Guimond et al. (2000) for averaging MR images. Instead of using structural MRI, diffusion tensor images were registered to create a tensor diffusion atlas. Tensor orientations were successively adjusted during each iteration. The combination of the intensity average and the shape average derived from mean of deformation fields renders the topology and morphology representative of the group.
In making an atlas, Jones et al. (2002) evaluated several averaging methods such as mean, median, and mode. The median tensor was obtained in order to be robust to outliers by finding a tensor that minimizes the distance to the sample of tensors in an absolute distance sense. We applied these mean and median methods in the averaging of normalized DT-MRIs, but instead of linear registration using FA information, we used the nonlinear registration using all the tensor components. In terms of the alignment of the major eigenvector of the tensor, nonlinear normalization showed better performance than linear normalization. As mentioned by several investigators (Alexander and Gee, 2000; Jones et al., 2002), due to noise effects, there may exist a possibility of misorientation of the diffusion tensors in nonlinear high-dimensional warping. However, this potential misorientation does not necessarily pose a larger problem than the misalignment obtained by an affine transformation. For voxel-based statistics, where finding corresponding positions is important, nonlinear warping technique is thought to be appropriate. More specifically, the nonlinear warping using all diffusion tensor information showed a lower dispersion index implying better registration of tensors compared with nonlinear registration using other types of input information. This provides further arguments supporting the thesis that the orientation information of diffusion tensor as well as anisotropy is necessary for the registration of fiber tracts.
Note that we used the average brain morphology, derived from the mean deformation field, as well as the average tensor intensity when creating the average brain. We believe that the average brain created by our nonlinear method using these two types of average information is a better approach than a strict linear one, in representing both tensor distribution and morphological distribution of the population.
Though further work will be required, including comparisons between the mean and median method in terms of better group representation, we think the selection of the averaging method can be dependent on the distributional model of sample tensors at each voxel and the use of an atlas. As was noted by Jones et al. 2002, especially for the case of outliers, the median method will be advantageous but for normally distributed or coherently distributed samples of tensors, the mean method is thought to be sufficient with a much lower computational cost.
Using the multiple channel registration method and a group diffusion tensor atlas, we are further exploring white matter abnormalities in schizophrenia in comparison to healthy control subjects, using statistics for scalar quantities such as FA and angles between vectors at the corresponding position across samples. Exploration of left and right hemispheric asymmetry for both populations has also been conducted using the proposed methods (e.g., Park et al., 2003).
Concluding remarks
In this article we have discussed spatial normalization of DT-MRI data in terms of the input information the registration algorithm utilizes. We have evaluated the methods using DT-MRI tractography. In addition, we have created a DT-MRI atlas based on the average diffusion tensor images. Nonlinear registration using all the components of the diffusion tensors resulted in the most reliable results and can be used for generation of a group atlas, where the mean of tensors and the mean of deformation fields are combined together.
Acknowledgments
The authors acknowledge Marie Fairbanks for her administrative assistance. Additionally, we gratefully acknowledge the support of the Post-doctoral Fellowship Program of Korea Science & Engineering Foundation (KOSEF) (H.J.P.), National Alliance for Research on Schizophrenia and Depression (M.K.), the National Institutes of Health (K02 MH 01110 and R01 MH 50747 to M.E.S., R01 MH 40799 to R.W.M., and R01 NS 39335 to S.E.M.), the Department of Veterans Affairs Merit Awards (M.E.S. and R.W.M.), and the National Center for Research Resources (11747 to RK and P41-RR13218 to F.A.J. and C.F.W.).
References
- Alexander DC, Gee JC. Elastic matching of diffusion tensor images. Comput Vison Imag Understand. 2000;7(2):233–250. [Google Scholar]
- Alexander DC, Pierpaoli C, et al. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging. 2001;20(11):1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Nonlinear spatial normalization using basis functions. Hum Brain Mapp. 1999;7(4):254–266. doi: 10.1002/(SICI)1097-0193(1999)7:4<254::AID-HBM4>3.0.CO;2-G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ. Voxel-based morphometry—the methods. Neuroimage. 2000;11(6 Pt 1):805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Basser PJ. Fiber-tractography via diffusion tensor MRI(DT-MRI). Six Annual Meeting of the International Society for Magnetic Resonance in Medicine; Berkeley, CA. 1998. p. 1226. [Google Scholar]
- Basser PJ, Mattiello J, et al. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S. Statistical artifacts in diffusion tensor MRI (DT-MRI) caused by background noise. Magn Reson Med. 2000;44(1):41–50. doi: 10.1002/1522-2594(200007)44:1<41::aid-mrm8>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, et al. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44(4):625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Bjornemo M, Brun A, et al. Regularized stochastic white matter tractography using diffusion tensor MRI. Medical Image Computing and Computer-Assisted Intervention—MICCAI 2002; Tokyo, Japan. 2002. pp. 435–442. [Google Scholar]
- Conturo TE, Lori NF, et al. Tracking neuronal fiber pathways in the living human brain. Proc Natl Acad Sci USA. 1999;96(18):10422–10427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson SH, Rugg-Gunn FJ, et al. Diffusion tensor imaging in patients with epilepsy and malformations of cortical development. Brain. 2001;124(Pt 3):617–626. doi: 10.1093/brain/124.3.617. [DOI] [PubMed] [Google Scholar]
- Frechet M. Les elements aleatoires de nature quelconque dans un espace distancie. Ann Inst Henri Poincare X. 1948:215–308. [Google Scholar]
- Friston KJ, Ashburner J, et al. Spatial registration and normalization of images. Hum Brain Mapp. 1995;2:165–189. [Google Scholar]
- Gossl C, Fahrmeir L, et al. Fiber tracking from DTI using linear state space models: detectability of the pyramidal tract. Neuroimage. 2002;16(2):378–388. doi: 10.1006/nimg.2002.1055. [DOI] [PubMed] [Google Scholar]
- Grenander U, Miller M. Computational anatomy: an emerging discipline. Q Appl Math. 1998;56(4):617–694. [Google Scholar]
- Gudbjartsson H, Maier SE, et al. Line scan diffusion imaging. Magn Reson Med. 1996;36(4):509–519. doi: 10.1002/mrm.1910360403. [DOI] [PubMed] [Google Scholar]
- Guimond A, Guttmann CRG. Deformable registration of DT-MRI data based on transformation invariant tensor characteristics. Proceedings of the IEEE International Symposium on Biomedical Imaging (ISBI'02); Washington, DC. USA. 2002. [Google Scholar]
- Guimond A, Meunier J, et al. Average brain models: a convergence study. Comput Vision Imag Understand. 2000;77:192–210. [Google Scholar]
- Guimond A, Roche A. Multimodal brain warping using the demons algorithm and adaptative intensity corrections. Institut National de Recherche en Informatique et en Automatique; Sopia Antipolis, France: 1999. [Google Scholar]
- Jones DK, Griffin LD, et al. Spatial normalization and averaging of diffusion tensor MRI data sets. Neuroimage. 2002;17(2):592–617. [PubMed] [Google Scholar]
- Jones DK, Simmons A, et al. Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI. Magn Reson Med. 1999;42(1):37–41. doi: 10.1002/(sici)1522-2594(199907)42:1<37::aid-mrm7>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Kubicki M, Westin CF, et al. Uncinate fasciculus findings in schizophrenia: a magnetic resonance diffusion tensor imaging study. Am J Psychiat. 2002;159(5):813–820. doi: 10.1176/appi.ajp.159.5.813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maier SE, Gudbjartsson H, et al. Line scan diffusion imaging: characterization in healthy subjects and stroke patients. AJR Am J Roentgenol. 1998;171(1):85–93. doi: 10.2214/ajr.171.1.9648769. [DOI] [PubMed] [Google Scholar]
- Mamata H, Mamata Y, et al. High-resolution line scan diffusion tensor MR imaging of white matter fiber tract anatomy. AJNR Am J Neuroradiol. 2002;23(1):67–75. [PMC free article] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, et al. A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM) Neuroimage. 1995;2(2):89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- McGraw P, Liang L, et al. Evaluation of normal age-related changes in anisotropy during infancy and childhood as shown by diffusion tensor imaging. AJR Am J Roentgenol. 2002;179(6):1515–1522. doi: 10.2214/ajr.179.6.1791515. [DOI] [PubMed] [Google Scholar]
- Mori S, Crain BJ, et al. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45(2):265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Mori S, Kaufmann WE, et al. Imaging cortical association tracts in the human brain using diffusion-tensor-based axonal tracking. Magn Reson Med. 2002;47(2):215–223. doi: 10.1002/mrm.10074. [DOI] [PubMed] [Google Scholar]
- Park HJ, Westin CF, et al. A method for hemispheric asymmetry of white matters using diffusion tensor MRI. Neuroimage. 2003;19:S918. [Google Scholar]
- Peled S, Gudbjartsson H, et al. Magnetic resonance imaging shows orientation and asymmetry of white matter fiber tracts. Brain Res. 1998;780(1):27–33. doi: 10.1016/s0006-8993(97)00635-5. [DOI] [PubMed] [Google Scholar]
- Poupon C, Clark CA, et al. Regularization of diffusion-based direction maps for the tracking of brain white matter fascictes. Neuroimage. 2000;12(2):184–195. doi: 10.1006/nimg.2000.0607. [DOI] [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, et al. Numerical Recipes in C Cambridge. Cambridge University Press; Cambridge, UK: 1992. [Google Scholar]
- Rugg-Gunn FJ, Eriksson SH, et al. Diffusion tensor imaging of cryptogenic and acquired partial epilepsies. Brain. 2001;124(Pt 3):627–636. doi: 10.1093/brain/124.3.627. [DOI] [PubMed] [Google Scholar]
- Ruiz-Alzola J, Westin CF, et al. Nonrigid registration of 3D tensor medical data. Med Image Anal. 2002;6(2):143–161. doi: 10.1016/s1361-8415(02)00055-5. [DOI] [PubMed] [Google Scholar]
- Ruiz-Alzola J, Westin CF, et al. Nonrigid registration of 3D scalar vector and tensor medical data. MICCAI 2000: Third International Conference on Medical Image Computing and Computer-Assisted Intervention; Pittsburgh, USA. New York: Springer-Verlag; 2000. pp. 541–550. [Google Scholar]
- Schroeder WJ, Volpe CR, et al. The stream polygon: a technique for 3D vector field visualization. Proceedings of Visualization '91; Los Alamitos, California. 1991. pp. 126–132. [Google Scholar]
- Tench CR, Morgan PS, et al. White matter mapping using diffusion tensor MRI. Magn Reson Med. 2002;47(5):967–972. doi: 10.1002/mrm.10144. [DOI] [PubMed] [Google Scholar]
- Thompson PM, Toga AW. Detection, visualization and animation of abnormal anatomic structure with a deformable probabilistic brain atlas based on random vector field transformations. Med Image Anal. 1997;1(4):271–294. doi: 10.1016/s1361-8415(97)85002-5. [DOI] [PubMed] [Google Scholar]
- Westin CF, Maier SE, et al. Image Processing for Diffusion Tensor Magnetic Resonance Imaging. Second International Conference on Medical Image Computing and Computer-Assisted Intervention-MICCAI 99; New York. 1999. pp. 441–452. [Google Scholar]
- Westin CF, Maier SE, et al. Processing and visualization for diffusion tensor MRI. Med Image Anal. 2002;6(2):93–108. doi: 10.1016/s1361-8415(02)00053-1. [DOI] [PubMed] [Google Scholar]
- Woods RP, Grafton ST, et al. Automated image registration. I. General methods and intrasubject, intramodality validation. J Comput Assist Tomogr. 1998;22(1):139–152. doi: 10.1097/00004728-199801000-00027. [DOI] [PubMed] [Google Scholar]
- Xu D, Mori S, et al. A framework for callosal fiber distribution analysis. Neuroimage. 2002;17(3):1131–1143. doi: 10.1006/nimg.2002.1285. [DOI] [PubMed] [Google Scholar]
- Zhang S, Curry C, et al. Visualizing Diffusion Tensor MR Images Using Streamtubes and Streamsurfaces. IEEE Visualization Conference; Utah. 2000. [Google Scholar]


