Patient Death as a Censoring Event or Competing Risk Event in Models of Nursing Home Placement

SUMMARY

Participant death is often observed in studies that examine predictors of events such as hospitalization or institutionalization in older adult populations. Cox proportional hazards modeling of the target event, whereby death is treated as a censoring event, is the standard analysis in this competing risks situation. However, the assumption of noninformative censoring applied to a frequently occurring competing event like death may be invalid and complicate interpretation in terms of the probability of the event. Multiple cause-specific hazard (CSH) models can be estimated, but ambiguities may arise when interpreting covariate effects across multiple CSH models and in terms of the cumulative incidence function (CIF). Alternatively, one can model the proportional hazards of the subdistribution of the CIF and evaluate covariate effects on the CIF directly. We examine and compare these two approaches with nursing home placement data from a randomized controlled trial of a counseling and support intervention for spouse caregivers of patients with Alzheimer’s disease. CSHs for nursing home placement (where death is treated as a censoring event) and death (where nursing home placement is treated as a censoring event) and subdistribution hazards of the CIF for nursing home placement are modeled separately. In the presence of multiple covariates, the intervention effect is significant in both approaches but the interpretation of the covariate effects requires joint evaluation of all estimated models.

1. INTRODUCTION

Time to event analyses in the health sciences test hypotheses about the occurrence of a target event in two or more experimental groups with data that are often subject to censored observations. Censoring may occur for multiple reasons including loss to follow-up, participant withdrawal, and study termination prior to observation of the target event. If it is reasonable to assume that those participants remaining in the risk set are representative of all who would be at risk for the target event, then we have independent censoring [1, Chapter III.2.2.]. Under this assumption, testing of group effects and modeling of the survival function may be carried out with the Kaplan-Meier (KM) method. The marginal probability of the event, the cumulative incidence function (CIF), may then be estimated by 1−KM. In the presence of covariates, evaluation of group and covariate effects on the hazard function and then the modeling of the hazard and survival functions may be performed with the Cox proportional hazards method [1–3].Additionally, other events may occur that preclude the occurrence of the target event. These alternative events are typically called competing risk events [4].The analysis of each cause-specific hazard (CSH) is the standard analysis procedure for these data, allowing for the covariate effects on the hazard of the target event to be evaluated in the presence of competing risk events. Computationally, individuals who experience the competing event are censored at that event time, and there is no differentiation between varying causes of censoring. Separate cause-specific proportional hazards models may then be fitted for each failure type, assuming only independent censoring [1, 2, 5].A chief drawback to this approach, however, is that independence of failure types must be assumed in order to directly translate group and covariate effects from the CSH to the marginal probabilities of failure of a specific event type [6].

In many time to event analyses in older adult populations where the target event is the institutionalization of the participant or the presence of an acute event such as a stroke, death of the participant before the target event occurs is common. In practice, participant death is typically treated as a noninformative censoring event, and treatment and covariate effects are often estimated with the Cox proportional hazards method [7–10]. While this approach is valid for evaluating the CSH of the target event, in practice the analysis of the complimentary CSH of death is often excluded. Furthermore, estimates of the target event probabilities are either overestimated with the 1−KM estimate or foregone completely. When the marginal probabilities are of interest, we may model the proportional hazards of the subdistribution, and therefore directly assess covariate effects on the probability of the target event in the presence of death as a competing risk [11].

In this article, we review proportional hazards models for the subdistribution, also known as the cumulative incidence function, for a specific failure type in a competing risks analysis. We then apply and compare cause-specific Cox proportional hazards models with proportional subdistribution hazards models in a re-analysis of nursing home (NH) placement data from the New York University Caregiver Intervention (NYUCI) study. The NYUCI study is a randomized controlled trial of a counseling and support intervention for spouse caregivers of patients with Alzheimer’s disease (AD) [12]. A primary outcome of interest is the time until NH placement of the person with AD. In this study, 32% of care recipients died under spousal care at home without previous NH placement. These cases were treated as censored cases in a previous analysis of the effect of the intervention [12]. Comparative analyses of these data illustrate the effects of death as a competing risk event on the inferences made for both the intervention condition and the model covariates. We estimate the CIF for NH placement based on the estimated proportional subdistribution hazards model and provide SAS and R programming code as a reference. We conclude with a discussion of the differences in the results from these two methods and offer some guidance to researchers in dealing with competing risk events.

2. METHODS

In time to event data with a single event type we observe for each individual X = min(T, C), where T is an event time and C is a censoring time, and censoring indicator, D, where D = I(T ≤ C). We are frequently interested in testing group and covariate effects on the time to the event and in modeling F(t), the CIF. The CIF determines the probability of observing the event at any time up to and including time t. For event times T, we denote F(t) = P(T ≤ t). In the absence of competing risk events, the CIF is frequently estimated with the nonparametric KM approach [1–3]. Specifically, F(t) = 1 – S(t), where S(t) = P(T > t), is the estimated survival function at time t. Conditional on a p×1 vector of time-independent covariates Z = (Z₁,…, Z_p), we define the hazard

$$h(t|\mathbf{Z})=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\frac{P(t\le T<t+\mathrm{\Delta }t|T\ge t,\mathbf{Z})}{\mathrm{\Delta }t}.$$ (1)

We interpret (1) as the instantaneous event rate at time t [2, 5]. In the presence of covariates, we may employ the Cox proportional hazards model to test treatment effects and evaluate covariate effects. We estimate the vector of coefficients β = (β₁,…, β_p) in the Cox proportional hazards model h(t|Z) = h₀(t)exp{Z^Tβ}, where h₀(t) is an arbitrary baseline hazard.

In the presence of k multiple event types, k = 1,…,K, we have separate cause-specific hazards for each event type:

$$h_i(t|\mathbf{Z})=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\frac{P(t\le T<t+\mathrm{\Delta }t,k=i|T\ge t,\mathbf{Z})}{\mathrm{\Delta }t}.$$ (2)

We may fit a separate cause-specific Cox proportional hazards model h_i(t|Z) = h_0i(t)exp{Z^Tβ_i} where β_i varies for each event type. In this framework, we assume only independent censoring [1, Chapter III.2.2, 2, Chapter 8.2, 5]. Individuals who experience the competing risk event before time t are excluded from the risk set at time t, as are those who are censored prior to time t. Thus, in the cause-specific model for NH placement, patients who die without NH placement are censored at the time of death. In the accompanying cause-specific model, NH placement is a censoring event with death as the target event. The procedures for obtaining the survival function and the CIF for a single event type are routine and are described in the texts by Andersen et al. [1], Kalbfleisch and Prentice [2], and Allison [3]. However, it is well documented that the 1 − S(t) estimate from the KM estimate may overestimate the CIF in the competing risks context [6, 13–15]. In addition, covariate effects from these CSH models have no direct interpretation on the marginal failure probability for a specific cause [6,11]. We briefly describe the connection between the CSH and the CIF later in this section. In the follow-up to the work of Pintilie [16], Latouche et al. [17] explicitly state this relationship. Beyersmann et al. [18] present this relationship for three failure types.

Alternatively, we may choose to directly model the cause-specific CIF for the target event. Gray [19] presents a method for estimating the CIFs and testing their equality across values of a categorical covariate in the presence of competing risks. The Fine and Gray model has the added utility of modeling multiple covariate effects, including those that may be continuous, in the proportional hazards framework. In addition, we may estimate the CIF for a fixed t and Z = Z₀. We highlight this capability in the following case study.

Using notation similar to Fine and Gray [11], the cause-specific cumulative incidence function is denoted F₁(t|Z) = P(T ≤ t, k = 1|Z), where k=1 specifies the event type of primary interest in the presence K−1 competing risk events. To estimate this function in the presence of covariates, we estimate parameters of a proportional hazards model for the subdistribution, where the hazard of the subdistribution is defined

$$h_{\mathit{\text{SUB}}}(t|\mathbf{Z})=\underset{\mathrm{\Delta }t\to 0}{\lim }\frac{P(t\le T<t+\mathrm{\Delta }t,k=1|T\ge t\cup (T\le t\cap k\ne 1)\mathbf{Z})}{\mathrm{\Delta }t}[11].$$ (3)

Note that the subdistribution hazard places the condition that the target event time has not yet occurred. In addition, there is an allowance for a competing risk event to have occurred prior to time t. Thus individuals for whom a competing event has already occurred prior to time t are weighted and included in the risk set at time t. Fine and Gray acknowledge the unusual risk set construction and point out that, despite its unconventional appearance, the parameter estimates for the subdistribution function have a straightforward interpretation, and present a weighted partial likelihood function for the estimation of model parameters [11]. We proceed by fitting a proportional hazards model of the form h_SUB(t|Z) = h_SUB,0(t)exp{Z^Tβ_SUB}.

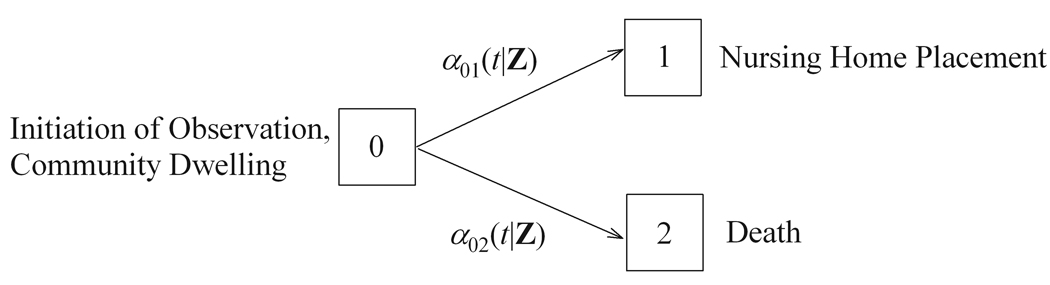
The CSH and the hazard of the subdistribution are two distinct, but related, functions [17–18, 20–21]. As such, β₁, and β_SUB do not share exactly the same interpretations. To illustrate the point, consider the competing risks example in the multistate process in Figure 1. Here we have two event types where NH placement is the target event and death is the competing risk event. All patients initiate observation in state 0 (community dwelling). Patients remain in state 0 until proceeding to either state 1 (NH) with cause-specific hazard α₀₁(t|Z) or state 2 (death) with cause-specific hazard α₀₂(t|Z). At any time in this multistate process a patient may be in only 1 state and, although some patients were observed to die after NH placement, we consider states 1 and 2 to be absorbing for this analysis. In this multistate process, define X_T, where X_T ε (0,1,2), and we observe the event time T when X_T ≠ 0. Patients who never proceed out of state 0 by the end of the study are censored. Dependent upon covariate values Z, each event has its own cause-specific hazard, α_0i(t|Z), where

$${\alpha }_{0i}(t|\mathbf{Z})=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\frac{P(t\le T<t+\mathrm{\Delta }t,X_T=i|T\ge t,\mathbf{Z})}{\mathrm{\Delta }t},i=1,2.$$ (4)

Fig 01.

Note that (4) is directly comparable to the more familiar CSH expression (2) where events other than the target event are treated as censoring events in the analysis. Modeling of the CSH then requires the assumption of independent censoring but no assumption of independence between event types. From here we note that, conditional on Z, the CIF for X_T = 1 is a function of both the all-cause survival, S(t|Z), and the cause-specific hazards, α₀₁(t|Z). We have

$$F_1(t|\mathbf{Z})={\displaystyle \underset{0}{\overset{t}{\int }}P(T>u|\mathbf{Z}){\alpha }_{01}(u|\mathbf{Z})du,}$$ (5)

where the all-cause survival is a function of both cause-specific hazards

$$P(T>t|\mathbf{Z})=S(t|\mathbf{Z})=\text{exp}\left\{-{\displaystyle \underset{0}{\overset{t}{\int }}{\alpha }_{01}(u|\mathbf{Z})+{\alpha }_{02}(u|\mathbf{Z})\mathit{\text{du}}}\right\}[2,\text{Chapter}8.2,21].$$ (6)

While we can estimate β_i for the CSHs with ease and interpret it in the usual way, extrapolating the group and covariate effects to the CIF is more difficult because of the relationship in (5–6). We alternatively model the hazard of the CIF directly. Fine and Gray [11] define the improper failure time, T*, that provides the foundation for proportional subdistribution hazards modeling. Briefly, we allow T* = T for X_T = 1 and T* = ∞ for X_T = 2. The subdistribution hazard is then:

$${\lambda }_{0i}(t|\mathbf{Z})=\underset{\mathrm{\Delta }t\to 0}{\text{lim}}\frac{P(t\le T^{*}<t+\mathrm{\Delta }t,X_T=i|T^{*}\ge t,\mathbf{Z})}{\mathrm{\Delta }t}i=1,2.$$ (7)

This is directly comparable to the hazard defined in (3). We then may estimate the CIF directly from the hazard of the subdistribution

$$F_1(t|\mathbf{Z})=1-\text{exp}\left\{-{\displaystyle \underset{0}{\overset{t}{\int }}{\lambda }_{01}(u|\mathbf{Z})\mathit{\text{du}}}\right\}[11,18,21].$$ (8)

By modeling the CIF as a function of the subdistribution hazard, we may then interpret the model and covariate effects, β_SUB, directly in terms of the marginal failure probabilities.

In the following analysis, an event other than the target event terminates the subject’s participation in the study. We demonstrate that the differences between treating this event as a censoring event in a cause-specific proportional hazards model and treating the event as a competing risk event in the proportional subdistribution hazards model can be substantial. We now illustrate and compare these methods using mortality and nursing home placement data from a randomized controlled trial of patients with dementia and their spouse-caregivers.

3. THE NYUCI STUDY OF NH PLACEMENT

A randomized controlled trial examined the effectiveness of an enhanced counseling and support intervention compared to usual care for spouse caregivers of persons with Alzheimer’s disease [22–26]. A primary hypothesis of this study was that the intervention would enable caregivers to provide care in the home longer and therefore delay placement of their spouses in NH facilities [12]. Between 1987 and 1997, 406 caregivers were enrolled into the study. A family counselor was assigned to the caregivers upon study enrollment and the caregivers were then randomly assigned to intervention or usual care. Regular structured interviews were completed, which made it possible to identify some of the mechanisms through which the intervention delayed NH placement. Baseline assessments were collected at enrollment but before randomization, with follow-up assessments of the caregivers occurring every 4 months during the first year after enrollment and every 6 months thereafter. Participation ended with severe caregiver illness, caregiver death, or refusal to continue, or 2 years after the death of the spouse with dementia.

Time to NH placement was measured in years from enrollment to the actual date of NH placement. Follow-up extended through July 1, 2007. Over the course of follow-up, NH placement occurred for 211 of the 406 patients. Dates of death were obtained for 128 of the 195 (65.6%) patients who were not placed in the NH (Table 1). Patients whose caregivers were lost to follow-up and for whom dates of NH placement and/or patient death were not known were right-censored at the last follow-up interview. Thus we assume independent censoring.

Table 1.

Patient Outcomes.

	Sample size	NH Placement	Deaths (without NH placement)	Total Deaths (overall)
Usual Care	203	111	61	193
Intensive	203	100	67	192
Total	406	211	128	385

Patient and caregiver demographic information was obtained at baseline assessments. The Global Deterioration Scale (GDS) was used to measure mild (GDS = 4), moderate (GDS = 5), and severe (GDS = 6,7) dementia. Both patient and caregiver physical health scores were determined from a subjective rating of overall health scored 1–4 (excellent/good/fair/poor) from a questionnaire adapted from the OARS Physical Health Form [27]. The 30-item Memory and Behavior Problems Checklist (MBPC) [27] was used to measure the frequency of patient memory and behavior problems and caregiver appraisals of the stress involved. Caregiver burden was assessed by the 22-item Burden Scale [28]. Caregiver depression was assessed using the 30-item Geriatric Depression Scale [29] and satisfaction with social support was assessed with the mean score of 3 questions ranging from 1 (very dissatisfied) to 6 (very satisfied) from the Stokes Social Network Questionnaire [30]. Year of study entry (1987–1997) was included as a predictor to account for possibly changing trends in overall NH placement rates at the time of enrollment.

4. ANALYSIS

As a primary goal of the NYUCI study is to evaluate the effectiveness of the caregiver intervention in delaying the time to NH placement, we examine this effect both without and with covariate adjustments. In all, we estimate six different models. In the first three models, intervention group is the only predictor. We first examine the role of the intervention on the CSH of both NH placement and patient death. By simultaneously studying the effect of the intervention on the CSH of the target event and the competing risk event, we assess intervention effectiveness more completely. We then model the proportional hazards of the subdistribution and compare the findings with the cause-specific Cox model for NH placement. Plots of the CIFs for both treatment groups complement the estimated intervention effects. The assumptions of proportional hazards and proportional subdistribution hazards were evaluated visually with residual plots and interactions with time were tested.

Next we extend our analytic comparisons to include multiple baseline covariates. Three models were estimated to parallel the intervention-only models: cause-specific proportional hazards model of NH placement, cause-specific proportional hazards model of death, and a proportional hazards model of the subdistribution for NH placement. Several baseline measures were included as covariates as in a previous Cox proportional hazards model for these data [12]. Covariates were included either because of clinical importance or because of imbalances in the characteristics in the two treatment groups at baseline despite randomization. All covariates are investigated in all models for a complete comparison.

Cox proportional hazards models are estimated using the PHREG procedure in SAS version 9.1 (SAS Institute, Cary, N.C.). Proportional hazards models for the subdistribution were estimated with the CRR function available in the CMPRSK library for R (www.r-project.org). Code used for programming in SAS and the R language is included in the appendix. Modeling the hazard of the subdistribution is straightforward with the CRR function in the CMPRSK package available for the R software package. This function allows the inclusion of several covariates to be included in the model and is also able to adjust for covariate interactions with time. At present no analogous procedure is available in SAS.

5. RESULTS

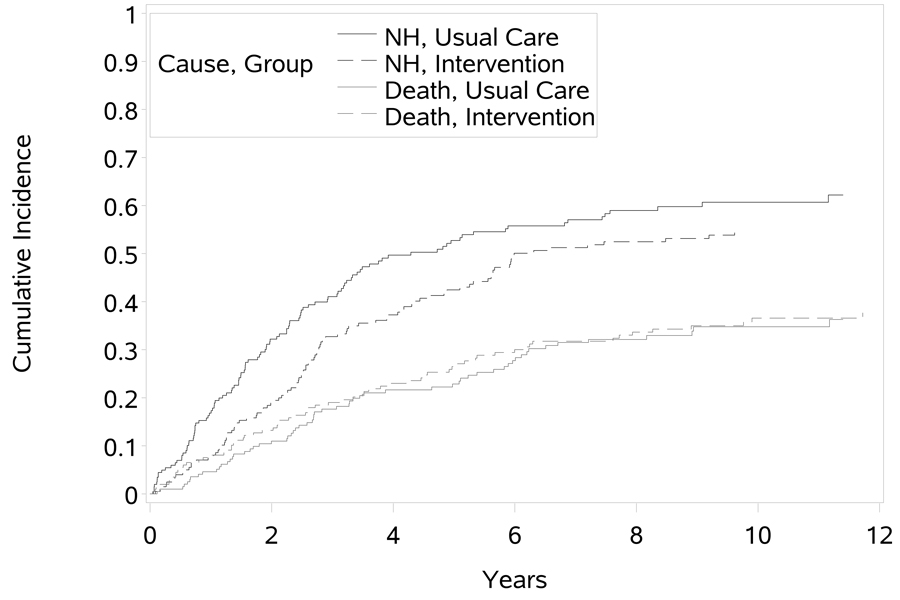
In the univariate cause-specific Cox proportional hazards models, the intervention group showed a statistically significant lower hazard of NH placement compared to the usual care control group (HR = 0.73, p = 0.025) and no difference in the hazard of death (HR = 0.85, p = 0.352). The absence of an intervention effect on the CSH of death and the presence of an effect on the CSH of NH placement is reflected in the CIFs of both events (Figure 2) where we see that the intervention group does have a lower incidence of NH placement. Despite the observed CSH effect, the effect on the CIF is a function of both CSHs and thus we cannot directly assign the observed CSH difference to the CIF. The proportional hazards model of the subdistribution does allow us to test and estimate the intervention effect (HR = 0.77, p = 0.052) on the CIF directly while treating patient death as a competing risk event. As we would expect, the probability of NH placement is lower for those in the intervention group. This reflects the lower hazard of NH placement for those in the intervention group and no difference in the hazard of death. Visual inspection of the proportional hazards assumption indicated minimal concern about non-proportional hazards and tests for an interaction with time were not statistically significant in either analysis of NH placement. Hence, no adjustment for non-proportional hazards was required.

Fig 02.

The covariate-adjusted cause-specific proportional hazards models for NH placement (Table 2) and death (Table 3) should be interpreted jointly. For each variable investigated, we may simultaneously examine the effects on each CSH, holding all other covariate values constant. Consider, for example, the effect of male gender on both outcomes. Males have a higher hazard of death (HR = 1.75, p = 0.016) than females, but males do not have a statistically significantly higher hazard of NH placement (HR = 1.28, p = 0.164). For most variables, we see a significant effect on at most one CSH. Moderate dementia and severe dementia are the exceptions, where more severe dementia increases the cause-specific hazards of both death and NH placement.

Table 2.

Covariate-adjusted hazard ratios for the cause-specific Cox proportional hazards model of nursing home placement. Death is treated as a censoring event.

	Hazard ratio (95% CI)	p value
Patient Variables
Patient Age	1.016 (0.990, 1.043)	0.2292
Log(1+Patient Income)	0.843 (0.764, 0.930)	0.0007
Patient Physical Health	0.979 (0.786, 1.220)	0.8515
Patient Gender (male vs female)	1.278 (0.905, 1.805)	0.1634
Frequency of Memory and Behavior Problems	0.987 (0.975, 1.000)	0.0498
Global Deterioration Scale
moderate vs mild	1.906 (1.311, 2.772)	0.0007
severe vs mild	2.431 (1.535, 3.850)	0.0002
Caregiver Variables
Caregiver Age	1.005 (0.980, 1.030)	0.7071
Caregiver Physical Health	1.080 (0.838, 1.393)	0.5515
Satisfaction with Support Network	1.137 (1.004, 1.288)	0.0426
Reaction to Memory and Behavior Problems	1.013 (0.999, 1.027)	0.0720
Depressive Symptoms	1.013 (0.986, 1.042)	0.3505
Caregiver Burden	1.008 (0.996, 1.021)	0.1904
Other Effects
Year of Study Entry (0 = 1987 – 10 = 1997)	0.901 (0.854, 0.951)	0.0002
Group (intervention vs usual care)	0.746 (0.559, 0.997)	0.0478

Table 3.

Covariate-adjusted hazard ratios for the cause-specific Cox proportional hazards model of death. Nursing home placement is treated as a censoring event.

	Hazard ratio (95% CI)	p value
Patient Variables
Patient Age	1.042 (1.010, 1.075)	0.0101
Log(1+Patient Income)	1.164 (0.969, 1.398)	0.1053
Patient Physical Health	1.423 (1.114, 1.819)	0.0048
Patient Gender (male vs female)	1.748 (1.108, 2.757)	0.0164
Frequency of Memory and Behavior Problems	1.007 (0.991, 1.023)	0.4132
Global Deterioration Scale
moderate vs mild	1.728 (1.057, 2.825)	0.0291
severe vs mild	2.708 (1.505, 4.873)	0.0009
Caregiver Variables
Caregiver Age	1.015 (0.985, 1.045)	0.3373
Caregiver Physical Health	0.826 (0.588, 1.161)	0.2711
Satisfaction with Support Network	0.980 (0.837, 1.148)	0.8013
Reaction to Memory and Behavior Problems	1.007 (0.988, 1.026)	0.4685
Depressive Symptoms	0.986 (0.950, 1.024)	0.4622
Caregiver Burden	1.002 (0.985, 1.018)	0.8423
Group Effect
Year of Study Entry (0 = 1987 – 10 = 1997)	0.958 (0.894, 1.028)	0.2328
Group (intervention vs usual care)	1.064 (0.736, 1.539)	0.7404

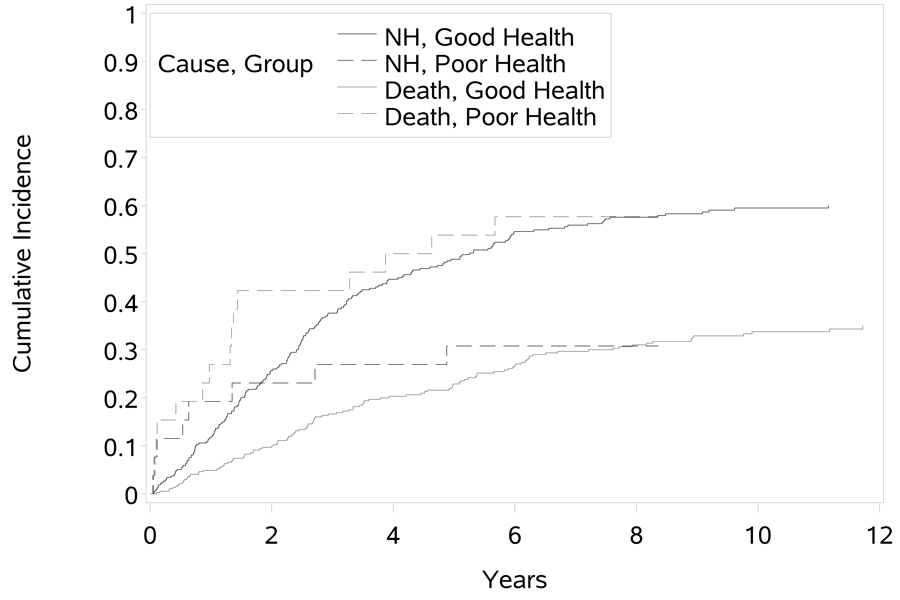
The parameter estimates from the proportional subdistribution hazards model of NH placement are presented in Table 4. Here we have tests of statistical significance that are largely in agreement with the cause-specific NH placement hazards analysis for the majority of covariates. For example, the effect of male gender on the subdistribution hazards is not statistically significant. This is not surprising since we observed that males had a significantly higher CSH of death, but not NH placement. In addition, the effect of the intervention in delaying NH placement is still statistically significant (HR = 0.75, p < 0.05). Inconsistent results are noted for patient physical health, frequency of memory and behavior problems (although marginal), severe dementia, and satisfaction with the support network. Patient physical health is particularly interesting, as it was not found to be statistically significant (HR = 0.979, p = 0.852) for the CSH of NH placement, but in the subdistribution hazards analysis, poorer patient health at baseline (higher scores of the measure) significantly lowered the hazard of the NH placement (HR = 0.796, p = 0.037). This is largely explained by the significant increase in the CSH of death. Consider the CIFs for patients with good (collectively including those evaluated as excellent, good, or fair) and poor health as identified on the OARS Physical Health Form at baseline (Figure 3). We see graphically that those in poor health have a higher incidence of death than those in better health, and initially have a higher incidence of NH placement until being surpassed after 2 years of follow-up. That is, over time patients in poor physical health at baseline are more likely to die (and hence not be placed in a nursing home) than those in better physical health. Our analysis reveals no effect of patient physical health on the instantaneous rate of NH placement, but does affect the cumulative probability of NH placement in the presence of death as a competing risk. This effect can be interpreted correctly only after considering both cause-specific hazards analyses and following with the subdistribution hazards analysis.

Table 4.

Covariate-adjusted hazard ratios of nursing home placement from a proportional hazards model of the subdistribution.

	Hazard ratio (95% CI)	p value
Patient Variables
Patient Age	1.003 (0.978, 1.028)	0.8327
Log(1+Patient Income)	0.824 (0.746, 0.910)	0.0001
Patient Physical Health	0.796 (0.642, 0.986)	0.0370
Patient Gender (male vs female)	1.039 (0.746, 1.448)	0.8199
Frequency of Memory and Behavior Problems	0.988 (0.976, 1.000)	0.0504
Global Deterioration Scale
moderate vs mild	1.510 (1.081, 2.109)	0.0156
severe vs mild	1.525 (0.973, 2.389)	0.0654
Caregiver Variables
Caregiver Age	1.000 (0.977, 1.024)	0.9935
Caregiver Physical Health	1.148 (0.894, 1.473)	0.2794
Satisfaction with Support Network	1.108 (0.980, 1.253)	0.1006
Reaction to Memory and Behavior Problems	1.009 (0.996, 1.023)	0.1831
Depressive Symptoms	1.009 (0.982, 1.037)	0.5022
Caregiver Burden	1.012 (0.999, 1.025)	0.0774
Group Effect
Year of Study Entry (0 = 1987 – 10 = 1997)	0.924 (0.877, 0.974)	0.0032
Group (intervention vs usual care)	0.748 (0.561, 0.999)	0.0494

Fig 03.

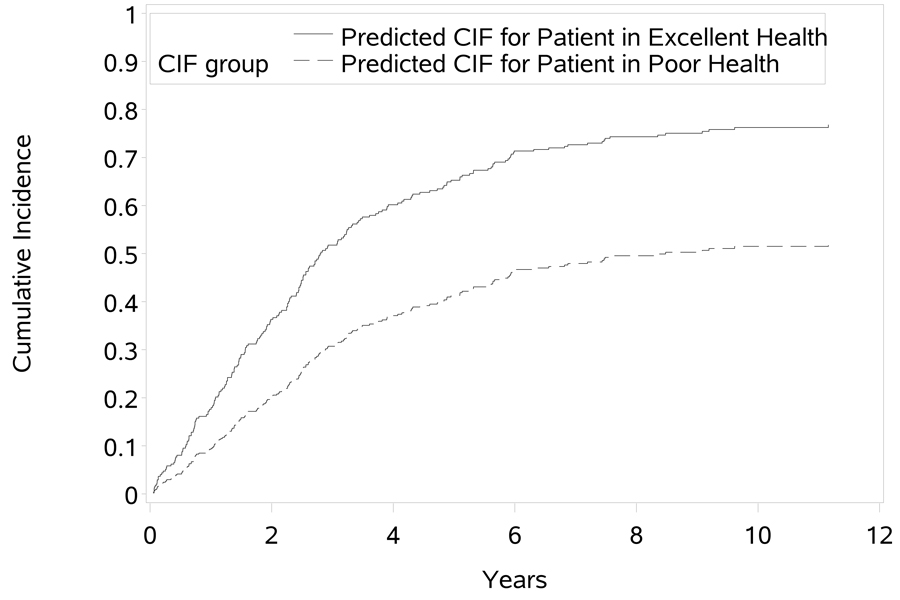
By modeling the subdistribution hazards directly, we may also estimate the cumulative incidence at a given time t and covariate values Z = Z₀. Fine and Gray [11] describe the estimation procedure and the probabilities may be estimated with the PREDICT.CRR function in the CMPRSK package for R. Suppose, for example, that we are interested in predicting the probability of NH placement for a male AD patient with moderate dementia who enters the study in year 4 in excellent physical health and is assigned to the intervention. We can estimate the cumulative incidence at a specific time or generate the estimated CIF (Figure 4).We can also compare this estimate with that for a similar patient who enters the study with poor physical health (Figure 4). The estimated CIFs in Figure 4 are evaluated at the covariate values specified above, and the remaining covariates are evaluated at the observed sample means. As we can see in the plot, the patient in better physical health has a much higher probability of NH placement than the patient in poorer physical health. This is not surprising, since the CSH for death was high for patients in poor physical health, indicating that these patients have a higher rate of death and hence are less likely to be placed in the NH.

Fig 04.

6. DISCUSSION

In these analyses, we compared cause-specific proportional hazards modeling and proportional subdistribution hazards modeling when analyzing the predictors of time to nursing home placement in a sample of older adults with dementia. Observation of the outcome in this study was complicated by the frequent occurrence of patient death as a terminal endpoint in the study. In practice, the analysis of such data is limited to only the cause-specific proportional hazards model for NH placement, with death usually treated as a noninformative censoring event and without considering the cause-specific death model. By including this component and the accompanying proportional hazards model of the subdistribution in the composite analysis, the researcher gains thorough understanding of the factors affecting the cumulative incidence of the target event.

The univariate models suggested that the method of handling death (either as a censoring event in a Cox proportional hazards model or a competing risk event in the proportional subdistribution hazards model) had only a minimal effect in estimating the intervention effect. This similarity is largely explained by the lack of an intervention difference on the CSH of death. The estimated intervention effect for delaying nursing home placement then can be interpreted as the effect on the CSH (HR = 0.73) or on the subdistribution hazards (HR = 0.77). In the models incorporating covariate effects we are able to consider known imbalances in the two treatment groups that affect the target event, and we once again saw minimal differences on the test for treatment effect. However, the examination of multiple predictors revealed that covariates deemed non-significant for the cause-specific analyses may be significant in the subdistribution hazards analysis (and vice versa). This is consistent with examples of group effects examined elsewhere [18, 19]. Specifically, we saw that treating death as a censoring event resulted in a non-significant effect of patient physical health on NH placement. After conducting the cause-specific analysis of death where poorer patient physical health showed a significantly increased the hazard of death, and then analyzing the subdistribution hazards model, did we uncover the significant effect of poor patient health in reducing the probability of NH placement.

Subdistribution hazards modeling is appealing because of its close relationship to the Cox proportional hazards model. Although the hazard constructs, risk sets, and partial likelihood functions differ somewhat, the two share the familiar proportional hazards modeling methodology. A researcher faced with competing risk events should pursue both analysis strategies: cause-specific analyses of all event types and proportional subdistribution hazards analyses.

The Fine and Gray model of the subdistribution hazard is restricted to the proportional hazards framework and other modeling methodologies of the CIF may be considered. Fine [31] presents a more flexible semi-parametric regression model for the cumulative incidence that is applicable to any transformation model. Similarly Sheike et al. [32] develop a semiparametric regression model for the CIF based on binomial regression methods. Andersen et al. [33] and Klein and Andersen [34] model the CIF based on pseudovalues from a jackknife statistic from the estimated cumulative incidence. Alternative inferences for differences in CIFs based on general summary measures, including risk ratios and odds ratios, are presented by Zhang and Fine [35]. A thorough description of these methods is beyond the scope of this paper.

In some instances, competing risk events that do affect the probability of the target event of interest may be present, but occur so infrequently that the effects on the Cox proportional hazards model parameter estimates may be negligible. The minimum frequency at which the researcher should be concerned is subjective. However, this may be assessed by conducting both the CSH and subdistribution hazards analyses and comparing the results. Latouche et al [20] studied the robustness of the subdistribution hazards analysis under a misspecified model and found, as we have seen here, that the estimates of the Fine and Gray model are impacted by the CSH of the competing risk. This further emphasizes the need for a complete analysis. In summary, we advise researchers to consider conducting both types of analyses in situations where competing risk events are common.

Appendix

The following R code was used to determine the cumulative incidence curves (CUMINC) and conduct proportional subdistribution hazards analysis (CRR). These functions are available in the CMPRSK package. Before these functions can be used, the package must be loaded. The SAS code that follows was used for the cause-specific proportional hazards models (note that R may be used for the cause-specific hazards analysis as well).

# read data into the table ×<- read.table("C:/analysis_dataset.txt",header=T,sep="\t")
# assign variable names
ftime <- x$years	# follow-up time to censor, death, or NH
fstatus <- x$fstatus	# status: 0=censor, 1=NH, 2=Death
pat_age <- x$pat_age	# patient age
pat_inc <- x$log_pat_income	# log patient income
pat_health <- x$pat_health	# patient health
gender <- x$pat_gender	# patient gender: female = 0 male = 1
freq <- x$freq_mb	# freq of M & B problems
gds5 <- x$gds5	# moderate dementia = 1, 0 otherwise
gds6 <- x$gds6	# severe dementia = 1, 0 otherwise
age <- x$caregiver_age	# caregiver age
c_hlth <- x$caregiver_health	# caregiver health
sat <- x$satisfaction	# satisfaction with support
react <- x$reaction	# reaction to M & B problems
dep <- x$depression	# depression scale
burden <- x$burden	# caregiver burden
entry <- x$entry_year	# year of study entry
tx <- x$group	# group: 0=usual, 1=intensive
# assign labels 0='usual', 1='intensive'
tx_lab <- factor(tx,label=c('usual tmt','intensive'))
# assign labels 0='censor',1='NH',2='Death'
fstatf <- factor(fstatus,label=c('censor','NH','Death'))
# get the CIFs for each intervention group
x <- cuminc(ftime,fstatf,tx_lab,cencode='censor')
plot.cuminc(x,main="CIFs",xlab="Years",ylab="Probability",lty=1, lwd=2, color=1:6)
# multiple covariate analysis for proportional subdistribution hazards
y <- crr(ftime, fstatf, cov1=cbind(pat_age, pat_inc, pat_health, gender, freq, gds5, gds6,
+ age, c_hlth, sat, react, dep, burden, entry, tx_lab), failcode='NH', cencode='censor')
# produce the estimated cumulative incidence function for a male Alzheimer’s patient
# with moderate dementia (excellent health vs poor health) with caregiver receiving the
# intensive support. This patient is assumed to be average with respect to the other
# covariates and enters the study in year 4.
y.plot <- predict.crr(y,cov1=rbind(cbind(74, 3.6, 1, 1, 44, 1, 0, 71, 2, 4, 24, 10, 36, 4, + 1),cbind(74, 3.6, 4, 1, 44, 1, 0, 71, 2, 4, 24, 10, 36, 4, 1)))
plot(y.plot,ylim=c(0,1),xlab="Years",ylab="Probability")
# produce the estimated cumulative incidence function without covariate adjustment
z <- crr(ftime, fstatf, cov1=cbind(tx_lab), failcode='NH', cencode='censor')
z.plot <- predict.crr(z,cov1=c(0,1))
plot(z.plot,ylim=c(0,1),xlab="Years",ylab="Probability")
SAS code for Cox Proportional Hazards Models
* This code conducts cause-specific hazards analysis in SAS;
* treatment effect only;
proc phreg data=new;
model years*fstatus(0,2) = group/ risklimits;
title 'cause specific hazards for NH placement - treatment effect only';
run; quit;
proc phreg data=new;
model years*fstatus(0,1) = group/ risklimits;
title 'cause specific hazards for death - treatment effect only';
run; quit;
* treatment effect with covariates;
proc phreg data=new;
model years*fstatus(0,2) = pat_age log_pat_income pat_health pat_gender freq_mb gds5 gds6 caregiver_age caregiver_health satisfaction reaction depression burden entry_year group / risklimits;
title 'cause specific hazards for NH placement ';
run; quit;
proc phreg data=new;
model years*fstatus(0,1) = pat_age log_pat_income pat_health pat_gender freq_mb gds5 gds6 caregiver_age caregiver_health satisfaction reaction depression burden entry_year group / risklimits;
title 'cause specific hazards for death ';
run; quit;