Accuracy of ¹³¹I Tumor Quantification in Radioimmunotherapy Using SPECT Imaging with an Ultra-High-Energy Collimator: Monte Carlo Study

Abstract

Accuracy of ¹³¹I tumor quantification after radioimmunotherapy (RIT) was investigated for SPECT imaging with an ultra-highenergy (UHE) collimator designed for imaging 511-keV photons.

Methods

First, measurements and Monte Carlo simulations were carried out to compare the UHE collimator with a conventionally used, high-energy collimator. On the basis of this comparison, the UHE collimator was selected for this investigation, which was carried out by simulation of spherical tumors in a phantom. Reconstruction was by an expectation–maximization algorithm that included scatter and attenuation correction. Keeping the tumor activity constant, simulations were carried out to assess how volume-of-interest (VOI) counts vary with background activity, radius of rotation (ROR), tumor location, and size. The constant calibration factor for quantification was determined from VOI counts corresponding to a 3.63-cm-radius sphere of known activity. Tight VOIs corresponding to the physical size of the spheres or tumors were used.

Results

Use of the UHE collimator resulted in a large reduction in ¹³¹I penetration, which is especially significant in RIT where background uptake is high. With the UHE collimator, typical patient images showed an improvement in contrast. Considering the desired geometric events, sensitivity was reduced, but only by a factor of 1.6. Simulation results for a 3.63-cm-radius tumor showed that VOI counts vary with background, location, and ROR by less than 3.2%, 3%, and 5.3%, respectively. The variation with tumor size was more significant and was a function of the background. Good quantification accuracy (<6.5% error) was achieved when tumor size was the same as the sphere size used in the calibration, irrespective of the other parameters. For smaller tumors, activities were underestimated by up to −15% for the 2.88-cm-radius sphere, −23% for the 2.29-cm-radius sphere, and −47% for the 1.68-cm-radius sphere.

Conclusion

Reasonable accuracy can be achieved for VOI quantification of ¹³¹I using SPECT with an UHE collimator and a constant calibration factor. Difference in tumor size relative to the size of the calibration sphere had the biggest effect on accuracy, and recovery coefficients are needed to improve quantification of small tumors.

Clinical trials of ¹³¹I-labeled radioimmunotherapy (RIT) are showing promise for the treatment of B-cell non-Hodgkin’s lymphoma (NHL) (1–4). At the University of Michigan, a phase I RIT trial of NHL using ¹³¹I-labeled anti-B1 monoclonal antibody has been completed and reports that, of 28 salvage-therapy patients, 79% achieved a response and 50% achieved a complete response (1). The success at this institution and others has renewed interest in accurate ¹³¹I quantification for dosimetric calculations. Both SPECT (5–9) and planar imaging (10–13) have been used to carry out quantitative imaging of ¹³¹I. However, SPECT is the preferred method for accurate estimation of activity in sites with significant activity in overlying or adjacent tissues.

The most significant ¹³¹I γ-ray emissions are at 364 keV (82%), 637 keV (7.2%), and 723 keV (1.8%), and typically imaging is carried out with a photopeak window at 364 keV. Collimator septal penetration by these medium-energy and high-energy (HE) emissions has been recognized as 1 of the principal limitations in accurate SPECT quantification of ¹³¹I (14–18). The camera-wide tails of the ¹³¹I point spread function (PSF), which are a result of scatter and penetration, degrade focal quantification accuracy caused by activity spillover from the surrounding tissue. This is especially important in intravenously administrated RIT where antibody uptake by surrounding organs is significant compared with tumor uptake. Work on compensation for scatter and septal penetration in ¹³¹I imaging has been limited to energy spectra–based methods (8,10,16). These methods are easy to implement in the clinic using multiwindow acquisitions but cannot compensate for the 364-keV photons that penetrate the collimator without undergoing a scatter interaction anywhere. Such events have the same energy spectrum as the desired events (no scatter and no penetration) and, hence, cannot be compensated by techniques that are based on differences in the energy spectra (18). Therefore, even if energy spectra-based compensation is used, it is important to minimize septal penetration by proper collimator design or selection.

Recently Smith and Jaszczak (17) and Smith et al. (7) designed and tested both a rotating parallel-hole collimator and a pinhole collimator for high-resolution SPECT imaging of ¹³¹I distribution in brain tumors. Typically, ¹³¹I imaging after RIT is carried out using commercial HE or mediumenergy, parallel-hole, general-purpose collimators. The HE collimators are designed for ¹³¹I, but Monte Carlo simulations (15,18) and experimental measurement (19) have shown that they allow a substantial amount of photon penetration. In this work we propose the use of a commercially available, ultra-high-energy (UHE), parallel-hole collimator for quantitative ¹³¹I SPECT. This collimator was designed for imaging the 511-keV photons in positron SPECT but can also be used to significantly reduce septal penetration in ¹³¹I SPECT. However, the thicker septa of the UHE collimator can result in loss of sensitivity and hole pattern artifacts. In the first part of this work we compare the performance of the HE and UHE collimators by experimental measurement and Monte Carlo simulation. On the basis of this comparison, the UHE collimator is selected for our investigation of quantitative imaging, which is carried out by simulating tumor phantoms. The SPECT quantification procedure we investigated is similar to that used to determine ¹³¹I tumor dosimetry of NHL patients at our clinic (20). Previously we have carried out some experimental phantom measurements with the HE collimator to show the accuracy of our clinical quantification procedure (8,21). This more detailed Monte Carlo study identifies some of the limitations in volume-of-interest (VOI) quantification of radioactive structures and establishes error limits for clinical ¹³¹I SPECT using an UHE collimator.

MATERIALS AND METHODS

SPECT System and Collimators

The SPECT camera used in this work was a Prism XP3000 (Picker International, Inc., Cleveland Heights, OH). The NaI crystal measured 24 × 40 × 0.95 cm. The measured energy resolution at 364 keV was 10.2% (full width at half maximum [FWHM]). The spatial resolution at 10 cm measured for ¹³¹I with the HE collimator was 1.2 cm (FWHM). In both measurement and simulation, tomographic acquisitions used 360°, 60 angles, and a 20% photopeak window at 364 keV. A 128 × 128 matrix with a pixel size of 3.6 mm was used for point source images, and a 64 × 64 matrix with a pixel size of 7.2 mm was used for phantom images. Phantom projections were reconstructed using a space-alternating generalized expectation–maximization algorithm (22). The algorithm used an attenuation-weighted strip integral and incorporated scatter estimates based on the triple-energy window (TEW) method into the Poisson statistical model. The attenuation coefficient of water at 364 keV (0.11 cm⁻¹) and the actual dimensions of the elliptic phantom were used to generate the attenuation map. The subwindows for the TEW correction were located adjacent to the main window and were 6% in width.

The hole size, septa, and thickness of the UHE, general-purpose, parallel-hole collimator (UHEGAP; Picker International) are 5.08, 3.43, and 77 mm, respectively, whereas those of the HE, generalpurpose, parallel-hole collimator (HEGAP; Picker International) are 3.81, 1.73, and 58.4 mm, respectively. Both collimators have a hexagonal hole shape. Note that the septal thickness of the UHE collimator is almost 2 times that of the HE collimator. The theoretic spatial resolution (FWHM) using Anger’s equation (23) at 10 and 15 cm is 1.03 and 1.36 cm for the HE collimator and 1.17 and 1.50 cm for the UHE collimator.

Monte Carlo Model

All simulations were carried out using the well-established SIMIND Monte Carlo code (24,25). The version of the code that is used here is coupled to a collimator routine (26) that explicitly models collimator scatter and penetration. The camera model includes a 5-cm glass layer behind the NaI crystal to model backscatter. We previously validated the SIMIND code for ¹³¹I imaging with the HE collimator (18). The modeling of the UHE collimator is verified in this work by comparing measured and simulated energy spectra and PSF. Note that for ease of implementation the collimator routine is restricted to a rectangular hole shape. As proposed by de Vries et al. (26), the hexagonal hole shape UHE collimator was approximated in the simulation by a square hole collimator that has the same open area and lead content. Although explicit modeling of the collimator is computationally tedious, SIMIND is relatively fast compared with some other Monte Carlo codes. For each of the studies presented, it took between 1 and 6 days of central processing unit time on a DEC Alpha XP1000 workstation (Compaq Computer Corp., Littleton, MA) to simulate all 60 projection angles with a large number of emitted photons (1 × 10⁸ to 6 × 10⁸ photons) per projection.

Comparison of HE and UHE Collimators

Experimental Measurements

To compare energy spectra, PSFs, and hole pattern artifacts, planar acquisitions were carried out for a point source in air 19 cm away from the collimator face. The source was a 6-mm-diameter filter paper soaked in ¹³¹I solution. These measured data were also used to validate Monte Carlo modeling of the UHE collimator.

To compare contrast and hole pattern artifacts in typical SPECT images, 3 NHL patients who had undergone RIT at our clinic were imaged using UHE and HE collimators consecutively. Acquisition time was 20 min, and the other parameters of the acquisition and reconstruction were as described. Note that to change the collimators it was necessary to move the patients between scans. Therefore, to carry out a valid comparison, the HE and UHE collimator images were registered to the same space using a mutual information image fusion program.

Monte Carlo Simulation

Monte Carlo simulation is ideal for assessing penetration and scatter because these events can be tracked separately, which is not possible in experimental measurements. To quantitatively compare scatter and penetration for the 2 collimators, the geometric, scatter, and penetration components of photopeak events were separated for a planar acquisition of a point source in air 19 cm from the collimator. Geometric implies traversing the collimator hole without interaction; scatter implies scattering in the collimator lead, whereas penetration implies penetration of 1 or more septa without scatter.

When comparing sensitivity, it is important to compare not only the total events but also the desired geometric events in the photopeak window. Because measurement will not allow for the latter comparison, simulation was used to compare sensitivity both in terms of total events and geometric events for the point source acquisition.

On the basis of the results of the comparison of the 2 collimators, the UHE collimator was selected for this investigation of SPECT quantification carried out by Monte Carlo simulation of tumor phantoms.

SPECT Quantification Using UHE Collimator

Phantom

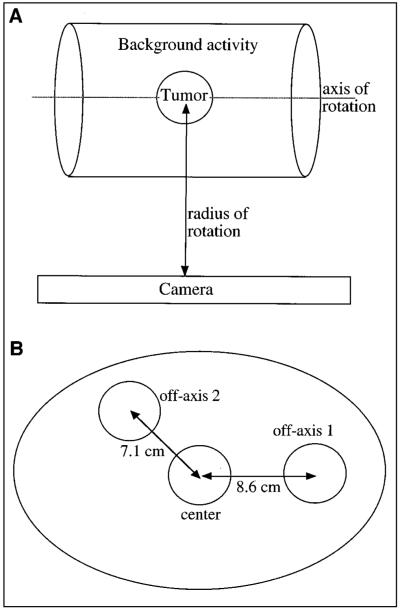
The tumors were modeled by hollow spheres filled with ¹³¹I solution and placed in a radioactive or cold water–filled elliptic phantom that represents the tissue of the rest of the body (Fig. 1A). The location, size, and number of spheres varied, but in all cases the elliptic phantom was centered with respect to the crystal and was constant in size (23 × 31.5 cm and 20.5 cm in height).

FIGURE 1.

(A) Simulated phantom consists of hot sphere centered in elliptic phantom. (B) Center plane of phantom shows 3 sphere locations.

A large number of emitted photons were simulated to produce low-noise images. Acquisition parameters and reconstruction were as described. Tight VOIs corresponding to the physical size of the simulated spheres were used to define tumor boundaries, and the physical size of the phantom was used to define the attenuation map. This is consistent with our clinical SPECT quantification procedure whereby patient-specific attenuation maps and tumor VOI are obtained by CT–SPECT fusion (5). Tumor VOIs correspond to physical size because they are outlined on the patient CT by a trained radiologist.

Several factors can affect VOI quantification of radioactive structures. The effects of tissue-background activity, tumor location, radius of rotation (ROR), and tumor size were assessed by varying each of these parameters and comparing tumor VOI counts in the reconstructed image. Note that typical values from patient imaging were used for these parameters. It is possible to simply compare VOI counts because, in all cases, the simulated tumor activity and acquisition time were the same and projection images were normalized by the number of histories. Effects of statistical noise, tumor shape, patient size, and nonuniform attenuation were not addressed in this study.

Background Activity

To investigate the effect of background activity, a 3.63-cm-radius tumor was positioned at the center of the standard phantom, with 4 different levels of uniform activity outside the tumor (Fig. 1A). The background level, b, is defined as the ratio of activity concentration in the elliptic phantom over that in the tumor. The tested b values were 0, 1/8, 1/5, and 1/3, and the ROR was 26 cm. Note that the background activity and sphere activity were simulated separately, and the 2 sets of projections were superimposed after scaling the sphere projections to achieve the required b value. This greatly reduced the simulation time because the same set of projections could be used to obtain different background levels. The range b = 0 to 1/3 was selected for simulation on the basis of typical tumor and organ counts in patient ¹³¹I SPECT images and conjugate view organ and tumor dosimetry (27) carried out at our clinic. The background level of 1/3 can be considered a worst case equivalent to a situation in which the tumor is adjacent to a high-uptake organ such as the liver or spleen.

The effect of nonuniform activity distribution was also evaluated. For this case 2 hot spheres, identical to the center sphere in activity and size, were located off-axis on the center plane of the phantom as shown in Figure 1B. In the case termed nonuniform 1 the water surrounding the spheres was nonradioactive, whereas in the case termed nonuniform 2 the water surrounding the spheres was radioactive with b = 1/8. The center sphere was considered the target sphere with the off-axis spheres forming the nonuniform background for the target.

Location

To investigate the effect of tumor location, simulations were carried out for 3 sphere positions at the center plane of the standard phantom. The sphere locations were as indicated in Figure 1B but only 1 of the 3 spheres was present at a time. The spheres were 3.63 cm in radius, and the ROR was 26 cm. All 4 background levels specified previously were simulated.

ROR

To investigate the effect of ROR, the distance between the phantom axis and the front face of the collimator was varied between 22 and 30 cm, which is a typical range for patient imaging. The 3.63-cm-radius sphere was centered in the phantom, with the background activity at zero.

Size

To investigate the effect of tumor size, simulations were carried out for tumors of 4 different sizes centered in the phantom. The sphere volumes were 20, 50, 100, and 200 mL, which corresponds to sphere radii of 1.68, 2.29, 2.88, and 3.63 cm, respectively. The ROR was 26 cm and all 4 levels of background activity specified previously were simulated. In our SPECT evaluations of 131 tumors in 31 NHL patients, the tumor volumes ranged from 1.27 to 795 mL with a mean of 59.2 mL and a median of 20.7 mL (20).

Calibration Factor and Absolute Quantification

A constant calibration factor was used to convert VOI counts in the reconstructed images to activities. The simulation with the 3.63-cmradius sphere, center location, ROR of 26 cm, and b = 1/5 was selected as the calibration experiment. The sphere VOI counts were divided by the simulated sphere activity and total acquisition time for all projection angles to obtain a calibration factor in units of counts per sec per megabecquerel (cps/MBq). Using this conversion, SPECT-estimated tumor activities were compared with the true activities for each of the simulations discussed previously.

RESULTS

Comparison of HE and UHE Collimators

Experimental Measurements

For the point source in air, the measured energy spectra are compared in Figure 2. In the spectrum corresponding to the HE collimator, the 637- and 722-keV photopeaks appear with much higher intensity than would be expected on the basis of their emission intensities. This is because the higher energy emissions have a higher probability of penetrating the collimator. As Figure 2 shows, this contribution from HE penetration is greatly reduced in the spectrum corresponding to the UHE collimator because of the thicker septa. The tail beyond the 364-keV photopeak is caused by the 637- and 722-keV photons that scatter in the collimator or detector or penetrate the collimator and also undergo scatter in the detector. Comparison of the 2 energy spectra shows that the UHE collimator greatly reduces the fraction of such events that would be included in the photopeak window at 364 keV. As a validation of the Monte Carlo code, Figure 2 also includes the simulated energy spectrum for the UHE collimator. Good agreement is shown between measurement and simulation.

FIGURE 2.

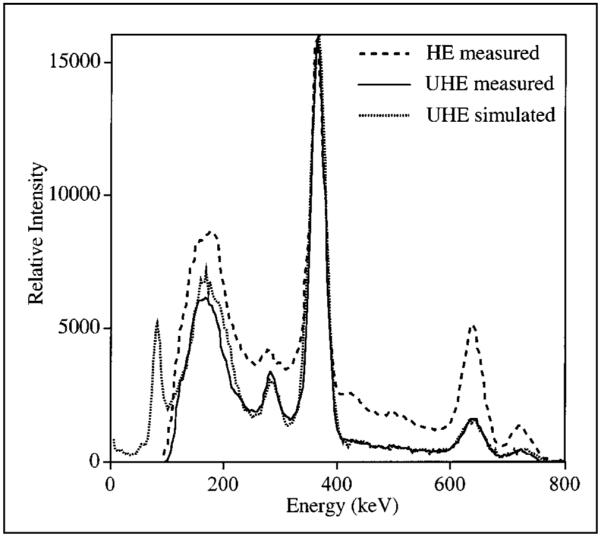
¹³¹I point source energy spectrum for 2 collimators.

The measured planar point source images and the corresponding line profiles are compared in Figure 3. The images have been normalized such that they have the same maximum intensity and the profiles such that they have the same total counts. As Figure 3 indicates, the camera-wide tails of the ¹³¹I PSF can be sharply reduced by using the UHE collimator. In the images, the fraction of counts in a small-diameter (5.76 cm), circular region of interest (ROI) centered on the peak compared with the counts in the total FOV is 0.34 for the HE collimator and 0.82 for the UHE collimator. When the PSFs are compared at a distance of 5 cm from the peak, the UHE collimator value is lower by a factor of 10. Because of the thicker septa and the larger hole size, the hexagonal hole pattern is clearly visible in the point source image and PSF corresponding to the UHE collimator. The hole pattern makes it difficult to measure the system resolution with the UHE collimator in terms of FWHM, but Figure 3C indicates that the 2 collimators have comparable resolution. The FWHM of the HE collimator PSF of Figure 3C is 1.7 cm. As a validation of the Monte Carlo code, Figure 3C also includes the simulated PSF for the UHE collimator. There is good agreement between measurement and simulation with the main difference being the absence of hole pattern artifacts in the simulated PSF. This is because the collimator response is spatially averaged in the simulation.

FIGURE 3.

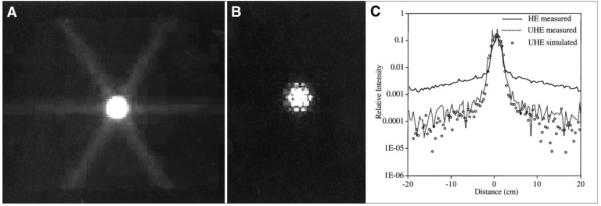
¹³¹I point source planar image measured with HE collimator (A) and UHE collimator (B). (C) Profiles from (A) and (B) and simulated profile for UHE collimator.

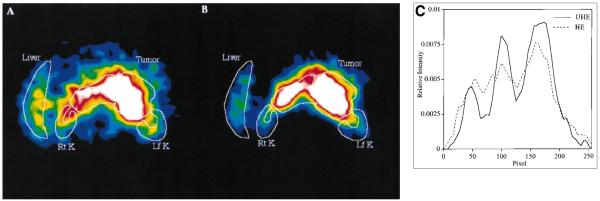
Figure 4 compares the same reconstructed slice and corresponding line profiles for 1 of the patients imaged with both collimators. The images are normalized such that they have the same maximum intensity and the profiles such that they have the same total counts. The reconstructed resolution (FWHM) in the transaxial and axial directions is 2.1 and 1.6 cm for the HE collimator and 2.3 and 1.9 cm for the UHE collimator. The area imaged was the abdomen, and Figure 4 shows some activity in the inferior tip of the liver and uptake in a large tumor surrounding the aorta. Patient images obtained with the UHE collimator show a clear improvement in contrast associated with reduction in penetration. Because of the relatively large object size and poor reconstructed resolution, hole pattern artifacts are not evident in typical patient images.

FIGURE 4.

Reconstructed slice in abdominal region of patient imaged with HE collimator (A) and UHE collimator (B) after ¹³¹I RIT. Rt K = right kidney; Lf K = left kidney. (C) Profiles from (A) and (B).

Monte Carlo Simulation

The geometric, penetration, and scatter components of the photopeak events for the point source in air are compared in Table 1. Use of the UHE collimator increases the geometric component from 27% to 72%. Reduction of penetration is especially significant because this component has the same energy distribution as the geometric component and compensation by energy spectra–based methods is not possible for these events.

TABLE 1.

Monte Carlo Comparison of Geometric, Penetration, and Scatter Component of Events Within Photopeak Window for Point Source in Air

Collimator	Geometric (%)	Penetration (%)	Scatter (%)
HE	27.3	43.3	29.4
UHE	72.4	17.3	10.3

Considering all events, the simulated sensitivities for the point source measurement were 64.6 and 15.1 cps/MBq for the HE and UHE collimators, respectively. According to Table 1, a large fraction of the total events includes scatter events that will be subtracted by the compensation method or unwanted penetration events. When only the desired geometric events are compared, the sensitivity with the UHE collimator is only a factor of 1.6 lower than that with the HE collimator. This loss of sensitivity is not of concern in high count rate situations such as imaging after ¹³¹I RIT where typically 1.9–3.7 GBq of activity is infused for therapy.

SPECT Quantification with UHE Collimator

Effect of Background

The sphere VOI counts at different values of the uniform background level are tabulated in Table 2. The values in parentheses are percentage differences from counts corresponding to the b = 0 case. The VOI counts as a function of the background level are plotted in Figure 5 both with and without scatter compensation in the reconstruction. As Figure 5 indicates, the VOI counts increase linearly with background, but the dependence is small when TEW scatter compensation is used. Going from b = 0 to 1/3, the VOI counts increase by 11.7% without scatter compensation and by only 1.8% with scatter compensation. For smaller tumors, the VOI counts increase much more significantly with background. Ideally, the sphere counts should be independent of background, but this is not achieved because of imperfect scatter correction or activity spillover associated with septal penetration and finite spatial resolution of the system. Table 2 also gives the VOI counts for the center sphere with off-axis spheres forming a nonuniform background. Because of activity spillover from the nearby hot spheres, the center sphere counts are overestimated but only slightly (<3.2%).

TABLE 2.

Tumor VOI Counts for 3.63-cm-Radius Sphere at Different Values of b for Uniform and Nonuniform Background Activity Distributions

	VOI counts*
Background	b = 0	b = 1/8	b = 1/5	b = 1/3
Uniform	541.2 (0)	547.2 (1.0)	548.5 (1.3)	551.2 (1.8)
Nonuniform 1	555.7 (2.7)
Nonuniform 2		558.3 (3.2)

^*Values in parentheses are percentage differences from counts corresponding to b = 0 case.

FIGURE 5.

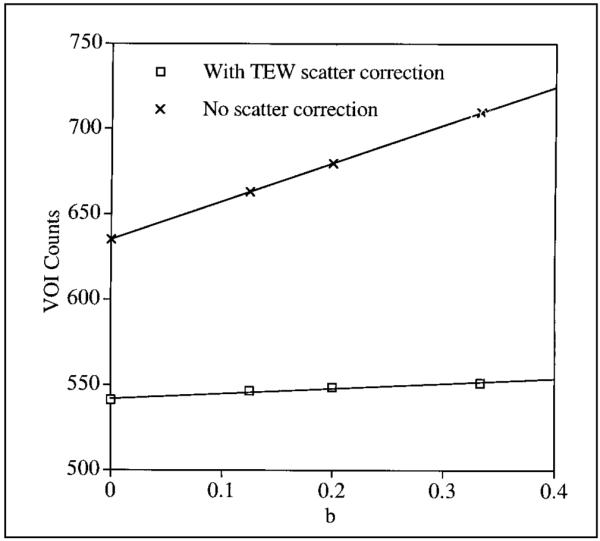
Tumor VOI counts as function of b with and without scatter correction for 3.63-cm-radius sphere.

Effect of Tumor Location and ROR

The VOI counts corresponding to the 3 sphere locations are compared in Table 3. The values in parentheses are percentage differences from the central sphere counts. These results show that there is very little dependence (<3%) of VOI counts on source location within the phantom, which gives us confidence in our scatter and attenuation correction. In all cases, the VOI counts corresponding to the off-axis spheres were slightly higher than the counts corresponding to the central sphere, perhaps because of improved resolution for objects closer to the phantom edge. In ¹³¹I patient SPECT dosimetry calculations, we have observed that axillary tumors close to the periphery of the body typically have a lower radiation dose than do tumors in other regions of the body such as the abdomen (20). The present results indicate that this is not an artifact of the quantification procedure associated with differences in tumor location.

TABLE 3.

Tumor VOI Counts for 3.63-cm-Radius Sphere at Different Locations and Different RORs

Tumor location	ROR (cm)	VOI counts*
		b = 0	b = 1/8	b = 1/5	b = 1/3
Center	26	541.2 (0)	547.2 (0)	548.5 (0)	551.4 (0)
Off-axis 1	26	550.4 (1.7)	560.1 (2.4)	562.8 (2.6)	568 (3)
Off-axis 2	26	542.1 (0.2)	553.9 (1.2)	558.3 (1.8)	566.5 (2.7)
Center	26	541.2 (0)
Center	22	568.2 (5)
Center	30	512.6 (−5.3)

^*Values in parentheses are percentage differences from central sphere counts.

The sphere VOI counts at 3 different values of the ROR are compared in Table 3. The values in parentheses are percentage differences from the counts corresponding to the ROR of 26 cm, which is the middle of the examined range. VOI counts decrease with increase in ROR because as the distance from source to detector increases the image will be more smeared and more counts will be excluded from the VOI. This is especially significant when a tight VOI corresponding to the physical object size is used. By plotting counts versus the ROR, the relationship between the 2 was found to be linear (r² = 1).

Effect of Tumor Size

The VOI counts corresponding to the 4 sphere sizes are compared in Table 4. The values in parentheses are percentage differences from the counts corresponding to the 3.63-cm-radius sphere. The VOI counts decrease significantly with decrease in object size because of limitations imposed by resolution. The dependence of VOI counts on sphere size varies with the background level. The underestimation of counts for the smaller spheres is most severe at b = 0. As background increases, the loss of counts is somewhat compensated by activity spillover from the background, which has a larger effect on the smaller spheres.

TABLE 4.

Tumor VOI Counts at Different Values of b for Different Tumor Sizes

Tumor radius (cm)	VOI counts*
	b = 0	b = 1/8	b = 1/5	b = 1/3
3.63	541.2 (0)	547.2 (0)	548.5 (0)	551.4 (0)
2.88	465.1 (−14.1)	484.3 (−11.5)	494.5 (−9.8)	512.1 (−7.1)
2.29	422.4 (−22)	468.2 (−14.4)	478.6 (−12.7)	511.8 (−7.2)
1.68	292.2 (−46)	343.8 (−37.2)	373.9 (−31.8)	423.9 (−23)

^*Values in parentheses are percentage differences from counts corresponding to 3.63-cm-radius sphere.

Calibration Factor and Absolute Tumor Activity

On the basis of the simulation of the calibration experiment, the calibration factor was determined to be 9.14 cps/MBq. Using this constant calibration factor, the tumor VOI counts corresponding to each of the previous simulations (28 cases in all) were converted to activity. The percentage difference between this SPECT estimated activity and the true simulated activity for each tumor is given in Table 5. Note that the case with an activity error of 0% corresponds to the calibration experiment. Results show that when the sphere size and ROR are the same as those used in the calibration, activity estimates are very accurate (<3.6% error) over the range of b values. Sphere activity estimates were also reasonable (<6.5%) when the ROR was changed to cover a typical range used in patient imaging. The error in activity estimates is greatest when the tumor size is less than the sphere size used in the calibration. Activity is underestimated by up to 47% for the smallest tumor simulated.

TABLE 5.

Tumor Activity Quantification

Tumor radius (cm)	b	ROR (cm)	Location	Activity error* (%)
3.63	0	26	Center	−1.3
3.63	1/8	26	Center	−0.2
3.63	1/5	26	Center	+0.0
3.63	1/3	26	Center	+0.5
3.63	0	22	Center	+3.6
3.63	0	30	Center	−6.5
3.63	0	26	Off-axis 1	+0.3
3.63	0	26	Off-axis 2	−1.2
3.63	1/8	26	Off-axis 1	+2.1
3.63	1/8	26	Off-axis 2	+1.0
3.63	1/5	26	Off-axis 1	+2.6
3.63	1/5	26	Off-axis 2	+1.8
3.63	1/3	26	Off-axis 1	+3.6
3.63	1/3	26	Off-axis 2	+3.3
3.63	Nonuniform 1	26	Center	+1.3
3.63	Nonuniform 2	26	Center	+1.8
2.88	0	26	Center	−15.2
2.88	1/8	26	Center	−11.7
2.88	1/5	26	Center	−9.8
2.88	1/3	26	Center	−6.6
2.29	0	26	Center	−23.0
2.29	1/8	26	Center	−14.6
2.29	1/5	26	Center	−12.7
2.29	1/3	26	Center	−6.7
1.68	0	26	Center	−46.7
1.68	1/8	26	Center	−37.3
1.68	1/5	26	Center	−31.8
1.68	1/3	26	Center	−22.7

^*Error is percentage difference between SPECT estimated value and true simulated value.

DISCUSSION

The reduction in ¹³¹I penetration that was observed with the UHE collimator comes at the expense of some loss in sensitivity. In a previous study on quantitative ¹³¹I scintigraphy, Specht et al. (14) recommended the following priorities for collimator selection listed in order of importance—namely, septal penetration, sensitivity, and resolution. In a review article on collimator design for SPECT, not specific for ¹³¹I, Moore et al. (28) suggested that improvement in image quality be given a greater weight than the loss in sensitivity.

Calibration procedures different from those described in this study have been used by previous investigators for ¹³¹I SPECT quantification. Recently, Smith et al. (7) reported on phantom measurements with pinhole SPECT to determine ¹³¹I distributions in brain tumors in the range 20–100 mL. The calibration factor was determined using an empiric threshold and a reference point source in air. Tumor counts were determined by applying a 10% threshold within a loose, manually drawn ROI. Their method was designed for estimating tumor uptake after intratumoral administration of activity where background uptake is very low. Israel et al. (9) also reported good correlation between measured and true concentration for ¹³¹I SPECT quantification of tumor phantoms in the range 25–127 mL. Volumes and concentrations were calculated by applying an empirically determined threshold within an ROI. Accurate activity estimates were also obtained by Green et al. (6) for an ¹³¹I source regardless of background activity.

The tumor quantification procedure investigated in this study is suitable for intravenously administered ¹³¹I RIT where tumor-to-background contrast is low. Because of the high background, target volumes were defined by physical size and not by establishing a threshold. Instead of using a reference point source, the system calibration factor was determined using a sphere centered in an elliptic phantom. The definition of the VOI, scatter correction, attenuation correction, and reconstruction for both the calibration data and the tumor data were carried out in the same manner. Note that the quantification results of Table 5 were obtained using a constant calibration factor without applying correction factors to account for variation in tumor size, background level, or ROR. To achieve accurate quantification with this methodology when tumor size is significantly different from the calibration sphere, recovery coefficients must be applied. In our clinical SPECT quantification procedure, recovery coefficients are used when quantifying objects that are <200 mL (29). Previously, Hoffman et al. (30) and Kessler et al. (31) investigated the effect of object size on quantitative imaging with positron emission CT. They also reported considerable degradation in activity recovery when imaging objects with limited size. Hoffman et al. introduced recovery coefficients to correct the apparent isotope concentration to the true isotope concentration for objects that fall into the size range <2 × FWHM.

In a future Monte Carlo study, the effect of tumor shape, nonuniform scattering, and attenuating media and statistical noise will be investigated. Of these factors not considered in this work, tumor shape is expected to have the most significant effect, especially when analyzing small tumors. Mazziotta et al. (32) showed previously that in positron emission CT brain imaging, quantitative measurement inaccuracies in small objects are a function of object shape. Assuming no error in the CT–SPECT fusion procedure, nonuniform attenuation is not expected to significantly affect our quantification accuracy because of the availability of patient-specific attenuation maps. The effect of nonuniform scattering media is also not expected to be significant because pixel-by-pixel scatter compensation is carried out by the TEW method. However, in the future, both nonuniform attenuation and scatter will be assessed further by simulating realistic imaging situations using a digitized anthropomorphic phantom (33). In ¹³¹I SPECT imaging after RIT, the count rate is sufficiently high that statistical noise is not expected to greatly affect quantification accuracy either.

CONCLUSION

The reduction in penetration associated with the use of the UHE collimator is especially significant in ¹³¹I RIT where activity spillover is a major limitation to accurate tumor quantification. The reduction in penetration came at the expense of some loss in sensitivity, but this is not a concern in post-therapy RIT imaging. With the UHE collimator typical patient images show an improvement in contrast and no effects of hole pattern visualization. On the basis of the results of this study we are considering using the UHE collimator for SPECT imaging of future NHL patients undergoing RIT at our clinic. The quantification procedure evaluated for the UHE collimator used a VOI corresponding to physical size and a constant calibration factor. When tumor size was the same as the sphere size used for the calibration, quantification error was <6.5% when other parameters were varied over typical values found in patient imaging. However, when tumor size was reduced, accuracy was significantly worse and recovery coefficients are needed to improve quantification.