Kinetics of M₁ muscarinic receptor and G protein signaling to phospholipase C in living cells

Abstract

G protein–coupled receptors (GPCRs) mediate responses to external stimuli in various cell types. Early events, such as the binding of ligand and G proteins to the receptor, nucleotide exchange (NX), and GTPase activity at the Gα subunit, are common for many different GPCRs. For G_q-coupled M₁ muscarinic (acetylcholine) receptors (M₁Rs), we recently measured time courses of intermediate steps in the signaling cascade using Förster resonance energy transfer (FRET). The expression of FRET probes changes the density of signaling molecules. To provide a full quantitative description of M₁R signaling that includes a simulation of kinetics in native (tsA201) cells, we now determine the density of FRET probes and construct a kinetic model of M₁R signaling through G_q to activation of phospholipase C (PLC). Downstream effects on the trace membrane lipid phosphatidylinositol 4,5-bisphosphate (PIP₂) and PIP₂-dependent KCNQ2/3 current are considered in our companion paper in this issue (Falkenburger et al. 2010. J. Gen. Physiol. doi:10.1085/jgp.200910345). By calibrating their fluorescence intensity, we found that we selected transfected cells for our experiments with ∼3,000 fluorescently labeled receptors, G proteins, or PLC molecules per µm² of plasma membrane. Endogenous levels are much lower, 1–40 per µm². Our kinetic model reproduces the time courses and concentration–response relationships measured by FRET and explains observed delays. It predicts affinities and rate constants that align well with literature values. In native tsA201 cells, much of the delay between ligand binding and PLC activation reflects slow binding of G proteins to receptors. With M₁R and Gβ FRET probes overexpressed, 10% of receptors have G proteins bound at rest, rising to 73% in the presence of agonist. In agreement with previous work, the model suggests that binding of PLC to Gα_q greatly speeds up NX and GTPase activity, and that PLC is maintained in the active state by cycles of rapid GTP hydrolysis and NX on Gα_q subunits bound to PLC.

INTRODUCTION

G protein-coupled receptors (GPCRs) transduce extracellular signals to initiate intracellular signaling cascades. This large receptor family serves diverse physiological functions and constitutes a good portion of pharmaceutical targets (Sautel and Milligan, 2000). We describe kinetic studies as one way to understand how GPCR signaling works. We focus on activation of the G_q-coupled M₁ muscarinic (acetylcholine) receptor (M₁R) and its consequences: activation of PLC, depletion of phosphatidylinositol 4,5-bisphosphate (PIP₂), and closure of PIP₂-dependent KCNQ channels (Suh et al., 2004; Jensen et al., 2009). M₁R signaling increases excitability in mammalian sympathetic neurons (Brown, 1983) and augments hippocampal long-term potentiation (e.g., Shinoe et al., 2005).

Using Förster resonance energy transfer (FRET) in an expression system, we have previously measured time courses of individual steps in the M₁R signaling cascade (Jensen et al., 2009). The first steps include the binding of the muscarinic agonist to the M₁R, activation of G proteins and the binding of the Gα_q subunit to PLC (Fig. 1). FRET allowed us to track the interactions of signaling proteins within intact cells. We monitored G protein activity by measuring both the interaction of Gβ subunits with receptors, which increased in the presence of agonist, and the interaction of Gβ with Gα, which decreased in the presence of agonist. The time courses of these interactions were different, and we interpreted them in the classical sense, that G proteins are recruited to the receptors with agonist and dissociate upon nucleotide exchange (NX). It is nonetheless possible that conformational rearrangement instead of binding/unbinding underlies these changes.

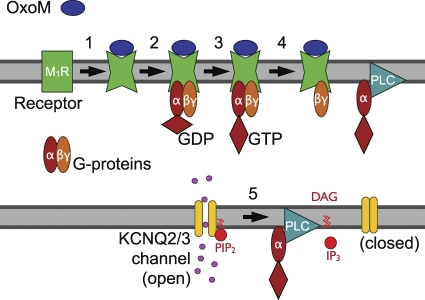
Figure 1.

Schematic representation of classical M₁R signaling. (1) Binding of the agonist Oxo-M to the M₁R increases receptor affinity for G proteins. (2) Binding of G proteins to the receptor leads to NX (3) on the Gα_q subunit. (4) G protein αβγ trimers dissociate, and Gα_q binds to PLC. (5) KCNQ2/3 potassium channels require PIP₂ to open. Activated PLC cleaves PIP₂ into DAG and IP₃. PIP₂ depletion turns off KCNQ2/3 channels.

The FRET probes needed to be overexpressed, with each signaling step being reconstituted using a different set of transfected proteins. Such changes in the amounts of signaling molecules affected the timing. To better analyze our measurements, we have therefore determined the amounts of expressed and endogenous signaling molecules and constructed a kinetic model of the M₁R signaling cascade. In quantifying FRET probes, the present study follows the lead of several studies that determined the density of fluorescent molecules by comparing intensities of cells to fluorescent beads and to solutions of recombinant fluorescent proteins (Chiu et al., 2001; An and Almers, 2004; Sugiyama et al., 2005).

We then combine this molecular census with our kinetic observations (Jensen et al., 2009) to develop a comprehensive, quantitative description for M₁R signaling. Previous models of GPCR signaling have been helpful in explaining high-affinity and low-affinity binding sites for ligands at GPCRs (De Lean et al., 1980), inverse agonism (Kinzer-Ursem and Linderman, 2007), GTPase-activating properties of PLC (Bornheimer et al., 2004; Turcotte et al., 2008), and modulation by regulators of G protein signaling (Hao et al., 2003). As our FRET time courses (Jensen et al., 2009) were collected from different steps of the M₁R signaling cascade in living cells, the model informed by these measurements allows us to extract kinetic rate constants for many steps of M₁R signaling, to ask whether our understanding of signaling is self-consistent and sufficient to explain the observed delays, and to suggest more general mechanisms by which GPCR signaling may function. Our companion paper (see Falkenburger et al. in this issue) makes new measurements of lipid metabolism and extends the model to regulation of phosphoinositides and KCNQ channels.

MATERIALS AND METHODS

Cell culture and plasmids

Cells (tsA201) cultured in DMEM (Invitrogen) with 10% serum and 0.2% penicillin/streptomycin were passaged once a week. Cells were transfected at 75% confluency, plated on polylysine-coated glass chips 24 h after transfection, and used for experiments the next day. Cells were transfected with Lipofectamine 2000 (10 µl for a 3-cm dish; Invitrogen) and 0.1–1.2 µg DNA per plasmid: mouse M₁R (provided by N. Nathanson, University of Washington, Seattle, WA); cerulean-tagged M₁R (M₁R-CFP) and M₁R-YFP-CFP (Jensen et al., 2009); mouse Gα_q-eCFP (provided by C. Berlot, Geisinger Clinic, Danville, PA); bovine eYFP-Gβ1 (provided by S. Ikeda, National Institutes of Health [NIH], Rockville, MD); rat eYFP-PLCβ1 (provided by L. Runnels, University of Medicine and Dentistry of New Jersey, Piscataway, NJ); human eCFP-PH(PLCδ1) and eYFP-PH(PLCδ1) (provided by K. Jalink, The Netherlands Cancer Institute, Amsterdam, Netherlands); human KCNQ2 and rat KCNQ3 (provided by D. McKinnon, State University of New York, Stony Brook, NY); and unlabeled human Gα_q, Gβ1, and Gγ2 (The Missouri S&T cDNA Resource Center). Hereafter, we refer to fluorophores simply as cyan fluorescent protein (CFP) or yellow fluorescent protein (YFP), regardless of whether regular or enhanced fluorescent proteins were used.

Flow cytometry

Cells were harvested, resuspended in Ringer’s buffer, and analyzed by a FACScan (BD) flow cytometer using a 488-nm laser and a 530/30-nm emission filter. Parameters were FSC E00, SSC 359, and FL1 401. Cells were selected based on forward and sideward scatter, using the same gate for all samples. At least 10,000 cells were counted per sample. A different gate and FSC E01 were used to measure fluorescent beads. Data were analyzed offline using FlowJo software (Tree Star, Inc.) and visualized with IGOR Pro 6.0 (Wavemetrics). Fluorescence intensity histograms were computed and displayed on a logarithmic scale for fluorescence intensity, which more closely mimics our visual impression than a linear scale.

Western blot

Cells were harvested in PBS, centrifuged, and resuspended in 50 µl of lysis buffer: PBS with 1% Triton X-100 and protease inhibitor cocktail (Thermo Fisher Scientific). Lysates were cleared by centrifugation (13,000 g for 20 min at 4°C), and the supernatant was transferred to new tubes. Protein concentration was determined by Bradford assay (Bio-Rad Laboratories). 20 µg of protein was separated by SDS-PAGE using standard techniques (as in Krenz et al., 2009). The primary antibody against PLCβ1 was used at 1:1,000 (BD Transduction Laboratories). The secondary antibody was coupled to horseradish peroxidase and visualized by chemiluminescence (AlphaImager; AlphaInnotech).

Recombinant CFP and YFP protein

His-tagged ECFP and EYFP DNA were cloned into pETGQ and transformed into Escherichia coli BL-21(DE3) cells, which were grown at 37°C in Luria broth for 4 h. To induce expression, isopropyl-1-thio-β-d-galactopyranoside was added to a concentration of 1 µM, and cells were grown overnight at 18°C. Bacteria were collected by centrifugation and resuspended in ice-cold lysis buffer. The lysate was harvested using a homogenizer and cleared by centrifugation, and the constructs were purified by Ni²⁺-NTA chromatography. Proteins were checked for contaminants by comparing Coomassie-stained bands on SDS-PAGE from 20 and 1 µg of protein. Absorbance was measured with a spectrophotometer (DU640; Beckman Coulter). For comparison of fluorescence intensities between CFP/YFP solutions and bead suspensions, emission spectra were acquired with a fluorometer (10-nm excitation slit, 3-nm emission slit, and 1-s sampling per point; Fluorolog FL-1039; Horiba Jobin Yvon).

Photometric measurement of proteins

To estimate expressed protein amounts, the fluorescence of live cells was measured in the epifluorescence photometry setup used in Jensen et al. (2009). In brief, a xenon arc lamp was used for excitation with 440/20- or 500/20-nm excitation filters; 480/30- and 535/25-nm emission filters were used for CFP and YFP channels. Fluorescence was detected by photon-counting photomultiplier tubes. We estimated the number of fluorescent proteins from the brightness of each cell. To be consistent with our previous work and to be able to compare the relative amounts of CFP and YFP, we cotransfected both CFP- and YFP-tagged proteins. When appropriate, untagged Gα, Gβ, and Gγ were included to complement any tagged G protein subunits (see legend to Fig. 3 A). As FRET is expected to reduce CFP fluorescence, we took the values for YFP fluorescence before acceptor photobleaching and for CFP fluorescence after acceptor photobleaching. To bleach ∼95% of YFP, we illuminated with the YFP filter set for 5 min, omitting the neutral density filter (0.2 ND) used for time course measurements. FRET efficiency was determined from the increase in CFP fluorescence upon acceptor photobleaching. The time constant for YFP bleaching was 51 s with continuous illumination. Using a 350 linear/log optometer (United Detector Technology Instruments), the light energy of the CFP-measuring light at the stage was ninefold less than that of the YFP-bleaching light.

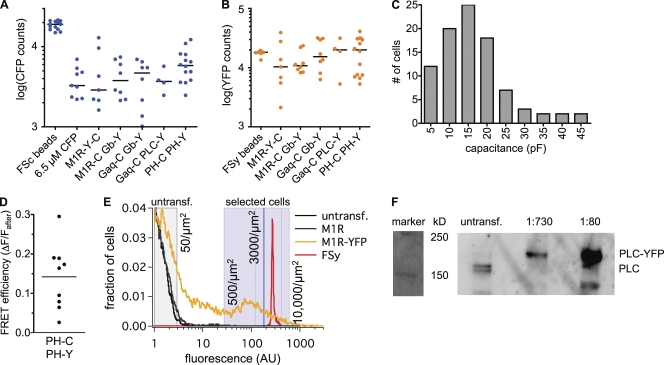
Figure 3.

Determining expression levels. (A) Fluorescence counts from epifluorescence microscopy with 440 nm excitation and 480 nm emission (CFP channel) of: FSc beads (FSc), cells equilibrated with a 6.5-µM CFP solution by whole cell patch clamp (6.5 µM CFP), and selected cells transfected with various FRET constructs after bleaching of YFP. Constructs: intramolecular FRET probe for M₁R activation (M₁R-Y-C); M₁R-CFP, Gβ-YFP, Gα, and Gγ (M₁R-C Gb-Y); Gα_q-CFP, Gβ-YFP, M₁R, and Gγ (Gaq-C Gb-Y); Gα_q-CFP, PLC-YFP, M₁R, Gβ, and Gγ (Gaq-C PLC-Y); PH-PLCδ1-CFP, PH-PLCδ1-YFP, and M₁R (PH-C PH-Y). (B) Epifluorescence counts with 500 nm excitation and 535 nm emission (YFP channel) for FSy beads (FSy) and the same transfected cells as in A before the bleaching of YFP. (C) Distribution of cell capacitance from whole cell patch clamp recordings (93 cells). (D) FRET efficiency estimated from donor dequenching by acceptor photobleaching. The calculation uses the fractional increase (ΔF) in CFP fluorescence after the bleaching of YFP and the final fluorescence F_after. (E) Flow cytometry of untransfected cells (black), of cells transfected with M₁R, Gα, Gβ, and Gγ (gray), or M₁R-YFP, Gα, Gβ, and Gγ (yellow), and of fluorescent beads (FSy; red). Excitation was 488 nm, and emission was 530/30 nm. Fluorescence intensity histograms were normalized to the maximum, which was in the first bin (offscale). Shaded gray area contains 99% of untransfected cells. Shaded blue area is the brightness range of cells selected for experiments (see B), as estimated from comparison to FSy beads. Dark blue line represents the median intensity of these cells, and lighter blue lines represent the 25th and 75th percentiles. Three independent experiments gave similar histograms. (F) Western blot of lysates from untransfected cells and from cells transfected with PLC-YFP at 1:730 and 1:80 dilutions. Primary antibody against PLC-β1. Two bands in untransfected cells around the 150-kD marker correspond to PLC-β1a (top; 138 kD) and PLC-β1b (bottom; 133 kD, nuclear localization). PLC-YFP is expected to run 27 kD higher. Endogenous PLC is comparable in intensity to the 1:730 dilution of transfected cells. Similar results were found in four independent experiments.

We assume that we sample light from the entire cell thickness when our imaging setup (40× oil objective; N.A. 1.3) is focused on a cell, as with a 1-µm diameter fluorescent bead, recorded fluorescence intensity changed only 5% within a 10-µm focus range around the z-plane of maximal intensity.

Modeling

A kinetic model of M₁R signaling was formulated as a compartmental model in the Virtual Cell framework (University of Connecticut). The Virtual Cell Model “FalkenburgerJGP2010” is available at http://www.vcell.org/ under shared models/hillelab. Model species and reactions are shown in Fig. 4. Model initial conditions are listed in Table II. They are mostly derived from measurements. Model rate constants are listed in Table IV. They were chosen manually and were not optimized by a statistical fit. When comparing model outputs to FRET data, we combine all molecular species that include the tagged pair of molecules. Thus, a term such as “receptor with ligand,” for example, refers to the sum of all species that include both receptor (R) and ligand (L).

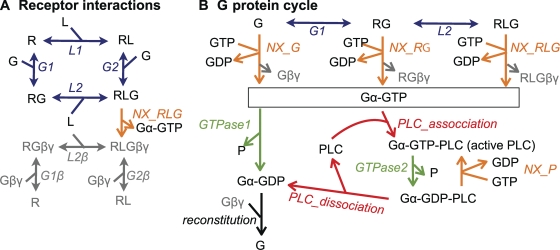
Figure 4.

Outline of the kinetic model. Model species are depicted with Roman letters, and reactions are in italics. For reversible reactions (double arrows), forward reactions are in the direction of association. Note that most species and some reactions occur in several places in the schema. (A) Binding of agonist ligand (L) and G protein heterotrimers (G) to the M₁R (R) are implemented as an allosteric (ternary complex) model (blue), where ligand binding increases the affinity for G proteins and G protein binding increases the affinity for ligand. It is assumed that after NX, Gα_q-GTP dissociates from the receptor, leaving behind Gβγ (gray). (B) G protein activation by NX (includes G protein dissociation; orange) and G protein deactivation by GTPase activity (green). Activated G proteins (Gα-GTP) deactivate slowly through their own GTPase activity (GTPase1) or much faster (GTPase2) when bound to PLC.

Table II.

Initial conditions

Species	Density	Source
	µm−2
R (endogenous)	1	From ratio of endogenous R to G
R (M1R-YFP)	3,000	From fluorescence
R (M1R, selected for FRET)	3,000	To reproduce Gα/Gβ FRET onset
R (M1R, current measurements)	500	Arithmetic mean of all cells (flow cytometry)
G protein (endogenous)	40	To fit concentration-response curve of current
G protein (overexpressed)	3,000	From fluorescence
PLCβ1 (endogenous)	3	From western blot
PLCβ1 (overexpressed)	3,000	From fluorescence
PLC (total endogenous)	10	To fit concentration-response curve of current
PH domains (membrane)	3,000	From fluorescence, consistent with FRETr

Table IV.

Rate constants

Parameter	Value	Units	Comment
α	100		Allosteric constant (cooperativity factor); Cortés and Palacios (1986); Vannucchi and Goldman-Rakic (1991)
KL1	2	µM	KL2 * α, similar to EC50 for M1R-Y-C FRET
KL2	0.02	µM	From EC50 for Oxo-M on M1R/Gβ FRET
KG1	25,500	µm−2	α * KG2
KG2	255	µm−2	kr_G2/kf_G2
kf_L1	2.8	µM−1 s−1	kr_L1/KL1
kr_L1	5.5	s−1	From M1R-Y-C FRET recovery
kf_L2	2.8	µM−1 s−1	As kf_L1
kr_L2	5.5 × 10−2	s−1	kf_L1 * KL2
kf_G1	2.7 × 10−4	µm2 s−1	Not well-constrained
kr_G1	6.8	s−1	kf_G1 * KG1
kf_G2	2.7 × 10−3	µm2 s−1	From M1R/Gβ FRET onset
kr_G2	0.68	s−1	From M1R/Gβ FRET recovery
k_NX_RLG	0.65	s−1	From Gα/Gβ FRET onset, fits Gα/PLC FRET onset
k_NX_G	1.5 × 10−5	s−1	From Turcotte model, d1a
k_NX_P	4.7	s−1	From Turcotte model, d4b
k_GTPase1	0.026	s−1	From Gα/Gβ FRET recovery
k_GTPase2	15.0	s−1	From Turcotte model, p4c
k_PLCassoc	1	µm2 s−1	Not rate-limiting
k_PLCdiss	0.71	s−1	From Gα-PLC FRET recovery
k_reconst	1	µm2 s−1	Reconstitution of Gαβγ trimers, affects timing if <1.0

^ad1 refers to the dissociation of GDP from Gα alone in Turcotte et al. (2008).

^bd4 refers to the dissociation of GDP from Gα bound to RL and PLC.

^cp4 refers to GTP hydrolysis bound to RL and PLC.

Statistics

Summarized data include one data point per cell. Bars and markers represent mean ± SEM.

RESULTS

The signaling steps from M₁R excitation to PIP₂ depletion and channel modulation are shown diagrammatically in Fig. 1. KCNQ channels need PIP₂ to function. Ligand binding to M₁Rs allows the G protein G_q to activate the enzyme PLC, which hydrolyzes PIP₂, thus shutting off the channel. Our laboratory has already formulated a preliminary kinetic description of these steps (Suh et al., 2004). It was based on published test tube measurements of the G protein cycle and plausible estimates of the subsequent steps from the final modulation of KCNQ channels from our studies. Subsequently, we measured the kinetics of four of the intermediate reactions in living cells using transfected FRET reporters for each step (Jensen et al., 2009). Nevertheless, to refine a more realistic kinetic model still requires several more measurements, particularly better estimates of the concentrations of reactants.

Transfected cells we select for study express roughly 3,000 proteins per µm² of plasma membrane

The study of Jensen et al. (2009) transfected CFP- and YFP-labeled signaling proteins into cells for optical measurements of the progression of muscarinic signals through intermediate signaling steps. We now want to estimate how many copies of the transfected molecules were expressed in those cells. Because no method seemed ideal, we accumulated determinations by numerous techniques based on the following five measurements. (1) We calibrated fluorescent beads (1-µm diameter) as fluorescence intensity standards by comparing their fluorescence to purified CFP and YFP solutions in a fluorometer. Transfected cells could then be compared with the calibrated beads. (2) We allowed the cytoplasm of untransfected cells to equilibrate with a CFP solution of known concentration in a whole cell patch pipette and measured the fluorescence intensity. (3) We estimated the density of expressed pleckstrin homology domain (PH)-YFP acceptor molecules from FRET efficiency. (4) We compared whole populations of transfected cells with fluorescent beads by flow cytometry. (5) For PLC expression, we compared levels of transfected proteins with levels of endogenous proteins using Western blot.

The calibration studies began with generation and purification of recombinant CFP and YFP proteins in bacteria (Fig. 2 A). To determine protein concentration several ways, we measured the absorbance (A₂₈₀) of tyrosine and tryptophan residues at 280 nm, absorbance of the fluorochromes at their peaks (440 nm for CFP and 505 nm for YFP), and absorbance of the alkali-denatured fluorochrome of YFP (Fig. 2, B and C). From published extinction coefficients, these values corresponded to ∼650 µmol of CFP and 400 µmol of YFP protein per liter of stock solution (Table I). We then compared the calibrated solutions to suspensions of fluorescent beads (cyan fluorescent [FSc] and yellow fluorescent [FSy]) in cuvettes using a fluorometer (Fig. 2, D and E). One FSc bead was as bright as 4 × 10⁷ CFP molecules, and one FSy bead was bright as 10⁷ YFP molecules. In the previous FRET work, we had selected cells to study by quantitative criteria based on their brightness (Jensen et al., 2009). Using the same epifluorescence photometry, we compared the fluorescence of cells we would select for those experiments to the calibrated FSc and FSy beads. Note that beads were calibrated against CFP or YFP in aqueous solution, but fusion to other proteins and the cellular environment can alter the quantum efficiency. We did not correct for such changes. Pooled across all transfections, the cells were on average 22% as bright as an FSc bead in the CFP channel (Fig. 3 A) and 88% as bright as an FSy bead in the YFP channel (Fig. 3 B), corresponding to roughly 10⁷ CFP and 10⁷ YFP molecules per typical cell. Our estimated numbers show internal consistency in that for the receptor construct that had stoichiometric amounts of YFP and CFP covalently linked, the calculated fluorophore ratio was 1.1 ± 0.1 (n = 7 cells).

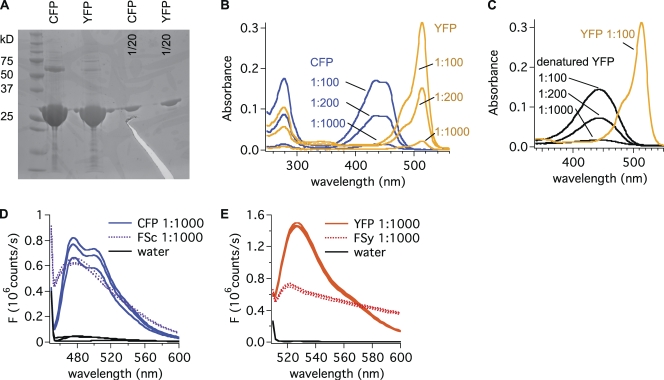
Figure 2.

Properties of purified recombinant CFP and YFP proteins. (A) Purity of protein solutions is >95%: 20 or 1 µg (1/20) of purified protein (CFP and YFP) was separated by SDS-PAGE and stained with Coomassie. The thick band above 25 kD corresponds to the molecular weight of CFP and YFP (27 kD). Impurities are less abundant than the 1/20 dilution. Upper band for CFP possibly reflects dimerization. (B) Absorbance spectra for CFP and YFP. CFP and YFP solutions were diluted at 1:100, 1:200, and 1:1,000, and absorbance was determined (1) at the peak around 280 nm (absorbance of tyrosine and tryptophan) and (2) at the peak of fluorophore absorbance (440 nm for CFP and 515 nm for YFP). Results are summarized in Table I. (C) Absorbance spectra for YFP denatured in 0.1 N NaOH as compared with native YFP. (D) Emission spectra for diluted CFP solution (CFP; 3.9 × 10¹¹ molecules/µl) and a suspension of FSc beads (FSc; 10⁴ beads/µl) suggest that 1 FSc bead is as bright as 4 × 10⁷ CFP molecules. Three different samples measured in the same experiment are shown. Similar results were found in three independent experiments. (E) Emission spectra from diluted YFP solution (YFP; 2.4 × 10¹¹ molecules/µl) and a suspension of FSy beads (FSy; 10⁴ beads/µl) indicate that 1 FSy bead is as bright as 10⁷ YFP molecules. Similar results were found in three independent experiments.

Table I.

Absorbance of CFP and YFP solutions

	ε	A	C
	mM−1		µM
CFP, 280 nm	25.9a	16.7 ± 0.7	646 ± 27
CFP, 440 nm	26b	16.0 ± 0.9	617 ± 33
YFP, 280 nm	23.4a	10.8 ± 0.3	460 ± 11
YFP, 515 nm	84b	30.5 ± 0.4	363 ± 5
YFP, denatured	44c	13.8 ± 1.3	313 ± 31

Measurements on three different days, mean ± SEM. ε, published extinction coefficients; A, measured absorbance of the stock solution; C, protein concentration of the stock solution estimated as A/ε.

^aCalculated from molar extinction coefficients for tyrosine (1.49 mM⁻¹) and tryptophan (5.5 mM⁻¹; from Oregon Medical Laser Center).

^bFrom Patterson et al. (2001).

^cFrom Ward (2006).

PH probes are CFP-tagged or YFP-tagged PH domains from PLCδ1 that bind PIP₂. In confocal images, the fluorescence of cells transfected with PH probes is brightest at the plasma membrane. When PIP₂ is depleted, PH probes leave the membrane and the cytosolic fluorescence increases two- to threefold (van der Wal et al., 2001; Horowitz et al., 2005; Winks et al., 2005). This suggests that 50–60% of the PH probe molecules are at the plasma membrane at rest. As the appearance of cells transfected with the other fluorescently tagged proteins (M₁R, Gα_q, Gβ, and PLC) was similar to cells transfected with PH probes, and in the absence of a better estimate, 50% plasma membrane localization was assumed for all of these proteins. The median surface area of our cells was 1,500 µm² judging from the membrane capacitance (median, 15 pF; Fig. 3 C). Collectively, these numbers give a surface density of 3,200 expressed PH probes per µm² (50% of the 10⁷ molecules per 1,500 µm² cell). Because we selected cells using the same brightness criteria for each of the transfected probes we studied, we now assume that the average density of any of them was around 3,200 µm⁻² in the subset of transfected cells we studied in Jensen et al. (2009).

As an independent check on these numbers, we equilibrated untransfected cells with a solution of purified CFP in the patch pipette chosen to give a similar brightness. The matching test solution contained 6.5 µM CFP (Fig. 3 A). Lacking a PH domain, these CFP molecules would all remain in the cytoplasm, but if 50% of them had translocated to the plasma membrane, they would have reached a surface density of 3,250 µm⁻², as estimated above, assuming a surface to volume ratio of 0.6 µm⁻¹. This factor is used in all places where we compare surface densities with cytoplasmic concentrations for our cells.

In principle, FRET efficiency can be used to estimate intermolecular distances. If donors and acceptors were placed randomly at the plasma membrane, FRET efficiency would depend only on the density of acceptor molecules within the expected range of mean densities (Fung and Stryer, 1978). The approximately linear theoretical relationship has an initial slope of 8.3% FRET efficiency per 1,000 acceptors per µm². (These numbers assume CFP/YFP fluorophores. A graph of the theoretical relationship is shown in Fig. S3 B of our companion paper by Falkenburger et al., 2010). In the PH-CFP– and PH-YFP–transfected cells we selected, the median resting FRET efficiency as determined by acceptor photobleaching was 14 ± 3% (Fig. 3 D). This corresponds to 1,700 acceptor PH-YFP molecules per µm², smaller than the previous values but in a similar range.

From the small fraction of bright cells in the epifluorescence microscope, we had initially supposed that the efficiency of our transfections was low (Jensen et al., 2009). However, experiments with flow cytometry on the entire population of cells showed that many more cells were expressing fluorescent proteins but at levels well below our selection criteria. Comparison with FSy beads calibrated the cytometer readings. Untransfected cells and cells transfected with untagged M₁Rs had low background fluorescence equivalent to <1.7 × 10⁵ YFP per cell or 50 YFP proteins per µm² (Fig. 3 E). Transfection with M₁R-YFP increased the fluorescence of most cells, but the values ranged over three orders of magnitude. In summary, the brightness range of cells selected for FRET experiments corresponded to a range of 500–10,000 fluorescent proteins per µm².

Based on the brightness distribution in flow cytometry, we can calculate the mean density of fluorescent proteins if we picked cells at random in a dish of transfected cells. The arithmetic mean of the brightness of all cells was 28 arbitrary fluorescence units with M₁R-YFP and 61 for PLC-YFP in transfections together with unlabeled G proteins (median of three independent experiments). This corresponds to 500 molecules µm⁻² for M₁R-YFP and 1,000 for PLC-YFP.

Endogenous levels of PLC are much lower

To obtain an estimate of endogenous levels of PLC, we compared PLC levels in untransfected cells with PLC-YFP–transfected cells by Western blot (Fig. 3 F). Protein lysates from PLC-YFP–transfected cells had to be diluted 600–700 times to produce immunostaining that was similar in intensity to endogenous PLC. Whereas a random cell in a dish transfected with PLC-YFP expresses on average 1,000 µm⁻² PLCs at the plasma membrane (from flow cytometry; plus an equal number in the cytosol), a native tsA cell might express only around 3 µm⁻². Thus, when we transfect with fluorescent PLC, our selection criteria pick cells with >>100-fold increased expression of PLCβ1, which explains why PLC transfection greatly speeds muscarinic suppression of KCNQ current compared with control cells (Jensen et al., 2009). Note that the Western blot determined only PLCβ1, and there may be other PLC subtypes also contributing to the G_q-coupled inhibition of KCNQ2/3 current. In an alternative approach below, we suggest from modeling that assuming 10 µm⁻² PLC in native cells would be appropriate to describe the Oxo-M concentration–response relationship measured for inhibition of KCNQ2/3 current in cells transfected with only untagged M₁R and KCNQ2/3 channel subunits (Jensen et al., 2009).

Modeling muscarinic signaling to G proteins and PLC

We then could develop a kinetic model of the entire M₁R signaling cascade. The model is outlined in Fig. 4. The signaling cascade is confined to the plasma membrane, and proteins are assumed to be at uniform density and freely diffusing. Tables II–IV list initial conditions, differential equations, and rate constants. The first part is an allosteric model for the binding of ligand (L) and G proteins (G) to the receptor (R) (Fig. 4 A). L and G bind to R to make the ternary complex RLG, which catalyzes formation of dissociated, active Gα_q-GTP (Fig. 4, A and B). This active moiety then binds to and activates PLC until the GTPase activity of Gα_q restores the inactive Gα_q-GDP (Fig. 4 B). The model is constrained by time courses and concentration–response curves of previously published FRET data (Jensen et al., 2009). Modeling hydrolysis of PIP₂ by active PLC, PIP₂ synthesis, and PIP₂ effects on KCNQ2/3 current is described in our companion paper (Falkenburger et al., 2010).

Table III.

Differential equations

Reaction	Rate equation
Bluea
L1	kf_L1 * R * L – kr_L1 * RL
L2	kf_L2 * L * RG – kr_L2 * RLG
G1	kf_G1 * G * R – kr_G1 * RG
G2	kf_G2 * G * RL – kr_G2 * RLG
Greya
G1β	kf_G1 * Gβγ * R – kr_G1 * RGβγ
G2β	kf_G2 * Gβγ * RL – kr_G2 * RLGβγ
L2β	kf_L2 * L * RGβγ – kr_L2 * RLGβγ
Orangea
NX_RLG	k_NX_RLG * RLG
NX_G	k_NX_G * G
NX_RG	k_NX_G * RG
NX_P	k_NX_P * Gα-GDP-PLC
Greena
GTPase1	k_GTPase1 * Gα-GTP
GTPase2	k_GTPase2 * Gα-GTP-PLC
Reda
PLCassoc	k_PLCassoc * Gα-GTP * PLC
PLCdiss	k_PLCdiss * Gα-GDP-PLC
Blacka
G-reconstitution	k_reconst * Gβ * Gα-GDP

Units of fluxes (reaction rates) are molecules µm⁻² s⁻¹.

^aColor of arrow in Fig. 4.

Our model of ligand binding to M₁R can be called a ternary complex model, but it does not distinguish between “activated” and “resting” forms of the receptor because our FRET data (Jensen et al., 2009) do not provide information about this distinction. In this regard it contrasts with cubic ternary complex models where the distinction is made (Weiss et al., 1996; Kinzer-Ursem and Linderman, 2007). Our experimental data also cannot discriminate NX from G protein dissociation; therefore, we lumped these steps in a single, first-order reaction. Some studies suggest that certain receptors and G proteins are preassembled even without agonist (for review see Hein and Bünemann, 2009). The observed agonist-induced increase in M₁R/Gβ FRET could then reflect a conformational change in such preassembled complexes rather than de novo binding of G proteins to the receptor. Similarly, the decrease in Gα/Gβ FRET could reflect a conformational change in the G protein heterotrimer rather than its dissociation. We did find it possible to construct an alternative model that uses conformational change instead of G protein binding and dissociation that reproduces our experimental results equally well. We have chosen the implementation of Fig. 4 as it relates to previous (classical) models and reflects a simple interpretation of our FRET findings. For the remainder of this paper, we continue with this binding/dissociation framework for clarity. However, our data do not allow us to favor this implementation over that of a preassembled complex.

Further, the model does not include desensitization of receptors (phosphorylation and/or internalization), which is more prominent in the termination of activity of some other GPCRs (Maeda et al., 2003; Gainetdinov et al., 2004). It also does not consider the dependence of PLC on cytosolic calcium, which constitutes a highly nonlinear positive feedback loop that is not well constrained by our experiments to date.

The initial conditions are taken from the measurements and estimates of protein amounts given in the previous sections. In addition to initial conditions, the model has five free parameters for binding of ligand and G proteins to receptor and eight parameters for the G protein cycle. These rate constants were chosen manually to reproduce the experimentally observed time courses (Jensen et al., 2009) for individual steps of the M₁R signaling cascade. Most rate constants are strongly constrained by at least one of the time courses (see comments in Table IV). The number of “hidden” steps in the model is therefore small. Some rate constants for NX and Gα_q GTPase activity were also informed by biochemical measurements (Turcotte et al., 2008). Rate constants are compared with literature values in the Discussion.

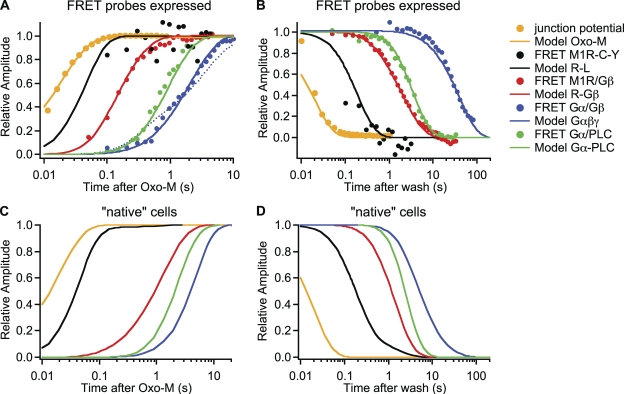
The model can reproduce our FRET results. Fig. 5 (A and B) summarizes the observed onset and recovery time courses of the first four steps of muscarinic signaling after agonist application, as measured by FRET (measured symbols from Jensen et al., 2009). The steps are agonist binding to receptor, G protein binding to receptor, Gα-Gβγ dissociation, and Gα binding to PLC. Smooth curves from the model are drawn on logarithmic axes. In comparing model results to the FRET time courses, initial conditions differed between traces to accommodate the different transfections required to measure FRET as listed in the legend.

Figure 5.

The model reproduces many individual steps of M₁R signaling. Rate constants for the kinetic model in Fig. 4 were chosen to mimic time courses of signaling steps previously measured by FRET (Jensen et al., 2009). Curves are model outputs, and circles are binned averages of FRET data from several experiments. Solution exchange was measured as the change in junction potential as 160 mM KCl is washed on. The exchange data are offset by 10 ms to the left. A and C show normalized onset time courses induced by the application of “saturating” M₁R agonist (10 µM Oxo-M). The vertical axis is like a reaction coordinate from the baseline level (0.0) to the final level (1.0). A logarithmic time axis is used to display fast and slow events. B and D show recovery time courses. R-L is the sum of all species with R and L (RL, RLG, and RLGβ); R-Gβ is the sum of all species with R and Gβ (RG, RLG, RLGβ, and RGβ); Gαβγ is the sum of all species with undissociated G proteins (G, RG, and RLG); and Gα-PLC is the sum of Gα-GTP-PLC and Gα-GDP-PLC. Note that the changes of Gα/Gβ FRET and Gαβγ model output are actually negative-going but become positive-going in the coordinates used. For the model outputs in A and B, amounts of receptors, G proteins, and PLC (in µm⁻²) were chosen to reflect the conditions with overexpressed FRET probes: R, 3,000; G proteins, 0 (R-L) or 3,000 (R-Gβ, Gαβγ, and Gα-PLC); PLC, 10 (R-L, R-Gβ, and Gαβγ) or 3,000 (Gα-PLC). For model outputs in C and D, amounts were chosen as estimated for native (untransfected) cells: R, 1; G proteins, 40; PLC, 10 µm⁻². The dotted line in A shows the predicted onset of Gα/Gβ FRET assuming 1,000 µm⁻² receptors. Note the biphasic time course, which is unlike the measured data.

We must consider how the choice of M₁R density (initial condition of R) was made. For any overexpressed proteins that are fluorescently labeled and selected for, we assumed a density of 3,000 µm⁻²; however, to measure Gα/Gβ FRET we had transfected an unlabeled M₁R. Its mean density should be between 500 and 3,000 µm⁻², depending on whether its expression level is uncorrelated or identical to that of the fluorescently tagged G proteins. It is not unreasonable to assume some correlation between expression levels. For example, we find that when cells are transfected with GFP and unlabeled KCNQ2/3 channel subunits, most GFP⁺ cells also show KCNQ2/3 current. At the same time, we find under such conditions that a cell’s brightness correlates poorly with the current amplitude (unpublished data). The time course of dissociation of Gα from Gβγ observed with FRET was better approximated with 3,000 µm⁻² receptors (solid line in Fig. 5 A) than with 1,000 (dotted line in Fig. 5 A) or 500 µm⁻² (not depicted). The model reproduced the time course of Gα/PLC FRET reasonably using the same receptor density. The predicted onset of G protein dissociation has two components (dotted line in Fig. 5 A) if the number of receptors is much lower than the number of G proteins (i.e., not all G proteins are activated at once) and the deactivation of G proteins is much slower than their activation (see Fig. 5 B).

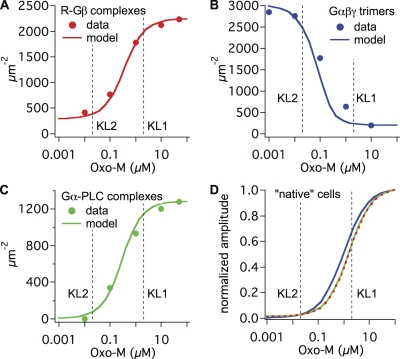
Fig. 6 shows predicted FRET time courses on an absolute scale and with a linear time axis (solid traces). In addition to time courses, we reproduced concentration–response data from the FRET measurements of Jensen et al. (2009). Fig. 7 overlays experimental Oxo-M concentration–response curves (symbols) with model curves (solid traces) for G protein binding to receptor (Fig. 7 A), G protein dissociation (Fig. 7 B), and Gα_q binding to PLC (Fig. 7 C). Again, the match is generally reasonable.

Figure 6.

Comparison of model predictions for cells overexpressing FRET probes and for native cells. Solid traces are the time courses from Fig. 5 (A and B) on an absolute y axis and a linear time axis, and dotted traces are from Fig. 5 (C and D). Naming conventions are as in Fig. 5. Initial conditions for solid traces (in µm⁻²): R, 3,000; G proteins, 0 (A) or 3,000 (B–D); PLC, 10 (A–C) or 3,000 (D). Initial conditions for dotted traces (in µm⁻²): R, 1; G proteins, 40; PLC, 10.

Figure 7.

The model reproduces Oxo-M concentration–response curves. Maximum formation of R–Gβ complexes (A), maximum depletion of Gαβγ trimers (B), and maximum formation of Gα–PLC complexes (C) predicted by the model for different concentrations of Oxo-M (lines) were compared with averaged and normalized Oxo-M concentration data (symbols; from Jensen et al., 2009) for M₁R/Gβ FRET (A), Gα/Gβ FRET (B), and Gα/PLC FRET (C). Initial conditions (in µm⁻²): R, 3,000; G proteins, 3,000; PLC, 10 (A and B) or 3,000 (C). (D) Superimposed, normalized concentration–response curves predicted for maximum formation of R–Gβ complexes (red), maximum depletion of Gαβγ trimers (blue; inverted), and maximum formation of Gα–PLC complexes (green) predicted by the model for native cells. Initial conditions (in µm⁻²): R, 1; G proteins, 40; PLC, 10. Vertical lines indicate dissociation constants KL1 and KL2 for receptors without and with G proteins bound.

As the initial conditions differed, the various FRET time courses could not be compared easily. To permit comparison, we used the model informed by the FRET measurements to calculate time courses for identical initial conditions. We used amounts of endogenous receptors, G proteins, and PLC estimated below (“native cells”; see Figs. 5, C and D, and 7 D). This also allowed us to ask how the FRET time courses we had measured with high amounts of receptors, G proteins, or PLC (Fig. 6, solid lines) would compare with those with endogenous amounts (Fig. 6, dotted traces).

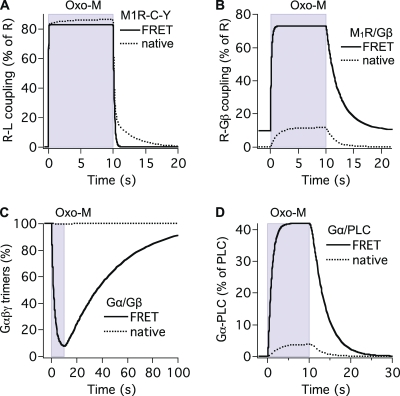
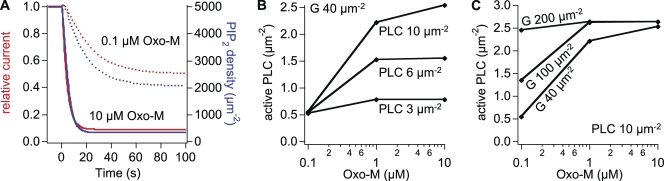
Endogenous amounts of PLC and G proteins were estimated by modeling the KCNQ current inhibition by M₁R activation seen in cells transfected only with unlabeled M₁R, KCNQ2/3 channel subunits and soluble GFP (Jensen et al., 2009; no explicit selection criteria concerning GFP brightness). We assumed 500 µm⁻² receptors in these experiments (the arithmetic mean of the population) and 5,000 µm⁻² PIP₂ molecules at rest (see Falkenburger et al., 2010). The observed steady-state block of KCNQ2/3 current by 0.1 and 10 µM Oxo-M was 50 and 90% (Jensen et al., 2009). If KCNQ2/3 current was simply linear with PIP₂, steady-state PIP₂ densities would have to be 2,500 µm⁻² with 0.1 µM and 500 µm⁻² with 10 µM Oxo-M. PIP₂ metabolism and PIP₂ effects on KCNQ2/3 current were in fact modeled as described in our companion paper (Falkenburger et al., 2010), with roughly similar results (Fig. 8 A). Achieving these steady-state PIP₂ densities (2,500 and 500 µm⁻²) in the face of ongoing constant PIP₂ synthesis requires a fivefold higher activity of active PLC with 10 µM as compared with 0.1 µM Oxo-M. When we tried different assumed amounts of PLC (Fig. 8 B) and G proteins (Fig. 8 C), we found that the combination of 10 PLC molecules µm⁻² and 40 G proteins µm⁻² produces fivefold more active PLC with 10 µM as compared with 0.1 µM Oxo-M (2.5 and 0.5 active PLC µm⁻²). The assumed density of PLC molecules is only slightly higher than that obtained above by Western blot (3 µm⁻²). An endogenous level of 40 µm⁻² G proteins compares well to 66 and 466 µm⁻² in other systems (10⁵ and 7 × 10⁵ per cell; Mahama and Linderman, 1994; Alt et al., 2001). The ratio of G proteins to receptors has previously been given as 20–50 (Luetje et al., 1987; Neubig, 1994; Alt et al., 2001). Although tsA201 cells do not express endogenous M₁Rs, we accordingly approximated a pseudo-endogenous situation in the model with 1 receptor µm⁻² and 40 G proteins µm⁻².

Figure 8.

Estimating endogenous densities of PLC and G proteins. (A) Predicted effect of 10 and 0.1 µM Oxo-M on KCNQ current and plasma membrane PIP₂. For reactions and parameters involving PIP₂ metabolism and KCNQ current see our companion paper (Falkenburger et al., 2010). (B and C) Predicted densities of active PLC for different initial amounts of PLC and G proteins. Unless otherwise noted, amounts were (in µm⁻²): R, 500; G proteins, 40; PLC, 10.

Comparing predicted time courses with the extrapolated “native” initial conditions revealed several interesting properties that are explored in more detail in the second half of the Discussion. (1) Modeling native tsA-like cells (Fig. 5 C) suggests a substantial delay between the binding of ligand and the binding of G proteins to the receptor. Such a “gap” is less apparent with overexpression of receptors and G proteins for FRET (Fig. 5 A). (2) G protein dissociation comes to steady state only after Gα/PLC binding does. (3) The very slow reassociation of G proteins seen by FRET (Fig. 5 B, blue trace) is likely a consequence of the G protein overexpression, as it goes away in simulations with native conditions (Fig. 5 D). (4) Ligand binding in modeled native cells includes a slow component. This was not seen with the intramolecular FRET probe for ligand binding (M₁R-Y-C) that does not couple to G proteins. (5) Ligand unbinding in modeled native cells is much slower than that seen with the overexpressed M₁R-Y-C FRET probe (Fig. 6 A). (6) Modeled native cells have only 0.3% of receptors bound to Gβ at rest, rising to 10% coupling during agonist. The fraction of G protein–bound receptors is much larger in cells transfected for M₁R/Gβ FRET (Fig. 6 B). (7) Only a very small fraction of G proteins is dissociated (to Gα and Gβγ) by agonist in modeled native cells, whereas most of the G proteins are dissociated by agonist in cells transfected for Gα/Gβ FRET (Fig. 6 C). (8) Fewer than 5% of the PLC enzymes are activated by agonist in modeled native cells, more in cells transfected for Gα/PLC FRET (Fig. 6 D). (9) For native cells, the model predicts similar Oxo-M EC50 values for three measured interactions: receptor–G protein, G protein dissociation, and Gα-PLC (Fig. 7 D). The EC50 values are also similar to KL1, the model’s dissociation constant for ligand binding to receptors without G proteins.

DISCUSSION

We have constructed a kinetic description of M₁R signaling to PLC based on measurements of protein amounts and on time courses of individual signaling steps obtained from our earlier FRET measurements (Jensen et al., 2009). This model combines several concepts. (1) An allosteric approach provides for cooperative binding of ligand and G proteins to the receptor. Predicted time courses and EC50 values were similar to those measured by FRET. (2) Important rate constants for NX and GTPase activities were taken from a model of G protein signaling that had been refined by in vitro measurement of GTPase activity (Turcotte et al., 2008). Those measurements complement ours because FRET does not inform well about GTPase activities but does constrain rate constants for protein–protein interaction (binding of receptor and PLC to G proteins; see Fig. 3 in Turcotte et al., 2008). We first compare numerical values we have chosen with those reported for other GPCR systems in the literature. Then we discuss the implications of our model for GPCR signaling.

Protein amounts

When performing transient transfection, we often think of transfected and untransfected cells as two distinct populations of cells. Flow cytometry showed, however, that there is a continuous spectrum of transfection with fluorescence levels spanning three orders of magnitude, starting in a range that overlaps with untransfected cells (Fig. 3 E). Others made similar observations (e.g., He and Hristova, 2008). A local maximum in our fluorescence intensity histogram (Fig. 3 E) falls within the range of selected cells and is close to our estimate of 3,000 molecules per µm². One can characterize this subset of cells by a median (or modal) expression level. However, the expression level averaged over the entire population falls pretty much between the two modes of the distribution (which includes the obviously transfected cells on the right and cells that are indistinguishable from untransfected cells on the left). Thus, comparing transient expression levels in individual cells to measurements averaged from the entire population, such as radioligand binding or Western blot, is not straightforward.

Several independent estimates of protein expression levels agree that in the cells we selected, overexpressed proteins have densities around 3,000 µm⁻² at the plasma membrane. (1) Comparisons of the fluorescence intensity of cells versus calibrated fluorescent beads suggest ∼3,000 fluorescent proteins per µm². (2) Filling untransfected cells with CFP by whole cell patch clamp yields a similar estimate. (3) The observed FRET efficiency of 14% for PH probes suggests a density of acceptors of 1,700 µm⁻². These values are in a range similar to the estimated density of expressed PH probes in N1E-115 cells (4,617 µm⁻²; Xu et al., 2003), but they are an order of magnitude higher than the copy numbers in identified synapses of scaffolding proteins fused to EGFP expressed in primary hippocampal neurons by adenoviral infection (Fig. 5 in Sugiyama et al., 2005). This is not unexpected as tsA201 cells were constructed for high expression of genes driven by the cytomegalovirus promoter we used.

As cells were selected based on their measured fluorescence, it is not surprising that the amounts of fluorescent proteins were similar across different cells and constructs. Our original selection of cells for the FRET experiments had been guided (1) on the lower end, by the sensitivity of our photometry apparatus to get adequate signal to noise ratio; (2) on the upper end, by the experience that very bright cells were often not as healthy or contained clusters of fluorescent proteins that do not participate in the response to agonist application; and (3) by an attempt to select a “typical” cell, i.e., one with a commonly observed level of expression. The resulting 3,000 proteins per µm² is a high number when compared with our estimate of endogenous PLC (3–10 µm⁻²) and is comparable to our model estimate for free PIP₂ lipids (5,000 µm⁻²). It is one to three orders of magnitude higher than typical ion channel densities (Hille, 2001). In cases where overexpressed proteins are supposed to report activities of native cells, it would be desirable to work with lower expression levels in the future. This would require some combination of more dilute transfection, stronger excitation light, better light collection and detection, longer integration of optical signals, and brighter and more bleach-resistant fluorophores.

We have quantified fluorescently tagged signaling molecules (receptors, G proteins, and PLC) mainly based on their fluorescence. Due to slow maturation of fluorescent proteins and cleavage, the number of fluorescent molecules need not be identical to the number of biologically active molecules. For PLC-YFP, we have evidence for ∼10% cleavage products (Fig. 3 F), which is small compared with the overall variance of fluorescence intensity between individual selected cells (Fig. 3 A). In addition, the biological activity of PLC to speed up GTPase activity was similar between our estimates, calibrated with fluorescence intensity, and in vivo measurements where PLC amounts were determined biochemically (Turcotte et al., 2008).

The native cells in our model primarily represent the tsA201 cells we used for our experiments. Estimates of PLC and G proteins were based on Western blots for untransfected tsA201 cells and on KCNQ2/3 current reduction. Amounts are likely quite different in primary cells where signaling by G_q-coupled receptors is important. For example, a (locally) higher density of G proteins is one possible explanation for the higher fraction of high-affinity binding sites for Oxo-M in the brain as compared with tsA201 cells (see below).

Rate constants for ligand binding and unbinding, G protein activation, and deactivation

We now consider the rationale for the values selected for equilibrium and rate constants. The model uses equilibrium dissociation constants KL1 and KL2 for ligand binding to receptors (without and with G proteins, respectively) to mimic our concentration–response curves measured with FRET (Fig. 6, A–C) (Jensen et al., 2009). KL1 and KL2 are in the range of reported values for low- and high-affinity Oxo-M–binding sites in the brain (0.1 and 10 µM, Cortés and Palacios, 1986; 0.024 and 0.944 µM, Potter et al., 1988). The allosteric constant (also termed the cooperativity factor) is KL1/KL2 = 100 (as in Cortés and Palacios, 1986; Vannucchi and Goldman-Rakic, 1991). The low-affinity equilibrium dissociation constant KL1 = 2 µM for ligand binding to receptor without G proteins is similar to our experimental K_D for Oxo-M binding to the intramolecular receptor FRET probe (M₁R-Y-C), which does not couple to G proteins (4 µM; Jensen et al., 2009).

The unbinding rate of Oxo-M from G protein–free receptor (kr_L1 = 5.5 s⁻¹; τ_off = 182 ms) was set to match the decay of M₁R-Y-C FRET. From KL1 and Kr_L1, we then calculated the ligand association rate constant kf_L1 as 2.8 µM⁻¹s⁻¹. This is similar to the binding of the radioactive muscarinic antagonist quinuclidinyl benzilate to cultured heart cells (3 µM⁻¹s⁻¹; Galper and Smith, 1978), radioactive α₂ adrenergic agonist UK14304 to platelet membranes (5 µM⁻¹s⁻¹; Neubig et al., 1988), fluorescently tagged neurokinin to EGFP-NK2R (5 µM⁻¹s⁻¹; Palanche et al., 2001), and phenylisopropyl adenosine to A₁-adenosine receptors (1 µM⁻¹s⁻¹; Lohse et al., 1984). It is faster than the estimated binding of the α₂ adrenergic antagonist yohimbine to platelet membranes (0.25 µM⁻¹s⁻¹; Neubig et al., 1988), and a little slower than the estimated association of N-formyl peptides to neutrophils (10 µM⁻¹s⁻¹, Waller et al., 2004; 20 µM⁻¹s⁻¹, Sklar, 1987). The resulting onset time constant for M₁R-Y-C FRET (40 ms) is in a range similar to that reported for ligand binding to α_2A or β₁ adrenergic receptors (40–60 ms; Vilardaga et al., 2003; Hein et al., 2005; Hoffmann et al., 2005; Rochais et al., 2007), but faster than for parathyroid receptors (1 s; Vilardaga et al., 2003). The forward rate constants for ligand binding to receptors are often fast and relatively insensitive to the ligand structure, whereas the off rate constants vary and give different ligands different affinities. For example, a series of N-formyl ligands differed more in their predicted unbinding than in their binding rate constant (Waller et al., 2004). Therefore, we set kf_L2 = kf_L1. FRET within M₁R-Y-C in fact reports the conformational change after ligand binding, not the actual binding itself. The fact that this event falls in the same time range as ligand binding, as reported by fluorescent or radioactive ligands, suggests that the conformational change after ligand binding is not a slow step.

The slower rate constant for unbinding of ligand from G protein–bound receptor (kr_L2 = 0.055 s⁻¹; τ_off = 18 s) derives from kf_L2 and KL2 = 20 nM (see Table II). This rate constant is similar to that determined for unbinding of radioactive Oxo-M from G protein–bound M₂ receptors (0.01 s⁻¹, Hirschberg and Schimerlik, 1994; K_d = 1.3 nM). As the unbinding reaction reflects affinity, it is slower than the unbinding of IgG from FcR (2 s⁻¹, Lieto et al., 2003; K_d = 2.4 µM), but faster than the unbinding of quinuclidinyl benzilate (0.005 s⁻¹, Galper and Smith, 1978; K_d = 1.8 nM), UK14304 (0.0065 s⁻¹, Neubig et al., 1988; K_d = 1 nM), yohimbine (0.001 s⁻¹, Neubig et al., 1988; K_d = 4.8 nM), N-formyl peptides (0.001 s⁻¹, Waller et al., 2004; K_ds = 0.04, 0.4, and 4.6 nM), or erythropoietin (0.005 s⁻¹, Jarsch et al., 2008; K_d = 2.9 nM) from their receptors.

Rate constants for receptor binding and unbinding of G proteins were determined from the time course of M₁R/Gβ FRET. (Again, in an alternative interpretation, this transition could represent a conformational change rather than de novo binding.) Because Oxo-M binds faster to the receptor than G proteins do, and 99.4% of receptors have ligand bound in the presence of 10 µM Oxo-M, the onset time course of M₁R/Gβ FRET (0.2 s) primarily constrained the rate constant kf_G2 (as opposed to kf_G1). Similarly, the recovery time constant of M₁R-Gβ FRET (3.7 s) mainly constrained the rate constant kr_G2. KG2 was set to kr_G2/kf_G2, and KG1 was set to α * KG2. As the reaction G1 does not contribute much to our measured time courses, G1 rate constants are not further constrained by our measurements. To avoid extreme values, we made them similar to the G2 rate constants.

The choice of model rate constants for NX and G protein GTPase activity (Fig. 4 B) was guided both by our prior FRET measurements and by values from biochemical measurements of GTPase activity (Turcotte et al., 2008). These two sources dovetail nicely. Our rate of NX at ligand-bound receptor (NX_RLG), informed by the onset of Gα/Gβ FRET, was 0.65 s⁻¹, which compares to 0.4 s⁻¹ in Biddlecome et al. (1996) and to 0.28 s⁻¹ for the rate-limiting step in Turcotte et al. (2008). The rate constant for the slow endogenous GTPase activity of Gα_q (0.03 s⁻¹), chosen to reproduce recovery of Gα_q/Gβ FRET, was similar to values obtained in vitro (0.01 s⁻¹, Mukhopadhyay and Ross, 1999; 0.018 s⁻¹ for step p1 and 0.0063 s⁻¹ for p3 in Turcotte et al., 2008; 0.013 for p1 and p3 in Bornheimer et al., 2004, where steps p1 and p3 refer to the GTPase activity of Gα_q in the absence and presence of receptor ligand).

Interpretation of the model: binding of ligand and G proteins to receptors

Our model suggests that ligand binding occurs mainly through reaction L1 (R + L). Binding of G proteins to the receptor occurs mainly through G2 (RL + G). It is much slower than the binding of ligand (compare kf_L1 and kf_G2 in Table IV). The slow G protein binding is responsible for the majority of the delay between ligand binding and later steps (black trace to red trace in Fig. 5 C). The binding of G proteins to receptors was accelerated by overexpression of receptors and G proteins, making this delay less apparent with FRET experiments (Fig. 5 A). Slow G protein binding also is responsible for a slower component in ligand binding (dotted trace in Fig. 6 A) that has been described with radioligands (e.g., Neubig et al., 1988; Lohse et al., 2008) but was not observed with our intramolecular receptor FRET probe (M₁R-Y-C), presumably because it does not interact with G proteins.

With 10 µM Oxo-M and “endogenous” amounts of receptor, G proteins, and PLC, our model predicts the following distribution of receptors: 74% RL, 15% R alone, and 11% RLG and RLGβ combined. The unbinding of ligand then occurs mainly from RL through the reversal of L1, producing the fast initial decrease in R-L complexes (Fig. 6 A). Ligand unbinding from RLG complexes occurs through the reversal of first G2 and then L1 (kr_L2 is slower than kr_G2), making slow unbinding of G proteins from RLG (kr_G2) rate limiting for a portion of ligand unbinding. This results in the slower component of ligand unbinding in native cells (Fig. 6 A, dotted trace). The overall speed of ligand unbinding thus depends on the balance of RL versus RLG. It is faster with endogenous amounts (mainly RL) and slower with overexpression of G proteins (more RLG).

One long-standing question about the signaling of receptors and G proteins is to what extent G proteins are complexed with receptors at rest (“preassembly”). Previous measures of preassembly by FRET have yielded mixed results (see Lohse et al., 2008; Hein and Bünemann, 2009). In our own data, the nonzero resting M₁R/Gβ FRET might suggest preassembly. However, expression levels of M₁R-CFP and Gβ-YFP were similar to those for PH-CFP and PH-YFP (Fig. 3, A and B), which already achieve 14% FRET efficiency (Fig. 3 D) simply from crowding at the membrane. We therefore have to assume that a substantial proportion of M₁R/Gβ resting FRET also arises from crowding after overexpression and not from specific binding to one another. FRET efficiency for M₁R/Gβ was not much higher than for PH probes, so that we too have no clear evidence for preassembly.

The time course of M₁R/Gβ FRET changes contains additional information about steady-state receptor G protein binding that is independent from resting FRET levels. Our model suggests that with overexpression of receptor and G proteins, 10% of receptors have G proteins bound at rest, a number that rises to 73% in the presence of saturating Oxo-M (Fig. 6 B). The fraction of receptor–G protein complexes in the presence of Oxo-M in the model is determined by the equilibrium dissociation constant KG2, which is well constrained by the time course of M₁R/Gβ FRET as outlined earlier. The extent of receptor–G protein binding at rest is determined by KG1 = α * KG2, where α is an allosteric constant (Table IV). The value for α was taken from the literature. The prediction of the model, that only a small fraction (10%) of G proteins are coupled to receptors at rest when both are overexpressed, is in line with observations by others on the mobility of transfected fluorescently tagged G proteins, assayed by fluorescence recovery after photobleaching. For example, Qin et al. (2008) reported that immobilizing α₂ adrenergic receptors in HEK293 cells did not lower measured G protein mobility.

In the model, the fraction of receptors with G proteins bound at rest depends on the density of G proteins (but not on the density of receptors). In cells transfected with receptors only, the much weaker inhibition of KCNQ current by 0.1 µM Oxo-M as compared with 10 µM is best reproduced with a low number of G proteins (40 µm⁻²; Fig. 8 C), i.e., many fewer G proteins than receptors. In that case, very few receptors can be G protein bound, and ligand would see only low-affinity binding sites (receptors without G protein). This is consistent with our radioligand binding studies of M₁R (Fig. S1 in Jensen et al., 2009), where we did not see evidence for high-affinity binding sites in cells transfected with M₁R or M₁R-YFP. Then, the EC50 values for the formation of receptor–G protein complexes, for G protein dissociation, and for Gα-PLC binding (Fig. 7) would also reflect low affinity, KL1. In contrast, with overexpression of G proteins for FRET measurements, high-affinity binding sites become more relevant and the EC50 values fall between KL1 and KL2.

Interpretation of the model: G protein activation and deactivation

Our FRET measurements showed a substantial gap between the change in M₁R/Gβ FRET (red in Fig. 5 A) and the change in Gα/Gβ FRET (blue in Fig. 5 A). In the model, this delay results from two factors. (1) The underlying reactions are sequential so G proteins have to be bound to receptors before meaningful NX and G protein dissociation can take place. (2) In agreement with the literature (Biddlecome et al., 1996; Turcotte et al., 2008), our time constant for the second reaction (NX) is >1 s, whereas that for the first reaction (G–R interaction) is 20-fold shorter.

Less intuitive is why Gα binding to PLC (green in Fig. 5) reaches steady state before the preceding G protein dissociation does (blue in Fig. 5), both in native and transfected cells. The answer is that when displayed on an absolute scale, G protein dissociation and Gα binding to PLC progress together, but even after PLC binding is saturated, dissociation of more G protein continues. Therefore, the time to steady state is longer for G protein dissociation than for PLC binding.

In our model, the NX activity and the GTPase activity are both ≥500 times faster for PLC-bound Gα_q than for PLC-free Gα_q, as in the Turcotte et al. (2008) model. Compare, for example, NX rate constant NX_P with NX_G and GTPase rate constant GTPase2 with GTPase1 in Table IV. The chosen values make PLC simultaneously a strong guanine NX factor (GEF) (Turcotte et al., 2008) and a strong GTPase accelerating protein (GAP) (Biddlecome et al., 1996).

Our model of native cells reveals that in the steady state during Oxo-M, NX at RLG (NX_RLG) is compensated by an equal production of new RLG through reaction G2. Hence, the reactions NX_RLG, G2β, and G2 create the cycle: RLG→RLGβγ→RL→RLG, etc. (see Fig. 4 A). Of the Gα-GTP formed, 99% binds to PLC, which accelerates GTP hydrolysis (GAP activity). However, 87% of Gα-GDP-PLC formed then becomes Gα-GTP-PLC again due to the fast NX at PLC (GEF activity). The activated PLC pool is thus not static but in a steady state of continual GTP-GDP NX and hydrolysis. In the model for native cells with agonist, ∼75% of Gα-PLC bears GDP, and just 25% bears GTP. The benefit of such dynamic GTP consumption is that it allows PLC to be turned off quickly when agonist is removed.

As a consequence of the rapid recycling of G proteins and the relatively low number of receptors in native cells, only a small fraction of their G proteins become dissociated into Gα and Gβγ subunits (Fig. 6 C), consistent with the observation that receptors generally do not have to compete for G proteins (e.g., Neubig, 1994). The situation changes markedly with overexpression of the Gα and Gβ FRET probes. The amount of G proteins then greatly surpasses endogenous PLC, and G protein deactivation must rely on the slow endogenous GTPase activity of Gα until most of the G proteins are deactivated. Thus, deactivation is slow (time constant of 30 s; Figs. 5 B and 6 C), and a larger proportion (93%) of G proteins accumulates in the active dissociated form waiting to deactivate. Under such conditions, we would expect competition for G proteins to generate crosstalk between GPCRs.

To measure Gα/PLC FRET, we coexpressed PLC and G proteins. Under such conditions, the model predicts that deactivation of G proteins is sped up and that the deactivation of PLC occurs at almost the same time (blue and green in Fig. 5 D). This is consistent with the faster recovery of Gα/PLC FRET (time constant of 3.6 s) as compared with Gα/Gβ FRET. The GAP effect of PLC on termination of signaling was thus evident in our FRET experiments (Jensen et al., 2009).

In our ligand-gated GPCR system, the binding of G protein to activated receptor takes several hundred milliseconds when both are overexpressed, and longer with native levels of G proteins. This contrasts with photodetection by rhodopsin and the G protein transducin. The vertebrate photoreceptor is optimized for rapid response and is the best kinetically described of all GPCR signaling systems. In amphibian rod disk membranes, the endogenous densities of rhodopsin (Rh) and transducin (G_T) molecules are 25,000 and 2,500 µm⁻², respectively (Pugh and Lamb, 1993). The activated form of rhodopsin Rh* is formed within a couple of milliseconds of light absorption, and, at room temperature, one Rh* initiates activation and subunit dissociation of transducins at 4,000 s⁻¹, ∼60% of the estimated collision rate in the disk membrane. Thus, in addition to having higher endogenous concentrations of the signaling proteins in the rod, the intrinsic rate constant for receptor activation of G proteins is ∼500 times larger than for the system we studied (Hamer et al., 2005). Even if there might be preformed Rh–G_T complexes in the dark, they must break and reform several times per millisecond to allow the amplification steps of photoactivation. As with the PLC system, the effector (phosphodiesterase) is the GAP for transducin GTP, shortening its lifetime to 2 s. Finally, in the rod, the deactivation of Rh* requires actions of GPCR kinase and arrestin rather than dissociation of the ligand. Nevertheless, these deactivation steps take <1 s in the rod.

Conclusion

We have constructed a quantitative description of M₁R signaling that is based on FRET time courses and protein amounts. We find that the transient transfection of our probes generates a very broad range of protein expression in different cells, and that choosing readily visible fluorescent cells selects cells with enormous overexpression of the proteins. Nevertheless, it is possible to work with such data to make a model that describes transfected and untransfected cells well, both in the time domain and in their steady-state concentration dependence on agonist. Indeed, the enormous overexpression allows approximating the density of signaling molecules as the number of fluorescent molecules. The model helps to interpret our FRET measurements further, showing clearly, for example, in living cells the GAP and GEF action of PLC on G_q. Several components of the model are not specific for M₁R and should be applicable to thinking about other signaling cascades.