Design and validation of a clinical instrument for spectral diagnosis of cutaneous malignancy

Abstract

We report a probe-based portable and clinically compatible instrument for the spectral diagnosis of melanoma and nonmelanoma skin cancers. The instrument combines two modalities—diffuse reflectance and intrinsic fluorescence spectroscopy—to provide complementary information regarding tissue morphology, function, and biochemical composition. The instrument provides a good signal-to-noise ratio for the collected reflectance and laser-induced fluorescence spectra. Validation experiments on tissue phantoms over a physiologically relevant range of albedos (0.35–0.99) demonstrate an accuracy of close to 10% in determining scattering, absorption and fluorescence characteristics. We also demonstrate the ability of our instrument to collect in vivo diffuse reflectance and fluorescence measurements from clinically normal skin, dysplastic nevus, and malignant nonmelanoma skin cancer.

1. Introduction

Skin cancer is the most common form of malignancy, with more than one million cases reported in the United States every year [1]. A majority of these cases are nonmelanoma skin cancers that are usually not life threatening and can be treated. For melanoma skin cancer, early detection is critical to the survival of the patient. At advanced stages, melanomas metastasize and spread to other organs, significantly decreasing five-year survival (~15%) [1]. The current procedure for the detection of skin cancers is a clinical examination by a qualified dermatologist or general practitioner followed by a tissue biopsy and histopathology—the current gold standard—to confirm the results. However, there are several limitations associated with the process. Tissue biopsies are time-consuming, invasive, and subjective procedures that have led to an increase in the morbidity associated with the diagnosis of skin cancers. Additionally, a recent clinical study showed that approximately 40% of suspicious biopsied lesions were classified as benign by pathology [2]. Therefore, there is a need for a real-time, noninvasive diagnostic method that can reduce the morbidity and mortality associated with skin cancers.

Optical techniques such as diffuse optical spectroscopy and laser-induced fluorescence spectroscopy offer a noninvasive alternative to tissue biopsies for determining the state of tissue. Light is delivered and collected with optical fiber probes that are placed in contact with the skin surface. The weak light pulses sample the tissue beneath the probe noninvasively and provide information regarding tissue morphology, function, and biochemical composition. As these physiological parameters change with progression of disease, optical spectroscopy offers a means to measure disease progression without tissue removal.

A number of studies have demonstrated the feasibility of diffuse reflectance spectroscopy (DRS) for the optical biopsy of sampled tissue using either a model-based [3] or empirical approach [4,5]. The model-based analysis of diffuse reflectance has the advantage of providing quantitative measures of the wavelength-dependent reduced scattering (μ_s′) and absorption coefficients (μ_a) that relate to tissue morphology and function, respectively. The reduced scattering coefficient in tissue can be described as an inverse power law function of wavelength in the visible range and is a function of the scatterer size and density [6]. The absorption coefficient of tissue is a function of physiological parameters such as blood volume fraction, oxygen saturation, blood vessel diameter, and melanin concentration. Each parameter provides a different perspective of sampled tissue, and a number of them have been demonstrated to change with progression to dysplasia in various organs [3,7,8].

Laser-induced fluorescence spectroscopy (LIFS) has been widely used to detect dysplasia in various organs [9–12]. LIFS is based on the study of prominent tissue fluorophores such as nicotinamide adenine dinucleotide (NADH), collagen, and flavin adenine dinucleotide (FAD). NADH and FAD are important indicators of metabolic activity. Hence, large-scale cell proliferation or tumor growth can be identified by significant changes in NADH and FAD fluorescence [13,14]. In addition, studies have reported an increase in production of matrix metalloproteinases (MMPs) with progression to dysplasia [15]. Metalloproteinases are a group of collagenases that cleave the collagen cross links, leading to a reduction in the levels of collagen fluorescence. Coghlan et al. demonstrated that such spectral changes in fluorescence precede morphological changes in tissue, thus offering a means for the early detection of dysplasia [16].

Although DRS and LIFS are independently capable of measuring tissue pathology, a combination of both techniques can provide complementary information about tissue morphology, function, and biochemical composition. In addition, acquiring DRS in combination with LIFS allows for correcting the fluorescence spectra distorted by absorption and scattering events [17,18]. Cottrell et al. [19] developed a clinical instrument that used both reflectance and fluorescence spectroscopy for monitoring the optical properties of basal cell carcinoma during treatment with photodynamic therapy. Ramanujam and collaborators have conducted extensive studies on malignant breast tissue, using a combination of DRS and intrinsic fluorescence (corrected LIFS) spectroscopy (IFS) [20–22]. Clinical studies in the cervix [23] and oral cavity [24] using combined DRS, IFS, and model-based light scattering spectroscopy have demonstrated that a multimodal approach provides a superior tool for differentiating between normal and dysplastic tissue compared with any one method alone. A combination of DRS and IFS has been used for in vivo cancer diagnosis in the breast with improved results [25].

The clinical studies described earlier use systems that collect white light reflectance and fluorescence excitation-emission matrices (EEMs) over a wide wavelength range. Zângaro et al. [26] developed a clinical instrument (fast-EEM) for simultaneously measuring spectrally resolved reflectance and fluorescence excitation-emission matrices (EEMs) in the wavelength range 350–700 nm that was subsequently used in diagnostic studies of the cervix [23], oral cavity [24], and esophagus [27]. The instrument consisted of an independent white light source, a nitrogen laser that pumped a series of 10 dye cuvettes to provide 11 different excitation wavelengths (337–505 nm) for fluorescence, and a multichannel diode detector for collecting tissue spectra. Subsequently Müller et al. [28] and Tunnell et al. [29] developed upgraded versions of the fast-EEM instrument that extended the wavelength range of collection (300–800 nm) and significantly improved the data acquisition time to less than 1 s. The improved fast-EEM was used in studies in the oral cavity [30], breast [25], and atherosclerotic plaques [31]. Zuluaga et al. [32] developed the FastEEM instrument for collecting fluorescence EEMs and spectrally resolved diffuse reflectance spectra at multiple source–detector separations. This instrument utilized a single light source coupled with filters for delivering white light (380–950 nm) and 18 fluorescence excitation wavelengths (330–500 nm) and was subsequently used in clinical studies to detect dysplasia in the cervix [33,34]. Freeberg et al. [35] have reported upgraded versions of this FastEEM instrument that was used at multiple sites for studies in the cervix [36]. Ramanujam and collaborators used both custom-built [37] and commercially available [22] clinical instruments that collected spectrally resolved diffuse reflectance at three different source–detector separations and fluorescence EEMs for nine excitation wavelengths.

We have developed a compact, portable and fast clinical instrument that combines DRS and IFS for the early detection of melanoma and nonmelanoma skin cancers. We measure white light reflectance in the wavelength range of 350–700 nm. However, in contrast to the clinical systems described previously, we employ only two excitation wavelengths for fluorescence measurements: 337 nm for exciting NADH and collagen and 445 nm for FAD. Several studies have identified the fluorescence from these excitation bands to be diagnostically relevant for separating normal and dysplastic tissue [25,38,39]. Using only two excitation wavelengths has two important advantages. First, it facilitates simple and compact instrument design by eliminating the need for large excitation and emission monochromators for collecting fluorescence EEMs. This makes the system portable and clinically compatible. Second, we can significantly reduce data acquisition and processing time because we do not record full fluorescence EEMs. We use a microelectromechanical systems-based (MEMS-based) fiber optic switch for controlling the excitation sequence of the white light and laser sources, instead of a filter wheel. This reduces the instrument complexity and eliminates losses due to additional optics. We use an interline transfer CCD cooled to −30°C that allows data collection with short integration times (50 μs) while affording a high signal-to-noise ratio by eliminating thermal noise and dark current. Using such gated detection techniques allows us to leave the room lights on while recording data, an important step toward developing a clinically compatible system. We use a fiber optic probe with a close source–detector separation of 250 μm to ensure a superficial sampling depth, because skin cancers originate in the superficial epidermal layer of tissue. In this paper, we discuss the design and instrumentation of a combined DRS–IFS clinical system and detail the features that make it clinically compatible, portable, and capable of rapid data acquisition from tissue. We also briefly describe the algorithms used to extract both optical properties and fluorophore contributions from in vivo measurements. The development and validation of a model to extract optical properties has already been discussed in a previous publication [40]. We demonstrate the accuracy of the system on tissue-simulating phantoms over a wide range of optical properties. We also present in vivo measurements from clinically normal skin, dysplastic nevi, and malignant non-melanoma skin cancers.

2. System Design

A. Clinical Instrument

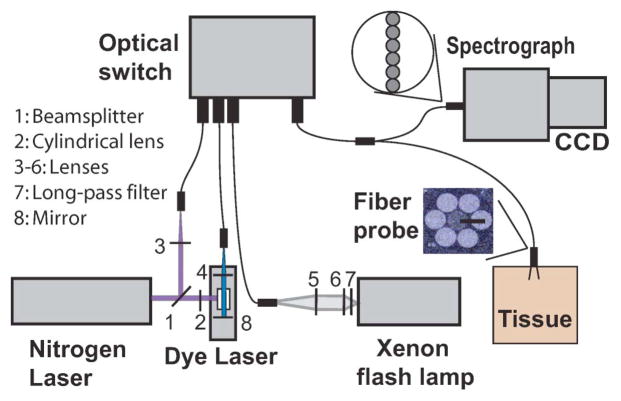
A schematic diagram of the probe-based clinical instrument is shown in Fig. 1. We used three light sources: (1) a pulsed xenon flashlamp (L7684, Hamamatsu Photonics, Bridgewater, New Jersey) for white light illumination, (2) a pulsed nitrogen laser (NL-100, Stanford Research Systems, Mountain View, California) at 337 nm to excite NADH and collagen fluorescence, and (3) a nitrogen-pumped dye laser at 445 nm to excite FAD fluorescence. We used Coumarin 450 (Exciton Inc., Dayton, Ohio) as the gain medium for the dye laser. We placed a long-pass filter (340 nm, Asahi Spectra, Torrance, California) in the optical path of the xenon flash lamp (Fig. 1, L7) to minimize exposure to UV light and eliminate second-order diffraction modes in the detection.

Fig. 1.

(Color online) Schematic representation of spectral diagnosis system.

The white light and laser pulses are coupled into optical fibers and guided into a 3 × 1 fiber optic switch (FSM-13, Piezosystems Jena, Germany). The optical switch is a MEMS-based device that controls the opening and closing of each port with microprisms. The switch helps control the excitation sequence and is triggered with TTL (transistor–transistor logic) signals. The switch’s output fiber is mated with the input fiber of the bifurcated fiber optic probe by using an SMA–SMA (subminiature version A) connector. There is an overall loss of ~30% of signal due to the fiber optic switch and the SMA–SMA connector. The distal end of the 2 m long bifurcated fiber optic probe [Fig. 2(c), FiberTech Optica, Ontario, Canada] consists of seven optical fibers arranged in a six-around-one configuration (Fig. 1). The central fiber (NA = 0.22, 200 μm core diameter) is used for delivering the light to the skin, while the six surrounding fibers (NA = 0.22, 200μm core diameter) collect the remitted light. The fiber optic probe is placed in gentle contact with the surface of the skin to acquire in vivo spectral measurements. Because we are interested in detection of early cancer lesions that originate in the epithelium, we chose a source–detector separation (center–center distance) of 250 μm. This distance is the closest separation that can be reasonably fabricated and allows us to sample the skin superficially. The proximal end of the six collection fibers are arranged in a linear configuration and aligned parallel to the entrance slit of the spectrograph (SP-150, Princeton Instruments, Trenton, New Jersey).

Fig. 2.

(Color online) (a), (b) Clinical instrument. (c) Fiber optic probe used with the clinical instrument.

The spectrograph contains a 150 groove/mm grating blazed at 500 nm that disperses the collected light onto a cooled CCD (Photometrics, Tucson, Arizona). The CCD is cooled to a temperature of −30°C to minimize dark current. The CCD is gated (50 μs) to acquire data only during an excitation pulse. This permits leaving the room lights on, making the system more clinically compatible. White light reflectance and laser-induced fluorescence is recorded in the spectral range of 350–700 nm in approximately 200 ms. We bin the pixels in a specific region along the slit axis corresponding to probe illumination and in groups of three pixels along the wavelength axis to increase the signal-to-noise ratio. We also average over three acquisitions for each light source to further improve the signal/noise ratio. The total acquisition time is typically less than a second. The spectral resolution of the system is 0.78nm.

Instrument control and spectral calibration is automated by using a personal computer running LabVIEW (National Instruments, Austin, Texas) and MATLAB (Mathworks, Natick, Massachusetts). We use a timer–counter board (NI 2121, National Instruments, Austin, Texas) that interfaces with the computer to generate trigger pulses for the light sources, the fiber optic switch, and the CCD. The light sources are triggered in a sequence, and the corresponding ports on the fiber optic switch are opened to allow for excitation. White light reflectance and laser-induced fluorescence spectra are saved and stored automatically on the computer.

The entire system was built on an optical bread-board and transferred to a portable rack (2 ft × 2 ft × 3 ft, where 1 ft = 30.5 cm, PTRK-1426, Middle Atlantic Products) [Figs. 2(a) and 2(b)]. The rack houses the power supplies for all the system components as well as a personal computer. Additionally, the system contains an uninterruptible power supply module on board (run time 15 min) that allows the system to run free of any wall socket and thus allows for its transport between exam rooms. The spectral diagnosis system has been approved as a Class I laser device according to the safety standards specified by the American National Standards Institute (ANSI) [41]. A Class I specification implies the lowest possible risk to skin due to laser exposure, similar to a handheld laser pointer. In addition, Class I devices typically do not require eye goggles to be worn by the patient. This classification also limits the total number of pulses that can be incident on a patient in a given period of time. It also limits the energy allowed for each light source. To conform to Class I stipulations, we incorporated a routine in the LabVIEW data acquisition algorithm that stops all data acquisition for a period of 30 s after 15 pulses have been fired. Care is taken to ensure that the stipulated energy levels are not exceeded during trials on phantoms as well as patients.

B. Instrument Calibration

Data calibration forms a crucial component of the spectral diagnosis system. The instrument relies on a comparison of absolute measures of tissue optical properties and fluorophore contributions for differentiating between normal and dysplastic tissue. Therefore, it is important to eliminate any differences in daily measurements due to source intensity and system response. This ensures that any changes in optical properties are due solely to variations in tissue morphology and function. First, we discuss the calibration routines employed for correcting the white light intensity measurements from samples and calculating the diffuse reflectance. The wavelength scale of the CCD is calibrated by using the wavelength peaks of a standard mercury–argon lamp. The spectrally resolved diffuse reflectance, R_diffuse(λ), is calculated by using the equation

$${\text{R}}_{\text{diffuse}}(\lambda )=\frac{I_{\text{sample}}(\lambda )-I_{\text{background}}(\lambda )}{[I_{\text{standard}}(\lambda )-I_{\text{background}}(\lambda )]\times 100/R_{\text{standard}}},$$ (1)

where I_sample is the white light intensity measured from a sample (phantom or patient). I_background(λ) refers to a background spectrum that is recorded with the light sources turned off to eliminate the effects of CCD dark current and ambient light. I_standard(λ) is recorded from a calibrated reflectance standard (Labsphere, North Sutton, New Hampshire). Dividing the background corrected sample intensity by the intensity from a calibrated standard removes the wavelength-dependent system response. A factor of 100/R_standard is used to normalize the denominator to 100%, where R_standard refers to the calibrated reflectance level from the standard used (20%). To account for possible daily variations in the white light intensity, we measured the diffuse reflectance spectrum [R_beads(λ)] from a standard solution of 1 μm diameter polystyrene microspheres in water (0.12%; Polysciences, Warrington, Pennsylvania) on each day. We then calibrated the diffuse reflectance spectra for each day as

$$R_{\text{calibrated}}(\lambda )=R_{\text{diffuse}}(\lambda )\times \frac{R_{\text{beads}(\text{LUT})}(\lambda )}{R_{\text{beads}}(\lambda )},$$ (2)

where R_beads(LUT) (λ) is recorded from a solution of polystyrene beads on the same day that we created a lookup table (LUT) for fitting the diffuse reflectance spectra (discussed in Section 3). This ensures that all reflectance measurements are calibrated to the LUT model before extraction of optical properties.

We calibrate the laser-induced fluorescence by using the equation

$$\begin{array}{l}{F}_{\text{calib}}(\lambda )=[f(\lambda )-I_{\text{bgd}}(\lambda )]\times \frac{I_{\text{NIST}}(\lambda )}{I_{\text{NIST}-\text{SD}}(\lambda )}\\ \times \frac{f_{\text{rhod}(\text{master})}({\lambda }_{max})}{f_{\text{rhod}}({\lambda }_{max})}.\end{array}$$ (3)

The first term in Eq. (3) represents the background-corrected fluorescence spectrum. f(λ) refers to the measured fluorescence intensity. To correct for the effects of wavelength-dependent system response, we recorded the spectrum of a NIST traceable tungsten calibration standard (LS-1-CAL, Ocean Optics, Dunedin, Florida) using our optical system [I_NIST(λ)]. By comparing this recorded spectrum with the calibrated lamp spectrum of the NIST standard [I_NIST(λ)], we calculated a wavelength-dependent correction factor to calibrate the laser-induced fluorescence spectrum. This is represented by the second term in the equation. Finally, we measured the fluorescence spectrum of a Rhodamine B solution in water (0.01 g/l) to calibrate both the nitrogen and the dye laser for variations in source intensity. Rhodamine B has an emission peak of 580 nm (λ_max) independent of the excitation wavelength. As with the beads measurement, the peak intensity of rhodamine fluorescence measured on each day [f_rhod(λ_max)] is compared to that of a master rhodamine measurement [f_rhod(master)(λ_max)] to calculate a correction factor. This correction factor is represented by the third term in Eq. (3).

3. System Performance

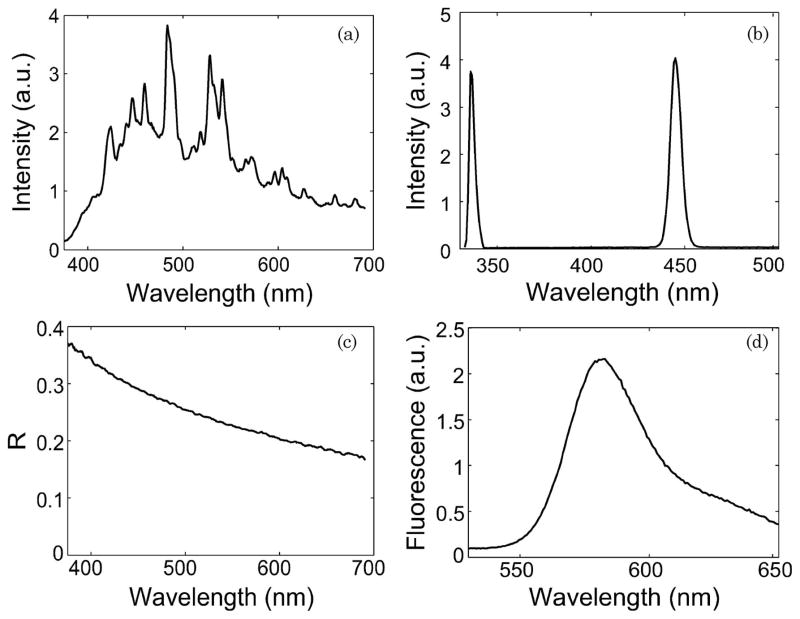
A typical white light spectrum from the xenon flash lamp reflecting off a 20% reflectance standard is shown in Fig. 3(a). Also shown are laser excitation pulses from the nitrogen laser at 337 nm and the dye laser at 445 nm [Fig. 3(b)]. The energy levels for each light source along with the respective pulse width and full width at half-maximum (FWHM) are specified in Table 1. These energy levels are well within the Class I maximum permissible exposure levels [41]. Figures 3(c) and 3(d) show a good signal-to-noise ratio for sample diffuse reflectance (~50 dB) and fluorescence spectra (>100 dB) measured from 1% intralipid and rhodamine solutions, respectively.

Fig. 3.

(a) White light spectrum from the xenon flash lamp reflecting off a 20% reflectance standard. (b) Excitation pulses from the nitrogen laser at 337 nm and the dye laser at 445 nm. (c) Diffuse reflectance spectrum of a 1% intralipid solution. (d) Laser-induced fluorescence spectrum of a Rhodamine B solution (0.01 g/l).

Table 1.

Light Source Specifications

Parameter	Xenon Flashlamp	Nitrogen Laser	Dye Laser
Energy/pulse	2.5 μJ	2.1 μJ	4.7 μJ
Operating wavelength	350–700 nm	337 nm	445 nm
FWHM	—	6 nm	6 nm
Pulse width	2.90 μs	3.5 ns	N/A

A. Determination of Optical Properties

Many current strategies for analyzing diffuse reflectance rely heavily on the solution to the diffusion approximation of the radiative transport equation [42], or a modified form [43]. However, the diffusion approximation is not valid at source–detector separations less than approximately one mean free path [1/(μ_s′ + μ_a)] and in tissues with low albedo [μ_s′/(μ_s′ + μ_a) < 0.9], where μ_s′ and μ_a refer to the reduced scattering and absorption coefficients, respectively. Because we are interested in the detection of early cancers that originate in the upper layers of skin, an inverse model that is accurate at short source–detector separations and in tissues with low albedo (e.g., dysplasia) is of paramount importance. Unfortunately, diffusion-approximation-based inverse models are not accurate in these regimes. To overcome this limitation, we recently developed a LUT-based inverse model that is valid for fiber-based probe geometries with close source–detector separations and tissues with low albedos. The LUT is a database of experimental reflectance measurements made on calibration standards of known optical properties and is specific to our probe geometry. The development of the LUT-based model has been described in detail elsewhere [40].

We validated the LUT by using a matrix of tissue-simulating phantoms of known optical properties. These phantoms were fabricated by using polystyrene microspheres (diameter 1 μm, Polysciences, Warrington, Pennsylvania) and ferrous stabilized hemoglobin powder (Sigma, St. Louis, Missouri) dissolved in water to simulate scattering and absorption, respectively. We used Mie theory to calculate the μ_s′ of the polystyrene microspheres and a spectrophotometer (DU 720, Beckman Coulter, Fullerton, California) to measure μ_a of a stock Hb solution. We created a matrix of tissue phantoms with scattering [μ_s′ (λ₀ = 630 nm) = 1–3 mm⁻¹] and absorption parameters ([Hb] = 0–2.5 mg/ml)) in a physiologically relevant range.

We implemented a nonlinear optimization fitting routine to fit the diffuse reflectance spectra. We constrained the reduced scattering coefficient to the form μ_s′ (λ) = μ_s′ (λ₀) × (λ/λ₀)^−B, where λ₀ = 630 nm. We assumed the absorption in the visible range to be due to oxyhemoglobin and deoxyhemoglobin. The absorption coefficient was calculated by using the absorption cross sections (σ_Hb and σ_HbO2) of these chromophores as μ_a(λ) = [Hb] × [α × σ_HbO2 + (1 − α) × σ_Hb], where α is the oxygen saturation and [Hb] is the total hemoglobin concentration. Depending on the type of tissue sampled and the wavelength range of interest, the expression for μ_a (λ) can be modified to include the absorption cross sections of other absorbing chromophores. The fitting routine minimized the value of χ² and determined the optical properties from the fit with the lowest value of χ². We defined a threshold for χ² (3 × 10⁻⁴) and described a χ² value lower than the threshold as a good fit.

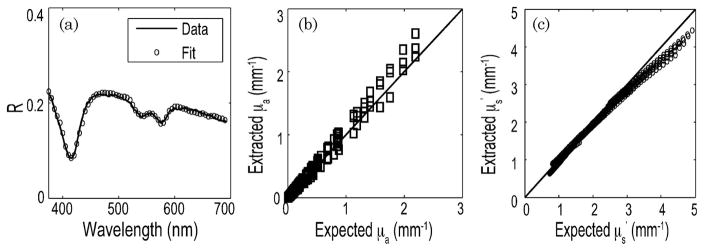
Figure 4(a) shows the diffuse reflectance spectrum from a sample tissue phantom with μ_s′ (λ₀) approximately 2.5 mm⁻¹ and [Hb] = 2 mg/ml. The general shape of the curve is derived from the scattering behavior of polystyrene beads in solution, and the depressions are due to the characteristic absorption peaks of hemoglobin at 420, 542, and 577 nm. The plot also illustrates a LUT-based model fit. The LUT-based inverse model estimated the absorption and reduced scattering coefficients over a wide range (μ_a(λ) = 0–2.29mm⁻¹ and μ_s′ (λ) = 0.71–4.91 mm⁻¹) with mean root-mean-square (rms) errors of 11.6% and 5.9% respectively [Figs. 4(b) and 4(c)]. The data show good agreement between the expected and the measured values of μ_s′ and μ_a. All experiments were performed immediately after preparation of phantoms. Therefore, the oxygen saturation of the phantoms was constant and did not vary by more than 2%.

Fig. 4.

(a) Diffuse reflectance spectrum (solid curve) and the corresponding LUT fit (circles) from a tissue phantom [μ_s′ (λ₀) = 2.46 mm⁻¹ and [Hb] = 2 mg/ml]. Scatter plot of the extracted versus expected values of (b) μ_a(λ) and (c) μ_s′ (λ) for all tissue phantoms. The solid line indicates perfect agreement.

B. Determination of Fluorophore Contributions

We used the model described by Zhang et al. [17], which builds on the photon migration model developed by Wu et al. [44], to extract the intrinsic fluorescence of a fluorophore. The intrinsic fluorescence can be described as the laser-induced fluorescence spectrum free of distortions due to scattering and absorption. To test the ability of our instrument to extract intrinsic fluorescence, we conducted experiments on tissue phantoms with scattering, absorption and fluorescence properties.

We used commercially available fluorophores to prepare tissue phantoms for measuring fluorescence. FAD (Sigma, St. Louis, Missouri) was available commercially and hence was used as the fluorophore under test with the dye laser (445 nm excitation). We chose Stilbene 3 (Exciton, Dayton, Ohio) to simulate NADH fluorescence because of the similar position of its peak emission wavelength. The tissue phantoms were fabricated in three stages. Nonscattering solutions of the two fluorophores were first prepared to measure the intrinsic fluorescence. The fluorophore concentrations were selected so that the solutions were optically dilute. We used 0.43 μM of Stilbene 3 and 42.1 μM of FAD in the experiments. To examine the combined effect of scattering and absorption, hemoglobin was added in concentrations ranging from 0–2 mg/ml. We added a fixed concentration of beads (μ_s′ (λ₀) = 1 mm⁻¹) to simulate scattering.

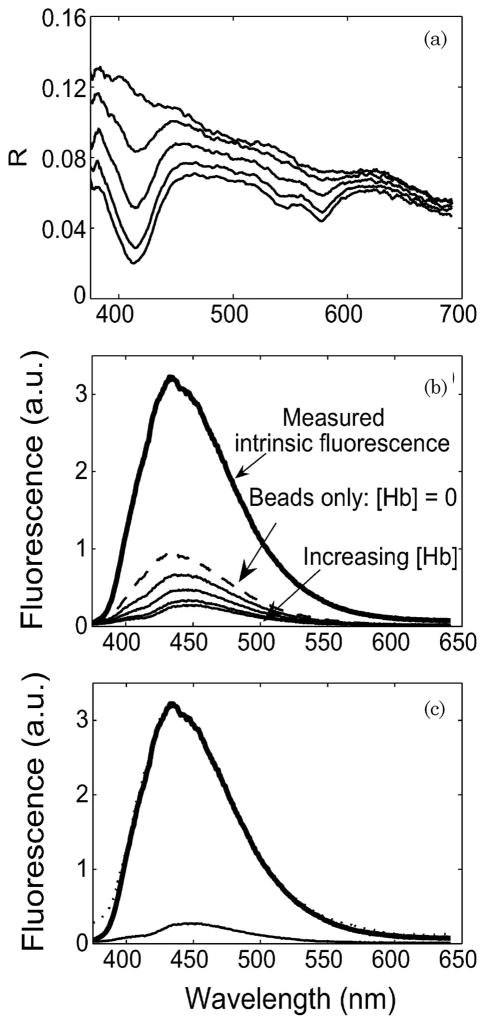
Figure 5 shows the results of fluorescence measurements on tissue-simulating phantoms at 337 nm excitation. We simultaneously measured the diffuse reflectance spectrum [Fig. 5(b)] for each phantom. Fluorescence spectra from tissue phantoms with varying concentrations of hemoglobin are plotted along with the intrinsic fluorescence spectrum of Stilbene 3 in Fig. 5(a). The addition of hemoglobin introduced a distortion in the fluorescence spectrum around 420 nm. This can be attributed to absorption by hemoglobin in the Soret band. There is good agreement between the extracted and the measured intrinsic fluorescence spectra, as shown in Fig. 5(c). We were able to recover the intensity and the line shape of the intrinsic fluorescence spectrum with an rms error of less than 10%. We repeated the same fluorescence experiments with FAD as the fluorophore by using 445 nm excitation (data not shown). As with Stilbene 3, we were able to recover both the intensity and line shape of the intrinsic fluorescence spectrum for each tissue phantom with an rms error less than 10%.

Fig. 5.

(a) Data recorded from tissue phantoms with Stilbene 3 as fluorophore under test. The tissue phantoms contained a fixed scatterer concentration [μ_s′ (λ ₀) = 1 mm⁻¹] and varying concentrations of hemoglobin [0–2 mg/ml]. (b) Corresponding diffuse reflectance spectrum for each phantom. No measurement was possible for the intrinsic fluorescence phantom. (c) Intrinsic fluorescence spectra measured from a phantom (bold solid curve) and extracted by using the IFS model (dotted curve) compared with the laser-induced fluorescence spectrum (lighter solid curve).

In these experiments, we used each laser source to excite only one fluorophore in solution. However, in tissue, a 337 nm excitation line causes both NADH and collagen fluorescence. In such a case, the relative contributions of these fluorophores can be determined from the intrinsic fluorescence spectrum by using a linear combination of the basis spectra of fluorophores, as

$$\begin{array}{l}{\text{IF}}_{337}(\lambda )=[\text{NADH}]\times {\text{IF}}_{\text{NADH}}(\lambda )+[\text{collagen}]\\ \times {\text{IF}}_{\text{collagen}}(\lambda ),\end{array}$$ (4)

where [NADH] and [collagen] refer to the relative contributions of the respective fluorophores and IF_NADH and IF_collagen are the basis intrinsic fluorescence spectra of NADH and collagen reported by Volynskaya et al. [25].

4. In vivo Skin Studies

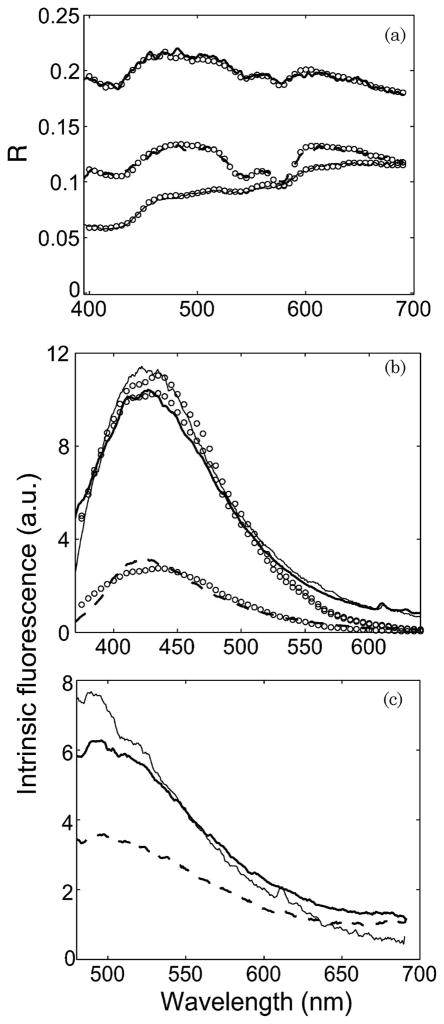
We are currently conducting a clinical feasibility study using the clinical instrument on nonmelanoma and melanoma skin cancers at the University of Texas Medical Branch, Austin (UTMB) and the Mohs surgery clinic at the M. D. Anderson Cancer Center, Houston (MDACC). Figure 6(a) shows diffuse reflectance spectra from three different groups: normal skin, dysplastic nevus, and a malignant form of non-melanoma skin cancer—basal cell carcinoma (BCC). These are representative spectra from three different patients. The data demonstrate a sufficient signal-to-noise ratio for in vivo diffuse reflectance measurements. The plot also illustrates good agreement between the LUT model and in vivo data. The extracted intrinsic fluorescence spectra due to 337 and 445 nm excitation are shown in Figs. 6(b) and 6(c). The fluorescence at 337 nm excitation is due to both NADH and collagen. Figure 6(b) shows a fit to the linear combination model that extracts the relative contributions of NADH and collagen.

Fig. 6.

In vivo measurements from normal skin (bold solid curve), dysplastic nevus (lighter solid curve) and malignant BCC (dashed curve) from three different patients. (a) Diffuse reflectance. The circles indicate the LUT model fit. (b) Intrinsic fluorescence spectra from 337 nm excitation. The circles indicate the fit to the linear combination model. (c) Intrinsic fluorescence spectra from 445 nm excitation.

5. Discussion

We have reported the design, calibration, and performance of a clinically compatible and portable instrument for the spectral diagnosis of cutaneous malignancies. The system acquires diffuse reflectance and laser-induced fluorescence from tissue within a fraction of a second. We use gated detection techniques (integration time 50 μs) that allow us to leave the room lights on, making the system clinically compatible. We employ only two wavelengths to excite endogenous fluorescence from tissue as compared with other devices currently in clinical trials [29,32,37] that record fluorescence EEMs and use more than ten different light sources or excitation wavelengths. We use a MEMS-based fiber optic switch to generate a sequence of light excitation pulses. This significantly reduces the size and complexity of our instrument, compared with other clinical systems that have used large monochromators [32] or dye cell filter wheels to change the excitation wavelengths [28,29]. The total time for data acquisition using our system is typically less than a second. We measure the spectrally resolved diffuse reflectance from tissue at only one short spatial distance from the source. This allows us to sample tissue at very shallow depths and target early cancers that originate in the upper layers of skin.

A majority of the spectroscopy-based clinical studies to date have utilized either DRS [4,45–47] or LIFS [48,49] to study melanoma and nonmelanoma skin cancers. Although a number of clinical studies using a combination of spectroscopic modalities have been reported for other organs, there are few studies detailing such an instrument for the study of skin cancer. Zeng et al. [50] described a combined reflectance and fluorescence spectroanalyzer to study normal skin. Borisova et al. [51] described a clinical instrument that combined DRS and LIFS for the empirical study ofpigmented nevi. However, the presence of absorbers like melanin in skin could potentially distort the line shape and intensity of the laser-induced fluorescence signal, leading to a loss in diagnostic accuracy [48]. In addition, studies by Sterenborg et al. employing uncorrected LIFS showed no significant differences in fluorescence between normal skin and nonmelanoma skin cancer [49]. A technique such as IFS that corrects distortions in the LIFS signal could potentially provide vital information to discriminate normal from dysplastic skin tissue. The spectral diagnosis system we describe combines DRS and IFS to provide complementary information regarding tissue morphology, function, and biochemical composition.

We use a LUT-based model [40] to fit our diffuse reflectance spectra and determine the optical properties of sampled tissue. The LUT is built on experimental measurements of diffuse reflectance on calibration standards of known optical properties and could potentially be adapted to any probe geometry. There are several advantages of using such an approach. First, the LUT is specific to our probe and was developed with the same system used to collect phantom and clinical data. Hence, it potentially accounts for the exact system response, which is not easy to reproduce by using an analytical or computational model. Second, LUTs provide a simple and fast approach to inverse solutions. The LUT approach extends the bounds of validity imposed by diffusion models to very short source-detector separations (~250 μm) and highly absorbing tissue. The LUT model was able to extract the scattering and absorption parameters for a tissue phantom of albedo 0.35 with accuracies of 6% and 8%, respectively. This is a major improvement over traditional diffusion-theory-based models that are inaccurate at albedos < 0.9. Our development and validation of the LUT is based on 1 μm polystyrene microspheres that are a good approximation of the typical value of anisotropy (g) found in tissue (g ~ 0.9). Previous studies have demonstrated that skin is strongly forward scattering [52,53]. Recently, Reif et al. demonstrated by using tissue phantoms that reflectance does not vary by more than 15% for g > 0.75 for all values of scattering and that this variation is almost negligible for g > 0.9 [54]. Their work was based on a fiber source-detector separation of 250 μm. To strengthen the validation of our LUT, we will assess the accuracy of the LUT in extracting optical properties from phantoms containing different sizes of scatterers that simulate different values of anisotropy (g ranging from 0.7 to 0.9). We also intend to study the effect of source-detector separation on the accuracy of the LUT. It is well known that the accuracy of diffusion models improves at distances larger than 1 mm [43]. Therefore, we intend to compare the performance of the LUT to diffusion models at distances ranging from our current source-detector separation to well over 1 mm.

The spectral diagnosis system has been classified as a Class I laser device [41] and has been approved for clinical trials on patients by the Institutional Review Boards at MDACC and UTMB. We are currently conducting a pilot clinical study to determine the feasibility of spectral diagnosis of nonmelanoma and melanoma skin cancer. The skin sites are classified into five groups according to histopathology: (1) benign lesions, (2) precancerous actinic keratosis, (3) malignant squamous cell carcinoma (SCC), 4) malignant BCC, and (5) melanoma. We also make a normal skin measurement adjacent to the lesion for comparison. Figure 6 illustrates sample in vivo data from normal skin, malignant BCC, and a dysplastic nevus on three different patients. There are visible differences in magnitude and line shape of both DRS and IFS spectra of the different groups. The plot shows reasonably good fits to the LUT-based model and the IFS model. These fitting algorithms are used to extract physiological parameters such as scatter density and size, oxygen saturation, blood vessel diameter, blood volume fraction, and fluorophore contributions. Our future work will use these parameters to assess the accuracy of this system in classifying various nonmelanoma and melanoma skin cancers.