Prometaphase spindle maintenance by an antagonistic motor-dependent force balance made robust by a disassembling lamin-B envelope

The lamin-B nuclear envelope stabilizes spindle microtubules by keeping the competitive motility of opposing-force kinesins in check.

Abstract

We tested the classical hypothesis that astral, prometaphase bipolar mitotic spindles are maintained by balanced outward and inward forces exerted on spindle poles by kinesin-5 and -14 using modeling of in vitro and in vivo data from Drosophila melanogaster embryos. Throughout prometaphase, puncta of both motors aligned on interpolar microtubules (MTs [ipMTs]), and motor perturbation changed spindle length, as predicted. Competitive motility of purified kinesin-5 and -14 was well described by a stochastic, opposing power stroke model incorporating motor kinetics and load-dependent detachment. Motor parameters from this model were applied to a new stochastic force-balance model for prometaphase spindles, providing a good fit to data from embryos. Maintenance of virtual spindles required dynamic ipMTs and a narrow range of kinesin-5 to kinesin-14 ratios matching that found in embryos. Functional perturbation and modeling suggest that this range can be extended significantly by a disassembling lamin-B envelope that surrounds the prometaphase spindle and augments the finely tuned, antagonistic kinesin force balance to maintain robust prometaphase spindles as MTs assemble and chromosomes are pushed to the equator.

Introduction

Mitosis depends on the mitotic spindle, a subcellular machine which uses microtubule (MT)-based force generators to assemble itself and to segregate chromosomes (Walczak et al., 1998; Sharp et al., 2000b; Mitchison and Salmon, 2001; Wadsworth and Khodjakov, 2004; Brust-Mascher and Scholey, 2007; Walczak and Heald, 2008). During prometaphase, i.e., the period between nuclear envelope breakdown (NEB) and metaphase, bipolar astral spindles use dynamically unstable MTs and motors to capture replicated, condensed chromosomes and to maneuver them onto the spindle equator (Mitchison and Kirschner, 1984; Alexander and Rieder, 1991; Echeverri et al., 1996; Wollman et al., 2005).

In many systems, an antagonistic sliding filament mechanism driven by MT plus end–directed kinesin-5 and minus end–directed kinesin-14 motors is proposed to produce balanced outward and inward forces on spindle poles to maintain these prometaphase spindles as they capture chromosomes (for reviews see Hoyt and Geiser, 1996; Kashina et al., 1997; Civelekoglu-Scholey and Scholey, 2007). For example, Saccharomyces cerevisiae cells contain two members of the kinesin-5 family (Hoyt et al., 1992), which are required for spindle pole separation during initial spindle assembly and resist a kinesin-14–generated spindle collapse during prometaphase (Saunders and Hoyt, 1992). Drosophila melanogaster embryo mitotic spindles contain only one kinesin-5, KLP61F (Heck et al., 1993; Cole et al., 1994), which is dispensable for initial spindle assembly but is required to prevent prometaphase spindle collapse driven by a kinesin-14, Ncd (Sharp et al., 1999b; Brust-Mascher et al., 2009).

Specifically, time-lapse imaging and functional perturbation of the living Drosophila embryo early prometaphase spindle suggest that it is maintained at a steady-state length of ∼8 μm by a force balance generated by KLP61F and Ncd (Sharp et al., 1999b, 2000a; Tao et al., 2006), and this balance is tipped by the up-regulation of other outward force generators, e.g., cortical dynein and KLP3A, causing the spindle to elongate to its new steady-state metaphase length of 10–12 μm (Sharp et al., 2000a; Kwon et al., 2004). This model was supported by observations that genetic or antibody-mediated inhibition of KLP61F caused wild-type prometaphase spindles to collapse and that loss of Ncd function in null mutants caused prometaphase spindles to elongate prematurely, but bipolar spindle length was maintained after the inhibition of both KLP61F and Ncd (Sharp et al., 1999b, 2000a; Brust-Mascher et al., 2009). However, several uncertainties remain because it is not known precisely when these motors act and whether they actually localize to interpolar MTs (ipMTs) during prometaphase or whether antagonistic MT sliding driven by KLP61F and Ncd can act alone to maintain the early prometaphase spindle. Moreover, a computational model questioned the validity of the antagonistic motor-dependent sliding filament model (Nédélec, 2002), and there are suggestions that other mechanisms may be involved (Johansen and Johansen, 2007; Gardner et al., 2008; Wollman et al., 2008; Brust-Mascher et al., 2009). In this context, it is significant that recent work suggests that a membranous lamin-B envelope derived from the nuclear membrane could contribute to spindle assembly and stability in some systems (Tsai et al., 2006).

The KLP61F–Ncd force-balance hypothesis gains further support from observations that purified KLP61F, which moves to the MT plus ends at 0.04 μm/s, and Ncd, which moves to the MT minus ends at 0.1 μm/s, can both cross-link and slide MTs and antagonize one another in competitive motility assays (McDonald et al., 1990; Walker et al., 1990; Cole et al., 1994; Kashina et al., 1996; Tao et al., 2006; Oladipo et al., 2007; Furuta and Toyoshima, 2008; van den Wildenberg et al., 2008; Fink et al., 2009). Thus, increasing the molar ratio of one motor slows down the motility of the other “winning” motor until a balance point is reached (at a mole fraction of ∼0.7 Ncd) where MTs display a mean velocity of zero (Tao et al., 2006). This competitive motility was described using a protein friction model in which the “losing” motors switch to a protein friction mode and exert a passive springlike resistance that slows the movement of the active, winning motors. We argued that small plus end– and minus end–directed fluctuations observed at the balance point could be dampened out to produce a stable steady-state length in the spindle itself by the coupling of multiple ipMT bundles acting on the poles (Tao et al., 2006). However, this protein friction model does not provide a good description of the balance point.

In this study, we have evaluated the role of the KLP61F–Ncd force balance in prometaphase Drosophila embryo spindles using quantitative modeling. First, we carefully reexamine prometaphase spindles with or without depletion of KLP61F or Ncd to investigate when and where these motors act. Then we present the results of significantly improved modeling of the in vitro KLP61F–Ncd force balance to derive motor parameters that are applied to a new model for the prometaphase spindle in living embryos. This allowed the identification of factors required for the maintenance of a stable steady-state spindle length, implicating a role for the lamin-B spindle envelope in augmenting the underlying motor-dependent force balance.

Results

Roles of kinesin-5 and -14 in prometaphase spindles

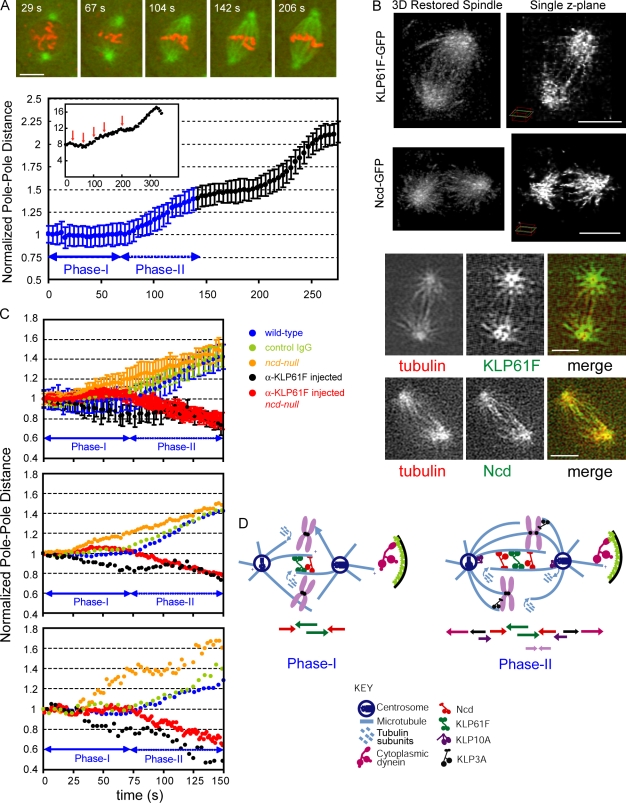
To determine when in prometaphase KLP61F and Ncd perform their function relative to the dynamic cytoskeletal and chromosomal rearrangements that follow NEB during prometaphase and whether they are localized along ipMT bundles, as predicted, we examined spindle and chromosome dynamics with improved spatial and temporal resolution. We monitored prometaphase, which consists of two phases in this system, in a new transgenic fly line coexpressing GFP-tubulin and histone-RFP. During phase I, lasting ∼75 s after NEB, the spindle poles were maintained, presumably by balanced inward and outward forces, at a steady spacing (where time-dependent spindle length S(t) = 8 μm and dS/dt = 0), and new ipMTs and chromosome-associated MTs were observed to assemble within the nucleus (Fig. 1 A). The chromosomal MTs apparently exerted the subpiconewton scale forces required to push chromosomes to the equator (Marshall et al., 2001; Kapoor et al., 2006), as seen by comparing images from 29 and 67 s in Fig. 1 A. Because many chromosomes lie outside the pole–pole plane during phase I (Fig. S1 A), we estimate that the minor component of these forces that acts parallel to the pole–pole axis is far too small to influence pole–pole spacing, which is controlled by ∼100 pN scale forces (see Discussion). During the subsequent 75-s long phase II, the force balance was tipped, and the spindle elongated (dS/dt > 0) to its metaphase steady-state length (S(t) = 10–12 μm; Fig. 1 A, Fig. S1 A, and Videos 1 and 2). During this phase, more robust kinetochore and chromosome-associated MT bundles could be seen, and they were very likely to influence the force balance acting on spindle poles. Previously, we noted that disruption of cortices overlying the spindle in scrambled and sponge mutants has no effect on spindle length during phase I but does impair spindle elongation during phase II (Brust-Mascher et al., 2009). Thus, forces generated solely by KLP61F and Ncd on nascent ipMTs could determine pole–pole spacing during phase I but not phase II, when cortical and chromosomal influences become more significant.

Figure 1.

Prometaphase spindle dynamics in Drosophila embryos: steady-state and elongation phases. (A, top) Time series of a spindle in living transgenic Drosophila embryos expressing GFP-tubulin (green) and histone-RFP (red) taken at the indicated time points on the plot of pole–pole spacing from the same spindle (red arrows on inset of bottom panel; t = 0 is NEB). (bottom) Averaged and normalized pole–pole dynamics in cycle 11 Drosophila embryo spindles; t = 0 is NEB. Prometaphase dynamics (blue): the steady-state (I) and elongation (II) phases are shown. Error bars show SD. (B) The top two rows show KLP61F-GFP (first row) and Ncd-GFP (second row) localization during prometaphase (phase I; steady-state) in restored spindles (deconvolved 3D image stacks), respectively. The left panels are 3D views of restored spindles, and the right panels show a single z plane from the same spindles. The bottom two rows show the colocalization of KLP61F-GFP and Ncd-GFP with rhodamine-tubulin on the nascent ipMTs during prometaphase (phase I; steady-state). (C, top) Averaged and normalized prometaphase pole–pole dynamics from cycle 11 embryos in wild type, control IgG, Ncd null, and KLP61F antibody–injected wild-type (black) and Ncd null (red). Error bars show SD. (middle) Data from the top panel are shown without SDs for clarity. (bottom) Pole–pole dynamics in individual representative spindles. (D) Cartoon of phase I (left) and II (right) prometaphase spindles based on in vivo functional perturbation and localization data. Colored arrows below the drawings indicate the direction of the forces generated by corresponding motors. Bars, 5 μm.

In support of this hypothesis, observations of GFP-KLP61F and GFP-Ncd in deconvolved and restored 3D confocal images of spindles in living embryos expressing functional fluorescent proteins in rescued mutants (Endow and Komma, 1997; Cheerambathur et al., 2008) revealed that both motors were aligned along filaments running from pole to pole, corresponding to the nascent ipMT bundles that assembled during phase I of prometaphase (Fig. 1 B). The fluorescent motors formed puncta that were somewhat reminiscent of myosin-II along stress fibers, possibly indicating that KLP61F and Ncd may multimerize as they associate with the ipMTs, as proposed recently for the MT–cross-linking MT-associated protein (MAP) Ase1p (Kapitein et al., 2008). After KLP61F inhibition resulting from antibody-induced dissociation of the motor from spindles (Brust-Mascher et al., 2009), pole–pole spacing began to decrease at a rate that was slow throughout phase I but accelerated at the onset of phase II, whereas loss of Ncd function in null mutant embryos led to premature pole–pole separation throughout both phases (Fig. 1 C). Loss of Ncd function in Ncd-null mutants led to the complete rescue of the phase I steady-state after KLP61F inhibition, and during phase II, loss of Ncd function substantially rescued spindle assembly (although the complete or very severe inhibition of KLP61F could cause spindle collapse during phase II, which was likely to be driven by another inward force generator; Fig. 1 C; Brust-Mascher et al., 2009).

These results are consistent with the idea that KLP61F and Ncd control spindle length throughout prometaphase, contradicting the surprising recent claim that Ncd acts only subsequent to metaphase (Hallen et al., 2008). During phase I, KLP61F and Ncd could have played the dominant role, acting on the newly assembling, overlapping antiparallel (AP) ipMTs to exert balanced outward and inward forces on spindle poles to maintain constant pole–pole spacing, but this was augmented during phase II by outward forces, e.g., as the result of cortical dynein plus chromosomal KLP3A and by an unknown inward force generator (Fig. 1 D; Sharp et al., 2000a; Kwon et al., 2004; Brust-Mascher et al., 2009).In the sections that follow, we test the idea that KLP61F and Ncd act alone to maintain spindle length during phase I.

A model for antagonistic sliding by KLP61F and Ncd using opposing power strokes with force-dependent detachment

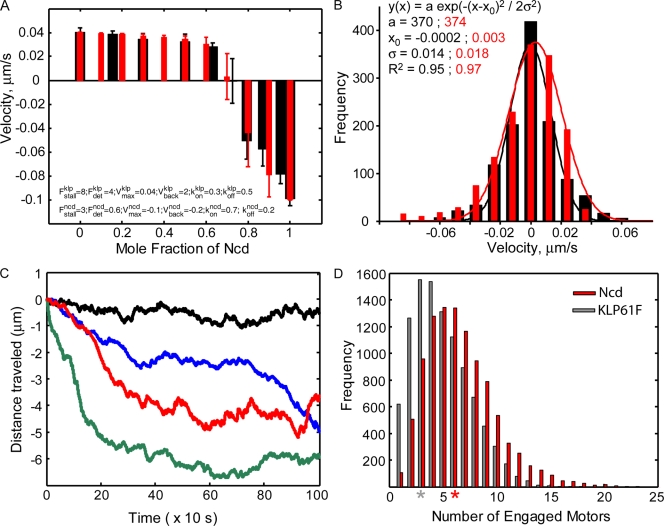
In competitive MT gliding assays, mixtures of purified KLP61F and Ncd oppose one another to stall MT movement at an appropriate molar ratio. This behavior could mimic the maintenance of a stable, steady-state phase I prometaphase spindle by these antagonistic motors (Tao et al., 2006). To explore this possibility and to derive motor parameters relevant to the development of an in vivo model for prometaphase, we developed a new force-balance model for these competitive MT motility assays (see Materials and methods sections In vitro model and Modeling methods). This model is based on opposing active power strokes and is fully stochastic because it incorporates MT–motor kinetics, most significantly a load-dependent detachment rate of motors, which yielded an excellent fit to the data (Fig. 2 A). We used our model to examine the behavior of MTs at the balance point and found that the histogram of MT velocities (Fig. 2 B) and trajectories of MTs (Fig. 2 C) are in very good agreement with experimental observations (Fig. S1, B and C). The model predicts that these velocities and trajectories occur when there are, on average, ∼10–15 (KLP61F + Ncd) motors bound per MT in a ratio of active and bound KLP61F:Ncd of 1:2 (∼4 KLP61F to 8 Ncd bound; Fig. 2 D).

Figure 2.

Stochastic force-balance model for antagonistic motility assays incorporating KLP61F and Ncd kinetics: model fit to assay data identifies motors’ biophysical parameters and suggests load-dependent kinetics and a specific superstall F–V relationship for motors. (A) Experimental (black) and computed (red) MT velocities in competitive gliding assays. The mole fraction is defined as (mole Ncd)/(mole Ncd + mole KLP61F), ignoring solvent/buffer concentrations. The stochastic force-balance model provides an excellent fit to the mean and the SD of the gliding data, even at the balance point. (B) Histogram of experimental (black) and computed (red) MT velocities at the balance point mole fraction with respective Gaussian fits. (C) Computed trajectories of four representative MTs at the balance point. (D) Histogram of the number of KLP61F and Ncd motors engaged with an MT (computed). Asterisks indicate peaks.

This new model fits the data far better than a previous macroscopic and deterministic protein friction model, which yielded plots of velocity versus mole fraction that were discontinuous and did not explain the behavior at the balance point (Tao et al., 2006). To further evaluate the two models, we performed competitive motility assays with Ncd and a purified, homotetrameric, headless (HL) subfragment, HL-KLP61F, which is capable of cross-linking MTs into bundles, displaying a threefold preference for AP versus parallel bundles (van den Wildenberg et al., 2008). We reasoned that this mutant should also exert protein friction–dependent drag on MTs being moved by active Ncd motors, so if the protein friction model is correct, the velocity–mole fraction curves for competitive motility assays involving HL-KLP61F should resemble those observed using full-length (FL) KLP61F (FL-KLP61F) in the mole fraction regime in which Ncd is winning (Tao et al., 2006). Instead, we observed that the mole fraction–velocity curve displayed a distinct switch-like behavior in which Ncd-driven motility abruptly stalled (Fig. 3 A, left). Such a switch was not seen using a homotetrameric KLP61F stalk subfragment lacking MT-binding activity (Fig. 3 A, right), suggesting that this is caused by HL-KLP61F binding to gliding MTs. The previous protein friction model (Tao et al., 2006) predicts that decreasing the ratio of Ncd to HL-KLP61F yields a gradual decrease in MT velocity at all frictional coefficients tested, which does not fit the observed switch-like behavior (Fig. 3 A and Fig. S2 A). In contrast, the new model (see Materials and methods sections In vitro model and Modeling methods) fits the HL-KLP61F data very well (Fig. 3 B). With the new model, we observed either a smooth, rapid transition in the Ncd-driven MT gliding velocity or an abrupt motility switch at decreasing Ncd mole fractions depending on whether the opposing force generators performed active unidirectional power strokes like FL-KLP61F (Fig. 2 A) or exerted tension as linear springs like HL-KLP61F (bidirectional, opposing extension or compression; Fig. 3 B).

Figure 3.

Gliding assays with purified Ncd and HL-KLP61F or KLP61F stalk: stochastic force-balance model that includes motors’ kinetics accounts for the results, but a protein friction model does not. (A) Competitive gliding assay results for Ncd with HL-KLP61F (left) and KLP61F stalk (right) for various mole fractions of Ncd, ranging from 0 to 1. (B) Results of stochastic, opposing power stroke force-balance model (red) including the kinetics of individual motors superimposed on experimental results (black). (A and B) Error bars show SD. (C) Histogram of distances MTs travel at the balance point mole fraction (∼0.7; in gliding assays shown in A) and the Gaussian distribution fit (red).

There are 12 parameters in the model (Table I; see Materials and methods section In vitro model), the maximal free velocities of KLP61F and Ncd plus the parameters listed in Table II. A search of this 12D parameter space yielded only a small set of parameter combinations that account for the data from competitive MT gliding assays (e.g., one set giving an excellent fit is shown in Fig. 2 A). By varying the parameter values one by one, we were able to assess their effect on the mole fraction–velocity relationship; for example, changing the kinetic properties of the motors had a profound effect on the position of the balance point (Table II), which occurred at the same mole fraction for both FL- and HL-KLP61F when the same kinetic parameters were used (Figs. 2 A and 3 B).

Table I.

Model variables and parameters

Symbol	Meaning	Parameter values used	References
$F_{stall}^{klp/ncd}$	Stall force of the motor	1–10 pN	Schnitzer et al., 2000; Valentine et al., 2006
$F_{det}^{klp/ncd}$	Detachment force of the motor	1–10 pN	Valentine et al., 2006
$V_{max}^{klp/ncd}$	Maximal velocity of the motor	0.01–0.5 μm/s	Tao et al., 2006
$V_{back}^{klp/ncd}$	Backward velocity of the motor	0.001–5 μm/s	Carter and Cross, 2005
$k_{on}^{klp/ncd}$	Binding rate of motors	0.01–10 s−1	Krzysiak et al., 2008
$k_{off}^{0,klp/ncd}$	Load-free detachment rate of motors	0.01–10 s−1	Krzysiak et al., 2008
k, n	Number of bound motors per unit length AP MT	up to 800 μm−1	Sharp et al., 1999a
κ	Spring constant of HL-KLP61F	10–200 pNs/μm	Tawada and Sekimoto, 1991
ζ(t)	Spring constant of nuclear lamin-B envelope	100–200 pNs/μm	Dahl et al., 2004; Cytrynbaum et al., 2005
μ	Effective spindle pole viscous drag coefficient	200 pNs/μm	Marshall et al., 2001
vMT	Instantaneous velocity of MT	variable	This study
vpole	Instantaneous velocity of spindle poles	variable	This study
νg	MT plus end growth rate	0.1–0.4 μm/s	Cheerambathur et al., 2007
νs	MT plus end shrinkage rate	0.1–0.4 μm/s	Cheerambathur et al., 2007
fres	MT plus end rescue frequency	0.01–0.5 s−1	Cheerambathur et al., 2007
fcat	MT plus end catastrophe frequency	0.01–0.5 s−1	Cheerambathur et al., 2007

Table II.

Impact of changing parameters

Parameter changed	Sharpness of velocity next to BP (KLP61F direction)	Position of BP mole fraction	Sharpness of velocity next to BP (Ncd direction)
$k_{on}^{ncd}$ ↑/↓	decrease/increase	left/right	increase/decrease
$k_{on}^{klp}$ ↑/↓	increase/decrease	right/left	decrease/increase
$k_{off}^{ncd}$ ↑/↓	unchanged/unchanged	right/left	unchanged/unchanged
$k_{off}^{klp}$ ↑/↓	unchanged/unchanged	left/right	unchanged/unchanged
$F_{stall}^{ncd}$ ↑/↓	decrease/increase	left/right	decrease/increase
$F_{stall}^{klp}$ ↑/↓	unchanged/decrease	unchanged/right	unchanged/unchanged
$F_{det}^{ncd}$ ↑/↓	unchanged/unchanged	left/right	unchanged/decrease
$F_{det}^{klp}$ ↑/↓	increase/decrease	right/left	unchanged/decrease
$V_{back}^{ncd}$ ↑/↓	unchanged/unchanged	unchanged/left	unchanged/unchanged
$V_{back}^{klp}$ ↑/↓	unchanged/decrease	unchanged/wider region	increase/decrease

BP, balance point. The effects of parameter changes (with respect to those in Fig. 2 A) on the mole fraction–velocity plot are font coded as follows: parameters for which a small (<20%), an intermediate (20–100%), and a large (>100%) change results in significant alteration on the plot are marked in bold, regular, and italic fonts, respectively. Note that parameters were changed one at a time and not simultaneously.

The model makes interesting predictions about the force–velocity (F–V) relationship of the motors, especially in the superstall regime, i.e., when the motor is exposed to forces exceeding its stall force, causing it to step backward (Fig. S2 B). Within the region of parameter space that provides a good fit to the data, the motor parameters could be uniquely determined: assuming that KLP61F has similar biophysical properties to Eg5 (Valentine et al., 2006; Korneev et al., 2007), the corresponding properties of Ncd emerge, e.g., unloaded velocity (v_max) = 0.1 μm/s, stall force (F_stall) ≤ 3 pN, and detachment force (F_det) is ∼1 pN, suggesting a relatively fast, weak motor that, in its superstall regime, would not have a profound effect on MT motility driven by the stronger KLP61F. To account for the experimentally observed high sensitivity of the balance point to changes in the Ncd mole fraction, our model predicts that the motors must exert a nearly constant force (≈F_stall) when stochastically and transiently attached to MTs in the superstall regime (Fig. S2 B). Exertion of forces greater than the stall forces would cause the balance point to persist over a much larger range of mole fractions (Fig. S3 A), although it was possible to recover the sharp transition under certain conditions if the weak Ncd motor exerted superstall forces while back stepping (Fig. S3 B).

A fully stochastic force-balance model for the prometaphase steady-state

The motor parameters obtained from the model fit to the competitive MT gliding assay data were applied to a new, fully stochastic force-balance model for the Drosophila embryo prometaphase spindle (see Materials and methods sections In vivo model and Modeling methods). This yielded several insights into the role of the KLP61F–Ncd force balance in prometaphase spindle maintenance, as discussed in the following sections.

KLP61F and Ncd can maintain the phase I prometaphase spindle at a stable length

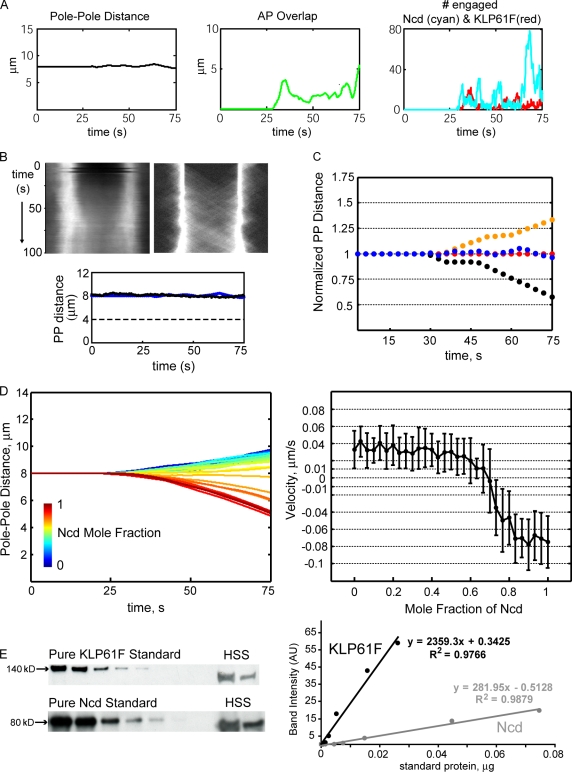
In the absence of any additional length-stabilizing factors, the model predicts that dynamic KLP61F and Ncd motors, at a mole fraction of ∼0.68 KLP61F to Ncd, could act on the rapidly maturing AP overlaps formed by dynamically unstable ipMT plus ends (Fig. 4 A, middle) to maintain the prometaphase spindle at a steady-state length of ∼8 μm (Fig. 4, A [left] and B). The motors acted as ensembles of dynamic cross-linkers that diffused and attached to the AP overlaps, exerted force, and detached in response to load (Cheerambathur et al., 2008). At the balance point, the ratio of engaged Ncd to KLP61F motors tended to fluctuate but remained, on average, lower than the available ratio of Ncd to KLP61F (∼2:1, as described by the nonfluctuating mole fraction) because of the load-dependent detachment of the motors from the highly dynamic ipMT tracks (Fig. 4 A, right; see Materials and methods section Modeling methods). Note that the MT dynamic parameters used in our model were entirely consistent with our previous experimental and theoretical studies of fly embryo mitosis (Brust-Mascher et al., 2004; Cheerambathur et al., 2007) and yielded virtual kymographs of fluorescent tubulin dynamics and pole–pole spacing similar to those obtained experimentally (Fig. 4 B). The (nonconvolved) model kymographs tracked only MT polymers whose dynamic ends appeared as distinct diagonal lines, which were somewhat masked in the experimental kymographs by the background of unpolymerized tubulin. Nevertheless, it was apparent in both cases that the AP MT overlaps began to form at 20–30 s after NEB and were becoming robust by the end of phase I (75 s).

Figure 4.

Quantitative stochastic force-balance model of the prometaphase phase I spindle: spindle MT and motor properties reveal a finely tuned steady-state. (A, from left to right) Spindle length, total AP overlap, and number of engaged Ncd and KLP61F motors on the AP overlaps during Phase I. Mole fraction of available Ncd is 0.7 (i.e., ∼2 Ncd per KLP61F). (B, top) Experimental (left) and computed (right) tubulin kymograph starting at NEB (t = 0) during prometaphase. (bottom) The corresponding pole–pole (PP) dynamics, experimental (black) and computed (blue), are shown. (C) Computed normalized spindle length dynamics in representative individual spindles: wild type (blue), Ncd null (orange), and KLP61F antibody injected into wild-type (black) or Ncd-null background (red). (D, left) Mean prometaphase phase I spindle dynamics for varying mole fractions of Ncd, increasing from 0 to 1 in 31 equally spaced steps. At t = 0 (NEB) MTs (not depicted) begin invading the spindle region. (right) Mean pole–pole separation rate (mean of instantaneous velocities during the last 40 s of prometaphase in 10 virtual spindles) plotted for varying Ncd mole fractions. The steady-state separation (mean velocity is ∼0) is confined to a narrow range of Ncd mole fractions. Error bars show SD. (E) Measurement of the molar ratio of endogenous KLP61F to Ncd. (left) Western blots showing (a) polypeptides from a serial dilution of recombinant protein (standard) purified from baculovirus expression system on the left and (b) corresponding polypeptides in high speed supernatants (HSS) from Drosophila embryo lysates; KLP61F was detected by anti-KLP61F antibody (top), and Ncd was detected by anti-Ncd antibody (bottom). (right) Corresponding standard curves showing polypeptide density versus standard protein’s amount from the left panels (KLP61F standards are shown as black dots, and Ncd standards are shown as gray dots). The amount of standard protein loaded was adjusted so that the densities of the endogenous protein (labeled as high speed supernatant; two different loading volumes for each protein) fell within the linear range, i.e., the middle of the standard curve. The amount of endogenous KLP61F and Ncd were calculated from linear fits to the standard curves. AU, arbitrary unit.

To simulate Ncd-null and KLP61F-inhibited embryos, we decreased the concentrations of the motors in the virtual spindles, and generally, we observed a good fit to the data (compare Fig. 4 C with Fig. 1 C). Interestingly, the virtual Ncd-null spindles elongated at a rate much lower than the free-sliding velocity of KLP61F, suggesting the kinesin-5 motors are loaded and work close to stall (Fig. 4 C). This is because the nascent AP overlaps remain sparse during phase I so the number of engaged KLP61F motors pushing apart the poles is sufficiently low to keep them loaded. Also, below a critical AP overlap level, the loaded KLP61F motors detach rapidly as a consequence of their kinetic parameters, ensuring the persistence of the slow elongation rate. This is different from the situation predicted for anaphase B when the motors work at their free-sliding rate on mature and rapidly turning over MT overlaps (Brust-Mascher et al., 2004; Cheerambathur et al., 2007).

The elongation of the virtual Ncd-null embryo spindles was interspersed with quiescent pauses, which may have resulted from transient reductions in the extent of overlap of AP force-generating ipMTs, as a result of them stochastically sliding apart or depolymerizing at their plus ends (e.g., compare Fig. 4 C with Fig. 1 C). In contrast, loss of KLP61F led to virtual spindle shortening as soon as the ipMT overlaps began forming (unless Ncd was absent as well; Fig. 4 C), which is in agreement with experiments (Brust-Mascher et al., 2009). Here, the viscous resistance of the spindle poles slowed the rate of spindle shortening below the free-sliding rate of Ncd, but the collapse was more persistent than the elongation of Ncd-null spindles because spindle shortening helped maintain the ipMT overlaps. This differs from the transient pauses observed in real KLP61F-inhibited spindles (Fig. 1 C), which we think were caused by steric hindrance from chromosomes dispersed between the poles, which is a situation not accounted for in our model.

Maintenance of the prometaphase steady-state by KLP61F and Ncd alone requires a specific ratio of KLP61F to Ncd that matches that measured in lysed embryo extracts

In our model, phase I prometaphase spindle length maintenance was very sensitive to the mole fraction of the KLP61F: Ncd force-balance motors, which must be maintained between 0.64 and 0.72 Ncd (Fig. 4 D). “Back of the envelope” calculations (Sharp et al., 1999a) suggest that ∼10⁴ KLP61F and 2 × 10⁴ Ncd motors per spindle can interact with the ipMT overlaps, but in vivo, these numbers could fluctuate because of changes in the rate of gene expression, posttranslational modifications, and proteolysis, etc. For example, fluctuations causing only a 20% increase in one motor plus a 20% decrease in the other yields a mole fraction of 0.57–0.75 Ncd, which lies beyond the acceptable range.

We measured the molar ratio of KLP61F to Ncd in Drosophila embryo extracts by quantitative immunoblotting and observed concentrations of 4.7 nM Ncd and 1.9 nM KLP61F, yielding a mole fraction of Ncd (4.9/(4.9 + 1.9)) of 0.71 (Fig. 4 E). It is striking that this lies well within the range that our model predicts to be required for the maintenance of a prometaphase spindle of constant length by the KLP61F–Ncd force balance acting alone. However, our experimental data obtained using KLP61F antibody–induced dissociation of KLP61F from spindles indicate that the steady-state is not very sensitive to the motors’ molar ratio (Brust-Mascher et al., 2009). Additionally, because natural phenotypic variations in this ratio may occur, we sought further stabilizing mechanisms that might produce a robust steady-state spindle length that is less sensitive to the relative amounts of these motors.

Effect of MT dynamics, MT geometry, and motor properties on the maintenance of a stable prometaphase spindle length

Stabilization of virtual spindle ipMT plus ends by a decrease in the catastrophe frequency, f_cat (which could correspond to inhibiting MT-depolymerizing kinesin-8 or -13 motors), did not extend the range of mole fractions capable of maintaining the prometaphase spindle length. When f_cat was decreased, the mean pole–pole separation rate remained near zero, but the SD around this balance point became very high (Fig. S4). For example, when f_cat = 0.2 s⁻¹, the unperturbed virtual spindles remained stable around a mole faction of 0.7 Ncd, but reducing this parameter to f_cat = 0.1 s⁻¹ tipped the force balance in favor of KLP61F, which prematurely elongated the spindle (Fig. S4). Thus, a narrow window of ipMT dynamics facilitates spindle stability, possibly because if f_cat is too high (f_cat ≥ 0.25 s⁻¹), MTs are unable to polymerize sufficiently and form overlaps, which is in contrast with our observations in GFP-tubulin kymographs (Fig. 4 B), whereas if f_cat is too low (f_cat ≤ 0.15 s⁻¹), ipMT may be too stable to facilitate MT–motor dissociation and switching, whereupon the system becomes trapped in a state in which either KLP61F or Ncd continues to win and the spindle either collapses or elongates.

We used the model to asses any influence of the geometry of the track upon which KLP61F and Ncd move on the motor’s processivity, with both ends on AP MTs as in the prometaphase spindle or with one end bound to a glass surface and the other moving along a single MT as in gliding assays (Sharp et al., 1999a; Tao et al., 2006; van den Wildenberg et al., 2008). Ncd is found to be highly processive when acting between MTs (Furuta and Toyoshima, 2008). Thus, we computed pole–pole separation in a virtual spindle where the KLP61F and Ncd motors are four times less likely to dissociate from AP ipMTs (prometaphase spindle) versus single MTs (gliding assays) and observed little effect on the sensitivity to variations in the Ncd mole fraction (Fig. S5 A). This suggests that such changes in the geometry of the motors’ tracks do not significantly influence the robustness of prometaphase spindle maintenance.

KLP61F is thought to be a bipolar homotetramer, whereas Ncd is a unipolar homodimer. To determine whether motor ultrastructure influences spindle maintenance by the KLP61F–Ncd force balance, we simulated a KLP61F motor having a monopolar structure instead (Fig. S5 B). We observed that the steady-state formed at a lower mole fraction of Ncd (∼0.56) but became more sensitive to changes in the mole fraction (i.e., increased variance and steeper slope at the steady-state). Thus, if both motors were to have a monopolar ultrastructure, their interaction with multiple dynamic AP MT overlaps would not lead to the maintenance of a stable prometaphase spindle.

Our aforementioned model of the competitive gliding assays predicted that, in the superstall regime, attached KLP61F motors should maintain a roughly constant force (≈F_stall). How protein motors function to produce force in the superstall regime merits further experimental investigation (Carter and Cross, 2005), but in previous theoretical models, it was suggested that motors must exert large, superstall forces while stepping backward (Müller et al., 2008). To examine how changing the behavior of motors in the superstall regime affects spindle pole dynamics, we simulated KLP61F motors displaying a sharp increase in the slope of the F–V curve in the superstall regime (as in Fig. S2 B). We found that, in this situation, a stable spindle pole separation was maintained for a wide range of Ncd mole fractions and was highly stable (Fig. S5 C). Thus, the nature of the motors’ F–V curve could contribute to the robustness of prometaphase spindle maintenance.

Lamin-B forms a gradually disassembling envelope that could maintain a robust prometaphase steady-state spindle length over a large range of KLP61F:Ncd molar ratios

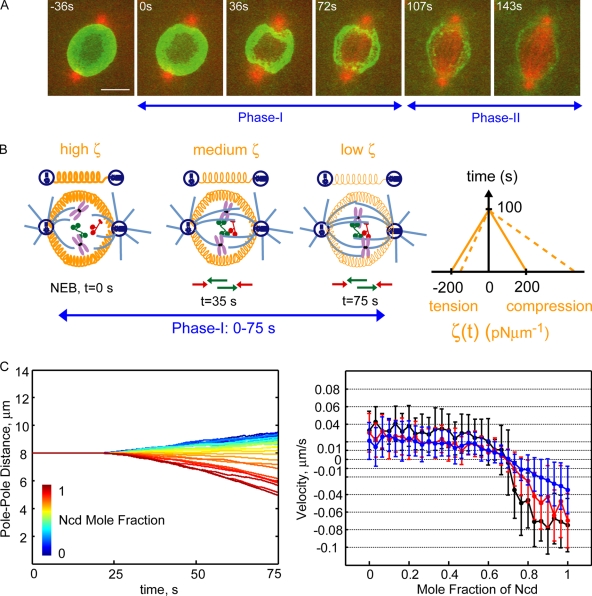
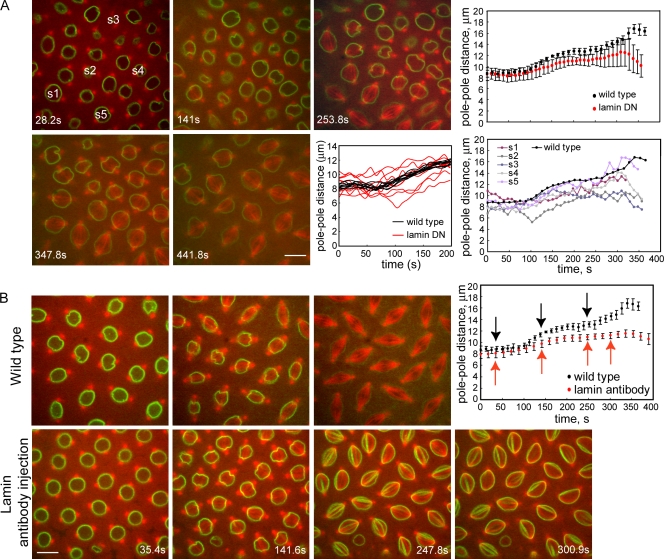
In considering three candidate structures that could potentially stabilize the prometaphase phase I spindle against naturally occurring fluctuations in KLP61F and Ncd ratios, namely chromatin (Bouck and Bloom, 2007), actin-rich cortices (Brust-Mascher et al., 2009), and a lamin-B spindle envelope (Stafstrom and Staehelin, 1984; Tsai et al., 2006), we tentatively concluded that neither chromatin nor cortical structures are likely to contribute significantly (see first section of Results; Brust-Mascher et al., 2009) but the lamin-B envelope could indeed confer robustness to the phase I prometaphase spindle. For example, we examined the dynamics of the Drosophila lamin-B (Dm0) around nuclei and spindles of living transgenic embryos expressing GFP-Dm0. We observed that a robust but gradually diminishing GFP-Dm0 signal persisted after NEB throughout prometaphase phase I (0–75 s), such that at the transition from phase I to II (the time when rapid spindle collapse begins after severe KLP61F inhibition), the disassembly was evident and persisted as the phase II spindle elongated and was complete only at the end of phase II (Fig. 5 A). Moreover, deformations were seen in the lamin-B envelope at the poles (e.g., Fig. 5 A, indentations at t = 36 s), which suggests the existence of mechanical interactions between the spindle envelope and the growing MTs that invade the nucleus to form nascent ipMTs. These observations indicate that the gradually disassembling nuclear lamina could serve as a mechanical stabilizer that augments the KLP61F–Ncd force balance to enhance the robustness of the system.

Figure 5.

A lamin-B envelope confers robustness to the steady-state prometaphase spindle by stabilizing it to phenotypic variations in the KLP61F to Ncd ratio. (A) Localization of the Drosophila lamin-B (Dm0) surrounding the prometaphase (phase I and II) spindle in fly embryos stably expressing GFP-Dm0; t = 0 is NEB. Images show a time series from a live embryo, each image being a projection of six z stacks along the x–y plane. Note the indentation of the lamin-B envelope surrounding the spindle by the centrosomes at the opposite ends of the spindle at t = 36 and 72 s during prometaphase phase I. (B) Schematic representation of an elastic lamin-B envelope surrounding the spindle during phase I of prometaphase and the representation of this envelope as a linear Hookean spring between the spindle poles (simple drawings above the spindle cartoons). Green and red arrows depict KLP61F- and Ncd-driven ipMT sliding. The time-dependent disassembly of this elastic envelope is incorporated into the quantitative model as a linearly decreasing spring constant, ζ(t), responding equally to extension and compression as shown in the graph on the right (solid line). Superimposed is an asymmetric spring constant of the lamin-B envelope with limited compressibility (dashed line). (C) Quantitative model results of the role of the elastic lamin-B envelope on the robustness of the prometaphase steady-state to the motors’ molar ratio. The left panel shows the mean prometaphase spindle length over time (averaged over 10 virtual spindles) for the varying mole fraction of Ncd, increasing from 0 to 1 in 31 equally spaced steps. The right panel shows the mean pole–pole separation rate for increasing Ncd mole fraction from 0 to 1; results of the model augmented with an elastic lamin-B envelope (red) are superimposed on the model solutions without lamin-B (black), as in Fig. 4 D, for comparison. A stable spindle length (mean velocity ≤|0.02| μm s⁻¹) is maintained for a wide range of motors’ molar ratio (approximately within [0.35 to 0.8] Ncd mole fraction) in the solution of the augmented model (red). The solution of the model including a lamin-B envelope with asymmetric response to extension and compression as in B (right, dashed line) is shown superimposed in blue. This extends the stability regime further, particularly at high Ncd mole fractions. Error bars show SD. Bar, 5 μm.

To determine whether the lamin-B envelope could indeed extend the range of motor concentrations that can maintain a prometaphase spindle at constant length, we first modeled it as a simple linear spring with an effective elastic spring constant of 100–200 pNs/μm at t = 0 (NEB; Dahl et al., 2004; Panorchan et al., 2004a,b; Cytrynbaum et al., 2005), decreasing linearly to 0–50 pNs/μm by the end of phase I (Fig. 5, A and B). This linear spring (with time-dependent constant ζ(t)) augments the motors to exert an inward–outward force on the virtual spindle poles according to the expression F_elastic = ζ(t)(S(t) − S₀), where S(t) and S₀ are spindle lengths at times t and 0 from NEB, respectively (see Materials and methods section Modeling methods). Solutions over time, with Ncd mole fraction varied between [0 1], reveal that the prometaphase spindle can now be maintained at a stable length over a much larger ratio of KLP61F:Ncd (Fig. 5 C). Indeed, for mole fractions varying from 0.35 to 0.8, the change in spindle pole separation remained <1 μm during phase I, which lies within the range of measurement error in our light microscopy experiments. This stabilization was further enhanced, especially in the region of high Ncd mole fractions, when a spring with asymmetrical resistance to extension and compression (corresponding to a piecewise linear elastic constant) was used to model an elastic lamin envelope that was limited in compressibility (Fig. 5, B and C), as described for the Xenopus laevis nuclear lamina (Dahl et al., 2004).

Proper lamin-B dynamics are required for spindle maintenance and elongation during prometaphase and anaphase B

Our model results predict that the disruption of the lamin-B envelope should destabilize the steady-state pole–pole distance during prometaphase phase I. To test this, we microinjected GFP–lamin-B–expressing transgenic embryos with a dominant-negative subfragment of the Drosophila lamin-B tail (nonhelical residues 407–622 of Dm0), which is expected to interfere with lamin–lamin interactions, thereby disrupting the architecture and mechanical resistance of the lamin-B envelope (Bray, 2001; Lopez-Soler et al., 2001; Tsai et al., 2006). This produced defects in prometaphase phase I spindle maintenance and in subsequent spindle elongation (Fig. 6 A). The timing of NEB was perturbed so that neighboring nuclei entered mitosis at different times, and in some nuclei, spindle assembly was delayed after tubulin invaded the nuclear space. As predicted, phase I was not as steady as in wild-type controls; spindle length was destabilized, with individual spindles displaying obvious bidirectional length fluctuations in plots of pole–pole spacing versus time (Fig. 6 A, bottom right), whereas the mean length of multiple spindles exhibited a significantly larger variance than controls (Fig. 6 A, top right [showing means with SDs] and bottom left [showing multiple individual wild-type and lamin dominant-negative spindles]), which is consistent with the lamin-B envelope playing a stabilizing role. Subsequently, spindles underwent a small prometaphase elongation, but after a while, they disassembled, and a single nucleus reformed; a few spindles formed two nuclei that then collapsed back together.

Figure 6.

Functional perturbation of the lamin-B envelope interferes with spindle length changes and the completion of mitosis. (A) Microinjection of the lamin-B tail dominant-negative (DN) subfragment disrupts the lamin-B nuclear lamina and causes delays in prometaphase spindle formation, destabilization and length fluctuations of the phase I spindles, defects in subsequent spindle morphogenesis, and failure to complete mitosis. (B) The microinjection of a mixture of anti–lamin-B mAbs cross-links the lamin-B envelope into a hyperstable network that fails to disassemble. This structure impedes spindle elongation during prometaphase phase II and anaphase B (graph; arrows show times when still images were captured). In A and B, panels show still images at times after NEB. In A, t = 0 corresponds to NEB for spindle s1. Top and bottom graphs show pole–pole spacing versus time after NEB (t = 0) for multiple spindles (mean with SD) and individual spindles (A, second row: the left graph shows multiple control spindles [black]; for clarity, the right graph shows a single control spindle [black]). Bars, 10 μm.

The microinjection of a mixture of anti–lamin-B mAbs apparently cross-linked lamin-B into a hyperstable network and prevented the normal disassembly of the lamin-B spindle envelope, which then persisted throughout mitosis (Fig. 6 B). Strikingly, this stabilized envelope impeded the normal elongation of the spindle during prometaphase phase II and during anaphase B (Fig. 6 B, graph). Thus, (a) the lamin-B envelope must disassemble during prometaphase phase II to allow force generation by MTs and mitotic motors to drive pole–pole separation, thereby supporting the notion of a mechanical effect of the lamina in resisting spindle elongation, and (b) the lamin-B envelope is not required for anaphase B, when MTs and motors alone can produce robust spindle elongation (Brust-Mascher et al., 2004), because it disassembles before metaphase (Fig. 5 A), and when it persists through anaphase B, spindle elongation cannot occur (Fig. 6 B).

Discussion

How antagonistic kinesin-5 and -14 motors control mitotic spindle length is unclear and may differ in different spindles (Saunders and Hoyt, 1992; Gaglio et al., 1996; Saunders et al., 1997a,b; Walczak et al., 1998; Cottingham et al., 1999; Sharp et al., 1999b, 2000a; Goshima and Vale, 2003). To explore this problem, we used a stochastic force-balance model for competitive in vitro motility assays of KLP61F and Ncd and obtained motor parameters that were applied to a model for prometaphase Drosophila embryo spindle maintenance by these motors.

Prometaphase spindle maintenance by the KLP61F–Ncd force balance

Our modeling suggests that a KLP61F–Ncd force balance, acting alone on highly dynamic, overlapping ipMTs, can maintain the phase I prometaphase spindle at a constant length as ipMTs assemble and chromosomes are pushed to the equator, so long as the molar ratio is maintained within a narrow range, i.e., 0.65–0.72 mole fraction of Ncd. Surprisingly, we measured the same ratio of total KLP61F:Ncd in embryo extracts, suggesting that regulatory mechanisms maintain the level of expression of the motors at the required ratio. A precedent for such a tight control of motor ratios is found in skeletal muscles, in which the ratio of myosin-II isotypes is regulated to match physiological performance (Tsika et al., 1987). The KLP61F–Ncd force balance is augmented by other force generators during phase II when robust chromosome fibers form, cortical organization becomes important, and the spindle elongates to its metaphase length.

Role of the lamin-B envelope

If fluctuations in the mole fraction beyond the range required for stability occur in living embryos, e.g., because of changes in gene expression or posttranslational modifications, additional length regulatory mechanisms must counteract spindle destabilization. Candidates for such regulators include MT polymerases–depolymerases (Kline-Smith and Walczak, 2004; Goshima et al., 2005), nonmotor MAPs (Cullen et al., 1999; Manning and Compton, 2008), or a spindle matrix (Kapoor and Mitchison, 2001; Scholey et al., 2001; Chang et al., 2004; Tsai et al., 2006; Johansen and Johansen, 2007). Our modeling suggests that the disassembling lamin-B envelope, which persists until the end of prometaphase, could fulfill this role, making the spindle robust in the face of kinesin-5 and -14 fluctuations. In complementary work, a stabilizing role for the nuclear lamina has been described for Xenopus extract spindles, where it anchors dynein to oppose kinesin-5–driven spindle elongation rather than conferring robustness to a kinesin-5–kinesin-14 force balance that is capable of functioning independently of the lamina as we propose (Tsai et al., 2006; Zheng, Y., personal communication).

Microinjecting dominant-negative subfragments and mAbs that disrupted and hyperstabilized the lamin-B envelope, respectively, perturbed spindle length in the manner predicted by our model. Significantly, disruption of the lamina by the dominant-negative subfragment caused a delay in prometaphase spindle assembly and the destabilization of length maintenance during phase I, as expected if the lamin-B envelope normally plays a stabilizing role. Hyperstabilization of the envelope inhibited subsequent spindle elongation, and this, together with observations that the lamin-B envelope is no longer visible by metaphase, suggests that the lamina must disassemble before metaphase to allow normal spindle length changes. Thus, the lamin-B envelope cannot contribute to the mechanisms of anaphase A or B (Brust-Mascher et al., 2004; Civelekoglu-Scholey et al., 2006).

Requirement for rapidly turning over, nascent AP ipMT overlaps

Our model suggests that a narrow range of ipMT dynamic instability parameters, matching those that are thought to exist in embryos (Cheerambathur et al., 2007), supports prometaphase spindle stability. For example, if the ipMT catastrophe frequency (f_cat) is too low, a substantial AP ipMT overlap forms rapidly, providing a large substrate for many Ncd and KLP61F motors (Fig. S4, B and C), but this does not support spindle stability mediated by the KLP61F–Ncd force balance because the opposing motors must frequently switch between episodes of winning and losing to keep the spindle at a steady-state length. A sufficiently high f_cat is needed to augment the load-dependent detachment of winning motors so that the losing motors can take over to sustain the balance of forces. Consequently, as f_cat increases, spindle stability also increases (Fig. S4 A). In contrast, if f_cat becomes too high (≥0.25 s⁻¹), the AP ipMT overlaps do not begin to form until much later than is observed in the tubulin kymographs of embryo spindles, and there are no tracks for the force-balance motors to work on during phase I. Therefore, a narrow range of MT dynamic instability parameters, as used in Fig. 4, is required for spindle stability.

Implications for motor F–V relations

Only certain forms of F–V relationships for KLP61F and Ncd in the superstall regime are compatible with both the sharp transition though the balance point and spindle stability; e.g., a robust steady-state spindle length occurs if KLP61F motors exert superstall forces when stepping backward. This differs from our anaphase B model, which predicts that KLP61F works in its unloaded regime and never enters the superstall regime during spindle elongation (Brust-Mascher et al., 2004). Measuring F–V curves in the superstall regime for KLP61F and Ncd will obviously be informative, but this is technically challenging. Our model also implicates different F–V relationships to explain the difference in response of Ncd motors to competition from ATP-hydrolyzing FL-KLP61F versus MAP-like HL-KLP61F, namely a gradual slowing down versus an abrupt motility switch. This is because a nonmotor MAP can exert symmetrical resistance to motility in both the plus and minus end directions, possibly indicating an important in vivo role for MAPs, and indeed for the MT-binding tail of kinesin-5 (Cahu et al., 2008; van den Wildenberg et al., 2008), in controlling motor-generated forces.

The new model for the competitive motility assay

The new force-balance model provided a better description of competitive KLP61F–Ncd MT gliding assay data than did a previous protein friction model (Tao et al., 2006). Only a small region of parameter space was consistent with the tight ratio of Ncd:KLP61F that produced the balance point in vitro where motors move taxol-stabilized MTs over glass coverslips (Tao et al., 2006), unlike the situation in vivo in which motors cross-link and slide dynamic AP ipMTs (Sharp et al., 1999a; Cheerambathur et al., 2008; van den Wildenberg et al., 2008). Despite this difference, when parameters from the in vitro assay were used to model the KLP61F–Ncd force balance in prometaphase of living embryos, a similar response to changing motor ratios was observed, suggesting that the in vitro study is relevant to the situation in vivo.

Relation to other models for motor competition

Our in vitro model for competitive motility between mitotic motors is similar to an independently derived mean field model for bidirectional vesicle transport involving a “tug of war” mechanism between antagonistic transport motors (Müller et al., 2008). Another recent related model describes vesicle transport by multiple motors of a single class working in or out of phase as a result of strain gapping at various velocities (Kunwar et al., 2008). The formation of a stable spindle by antagonistic motors with linear F–V relationships was not found in a comprehensive computational search for combinations of motors that give rise to robust steady-states when MT asters are fused together (Nédélec, 2002), but that search targeted steady-states that were relatively insensitive to parameter variations, so the narrow range of mole fractions required in our study very likely precluded its discovery. The study by Nédélec (2002) agrees with ours that a stable spindle length cannot be maintained by antagonistic motors acting on stable (slowly turning over) AP ipMT overlaps, as investigated in his study, but we find that a steady spindle length can be maintained if the MT tracks are sufficiently dynamic. Our system level search for combinations of force generators acting in Drosophila embryos did not find the KLP61F–Ncd force balance to be important for early prometaphase (Wollman et al., 2008). That study incorporated forces generated by robust chromosomal/kinetochore fibers and cortical dynein, but such forces are thought to be insignificant during much of phase I of prometaphase (e.g., see Results and Brust-Mascher et al., 2009). A very different “slide and cluster” model was developed to explain how antagonistic motors establish and maintain anastral spindle length (Burbank et al., 2007), but it is unclear whether this is relevant to astral Drosophila embryo spindles. A significant advance in our work over previous models for mitosis (Brust-Mascher et al., 2004; Burbank et al., 2007; Wollman et al., 2008) is its fully stochastic nature, which underscores the notion that stochasticity, e.g., load-dependent motor kinetics and ipMT dynamic instability, has a stabilizing effect on spindle length.

Conclusions

Our results suggest that ensembles of KLP61F and Ncd motors, acting on their own, can cross-link and slide multiple nascent, dynamic AP ipMTs to maintain the prometaphase spindle at a stable spacing as chromosomes are pushed to the equator, so long as the concentration ratio of the force-balance motors is maintained within a narrow range. However, the prometaphase spindle can be made robust to natural fluctuations in motor ratios by a disassembling lamin-B envelope.

Materials and methods

In vitro model: description of the stochastic force-balance model, including the kinetics and load-dependent detachment rates of KLP61F–Ncd

In our stochastic force-balance model for the in vitro MT gliding assays, we first randomly positioned MTs and KLP61F and Ncd motors on a virtual coverslip (∼20 MTs; MT lengths [4,8] μm; total of 500,000 motors). The motors’ positions and MTs’ lengths were kept constant throughout each simulation. At each time step for each MT, we first executed the binding and detachment events of the motors and then calculated the instantaneous velocity of the MT, v_MT, based on the current number of attached motors and a force-balance equation (Eq. 1), incremented the time step, updated the position of the MT according to v_MT, and repeated the sequence of events (see Modeling methods). New binding events of motors to MTs were executed according to the current position of the MT, the position of the motors on the virtual coverslip, a preset minimal interaction distance, a pseudo–first order binding rate constant (k_on), and a random number generator algorithm. Similarly, detachment of motors were executed based on the current load on the motor, F, the load-dependent detachment rate of the motor,

$$k_{off}\left(F\right)=k_{off}^0\exp \left(\frac{F}{F_{det}^{klp/ncd}}\right),$$

where $k_{off}^0$is the motor’s detachment rate in the absence of load and $F_{det}^{klp/ncd}$is the critical detachment force of the motor, and a random number generator algorithm. The magnitude of the force exerted on the MT and the MT’s velocity, v_MT, were calculated based on the current number of engaged motors (k and n for KLP61F and Ncd, respectively), and the motors’ F–V relations, incorporating each motors’ stall force, F_stall, and unloaded velocity, V_max (ignoring the fN level drag forces on the MT), according to

$$k{F}_{stall}^{klp}(1-\frac{v_{MT}}{V_{max}^{klp}})-n{F}_{stall}^{ncd}(1-\frac{v_{MT}}{V_{max}^{ncd}})=0$$

(see Modeling methods). The motors were assumed to have piecewise linear F–V relationships (Fig. S2 B). For the HL-KLP61F motors, the following force-balance equation was solved to calculate the velocity of the MT:

$${\displaystyle \sum _k\kappa v_{MT}\Delta t}-n{F}_{stall}^{ncd}(1-\frac{v_{MT}}{V_{max}^{ncd}})=0,$$

where κ is the spring constant associated with the HL-KLP61F motor and Δt is the time step.

In vivo model: the stochastic prometaphase force-balance model

Our stochastic prometaphase spindle force-balance model describes a system of dynamic MTs and antagonistic motors acting on AP MT overlaps to generate opposing forces on the spindle poles. MTs are growing from the centrosomes at time t = 0 (NEB) toward the spindle equator to form transient AP overlaps, and individual KLP61F and Ncd motors bind to/detach from these dynamic AP ipMT overlaps. In our computational model (see Modeling methods), we kept track of each MT’s plus and minus ends, positions of the MT-bound motors, and the positions of the poles. At each time step, first the binding/detachment events of new and bound motors to AP MT overlaps were executed. Then, with the current number of engaged motors on AP MT overlaps, the instantaneous velocity of the MTs and the spindle poles, v_pole, were calculated based on the total force exerted on the spindle poles by all engaged motors. To do so, we used the following force-balance equation on the spindle poles (Eq. 5), with the motor F–V relations and parameters derived from the model fit to the in vitro competitive gliding data:

$$\mathit{\mu }{v}_{pole}={\displaystyle \sum _{M{T}_i}\left(k_i{F}_{stall}^{klp}(1-\frac{v_{pole}}{V_{max}^{klp}})-n_i{F}_{stall}^{ncd}(1-\frac{2v_{pole}}{V_{max}^{ncd}})\right)}.$$

Here, μ and v_pole are the drag coefficient and the velocity associated with a spindle pole, respectively, and MT_i and k_i or n_i denote the i^th pair of MTs with an AP overlap and the number of engaged KLP61F and Ncd motors on AP overlap on MT_i, respectively (for other terms, see In vitro model and Modeling methods; Table I). Then, the time step was incremented, and the positions of the MTs, bound motors, and the spindle poles were updated. MT dynamics of the plus ends were computed using the MT dynamic instability parameters, and the positions of plus ends were updated based on the current MT dynamic states and rates. In the new time step, with the new positions of MTs, motors, and the poles, the sequence of events was repeated, typically for 1,000 time steps, corresponding to 100 s in real time.

Modeling methods

Stochastic force-balance model of competitive MT gliding assays

Force-balance equations and F–V relations

In the antagonistic MT gliding assay model, the time-dependent rate of movement of MTs on the coverslip surface coated with KLP61F and Ncd motors of various molar ratio was determined by the force-balance equation under low Reynolds number conditions:

$$\mathit{\eta }{v}_{MT}\left(\text{t}\right)=F_{MT}\left(\text{t}\right),$$ (1)

where η is the viscous drag coefficient associated with the MT (assumed to be a rigid rod of length L), v_MT(t) is the velocity of the MT at time t, and F_MT(t) = F_KLP61F(t) − F_Ncd(t) is the total force exerted on the MTs by the attached and active KLP61F and Ncd motors at time t. The general form of the force-balance equation and the F–V relations are given in the In vitro model section, but details are given here. The KLP61F and Ncd motors in the model are characterized by piecewise linear F–V relations:

$$v_{KLP61F}\left(F\right)=\{\begin{array}{l}{V}_{max}^{klp}(1-\frac{F}{F_{stall}^{klp}})\hspace{1em}\text{if}\hspace{0.17em}F\le F_{stall}^{klp}\\ V_{back}^{klp}(1-\frac{F}{F_{stall}^{klp}})\hspace{1em}\text{if}\hspace{0.17em}F>F_{stall}^{klp}\end{array},$$ (2)

where F is the magnitude of the load exerted on the motor, v_KLP61F is the corresponding velocity of the motor on its MT track, and$F_{stall}^{klp}$, $V_{max}^{klp}$, $V_{back}^{klp}$ are the stall force, the unloaded (maximal) forward velocity, and the backward velocity for KLP61F, respectively (Fig. S2 B and Table I), and similarly for Ncd (Fig. S2 B and Table I). Note that with the piecewise linear F–V relation in Eq. 2, the resistance of the motor proteins to substall and superstall loads (forward and backward motion regime) are defined separately but continuously (Müller et al., 2008). In our model, the time-dependent force exerted on an MT by k number of attached KLP61F and n number of attached Ncd motors was determined by assuming piecewise linear F–V relations for the motors (as in Eq. 2), and multiple attached motors were assumed to share the load equally (additive forces). Thus, for an MT gliding with the minus end leading (KLP61F direction) by the action of k number of attached KLP61F and n number of attached Ncd, the force exerted on the MT by the motors and therefore its velocity v_MT are given by:

$$\mathit{\eta }{v}_{MT}=F_{KLP61F}-F_{Ncd}=k{F}_{stall}^{klp}(1-\frac{v_{MT}}{V_{max}^{klp}})-n{F}_{stall}^{ncd}(1-\frac{v_{MT}}{V_{back}^{ncd}}).$$ (3)

We further assumed that the viscous drag force associated with the MT was of negligible magnitude (in the order of fN; Howard, 2001). Therefore, KLP61F- and Ncd-generated forces antagonize one another on the MT at any given moment, and the velocity of the MT is

$$v_{MT}\left(t\right)=\frac{\gamma k{V}_{max}^{klp}-n{V}_{back}^{ncd}}{(\gamma k-n)},$$ (4)

where

$$\gamma =\frac{F_{stall}^{klp}/V_{\max }^{klp}}{F_{stall}^{ncd}/V_{back}^{ncd}}.$$

The velocity of an MT gliding with the plus end leading (Ncd direction) by the action of k number of attached KLP61F and n number of attached Ncd is described similarly, using the backward and the forward velocities of the KLP61F and Ncd motors, respectively.

Numerical simulations

Initial conditions.

The initial conditions were set to mimic the experimental gliding assay. A grid (coverslip surface) of 100 × 100 μm was defined. On average, 20–30 MTs of random lengths between 4 and 8 μm were positioned randomly (at randomly selected directions and an angle between [−π π]) on the grid. The initial, randomly determined lengths of the MTs were kept constant (i.e., representing taxol stabilized MTs) throughout each gliding assay simulation. Then, a total number of 500,000 motors (e.g., 250,000 Ncd and 250,000 KLP61F motors for an Ncd mole fraction of 0.5) were positioned randomly on the grid. The motors were assumed to remain static on the grid throughout each gliding assay simulation (i.e., representing motors that were stuck on the coverslip surface).

Motor–MT binding.

At each time step t_n for each MT, first the motors in reach of the MT were determined (shortest distances between the motors and MTs were calculated, and the orientation of the motors was not taken into account) and stored in arrays. The critical interaction distances for Ncd and KLP61F and the MTs were 40 nm and 65 nm, respectively. To minimize the computational time in the calculation of motor–MT distances, in each simulation at the initial time step, once the positions of the motors were randomly determined on the coverslip (100 × 100 μm), the coverslip was divided into grids (typically square grids of 5 × 5 μm), and the motors’ x–y positions were stored in separate arrays (cell) for each grid (note that the number of KLP61F and Ncd motors in each grid was different). To identify the motors that can interact with an MT at time step t_n, first the grid or grids in which the MT resided were determined based on the current position of the MT (i.e., minimum of one and maximum of four grids because the MT length is ≤8 μm, and the maximal interaction between a motor and an MT was also taken into account in the identification of the grids). This process reduced the computation time for distances between an MT and motors greatly. Thus, only the distances between all of the free/unattached motors in this grid and the MT were computed using the scalar product, and motors that were closer than the critical interaction distance were stored in an array for potential binding. Each motor in this array was allowed to bind to the MTs if a randomly chosen number r (Matlab built-in random number generator, rand) was less than P_on, P_on = 1 − exp(−k_on Δt), where k_on is the pseudo–first order binding rate constant (Table I) and Δt is the simulation time step. In this way, KLP61F and Ncd motors newly bound to an MT were determined and stored at each time step t_n.

Motor detachment from the MT.

At each time step t_n for each MT, the number of attached KLP61F and Ncd motors (k and n, respectively) in step t_n-1 was determined (this is equal to zero at the initial time step). The motors detach in two ways: (1) stochastically and (2) if they were further than a critical distance from the MT ends in the current time step (note that the MTs glided on the coverslip, but the motors were immobile). The stochastic detachment of each motor was executed by comparing a random number r (Matlab built-in random number generator, rand) with the detachment probability P_off(F), where P_off(F) = 1 − exp(−k_off Δt), F is the load on the motor, k_off is the load-dependent detachment rate of the motor, and Δt is the simulation time step. The load-dependent detachment rate is described by

$$k_{off}\left(F\right)=k_{off}^0\exp \left(\frac{F}{F_{det}^{klp/ncd}}\right),$$

where $k_{off}^0$is the motor’s detachment rate in the absence of load, and $F_{det}^{klp/ncd}$is the critical detachment force of the motor (Table I). At time step t_n, F is given by

$$F=F_{stall}^{klp/ncd}(1-\frac{v_{MT}}{V_{max/back}^{klp/ncd}}),$$

where v_MT is the velocity of the MT in the previous time step, t_n-1, and the stall forces and maximal or backward velocity of the motor were chosen appropriately for KLP61F and Ncd, depending on the sign of v_MT. At each time step for each MT, once all of the stochastic detachment events were executed, the current distances between the MT ends and the motors were checked for the remaining “not detached” motors, and motors that were farther than the critical distance required for interaction were detached. Motors that detached at time step t_n were not permitted to rebind until the subsequent step. Motors that did not detach were stored and combined with the array containing the newly bound motors in time step t_n, defining the engaged KLP61F and Ncd motors interacting with the MT in the current time step. These motors were used for the force balance on, and thus the velocity of, the MT.

Algorithm.

At each time step, first the binding and detachment of the motors were computed for each MT. Then, the velocity of the MT at the current time step t_n was computed as follows. First, for each MT, the appropriate part (substall or superstall) of the F–V relation for KLP61F or Ncd was determined based on the current number of bound motors. For example, if k and n number of KLP61F and Ncd motors were engaged on an MT at the current time step, the maximal force the motors could exert on the MT, $k{F}_{stall}^{klp}$and$n{F}_{stall}^{ncd}$, respectively, were calculated and compared. If $k{F}_{stall}^{klp}>n{F}_{stall}^{ncd}$ (i.e., the KLP61F motors are winning), the instantaneous velocity of the MT, v_MT, was calculated using force-balance Eqs. 3 and 4 (otherwise, the reciprocal force-balance equation, in which the maximal velocity of KLP61F was replaced by its backward velocity, and the backward velocity of the Ncd was replaced by its maximal velocity in Eqs. 3 and 4, was used). Once the velocity of the MT was determined, the time step was incremented, the MT was moved by v_MTΔt defining the position of the MT in time step t_n+1, and the sequence of events was repeated. Finally, when all of the MTs’ force-balance and velocity calculations were completed, typically for 10,000 time steps (1,000 s in real time), the observed velocity of each MT was calculated by the distance traveled per 100 time steps (10 s in real time) to be compared with the experimental data.

For the HL-KLP61F motors, we made the following modifications in the force-balance equations and the calculation of the load-dependent detachment kinetics of the motors in the numerical scheme. The HL-KLP61F motors were associated with a spring constant, κ, and a rest length, d₀. The tension force exerted because of the extension of these linear springs was calculated separately for each motor (determined by the distance the MT moved as the motor remained attached) and was bidirectional; i.e., a newly attached HL-KLP61F could be assisting or opposing Ncd, depending on the sign of the velocity of the MT. At each time step for each HL-KLP61F, the load-dependent detachment rate was calculated based on the current tension force (F = κ(d − d₀)), where d is the current extension of the motor and

$$k_{off}\left(F\right)=k_{off}^0\exp \left(\frac{F}{F_{det}^{klp}}\right).$$

Qualitative explanation for motor competition in the assays.

We imagine that motors of either type stochastically bind to an MT, and the MT begins gliding in the direction of the winning type of motor. The losing motors feel forces greater or near their detachment force and thus enter a detachment cascade. This, in turn, decreases the load on the winning motors, allowing them to step processively on the MT, producing persistent directional motility. Indeed, when the binding events of the losing motors were rare (lower concentrations of the unbound losing motors), the winning motors maintained a fairly high (near unloaded) MT gliding velocity. When the binding events of the losing motors became more frequent (higher concentration of unbound losing motors), newly and transiently bound motors kept the winning motors loaded, reducing their processivity and thus reducing the number of engaged winning motors. In this situation, when the number of engaged winning motors stochastically reached a critical low level, a rapid detachment cascade was initiated, allowing the losing motors to take the lead, switching the gliding direction of the MT. In the balance point regime, in which the motors’ concentration was such that the binding events of the winning and losing motors enabled bound motors of either type to impose sufficient load on the other, neither KLP61F nor Ncd motors could reach or maintain their unloaded gliding velocity, and the detachment cascades were initiated stochastically and frequently, leading to stochastic reversals in the MT’s gliding direction. However, this reversal process took typically hundreds of seconds, and the number of motors bound to an MT was in the order of tens.

In the case of the non-ATP–hydrolyzing HL-KLP61F, a motility switch rather than a gradual slowing down of gliding in the Ncd direction occurred because of the lack of directionality of HL-KLP61F. In this situation, it is important to point out that any newly attached HL-KLP61F motors will resist movement equally in both the Ncd gliding direction (e.g., if an MT is gliding in the Ncd direction) and in the direction opposing Ncd (newly bound HL-KLP61F motors assist Ncd and oppose previously engaged and stretched HL-KLP61F motors when Ncd begins losing). Indeed, it was this bidirectional resistance of HL-KLP61F to motility in either direction that prevented the Ncd motors from entering a rapid detachment cascade and to effectively reduce their velocity until a critical mole fraction was reached, at which point the MT stalled. This symmetrical resistance to motility of the springlike HL-KLP61F was unlike the KLP61F motors, which persistently resisted motility in the Ncd direction.

Stochastic force-balance model of prometaphase spindle dynamics

Force-balance equations and F–V relations

In the stochastic force-balance model for the prometaphase spindle, the time-dependent rate of movement of the spindle poles (and the MTs) is determined by the force-balance equation in low Reynolds number conditions:

$$\mathit{\mu }{v}_{pole}\left(t\right)={\displaystyle \sum _i{F}_{M{T}_i}\left(t\right)},$$ (5)

where μ is the viscous drag coefficient associated with the spindle pole, v_pole(t) is the velocity of pole (and the MTs sliding rate) at time t, and

$$F_{M{T}_i}\left(t\right)=F_{M{T}_i}^{klp}\left(t\right)-F_{M{T}_i}^{ncd}\left(t\right)$$

is the total force generated on the overlap region of the i^th pair of MTs by bound KLP61F and Ncd motors at time t. Note that the forces generated by KLP61F on AP MT overlaps were in the outward direction and those generated by Ncd were in the inward direction and motor-generated forces were assumed to be additive. The general form of this force-balance equation is given in the In vivo model section, but details are given here.

The F–V relationship for KLP61F and Ncd are as in Eq. 2. However, it is worth noting that, because of structural differences between the KLP61F and Ncd motors, when an MT in an AP overlapping MT pair was sliding in/out at rate v_MT, the corresponding effective velocity of KLP61F and Ncd on its MT track differed. Namely, while KLP61F steps along its MT track at rate v_klp = v_MT, Ncd must step along its MT track at rate v_ncd = 2v_MT. This is because KLP61F has a bipolar structure with motor heads at opposite ends, whereas Ncd has a monopolar structure with a motor domain at one end and an MT-binding tail domain at the opposite end and therefore gets cotransported with the MT to which it is bound through its tail domain. Thus, in the force-balance equation in the In vivo model section, the effective instantaneous velocity of Ncd is scaled by two. In solving the model, the force-balance equation in the In vivo model section was modified as follows to account for the piecewise linear form of the motors’ F–V relationships. At a given time step, before solving the force-balance equation, the current number of engaged KLP61F and Ncd motors (k and n, respectively) in the spindle were identified. If $k{F}_{stall}^{klp}>n{F}_{stall}^{ncd}$ (i.e., the KLP61F is winning), the maximal velocity of the Ncd ($V_{max}^{ncd}$) was replaced by its backward velocity ($V_{back}^{ncd}$) in the force-balance equation in the In vivo model section, and the reciprocal change was made for KLP61F if$k{F}_{stall}^{klp}<n{F}_{stall}^{ncd}$. As can be seen from the force-balance equation in the In vivo model section, the antagonistic forces generated by the engaged KLP61F and Ncd motors on all of the AP MT overlaps in the spindle were exerted collectively on the spindle poles; therefore, the MTs were coupled at their minus ends, and all minus ends were assumed to end at the spindle poles at this stage (early prometaphase). However, each MT plus end underwent dynamic instability independently (see MT plus ends’ dynamics).

Numerical simulations

Initial conditions.

In our prometaphase spindle model, at the initial time step (t = 0), 100 dynamically unstable MT plus ends were positioned randomly at 0–0.5 μm distance from the opposing centrosomes, extending into the nuclear region. All MT minus ends were positioned at the centrosomes and were assumed to move along with the centrosomes. The centrosomes were assumed to be located ∼8 μm away from one another at t = 0 to mimic the experimentally observed pole–pole separation at NEB.

MT plus ends’ dynamics.

As previously described (Cheerambathur et al., 2007), the dynamics of the plus ends of the MTs were computed in a Monte Carlo approach. To summarize, the MTs were either in a growth or a shrinkage state at all times, and their dynamics were fully described by the four parameters of dynamic instability: v_g and v_s and f_cat and f_res. The growth/polymerization and shrinkage/depolymerization rates and the rescue frequency (switch from shortening to growth) were fixed, and the catastrophe frequency (switch from growth to shortening) was position dependent along the spindle pole–pole axis, with lowest catastrophe at the spindle equator to mimic a hypothetical Ran-GTP gradient around the chromosomes (f_cat at the poles and 0.5 f_cat at the equator, linearly decreasing from the pole toward spindle equator). At each time step, t_n, for each MT plus end undergoing growth (or shrinkage) in the previous time step, t_n-1, a catastrophe (or rescue) event occurred if a random number r (Matlab function rand) satisfied r < P_cat(x) = 1 − exp(−f_cat(x) Δt) (or if r < P_res = 1 − exp(−f_res Δt)), where Δt is the simulation time step and x is the position of the MT plus end along the pole–pole axis at time t_n. Once the state of each MT tip was determined in time step t_n, the growth/shrinkage of MT tips and their new positions were computed. If an MT plus tip reached the opposing pole, it switched to shrinkage, or if it shrunk to its pole, it rescued.

Motor diffusion and binding to AP ipMT overlaps.

In our simulation, we explicitly modeled the dynamics of individual motors associated with AP MTs based on the properties of the motors derived from the fit to our in vitro gliding assays and in agreement with the motors’ known properties. The free/unbound KLP61F and Ncd motors were assumed to diffuse rapidly in the spindle region, and the time scale of diffusion of motors was assumed to be faster than the time scale for rebinding of motors to AP ipMT overlaps for force generation (i.e., binding of both motor heads for KLP61F and the tail and the motor head for Ncd). The density of free motors (per unit AP MT overlap length) was time dependent, and all motors were assumed to be free at the initial time step. In our model, we did not explicitly consider the binding of motors to parallel MT overlaps because motors on parallel MTs did not generate force for movement, and the residence time of motors on MTs was short (∼5 s), as assayed by FRAP and fluorescence speckle microscopy in GFP-KLP61F and GFP-Ncd rescued fly embryos (for KLP61F and for Ncd), giving rise to short-run lengths of motors on all spindle MTs. In addition, KLP61F displays a threefold preference for binding to AP MT overlap regions (van den Wildenberg et al., 2008). Also, single MT-bound conformations of motors are assumed to be short lived and therefore not accounted for (Furuta and Toyoshima, 2008). Finally, we did not account for the transport of KLP61F and Ncd by other plus–minus end MT–based motors or by MT plus end tip–tracking proteins or the binding of motors to freely diffusing tubulin subunits.

The free motors bound to AP MT overlaps stochastically depending on the pseudo–first order binding rate of the motor k_on,(derived from the model fit to our in vitro gliding assay model fit) and a random number r for each potential MT–motor binding interaction and were executed if r < P_on, where P_on = 1 − exp(−k_on Δt). Because free motors were assumed to rapidly diffuse in the nuclear region maintaining a homogeneous distribution, the number of motors that reached the interaction distance to AP overlaps for binding were computed based on a mean density Ρ_motor of free motors per micrometer length of MT in the spindle and variance σ² (σ = x_rms ∼2–5 μm). We estimated the density of KLP61F in the spindle region to be ∼100–250 per square micrometer in an early prometaphase spindle, corresponding to approximately ∼0.1–0.5 μM in the spindle (250 motors per square micrometer corresponding to ∼20,000 motors in an ellipsoid of dimensions 8 × 4 μm; ∼70 μm³). Note that Sharp et al. (1999a) reported ∼250 KLP61F-associated gold particles per square micrometer within the spindle region of a metaphase/anaphase fly embryo spindle, and assuming that between 1 and 10 gold particles (ideally 4) could be associated with each homotetrameric KLP61F motor, the aforementioned value is likely to be an upper limit. This corresponds to a density of ∼10–25 KLP61F potentially interacting with a 1-μm-long MT (surface area of a unit lattice length = 0.025π ∼0.1 μm²). In the absence of an estimate for the number of Ncd motors, we simply assume the same order of magnitude for the density of Ncd. Indeed, in the simulations, we assumed that the initial density of free KLP61F and Ncd motors potentially interacting with a 1-μm-long MT lattice surface was 50, and we varied the ratio of this density with the Ncd mole fraction (for example Ρ_motor = 25 of each type for 0.5 Ncd mole fraction, and Ρ_klp = 40 and Ρ_ncd = 10 for a 0.2 Ncd mole fraction). As motors bind along the length of individual or parallel and AP MTs as MT polymerize and invade the nuclear region, the density of the free motor decreases. This effect is not included in the model because at the early prometaphase stage of mitosis, the total MT density remains low and freely diffusing motors are abundant (unlike in later stages when the total length of spindle MTs reaches a steady-state and most motors are in an MT-bound state; Cheerambathur et al., 2008). Furthermore, including a moderate linear decrease in the density of free motors over time proportional to the increase in the total MT length did not affect the conclusions of our model. A maximal number of 800 motors (total of Ncd and KLP61F) per unit AP MT overlap is permitted to be bound at any time (the number of subunits in the lattice = 13/8 × 1,000 divided by 2 because of the binding of motors between AP MTs). However, it is important to note that the lattice never came close to saturation in the simulations, reflecting low density of motors with respect to tubulin. The aforementioned simplifying assumptions, which greatly reduced the computational time and effort, by no means affected the stochastic aspects of motor–MT interactions, and, as expected, large variations in the number of engaged motors per unit AP MT overlap were observed in the simulations.

In the simulations, at each successful binding event (r < P_on), the position of each newly bound motor along the AP MT was randomly selected and stored. For every new Ncd binding event, in addition to the position of the motor along the AP overlap, an MT between the left pole– and the right pole–associated MT was randomly selected and stored as the MT to which Ncd was bound by its tail. This is because Ncd co-translocates with the MT to which it is bound by its tail domain, whereas KLP61F stays put on the AP MT overlaps as MTs themselves slide inward/outward. Once all binding events were executed, the detachment events were computed.

Motor detachment from AP MT overlaps.

Motor detachment was executed based on a random number, and the load-dependent detachment rate of the motors as in the gliding assay model. The current load per motor on AP MT overlaps at time step t_n was computed using the velocity of the MTs (or poles) in the previous time step, t_n-1. Detachment of newly bound motors was not permitted until the subsequent time step. All motors that moved out of the AP overlap regions of the MTs because of MT plus end dynamics or sliding were forced to detach.

Algorithm.

At each time step first, the AP overlap distance was computed for each pair of MTs emanating from the centrosomes, and the current overlap length of all of the MT pairs was stored. Next, the binding and detachment events of KLP61F and Ncd motors at each AP MT overlap were executed. Then, based on the current number of motors on the AP overlaps, the velocity of the poles and MTs was determined. Finally, the position of the poles and all MT minus ends was updated: poles and MT minus ends were moved by v_pole Δt, where v_pole is the velocity of the poles computed at the current time. The position of the MT plus ends was updated according to the movement of the poles (v_pole Δt) and the rates of dynamic instability of the plus ends (v_g, v_s, f_cat, and f_res; Table I). The new positions of the poles and the ends of the MTs were recorded for the next time step. The time step was incremented, and the sequence of events was repeated typically for 1,000 time steps, corresponding to 100 s in real time.

Incorporation of lamin-B in the force-balance equations

In the situation in which an elastic lamin-B envelope was surrounding the spindle (Fig. 5 B), the force-balance equations were modified as follows. For example, consider the case in which k KLP61F and n Ncd motors are engaged on all of the AP MT overlaps in the spindle at time t = t_n. If

$$k{F}_{stall}^{klp}>\left(n{F}_{stall}^{ncd}\text{+}\zeta \text{(}{t}_n\text{)}\left(S\text{(}{t}_{n-1}\text{)-}S\text{(}{t}_0\text{)}\right)\right)$$

(i.e., the KLP61F motors are winning), where ζ(t_n) is the elastic spring constant associated with the lamin-B envelope at time t = t_n and S(t_n-1) and S(t₀) are the spindle pole–pole distances at time t = t_n-1 and the initial time, respectively, then the following equation is used to calculate the instantaneous velocity of the poles at time t = t_n:

$$\mathit{\mu }{v}_{pole}={\displaystyle \sum _{M{T}_i}\left(k_i{F}_{stall}^{klp}(1-\frac{v_{pole}}{V_{max}^{klp}})-n_i{F}_{stall}^{ncd}(1-\frac{2v_{pole}}{V_{max}^{ncd}})\right)}\text{−}\zeta \text{(}{t}_n\text{)}\left(S\text{(}{t}_n\text{)-}S\text{(}{t}_0\text{)}\right).$$ (6)

In the case of

$$k{F}_{stall}^{klp}<\left(n{F}_{stall}^{ncd}\text{+}\zeta \text{(}{t}_n\text{)}\left(S\text{(}{t}_{n-1}\text{)-}S\text{(}{t}_0\text{)}\right)\right),$$

meaning that the Ncd motors are winning based on the current number of engaged motors and the stretch/compression of the lamin-B envelope, we used the reciprocal of the Eq. 6, in which the maximal velocity of KLP61F was replaced with its backward velocity, $V_{back}^{klp}$, and the backward velocity of Ncd was replaced by its maximal velocity, $V_{max}^{ncd}$. For the situation in which the response of the lamin-B envelope to compression and extension differ (Dahl et al., 2004), the resistance to compression was taken to be twofold higher than that for extension (i.e., ζ_compression(t_n) = 2 ζ_extension(t_n) while both diminish linearly over time). Finally, as reported in Dahl et al. (2004), the lamin-B envelope considered in this study was assumed to be fully elastic capable to return to its initial unstretched state once the forces were removed, and the relaxation time scale of the nuclear lamina under stress was assumed to be longer than the prometaphase phase I duration, in the order of several minutes, as observed for keratin networks (Sivaramakrishnan et al., 2008).

Generation of virtual tubulin kymographs

The virtual tubulin kymographs (as in Fig. 4 B, right) were generated as follows. When a numerical simulation of the spindle pole dynamics was completed, the positions of the spindle MTs’ plus and minus ends emanating from the left and right poles and the position of the spindle poles over time were stored. In the simulations, there were 50 MTs emanating outward from the centrosomes (astral MTs) in random directions between [π/2 3π/2] and of random initial lengths between [0 3] μm. The astral MT plus ends underwent dynamic instability similar to the spindle MTs, but with a constant catastrophe frequency; they were not force-generating components of the spindle at this stage, and their minus/plus ends passively moved together with the spindle poles.

To generate the virtual kymographs, first a segment of 20 μm (x varying from −10 to 10 μm), in which the spindle equator was positioned at the origin (x = 0), was defined. This was divided into 300 subregions (num_sr = 300), each of 150-nm length, and the left and right position of each subregion was stored in an array. To store the number of MTs in each subregion at each time point, we generated an all zero array of size (num_sr by t_final; here, the final iteration time step is t_final). Then, for each iteration time point and for each subregion, the number of spindle MTs with segments within the boundary of the subregion was determined, and the value of the array was updated. For the astral MTs, which did not necessarily lie parallel to the pole–pole axis, the projection of the MT segment onto the pole–pole axis was used to calculate its contribution to fluorescence along an x position between [−10 10] μm. Once the array was fully updated, it was plotted using the built-in imagesc function in Matlab.

All models were solved numerically using custom made Matlab codes run on a personal laptop computer. The parameter space search was performed on a Linux cluster (11 nodes each with a 2× Opteron-246 processor).

Experimental materials and methods

Drosophila stocks and live imaging.

Flies were maintained, and embryos were collected as described previously (Sharp et al., 1999b). Flies expressing both GFP-tubulin and histone-RFP were obtained by crossing flies expressing GFP-tubulin (provided by T. Kaufman, Indiana University, Bloomington, IN) with flies expressing histone-RFP (from Bloomington Drosophila Stock Center). Flies expressing GFP-KLP61F and GFP-Ncd were described previously (Endow and Komma, 1997; Cheerambathur et al., 2008). Flies with UASp–GFP-Dm0 (Drosophila lamin-B) were obtained from J. Szabad (University of Szeged, Szeged, Hungary), and expression was driven by crossing them with w*; P{w[+mC]=matalpha4-GAL-VP16}V2H flies (from Bloomington Drosophila Stock Center). Embryos were collected at 25°C for 1 h, allowed to mature for 40 min, and then dechorionated, placed on heptane glue, and covered with halocarbon oil. For injections, embryos were dehydrated for 3–6 min, covered with halocarbon oil, and injected (Brust-Mascher and Scholey, 2009). For double injections, embryos were allowed to recover for 5–20 min between injections. Time lapse images were acquired with an inverted microscope (IX-70; Olympus) equipped with an Ultra-View spinning disk confocal head (PerkinElmer) and a UPlan-Apochromat 100× NA 1.35 or a Plan-Apochromat 60× NA 1.4 oil immersion objective. Either a single confocal plane or a stack of four to six planes spaced by 0.5 μm was acquired at time intervals of 3 to 10 s at room temperature (20–22°C). Images were acquired with a charge-coupled device camera (Orca II; Hamamatsu Photonics) and analyzed with MetaMorph Imaging software (Universal Imaging). Pole to pole distance as a function of time was measured from the position of the poles in each image. Calculations and statistical analyses were performed on Excel (Microsoft). All error bars shown in experimental and model solution figures are ±SDs.

3D restoration of the spindles from time lapse images of GFP-KLP61F or GFP-Ncd rescued fly embryos.

The raw data used for 3D restoration of spindles consist of time series of confocal z stacks (typically 30–60 stacks of z planes with 300–600-ms exposure time for each z plane, 0.1–0.2-μm spacing between z planes, and with x–y pixel size of 0.064–0.129 μm) acquired in live embryos obtained from GFP-KLP61F or GFP-Ncd rescued flies. GFP-tubulin flies were also imaged similarly. The raw images were then exported to, processed, and deconvolved using Huygens Essential (version 3.3.5; Scientific Volume Imaging BV) with the Nipkow option for 3D deconvolution (Huygens uses the CMLE [classical maximum likelihood estimation] algorithm for 3D deconvolution). 3D volume visualization of GFP-KLP61F spindles from the deconvolved image stacks or individual z planes were generated using the MIP renderer or the Twin Slicer functions of the Huygens Essential or Huygens Professional (version 3.3.0; Scientific Volume Imaging BV), respectively.

Protein preparation and characterization.

Different constructs for FL-KLP61F, HL-KLP61F, KLP61F stalk, and FL Ncd were generated as described previously (Tao et al., 2006). After verification by sequencing, the recombinant constructs were used to generate recombinant baculoviruses (Baculovirus Expression System; Invitrogen). The amplified viruses were used to infect sf9 cells. The proteins were purified from cell lysates with Ni–nitrilotriacetic acid affinity columns (QIAGEN) followed by superose 6 gel-filtration fast performance liquid chromatography (GE Healthcare). Fresh protein fractions from the gel filtration columns were used for in vitro assays. All in vitro assays were performed in buffer L (20 mM Tris, pH 8.0, 75 mM KCl, 2 mM MgCl_2, 2 mM DTT, and protease inhibitors).

In vitro competitive gliding assays.

In vitro motility assays were performed as previously described (Tao et al., 2006). Assays were performed in buffer L (20 mM Tris, pH 8.0, 75 mM KCl, 2 mM MgCl₂, 2 mM DTT, and protease inhibitors). In a 25-μl flow cell, a casein-treated glass coverslip was coated with a mixture of pure rNcd and rKLP61F fragments in different molar ratios, and then rhodamine-labeled MTs (Cytoskeleton, Inc.) were added in. Pure rKLP61F fragments and rNcd were used right after the gel-filtration column. Within the assay’s concentration range, the adsorption efficiency of the motor/fragment proteins to the casein-coated coverslip was ∼100%. Assays of different motor ratios were performed with the same batches of purified proteins. Serial dilution of rNcd to find the minimum concentration required for motility was used as a control for dilution effects. Similarly, serial dilution of HL-KLP61F was used to find the minimum concentration required for MT bundling as a measure of the activity.

Rhodamine-labeled MTs were imaged on a microscope (E600; Nikon) with a Plan-Apochromat 100× NA 1.4 oil immersion objective using a charge-coupled device camera (SenSys; Photometrics) at room temperature. Images were acquired and analyzed with MetaMorph Imaging software.

Western blotting.

Western blot analysis was performed using either known amounts of purified recombinant KLP61F and Ncd as standards (Tao et al., 2006) or high speed supernatants from Drosophila embryo lysates. Anti-KLP61F pAb (Brust-Mascher et al., 2009) or anti-Ncd pAb (Morales-Mulia and Scholey, 2005) was used to detect KLP61F and Ncd, respectively.

Lamin-B antibody and tail-fragment purification and injection.

Three different anti–lamin Dm0 (Drosophila lamin-B) mAbs (ADL101, ADL67.10, and ADL84.12; Developmental Studies Hybridoma Bank) were purified using the Montage antibody purification kit (Millipore). Purified antibodies were mixed and concentrated to 5–15 mg/ml. The C-terminal nonhelical tail (aa 407–622) of Dm0 was amplified by PCR and cloned into the baculovirus expression system. The tail fragment was expressed and purified using standard procedures (Tao et al., 2006). 1× PBS buffer was used instead of the previous Tris buffer system for microinjection. Embryos expressing fluorescent lamin-B (GFP-Dm0) were first injected with rhodamine-labeled tubulin, allowed to recover for 10–30 min, and then injected with either the lamin antibody mixture or the lamin tail fragment as previously described (Brust-Mascher and Scholey, 2009; Brust-Mascher et al., 2009).

Online supplemental material

Fig. S1 shows the spindle dynamics in Drosophila embryos and the results of the in vitro competitive gliding assays with Ncd and KLP61F. Fig. S2 shows the results of the protein friction model for competitive gliding assays with Ncd and HL-KLP61F and the form of the F–V relations considered in the models. Fig. S3 shows the impact of the motors’ F–V relationship on the mole fraction versus MT velocity curve in the competitive gliding assay model. Fig. S4 shows the impact of the MT dynamics on the spindle steady-state length in the prometaphase spindle model. Fig. S5 shows the effect of the motors’ kinetics, ultrastructural organization, and F–V relationships on the steady-state spindle length in the prometaphase spindle model. Videos 1 and 2 show the dynamics of MTs and chromosomes in transgenic Drosophila embryos expressing GFP-tubulin and histone-RFP. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200908150/DC1.