From stimulus estimation to combination sensitivity: Encoding and processing of amplitude and timing information in parallel, convergent sensory pathways

Abstract

Information theoretical approaches to sensory processing in electric fish have focused on the encoding of amplitude modulations in a single sensory pathway in the South American gymnotiforms. To assess the generality of these studies, we investigated the encoding of amplitude and phase modulations in the distantly related African fish Gymnarchus. In both the amplitude- and time-coding pathways, primary afferents accurately estimated the time course of random modulations whereas hindbrain neurons extracted information about specific stimulus features. Despite exhibiting a clear preference for encoding amplitude or phase, afferents and hindbrain neurons could encode significant amounts of modulation of their nonpreferred attribute. Although no increase in feature extraction performance occurred where the two pathways converge in the midbrain, neurons there were increasingly sensitive to simultaneous modulation of both attributes. A shift from accurate stimulus estimation in the periphery to increasingly sparse representations of specific features appears to be a general strategy in electrosensory processing.

1 Introduction

In many sensory systems, parallel sensory pathways are specialized for processing different stimulus attributes (Young 1998). Two well-studied examples include the parallel processing of timing and intensity information in the barn owl auditory system (Takahashi et al. 1984), and the separate pathways that are devoted to processing object/form information and spatial/motion information in primate visual cortex (Merigan and Maunsell 1993). Similarly, in wave-type weakly electric fish, two separate pathways are specialized for processing amplitude and timing information in electrosensory stimuli (Carr and Maler 1986; Heiligenberg 1991; Kawasaki 2005). The African fish Gymnarchus niloticus and several species of South American gymnotiform fish generate nearly sinusoidal electric organ discharges (EODs) that are subjected to amplitude modulation (AM) and phase modulation (PM) due to the presence of nearby objects or interference from conspecific EODs. Despite the independent evolutionary origin of electrogenesis and electroreception in these two groups of fish (Lauder and Liem 1983), their electrosensory systems share a number of similarities (Bullock et al. 1983; Hopkins 1995). In both groups, AM and PM are encoded by two distinct types of primary electrosensory afferents that give rise to separate amplitude- and time-coding pathways (Scheich et al. 1973; Bullock et al. 1975; Carr and Maler 1986; Zakon 1986; Heiligenberg 1991; Kawasaki 2005). S-afferents in Gymnarchus and T-afferents in gymnotiforms fire a single, phase-locked spike with each cycle of the EOD and thereby provide information about PM via shifts in spike timing. O-afferents in Gymnarchus and P-afferents in gymnotiforms are relatively loosely phase-locked to the EOD and do not fire with each cycle. However, their probability of firing during each cycle is proportional to stimulus amplitude, and their firing rate thereby provides information about AM.

Information theoretic approaches to neural coding have proven extremely useful in quantifying the encoding and processing of time-varying stimuli by sensory systems (Bialek et al. 1991; Borst and Theunissen 1999). In weakly electric fish, the focus of such studies has been on the encoding of AM by P-afferents in gymnotiforms and the computations performed by their postsynaptic targets in the hindbrain electrosensory lateral line lobe (ELL) (for reviews see Gabbiani and Metzner 1999; Sawtell et al. 2005; Fortune 2006). Individual P-afferents linearly encode as much as 80% of the time course of low-frequency (<40 Hz) random AM (Gabbiani et al. 1996; Wessel et al. 1996; Kreiman et al. 2000; Carlson and Kawasaki 2006a). By contrast, pyramidal neurons in ELL that receive direct or indirect synaptic input from P-afferents encode AM nonlinearly (Chacron 2006; Middleton et al. 2006), and reliably signal the occurrence of upstrokes or downstrokes in stimulus amplitude (Gabbiani et al. 1996; Metzner et al. 1998; Krahe et al. 2002). The encoding and processing of random PM in the time-coding pathway of gymnotiforms has not been extensively studied. However, we recently found that, similar to P-afferents, individual T-afferents can linearly encode as much as 84% of the time course of low-frequency (<20 Hz) random PM (Carlson and Kawasaki 2006a). Despite exhibiting a clear preference for encoding either random AM or random PM (preferred stimulus attribute), individual afferents can also encode the time course of random modulations in their nonpreferred stimulus attribute when it is presented in isolation or when modulation of the preferred attribute is sufficiently weak (Carlson and Kawasaki 2006a). In the absence of PM, T-afferents can encode as much as 52% of the time course of random AM due to an amplitude-dependent latency shift in their spike times. In the absence of AM, P-afferents can encode as much as 82% of the time course of random PM, due to their sporadic phase locking to the stimulus. This lack of complete independence in the processing of these two attributes results in ambiguity in the information content of individual primary afferent responses and predictable distortions in the fish’s perception of stimulus amplitude and timing, at least in the context of a particular behavior, the jamming avoidance response (Carlson and Kawasaki 2006a, 2007).

The amplitude-coding pathway of Gymnarchus exhibits a similar organization to gymnotiforms, with O-afferents projecting to AM-sensitive pyramidal neurons in the hindbrain ELL (Kawasaki and Guo 1998). Unlike gymnotiforms, in which PM information is extracted in the midbrain (Carr et al. 1986a; Carr et al. 1986b), S-afferents in Gymnarchus give rise to PM-sensitive pyramidal neurons in the ELL through a combination of direct and indirect synaptic inputs (Kawasaki and Guo 1996,Kawasaki and Guo 1998; Matsushita and Kawasaki 2004). Both AM-and PM-sensitive pyramidal neurons project to the midbrain torus semicircularis, where the amplitude- and time-coding pathways converge (Kawasaki and Guo 1998), and many neurons are sensitive to particular combinations of AM and PM (Kawasaki and Guo 2002; Carlson and Kawasaki 2004, 2006b), similar to the convergence of amplitude- and time-coding pathways in the midbrain of the barn owl auditory system (Knudsen and Konishi 1978; Peña and Konishi 2001).

In the current study, we used an information theoretic approach to quantify the encoding and processing of random AM and random PM at three different stages in the electrosensory system of the African fish Gymnarchus. Our goals were to: (1) determine whether the amplitude-coding pathway of Gymnarchus exhibits a transformation from linear stimulus encoding by primary afferents to feature extraction by ELL pyramidal neurons, as described in gymnotiforms; (2) determine whether the time-coding pathway of Gymnarchus exhibits a similar transformation in coding schemes between the primary afferents and ELL pyramidal neurons; (3) characterize the transformation in coding between hindbrain ELL pyramidal neurons and midbrain electrosensory neurons; (4) determine whether there is ambiguity in the encoding of AM and PM at the level of individual primary afferents in Gymnarchus, as is found in gymnotiforms; and (5) determine whether this ambiguity, if it exists, is reflected in the responses of downstream neurons in ELL and the midbrain, or whether it is somehow resolved. To address these questions, we made intracellular recordings from primary afferent fibers, ELL pyramidal neurons, and midbrain neurons, and characterized the encoding of AM and PM, presented both separately and simultaneously, using linear stimulus estimation and statistical pattern recognition techniques (see Gabbiani and Koch 1998; Gabbiani and Metzner 1999), as well as traditional measures of neuronal activity.

2 Materials and Methods

2.1 Animals

We used 79 Gymnarchus niloticus of both sexes (10–25 cm in total length). They were collected in West Africa at lengths of 5 to 6 cm and raised to the experimental size in the laboratory. Fish were housed individually, with the temperature set at 24–28°C, and the conductivity set at 100–200 μS/cm. The EOD frequency of each fish was measured before the start of an experiment, and ranged from 350 to 480 Hz. Following anesthesia with tricaine methanesulfonate (MS-222, 1:10000; Sigma, St. Louis, MO), we immobilized fish with an intramuscular injection of flaxedil (gallamine triethiodide: 8 to 20 μl of a 0.1% solution; Sigma), which greatly attenuated EOD amplitude. Activity of the EOD pacemaker command signal was recorded from the tail to monitor the fish’s condition throughout each experiment.

Fish were placed inside a Plexiglas chamber, gently held with a sponge-lined clamp and submerged in water except for a small area along the dorsal surface of the head. Oxygen-saturated water was provided to the gills with a tube inserted in the mouth. After local application of Xylocaine (2%; Barber Veterinary Supply, Richmond, VA), we removed a small portion of skin covering the skull and glued a plastic holder to the skull to hold the fish rigidly in position.

For recordings from primary afferent neurons, we exposed the posterior branch of the lateral line nerve by making an incision just caudal to the occipital bone and dissecting down through the tissue until the nerve was free (Bullock et al. 1975). For recordings from hindbrain ELL pyramidal neurons, we removed a small portion of the skull and meninges above the corpus cerebelli (Kawasaki and Guo 1996,Kawasaki and Guo 1998), and exposed the dorsal surface of the ELL by using the grounding wire to displace the corpus cerebelli. For recordings from torus semicircularis neurons, we removed a small portion of the skull and meninges above the midbrain, and exposed the dorsal surface of the torus semicircularis by using the grounding wire to displace the valvula cerebelli. (Carlson and Kawasaki 2004,Carlson and Kawasaki 2006b). At the conclusion of experiments, fish were euthanized by deep anesthesia in MS-222 (1:1000). These procedures are in accordance with the guidelines established by the National Institutes of Health and were approved by the University of Virginia Animal Care and Use Committee.

2.2 Electrophysiology

Intracellular recordings from primary afferent fibers were obtained with sharp glass capillary electrodes that were pulled using a Flaming/Brown micropipette puller (Sutter Instruments model P-97, Novato, CA) and filled with 3M KCl to yield resistances of 30–50 MΩ. Individual fibers were penetrated using mechanical vibration. S-afferents were distinguished from O-afferents based on whether or not a given unit fired during each cycle of the carrier signal in the absence of any stimulus modulation (Bullock et al. 1975; Kawasaki and Guo 1996; Carlson and Kawasaki 2006a).

We obtained whole-cell intracellular recordings from ELL pyramidal neurons and torus semicircularis neurons following the method of Rose and Fortune (1996). Electrodes were pulled in three stages to a tip diameter of ~1.2 μm and filled with a tip solution containing (in mM): potassium acetate (100), KCl (2), MgCl₂ (1), EGTA (5), HEPES (10), KOH (20), and biocytin (43). The shank was filled with an identical solution except that the biocytin was replaced with mannitol. This yielded pipette resistances of 20–30 MΩ and initial seal resistances > 1 GΩ. Some of the data presented were obtained from extracellular recordings, either using whole-cell electrodes or broken-tip electrodes (tip diameter of 5–12 μm) filled with a solution of either 3M NaCl or 3M KCl, or filled with Woods metal and electroplated with gold and platinum (Carlson and Kawasaki 2004).

Intracellular activity was amplified 10x on an AxoClamp 2B amplifier (Molecular Devices, Palo Alto, CA), then sent to an analog-to-digital converter and a Schmitt Trigger with an output to an event timer that recorded spike times at a clock rate of 1 MHz (Tucker-Davis Technologies models AD1 and ET1, respectively, Gainesville, FL). The A/D sampling rate was set at 20 kHz for primary afferent recordings and 2 kHz for ELL and torus semicircularis recordings. Intracellular potentials and spike times were saved using custom-made software for Matlab 7.0.1 (The Mathworks, Inc., Natick, MA).

2.3 Stimulus generation and delivery

Stimuli were numerically generated using custom-made software for Matlab 7.0.1, according to the following equation:

$$V(t)=A_c[1+s_{AM}(t)]sin(2\pi f_{c}t-s_{PM}(t))$$

where V(t) is the stimulus voltage at time t, A_c is the carrier amplitude, f_c is the carrier frequency, and s_AM(t) and s_PM(t) are time-varying modulations in amplitude and phase, respectively. The carrier frequency (f_c) was set to within 20 Hz of the fish’s EOD frequency as measured before the experiment. The carrier amplitude (A_c) was adjusted to values of 1–2 mV/cm near the gill cover. The AM (s_AM(t)) and PM (s_PM(t)) waveforms were generated independently and could therefore be presented completely in isolation (i.e. stimuli with only AM, for which s_PM(t) = 0 for all values of t, or stimuli with only PM, for which s_AM(t)=0 for all values of t), or both amplitude and phase could be modulated simultaneously with independent variation in s_AM(t) and s_PM(t).

Three types of random stimulus modulations were used, including simultaneous random AM and random PM (s_AM(t) and s_PM(t) were both randomly modulated independently), separate random AM (s_AM(t) was randomly modulated while s_PM(t) = 0 for all values of t), and separate random PM (s_PM(t) was randomly modulated while s_AM(t) = 0). Each random modulation waveform consisted of low-pass filtered (cutoff frequency = 10 or 20 Hz) Gaussian distributions with the standard deviation of random AM (σ_AM) varying from 5 to 25% of the carrier amplitude and the standard deviation of random PM (σ_PM) varying from 5 to 30° of the carrier phase.

Four types of sinusoidal stimulus modulations were used, including AM presented alone (s_AM(t) was sinusoidally modulated while s_PM(t) = 0 for all values of t), PM presented alone (s_PM(t) was sinusoidally modulated while s_AM(t) = 0 for all values of t), and two stimuli that simulated the modulations caused by combining the fish’s own EOD (frequency = f₁) with a neighbor’s EOD (frequency = f₂), where the difference in frequency (Df = f₂ − f₁) was either positive (Df >0, for which both s_AM(t) and s_PM(t) were sinusoidally modulated and the PM angle was advanced by 90° relative to AM) or negative (Df<0, for which both s_AM(t) and s_PM(t) were sinusoidally modulated and the PM angle was delayed by 90° relative to AM). For all four stimuli, the modulation rate was set at 1–4 Hz, AM depths were equal to 25%, and PM depths were equal to 15°.

Electric stimuli were digital-to-analog converted at a sampling rate of 20 kHz (Tucker-Davis Technologies model DA3-4), attenuated to the desired carrier amplitude using a programmable attenuator (Tucker-Davis Technologies model PA4), low-pass filtered at a cutoff frequency of 5 kHz, and then delivered to the fish using custom-made isolators with field effect transistors. For recordings from primary afferent fibers, stimuli were delivered through an anodal electrode placed in the mouth and a pair of cathodal electrodes placed on either side of the fish. Although timing information is represented by phase-locking in the periphery, information about PM is extracted centrally by comparing differences in phase between different portions of the body surface (differential PM). For recordings from ELL and torus semicircularis neurons, we therefore used a phase chamber to electrically isolate the head and trunk of each fish so that we could independently stimulate fish with AM and differential PM (Carlson and Kawasaki 2004,Carlson and Kawasaki 2006b). Stimuli to the head compartment were provided through an anodal electrode placed in the mouth, and two cathodal electrodes placed on either side of the fish’s head. Stimuli to the trunk compartment were provided through an anodal pin electrode placed in the dorsal musculature, and two cathodal electrodes placed on either side of the fish’s trunk. Unless otherwise stated, all stimulus modulations were applied to one compartment, while the other compartment was unmodulated. Display and analysis of stimulus-response relationships are based on the modulated compartment, considering differential phase (in μs) rather than absolute phase (in °).

2.4 Linear stimulus estimation and feature extraction during random modulation

Spike trains from primary sensory afferents were represented as:

$$x(t)=\sum _i\delta (t-t_i)-x_0$$

where t_i are the spike occurrence times and x₀ is the mean spike rate. Linear estimates of random modulation waveforms were generated by convolving spike trains with a filter, h(t):

$$s_{\mathit{est}}(t)={\int }_0^{T}d{t}^{\prime }h(t-t^{\prime })x(t^{\prime })$$

chosen so as to minimize the mean square error (ε²) between the stimulus and the estimate (Wessel et al. 1996; Gabbiani and Koch 1998; Gabbiani and Metzner 1999). We quantified the ability of spike trains to encode information about random AM and random PM using the coding fraction (γ), which represents the error (ε) in the linear estimate of the stimulus normalized by the standard deviation of the actual stimulus (σ):

$$\gamma =1-\frac{\epsilon }{\sigma }$$

The coding fraction ranges from 0 when estimation is at chance level to 1 when the stimulus is perfectly estimated, or 0% to 100% when expressed as a percentage of the stimulus encoded (Wessel et al. 1996; Gabbiani and Koch 1998; Gabbiani and Metzner 1999).

We calculated lower bound estimates of the rates of mutual information transmission (in bits/s) as the ε-entropy or rate distortion function:

$$I_{\epsilon }=\frac{-f_c}{log(2)}log\left(\frac{\epsilon }{\sigma }\right)$$

and obtained the mutual information transmitted per spike by diving this value by the mean firing rate (Gabbiani 1996; Wessel et al. 1996).

We evaluated the performance of neurons in extracting upstrokes or downstrokes in amplitude and advances or delays in phase using a modification of a statistical pattern recognition technique previously used to evaluate responses to upstrokes or downstrokes in amplitude only (for details see Gabbiani et al. 1996; Metzner et al. 1998; Gabbiani and Metzner 1999; Krahe et al. 2002). Spike trains were binned using a bin size of 0.5 ms, such that bins containing a spike were denoted as λ=1 and bins containing no spike were denoted as λ=0. For each stimulus attribute, two distributions of stimulus vectors (s) were generated, those that occurred in the period from 300 to 0 ms preceding bins containing a spike, P(s|λ=1), and those that that occurred in the period from 300 to 0 ms preceding bins containing no spike, P(s|λ=0). We calculated the mean stimulus preceding bins containing a spike (m₁) and the mean stimulus preceding bins containing no spike (m₀) and used the Euclidean classifier, f = m₁ − m₀, to discriminate stimulus vectors preceding spikes from stimulus vectors preceding no spikes.

When assessing performance in extracting a single attribute (either AM or PM), stimulus vectors were projected onto the Euclidean classifier to yield one-dimensional distributions of P(s|λ=1) and P(s|λ=0). Wequantitatively assessed the performance of the classifier in predicting the occurrence of a spike using a receiver operating characteristic (ROC) analysis (Macmillan and Creelman 2004). Putative spikes were identified whenever the projection of the stimulus onto the Euclidean classifier was larger than a certain threshold, θ. We then determined the probabilities of correct detection, P_CD (correctly classifying a stimulus vector as eliciting a spike), and false alarm, P_FA (incorrectly classifying a stimulus vector as eliciting a spike), as a function of variation in θ. Overall performance was assessed by plotting ROC curves (P_CD vs. P_FA) and calculating the area under the curve, which ranges from 0.5 for chance performance to 1 for perfect discrimination (Macmillan and Creelman 2004).

To assess the performance of neurons in extracting features characterized by simultaneous modulations in amplitude and phase, we projected both the AM stimulus vectors and the PM stimulus vectors onto their respective Euclidean classifiers to yield two-dimensional distributions of P(s|λ=1) andP(s|λ=0), one dimension for the AM projection and one dimension for the PM projection. These two-dimensional distributions were then reduced to one-dimensional distributions using discriminant function analysis (McLachlan 2004), a data reduction method that maximizes between group variance while minimizing within group variance (in this case the two groups being the distributions of P(s|λ=1) andP(s|λ=0)). We then performed an ROC analysis on the resulting one-dimensional distributions of P(s|λ=1) andP(s|λ=0), as described above. To assess the importance of each attribute (AM and PM) to overall feature extraction performance, we randomized either the AM or PM stimulus time course, low-pass filtered the resulting waveform using the same cutoff frequency as the actual stimulus, and then performed the same ROC analysis of feature extraction performance. We analyzed the effect of randomizing the AM or PM stimulus time course on ROC performance by calculating a normalized z-statistic:

$$z=\frac{\mid {\mathit{AUC}}_1-{\mathit{AUC}}_2\mid }{\sqrt{{{SE}_1}^2+{{SE}_2}^2}}$$

where the subscripts 1 and 2 refer to the two different ROC curves (the original ROC curve and the ROC curve obtained after randomizing either the AM or PM stimulus time course), AUC refers to the area under an ROC curve, and SE refers to its standard error (Green and Swets 1966). Absolute values of z greater than 3.28 were considered to represent significant differences between the areas of the two ROC curves (α = 0.001).

2.5 Analysis of responses to sinusoidal modulation

We estimated the spike rates of O-afferents using a low-pass filter with a cutoff frequency equal to 2.5 times the modulation rate for sinusoidal modulations (Carlson and Kawasaki 2006a). Spike rates were then expressed as a percentage of the mean value. To analyze changes in the spike times of S-afferents, we computed spike times relative to an arbitrary, constant phase of the unmodulated stimulus carrier cycle (Heiligenberg and Partridge 1981; Carlson and Kawasaki 2006a). Because the sampling rate of S-afferent spike times was dependent on the stimulus carrier frequency, which varied from fish to fish and differed from the sampling rate of O-afferent spike rates (20 kHz), the spike time values were low-pass filtered to yield a universal sampling rate of 20 kHz. This allowed us to make direct comparisons between O-afferent spike rates and S-afferent spike times.

We analyzed the spiking responses of ELL neurons and torus neurons to sinusoidal modulations by constructing spike histograms relative to the modulation cycle. For each response, we determined the mean spike rate (SR), the vector strength of synchronization to the modulation cycle (VS), and the mean vector angle of the responses relative to the modulation cycle (Batschelet 1981). The overall magnitude of responses was assessed using the magnitude of the Fourier component (FC):

$$FC=2^{\ast }{SR}^{\ast }VS$$

which represents the spike rate synchronized to the modulation waveform (Rees and Palmer 1989).

3 Results

3.1 Linear stimulus estimation by primary sensory afferents

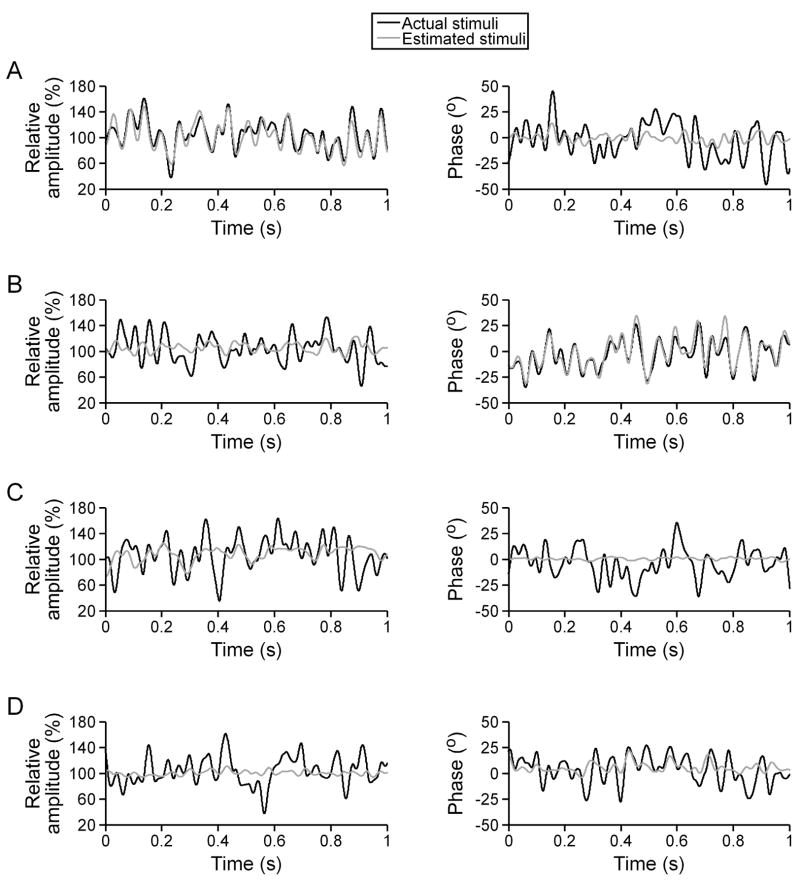
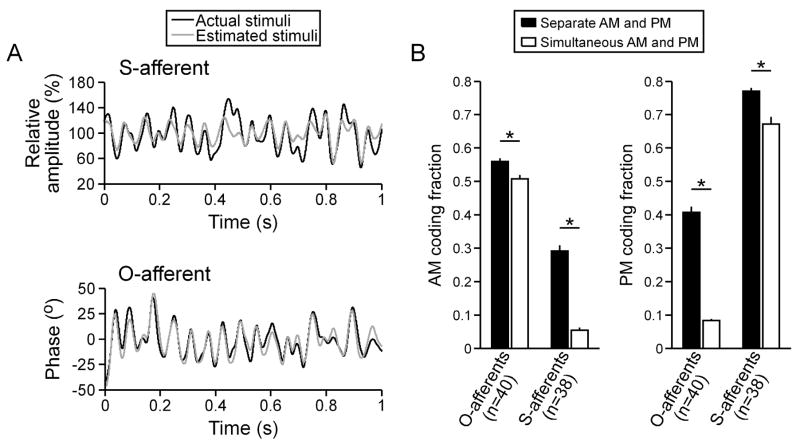
During simultaneous random AM and random PM, the firing rate of individual O-afferents closely followed the time course of random AM, but not random PM (Fig. 1(A)). As a result, individual O-afferents accurately estimated the time course of random AM (Fig. 2(A)), with coding fractions ranging from 31.32% to 62.88% (mean ± sem = 50.72 ± 1.22%, n = 40 units). Individual O-afferents poorly estimated random PM (Fig. 2(A)), resulting in substantially lower coding fractions (8.31 ± 0.51%). O-afferents therefore exhibited a clear preference for encoding AM over PM (Wilcoxon matched pairs test, z = 5.51, p < 0.000001).

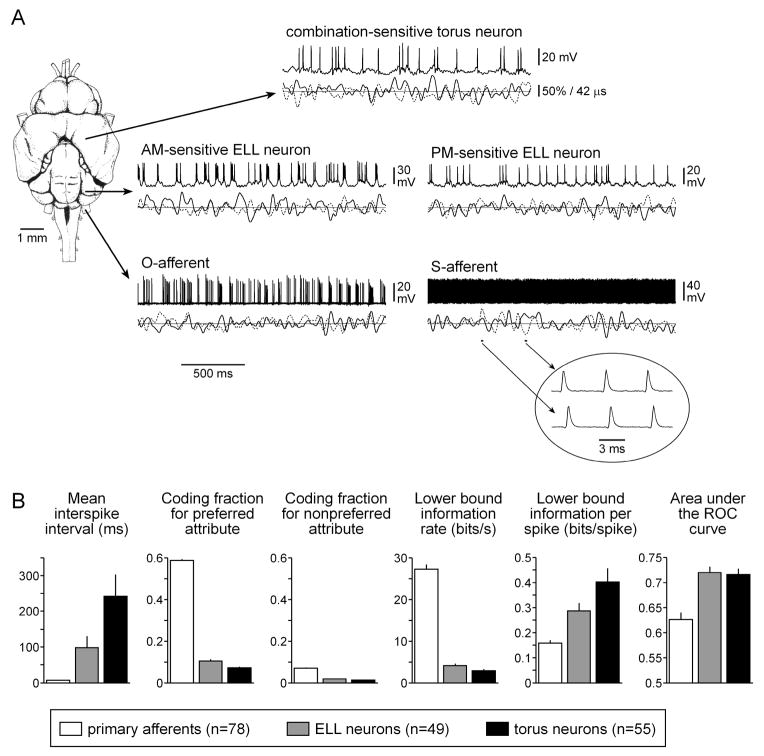
Fig. 1.

Encoding and processing of random modulations in the electrosensory pathway of Gymnarchus niloticus. (A) Dorsal view of the brain of Gymnarchus niloticus, showing the approximate locations of primary afferent fibers, hindbrain ELL neurons, and midbrain torus semicircularis neurons. Intracellular recordings of the responses to simultaneous random modulations in amplitude and phase are shown for the different types of neurons studied. Below each trace, the amplitude of the signal is represented by a solid line and the phase of the signal is represented by a dashed line, with the solid horizontal line indicating 100% of the carrier amplitude and 0° of phase modulation. For the recording from the S-afferent, the two portions shown are magnified in the inset to show the shift in spike timing that occurs with changes in phase (the time scales for the two examples in the inset are aligned to the carrier period). (B) Summary of activity patterns (mean ± sem) and information processing in the electrosensory system during simultaneous random AM and random PM.

Fig. 2.

Estimation of simultaneous random AM and random PM for an O-afferent (A), S-afferent (B), AM-sensitive ELL neuron (C), and PM-sensitive ELL neuron (D).

By contrast, individual S-afferents fired with each carrier cycle during simultaneous random AM and random PM, and their precise spike times closely followed the time course of random PM, but not random AM (Fig. 1(A)). As a result, individual S-afferents accurately estimated the time course of random PM, but not random AM (Fig. 2(B)). The PM coding fractions of individual S-afferents ranged from 31.86% to 83.77% (mean ± sem = 67.10 ± 2.17%, n = 38 units), while the AM coding fractions were substantially lower (5.46 ± 0.74%). S-afferents therefore exhibited a clear preference for encoding PM over AM (z = 5.37, p < 0.000001).

For each individual unit we determined the greater of the AM and PM coding fractions (coding fraction for the preferred attribute, which is AM for O-afferents, and PM for S-afferents) and the lesser of the AM and PM coding fractions (coding fraction for the nonpreferred attribute, which is PM for O-afferents, and AM for S-afferents). Across the entire population of primary afferents, coding fractions for the preferred attribute ranged from 31.32% to 83.77% and coding fractions for the nonpreferred attribute ranged from 0.90% to 23.17% (Fig. 1(B)). Expressed in terms of a lower bound estimate on mutual information transmission, rates of total information transmitted by individual afferents about both attributes ranged from 10.33 bits/s to 52.97 bits/s (Fig. 1(B)). For O-afferents, this corresponds to 0.11 to 0.54 bits/spike, and for S-afferents, 0.03 to 0.13 bits/spike (Fig. 1(B)).

3.2 Feature extraction by central electrosensory neurons

There was a significant increase in mean interspike interval at each successive step in the electrosensory pathway (Kruskal-Wallis ANOVA, H_2,182 = 134.04, p < 0.001; Fig. 1). Unlike primary afferents, ELL pyramidal neurons and torus neurons performed relatively poorly at linear stimulus estimation (Fig. 2(C, D)). The mean coding fractions (± sem) for the preferred and nonpreferred attributes of ELL neurons were 10.47 ± 1.29% and 1.80 ± 0.25%, respectively (n = 49) (Fig. 1(B)). For torus neurons, the mean coding fractions for the preferred and nonpreferred attributes were 7.10 ± 1.07% and 1.24 ± 0.21%, respectively (n = 55) (Fig. 1(B)). This corresponds to lower bound estimates of mutual information rates for both attributes of 3.89 ± 0.48 bits/s for ELL neurons and 2.60 ± 0.42 bits/s for torus neurons (Fig. 1(B)). There were therefore significant reductions in coding fractions for the preferred attribute (H_2,182 = 133.73, p < 0.001), coding fractions for the nonpreferred attribute (H_2,182 = 106.11, p < 0.001), and lower bound estimates of mutual information rates (H_2,182 = 134.95, p < 0.001). However, because of the concomitant decrease in spike rate, lower bound estimates of mutual information transmitted per spike increased at each successive step in the electrosensory pathway (H_2,182 = 27.77, p < 0.001; Fig. 1(B)).

Although ELL and torus neurons did not linearly encode significant amounts of information on the detailed time course of random AM or random PM, they did respond reliably to random modulations of one or both attributes. During simultaneous random AM and random PM, ELL pyramidal neurons tended to respond to modulations in only one of the two attributes. For instance, one of the ELL neurons in figure 1(A) shows a marked tendency to fire shortly after downstrokes in stimulus amplitude (‘AM-sensitive ELL neuron’), a trend that is clearly evident in the spike-triggered average stimulus from that neuron (Fig. 3(A)). The other ELL neuron in figure 1(A) tends to fire during phase advances (‘PM-sensitive ELL neuron’), which is also apparent in that neuron’s spike-triggered average stimulus (Fig. 3(C)). By contrast, several torus neurons did not respond reliably to random modulations of a single attribute, but instead tended to respond to particular combinations of amplitude and phase modulation. For example, the torus neuron in figure 1(A) tends to fire when upstrokes in amplitude co-occur with phase advances, but not when either feature occurs in isolation, which can also be seen in the spike-triggered average stimulus from that neuron (Fig. 4(A)).

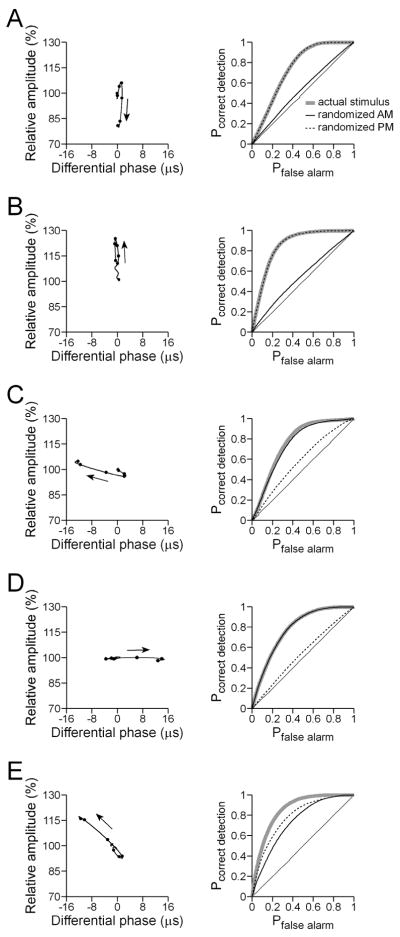
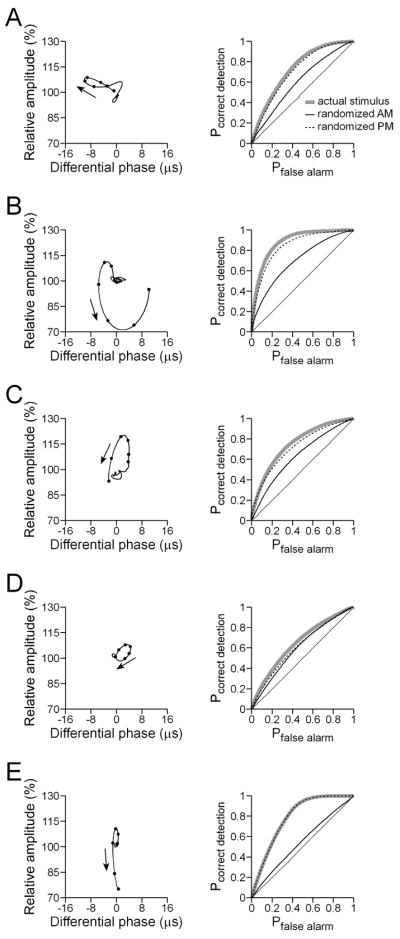
Fig. 3.

Feature extraction in ELL during simultaneous random AM and random PM for an I-unit (A), E-unit (B), advance-unit (C), delay-unit (D), and combination E/advance-unit (E). The left column shows the spike-triggered average stimulus from -300 ms to 0 ms relative to the spike time, with amplitude plotted against phase. The arrows denote the direction of modulation with respect to time, and the solid circles mark the points occurring at 0, -10, -20, -30, -40, and -50 ms before the spike time. The right column shows the receiver operating characteristic (ROC) curves for the actual stimulus, and the curves that result from randomizing either the AM or the PM in the stimulus. In each case, the solid, thin, straight line denotes chance performance.

Fig. 4.

Feature extraction in the torus during simultaneous random AM and random PM for four combination-sensitive neurons (A–D), and an I-unit (E), presented as in Fig. 3.

We examined the feature extraction performance of neurons using a receiver operating characteristic (ROC) analysis, and quantified the ability of neurons to detect specific stimulus features during simultaneous random AM and random PM by measuring the area under the ROC curve (see Methods). Both ELL and torus neurons performed comparably in extracting information about specific stimulus features, with mean areas under the ROC curve (± sem) of 0.7192 ± 0.0124 (n = 49 units) and 0.7151 ± 0.0122 (n = 55 units), respectively (Fig. 1(B)). Primary afferents did not perform as well at feature extraction (Fig. 1(B)); the mean area under the ROC curves of primary afferents was 0.6262 ± 0.0140 (n = 78 units). There was therefore a significant increase in feature extraction performance within the central electrosensory pathway (H_2,182 = 20.02, p < 0.001).

Figures 3 and 4 show spike-triggered average stimuli and ROC curves from representative ELL and torus neurons, calculated from 300 to 0 ms before each spike, and plotted as Lissajous graphs of relative amplitude versus differential phase. The spike-triggered averages reveal that most ELL pyramidal neurons responded primarily to particular modulations in either amplitude or phase. Thus, the neuron shown in Fig. 3(A) responded to amplitude decreases (I-unit) and the neuron shown in Fig. 3(B) responded to amplitude increases (E-unit), whereas the neuron shown in Fig. 3(C) responded to phase advances (advance-unit), and the neuron shown in Fig. 3(D) responded to phase delays (delay-unit). A small number of ELL pyramidal neurons responded to combinations of amplitude and phase, such as the neuron shown in Fig. 3(E), which responded to a combination of amplitude increases and phase advances. The spike-triggered averages of this latter group of neurons were characterized by simple, nearly linear streaks in Lissajous plots of amplitude vs. phase, consisting either of combined phase advances/amplitude increases (e.g. Fig. 3(E)), or phase delays/amplitude decreases.

In general, the spike-triggered averages of torus neurons revealed a greater number of neurons responsive to combinations of amplitude and phase (Fig. 4(A–D)). Furthermore, the spike-triggered averages of these neurons were generally more complex than those of their ELL counterparts (Fig. 3(E)), revealing sensitivity to a wide variety of amplitude and phase combinations. Similar to the majority of ELL pyramidal neurons, some torus neurons responded primarily to modulations in one particular attribute, such as the neuron in Fig. 4(E) that responded to decreases in amplitude (I-unit).

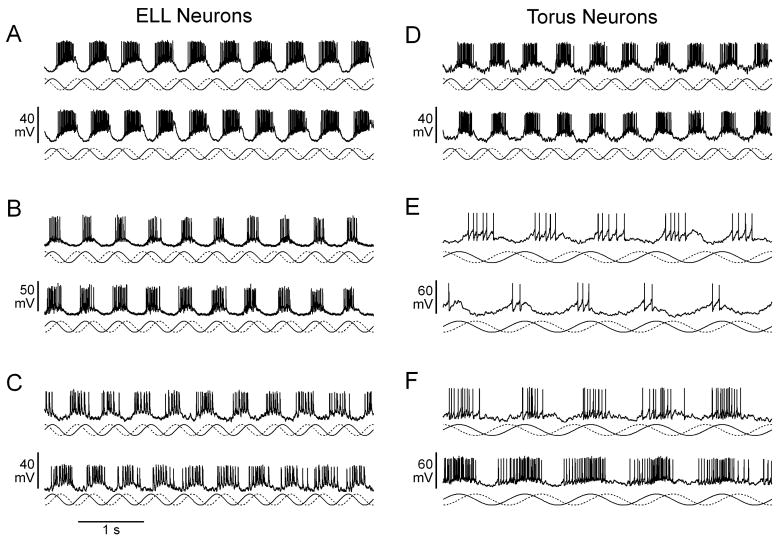
To evaluate the relationship between feature extraction performance and the encoding of naturalistic stimuli, we recorded responses to sinusoidal modulations in amplitude and phase such as those that occur naturally due to interference (‘jamming’) from neighboring conspecifics (Fig. 5). When a neighboring fish has a higher EOD frequency (positive frequency difference, or Df>0) it results in sinusoidal modulations in amplitude and phase at a rate equal to the difference in EOD frequency, with the phase modulation advanced by 90° relative to the amplitude modulation. For negative frequency differences (Df<0), the rate of modulation is also equal to the difference in EOD frequency, but the phase modulation is delayed by 90° relative to the amplitude modulation. The spike-triggered averages of ELL and torus neurons were predictive of their responses to Df>0 and Df<0 (Fig. 5). For example, the ELL neuron in Fig. 3(A) is responsive to downstrokes in amplitude; when stimulated with Df>0 or Df<0, it responds primarily to amplitude decreases and not phase modulation (Fig. 5(A)). Similarly, the torus neuron in Fig. 4(E), which likewise responds to downstrokes in amplitude, also responds consistently to amplitude decreases (Fig. 5(D)). By contrast, the ELL neuron in Fig. 3(B) responds consistently to amplitude increases (Fig. 5(B)), and the ELL neuron in Fig. 3(D) responds consistently to phase delays (Fig. 5(C)). Torus neurons that were responsive to unique combinations of amplitude and phase responded preferentially to one sign of Df (Fig. 5(E, F)). Thus, the torus neuron in Fig. 4(C) was responsive to increases in amplitude co-occurring with phase delays, followed by decreases in amplitude co-occurring with phase advances, and was therefore Df>0-selective (Fig. 5(E)). By contrast, the torus neuron in Fig. 4(D) responded primarily to decreases in amplitude during phase delays, and was therefore Df<0-selective (Fig. 5(F)).

Fig. 5.

Responses of ELL (A–C) and torus neurons (D–F) to jamming stimuli. In each case, an intracellular recording during Df>0 stimulation (top trace) and Df<0 stimulation (bottom trace) is shown. Below each trace, the amplitude of the signal is represented by a solid line and the phase of the signal is represented by a dashed line. (A) Same neuron as Fig. 3(A). (B) Same neuron as Fig. 3(B). (C) Same neuron as Fig. 3(D). (D) Same neuron as Fig. 4(E). (E) Same neuron as Fig. 4(C). (F) Same neuron as Fig. 4(D).

We determined the extent to which the overall feature extraction performance of ELL and torus neurons was dependent on detecting amplitude- or phase-specific features of stimuli by separately randomizing the random AM and random PM time courses and comparing the resulting ROC curves with the original ROC curve, as illustrated in figures 3 and 4. We then analyzed the effect of these randomizations on feature extraction performance by calculating a normalized z-statistic (see Methods). Neurons whose feature extraction performance was significantly reduced by randomizing the time course of one attribute but not the other were categorized as selective for a particular attribute (‘AM-sensitive’ or ‘PM-sensitive’). The remaining ELL and torus neurons were categorized as ‘combination-sensitive’. Of the 49 ELL neurons, 44 (89.80%) were categorized as selective for a particular attribute (35 AM-sensitive and 9 PM-sensitive), and 5 (10.20%) were categorized as combination-sensitive. Of the 55 torus neurons, 39 (70.91%) were categorized as selective for a particular attribute (38 AM-sensitive and 1 PM-sensitive), and 16 (29.09%) were categorized as combination-sensitive. There was therefore a significantly greater proportion of combination-sensitive neurons in the torus than in the ELL (Fisher exact test, p < 0.05). In addition, there was a significant negative correlation between the degrees of AM- and PM-sensitivity across the entire population of ELL pyramidal neurons (Spearman rank R = −0.5417, p < 0.0001). Among torus neurons, however, the degrees of AM- and PM-sensitivity were completely independent (R = 0.0117, p > 0.9).

3.3 Characteristic differences between AM- and PM-sensitive electrosensory neurons

We recorded baseline activity in the absence of any stimulus modulation from a total of 15 AM-sensitive ELL neurons, 9 PM-sensitive ELL neurons, 21 AM-sensitive torus neurons, and 6 combination-sensitive torus neurons, and calculated the vector strength of synchronization to the carrier cycle (Batschelet 1981). There was no significant difference between AM-sensitive ELL and torus neurons, which had vector strengths of 0.1161 ± 0.0272 and 0.1378 ± 0.0244, respectively (t₃₄ = 0.59, p > 0.55). The vector strength of PM-sensitive ELL neurons, which was 0.3948 ± 0.1069, was significantly greater than the vector strength of AM-sensitive neurons in the torus and ELL (t₄₃ = 4.22, p < 0.001). Similarly, the vector strength of combination-sensitive neurons in the torus, which was 0.3577 ± 0.1507, was significantly greater than the vector strength of AM-sensitive neurons in the torus and ELL (t₄₀ = 3.14, p < 0.01).

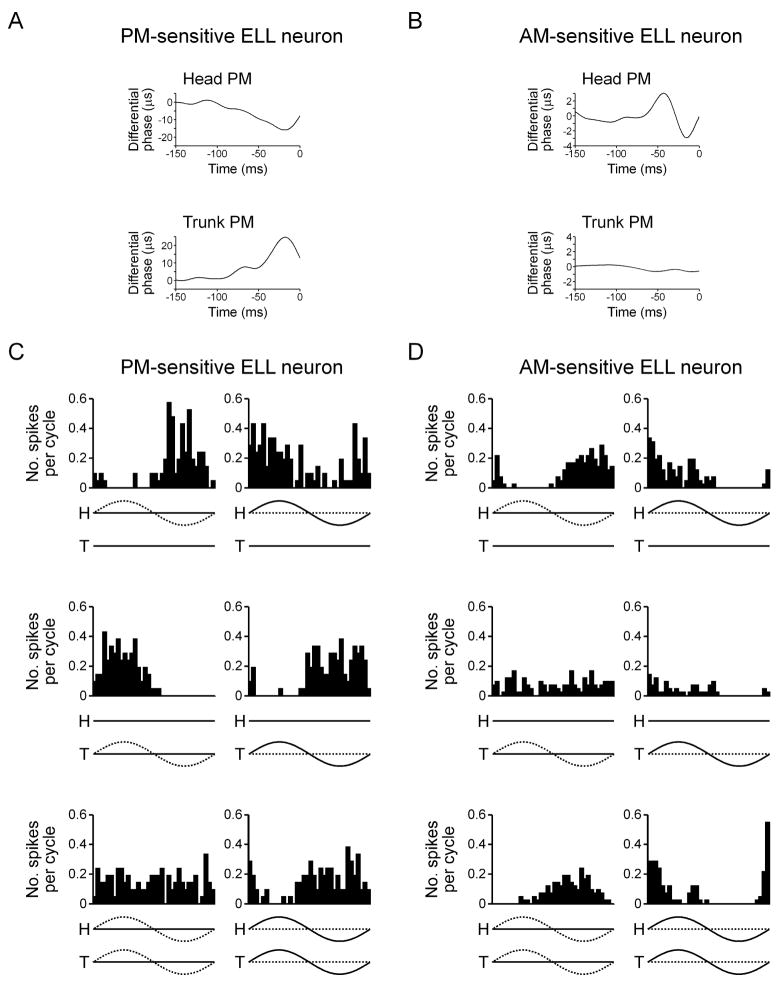
PM-sensitive neurons responded differentially to phase modulation. That is, neurons that responded to phase advances in the head compartment of the phase chamber responded to phase delays in the trunk compartment (Fig. 6(A)), revealing that the relevant variable was the difference in phase between the signals in the two compartments. By contrast, AM-sensitive neurons typically did not respond differentially to phase modulation. For example, the neuron shown in figure 6(B) responded to phase advances preceded by phase delays in the head compartment, but did not respond to phase modulation in the trunk compartment. Therefore, the neuron responded specifically to the modulation of phase in the head compartment, not to differences in phase between the two compartments.

Fig. 6.

PM-sensitive ELL neurons are responsive to differential modulation, whereas AM-sensitive ELL neurons typically are not. (A,B) Spike-triggered average phase from a PM-sensitive ELL neuron (A) and AM-sensitive ELL neuron (B) during random PM presented to the head compartment (trunk unmodulated) and trunk compartment (head unmodulated). (C,D) Histograms of spike times relative to the modulation cycle for a PM-sensitive ELL neuron (C) and AM-sensitive ELL neuron (D) during sinusoidal PM (left column) and sinusoidal AM (right column) presented to the head compartment (top row), trunk compartment (middle row), and both compartments (bottom row). Below each histogram, the amplitude of the signal is represented by a solid line and the phase of the signal is represented by a dashed line, with ‘H’ referring to the head compartment, and ‘T’ referring to the trunk compartment.

We systematically explored responses to differential modulation in 6 PM-sensitive ELL neurons and 4 AM-sensitive ELL neurons. All 6 PM-sensitive neurons responded differentially to phase modulation. For example, the neuron shown in figure 6(C) responded to phase advances in the head and phase delays in the trunk, but did not respond to simultaneous modulation of the phase in both compartments. Across the 6 PM-sensitive ELL neurons, the response to simultaneous PM in both compartments was therefore significantly weaker than the response to PM in either compartment alone (F_2,10 = 9.03, p < 0.01). PM-sensitive neurons responded similarly to AM. Neurons that responded to phase advances in the head and phase delays in the trunk responded to amplitude increases in the head and amplitude decreases in the trunk (Fig. 6(C)), whereas neurons with the opposite pattern of PM-sensitivity showed a reversed response to AM. Unlike the responses to PM, however, the responses to head AM and trunk AM were not always equal in magnitude, and as a result, PM-sensitive neurons often responded to simultaneous AM in the head and trunk compartments, although the response was not as strong as the greater of the head AM and trunk AM responses (Fig. 6(C)).

By contrast, most AM-sensitive neurons did not respond differentially (3 out of 4 neurons). For example, the neuron shown in figure 6(D) responds to phase advances in the head, but does not respond to phase modulation in the trunk. When both the head and trunk compartments are stimulated with simultaneous PM, the neuron in figure 6(D) continues to respond to phase advances in the head. Across the 4 AM-sensitive ELL neurons, the response to simultaneous PM in both compartments was therefore not significantly different from the response to PM in either compartment alone (F_2,6 = 1.06, p > 0.4). The neuron shown in figure 6(D) also responds strongly to amplitude increases in the head, but weakly to amplitude increases in the trunk. When the amplitude in both compartments is modulated simultaneously, the neuron continues to respond strongly to amplitude increases.

3.4 Ambiguity in the encoding and processing of amplitude and timing information

Although S-afferents exhibited a strong preference for encoding random PM, they were able to encode as much as 57.31% of the time course of random AM when stimulus phase was unmodulated (n = 38 units; mean ± sem = 29.17 ± 1.73%; Fig. 7(A)). Similarly, O-afferents were able to encode as much as 64.01% of the time course of random PM when stimulus amplitude was unmodulated (n = 40 units; mean ± sem = 40.75 ± 1.75%; Fig. 7(A)), despite a strong preference for encoding random AM. As a result, encoding of the nonpreferred stimulus attribute by both types of afferents was significantly reduced when the preferred attribute was also randomly modulated (Fig. 7(B); Wilcoxon matched pairs test for S-afferents: z = 5.37, p < 0.000001; O-afferents: z = 5.51, p < 0.000001).

Fig. 7.

Estimation of preferred and nonpreferred stimulus attributes by primary afferents. (A) Estimation of random AM by an S-afferent and estimation of random PM by an O-afferent. (B) AM and PM coding fractions (mean ± sem) for O-afferents and S-afferents during separate and simultaneous random AM and random PM. Significant differences, as determined by a Wilcoxon matched-pairs test, are noted by asterisks (p < 0.000001).

By contrast, both types of afferents encoded a large fraction of their preferred stimulus attribute regardless of whether it was presented alone or in the presence of random modulations of the nonpreferred attribute (Fig. 7(B)). However, the encoding of the preferred attribute was slightly greater when it was modulated alone (Fig. 7(B)). Adding random modulation of the nonpreferred attribute therefore resulted in a small, but significant decrease in the encoding of the preferred attribute for both types of afferents (Wilcoxon matched pairs test for S-afferents: z = 5.11, p < 0.000001; O-afferents: z = 5.26, p < 0.000001).

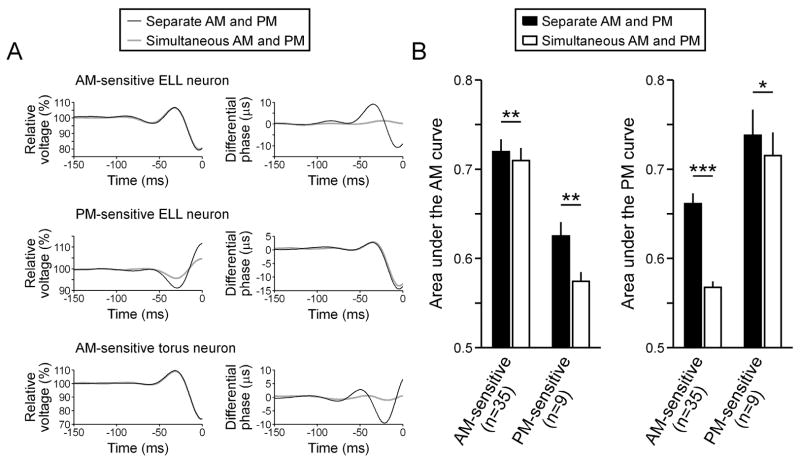
This same pattern was observed in the feature extraction performance of AM- and PM-sensitive ELL neurons (Fig. 8). That is, both types of neurons reliably signaled the occurrence of specific patterns of modulation in their nonpreferred attribute when they occurred in the absence of random modulations in their preferred attribute (Fig. 8(A)). Thus, the AM-sensitive ELL neuron in figure 8(A) responds to phase advances preceded by phase delays in the absence of random AM, but not in the presence of random AM. Similarly, the PM-sensitive ELL neuron in figure 8(A) responds to amplitude increases preceded by amplitude decreases in the absence of random PM, but not as reliably in the presence of random PM.

Fig. 8.

Extraction of preferred and nonpreferred stimulus features by central electrosensory neurons. (A) Spike-triggered average amplitude and phase from an AM-sensitive ELL neuron, PM-sensitive ELL neuron, and AM-sensitive torus neuron during separate and simultaneous random AM and random PM. (B) Areas under the ROC curve (mean ± sem) for AM and PM feature extraction from AM-sensitive and PM-sensitive ELL neurons during separate and simultaneous random AM and random PM. Significant differences, as determined by a Wilcoxon matched-pairs test, are noted by asterisks (*p < 0.05, **p < 0.01, ***p < 0.000001).

We quantified the AM and PM feature extraction performance of ELL neurons using an ROC analysis that only considered the particular attribute of interest and determined the area under the curve (see Methods). Similar to the primary afferents, the area under the curve for the nonpreferred stimulus attribute was significantly reduced when the preferred attribute was also randomly modulated (Fig. 8(B); Wilcoxon matched pairs test for AM-sensitive ELL neurons: n = 35 units; z = 5.16, p < 0.000001; PM-sensitive ELL neurons: n = 9 units; z = 2.66, p < 0.01). Also similar to the primary afferents, the area under the curve for the preferred stimulus attribute was slightly, but significantly reduced when the nonpreferred attribute was also randomly modulated (Fig. 8(B); Wilcoxon matched pairs test for AM-sensitive ELL neurons: z = 2.30, p < 0.01; PM-sensitive ELL neurons: z = 2.19, p < 0.05).

Like the AM-sensitive ELL neurons, the AM-sensitive neurons in the torus signaled the occurrence of specific patterns of phase modulation when they occurred in the absence of random AM, but not in the presence of random AM (Fig. 8(A)). Thus, the area under the ROC curve for random PM presented alone (n = 38 units; mean ± sem = 0.6628 ± 0.0148) was greater than the area under the ROC curve for random PM presented during random AM (0.5632 ± 0.0053), a difference that was highly significant (Wilcoxon matched pairs test: z = 5.33, p < 0.000001). For the AM-sensitive torus neurons, the area under the ROC curve for random AM presented alone (0.7284 ± 0.0147) was only slightly greater than the area under the ROC curve for random AM presented during random PM (0.7213 ± 0.0143), a difference that was nevertheless significant (z = 2.01, p < 0.05).

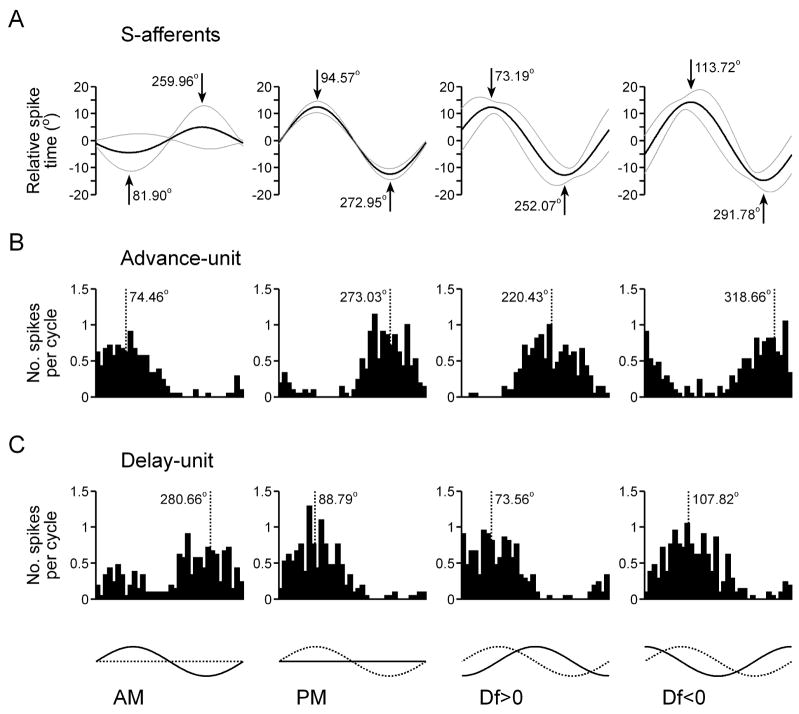
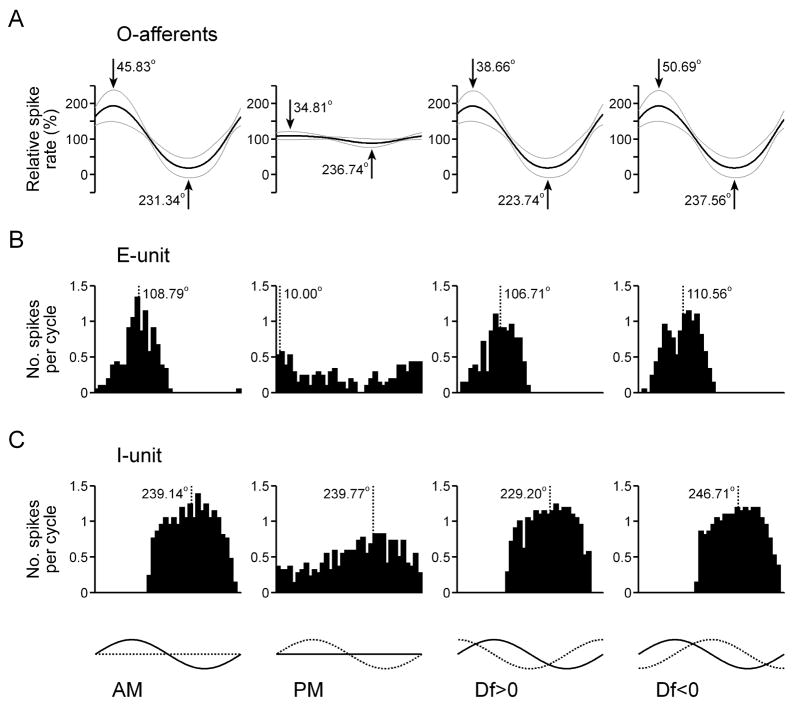
To systematically analyze the relationship between stimulus encoding by primary afferents and the feature extraction performance of ELL neurons, we recorded responses to sinusoidal AM, sinusoidal PM, Df>0, and Df<0 (AM depth = 25%, PM depth = 15°). Figure 9 shows the average shifts in the spike times of S-afferents in response to these four stimuli (Fig. 9(A), n = 21 units), as well as histograms of the action potential responses of two different PM-sensitive ELL neurons, one that responds to phase advances (Fig. 9(B)) and one that responds to phase delays (Fig. 9(C)). The shift in the spike times of S-afferents in response to AM reveals a clear amplitude-dependent shift in spike times, with amplitude increases causing advances and amplitude decreases causing delays (Fig. 9(A)). Accordingly, advance-type ELL neurons responded to amplitude increases (Fig. 9(B)), whereas delay-type ELL neurons responded to amplitude decreases (Fig. 9(C)). When sinusoidal AM and PM were combined, the amplitude-dependent shift interacted with the phase-induced shift to cause predictable differences in the responses of S-afferents to Df>0 and Df<0 (Fig. 9(A)). Relative to the response to PM presented alone, the amplitude-dependent shift in S-afferent spike times caused the maximum delay and maximum advance in spike times to occur slightly earlier in response to Df>0 and slightly later in response to Df<0 (Fig. 9(A)). Accordingly, the responses of PM-sensitive ELL neurons were also slightly advanced in response to Df>0 and slightly delayed in response to Df<0 (Fig. 9(B,C)). The amplitude-dependent latency shift also resulted in a small difference in the depth of modulation in S-afferent spike times in response to Df>0 and Df<0, with Df<0 causing significantly greater modulations in spike timing than Df>0 (15.89 ± 0.87° vs. 14.22 ± 0.75°, respectively; Wilcoxon matched pairs test: z = 3.80, p < 0.001). Accordingly, PM-sensitive ELL neurons gave slightly stronger responses to Df<0 than to Df>0 (17.38 ± 3.11 spk/s vs. 15.31 ± 3.01 spk/s, respectively; n = 15 units; z = 2.10, p < 0.05).

Fig. 9.

Responses to sinusoidal AM and PM in the time-coding pathway. (A) S-afferent spike times (mean is represented by the black line, mean ± st. dev. is represented by grey lines, n = 34 units). The timing of the maximum and minimum shift in spike timing is shown in degrees relative to the modulation cycle. (B,C) Histograms of spike times relative to the modulation cycle for an ELL advance-unit (B) and ELL delay-unit (C). The dashed line shows the average vector angle of the spikes relative to the modulation cycle. At the bottom of the figure, the amplitude of each stimulus is represented by a solid line and the phase of each stimulus is represented by a dashed line.

Figure 10 shows the average spike rates of O-afferents in response to the same four stimuli (Fig. 10(A), n = 34 units), as well as histograms of the action potential responses of two different AM-sensitive ELL neurons, one that responds to amplitude increases (i.e. E-unit, Fig. 10(B)) and one that responds to amplitude decreases (i.e. I-unit, Fig. 10(C)). In general, the effect of sinusoidal PM on O-afferent spike rates was not as dramatic as the effect of sinusoidal AM on S-afferent spike times. There was a general trend for O-afferent spike rates to increase slightly as phase was starting to delay, and to decrease slightly as phase was starting to advance (Fig. 10(A)), but several units showed the reverse trend (6 out of 34). Accordingly, E-units typically responded to phase delays (Fig. 10(B)), whereas I-units typically responded to phase advances (Fig. 10(C)). However, like the primary afferents, a few units showed a reverse trend (e.g. the E-unit shown in Fig. 6(D)). Like the S-afferents, the modulations in the spike rates of O-afferents were slightly shifted in response to Df>0 and Df<0 when compared to AM presented alone, reflecting the influence of PM (Fig. 10(A)). Compared to the response to AM, the maximum and minimum spike rates of O-afferents occurred slightly earlier in response to Df>0 and slightly later in response to Df<0. The responses of AM-sensitive ELL neurons showed the same shift in the timing of their activity (Fig. 10(B,C)). Unlike the S-afferents, there was no significant difference in the depth of modulation in O-afferent spike rates in response to Df>0 and Df<0 (87.62 ± 25.70% vs. 88.03 ± 24.20%, respectively; z = 0.54, p > 0.5), and no significant difference in the magnitude of responses of AM-sensitive ELL neurons to Df>0 and Df<0 (20.28 ± 3.40 spk/s vs. 21.50 ± 3.08 spk/s, respectively; n = 16 units; z = 1.19, p > 0.23).

Fig. 10.

Responses to sinusoidal AM and PM in the amplitude-coding pathway. (A) O-afferent spike times (mean is represented by the black line, mean ± st. dev. is represented by grey lines, n = 21 units). The timing of the maximum and minimum spike rate is shown in degrees relative to the modulation cycle. (B,C) Histograms of spike times relative to the modulation cycle for an ELL E-unit (B) and ELL I-unit (C). The dashed line shows the average vector angle of the spikes relative to the modulation cycle. At the bottom of the figure, the amplitude of each stimulus is represented by a solid line and the phase of each stimulus is represented by a dashed line.

3.5 Ambiguity and the jamming avoidance response

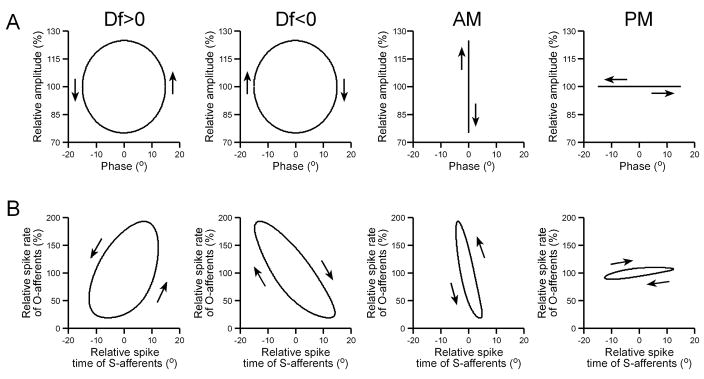
The jamming avoidance response of wave-type weakly electric fish relies on combining information about the temporal relationship between AM and PM to determine whether a neighboring fish has a higher or lower EOD frequency (Df>0 or Df<0, respectively) (Heiligenberg 1991; Kawasaki 1993). The difference between Df>0 and Df<0 can easily be visualized by plotting AM against PM in a Lissajous graph that develops over time, which reveals a circle with a counterclockwise sense of rotation for Df>0 and a clockwise sense of rotation for Df<0 (Fig. 11(A)). Plotting Lissajous graphs of the mean spike rate of O-units against the mean spike time of S-units reveals the same sense of rotation for Df>0 and Df<0 as the actual stimulus modulations (Fig. 11(B)). When sinusoidally modulating only one stimulus attribute (either AM or PM), there is no sense of rotation in a Lissajous plot of the stimulus modulations, only vertical (AM) or horizontal (PM) oscillations (Fig. 11(A)). However, when plotting Lissajous graphs of the primary afferent responses, sinusoidal AM elicited a counterclockwise rotation, and sinusoidal PM elicited a clockwise rotation (Fig. 11(B)), due to the responses of primary afferents to their nonpreferred stimulus attribute.

Fig. 11.

Primary afferent representations of sinusoidal stimulus modulations. (A) Sinusoidal stimulus modulations, plotted as Lissajous graphs of relative amplitude vs. phase. (B) Primary afferent representations of the stimuli in (A), plotted as Lissajous graphs of the mean relative spike rate of O-afferents (n = 34) vs. the mean relative spike time of S-afferents (n = 21).

The amplitude- and time-coding pathways converge within the midbrain, where many neurons respond selectively to a particular sign of Df. If ambiguity in the encoding of AM and PM persists within the central electrosensory pathway, then the responses of midbrain electrosensory neurons to sinusoidal AM should be more similar to their responses to Df>0 than Df<0, whereas their responses to sinusoidal PM should be more similar to their responses to Df<0 than Df>0, due to the shared sense of rotation in Lissajous plots of the primary afferent responses (Fig. 11(B)). We used multiple regression to compare the responses to Df>0 and Df<0 with the responses to sinusoidal AM and sinusoidal PM (n = 213 units; for AM correlation, total r² = 0.78; PM correlation, total r² = 0.51). Responses to AM were correlated with responses to both Df>0 and Df<0, but the correlation with Df>0 responses (β = 0.6519 ± 0.0675, t₂₁₀ = 9.66, p < 0.000001) was stronger than the correlation with Df<0 responses (β = 0.2525 ± 0.0675, t₂₁₀ = 3.74, p < 0.001). By contrast, responses to PM were correlated with responses to Df<0 (β = 0.5634 ± 0.1003, t₂₁₀ = 5.62, p < 0.000001), but not with responses to Df>0 (β = 0.1650 ± 0.1003, t₂₁₀ = 1.64, p > 0.1).

3.6 Bursting in ELL pyramidal neurons

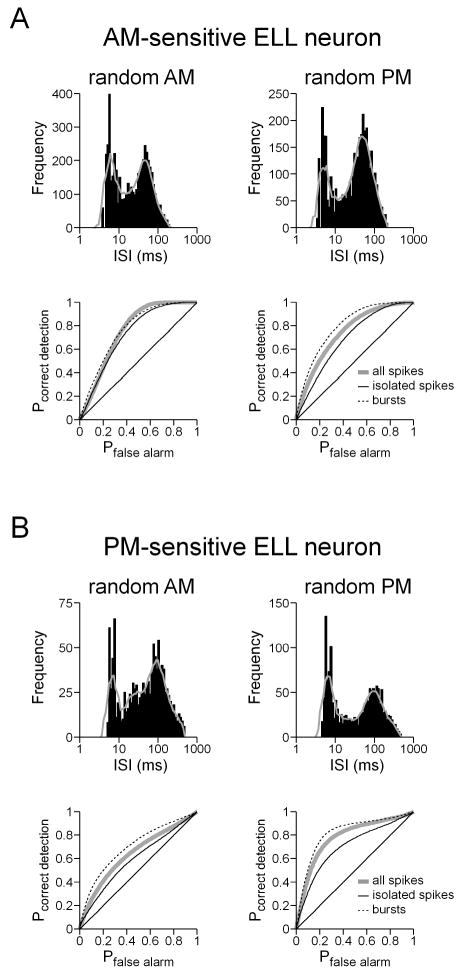
ELL pyramidal neurons in the South American gymnotiforms have a distinct tendency to fire in bursts, and these bursts can contain unique information beyond that carried by individual spikes (Krahe and Gabbiani 2004). Bursts could potentially transmit information about AM and PM more reliably than individual spikes, i.e. with less ambiguity. We did indeed find that ELL pyramidal neurons in Gymnarchus frequently responded in a burst-like pattern to random modulations, as seen in figure 1(A) and in histograms of the logarithm of interspike interval, or ISI (Fig. 12) (Selinger et al. 2007). Such histograms revealed two ISI modes, one at short intervals corresponding to intra-burst ISIs and one at longer intervals corresponding to inter-burst ISIs (Fig. 12). We identified bursts on the basis of these histograms, first by smoothing the histograms using a seven-point moving average, and then selecting the local minimum between the two peaks in the histogram as the ISI cutoff between burst and non-burst ISIs. An individual burst was defined as a continuous series of spikes with ISIs below this cutoff value, and the first spike in each burst was defined as the burst event time. We then performed a feature extraction analysis for AM and PM presented separately, using both bursts and isolated spikes as events.

Fig. 12.

Bursting in ELL pyramidal neurons. (A,B) Histograms of ln(ISI) during random AM and random PM (the solid grey line shows the smoothed, seven-point moving average), along with the ROC curves for all spikes, isolated spikes, and bursts for an AM-sensitive ELL neuron (A) and a PM-sensitive ELL neuron (B).

For both AM- and PM-sensitive ELL neurons that gave burst-like responses, the feature extraction performance of bursts was better than that of isolated spikes (Fig. 12). However, this was true for the preferred stimulus attribute as well as the nonpreferred attribute. In addition, there was no apparent difference in the location of the intra-burst and inter-burst ISI modes for the responses to the preferred and nonpreferred attributes (Fig. 12). Therefore, both individual spikes and bursts provided ambiguous information about AM and PM.

4 Discussion

4.1 Summary

We found that time-varying information about stimulus amplitude and timing is accurately encoded by two distinct populations of primary electrosensory afferents (Figs. 1 and 2). These two populations of afferents give rise to separate populations of hindbrain electrosensory neurons, one that responds preferentially to AM, and one that responds preferentially to PM. As information flows through both of these pathways, there is a reduction in lower bound estimates of mutual information rates, and a shift from accurate representations of the stimulus time course to representations of specific stimulus features (Figs. 1, 2, and 3). In the midbrain, these two pathways converge, where there is a general shift from representations of specific stimulus features in one attribute (AM or PM) to representations of combined features in both attributes (Figs. 1 and 4). Despite the apparent functional separation of amplitude- and time-coding into two distinct sensory pathways, we also found that the activity of both types of primary afferents is affected by modulations of their nonpreferred stimulus attribute, revealing ambiguity in the information content of peripheral sensory neurons (Fig. 7). This ambiguity was reflected in the responses of postsynaptic neurons in the hindbrain, as well as downstream neurons in the midbrain (Fig. 8), indicating that this ambiguity is not resolved within the central nervous system, but persists and therefore likely affects electrosensory perception.

4.2 Separate pathways for amplitude-coding and time-coding

The existence of two separate classes of primary electrosensory afferents in Gymnarchus has been recognized for some time (Bullock et al. 1975; Zakon 1986; Kawasaki and Guo 1996). The threshold for 1:1 spiking of S-afferents is about 20 dB lower than that of O-afferents, and at natural stimulus intensities, this translates into a 1:1 relationship between the carrier cycle and S-afferent spikes, but more sporadic activity in O-afferents (Bullock et al. 1975). In addition, across a wide range of intensities, S-afferent activity is much more tightly synchronized to the carrier signal (Bullock et al. 1975). As a result, S-afferents are well-suited to encoding precise modulations in phase through shifts in spike timing, whereas O-afferents are better suited to encoding modulations in amplitude with changes in firing rate.

Given the clear lack of independence in the processing of amplitude and timing information we found in the current study, one possibility is that the O- and S-afferent pathways do not remain segregated within the hindbrain. However, both anatomical and physiological evidence strongly indicate that this is not the case. S-afferents project exclusively to the inner cell layer of the ELL, where they terminate on the dendrites of ovoidal cells and pyramidal cells as well as on the soma of giant cells (Kawasaki and Guo 1996; Matsushita and Kawasaki 2004). The giant cells, like the S-afferents, terminate on the dendrites of ovoidal cells and pyramidal cells (Kawasaki and Guo 1996; Matsushita and Kawasaki 2004). As one would predict from the anatomical convergence of precise timing information from two different sources, the pyramidal cells within the inner cell layer are highly sensitive to differential phase modulation (Kawasaki and Guo 1996,Kawasaki and Guo 1998; Matsushita and Kawasaki 2005). Although the O-afferent pathway has not been as well studied, the O-afferents do not appear to project to the inner cell layer of the ELL, but instead to other regions of the ELL (Kawasaki and Guo 1996), where pyramidal neurons that are more sensitive to AM than PM are found (Kawasaki and Guo 1998).

In the current study, we did not characterize the anatomy of the ELL pyramidal neurons we recorded from, but the responses to simultaneous random amplitude and random phase modulation clearly revealed the existence of two distinct classes of neurons, ones that responded preferentially to AM, and others that responded preferentially to PM. As previously described, PM-sensitive neurons were more highly synchronized to the carrier cycle than AM-sensitive neurons, reflecting their distinct presynaptic input from S- and O-afferents, respectively (Kawasaki and Guo 1998). In addition, all the PM-sensitive neurons tested responded to differences in phase or amplitude between the head and trunk, whereas the majority of AM-sensitive neurons responded to absolute modulations in amplitude and phase (Fig. 6). Nevertheless, a small number of AM-sensitive neurons did respond to differences in amplitude between the two chambers, which was previously found in a subset of torus neurons (Carlson and Kawasaki 2004).

The responses of ELL pyramidal neurons to modulation of their preferred and nonpreferred attributes were accurately predicted by the response patterns of their respective primary afferents. That is, PM-sensitive neurons responded to either advances or delays in S-afferent spike times, regardless of whether those shifts in spike timing were caused by changes in amplitude or phase (Fig. 9). Similarly, AM-sensitive neurons responded to either increases or decreases in O-afferent spike rates, regardless of whether those changes in firing rate were caused by AM or PM (Fig. 10). If ELL pyramidal neurons received independent input from both types of afferents, then there is no reason to expect that the response to modulation of one attribute should be predictive of the response to modulation of the other attribute. Therefore, this finding provides further evidence to support the continued segregation of amplitude- and time-coding within the ELL. This reasoning also sheds light on the small number of exceptional ELL neurons identified as combination-sensitive (5 out of 49 neurons). In each case, these neurons responded either to a combination of amplitude increases and phase advances (e.g. Fig. 3(E)), or amplitude decreases and phase delays, indicating that they were “PM-sensitive” neurons (i.e. received S-afferent input) that were relatively strongly affected by amplitude-dependent shifts in spike timing.

4.3 The flow of information in sensory systems

Two distinct types of primary electrosensory afferents are also found in the distantly-related wave-type weakly electric gymnotiform fish from South America, amplitude-coding P-afferents and time-coding T-afferents (Scheich et al. 1973; Zakon 1986). Like Gymnarchus, these two populations of primary afferents give rise to distinct amplitude- and time-coding central electrosensory pathways (Maler et al. 1981; Carr and Maler 1986; Mathieson et al. 1987; Heiligenberg 1991; Kawasaki 2005). The encoding of AM by the P-afferent pathway has been extensively studied using information theoretical approaches similar to the methods used in the current study (see Gabbiani and Metzner 1999). In general, P-afferents linearly encode electrosensory stimuli and accurately represent the detailed time course of AM, whereas their postsynaptic targets in the ELL encode AM nonlinearly and accurately signal the occurrence of specific stimulus features, i.e. increases or decreases in amplitude (Gabbiani et al. 1996; Wessel et al. 1996; Metzner et al. 1998; Kreiman et al. 2000; Krahe et al. 2002; Chacron 2006).

We found an identical transformation in Gymnarchus from linear stimulus encoding in the periphery to feature extraction centrally, not only in the amplitude-coding O-afferent pathway, but also in the time-coding S-afferent pathway (Fig. 1). The overall feature extraction performance of hindbrain and midbrain electrosensory neurons was comparable. The difference, however, was that many more neurons in the midbrain signaled the occurrence of joint modulations in amplitude and phase, rather than modulations in only one attribute (compare Figs. 3 and 4). This finding was expected, given the anatomical convergence of the amplitude- and time-coding pathways in the midbrain (Kawasaki and Guo 1998), and the sensitivity of midbrain neurons to different temporal combinations of sinusoidal AM and PM (Kawasaki and Guo 2002; Carlson and Kawasaki 2004, 2006b).

Because of the increasing selectivity to particular stimulus features, the lower bound estimates of information rates by individual neurons decreased significantly from the periphery to the hindbrain to the midbrain (Fig. 1(B)). In other words, information about stimulus modulations other than a particular neuron’s feature of interest was discarded. However, this reduction in information rate was concomitant with a decrease in firing rate, revealing a significant increase in the amount of information transmitted per spike (Fig. 1(B)). We therefore found a shift from high firing rates necessary to accurately encode the time course of modulations in a particular attribute to increasingly sparse representations of increasingly complex stimulus features. The finding that a similar type of transformation in information processing occurs in the electrosensory pathways of unrelated species, and in two different pathways within the same species, suggests that this type of transformation is likely a general feature of sensory systems.

We used the indirect method to estimate a lower bound on mutual information rates based on linear decoding that does not take into account information that may be encoded nonlinearly (Strong et al. 1998; Borst and Theunissen 1999; Roddey et al. 2000). A recent study on the gymnotiform electrosensory system applied the direct method for estimating mutual information transmission in ELL pyramidal neurons, and revealed information rates that are significantly greater than lower bound estimates (Chacron 2006). It is therefore possible that our lower bound estimates of mutual information rates underestimate the actual amount of information transmitted by ELL and torus neurons in Gymnarchus. However, in the gymnotiform electrosensory system, upper bound estimates on information rates for pyramidal neurons are on average less than the lower bound estimates for P-afferents (Chacron 2006). Therefore, even under the assumption that actual information rates in pyramidal neurons achieve their theoretical maximum, much of the information on the detailed time course of stimuli is lost in central processing.

The feature extraction performance of ELL pyramidal neurons in gymnotiforms reveals a number of additional subtleties beyond the simple detection of upstrokes or downstrokes in amplitude. For instance, the linear stimulus estimation performance of pyramidal neurons is significantly better for spatially localized AM than for global AM, although in general it is still not as good as that of primary afferents (Bastian et al. 2002; Chacron 2006). Global AM also induces oscillatory behavior, but local AM does not (Doiron et al. 2003). In addition, bursts of spikes play a critical role in information processing: they serve as more reliable indicators of specific stimulus features than individual spikes (Gabbiani et al. 1996; Metzner et al. 1998), they selectively encode lower frequencies of modulation whereas individual spikes encode the entire frequency range (Oswald et al. 2004), and the intervals between spikes within bursts encode stimulus intensity (Oswald et al. 2007). Furthermore, gain control and synaptic plasticity actively regulate responses to stimuli (Bastian 1986a, b, 1999; Berman and Maler 1999; Mehaffey et al. 2005). The complex, nonlinear nature of stimulus encoding in the pyramidal neurons of gymnotiforms largely relates to a complex center-surround receptive field organization, active apical dendrites, and prominent feedback pathways that terminate onto the apical dendrites (see Bell and Maler 2005; Kawasaki 2005). We did not address any of these issues in detail, but the relatively little we know about the ELL of Gymnarchus suggests that similar computations may be occurring in the AM- and PM-sensitive pyramidal neurons, since their morphological and anatomical organization is very similar to that of gymnotiforms (Kawasaki and Guo 1998; Bell and Maler 2005; Kawasaki 2005). Indeed, we did find that both types of pyramidal neurons often fired in bursts and the feature extraction performance of bursts was greater than that of isolated spikes (Fig. 12). Future experiments will be needed to further assess the complexity of information processing by ELL pyramidal neurons in the amplitude- and time-coding pathways of Gymnarchus.

4.4 Ambiguity in neuronal representations of stimulus amplitude and timing

When the amplitude and phase of electrosensory stimuli are both randomly modulated, O-afferents exhibit a clear preference for encoding AM, whereas S-afferents exhibit a clear preference for encoding PM (Figs. 2(A,B), 7(B)). However, S-afferents encode a significant amount of the time course of random AM when it occurs without any PM, and O-afferents encode a significant amount of the time course of random PM when it occurs without any AM (Fig. 7). As a result, it is not possible to unequivocally determine whether the response of a given primary afferent is caused by modulations in amplitude or phase, and there is therefore ambiguity about the information content of primary afferent spike trains. This same effect was found for P- and T-afferents in the gymnotiform fish Eigenmannia, as well as for leaky integrate-and-fire models of amplitude- and time-coding afferents (Carlson and Kawasaki 2006a), indicating that ambiguity is an unavoidable feature of a sensory system designed to encode both the amplitude and precise timing of stimuli. In addition, the encoding of the preferred stimulus attribute was degraded when the nonpreferred attribute was simultaneously modulated (Fig. 7(B)). This reveals that the nonpreferred attribute can also serve as a source of noise for the encoding of the preferred attribute, which is also the case in Eigenmannia (Carlson and Kawasaki 2006a).

A major goal of the current study was to assess the effects of this ambiguity on the responses of downstream neurons in the electrosensory pathway. We found that the responses of both AM- and PM-sensitive neurons in the hindbrain and midbrain reflected the ambiguity present in the responses of primary afferent neurons. When the preferred stimulus attribute was unmodulated, central electrosensory neurons reliably signaled the occurrence of specific features in their nonpreferred attribute (Fig. 8). In addition, the nonpreferred attribute served as a source of noise that reduced the performance of central electrosensory neurons in extracting information about specific features in their preferred attribute (Fig. 8(B)). Furthermore, the responses of S- and O-afferents to sinusoidal modulation of their preferred and nonpreferred attributes accurately predicted the responses of ELL pyramidal neurons in the time- and amplitude-coding pathways, respectively (Figs. 9, 10). These results indicate that ambiguity in the information content of primary afferent responses is not resolved through central processing, but persists and ultimately affects the perception of electrosensory stimuli.

This conclusion is consistent with the effects of this ambiguity on electrosensory perception as related to the jamming avoidance response in Eigenmannia (Carlson and Kawasaki 2006a, 2007). This behavior relies on particular temporal relationships between AM and PM to determine whether a neighboring fish has a higher or lower EOD frequency (Df>0 or Df<0, respectively), as shown in figure 11. In Eigenmannia, as in Gymnarchus, the responses of primary afferents to sinusoidal AM signal a combination of AM and PM with the same temporal relationship as occurs with Df>0, whereas the responses to sinusoidal PM signal a combination of AM and PM with the same temporal relationship as occurs with Df<0 (Fig. 11). As a result, both Df>0 and sinusoidal AM cause Eigenmannia to lower its EOD frequency, whereas Df<0 and sinusoidal PM cause Eigenmannia to raise its EOD frequency (Carlson and Kawasaki 2006a). Similarly, we found that the responses of midbrain neurons in Gymnarchus to sinusoidal AM were more correlated with their responses to Df>0 than their responses to Df<0, whereas the reverse was true for the responses to sinusoidal PM. This indicates that in both species the neural circuitry for controlling the jamming avoidance response is likely to be similarly affected by encoding ambiguity. In Eigenmannia, this can result in EOD frequency shifts in response to a variety of stimuli that may be encountered in a natural environment, such as random AM, AM presented to a localized portion of the body surface, transient changes in amplitude, and movement of resistive objects through the electric field (Carlson and Kawasaki 2007).

It remains to be seen how ambiguity in the encoding of AM and PM affects electrosensory perception during active electrolocation. In this context, the amplitude and phase of electrosensory feedback is directly related to the resistance and capacitance of objects within the electric field (von der Emde 1999). Eigenmannia and other electric fish are able to distinguish complex from simple impedances (those with and without capacitance, respectively) (von der Emde 1990; von der Emde and Ringer 1992; von der Emde 1998), but ambiguity may limit the ability to discriminate fine differences in these two features of objects. In addition, the stimuli used in the current study consisted of modulations distributed over a large portion of the body surface, and the responses of central electrosensory neurons may become less ambiguous with highly localized stimuli, such as those caused by small prey items (Nelson and MacIver 1999; Nelson et al. 2002; Chacron et al. 2003). However, it is important to note that EOD frequency decreases can be elicited in Eigenmannia by highly localized AM (Carlson and Kawasaki 2007), suggesting that ambiguity occurs under both local and global stimulation. On the other hand, it may not be important to obtain unambiguous information about the actual resistance and capacitance of encountered objects. Instead, the amplitude- and time-coding pathways may each provide unique, complementary information about various characteristics of objects. Addressing this question can be fruitfully approached using methods analogous to those used in the current study. For example, an object could be placed in the electric field and subjected to random motion and information theoretical approaches could be used to objectively determine the information that electrosensory neurons in both pathways convey about various aspects of the object, such as its size, shape, electrical characteristics, position, velocity, and acceleration. As this study and many others reveal, it is best to make minimal assumptions about which aspects of stimuli are encoded by a particular type of neuron, and which variables are relevant to that encoding. Further studies on electrosensory processing in the amplitude- and time-coding pathways of weakly electric fish may reveal surprising insights into the information that can be transmitted by these two distinct types of primary afferents.