Generalized gradient approximation model exchange holes for range-separated hybrids

Abstract

We propose a general model for the spherically averaged exchange hole corresponding to a generalized gradient approximation (GGA) exchange functional. Parameters are reported for several common GGAs. Our model is based upon that of Ernzerhof and Perdew [J. Chem. Phys. 109, 3313 (1998)]. It improves upon the former by precisely reproducing the energy of the parent GGA, and by enabling fully analytic evaluation of range-separated hybrid density functionals. Analytic results and preliminary thermochemical tests indicate that our model also improves upon the simple, local-density-based exchange hole model of Iikura et al. [J. Chem. Phys. 115, 3540 (2001)].

INTRODUCTION

Kohn–Sham density functional theory^{1, 2} (DFT) using semilocal exchange-correlation (XC) functionals has become an indispensable tool for computational chemistry and solid state physics.³ Semilocal exchange-correlation functionals provide computationally tractable approximations to the many-body exchange-correlation energy, E_xc. The simplest semilocal functional is the local density approximation (LDA), which models the exchange-correlation energy density at each point r as that of a homogeneous electron gas (HEG) with electron density n=n(r). More sophisticated semilocal functionals include generalized gradient approximations (GGAs) incorporating |∇n(r)| and meta-GGAs incorporating the kinetic energy density and∕or density Laplacian.⁴ These functionals significantly improve upon the LDA for a wide variety of properties. But while the LDA has a simple derivation, constructing GGAs and meta-GGAs is not as straightforward.

One powerful guide to constructing new semilocal exchange-correlation functionals is the exchange-correlation hole,⁵n_xc(r₁,r₂). Given a test electron located at r₁, n_xc(r₁,r₂) represents a one-electron charge distribution—a “hole” in the N-electron density n(r₂)—that adds self-interaction and exchange-correlation effects to the classical Coulomb interaction between the test electron and n(r₂). Functionals built from proper exchange-correlation hole models ensure satisfaction of additional exact constraints beyond those known for E_xc itself.

In addition to their important formal properties, model exchange holes are essential for constructing range-separated hybrid functionals.^{6, 7, 8, 9} Hybrid functionals incorporate a fraction of exact nonlocal Hartree–Fock-type (HF) exchange, and can accurately model many properties with moderate computational effort.^{10, 11, 12, 13, 14} Range-separated hybrids are obtained by partitioning the Coulomb operator into short- and long-range components,

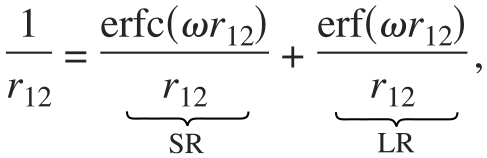(1)

and using different fractions of exact and semilocal DFT exchange for the two components. Range-separated hybrids that eliminate long-range exact exchange have demonstrated utility for condensed systems,^{15, 16, 17, 18} in which full range exact exchange presents computational and formal problems. Long-range-corrected (LC) hybrids incorporating 100% long-range exact exchange yield the exact asymptotic exchange-correlation potential and can accurately model many properties of finite systems.^{19, 20, 21, 22} A functional incorporating exact exchange only in the middle range has recently been introduced²³ and shows promise in both extended and finite systems. Evaluating the range-separated components of the semilocal DFT exchange energy requires a model for the corresponding exchange hole. As the number of ranges increases, analytic evaluation of the range-separated exchange energy becomes important.

There have been many attempts to construct model exchange holes that reproduce the energies of a parent exchange functional—to “reverse-engineer” an exchange hole from an exchange energy rather than obtaining an exchange energy from the exchange hole.^{19, 24, 25} Such model exchange holes are nonunique: even the LDA exchange energy, which can be directly obtained from the homogeneous electron gas model system, can also be constructed from nonoscillating models (Sec. 3). Unfortunately, there is to date no completely satisfactory prescription for constructing such models. The widely used model of Iikura et al.¹⁹ uses a simple LDA-based ansatz and fails to satisfy known exact conditions (see Sec. 6B). Perdew and co-workers have proposed a variety of exchange hole models, some used to derive exchange functionals,^{26, 27, 28} and others designed to reproduce existing exchange functionals.^{24, 25} The GGA model exchange hole of Ernzerhof and Perdew²⁴ (EP) is particularly relevant to the present work. While parametrized to reproduce the Perdew, Burke, and Ernzerhof (PBE) GGA,²⁹ it provides a framework for modeling any GGA exchange hole. However, the model satisfies some exact constraints only approximately, and generally does not yield the same exchange energy as its parent GGA. Nevertheless, it is a helpful point of departure. The recent work of Bahmann and Ernzerhof³⁰ provides another construction of the PBE exchange hole which can be readily generalized to other GGAs.

In this work, we present a general-purpose model for the exchange hole corresponding to a GGA exchange functional. Our model refines that of EP, and is particularly designed for use in range-separated hybrids. The remainder of this paper is organized as follows. In Sec. 2, we briefly review the exchange hole formalism, before reviewing the EP construction in Sec. 3. After pointing out a few practical concerns with the EP construction in Sec. 4, we introduce our own (HJS) exchange hole model in Sec. 5. In Sec. 6 we compare our model for the PBE exchange hole to those of EP and Iikura and co-workers, paying particular attention to implications for range-separated hybrids. We summarize in Sec. 7.

THE EXCHANGE HOLE

In order to evaluate the exact exchange energy in the Kohn–Sham (KS) framework, we proceed through the KS one-particle density matrix n₁(r₁;r₂), defined in terms of the KS occupied orbitals {ϕ_i(r)} as

$$n_1({\mathbf{r}}_1;{\mathbf{r}}_2)=\sum _{i=1}^N{\varphi }_i^{\star }\left({\mathbf{r}}_1\right){\varphi }_i\left({\mathbf{r}}_2\right),$$ (2)

where N is the number of electrons. The exact exchange energy is given, in the hartree atomic units used throughout this work, by

$$E_x=-\frac{1}{2}\int \mathrm{d}{\mathbf{r}}_1\mathrm{d}{\mathbf{r}}_2\frac{n_1({\mathbf{r}}_1;{\mathbf{r}}_2)n_1({\mathbf{r}}_2;{\mathbf{r}}_1)}{r_{12}},$$ (3)

where r₁₂=|r₁−r₂|. Since the exchange hole represents an effective charge distribution with which electrons interact Coulombically, the exchange hole is defined by

$$n\left({\mathbf{r}}_1\right)n_x({\mathbf{r}}_1,{\mathbf{r}}_2)=-n_1({\mathbf{r}}_1;{\mathbf{r}}_2)n_1({\mathbf{r}}_2;{\mathbf{r}}_1),$$ (4)

where n(r)=n₁(r;r) is the electron density.

The exact exchange hole satisfies several known constraints. Among those most important for our purposes are the following:

• The exchange hole is negative semidefinite.

• As seen from Eq. 4, for spin-unpolarized systems, the exchange hole obeys

  $$n_x(\mathbf{r},\mathbf{r})=-\frac{1}{2}n\left(\mathbf{r}\right).$$ (5)
• The exchange hole obeys the normalization condition

  $$\int \mathrm{d}{\mathbf{r}}_2{n}_x({\mathbf{r}}_1,{\mathbf{r}}_2)=-1,$$ (6)

  which follows ultimately from decomposing the pair density n₂(r₁,r₂) into Coulomb, exchange, and correlation pieces, and using idempotency of the KS one-particle density matrix along with the quadrature relation between the density and the pair density.
• The exchange hole yields the exchange energy via

  $$\frac{1}{2}\int \mathrm{d}{\mathbf{r}}_1\mathrm{d}{\mathbf{r}}_2\frac{n\left({\mathbf{r}}_1\right)n_x({\mathbf{r}}_1,{\mathbf{r}}_2)}{r_{12}}=E_x,$$ (7)

  which follows from inserting the definition of the exchange hole into the energy expression of Eq. 3.

As a six-dimensional object, the exchange hole is difficult to visualize, and it is generally easier to work with the system- and spherically averaged exchange hole,

$${\overline{n}}_x\left(u\right)=\int \mathrm{d}{\mathbf{r}}_1\frac{n\left({\mathbf{r}}_1\right)}{N}\int \mathrm{d}{\mathbf{r}}_2\frac{\delta (r_{12}-u)}{4\pi u^2}{n}_x({\mathbf{r}}_1,{\mathbf{r}}_2).$$ (8)

This quantity has a simple representation in terms of the exchange part of the pair distribution function (x-PDF), given through

$$-n_1({\mathbf{r}}_1;{\mathbf{r}}_2)n_1({\mathbf{r}}_2;{\mathbf{r}}_1)=n\left({\mathbf{r}}_1\right)n_x({\mathbf{r}}_1,{\mathbf{r}}_2)=n\left({\mathbf{r}}_1\right)n\left({\mathbf{r}}_2\right)g_x({\mathbf{r}}_1,{\mathbf{r}}_2).$$ (9)

In conventional semilocal exchange-correlation functionals, one usually writes instead

$$n\left({\mathbf{r}}_1\right)n_x({\mathbf{r}}_1,{\mathbf{r}}_2)=n{\left({\mathbf{r}}_1\right)}^2{J}_x(n\left({\mathbf{r}}_1\right),r_{12}).$$ (10)

We seek to model this quantity J_x. We begin by reviewing the EP model. Note that throughout, we discuss only spin-unpolarized models; the spin-polarized exchange hole can be obtained through the spin-scaling relation

$$n\left(\mathbf{r}\right)n_x[n_{\uparrow },n_{\downarrow }](\mathbf{r},\mathbf{r}+\mathbf{u})=\sum _{\sigma }{n}_{\sigma }\left(\mathbf{r}\right)n_x\left[2n_{\sigma }\right](\mathbf{r},\mathbf{r}+\mathbf{u}).$$ (11)

THE EP MODEL EXCHANGE HOLE

The LDA exchange hole and a nonoscillating approximation thereto

Since PBE reduces to LDA for homogeneous densities, and the LDA exchange hole is exact in this limit, constructing a GGA hole in principle requires only that gradient corrections to the LDA exchange hole be constructed. Within the LDA, the exchange hole at point r is approximated by the exchange hole of a HEG with density n equal to the density at the point r,

$$n_x^{\mathrm{LDA}}(\mathbf{r},\mathbf{r}+\mathbf{u})=n_x^{\mathrm{HEG}}(n\left(\mathbf{r}\right),u),$$ (12)

with

$$n_x^{\mathrm{HEG}}(n,u)=n{J}_x^{\mathrm{HEG}}\left(y\right),$$ (13)

where y=k_Fu and the Fermi wave vector k_F is given by

$$k_F={\left(3{\pi }^{2}n\right)}^{1∕3}.$$ (14)

The x-PDF for the spin-unpolarized HEG is

$$J^{\mathrm{HEG}}\left(y\right)=-\frac{9}{2}{\left(\frac{\sin \left(y\right)-y\cos \left(y\right)}{y^3}\right)}^2.$$ (15)

The long-range oscillations in J^HEG are energetically unimportant, and are unphysical in finite systems. Therefore, EP begin their construction of the PBE hole by building a nonoscillating approximation to J^HEG, denoted here by ${\tilde{J}}^{\mathrm{LDA}}\left(y\right)$. This approximation is constructed to satisfy the exact constraints listed in Sec. 2, as well as three additional constraints. The on-top constraint of Eq. 5 implies that

$${\tilde{J}}^{\mathrm{LDA}}\left(0\right)=-\frac{1}{2}.$$ (16)

The normalization constraint of Eq. 6 leads to

$$\frac{4}{3\pi }{\int }_0^{\infty }\mathrm{d}y{y}^2{\tilde{J}}^{\mathrm{LDA}}\left(y\right)=-1.$$ (17)

The energy constraint of Eq. 7 yields

$$\frac{8}{9}{\int }_0^{\infty }\mathrm{d}yy{\tilde{J}}^{\mathrm{LDA}}\left(y\right)=-1.$$ (18)

Three further constraints are chosen. First, ${\tilde{J}}^{\mathrm{LDA}}\left(y\right)$ should have the same curvature at y=0 as J^HEG(y),

$$\frac{{\partial }^2}{\partial y^2}{\tilde{J}}^{\mathrm{LDA}}{\phantom{|}\left(y\right)|}_{y=0}=\frac{1}{5}.$$ (19)

Second, ${\tilde{J}}^{\mathrm{LDA}}\left(y\right)$ should have the same behavior at large y as does the nonoscillating part of J^HEG(y). This implies that

$${\tilde{J}}^{\mathrm{LDA}}\left(y\right)\approx -\frac{9}{4y^4}$$ (20)

for large y. Finally, EP eliminate all structure in ${\tilde{J}}^{\mathrm{LDA}}\left(y\right)$ that is not needed to fulfill the preceding constraints by maximizing the information entropy,

$$S[-{\tilde{J}}^{\mathrm{LDA}}\left(y\right)]={\int }_0^{\infty }\mathrm{d}y4\pi y^2{\tilde{J}}^{\mathrm{LDA}}\left(y\right)\ln [-{\tilde{J}}^{\mathrm{LDA}}\left(y\right)]$$ (21)

of $-{\tilde{J}}^{\mathrm{LDA}}\left(y\right)$.

The nonoscillating model in EP, based on an earlier model of Perdew and Wang,³¹ writes

$${\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}\left(y\right)=-\frac{9}{4y^4}\frac{\overline{\mathcal{A}}{y}^2}{1+\overline{\mathcal{A}}{y}^2}+(\frac{9}{4}\frac{\overline{\mathcal{A}}}{y^2}+\mathcal{B}+\mathcal{C}{y}^2+\mathcal{E}{y}^4){\mathrm{e}}^{-\mathcal{D}{y}^2}.$$ (22)

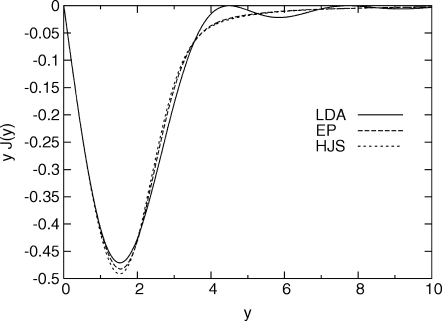
The first term controls the long-range behavior and guarantees satisfaction of the large y constraint of Eq. 20, while the parameters $\overline{\mathcal{A}}$, B, C, D, and E enforce the other constraints. In Fig. 1 we show yJ^HEG(y) and $y{\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}\left(y\right)$, the integrands required to obtain the exchange energy density. Note that here and in the following, we have renamed a few parameters or functions in the EP model. Specifically,

• Our parameter $\overline{\mathcal{A}}$ is defined as 4∕9A, where A≈1.106 is the parameter of EP.

• Our functions ${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)$ and ${\overline{\mathcal{G}}}_{\mathrm{EP}}\left(s\right)$ (see below) are defined as, respectively, 1+s²F(s) and 1+s²G(s) as given in Ref. 24.

• In Eq. (25) of Ref. 24, EP have written [16A²+36(B−AD)]∕36, which is identically equal to −1∕2 due to the on-top constraint of Eq. 16.

Figure 1.

Exact and model LDA energy-weighted exchange pair-distribution functions.

Gradient corrections

Given this zero-gradient limit, EP introduce gradient corrections in terms of the reduced density gradient

$$s=\frac{|\nabla n|}{2k_{F}n}$$ (23)

by writing

$${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}(s,y)=[-\frac{9}{4y^4}\frac{\overline{\mathcal{A}}{y}^2}{1+\overline{\mathcal{A}}{y}^2}+(\frac{9}{4}\frac{\overline{\mathcal{A}}}{y^2}+\mathcal{B}+\mathcal{C}{\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)y^2+\mathcal{E}{\overline{\mathcal{G}}}_{\mathrm{EP}}\left(s\right)y^4){\mathrm{e}}^{-\mathcal{D}{y}^2}]{\mathrm{e}}^{-s^2{\mathcal{H}}_{\mathrm{EP}}\left(s\right)y^2}.$$ (24)

The function ${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)$ is chosen to get a more general on-top curvature,

$${\partial }_s^2{\partial }_y^2{\tilde{J}}^{\mathrm{GGA}}{\phantom{|}{(s,y)}_{\mathrm{EP}}|}_{y=s=0}=-\frac{4}{27}.$$ (25)

The other two functions, ${\overline{\mathcal{G}}}_{\mathrm{EP}}\left(s\right)$ and H_EP(s), are chosen to yield the normalization constraint of Eq. 17 and the desired enhancement factor

$$-\frac{8}{9}{\int }_0^{\infty }\mathrm{d}yy{\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}(s,y)=F_x^{\mathrm{GGA}}\left(s\right),$$ (26)

where the GGA enhancement factor is defined by

$$E_x^{\mathrm{GGA}}=-\frac{3}{4\pi }\int \mathrm{d}\mathbf{r}n\left(\mathbf{r}\right)k_F\left(\mathbf{r}\right)F_x^{\mathrm{GGA}}\left(s\right).$$ (27)

These three constraints are not enough to determine ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}$ uniquely, since the constraint of Eq. 25 only affects the small s behavior of ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}$. Thus, EP write ${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)$ in terms of H_EP(s) as

$${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)=1-\frac{1}{27\mathcal{C}}{s}^2-\frac{1}{2\mathcal{C}}{s}^2{\mathcal{H}}_{\mathrm{EP}}\left(s\right).$$ (28)

The EP model is thereby completely specified. Equation 28 defines ${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)$, the normalization condition Eq. 17 defines ${\overline{\mathcal{G}}}_{\mathrm{EP}}\left(s\right)$, and given those the energy condition can be used to solve for H_EP(s). Unfortunately, H_EP(s) cannot be solved for in closed form, and, in fact, for the PBE GGA, there is no solution at all for s≳10. Thus, EP recommend simply writing s=min(s,10).

As EP noted in discussing their model, while the parameters defining H_EP(s) were chosen so that the model reduces to the PBE GGA [modulo difficulties in solving for H_EP(s)], nothing in the work requires this choice, and the EP procedure can be followed to construct model exchange holes for any GGA.

CRITIQUE OF THE EP MODEL EXCHANGE HOLE

While the EP model is quite straightforward and simple to construct, it contains deficiencies which we would like to remedy. Most importantly, the PBE model exchange hole of EP does not provide a closed-form expression for the range-separated PBE energy. Specifically, we may write a range-separated enhancement factor

$$F_x^{\omega \mathrm{PBE}}(s,\omega ,k_F)=-\frac{8}{9}{\int }_0^{\infty }\mathrm{d}yy{\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}(s,y)\mathrm{erfc}\left(\frac{\omega }{k_F}y\right),$$ (29)

where ω is the range-separation parameter of Eq. 1. Inserting the explicit form of ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}$, we see that one term contributing to $F_x^{\omega \mathrm{PBE}}(s,\omega ,k_F)$ is

$$\mathcal{F}(s,\omega ,k_F)=-\frac{8}{9}{\int }_0^{\infty }\mathrm{d}y\frac{9\overline{\mathcal{A}}}{4}y(-\frac{1}{y^4}\frac{y^2}{1+\overline{\mathcal{A}}{y}^2}+\frac{1}{y^2}{\mathrm{e}}^{-\mathcal{D}{y}^2}){\mathrm{e}}^{-s^2{\mathcal{H}}_{\mathrm{EP}}\left(s\right)y^2}\mathrm{erfc}\left(\frac{\omega }{k_F}y\right).$$ (30)

This term has, to date, defied analytic integration. Existing range-separated hybrids constructed from the EP model either approximate this integral or evaluate it numerically.^{15, 18, 21} Further, most of the approximations used in evaluating F(s,ω,k_F) fail for large ω∕k_F, and these approximations often complicate the functional differentiation needed to extract the range-separated exchange potential.

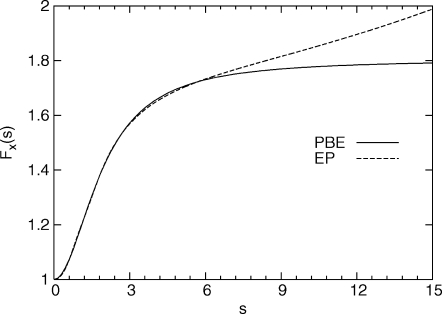
A second problem with the EP model is its behavior at large s. As the gradient gets large, the EP exchange hole becomes unphysically deep near y=1. Sufficiently large s make the EP exchange hole positive for large y, violating the negativity constraint discussed in Sec. 2. Moreover, as previously alluded to, the energy constraint cannot be satisfied for s≳10. This causes the enhancement factor $F_x^{\mathrm{EP}}\left(s\right)$ to violate the local Lieb–Oxford bound. In Fig. 2, we show the PBE enhancement factor and the enhancement factor due to the PBE hole of EP. Clearly, they begin to differ significantly as s gets larger. One consequence is that the exchange energy from the PBE hole model of EP differs non-negligibly from the PBE exchange energy. As mentioned, EP were aware of this difficulty and suggested simply setting s=10 for s>10. We present a somewhat more sophisticated rescaling in the Appendix. However, such rescalings remain unsatisfactory.

Figure 2.

Enhancement factors from PBE and the EP models of the PBE exchange hole.

The divergence of ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}$ for large s, the inability to obtain any solution for H_EP(s) for large s, and the resulting violation of the Lieb–Oxford bound are all due to the EP form of ${\overline{\mathcal{F}}}_{\mathrm{EP}}\left(s\right)$, which for large s tends to infinity. When a rescaled gradient is introduced, ${\overline{\mathcal{F}}}_{\mathrm{EP}}$ remains finite for all s.

Our model proposed below sets out to do two things. First, we desire the GGA hole model to lead to closed-form expressions for range-separated GGAs. Second, we wish the GGA hole model to be well behaved for all s, thereby allowing us to satisfy the energy constraint for all s without rescaling the reduced gradient. With such a model in hand, building exchange holes for different GGAs reduces to parameterizing the numerically defined function H(s), and building range-separated GGAs becomes trivial.

A NEW GGA EXCHANGE HOLE MODEL

Our first concern is to build a non-oscillating LDA exchange hole which takes a similar form to ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}\left(y\right)$ (thus minimizing additional implementation), but whose range-separated energy can be evaluated analytically. We accordingly choose the functional form to be

$${\tilde{J}}_{\mathrm{HJS}}^{\mathrm{LDA}}\left(y\right)=-\frac{9}{4y^4}(1-{\mathrm{e}}^{-\overline{\mathcal{A}}{y}^2})+(\frac{9}{4}\frac{\overline{\mathcal{A}}}{y^2}+\mathcal{B}+\mathcal{C}{y}^2+\mathcal{E}{y}^4){\mathrm{e}}^{-\mathcal{D}{y}^2}.$$ (31)

Comparison with the EP model of Eq. 22 shows that the only difference lies in the manner in which the long-range term goes from $-\frac{9}{4}\overline{\mathcal{A}}{y}^{-2}$ at small y to $-\frac{9}{4}{y}^{-4}$ at large y. We impose the same additional constraints as do EP.⁴¹

Enforcing the on-top constraint of Eq. 5 gives us

$$\mathcal{B}=\frac{9}{4}(\overline{\mathcal{A}}\mathcal{D}-\frac{1}{2}{\overline{\mathcal{A}}}^2)-\frac{1}{2}.$$ (32)

Enforcing the curvature constraint of Eq. 19 yields

$$\mathcal{C}=\frac{1}{10}-\frac{9}{8}\overline{\mathcal{A}}({\mathcal{D}}^2-\frac{1}{3}{\overline{\mathcal{A}}}^2)+\mathcal{B}\mathcal{D}.$$ (33)

Enforcing the normalization integral of Eq. 6 leads to

$$\mathcal{E}=-\frac{2}{5}\mathcal{C}\mathcal{D}-\frac{4}{15}\mathcal{B}{\mathcal{D}}^2-\frac{4}{5}\sqrt{\pi }{\mathcal{D}}^{7∕2}+\frac{6}{5}{\overline{\mathcal{A}}}^{1∕2}{\mathcal{D}}^3(2{\mathcal{D}}^{1∕2}-{\overline{\mathcal{A}}}^{1∕2}).$$ (34)

The other two parameters, $\overline{\mathcal{A}}$ and D, are obtained by imposing the energy constraint of Eq. 7 and maximizing the information entropy. Neither parameter can be solved for analytically. Numerical solutions, however, are perfectly straightforward. Plots of yJ^HEG(y) and various nonoscillating approximations to it are given in Fig. 1. The parameters defining ${\tilde{J}}_{\mathrm{HJS}}^{\mathrm{LDA}}$ are reported in Table 1, along with the parameters defining ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}$.

Table 1.

Parameters in the smoothed LDA exchange hole models of Eqs. 22, 31.

Model	$\overline{\mathcal{A}}$	B	C	D	E
${\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}$	0.451 606	−0.371 708	−0.077 2155	0.577 863	−0.051 955 7
${\tilde{J}}_{\mathrm{HJS}}^{\mathrm{LDA}}$	0.757 211	−0.106 364	−0.118 649	0.609 650	−0.047 796 3

Figure 1 shows that the model of Eq. 31 is similar to the model of EP, though closer inspection reveals that the minimum in $y{\tilde{J}}_{\mathrm{HJS}}^{\mathrm{LDA}}\left(y\right)$ is deeper than that of either $y{\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}\left(y\right)$ or yJ^HEG(y). We do not believe this to be of critical importance, but we do wish to point out that a range-separated LDA based on either ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{LDA}}\left(y\right)$ or ${\tilde{J}}_{\mathrm{HJS}}^{\mathrm{LDA}}\left(y\right)$ will give different results from one based on the HEG.

Having built a nonoscillating LDA model, we proceed to add gradient corrections. Still following the general design of EP, we have

$${\tilde{J}}_{\mathrm{HJS}}^{\mathrm{GGA}}(s,y)=[(\frac{9}{4}\frac{\overline{\mathcal{A}}}{y^2}+\mathcal{B}+\mathcal{C}\overline{\mathcal{F}}\left(s\right)y^2+\mathcal{E}\overline{\mathcal{G}}\left(s\right)y^4){\mathrm{e}}^{-\mathcal{D}{y}^2}-\frac{9}{4y^4}(1-{\mathrm{e}}^{-\overline{\mathcal{A}}{y}^2})]{\mathrm{e}}^{-s^2\mathcal{H}\left(s\right)y^2}.$$ (35)

We part company with EP, however, in writing

$$\overline{\mathcal{F}}\left(s\right)=1-\frac{1}{27\mathcal{C}}\frac{s^2}{1+s^2∕s_0^2}-\frac{1}{2\mathcal{C}}{s}^2\mathcal{H}\left(s\right).$$ (36)

This is similar to the functional form used by Constantin et al. in their meta-GGA exchange hole model of Ref. 25. By forcing $\overline{\mathcal{F}}\left(s\right)$ to be bounded so long as H(s) is bounded, we eliminate the unphysical large-s behavior of ${\tilde{J}}_{\mathrm{EP}}^{\mathrm{GGA}}$ and make it possible to solve for H(s) for all s. This eliminates the need to introduce a computational reduced gradient σ(s). At present, we use s₀=2, but with little compelling reason. Note that, in fact, we could have

$$\overline{\mathcal{F}}\left(s\right)=1-\frac{1}{27\mathcal{C}}{s}^{2}f\left(s\right)-\frac{1}{2\mathcal{C}}{s}^2\mathcal{H}\left(s\right),$$ (37)

for any well-behaved function f(s) satisfying f(0)=1.

We must still solve for $\overline{\mathcal{G}}\left(s\right)$ and give the equation for H(s). To simplify the expressions, it is helpful to write

$$s^2\mathcal{H}\left(s\right)=\zeta ,$$ (38a)

$$\overline{\mathcal{A}}+s^2\mathcal{H}\left(s\right)=\eta ,$$ (38b)

$$\mathcal{D}+s^2\mathcal{H}\left(s\right)=\lambda .$$ (38c)

The normalization integral is then

$$\frac{4}{3\pi }{\int }_0^{\infty }\mathrm{d}y{y}^2{\tilde{J}}_{\mathrm{HJS}}^{\mathrm{GGA}}(s,y)=\frac{3}{\sqrt{\pi }}(\sqrt{\zeta }-\sqrt{\eta })+\frac{5}{4\sqrt{\pi }}\frac{\mathcal{E}\overline{\mathcal{G}}\left(s\right)}{{\lambda }^{7∕2}}+\frac{1}{2\sqrt{\pi }}\frac{\mathcal{C}\overline{\mathcal{F}}\left(s\right)}{{\lambda }^{5∕2}}+\frac{1}{3\sqrt{\pi }}\frac{\mathcal{B}}{{\lambda }^{3∕2}}+\frac{3}{2\sqrt{\pi }}\frac{\overline{\mathcal{A}}}{{\lambda }^{1∕2}}.$$ (39)

Setting this equal to −1 and solving for $\mathcal{E}\overline{\mathcal{G}}\left(s\right)$, we obtain

$$\mathcal{E}\overline{\mathcal{G}}\left(s\right)=-\frac{2}{5}\mathcal{C}\overline{\mathcal{F}}\left(s\right)\lambda -\frac{4}{15}\mathcal{B}{\lambda }^2-\frac{6}{5}\overline{\mathcal{A}}{\lambda }^3-\frac{4}{5}\sqrt{\pi }{\lambda }^{7∕2}-\frac{12}{5}{\lambda }^{7∕2}(\sqrt{\zeta }-\sqrt{\eta }).$$ (40)

The energy integral is

$$-\frac{8}{9}{\int }_0^{\infty }\mathrm{d}yy{\tilde{J}}_{\mathrm{HJS}}^{\mathrm{GGA}}(s,y)=\overline{\mathcal{A}}-\frac{4}{9}\frac{\mathcal{B}}{\lambda }-\frac{4}{9}\frac{\mathcal{C}\overline{\mathcal{F}}\left(s\right)}{{\lambda }^2}-\frac{8}{9}\frac{\mathcal{E}\overline{\mathcal{G}}\left(s\right)}{{\lambda }^3}+\zeta \ln \left(\frac{\zeta }{\lambda }\right)-\eta \ln \left(\frac{\eta }{\lambda }\right).$$ (41)

We set this equal to the target enhancement factor $F_x^{\mathrm{GGA}}\left(s\right)$ and solve for H(s) numerically at each value of s, then fit a rational function to the numerical solution. We find that a rational function of the form

$$\mathcal{H}\left(s\right)=\frac{a_2{s}^2+a_3{s}^3+a_4{s}^4+a_5{s}^5+a_6{s}^6+a_7{s}^7}{1+b_{1}s+b_2{s}^2+b_3{s}^3+b_4{s}^4+b_5{s}^5+b_6{s}^6+b_7{s}^7+b_8{s}^8+b_9{s}^9}$$ (42)

gives uniformly excellent results.

We have parametrized model exchange holes for the PBE, PBEsol,³² B88,³³ and B97-x (Ref. ³⁴) GGAs. The parameters defining H(s) for each functional are listed in Table 2; parametrizing other GGAs is straightforward. Substituting our model into Eq. 29 yields an analytic range-separated enhancement factor,

$$F_x^{\omega \mathrm{PBE}}(s,\omega ,k_F)=\overline{\mathcal{A}}-\frac{4}{9}\frac{\mathcal{B}}{\lambda }(1-\chi )-\frac{4}{9}\frac{\mathcal{C}\overline{\mathcal{F}}\left(s\right)}{{\lambda }^2}(1-\frac{3}{2}\chi +\frac{1}{2}{\chi }^3)-\frac{8}{9}\frac{\mathcal{E}\overline{\mathcal{G}}\left(s\right)}{{\lambda }^3}(1-\frac{15}{8}\chi +\frac{5}{4}{\chi }^3-\frac{3}{8}{\chi }^5)+2\nu (\sqrt{\zeta +{\nu }^2}-\sqrt{\eta +{\nu }^2})+2\zeta \ln \left(\frac{\nu +\sqrt{\zeta +{\nu }^2}}{\nu +\sqrt{\lambda +{\nu }^2}}\right)-2\eta \ln \left(\frac{\nu +\sqrt{\eta +{\nu }^2}}{\nu +\sqrt{\lambda +{\nu }^2}}\right),$$ (43)

where ν=ω∕k_F and

$$\chi =\frac{\nu }{\sqrt{\lambda +{\nu }^2}}.$$ (44)

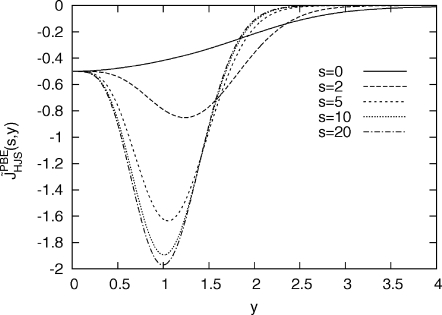
Range-separated hybrids built upon the functionals listed above will be presented in a following paper. In Fig. 3, we show our model for the PBE exchange pair distribution function at various reduced gradients. As the gradient increases, the exchange hole becomes shorter in range and, in order to maintain normalization, deeper.

Table 2.

Parameters in the rational functions defining H(s) for various GGAs.

	PBE	PBE-sol	B88	B97x
a2	0.015 994 1	0.004 733 3	0.009 686 15	0.002 735 5
a3	0.085 299 5	0.040 330 4	−0.024 249 8	0.043 297 0
a4	−0.160 368	−0.057 461 5	0.025 900 9	−0.066 937 9
a5	0.152 645	0.043 539 5	−0.013 660 6	0.069 906 0
a6	−0.097 126 3	−0.021 625 1	0.003 096 06	−0.047 463 5
a7	0.042 206 1	0.006 372 1	−7.325 83×10−5	0.015 309 2
b1	5.333 19	8.520 56	−2.503 56	15.827 9
b2	−12.478 0	−13.988 5	2.796 56	−26.814 5
b3	11.098 8	9.285 83	−1.794 01	17.812 7
b4	−5.110 13	−3.272 87	0.714 888	−5.982 46
b5	1.714 68	0.843 499	−0.165 924	1.254 08
b6	−0.610 380	−0.235 543	0.011 837 9	−0.270 783
b7	0.307 555	0.084 707 4	0.003 780 6	0.091 953 6
b8	−0.077 054 7	−0.017 156 1	−1.579 05×10−4	−0.014 096 0
b9	0.033 484 0	0.005 055 2	1.453 23×10−6	0.004 546 6

Figure 3.

HJS model exchange pair-distribution functions for the PBE GGA at several reduced gradients.

COMPARISON TO OTHER GGA HOLE MODELS

Having now constructed our exchange hole model, we wish to examine its performance and to compare it to previous models. The calculations presented here use the large 6−311++G(3df,3pd) basis set and a development version of the GAUSSIAN electronic structure program.³⁵

EP model

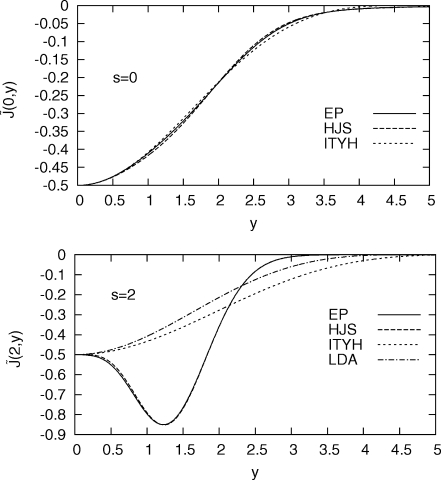
We begin by comparing our model for the PBE exchange hole to that of Ernzerhof and Perdew. As we have followed many of the same principles, we expect that our model will yield very similar results for the exchange hole in practical calculations. This is indeed the case; as seen in Fig. 4, the two exchange holes are almost superimposable for physically realistic reduced gradients (s≲3). Figure 5 shows that our model also yields molecular system- and spherically averaged exchange holes that are essentially identical to EP.⁴² Both our model and the EP model tend to overestimate the amount of exchange energy contained in small interelectronic separations as compared to exact exchange. Preliminary tests on the small AE6 and BH6 sets³⁶ (see below, and Fig. 7) show that our model gives similar results to that of EP in long-range-corrected hybrid functionals. More extensive tests of our model in range-separated hybrids will be reported in subsequent work.

Figure 4.

Model exchange pair-distribution functions for PBE. Top panel. s=0. Bottom panel. s=2. The bottom panel also shows the LDA result (identical to ITYH at s=0).

Figure 5.

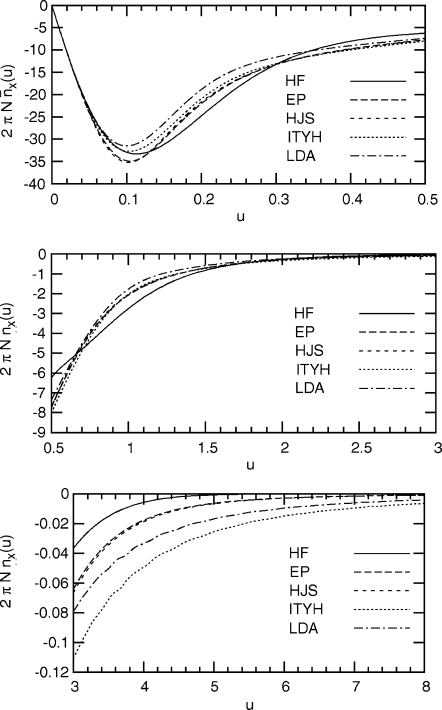
Energy-weighted system- and spherically averaged exchange hole in the Neon atom, from several models. Top panel. Core-dominated region. Middle panel. Core-valence and valence-dominated region. Bottom panel. Tail-dominated region. Note that the HJS and EP curves are essentially superimposable. Note also the Friedel oscillations in the LDA and ITYH curves for large u.

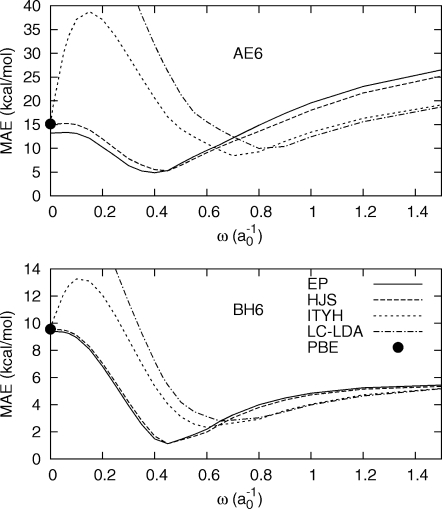
Figure 7.

Mean absolute error (kcal∕mol) in AE6 atomization energies (top) and BH6 reaction barrier heights (bottom) for LC functionals. Details are as in Fig. 6.

ITYH model

Iikura, Tsuneda, Yanai, and Hirao (ITYH) have presented an LDA-based ansatz for the exchange hole corresponding to any semilocal exchange functional.¹⁹ Given an enhancement factor defined as in Eq. 27, the ITYH exchange hole is obtained by substituting a modified Fermi wavevector,

$$k_{\mathrm{ITYH}}=\frac{k_F}{\sqrt{F_x^{\mathrm{GGA}}\left(s\right)}},$$ (45)

into the HEG hole of Eq. 13. The ITYH model possesses an admirable simplicity, and satisfies the on-top condition of Eq. 5 and the energy condition of Eq. 7. However, it violates the normalization constraint of Eq. 6, instead being normalized to $-{\left[F_x^{\mathrm{GGA}}\left(s\right)\right]}^{3∕2}$. (A “complementary” model with the correct normalization and incorrect on-top value was presented in Ref. 37.) The ITYH model also violates the on-top curvature condition of Eq. 25, giving −2μ∕5 for a GGA with $F_x^{\mathrm{GGA}}\left(s\right)=1+\mu s^2+\dots$ . The model is thus too delocalized at finite reduced gradient. To illustrate this, Fig. 4 compares the ITYH, EP, and HJS models for the energy-weighted PBE exchange pair distribution function. While the three models are nearly identical at s=0, the ITYH model is far too delocalized at the physically realistic reduced gradient s=2, and is still quite similar to the LDA exchange hole. Figure 5 illustrates this excessive delocalization for the system- and spherically averaged Neon exchange hole. Though the ITYH model follows the exact exchange curve rather well for small u, it is significantly too delocalized for larger interelectronic separations.

The ITYH model has been extensively applied in constructing range-separated hybrids.^{20, 38} Unfortunately, results to date suggest that it gives relatively poor thermochemistry. For example, an LC-BOP functional with range-separation parameter $\omega =0.53a_0^{-1}$ was recently reported to yield a mean absolute error (MAE) of 8.6 kcal∕mol in the G2 (Ref. ³⁹) ${\Delta }_f{H}_{298}^o$ set (148 molecules).²⁰ A significantly smaller G2 MAE of 3.73 kcal∕mol was reported for the LC-ω PBE functional constructed from the EP hole model.²¹ We suggest that this is a consequence of the ITYH exchange hole’s excessive delocalization at finite s. This can be seen from Fig. 6, which shows the N₂ dissociation energy D_e=E(N₂)−2E(N) evaluated with long-range-corrected⁴³ PBE functionals that use the ITYH, EP, and HJS PBE exchange hole models. Results are also presented for LDA and long-range-corrected LDA exchange. The calculations use Hartree-Fock orbitals, PBE correlation, and the experimental N₂ bond length, such that the only difference between the curves is the short-range exchange energy. Results are plotted as a function of the range-separation parameter ω, with ω=0 (ω=∞) corresponding to 0% (100%) exact exchange. The ITYH model strongly overbinds when exact exchange is included in the very long range $(\omega \sim 0.2a_0^{-1})$. Because the ITYH exchange hole is too delocalized in inhomogeneous systems, replacing its long-range contribution with exact exchange destabilizes inhomogeneous systems and increases atomization energies. The ITYH exchange hole is similar to LDA at short range (cf. Fig. 4), such that the long-range-corrected LDA and ITYH results become similar at large ω.

Figure 6.

N₂ dissociation energy from LC functionals, plotted as a function of the range separation parameter ω. Results are presented for LDA and for the EP, HJS, and ITYH models for the PBE exchange hole.

Figure 7 shows MAE (kcal∕mol) in the small, representative AE6 set of atomization energies and BH6 set of reaction barrier heights³⁶ for LC-PBE with the ITYH, EP, and HJS PBE hole models, evaluated as a function of ω.⁴⁴ Results are also presented for a long-range-corrected functional using LDA exchange and PBE correlation. Again, the excessive delocalization of the ITYH model yields significant overbinding at small ω, and results that are rather similar to LC-LDA for moderate ω. These results indicate that our GGA exchange hole model provides nontrivial improvements to the simple model of ITYH.

CONCLUSIONS

Semilocal DFT models for the exchange hole have a great deal of formal and practical value. They provide insight into the successes and failures of approximate exchange-correlation functionals: for example, the surprising accuracy of LDA has been attributed to the exact constraints satisfied by its exchange-correlation hole.⁴⁰ They also provide routes to constructing new approximations, such as range-separated hybrid functionals. In this work, we have illustrated what we believe to be important formal and computational difficulties with some popular exchange hole models. We have presented a new general-purpose GGA exchange hole model that is particularly designed for use in range-separated hybrid functionals. Changing from one GGA to another merely requires one to adjust the parameters defining a component function H(s), and the range-separated exchange energy using erf(ωr₁₂) to separate ranges can be evaluated analytically. We believe that this model will be useful for continued investigation of the exchange hole in density functional theory.

APPENDIX: RESCALED REDUCED DENSITY GRADIENTS

As discussed in Sec. 4, the EP model exchange hole violates the local Lieb–Oxford bound for reduced gradients s≳10. Ernzerhof and Perdew fixed this by setting s=10 for s>10, while Ref. 15 used a different scheme to enforce the local Lieb–Oxford bound. Other schemes have also been proposed. These schemes amount to introducing a computational reduced gradient σ(s). To the best of the authors’ knowledge, it has not been noticed that one can uniquely define σ(s) by writing

$$F_x^{\mathrm{EP}}\left(\sigma \left(s\right)\right)=F_x^{\mathrm{PBE}}\left(s\right).$$ (A1)

We fit the resulting σ(s) as

$$\sigma \left(s\right)=s\frac{1+p_4{s}^4+p_5{s}^5+p_6{s}^6+q_8{s}_0{s}^7}{1+q_4{s}^4+q_5{s}^5+q_6{s}^6+q_7{s}^7+q_8{s}^8}$$ (A2)

with parameters for the PBE hole given by s₀=8.572 844, p₄=0.615 482, p₅=1.136 921, p₆=−0.449 154, q₄=1.229 195,q₅=−0.026 925 3, q₆=0.313 417, q₇=−0.050 831 4, and q₈=0.017 573 9. The effect of this computational gradient is to keep $\overline{\mathcal{F}}\left(s\right)$ finite, and therefore the exchange hole negative semidefinite and bounded from below.

Note that different GGAs based on the EP form lead to different computational reduced gradients σ(s). We emphasize that while introducing a computational gradient resolves some difficulties, it is not a panacea. The integrations required to build range-separated hybrids still cannot be done in closed form, functional derivatives become more complicated, and σ(s) must be reparametrized for every GGA.