Volumetric restrictions in single particle 3DEM reconstruction

Abstract

3D electron microsscopy aims at the reconstruction of density volumes corresponding to the electrostatic potential distribution of macro-molecules. There are many factors limiting the resolution achievable when this technique is applied to biological macromolecules: microscope imperfections, molecule flexibility, lack of projections from certain directions, unknown angular distribution, noise, etc. In this communication we explore the quality gain in the reconstruction by including a priori knowledge such as particle symmetry, occupied volume, known surface relief, density nonnegativity and similarity to a known volume in order to improve the quality of the reconstruction. If the reconstruction is represented as a series expansion, such constraints can be expressed by set of equations that the expansion coefficients must satisfy. In this work, these equation sets are specified and combined in a novel way with the ART + blobs reconstruction algorithm. The effect of each one on the reconstruction of a realistic phantom is explored. Finally, the application of these restrictions to 3D reconstructions from experimental data are studied.

1. Introduction

3D electron microscopy (3DEM) is a powerful technique for structural studies of biological macromolecules due to the wide range of specimens that can be addressed. One of the biggest challenges in 3DEM lies in the area of “single particles” (specimens with low or no symmetry) where results worse than 6 Å resolution seem to be the best currently achievable [1–6]. Therefore, there are ongoing research activities to identify the limitations of the current methodologies and to introduce improvements in the experimental and computational procedures. One of these is the investigation of how one can introduce a priori information about the specimen to restrict the possible set of solutions and, thus, increase the reconstruction quality.

For example, Zheng et al. [7] studied the incorporation of several a priori constraints into the estimation of the autocorrelation function of the 3D structure of crystallized virus capsids. They translated constraints with physical meaning such as icosahedral symmetry, bounded support (the virus was assumed to fit within a known spherical shell) and nonnegativity into information used during interpolation in Fourier space. Two technical constraints were also considered: real-valuedness (the autocorrelation of a real function is real-valued) and invertibility (the autocorrelation of a real function is even). They performed the constrained interpolation by expanding the autocorrelation function into a series of icosahedral harmonics. However, this approach cannot be directly applied to single particles in 3DEM. First of all, the interpolation is for the autocorrelation function and not for the particle volume. Further, the support constraint assumed that the virus capsid was fully contained in a spherical shell, rather than a general mask, potentially representing a surface relief more accurately. Finally, micrographs of crystallized specimen yield relatively clean Fourier images and, therefore, interpolation can be carried out safely. This is not the case in single particle 3DEM, where the signal-to-noise ratio may be as low as $\frac{1}{3}$.

In this work, we propose the incorporation of a priori information into the ART + blobs process [8] in a nonlinear and adaptive way. Particularly, support (with complicated surface reliefs), density nonnegativity, total mass, similarity to a known volume and symmetry are considered. This kind of a priori constraints are easily expressed in real space. In this way, starting from the well-known ART reconstruction algorithm, we have defined a new constrained reconstruction algorithm incorporating a priori information. ART is a linear equation solving algorithm that treats the tomographic problem as a feasibility problem, i.e., finding a volume that is feasible considering that it must be near to all the hyperplanes defined by each of the projection pixels. In this work, we show how to solve the constrained tomographic problem in the same mathematical framework using a very simple modification of the tomographic equation set. Alternatively, the constrained tomographic problem might have been expressed as a series of feasibility problems associated with each of the constraints, as has been previously presented in the context of Projection Onto Convex Sets (POCS) by Carazo [9], Sezan and Stark [10], Stark and Peng [11] and Yeh and Stark [12]. Note, however, that the method proposed here allows for the incorporation of nonconvex constraints (like total mass), extending in this way previous works. Another difference with the previous POCS approach is that in the proposed algorithm the constraints are applied while the volume is being reconstructed instead of waiting to the end of the reconstruction step.

2. Materials and methods

Block-ART with blobs [8] is a series-expansion reconstruction algorithm that assumes that the volume to be reconstructed f (r) (r ∈ ℝ³ is the point at which the volume is evaluated) can be expressed as a linear combination of a set of basis functions obtained by shifting a fixed function b(r) to fixed points r_j ∈ ℝ³ in space. The set of fixed points is called a grid and they can be obtained as r_j = gz_j, where the z_j come from a subset of ℤ³. For this work a generalized Kaiser–Bessel window function (also known as blob) [13] has been used as the b(r), and

$$f(\mathbf{r})={\displaystyle \sum _{j=1}^J{x}_j·b(\mathbf{r}-{\mathbf{r}}_j).}$$ (1)

Both, the blob’s shape and the grid are fixed and the unknowns are the coefficients x_j. Given this volume representation it is easy to calculate the ideal projection (line integrals along lines perpendicular to the projection plane). This is because the integration can be brought inside the summation and can be analytically evaluated for the known blob b and the grid point r_j. In this way, the projection can be simply calculated as a weighted sum over the blob coefficients x_j. If the projection direction is specified by a vector $\overrightarrow{\omega }\in S^2$ (S² is the unit sphere in ℝ³), and ψ is the in-plane rotation, then the projection operation can be written in a matrix form as

$$\mathbf{y}\overrightarrow{\omega },\psi =P_{\overrightarrow{\omega },\psi }\mathbf{x},$$ (2)

where ${\mathbf{y}}_{\overrightarrow{\omega },\psi }$, is a vector formed by all the pixel values of the experimental projection in the direction $\overrightarrow{\omega }$ and with an in-plane rotation $\psi ,P_{\overrightarrow{\omega },\psi }$ is the projection matrix and x is the vector of all blob coefficients. The (i, j)th element of the matrix $P_{\overrightarrow{\omega },\psi }$ represents the projection of the blob j onto the pixel i. Therefore, this matrix has as many columns as there are blobs in the volume, and as many rows as there are pixels in the projection. When several projections are available, then all pixel values are stacked in a single vector, y, and the projection operator becomes a block matrix, P, whose blocks are the $P_{\overrightarrow{\omega },\psi }$ previously introduced. Finally, the experimental projection set poses an equation system described by

$$\mathbf{y}=P\mathbf{x}.$$ (3)

In this paper we discuss, in addition to Eq. (3) that arise from measurements, additional equations that arise from prior knowledge. Such prior knowledge will be of the form that f (r) has values at particular points r ∈ ℝ³ that are similar to given values. Typically, such points form the whole or a subset of a simple cubic grid over ℝ³ (i.e., a set of voxel centers). Using (1), this leads to additional equations of the form

$$\mathbf{w}=V\mathbf{x},$$ (4)

in which the ith equation expresses the fact that the reconstructed volume should have a value similar to w_i at a point r (the entries in the matrix V in the ith row are of the form b(r – r_j), for j = 1, … , J).

We solve such equation systems using a variant of block-ART [14]. This algorithm produces a sequence of iterates ${\{{\mathbf{x}}^{(n)}\}}_{n=0}^{\infty }$, each one defining a volume using our volume representation.

A decision that one has to make is the choice of the initial vector x⁽⁰⁾. It is known that ART-type reconstruction algorithms tend to minimize the distance from the initial vector x⁽⁰⁾ while searching for a solution of Eq. (3) [15]. Usually a zero-valued initial vector is provided as the starting point to the iterative algorithm. This initial guess expresses our uncertainty about the correct reconstructed volume and tends to minimize the variance of the resulting reconstruction. However, there are many situations where a reasonable approximation to the desired reconstruction is available at voxel centers. This approximation can be used as starting point for the ART iterations. This was already done in Ref. [15]. However, our volumes are expressed in blobs and some translation is needed to convert a voxel volume approximation into a blob volume. To obtain x⁽⁰⁾ we make use of Eq. (1). Each of the values of f (r) at a voxel center r provides us with a single instance of this equation, and the collection for all the voxel centers will result in a system of equations, as in Eq. (4), which can then be solved to obtain x⁽⁰⁾. Below we report on results using both of the above-mentioned choices for x⁽⁰⁾.

Having chosen x⁽⁰⁾, each iterate is calculated after presenting a subset (block) of the equation system (3) to the algorithm by

$${\tilde{x}}_j^{(n)}=x_j^{(n)}+\frac{\lambda }{N_j^{(n)}}{\displaystyle \sum _{l\in K_j^{(n)}}\frac{y_l-\langle {\mathbf{p}}_l,{\mathbf{x}}^{(n)}\rangle }{{\Vert {\mathbf{p}}_l\Vert }^2}}{\mathbf{p}}_{l,j},$$ (5)

where x⁽ⁿ⁾ represents the vector x at iteration n and $x_j^{(n)}$ its jth element, p_l is the transpose of the lth row of P, $K_j^{(n)}$ is the set of row indices within the block considered at iteration n such that the (l, j)th element of P is not null, $N_j^{(n)}$ is the cardinality of $K_j^{(n)}$ (in practice, it is never zero), λ is a relaxation factor, y_l is the lth measurement and ${\tilde{x}}_j^{(n)}$ is the jth element of an auxiliary vector representing a volume in blobs.

Without taking into consideration additional constraints on the volume to be reconstructed, x̃⁽ⁿ⁾ would in fact be taken as the next iterate. The subject matter of our paper is the introduction of volumetric restrictions into the iterative process. This is done by making use of Eq. (4), obtained as follows. Each volumetric constraint that we discuss below gives rise to a subset Ω of the set of voxel centers and a value w, both of which may depend on x̃⁽ⁿ⁾. The collection of such constraints will give rise to a system of equations (4), in the manner discussed above (4), which is then treated as a single block of additional equations to obtain x⁽ⁿ⁺¹⁾ by a single application of a step, as in Eq. (5), to x̃⁽ⁿ⁾. (We remark that this way of proceeding is a bit of an overkill: the constraints (4) are repeatedly applied after every use of a single block of data. It is a reasonable alternative to apply the constraints (4) only after all the equation in Eq. (3) have been treated; and we indeed report below that this alternate way of proceeding usually does not make a significant difference, although there is a single exception to this.)

We now discuss how prior constraints such as surface relief, symmetry, density nonnegativity and total mass can be expressed using this approach. In any application, one can use all, or some, or none of these constraints; the experiments reported below will illustrate this.

2.1. Surface relief

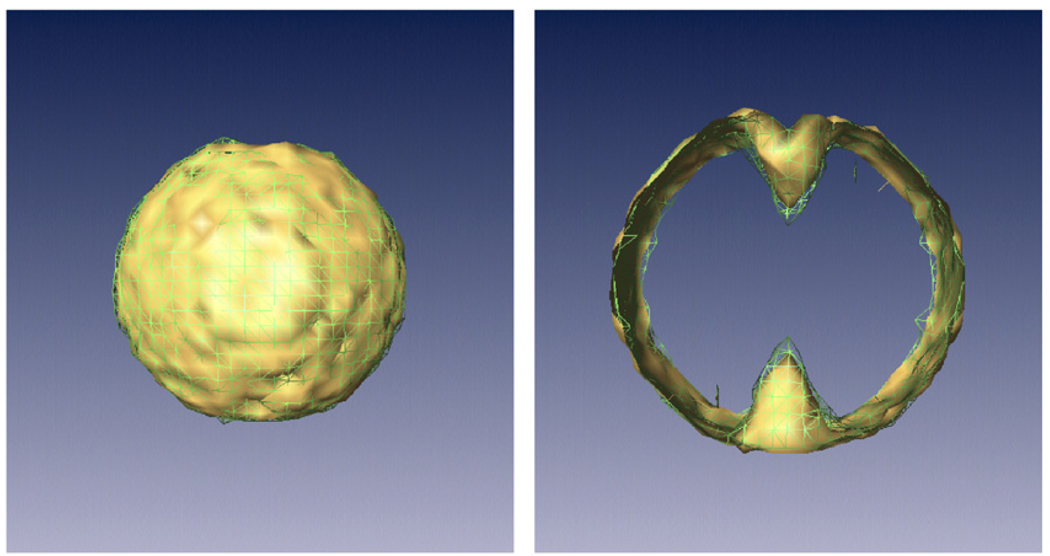
There exist experimental microscopy techniques that produce an image of the surface of a protein, such as metal shadowing [16] or atomic force microscopy [17]. Such surface information can be used to produce a mask, outside which the volume should be zero-valued (see Fig. 1). Furthermore, such a mask can also be obtained by application to x̃⁽ⁿ⁾, for selected n’s, nonlinear image processing methods such as thresholding, segmentation, connected component extraction and mathematical morphology [18]. Such information is modeled by setting w_i to 0 for those voxel centers r_i that are not within the mask.

Fig. 1.

Top: example of surface constraint: outside the mask shown, the volume must be zero-valued. Bottom: During the reconstruction, this knowledge translates into a new equation set that the blob coefficients must also satisfy. At each point outside the mask, the sum of all the blobs must be zero.

2.2. Symmetry

The classical way of imposing symmetry in a 3DEM reconstruction is either by symmetrizing the output volume at the end of the reconstruction process or by replicating the experimental projections with different angular assignments. However, volumetric constraints allow us to impose symmetry during the reconstruction process itself. In this case, Ω is the set of all voxel centers and, for any voxel center r_i, w_i is the estimated average of the f (r) values that are provided by x̃⁽ⁿ⁾ at all those points r that are symmetrically related to r_i.

2.3. Total mass

Experimentalists can determine the molecular weight of the complex under study via biochemical experiments or some estimation based on the protein aminoacid-sequence length and composition. Given the image sampling rate, this weight can easily be translated into an estimated number of voxels that the reconstructed volume should occupy, i.e., the number of voxels that are not zero-valued is fixed by the mass of the particle. In fact, this is the most used criterion in the field for segmenting reconstructions. Let us define t be the threshold such that the total mass of the voxels centered at r_i, whose value f (r_i) based on x̃⁽ⁿ⁾ is not less than t, is the desired mass m. This leads to constraints given by w_i = 0 at voxel centers r_i in Ω_mass = {r_i: f (r_i) < t} and $c\overline{({\Omega }_{\mathit{\text{mass}}})}=m$, where c(A) is the cardinality of the set A, and A̅ is the complement of A.

2.4. Density nonnegativity

In principle, the reconstructed volume corresponds to an electrostatic potential density estimate of the protein under study. Image normalization procedures guarantee that the volume density at all points should be nonnegative if there were no aberration introduced by the microscope [19]. However, the contrast transfer function (CTF) of the microscope introduces contrast modulations changing the sign of the Fourier transform at specific frequencies. Therefore, in the absence of ideal CTF-correction, the density nonnegativity would only be an approximate constraint. Still, the results presented in Ref. [19] and the ones in this work indicate that in spite of the practical violation of this constraint, the final result gets better when this constraint is imposed. Furthermore, since a large amount of noise is present in the experimental projections, it may turn out that, even with ideal normalizations and CTF corrections, for certain positions r, the f (r) that corresponds to x̃⁽ⁿ⁾ has negative values. To force these negative values towards zero, we use w_i = 0 for the voxel centers r_i in the set Ω_nonneg = {r_i: f (r_i) < 0}, and introduce the corresponding equation into Eq. (4).

3. Results

To test the efficacy of the proposed constraints, experiments were carried out. The first set of experiments explored all constraints independently to check the utility of each one. Then, these constraints were tested on the reconstruction of the DnaB–DnaC complex [20].

3.1. Application to simulated data

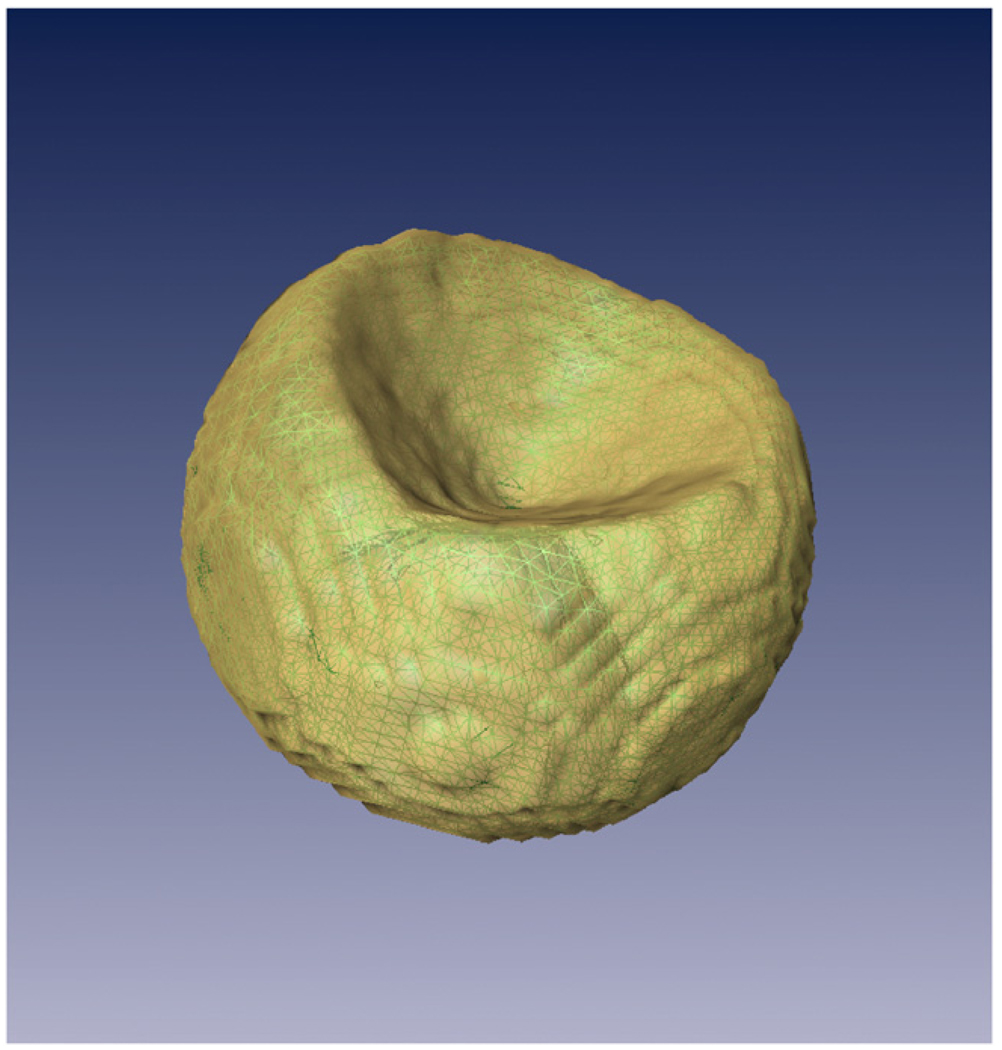
In order to quantitatively assess the utility of each restriction, simulation experiments were carried out. We started from a realistic phantom based on the protein data base (PDB) entry 1BRD, namely the bacteriorhodopsin [21], see Fig. 2. Projections were taken from this phantom and Gaussian white noise was added to the projections. Furthermore, noise was added to the Euler angles describing the projection direction and the projection center was shifted randomly. Then the reconstruction algorithm with the constraint under study was applied. To compute the number of iterations we followed the strategy proposed by Marabini et al. [8] and Sorzano et al. [22]. Finally, the reconstructed volume was compared with the phantom using objective figures of merit (FOM). The analysis of these numerical observers helped us to assess the utility of each one of the constraints. We performed three different experiments with this protein. In the first and second, the capability of the volumetric constraints to improve the reconstruction quality was explored with a medium (1000) and a large number of images (10,000). In the third experiment, volumetric constraints were applied to a single axis tomography problem as a possible way to fill information within the missing wedge. In the first two cases, the algorithm was stopped after cycling through the data exactly once, for the third case 500 iterative steps were used.

Fig. 2.

Isosurface containing 100% of the bacteriorhodopsin mass for the atomic phantom from PDB.

3.1.1. Experiment with a medium number of images

A thousand projection images were simulated from an atomic model of bacteriorhodopsin whose resolution was lowered down to 7 Å. The collection geometry was randomly chosen (uniform distribution in all angles) with a maximum tilt angle of 60°. Noise was added to obtain a signal-to-noise ratio of $\frac{1}{3}$. A random number with a Gaussian distribution with zero mean and standard deviation equal to 5° was added to each one of the three Euler angles. The projection center was shifted randomly in X and Y directions with zero mean and a standard deviation of 2 pixels. The relaxation factor of ART was optimized for this data collection geometry following Ref. [22] and its optimal region was found to be between 0.05 and 0.07. For this reason, the relaxation parameter was picked randomly from this interval for each one of the reconstructions performed. (The same relaxation parameter was used when dealing with a block of Eq. (3) and when dealing with the constraints (4).)

We compared the benefits obtained by each constraint independently and with all restrictions applied at the same time. For our pixel size (3.5 Å/pixel), 100% of the bacteriorhodopsin occupied 26,000 voxels, so the total volume of the reconstruction, when the total volume restriction was applied, was limited to 40,000 voxels. The surface for the support constraint was computed by dilating the surface enclosing the 100% of the mass of the bacteriorhodopsin phantom with a 2 × 2 × 2 cube as structuring element. This surface limited the number of voxels to 48,000 (note that when the surface constraint is used in combination with the total mass constraint only the 40,000 voxels within the known surface with highest values are left). The phantom was filtered to 40 Å and this volume was provided as the starting point to ART when similarity to known volume was considered. The symmetry constraint imposed a 3-fold symmetry around a rotational axis passing through the center of the channel formed by the seven monomers.

Thirty reconstructions with each of these constraints were performed. We measured the correlation between the reconstruction and the phantom. Fig. 3 represents the correlation values obtained for each constraint. These values were statistically different from each other with a confidence of 99%. The average resolution (measured by Fourier shell correlation (FSC) [23, Chapter 5] at a threshold of 0.5) of the 30 reconstruction without constraints is 24.85 ± 0.88 and for the 30 reconstructions with all constraints 18.27 ± 0.42 (the difference in resolution is significant with a confidence higher than 99%). This resolution estimation was performed comparing the reconstructed volume to the bacteriorhodopsin phantom.

Fig. 3.

Plot of the dependence of the correlation between the reconstruction and the phantom for different sets of constraints. The plotted line is a square distance fit to the data as described in Ref. [29].

Since similarity to a known volume seems to be the most informative a priori information, we performed an extra experiment to test how much the results in Fig. 3 depend on the quality of the initial volume. White, Gaussian noise with zero mean and standard deviation σ was added to the phantom volume before filtering it to 40 Å. While σ was below 0.2, the results applying similarity to known volume were similar to the ones when the noiseless filtered phantom was supplied (see Fig. 3). With increasing σ the results deteriorated. At σ= 0.3, the results were similar to the results of “All but similarity” in Fig. 3. At σ= 0.4 and 0.5, the results were similar to the ones with symmetry constraints. Finally, at σ= 0.6, supplying an initial noisy volume was comparable to using a surface constraint.

We further tested the applicability of the volumetric constraints when a CTF is present. The following CTF parameters were used: sampling rate = 3.5 Å/pixel, accelerating voltage = 200 kV, defocus = −6000 Å, spherical aberration coefficient = 20mm, chromatic aberration coefficient = 6.44mm, energy loss = 0.024, longitudinal displacement = 21.3, traversal displacement = 3.77 and fraction of multiply scattered electrons=0.36 [24]. When all constraints but similarity were applied, the achieved resolution in the 30 experiments was 22.4 ± 0.64 Å, while the resolution when no constraint was used was 32.3 ± 1.13 Å. The rest of the results for the constraints alone were 28.0 Å when the initial volume was provided or symmetry constraints were used, 29.9 Å for the mass constraint and 31.0 Å for the nonnegativity constraint. The resolution achieved when any of these constraints was used was significantly different from the case where no constraints were used. However, the resolution achieved by the surface constraint (32.1 Å) was not significantly different from the case with no constraint. It is interesting to note that there was no statistical difference between applying the symmetry via volumetric constraints or via considering the same projections from symmetric projection directions.

As it has been previously commented, the CTF introduces sign changes in the images that invalidates the strict application of nonnegative constraints. However, the application of this constraint has been shown in the previous paragraph and in Ref. [19] to still produce better reconstructions with statistical significance. The first zero of the CTF was at 12.54 Å. To check to what extent a correction for the CTF could improve the results, images were CTF-corrected by phase flipping. However, no significant change was observed in the final reconstructions, except if, additionally, the symmetry constraint was applied, in which case the resolution was marginally, but significantly, improved by 2 Å with respect to the reconstruction performed with symmetry constraint but no CTF correction. We observed no statistical difference between applying symmetry as a volumetric constraint and applying symmetry simply by repeating the experimental views with their symmetric equivalent angles.

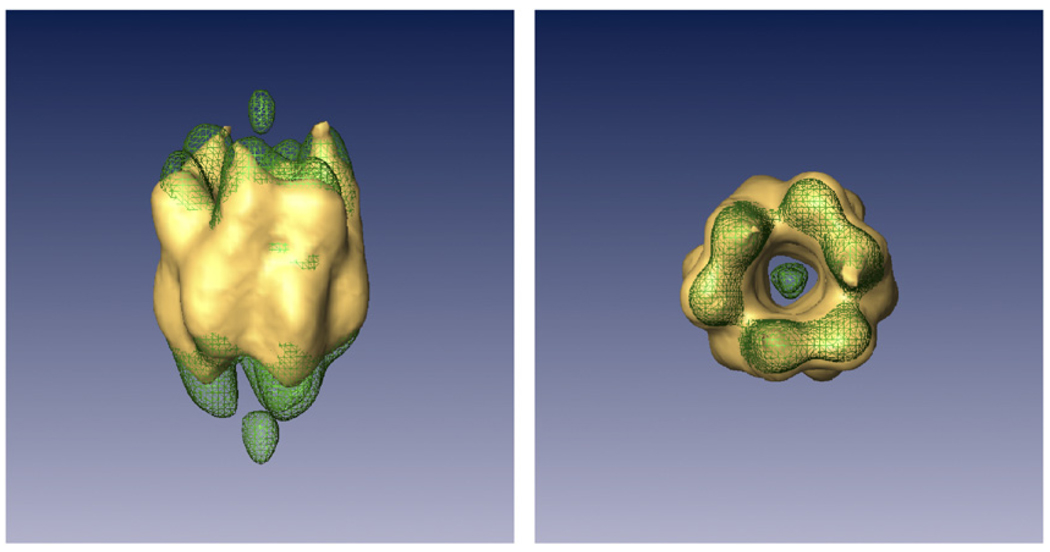
In the previous experiments, for each reconstruction with each constraint a new set of projections with a different noise realization was generated. In order to compare results when the different constraints were applied to the same projection set, reconstructions were performed applying the different constraints to the same projection data. Fig. 4 shows the resulting volumes without constraints and with all the constraints except similarity, which is less likely to be available in an experimental setup. Fig. 5 represents the achieved resolution (measured by FSC with the bacteriorhodopsin phantom) when every constraint is applied separately, when none is applied and when all are applied. This experiment was repeated several times observing always the same behavior. The improvement in resolution is about 7 Å (from 26 to 19 Å) in the example shown. Fig. 6 shows the volumetric spectral signal-to-noise ratio (VSSNR) [25] for the reconstruction performed without constraints and the reconstruction performed with all constraints except similarity to a known volume. The VSSNR is a volume in Fourier space that estimates the signal-to-noise ratio for each frequency. It can be seen that the reconstruction performed with the volumetric constraints is better than reconstruction without constraints in most directions. This is especially important in the missing cone where the improvement goes from 37.3 to 28 Å.

Fig. 4.

Different views of the isosurface containing 100% of the bacteriorhodopsin mass for the volume reconstructed without constraints (solid) and with all volumetric constraints but similarity (wire).

Fig. 5.

Fourier shell correlation of the reconstructions obtained after applying the different constraints.

Fig. 6.

Left: isosurface of the VSSNR at SSNR = 1 of the reconstruction performed without constraints (wire) and the reconstruction with volumetric constraints (all constraints but similarity) (solid). It can be seen that the one with constraints outperforms the one without constraints at most directions in Fourier space. Right: we have removed some of the rendered planes of the VSSNR to better show that the improvement is larger in the missing cone where the reconstruction without constraints has a vertical-direction resolution of 37.3 Å, while the reconstruction with constraints has a resolution of 28Å. The VSSNR of the reconstruction without constraints is now represented by the wireframe, and the VSSNR of the reconstruction with all constraints but similarity is solid.

Finally, we checked the reconstruction improvement obtained by imposing the volumetric constraints during the reconstruction process as proposed in this article and the improvement obtained by simply imposing them at the end of the reconstruction when they are applicable (for instance, the similarity to a known volume cannot be applied at the end of the reconstruction). The experimental setup is identical to the one that has been introduced so far. We did not observe significant differences between applying them at the end of the reconstruction process or during the reconstruction process for this medium-sized problem, except for the case of the surface constraint for which a resolution increase of 10% was observed when applying the constraints repeatedly rather than just at the end. However, as already demonstrated, there is a big difference between applying each of the volumetric constraints and not applying it (either during the reconstruction process or at its end).

3.1.2. Experiment with a large number of images

We explored the effect of the volumetric constraints when a large number of views were used. Ten thousands images were used with the same experimental setup as for the medium-size experiment described above. The experiment was repeated 30 times changing the realization of the noise added to the images and the realization of the collection geometry (uniform distribution in all angles with a maximum tilt of 60°). No CTF was considered in this case. The average resolution of the reconstructions without constraints was 23.00±0.96 Å. There was no significant difference between applying all constraints (including the initial volume) or applying all constraints but the initial volume. In the same way, there was no significant difference between applying no constraint and applying the symmetry or mass constraints or supplying an initial volume. Therefore, the only two conditions that seemed to be informative in this case were the surface constraint and nonnegativity which increased the resolution achieved to 20.00 ± 0.50 Å. The average resolution with all constraints was 17.60±0.38 Å. Thus, it seems that although individual constraints may not add extra information, there is a synergistic interaction when all of them are applied at the same time.

3.1.3. Experiment with a small number of images

In order to elucidate if this behavior was maintained even with a small number of projections we conducted the following experiment. Sixty-one images were taken every 2° simulating a single-axis tilt series with a maximum angle of ±60°. No noise was added either to the Euler angles or the particle center. The reconstruction algorithm was run 500 iterations with and without nonnegativity constraint (one of the constraints for which it seemed not to be any difference between applying it during the process or at the end of the process). We observed a general increase of about 6% of the FSC value at all frequencies.

3.2. Application to experimental data

We also applied our volumetric constraints to experimental data. In particular, we performed the reconstruction of the DnaB–DnaC complex with the same images as used by Barcena et al. [20]. Since the true volume was unknown, we performed a constrained reconstruction with all the images whose tilt angle was smaller than 45° (that we will refer to as the limited-angle image set). This yielded a total of 4182 out of 6995 images. The sampling rate was 3.5 Å, and images were of size 81 × 81 pixels. Images were normalized in such a way that the background (defined by a surrounding circle of radius 40 pixels) had 0 mean and standard deviation 1. The properties of this normalization procedure are reported by Sorzano et al. [19] and they correspond to the same conditions used with the simulated data sets. We imposed the mass of the reconstruction to be at most $\frac{5}{3}$ of the known mass of the complex (this threshold has been arbitrarily chosen so as to generously constrain the volume). The molecule surface was computed by nonlinear image processing on the reconstruction obtained from the limited-angle image set without constraints: this reconstruction was thresholded to hold 110% of the known mass; then, a rough approximation of the molecular surface was built by dilating the biggest connected component of the binary volume with a cube of size 2 × 2 × 2 voxels as the structural element [26].

The reconstruction obtained applying the symmetry, total mass, nonnegativity and surface constraints on the limited-angle image set as well as the reconstruction obtained from the same data set without constraints were compared to the reconstruction obtained with the full image set without constraints (see Fig. 7). Fig. 8 shows the corresponding FSCs when each reconstruction (unconstrained and constrained) is compared to the reconstruction carried out using the full data set (with all the images available and not only with those whose tilt angle was smaller than 45°). To perform a fair comparison, all volumes were masked (using the same mask) prior to computing the FSC; this explains why the FSC never drops below 0.5 and the deep minimum shown at middle frequencies. The mask used was extracted by dilation (with a cube 2×2×2) of the biggest connected component of the volume reconstructed from the full data set without constraints, thresholded to hold 110% of the known mass. This mask is necessarily a hard mask since the surface constraint applied during the reconstruction process is rather tight (3 or 4 voxels away from the reconstructed volume) and is applied in a hard way in the equation system as already shown. Fig. 9 shows the corresponding VSSNR of both reconstructions. Again, we see a noticeable increase of the FSC values as well as the VSSNR.

Fig. 7.

Isosurface containing 66% of the DnaBC mass for the volume reconstructed without constraints (wire) and with all volumetric constraints but similarity (solid). The vertical elongation due to the 45° missing cone is very pronounced. The threshold of 66% of the mass was chosen to concentrate the attention on the most central part of the structure with higher density values.

Fig. 8.

Fourier shell correlation of the reconstruction of the DnaB–DnaC complex from a limited-angle image set using and not using volumetric constraints.

Fig. 9.

Isosurface of the VSSNR at SSNR = 1 of the reconstruction performed without constraints (solid) and the reconstruction with volumetric constraints (wire).

4. Discussion

In this paper we explored how to restrict the set of possible solutions of the tomography problem by imposing extra conditions on the reconstruction in the specific case of 3DEM using ART+blob as the reconstruction algorithm. Several restrictions, not necessarily convex, have been considered: symmetry, total volume, similarity, nonnegativity and support constraint; these share the property of being easily expressed in real space. This is the first time that this kind of constraints are combined with methods using blobs as expansion basis. Blobs, by themselves, incorporate the a priori information of smoothness and continuity. A very pragmatic approach has been followed throughout this work in terms of justifying the theoretical goodness of applying some of these constraints. In general, for the case of nonconvex constraints, there is no mathematical proof of convergence of the algorithm. However, it is to be noted that even using convex constraints related to projection matching, which are at the core of ART, the presence of noise in the data may preclude the intersection set from being nonempty, which is a prerequisite in POCS-based methods [9–12,27]. The application of nonnegativity may be more controversial since even if our results do show that, in general, it has a positive effect, the practical use of the microscope with its associated image degradation by the CTF makes the use of this constraint a kind of compromise. Finally, it is to be noted that in all cases the reconstruction algorithms are stopped at a relatively early stage. This is so because strong noise may dominate the outcome of long iterative procedures that in many cases tend to be related to some form of least-squares solution.

The constraints are supposed to be especially useful in those situations where projections alone fail to provide enough information to achieve a high resolution reconstruction; for instance, for those data collection geometries that do not fully cover the Fourier space. This is confirmed by the VSSNR volumes in which it can be seen that the missing cone is partially filled and that, in general, the resolution of the constrained reconstruction is better than that of the unconstrained one in most directions. Although there is a general improvement as measured by all FOM, no drastic changes should be expected. This is specially true for medium–low resolution experiments. As the quality of the data improves, more important gains should be expected as is the case for solvent-flattening in crystallography [28].

The simulations carried out show that the total volume and the surface constraints are close to each other in terms of the amount of information supplied to the algorithm. In fact, the amount of information supplied by these two constraints depend on how accurate these restrictions are with respect to the macromolecule. In our experiments it has been considered that in experimental situations there exists uncertainty about the exact number of voxels occupied by the reconstruction or about the exact shape of its surface and we have supplied generous constraints.

Simulation experiments show that nonnegativity is a restriction whose improvement is not highly reflected by global FOMs although its effect is clearly seen in the FSC (see Fig. 5) specially at medium–high frequencies. Nonnegativity is a constraint that, in principle, should not be directly applied to experimental EM images which suffer from degradation due to CTF, since this function inverts the sign of the Fourier transform of images at certain frequencies. However, previous experiments [19] as well as the ones carried out in this paper show that nonnegativity can help to achieve better resolution even if the images are corrupted by the CTF. Some researchers consider that nonnegativity can be safely applied if the CTF of the experimental images is phase corrected, although it is not guaranteed that such corrected spectrum necessarily conforms to nonnegativity.

In our experiments, the resolution achieved by applying non-negativity was not statistically significantly different when the phase was corrected and when it was not. Furthermore, in both cases the application of the nonnegativity constraint implied an improvement in resolution with respect to the not constrained situation.

Symmetry is a restriction that, as expected, may be very little or very much informative depending on the symmetry elements used and the lack of angular coverage present. In the reconstruction of the bacteriorhodopsin, the symmetry constraint was not adding much information since the symmetry axis was aligned with the missing cone. Most of the improvement in that experiment reflected by global FOMs were due to the suppression of noise, not by a better agreement of the reconstruction with the phantom.

Similarity to a known volume is a very powerful tool. In our simulations we provided volumes that were filtered to 40 Å, while the resolution achieved by applying no constraints was 26 Å. Similarity to known volume alone strongly improves the correlation at low frequencies as well as global FOMs, but when it is combined with the rest of restrictions an important boost of the correlation at most frequencies, and therefore of the resolution achieved, is seen.

The application of all these constraints during the reconstruction process or applying it simply at the end once the reconstruction obtained seems not to make any difference except for the surface constraint in which case an increase of the resolution of a 10% has been observed due to repeated application. This is an important issue since it would be validating common practice in which these constraints are not applied during the reconstruction but at the end of the reconstruction. This fact would save a lot of computing time since the application of the volumetric constraints within the reconstruction process significantly slows down the ART + blobs algorithm due to the frequent blob to voxel conversion needed by the constraints. As has already been mentioned, the surface constraint is more or less informative depending on the faithfulness of these constraint, the number of images available and their orientations with respect to the surface.

The reconstructions from experimental data showed that these constraints can be successfully applied to a real case. The FSC showed that the constrained reconstruction correlated better to the full-coverage reconstruction than the unconstrained reconstruction. This was confirmed by the VSSNR where a general improvement in all directions, not only in the missing cone, could be seen. The two reconstructed volumes themselves are also different. The constrained volume is fatter and is less elongated along the missing cone direction.

5. Conclusion

In this paper, we have explored the gain of incorporating a priori knowledge within the tomographic reconstruction process. This knowledge includes symmetry, nonnegativity, surface constraint, total volume and similarity to a known volume. All these restrictions are easily expressed in real space and, thus, their incorporation into a reconstruction algorithm such as ART, that works in real space, is quite natural. The amount of information provided by these constraints depends on their accuracy and the amount of information not present in the projection data set. In our simulations improvements were observed in the FSC at all frequencies and the resolution achieved was higher. These observations were confirmed when using experimental data. However, except for the surface constraint, similar improvements can be achieved by applying these constraints at the end of the reconstruction process instead of during it. The algorithm described in this paper is freely available in the Xmipp software package.

Biographies

CARLOS OSCAR S. SORZANO (coss@cnb.uam.es) received the M.Sc. degree in electrical engineering and the B.Sc. degree in computer science from the University of Malaga, in 1997 and 2000, respectively. He received the Ph.D. degree in 2002, from the University Politecnica de Madrid. He joined the National Center of Biotechnology (CSIC, Madrid, Spain) in 1997, where he worked on electron microscopy of single particles. From 2003 to 2004, he worked as a research assistant in the Biomedical Imaging Group, Swiss Federal Institute of Technology, Lausanne, Switzerland. He then joined the University of San Pablo CEU, where he continues his research and teaches at the Polytechnic School. His research interests include image processing, tomography, system identification, multiresolution approaches and electron microscopy.

J.A. VELAZQUEZ-MURIEL was born in 1976 (Salamanca, Spain). He obtained in 2000 his M.S. in Chemical Engineering from the University of Salamanca, and in 2005 his Ph.D. in Biochemistry and Molecular Biology from the Autonomous University of Madrid, working on three-dimensional electron microscopy (3DEM). Specificially, in CTF determination, protein superfamily recognition and flexible fitting on 3DEM maps. Currently he is a Postdoctoral Scholar at the Biopharmaceutical Department of the University of California, San Francisco. His major interest is protein modeling applied to protein structure and function determination.

ROBERTO MARABINI (roberto@cnb.uam.es) received the M.Sc. degree from the University Autonoma de Madrid, Madrid, Spain, in 1989 and the Ph.D. degree from the University of Santiago de Compostela, Spain, in 1995, both in physics. He was previously with the BioComputing Unit of the National Center for BioTechnology, Spanish National Council of Scientific Research, Madrid, Spain, and then with the University of Pennsylvania, Philadelphia, and the City University of New York from 1998\u20132002. At present, he is an Associate Professor in the Escuela Superior Politecnica, University Autonoma de Madrid. His current research interests include electron microscopy, inverse problems, image processing and high-performance computing.

GABOR T. HERMAN received the Ph.D. degree in mathematics from the University of London, London, UK, in 1968, and honorary doctoral degrees from the University of Linkoping, Sweden, in 1989, the University of Szeged, Hungary, in 1998 and University of Haifa, Israel, in 2000. He is a pioneer in the field of X-ray computerized tomography and the author of several books and over 100 articles, including many classic works in the field. He is recognized internationally for his major contributions to image processing and its biomedical applications. He was the leader of successful image processing groups at SUNY Buffalo and at the University of Pennsylvania and has garnered millions of dollars in research funding. He is currently a Distinguished Professor of Computer Science at The Graduate Center of the City University of New York.

JOSE-MARIA CARAZO (carazo@cnb.uam.es) received the M.Sc. degree in theoretical physics and the Ph.D. degree in molecular biology. He is a research professor of the Spanish Research Council, CSIC, where he directs the Biocomputing Unit of the National Center for Biotechnology in Madrid. He worked at the IBM Madrid Scientific Center from 1981 to 1986 and from 1987 to 1989 at the Howard Hughes Medical Center at the New York State Health Department in Albany before joining the CSIC in 1989. His research interests are in the area of multidimensional image classification and tomographic reconstruction in electron microscopy. He has published more than 120 papers in biological and engineering journals and directed large international projects.