Accelerated Recurrence Time Models

Abstract

For the analysis with recurrent events, we propose a generalization of the accelerated failure time model to allow for evolving covariate effects. These so-called accelerated recurrence time models postulate that time to expected recurrence frequency, upon transformation, is a linear function of covariates with frequency-dependent coefficients. This modeling strategy shares the same spirit as quantile regression. An estimation and inference procedure is developed by generalizing the celebrated Powell’s (1984, 1986) estimator for censored quantile regression. Consistency and asymptotic normality of the proposed estimator are established. An algorithm is devised to attain good computational efficiency. Simulations demonstrate that this proposal performs well under practical settings. This methodology is illustrated in an application to the well-known bladder cancer study.

1. INTRODUCTION

Recurrent events are common in longitudinal studies where each individual may experience multiple episodes of the same event, e.g., machine breakdowns, epileptic seizures, tumor recurrences, or hospitalizations. Often the investigators are interested in the effects of covariates on the recurrent event times. Since the intra-individual correlation is typically evident in the data, many semiparametric models formulate the covariate effects on the mean frequency or rate function of the recurrences marginally, rather than the event intensity function conditionally on the process history. Such parsimonious models have been well accepted in practice. One popular modeling approach is to specify the covariate effects on the frequency scale of the mean frequency function. Pepe & Cai (1993), Lawless & Nadeau (1995), and Lin et al. (2000) among others suggested and investigated the proportional means and rates models with multiplicative covariate effects on mean frequency and rate. These models can be extended to the more general class of semiparametric linear transformation models (Lin et al., 2001). As an alternative approach, the covariate effects may be specified as time scale changes of the mean frequency function, as in the accelerated failure time model (Lin et al., 1998). Many have argued the advantage of ‘direct physical interpretation’ with the latter specification (Reid, 1994).

All these aforementioned models hold the covariate effects constant. Unfortunately, this assumption is not always reasonable and indeed covariate effects may evolve. In clinical trials, it is unrealistic to expect an intervention to take full effect instantaneously right after randomization. On the other hand, drug resistance with, say, AIDS therapies might develop over time, which erodes the treatment effect (e.g., Eshleman et al., 2001; Wu et al., 2005). These circumstances call for varying-coefficient models, but such developments are fairly limited for recurrent events. Fine et al. (2004) suggested the temporal process regression model to allow for varying covariate effects on the frequency scale of the mean frequency function. Chiang & Wang (2009) proposed a varying- coefficient model for the rate function and developed an estimation procedure based on kernel smoothing. In this article, we consider covariate effects as time scale changes, and propose a generalization of the accelerated failure time model. These so-called accelerated recurrence time models are presented in section 2. Our modeling strategy shares the same spirit as quantile regression. We present an estimation and inference procedure in sections 3 and 4, and a computational algorithm in section 5. Section 6 provides simulation results and an application to the well-known bladder cancer study. Section 7 concludes with final remarks. All proofs are collected in the appendix.

2. THE DATA AND MODELS

Denote the recurrent event times in order by T^(j), j = 1, 2, ….They are equivalently represented by a counting process $R(.)={\displaystyle {\sum }_{j=1}^{\infty }I(T^{(j)}\le .)}$, where I(.) is the indicator function. However, the observation is limited to follow-up time L. That is, only the first M = R(L) events are observed. Denote the observed counting process by N(.) = R(.∧ L), where ∧ is the minimization operator. Write a p-vector Z as the covariates of interest. The data consist of $\{N_i(.);M_i;T_i^{(j)}:j=1,\dots ,M_i;L_i;Z_i\},i=1,\dots ,n,$, i = 1,…., n, as n iid replicates of {N(.); M; T^(j) : j = 1,…, M; L; Z}.

The distribution of the counting process R(.) is fully governed by its intensity function. But, as indicated in section 1, its appropriate specification can be practically challenging due to the presence of intra-individual correlation. Therefore, we consider the mean frequency function instead:

$${\mu }_Z(t)=E\{R(t)|Z\},$$

i.e., the expected frequency at time t given covariates Z. Define its inverse function as

$${\tau }_Z(u)=\text{inf}\{t:{\mu }_Z(t)>u\},$$

which is time to expected frequency u. Note that expected frequency is a positive number, but not necessarily an integer. Let X = (1,Z^T)^T. We propose the accelerated recurrence time models taking the form:

$$\text{log}{\tau }_Z(u)=\text{log}{\tau }_Z(u-)={\beta }_0{(u)}^{T}X\forall u\in 𝒮,$$ (1)

where the (p+1)-vector of coefficients β₀(u) is a function of the expected frequency u. In the above specification, 𝒮 can be any subset of (0,∞). Nevertheless, we shall consider two specific cases: (i) 𝒮 is a singleton, and (ii) 𝒮 = (0,∞). Correspondingly, they will be appropriately referred to as singleton and global models. A singleton model is useful when a particular expected frequency is of interest but not necessarily others. In contrast, the global model facilitates the investigation of potentially evolving covariate effects, although the model is obviously somewhat more restrictive.

To complete the model specification, we assume

$$R\{{\tau }_Z(u)\}\perp L|Z\forall u\in 𝒮.$$ (2)

Under the global model, the above is equivalent to that R(.) is independent of L conditionally on Z. For a singleton model, this censoring mechanism becomes even weaker.

These proposed accelerated recurrence time models have a connection with the quantile regression model. When each individual may experience at most one event, μ_Z(.) and τ_Z(.) become the distribution and quantile functions of the event time, respectively. Then, (1) reduces to a quantile regression model. On the other hand, the accelerated failure time model of Lin et al. (1998) is a special case of the global accelerated recurrence time model when all components of β₀(u) except the intercept are constant in u. Allowance for frequency dependence of coefficients in this proposal greatly enhances the model flexibility. Meanwhile, our inference procedure may be used to assess the goodness-of-fit of the accelerated failure time model as will be shown later.

3. ESTIMATION WITH A SINGLETON MODEL

Under the singleton model, 𝒮 = {u} in (1) and (2) for a certain expected frequency of interest u. Throughout this section, u is held fixed.

Under mild regularity conditions, model (1) implies

$$E(X[R\{\text{exp}({\beta }^{T}X)\}-u])=0\text{ iff}\beta ={\beta }_0(u),$$

where the left hand side is a monotone function of β. This identity is equivalent to

$${\beta }_0(u)=\underset{\beta }{\text{arg}\text{min}E}\left\{{\displaystyle \sum _{j=1}^{\infty }{({\beta }^{T}X-\text{log}{T}^{(j)})}^{+}-{\beta }^{T}Xu}\right\},$$

where a⁺ = a ν 0 and ν is the maximization operator. Unfortunately, these identities cannot be directly used in the estimation of β₀(u) since the observation of recurrent events is limited by L. Nevertheless, they motivate the following result that accommodates limited follow up.

THEOREM 1

Suppose that (1) and (2) hold for 𝒮 = {u}. If E[X^⊗2I{L > τ_Z(u)}] is nonsingular, then β₀(u) is identifiable, where ν^⊗2 = νν^T for vector ν. Furthermore,

$${\beta }_0(u)=\underset{\beta }{\text{arg}\text{min}\psi }(\beta ;u),$$ (3)

where

$$\psi (\beta ;u)=E\left\{{\displaystyle \sum _{j=1}^M{\left({\beta }^{T}X\wedge \text{log}L-\text{log}{T}^{(j)}\right)}^{+}-({\beta }^{T}X\wedge \text{log}L)u}\right\}.$$

This result extends that established by Powell (1984, 1986) for censored quantile regression when the censoring time is observed.

Define an objective function

$$\mathrm{\Psi }(\beta ;u)=n^{-1}{\displaystyle \sum _{i=1}^n\left\{{\displaystyle \sum _{j=1}^{M_i}{\left({\beta }^T{X}_i\wedge \text{log}{L}_i-\text{log}{T}_i^{(j)}\right)}^{+}-({\beta }^T{X}_i\wedge \text{log}{L}_i)u}\right\}}.$$

Theorem 1 leads to an estimator for β₀(u):

$$\widehat{\beta }(u)=\underset{\beta }{\text{arg}\text{min}\mathrm{\Psi }}(\beta ;u).$$ (4)

THEOREM 2

Suppose that the assumptions in theorem 1 hold. Given that β₀(u) is in the interior of a compact parameter space ℬ, β̂(u) is strongly consistent for β₀(u). In addition, assume that

• (C1) Z and M are bounded;

• (C2) μ̇_Z(t) = dμ_Z(t)/dt is bounded and continuous at t = τ_Z(u), uniformly in Z;

• (C3) The conditional distribution function of L given Z has a bounded density function at τ_Z(u) for all Z; and

• (C4) D(u) = E[X^⊗2μ̇_Z{τ_Z(u)}τ_Z(u)I{L > τ_Z(u)}] is nonsingular.

Then, n^1/2{β̂(u)−β₀(u)} is asymptotically normal with mean 0 and variance D(u)⁻¹∑(u, u)D(u)⁻¹, where ${{\displaystyle \sum (u,u)=E(X^{\otimes 2}{\sigma }_Z^2[\text{exp}\{{\beta }_0{(u)}^{T}X\}]I\{\text{log}L>{\beta }_0(u)}}^{T}X\})\mathit{\text{ and }}{\sigma }_Z^2(t)=\text{var}\{R(t)|Z\}.$

Unfortunately, the sandwich variance estimate of β̂(u) is not available, since the asymptotic variance of β̂(u) involves the rate function μ ˙_Z(.) and the gradient

$$\dot{\mathrm{\Psi }}(\beta ;u)=n^{-1}{\displaystyle \sum _{i=1}^n{X}_i[N_i\{\text{exp}({\beta }^T{X}_i)\}-u]I(\text{log}{L}_i>{\beta }^T{X}_i)}$$

is not continuous. Nevertheless, several methods have recently been developed for variance estimation of this type. In particular, the resampling approach of Jin et al. (2001) may be employed by perturbing the objective function. Let ν_i, i = 1,…., n, be iid nonnegative random variables of unit mean and unit variance, e.g., an exponential distribution of unit rate. Write

$${\mathrm{\Psi }}^{*}(\beta ;u)=n^{-1}{\displaystyle \sum _{i=1}^n{\nu }_i}\left\{{\displaystyle \sum _{j=1}^{M_i}{\left({\beta }^T{X}_i\wedge \text{log}{L}_i-\text{log}{T}_i^{(j)}\right)}^{+}-({\beta }^T{X}_i\wedge \text{log}{L}_i)u}\right\},$$

which gives a perturbed estimator β̂ ^*= arg min_βΨ^*(β;u). It can be shown that the distribution of n^1/2{β̂^*(u) − β̂(u)} conditionally on the data is asymptotically the same as n^1/2{β̂(u) − β₀(u)}. Thus, the distribution of the latter may be approximated by a simulated distribution of the former.

4. INFERENCE WITH THE GLOBAL MODEL

Under the global model, model (1) holds for 𝒮 = (0,∞). Since the global model implies singleton models for all points in 𝒮, we apply the estimation procedure described in section 3 in a pointwise fashion to obtain the estimator β̂(.).

THEOREM 3

Suppose that (1) and (2) hold for 𝒮 = (0,∞). If there exists r > 0 such that E[X^⊗2I{L > τ_Z(r)}] is nonsingular, then β₀(.) is identifiable on (0, r]. Furthermore, if β₀(u) is in the interior of the compact parameter space ℬ for all u ∈ [l, r], then

$$\underset{u\in [l,r]}{\text{sup}}\Vert \widehat{\beta }(u)-{\beta }_0(u)\Vert \to 0$$

almost surely, where ‖.‖ is the Euclidean norm.

The lower and upper bounds, l and r, are imposed for different reasons. The lower one ensures that β₀(.) on [l, r] is bounded; note that β₀(u) may not be so as u approaches 0 if τ_Z(0) = 0. On the other hand, the upper bound is typically necessary for identifiability given limited follow-up.

THEOREM 4

Suppose that the assumptions in theorem 3 hold. In addition, assume condition

• (C1) along with

• (C2°) μ̇_Z (t) is bounded and continuous, uniformly in t ∈ [τ_Z(l), τ_Z(r)] and in Z;

• (C3°) The conditional distribution function of L given Z has a bounded density function on [τ_Z(l), τ_Z(r)] for all Z; and

• (C4°) inf_u∈[l,r] eigmin{D(u)} > 0, where eigmin(.) denotes the minimum eigenvalue of a matrix.

Then, n^1/2{β̂(.)−β₀(.)} on [l, r] converges weakly to a Gaussian process with mean 0 and covariance function D(u₁)⁻¹∑(u₁, u₂)D(u₂)⁻¹, where

$$\begin{array}{c}{\displaystyle \sum (u_1,u_2)=E(X^{\otimes 2}{\sigma }_Z^2)[\text{exp}\{{\beta }_0{(u_1)}^{T}X\},\text{exp}\{{\beta }_0{(u_2)}^{T}X\}]I\{\text{log}L>{\beta }_0{(u_1)}^{T}X\vee {\beta }_0{(u_2)}^{T}X\}),}\hfill \\ \mathit{\text{and}}{\sigma }_Z^2(t_1,t_2)=\text{cov}\{R(t_1),R(t_2)|Z\}.\hfill \end{array}$$

To estimate the distribution of n^1/2{β̂(.) − β₀(.)}, we use the same stochastic perturbation approach in section 3 except for that the estimand now is a functional. We thus obtain β̂^*(.). The distribution of n^1/2{β̂^*(.) − β̂(.)} conditionally on the data is asymptotically the same as n^1/2{β̂(.) − β₀(.)}. The simulated distribution by the resampling procedure provides a basis for inference. In the following, we describe a number of practically useful procedures. Focusing on a scalar component of the coefficient process, we shall abuse the notation, β₀(.), β̂(.) and β̂ ^*(.), to denote the component of interest.

With the simulated distribution of β̂^*(.), pointwise confidence intervals for β₀(.) can be obtained by the Wald or percentile method. The 95% equal-precision confidence band for β₀(u) on [l, r] is given by

$$\widehat{\beta }(u)\pm {\nu }_{0.95}\text{SE}\{\widehat{\beta }(u)\},$$

where SE{β̇(u)} is the standard error of β̂(u), and ν_0.95 is the estimated 95th percentile of supu∈[l,r]|β̂^*(u)− β̂(u)|/SE{β̂(u)}.

With evolving covariate effect, one may still wish to succinctly summarize β₀(.). To do so, we introduce an average measure

$${\eta }_0={(r-l)}^{-1}{\displaystyle {\int }_l^r{\beta }_0(u)}\mathit{\text{du}}.$$

A natural estimator is the plug-in estimator denoted by η̂, and its variance can be obtained from the resampling procedure. In comparison with, say, adopting the accelerated failure time model, this approach is more robust since η₀ is still meaningful when the covariate effect is not constant.

The accelerated recurrence time model is fairly general. However, one would opt for a more restrictive model, e.g., the accelerated failure time model, for potential efficiency gain if some or all covariates are known to have constant effects. Therefore, it is of interest to test whether a certain covariate indeed has evolving effect. To be specific, the null hypothesis is β₀(u) = η₀ for all u ∈ [l, r]. We propose a test statistic as follows

$$\widehat{\xi }=\underset{u\in [l,r]}{\text{sup}}\left|\widehat{\beta }(u)-\widehat{\eta }\right|/\text{SE}\{\widehat{\beta }(u)-\widehat{\eta }\},$$

where the standard error SE{β̂(u) − η̂} is obtained from the resampling procedure. Under the null hypothesis, ξ̂ is consistent for 0. To obtain the p-value of the test, one may compare ξ̂ to the simulated distribution of

$$\widehat{{\xi }^{*}}=\underset{u\in [l,r]}{\text{sup}}|\widehat{{\beta }^{*}}(u)-\widehat{\beta }(u)-\widehat{{\eta }^{*}}+\widehat{\eta }|/\text{SE}\{\widehat{\beta }(u)-\widehat{\eta }\}.$$

5. A COMPUTATIONAL ALGORITHM

Despite the fact that the estimator β̂(u) is well defined, its numerical implementation is not trivial. Note that the objective function Ψ(β;u) is not convex, and the gradient Ψ̇(β u) is not continuous. Nevertheless, these issues are shared by Powell’s (1984, 1986) estimator for censored quantile regression, which has received much attention and algorithmic developments over the years (e.g., Womersley, 1986; Buchinsky, 1994; Koenker & Park, 1996; Fitzenberger, 1997). By taking advantage of them, we develop an algorithm for the computation of β̂(u).

One important feature of Ψ(β; u) is its piecewise linearity in β. As a result, a minimizer along a given line is a nonsmooth point of Ψ̇(β u), i.e., in $\{\beta :{\beta }^T{X}_i=\text{log}{L}_i\text{or log}{T}_i^{(j)},j=1,\dots ,M_i;i=1,\dots ,n\}.$ Then, a line search algorithm follows immediately by evaluating a finite number of candidate points on the line. One may slightly strengthen this search by eliminating any nonsmooth point resulting only from β^TX_i = log L_i in the case of M_i ≥ u, at which the ith individual’s contribution to Ψ(β; u) is locally concave.

Furthermore, the global minimization has the interpolation property. Such a property was established for the Powell’s estimator by Womersley (1986); see also Fitzenberger (1997). We now extend it to the present problem. Specifically, if the design matrix (X₁…X_n)^T has full rank of p + 1, then there exists a global minimizer β̂(u) of Ψ(β; u) which interpolates at least p + 1 data points in the sense that

$$\widehat{\beta }{(u)}^T{X}_{k_l}=\text{a single value of}\{\begin{array}{cc}\{\text{log}{L}_{k_l},\text{log}{T}_{k_l}^{(j)},j=1,\dots ,M_{k_l}\}\hfill & \text{ if }{M}_{k_l}<u\hfill \\ \{\text{log}{T}_{k_l}^{(j)},j=1,\dots .M_{k_l}\}\hfill & \text{ otherwise}\hfill \end{array}$$

for {k_l : l = 1,…, p + 1} ⊆ {1,…, n} and the rank of (X_k1 …X_kp+1)^T is p + 1.

This interpolation property suggests that an enumeration algorithm guarantees to locate a global minimizer by considering all candidate interpolation sets. However, the computation is prohibitively intensive for most practical problems. For this reason, we propose an efficient algorithm as follows. Start with an interpolation set, and calculate the associated β and subsequently the objective function Ψ(β; u). At each step, update the interpolation set, with one point replaced, to reduce the objective function. By keeping the other p data points, a search line is determined and the aforementioned line search algorithm is used to locate the replacement data point. The algorithm stops when no point in the interpolation set can be replaced to further reduce Ψ(β; u).

This algorithm is motivated by those of Womersley (1986) and Fitzenberger (1997) for censored quantile regression. Similarly, it guarantees algorithmic convergence, to a local minimizer of Ψ(β; u). Although a global minimizer may not be located, a local strict minimizer is asymptotically equivalent to β̂(u) under mild conditions. In fact, it can be shown that the limit of the objective function, ψ(β; u), has a unique strict minimizer at β₀(u). For this reason, the line search component of the preceding algorithm may target a local minimizer rather than a global one on the line. From our experience, this substantially improves the computational efficiency.

6. NUMERICAL STUDIES

6.1 Simulations

We imposed a unit mean gamma frailty on a homogeneous Poisson process to generate recurrent events with unit baseline rate. The level of intra-individual correlation is determined by the variance of the gamma distribution. Two covariates were considered. The first covariate followed the equal-probability Bernoulli distribution, and had a ramp-up effect going from none to full effect linearly with mean recurrence frequency and staying constant afterwards. This effect pattern is reasonable for an intervention in a typical clinical trial. The second covariate followed a uniform distribution on [−0.5, 0.5] and had a constant effect.

Two variance values, 0 and 0.5, of the gamma frailty were chosen, where 0 corresponds to zero intra-individual correlation. The first coefficient was set to 1 ∧ (u/1.5) as a function of expected frequency u, and the second coefficient was 1. The follow-up time followed the uniform distribution between 0 and 12, resulting in an average of 4.3 observed recurrent events. The sample size was 100. For interval estimation and inference, the resampling size of 99 was chosen. This size is adequate for simulation purposes although a much larger size is needed for a specific dataset to obtain reliable results. Under each of the two intra-individual correlation scenarios, simulation studies were conducted with 1,000 iterations.

Table 1 reports the estimation of β₀(u) at five expected frequencies from 0.5 to 2.5. The estimator was virtually unbiased. Furthermore, the standard error based on the resampling approach tracked the standard deviation well. Finally, the Wald 95% confidence interval had a coverage close to the nominal level. Such performance is remarkable particularly when the censoring rate measured by E[I{log L < β₀(u)^TX}] reached 40% at u = 2.5.

Table 1.

Simulation summary for the estimation of β₀(u): BS, bias (×10³); SD, standard deviation (×10³); SE, mean standard error (×10³); CP, coverage probability (%) of the Wald 95% confidence interval

u		0.5			1.0			1.5			2.0			2.5
censoring†		5%			13%			24%			32%			40%
β0(u)	−0.69	0.33	1.00	0.00	0.67	1.00	0.41	1.00	1.00	0.69	1.00	1.00	0.92	1.00	1.00
Zero intra-individual correlation
BS	6	1	27	0	15	18	0	−55	16	−3	3	9	−1	3	14
SD	208	336	568	157	306	461	126	238	375	110	179	302	105	182	295
SE	208	353	587	150	297	459	123	238	376	109	191	323	101	181	305
CP	93.4	96.1	94.8	91.9	92.2	94.1	91.5	93.7	93.7	93.4	95.6	95.5	93.2	93.6	94.7
Gamma frailty of variance 0.5
BS	0	31	−29	7	18	−28	6	−62	−14	5	17	13	8	36	16
SD	231	396	678	185	367	583	164	318	526	158	283	479	156	301	492
SE	229	385	646	181	352	550	160	310	495	153	281	467	153	279	469
CP	93.9	92.9	92.5	92.7	93.3	92.9	92.8	94.1	93.1	93.5	95.0	93.5	93.8	93.8	93.5

^†censoring rate given by E[I{log L < β₀(u)^TX}].

Three columns under each u value corresponds to the intercept and slopes for the two covariates.

We also evaluated the estimation and inference procedures described in section 4 for the global accelerated recurrence time model on [0, 2.5]. Numerically, β̂(.) was obtained at 100 equally-spaced points. The results are summarized in table 2. The estimation of the average coefficient η₀ had good performance in terms of estimator bias, standard error, and coverage of the Wald 95% confidence interval. The 95% equal-precision band for β₀(.) on [0, 2.5] performed reasonably well for the two slopes, but had an under-coverage for the intercept. The constant coefficient test was applied to the intercept and two slopes. Note that only the second slope was constant. For the intercept, the null hypothesis of constant coefficient was rejected 100%. The power to detect a varying coefficient for the first slope was higher under zero intra-individual correlation, which is expected. Finally, the empirical size of the test for the second slope was reasonably close to the 0.05 nominal level.

Table 2.

Simulation summary for the estimation of β₀(.) over [0, 2.5]. Estimator of η₀ (a) bias (×10³), (b) standard deviation (×10³), (c) mean standard error (×10³), (d) coverage (%) of the Wald 95% confidence interval. Equal-precision confidence band: (e) coverage (%) of the 95% band. Constant coefficient test: (f) size and power (×10²) at 0.05 nominal level

		Zero intra-individual correlation						Gamma frailty of variance 0.5
	η0	(a)	(b)	(c)	(d)	(e)	(f)	(a)	(b)	(c)	(d)	(e)	(f)
Intercept	−0.08	36	132	123	89.9	86.5	100.0	40	166	157	91.0	86.5	100.0
1st slope	0.70	2	221	211	94.3	94.1	30.2	16	284	270	93.0	93.9	22.1
2nd slope	1.00	23	360	344	93.3	93.0	4.1	−9	493	445	90.9	89.1	3.8

6.2 Application to the bladder tumor study

We applied our proposal to the well-known bladder tumor study (Byar, 1980). This randomized clinical trial was conducted to determine the effects of two treatments, pyridoxine and thiotepa, on the recurrences of bladder tumor. The dataset has been extensively analyzed with various methods for recurrent events, including Wei et al. (1989) and Lin et al. (1998). At study enrollment, all participants had superficial bladder tumors. Following transurethral removal of these tumors, a total of 118 participants were randomized to three treatment arms: 48 to placebo, 32 to pyridoxine, and 38 to thiotepa. The average follow-up was 31 months, and 189 tumor recurrences were observed in 62 participants. The numbers of participants who experienced from 1 to the maximum 9 tumor recurrences were 23, 11, 8, 4, 8, 1, 1, 3, and 3, respectively.

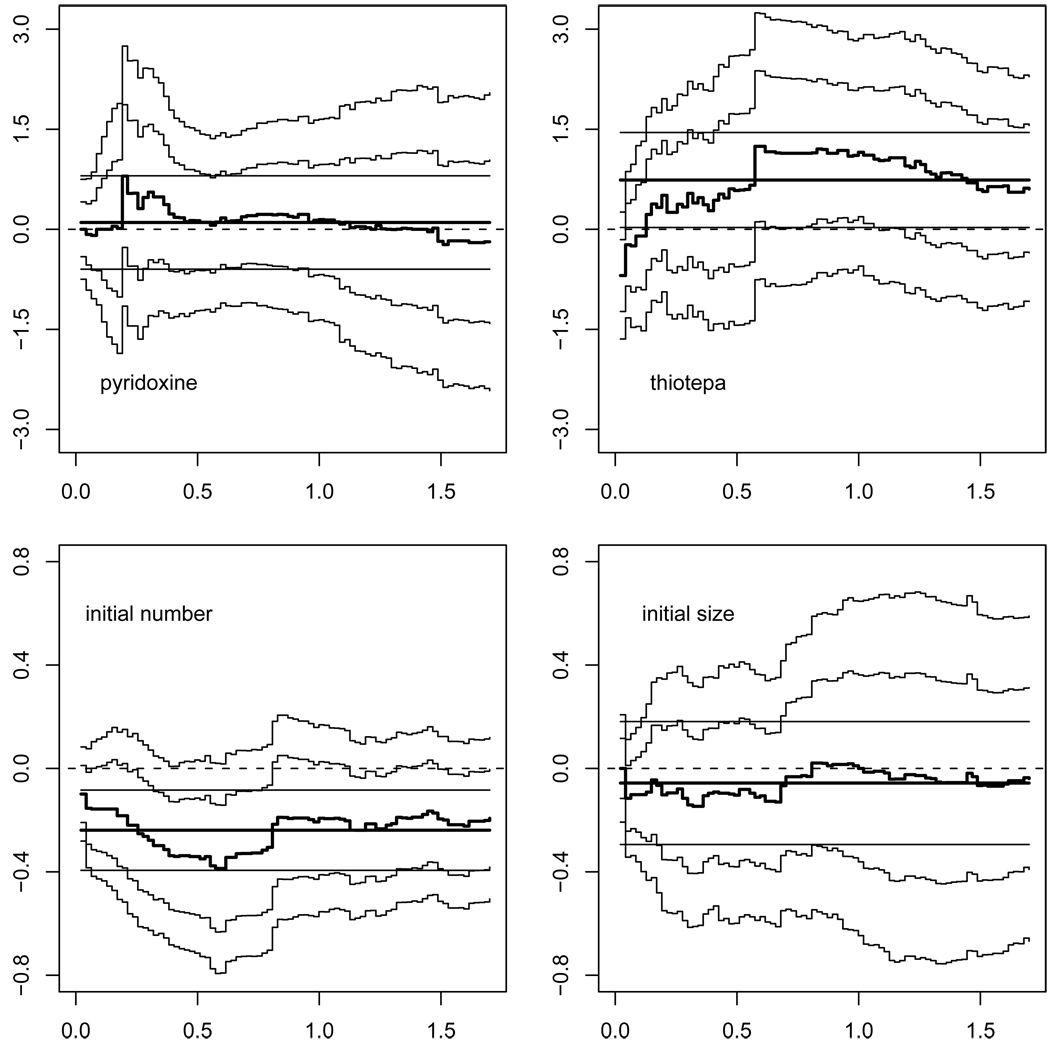
The global accelerated recurrence time model was adopted with four covariates: the two treatment indicators as well as initial tumor number and size. The regression coefficients were estimated over [0, 1.7] of expected frequency at 80 equally-spaced points. A resampling size of 999 was used to ensure reliable interval estimation and inference. Figure 1 provides the estimated coefficients along with pointwise Wald 95% confidence intervals and 95% equal-precision confidence band. To summarize the covariate effects, estimated average coefficients are given in Fig. 1 and reported in table 3. Constant coefficient test results are also presented in table 3. As shown, pyridoxine and initial size had little effect. But a larger number of initial tumors tended to be associated with higher recurrences. On the other hand, thiotepa on average reduced tumor recurrences. Interestingly, the effect of thiotepa appeared to be increasing over time, which was supported by the constant coefficient test with a p-value of 0.044. This suggests a time delay of thiotepa in reaching the full effect after its administration. In this case, the average effect of thiotepa might be a more meaningful effect summary than an estimate obtained from, e.g., the accelerated failure time model as in Lin et al. (1998).

Figure 1.

Bladder tumor study. Estimated coefficients are shown in rugged lines, surrounded by pointwise Wald 95% confidence intervals and further out by 95% equal-precision confidence band. Estimated average coefficients and Wald 95% confidence intervals are given by straight lines.

Table 3.

Analysis results of the bladder tumor study

	Average coefficient			Constant coefficient
Covariate	Estimate	SE	Wald 95% CI	test p-value
pyridoxine	0.102	0.357	(−0.598, 0.802)	0.617
thiotepa	0.739	0.363	(0.027, 1.451)	0.044
initial number	−0.239	0.079	(−0.394, −0.084)	0.526
initial size	−0.057	0.121	(−0.294, 0.181)	0.978

7. REMARKS

In this article, we have introduced the accelerated recurrence time models for recurrent events. Sharing the same spirit as quantile regression, they generalize the accelerated failure time model to allow for the dependence of covariate effects on the expected recurrence frequency. In comparison with other existing varying-coefficient models (Fine et al., 2004; Chiang & Wang, 2009), these new models provide direct interpretation of covariate effects on recurrence times instead of rates or cumulative rates. While an estimation and inference procedure has been developed, a number of issues might be worth further investigation.

For interval estimation, the resampling method of Jin et al. (2001) is employed. Our experience has shown that it has good performance both numerically and statistically. But its computation is burdensome, especially when the global model is estimated. To deal with nonsmooth estimating functions, Huang (2002) proposed a sample-based method that is computationally much more efficient. This method can be directly applied to the singleton model. But its application to the global model, i.e., with a functional estimand, does not appear to be straightforward. This topic is under current research.

The objective function Ψ(β; u) is proposed for the purpose of estimation. However, a weighted version of the objective function may also be constructed to obtain consistent estimators, and more efficient estimation may then be pursued. Newey & Powell (1990) investigated the efficiency issue with censored quantile regression. Their results can be extended to the singleton accelerated recurrent time model. Nevertheless, the optimal weight would involve the rate function μ̇_Z and its feasibility in practice requires further study.

In the global accelerated recurrence time model, all coefficients are allowed to depend on expected frequency with full flexibility. This may be viewed as the other extreme from the accelerated failure time model. There are, however, practical situations where limited flexibility in modeling is both reasonable and desirable. For example, in many clinical trials, the effect of an intervention is of primary interest and indeed evolving intervention effect is often scientifically plausible as in the bladder tumor study. But it might be reasonable to postulate that certain baseline characteristics as included for adjustment purposes have fairly stable effects. In this case, a model with a mixture of constant- and varying-coefficients would be more appealing. As the referee pointed out, even for a varying coefficient, its evolution may be known a priori to follow certain pattern, e.g., a step function. Again, this situation calls for a less flexible model. These models open the possibility of more efficient estimation and are under further developments.

With recurrent events, the follow-up time L, or censoring time, is always observed. However, it is not necessarily the case with univariate survival data. Censored quantile regression methods have also been developed under the circumstance that the censoring time is not observed for uncensored individuals, including Portnoy (2003) and Peng & Huang (2008). These methods might potentially be extended to address the global recurrence time model. Since they are not applicable under a singleton model, conceivably robustness would be somewhat compromised in comparison with our current proposal for the global model. Nevertheless, efficiency gain is hopeful. These extensions are under investigation.

Finally, despite the flexibility of the proposed models, their goodness-of-fit can still be an issue of concern. In light of their intimate relationship with the quantile regression model, diagnostic techniques developed for the latter may again provide a good starting point, e.g., He & Zhu (2003), Peng & Huang (2008), and the references therein. Careful development and thorough research are, nevertheless, needed.

APPENDIX

Proofs

Proof of theorem 1. Straightforward algebra gives

$$\begin{array}{cc}\varphi (\beta ;Z,L)\hfill & =E\left\{{\displaystyle \sum _{j=1}^M{\left({\beta }^{T}X\wedge \text{log}L-\text{log}{T}^{(j)}\right)}^{+}-({\beta }^{T}X\wedge \text{log}L)u|Z,L}\right\}\hfill \\ & {\displaystyle ={\int }_{-\infty }^{{\beta }^{T}X\wedge \text{log}L}\mu Z\{\text{exp}(s)\}\text{ds}-({\beta }^{T}X\wedge \text{log}L)u.}\hfill & \hfill \end{array}$$

We shall show ψ{β₀(u); u} = Eφ {β₀(u);Z,L} < ψ(β; u) = Eφ(β;Z,L) for any given β ≠ β₀(u).

When log L ≤ β₀(u)^TX and log L ≤ β^TX,

$$\varphi \{{\beta }_0(u);Z,L\}=\varphi (\beta ;Z,L).$$

When log L ≤ β₀(u)^TX and log L > β^TX,

$$\varphi \{{\beta }_0(u);Z,L\}-\varphi (\beta ;Z,L)={\displaystyle {\int }_{{\beta }^{T}X}^{\text{log}L}[{\mu }_Z\{\text{exp}(s)\}-u]\mathit{\text{ds}}\le 0.}$$

It remains to consider the case when log L > β₀(u)^TX. First, monotonicity of μ_Z(.) implies that ${\displaystyle {\int }_{-\infty }^{\nu }{\mu }_Z\{\text{exp}(s)\}\mathit{\text{ds}}-\nu u}$ is minimized at ν = log τ_Z(u), and the minimizer is unique since τ_Z(.) is continuous at u. Therefore, φ{β₀(u);Z,L} ≤ φ(β;Z,L) and the equality holds if and only if β₀(u)^TX = β^TX. By the nonsingularity of E[X^⊗2I{L > τ_Z(u)}],

$$\text{pr}[{\{{\beta }_0(u)-\beta \}}^{T}XI\{\text{log}L>{\beta }_0{(u)}^{T}X\}\ne 0]>0$$

for β ≠ β₀(u). Thus,

$$E[\varphi ({\beta }_0(u);Z,L)I\{\text{log}L>{\beta }_0{(u)}^{T}X\}]<E[\varphi (\beta ;Z,L)I\{\text{log}L>{\beta }_0{(u)}^{T}X\}].$$

This completes the proof.

Proof of theorem 2. First, consider the consistency of β̂(u). Note that the objective function

$$\begin{array}{cc}\mathrm{\Psi }(\beta ;u)={\mathrm{\Psi }}_1(\beta )+{\mathrm{\Psi }}_2(\beta )+{\mathrm{\Psi }}_3(\beta )\hfill & =n^{-1}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{M_i}\left\{{\left({\beta }^T{X}_i-\text{log}{T}_i^{(j)}\right)}^{+}+{\left(\text{log}{L}_i-\text{log}{T}_i^{(j)}\right)}^{+}\right\}}}\hfill \\ & -n^{-1}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{M_i}{\left({\beta }^T{X}_i\vee \text{log}{L}_i-\text{log}{T}_i^{(j)}\right)}^{+}}}\hfill \\ & -n^{-1}{\displaystyle \sum _{i=1}^n({\beta }^T{X}_i\wedge \text{log}{L}_i)u.}\hfill \end{array}$$

The above three components are either concave or convex functions of β. This fact coupled with pointwise convergence by the strong law of large numbers implies the uniform convergence of Ψ(β; u) (Andersen & Gill, 1982). Then, the strong consistency of β̂(u) follows from identity (3).

To study the asymptotic distribution of β̂(u), we shall establish the asymptotic normality of Ψ̇{β₀(u); u} and the asymptotic linearity of Ψ̇(β; u) at β₀(u). By the central limit theorem, n^1/2Ψ̇{β₀(u); u} is asymptotically normal with mean 0 and variance ∑(u, u). To establish the asymptotic linearity, it can be shown that, under conditions (C1), (C2) and (C3),

$$\text{var}(n^{1/2}[{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)+n^{-1/2}\mathrm{\Delta }\}-{\dot{\mathrm{\Psi }}}_k\{{\beta }_{0}u\}-E{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)+n^{-1/2}\mathrm{\Delta }\}+E{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)\}])\to 0$$

for k = 1, 2, 3 and any fixed Δ, where Ψ̇_k(β) = dΨ̇_k(β)/dβ. Therefore,

$$n^{1/2}\Vert {\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)+n^{-1/2}\mathrm{\Delta }\}-{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)\}-E{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)+n^{-1/2}\mathrm{\Delta }\}+E{\dot{\mathrm{\Psi }}}_k\{{\beta }_0(u)\}\Vert \to 0$$

in probability. By the result of Ritov (1987), the preceding pointwise convergence for those monotone functions implies a uniform one, which further leads to

$$\underset{\Vert \beta -{\beta }_0(u)\Vert \le n^{-1/2}d}{\text{sup}}{n}^{1/2}\Vert \dot{\mathrm{\Psi }}(\beta ;u)-\dot{\mathrm{\Psi }}\{{\beta }_0(u);u\}-E\dot{\mathrm{\Psi }}(\beta ;u)+E\dot{\mathrm{\Psi }}\{{\beta }_0(u);u\}\Vert \to 0$$

in probability for any d > 0. With conditions (C2) and (C3), Taylor expansion yields

$$\begin{array}{cc}E\dot{\mathrm{\Psi }}(\beta ;u)\hfill & =E[X({\mu }_Z\{\text{exp}({\beta }^{T}X)\}-{\mu }_Z[\text{exp}\{{\beta }_0{(u)}^{T}X\}])I(\text{log}L>{\beta }^{T}X)]\hfill \\ \hfill & =\{D(u)+o(1)\}\{\beta -{\beta }_0(u)\}\hfill \end{array}$$

for β → β₀(u). Since E Ψ̇{β₀(u); u} = 0, we then have the following asymptotic linearity result:

$$\underset{\Vert \beta -{\beta }_0(u)\Vert \le n^{-1/2}d}{\text{sup}}{n}^{1/2}\Vert \dot{\mathrm{\Psi }}(\beta ;u)-\dot{\mathrm{\Psi }}\{{\beta }_0(u);u\}-D(u)\{\beta -{\beta }_0(u)\}\Vert \to 0$$

in probability for any d > 0. Since β̂(u) minimizes Ψ(β; u), Ψ̇{β̂(u); u} = O(n⁻¹) almost surely by condition (C1). Arguing as in Tsiatis (1990), it can be shown that β̂(u) − β₀(u) converges in distribution to −D(u)⁻¹ Ψ̇{β₀(u); u} given condition (C4). The asymptotic normality of β̂(u) then follows.

Proof of theorem 3. Note that the nonsingularity of E[X^⊗2I{L > τ_Z(r)}] implies that of E[X^⊗2I{L > τ_Z(u)}] for any u ∈ (0, r]. The identifiability result then follows directly from theorem 1.

To establish the uniform consistency, we note that the proof of theorem 2 actually gives a stronger convergence result:

$$\underset{\beta \in B,u\in [l,r]}{\text{sup}}\left|\mathrm{\Psi }(\beta ;u)-\psi (\beta ;u)\right|\to 0$$

almost surely. Then

$$\psi \{\widehat{\beta }(u);u\}-\psi \{{\beta }_0(u);u\}\le \psi \{\widehat{\beta }(u);u\}-\mathrm{\Psi }\{\widehat{\beta }(u);u\}+\mathrm{\Psi }\{{\beta }_0(u);u\}-\psi \{{\beta }_0(u);u\}$$

leads to

$$\underset{u\in [l,r]}{\text{sup}}\psi \{\widehat{\beta }(u);u\}-\psi \{{\beta }_0(u);u\}\to 0$$

almost surely.

Now, it remains to show that, for any ∊ > 0, there exists δ > 0 such that if sup_u∈[l,r] Ψ{β(u); u}− Ψ{β₀(u); u} < δ, then sup_u∈[l,r] ‖β(u) − β₀(u)‖ < ∊. Suppose that this is not true. Thus, for each δ > 0, there exists (ζ,ν) such that Ψ(ζ; ν)−Ψ{β₀(ν); ν} < δ and ‖ζ − β₀(ν) ‖ > c for some constant c > 0. Then there is a subsequence of (ζ, ν) that converges to, say, (ζ₀, ν₀), which implies that ζ₀ ≠β₀(ν₀) also minimizes Ψ(β; ν₀). This contradicts the fact that β₀(u) is the unique minimizer of Ψ(β; u) for all u ∈ [l, r]. This completes the proof.

Proof of theorem 4. We first establish the weak convergence of n^1/2 Ψ̇{β₀(u); u} on u ∈ [l, r]. Under model (1), β₀(u)^TX is increasing in u. Therefore, N{exp{β₀(u)^TX} and I{log L > β₀(u)^TX} are monotone cadlag stochastic processes, respectively, and thus Donsker. By Donsker permanence, {X (N{exp{β₀(u)^TX} − u) I{log L > β₀(u)^TX} : u ∈ [l, r]} is then Donsker. Therefore, n^1/2 Ψ̇{β₀(u); u} on u ∈ [l, r] converges weakly to a Gaussian process. The covariance function ∑(u₁, u₂) can be easily established.

Now, we consider the asymptotic linearity of Ψ̇(β; u). Using the techniques of Alexander (1984), Lai & Ying (1988, theorem 1) established the asymptotic linearity for so-called ‘empirical-type’ processes. The same arguments can be applied to establish the asymptotic linearity of Ψ̇(β; u): For any sequence d_n → 0,

$$\underset{\Vert \beta -\beta \prime \Vert \le d_n,u\in [l,r]}{\text{sup}}\Vert \dot{\mathrm{\Psi }}(\beta ;u)-\dot{\mathrm{\Psi }}\{\beta \prime ;u\}-E\dot{\mathrm{\Psi }}(\beta ;u)+E\dot{\mathrm{\Psi }}\{\beta \prime ;u\}\Vert =o(n^{-1/2}+\Vert \beta -\beta \prime \Vert )$$

almost surely.

Finally, using the arguments in the proof of theorem 2 with possibly minor extensions, we can then obtain

$$\widehat{\beta }(u)-{\beta }_0(u)=-D{(u)}^{-1}\dot{\mathrm{\Psi }}\{{\beta }_0(u);u\}+o(n^{-1/2})$$

uniformly in u ∈ [r, l] almost surely. Thus, the weak convergence result follows.