Geographic Information Systems and Applied Spatial Statistics Are Efficient Tools to Study Hansen's Disease (Leprosy) and to Determine Areas of Greater Risk of Disease

Abstract

Applied Spatial Statistics used in conjunction with geographic information systems (GIS) provide an efficient tool for the surveillance of diseases. Here, using these tools we analyzed the spatial distribution of Hansen's disease in an endemic area in Brazil. A sample of 808 selected from a universe of 1,293 cases was geocoded in Mossoró, Rio Grande do Norte, Brazil. Hansen's disease cases were not distributed randomly within the neighborhoods, with higher detection rates found in more populated districts. Cluster analysis identified two areas of high risk, one with a relative risk of 5.9 (P = 0.001) and the other 6.5 (P = 0.001). A significant relationship between the geographic distribution of disease and the social economic variables indicative of poverty was observed. Our study shows that the combination of GIS and spatial analysis can identify clustering of transmissible disease, such as Hansen's disease, pointing to areas where intervention efforts can be targeted to control disease.

Introduction

Hansen's disease, as leprosy is called in Brazil, is a communicable disease caused by Mycobacterium leprae infection, which is principally transmitted by the upper respiratory tract. Not everyone infected with M. leprae will go on to develop the disease, but a subset of infected people develop clinical signs that have been used to classify a spectrum from tuberculoid or paucibacillary to lepromatous or multibacillary forms of disease.¹ People who evolve the lepromatous form of disease present a heavy burden of Mycobacterium, release more microorganisms to the environment, and are therefore potentially more contagious.^2,3

Hansen's disease can be disfiguring and impact heavily on quality of life, contributing to a high estimate of disability adjusted life years (DALY).⁴ The Prevention of disability is a crucial target to decrease morbidity. The introduction of multidrug therapy for the treatment of Hansen's disease in 1981 led to a dramatic reduction in the global disease burden: from the approximate 10 million cases registered in the mid 1970s to 212,802 at the end of 2007 (http://www.who.int/lep).^5–8 Nevertheless, the more endemic countries such as India and Brazil continue to diagnose around 250,000 new cases yearly.^9–11 Although the prevalence of leprosy in Brazil has been reduced from 19 cases per 10,000 population in 1985 to 2.02 in 2006 (http://tabnet.datasus.gov.br/cgi/tabcgi.exe/hans/hanswbr.def), there are still around 42,000 new cases of Hansen's disease diagnosed yearly.^12–14 The disease is spread throughout the country, but is more clustered in the North and Western Central Regions.^15–17

The risk of Hansen's disease is increased in neighborhoods where there is a previous report of disease.^18–20 Therefore, finding these high-risk areas is essential for the design of effective long-term intervention strategies. Spatial localization of a transmissible disease can provide hints as to why it occurs in that particular geographic area. Methods such as geographic information systems (GIS) combined with spatial statistics can be used to identify disease clusters and determine the potential risk factors involved with clustering.^{3,18,19,21,22} Spatial analysis tools are commonly used to characterize spatial patterns of diseases.^23–26 Spatial autocorrelation analysis is performed to verify whether pairs of observations taken nearby are more alike than those taken farther apart.²⁷ However, because each spatial statistical technique has advantages and disadvantages, more than one method is sometimes needed to validate results. For instance, the use of Kernel intensity, which is calculated from the point map of cases, can show areas of greater disease risk. Methods such as Correlogram, local indicator of spatial association (LISA), and Scan Statistics can also be used to map relative risk (RR) of disease by area.²⁸ The correlogram calculated using Moran's I, which is a global index of spatial autocorrelation, can potentially indicate spatial autocorrelation and existence of spatial clustering. The LISA can show local spatial autocorrelation. Last, the spatial scan statistic, as defined by Kuldorff, is able to identify the existence of clusters of both high and low risk and also assess its significance by testing the null hypothesis that the RR of the disease is homogeneous throughout the study area.²⁹ The use of spatial linear models can refine a particular conclusion by adjusting the analyses and maps for important covariate information.³⁰

In this study, we conducted GIS-based spatial analysis and used exploratory spatial data analysis and the spatial scan statistics to characterize the geographical distribution of Hansen's disease cases in Mossoró, a city located in the western region of the state of Rio Grande do Norte, Brazil. Mossoró had a low detection rate of Hansen's disease but recently high detection rates of disease have been registered.³¹ We found clustered areas of Hansen's disease there, which was confirmed by multiple statistical tools. The use of spatial statistical analysis can identify areas of disease risk, facilitating cost-effective targeting of intervention measures and allowing more efficient use of public resources.

Material and Methods

Study site.

Mossoró is a city located in the State of Rio Grande do Norte, Brazil, with an urban population that increased from 192,267 in the 1991 census to 213,841 inhabitants in the last census, which was conducted in the year 2000. The city of Mossoró covers a geographic area of 150 km², although the municipality covers 2,110.207 km², including the rural area. The downtown coordinates are UTM 683530; 9426311S.

Ethical considerations.

This protocol was approved by the Universidade Federal do Rio Grande do Norte (UFRN) Ethical Committee (CEP-UFRN 145-05) and by the Brazilian Committee of Ethics in Research (Comissão Nacional de Ética em Pesquisa, CONEP 12504). The certificate number assigned by CONEP to this study was 006.0.051000-06 (http//:www.sisnep.gov.br).

Data collection and management.

A sample of 808 Hansen's disease cases diagnosed between 1995 and 2006 was selected from the total list of cases reported in Mossoró (N = 1,293 cases). The household in which the case resided when the diagnosis of Hansen's disease was made was geocoded (GPS, Magellan, Magellan Corp., San Dimas, CA). The software ESRI-ArcMap 9.0 (ESRI, Redland, CA) was used to create the layers of the geocoded points using the coordinate system UTM 24S Zone with projection transverse Mercator. The coordinates were plotted in a layered map of 170 census tracts, numbered from 1 to 170, identified by column ID in the dataset. The point data were projected over the layer of census tract polygons for each census sector yielding a map of the area. Demographic information based on the year 2000 census was integrated with the census tracts (http://www.ibge.gov.br). The population residing in Mossoró between 1995 and 2006 was estimated for each census tract using the DATASUS database. The Brazilian Ministry of Health has an agency aimed to collect, process, and make available through a public database, records related to health and demographic issues for the Brazilian population (http://www.datasus.gov.br). The database of the Ministry of Health also contains socio-demographic information and projected intercensus population estimates for each municipality. The Brazilian census is usually conducted every 10 years; the last census was conducted in 2000. The population of the census tract for each year was estimated by combining its reported population obtained in the 2000 census and the estimated municipality population by year as indicated in the DATASUS. Assuming proportional spatial growth, we determined the detection rate of Hansen's disease per year and estimated the RR of disease in each census tracts.

Statistical methods.

Kernel intensity.

The Kernel intensity of the spatial point pattern was estimated using ArcMap 9.0 over the map of cases of disease with the adjusted bandwidth of 270 m and quartic kernel function, which is the function used most commonly to identify spots with high intensity (as seen later in Figure 1). The bandwidth is equivalent to the third percentile of the distance between cases distribution, i.e., 3% of the distances between cases are less than 270 m apart. The Kernel intensity function is an exploratory tool, similar to the probability density function, differing by a constant of proportionality, resulting in a contour or intensity plot.^32–34

Figure 1.

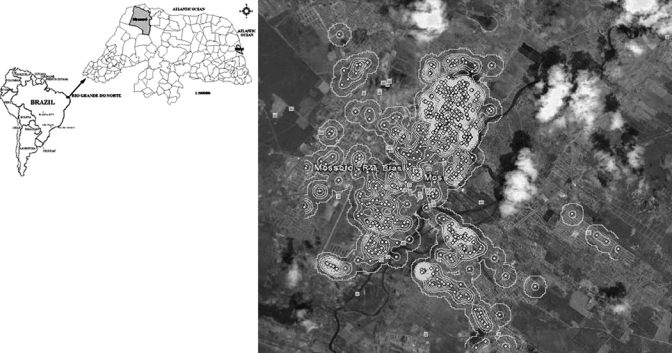
Geographic location of Hansen's disease cases in Mossoró, Brazil. The spots indicate areas of greater risk determined by Kernel intensity. This allowed the estimate of distance between house cases, yielding a map of standard points, which revealed high spatial variation of Hansen's disease cases in the city.

Spatial autocorrelation analysis.

Global spatial autocorrelation analysis was performed in R software version 2.6.1, downloaded on 01/25/2008 (http:/www.r.project.org). We used the sp.correlogram function in the package spdep. Moran's I spatial autocorrelation statistic, which is similar to Pearson's linear coefficient, was used to assess the degree of relatedness of the sets of census tracts with respect to RR, i.e., the extent to which adjoining or neighboring spatial tracts influence the RR on those tracts. The RR of Hansen's disease was calculated in the 170 tracts and data visualized using correlogram. The correlogram is a graph that records the degree of spatial autocorrelation among the set of census tracts at different spatial lags, where the first lag involves adjoining or neighboring tracts, the second lag neighbors of neighbors, and so on. The presence of significant values in the first lags and intense decrease in the subsequent lags assert the existence of significant spatial autocorrelation. Although the correlogram is a good tool to assess patterns of spatial similarity, it is based on a global index,³⁵ possibly placing it under a number of sources like a spatial trend in the expected risk. Furthermore, it can suggest clustering, but it cannot identify individual ones. To identify clusters, we used the localmoram function in Local Indicators of Spatial Association (LISA) using the spdep package in R. The main purpose of LISA indicators is to provide a local measure of similarity (Moran's I) between each census tract and its neighbor, generating the map of P values related to the hypothesis of no autocorrelation in each tract.³⁶ Dark regions on the map indicate the existence of clusters. A Moran scatter plot was plotted using the function moran.plot in spdep from R. It provides a graphic of the points (x, Wx) with a linear regression line superimposed indicating the influence of each point on the global association measure. The vector x represents the census tract's standard RR deviations. W is the spatial weights matrix of proximity among the tracts. Outliers can be visualized as points further than two units away from the origin.^32,33

Spatial cluster analysis.

The implementation of Spatial Scan Statistic for data area, as defined by Kulldorff, has the main goal of finding a collection of adjacent census tracts, among the 170 tracts, which were least consistent with the hypothesis of constant risk. It provides a significance value representing the rarity of the detected cluster, named “the most likely cluster.” It can identify a higher or lower risk cluster. The method defines circles, or ellipses, with radii ranging from the smallest distance between two tracts to one-half of the width of the study area. It identifies a region formed by all tracts whose intercentroid falls within the circle, and tests the null hypothesis of constant risk versus the specific alternative that the risks within and outside this region are different. The test's statistic is a likelihood ratio statistic (LRS) based on the Poisson distribution and defined as

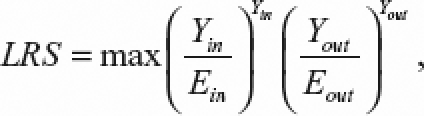where Y_in is the number of cases observed in the region defined by the circle of interest and E_in is the number expected within this region under the null hypothesis. Y_out and E_out are the corresponding number of cases observed and expected occurring outside the region, respectively.

Using Monte Carlo simulation, we generated independent datasets under the null hypothesis and calculated the empirical distribution of LRS for each region to assess the significance of the observed statistic. StatScan version 7.0.3 (http:/www.satscan.org) was applied. The spatial scan methods take into account both areas of high and low risk of disease.

Factorial analysis.

A factorial analysis was performed using census tract data from the 2000 census to determine the spatial dimension of 10 socio-economic variables, which are listed in Table 1. The purpose of this analysis was to extract a few latent variables from the socio-economic variables’ structure and to determine the level of aggregation with the risk of Hansen's disease. The factorial analysis results are sets of statistically independent linear combinations extracted from the socio-economic variables by principal components analysis,³⁴ which is performed on the correlation matrix calculated from the data frame that contained the values of these 10 socio-economic variables in each census tracts (a 170 × 10 matrix). The function princomp in R was used. The varimax rotation was determined in STATISTICA (version 6.0, StatSoft, Tulsa, AZ).

Table 1.

Correlations between each variable and each factor extracted by principal components analysis^*

Variables	Factor 1	Factor 2	Factor 3
Average income	0.1074	0.9623	0.0550
Years-of-schooling	0.2464	0.8501	0.4183
Literacy	0.5140	0.7217	0.2392
Lack of access to get bank loaning	−0.2360	−0.2094	−0.7853
Water-supply	0.7947	0.2922	0.0331
Household with toilet	0.7816	0.2770	0.0933
Number of bathrooms	0.2894	0.9140	−0.0825
Trash collection	0.9390	0.1396	0.0258
Dumping of waste adjacent to the house	−0.9054	−0.1367	−0.0379
Number of residents in the household	0.1074	−0.0042	−0.8680

^*The values in bold are greater than 0.7.

Linear regression models for spatial data.

Spatial linear regression models were adjusted to assess the significance of association between socio-economic factors and the RR of disease,²⁹ i.e., to understand how the tracts with different levels of a factor match with different levels of risk of disease. The function lagsarlm in package spdep from R was used to adjust a spatial simultaneous autoregressive lag model (SAR) of the kind y = ρWy + Xβ + ɛ where y is the vector RR in the census tracts, W is the spatial proximity matrix measuring a tract that is next to the other. X is the design matrix with the covariates (factors) values, ɛ is the vector of random Gaussian error, and ρ and β are estimated parameters where ρ assesses the spatial autocorrelation involving each census tracts and its neighbors by the so-called lag term, ρWy, in the previous formula. On the other hand, ρ is the vector of regression parameters that estimate the association between the covariates and the response y.

The model's parameters were estimated by maximum likelihood methods and we tested the hypothesis H₀: ρ = 0 using the likelihood ratio test (LR test).²⁸ A comparison between the SAR model and an Ordinary Least Square (OLS) model was made by the Wald test, and we used the Lagrange Multiplier test (LM test) to verify the absence of spatial autocorrelation in the model residuals.^33,35 The factors extracted by the principal components analysis were used instead of the original covariates because these were highly correlated, verifying a heavy degree of multicolinearity among these variables, in conformity with a coefficient of multicolinearity degree, CD = 1243.4, greater than 30. This coefficient was calculated using the eigenvalues (e_i) for X′X, where X′ is the transposed matrix of X enclosing the values of the 10 socio-economic variables. Its formula is

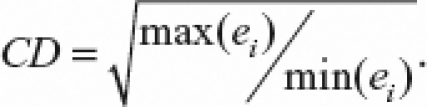A value greater than 30 denotes a strong multicolinearity.³⁶ The RR of the tract was calculated based on the cases and exposed population in and out of the tract. The calculation is performed by using the following expression:

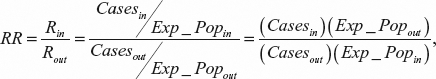where Cases_in and Cases_out are the number of cases in and out of the tract, respectively. Exp_Pop_in and Exp_Pop_out are the exposed population in and out of the tract, respectively. The hypothesis of homogeneous distributions of nominal variables was performed using the χ² test. The comparison of the proportions of disease between males and females was performed by testing the hypothesis H₀: P = 0.5 by a one-sample t student test for proportion.

Results

Spatial aggregation of Hansen's disease in Mossoró, state of Rio Grande do Norte, Northeastern Brazil.

A total of 1,293 cases of Hansen's disease were diagnosed in Mossoró between 1995 and 2006 (Figure 2). There were no differences in Hansen's disease between sexes (P = 0.723), with 48.3% of the cases being males and 51.7% females. The mean age of the cases was 39.6 (±19.5 years). Of these cases, 808 (62.5%) were geocoded and the pattern of distribution and Kernel intensity for these cases is shown in Figure 1. The cases were more frequently found in the proximity of the river, a region with homogeneous population density and a high level of poverty. The study area shown in Figure 1 comprised 8.5 km longitudinal by 12 km latitudinal, with a residing population of 218,591 persons/year. The distance between the house cases was analyzed on a map of point patterns (Figure 1). The spots as determined by Kernel intensity methods revealed areas of greater risk of Hansen's disease with high spatial variation of cases found from 0 to 12 km. The distribution of distance between the house cases had the first quartile q₂₅ = 1,177 m and third quartile q₇₅ = 4,237 m, so 50% of them are between these two values. The mean average distance between house cases was 2,890 m and median 2,841 m, with 10% of the cases falling within 580 m and 5% around 380 m, with a modal value of 750 m (Figure 3).

Figure 2.

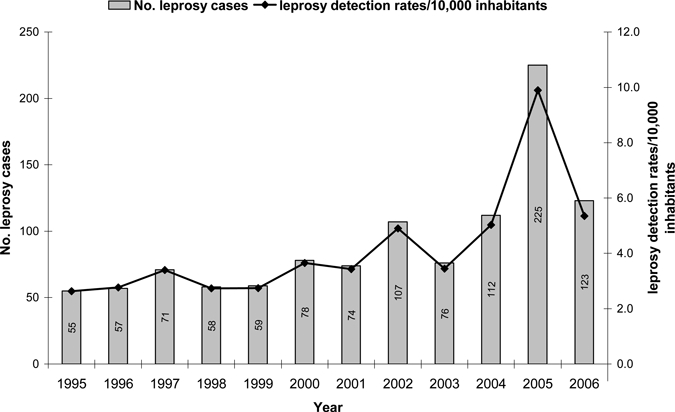
Time series of Hansen's disease cases and the average detection rate per 10,000 people for the city of Mossoró (1995–2006). The graph shows an increase of Hansen's disease cases peaking in 2005. This peak of detection was a result of active surveillance in the area.

Figure 3.

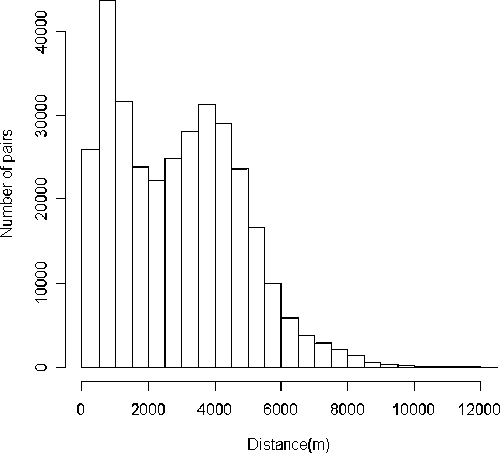
Histogram of the distance between pairs of cases of Hansen's disease in Mossoró determined by Euclidean formula applied into its geographical coordinates. The bimodal distribution indicates the non-random distribution of Hansen's disease cases in the area.

The average detection rate of leprosy ranged from 0.00 to 31.69 cases per 10,000 persons per year and this was calculated for each census tract (Table 2). No cases of Hansen's disease were found in 19% of the tracts, but in 20% of the tracts the detection rate was at least 5.14. Overall, the RR varied from 0.00 to 9.40 (Table 2). The spatial variability of the risk of disease is shown in Figure 4A, where the darker regions in the map indicate increased risk of developing Hansen's disease with an RR over 2.16. The spatial association of Hansen's disease cases in Mossoró was estimated and confirmed by Moran's I correlogram, as shown in Figure 4B. Significant positive autocorrelations in lags 1 to 3 are seen, decaying from the first lag on, indicating the existence of clusters whose ascertainment and localization were performed by the use of the Spatial Scan Statistic and LISA. Using the first method, we tested the hypothesis of constant rate of Hansen's disease throughout the area and found two clusters of Hansen's disease as shown in Figure 4A. The most likely cluster, the main one, was composed by nine census tract of numbers {132, 146, 160, 161, 162, 163, 164, 169, 170}, covering a circle, with a radius of 588 m and an RR of 5.9 (P = 0.001), Figure 4A, cluster A. The second cluster had only one tract number {29} with an RR of Hansen's disease of 6.5 (P = 0.001), Figure 4A, cluster B. Using LISA indicators through the function localmoram in R, the map of P values was generated (Figure 5A) that shows a dark cluster very similar to cluster A in Figure 4A. The Moran scatter plot in Figure 5B, plotted using the function moran.plot identified the tracts in this cluster. They are {141, 147, 159, 160, 161, 162, 163, 164, 165, 166, 170}, verifying that the set of tracts {160, 161, 162, 163, 164, 170} is in the main cluster A. In addition, note that the tract of number {29}, which is the cluster B shown in Figure 4A, is not seen in Figure 5A, because it is isolated, i.e., few cases of Hansen's disease cases are found around it.

Table 2.

Parameters of the detection rate of leprosy and relative risk (RR) per census tract

Parameter	Detection rate	Relative risk
Minimum	0.00	0.00
1st quartile	0.70	0.21
Median	1.82	0.54
Mean	3.24	0.96
3rd quartile	4.13	1.22
Maximum	31.69	9.40

Figure 4.

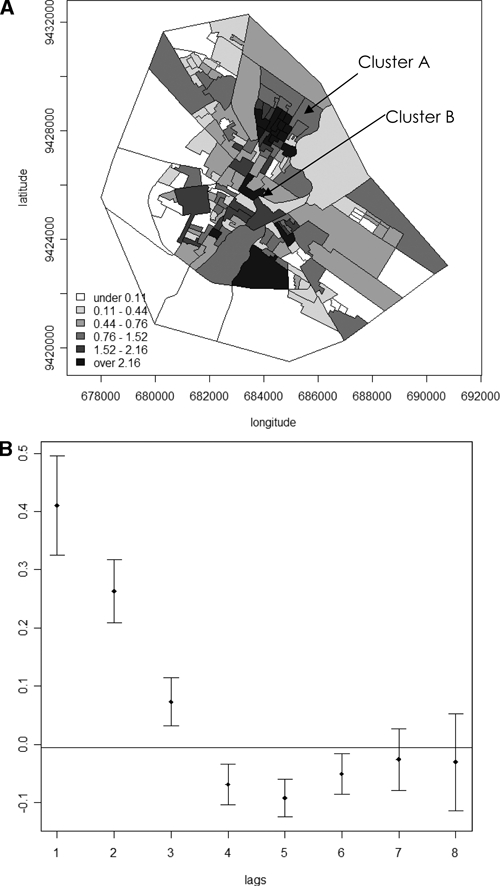
A, Map of relative risk (RR) of Hansen's disease and clusters A and B as determined by the scan statistics Kulldoff's method. B, Moran's correlogram of the RR of Hansen's disease in Mossoró. The correlogram with the Moran's I of the RR and confidences interval are shown in the Y axis. Note that there are high autocorrelations in low lags with high decrease characterizing spatial autocorrelation.

Figure 5.

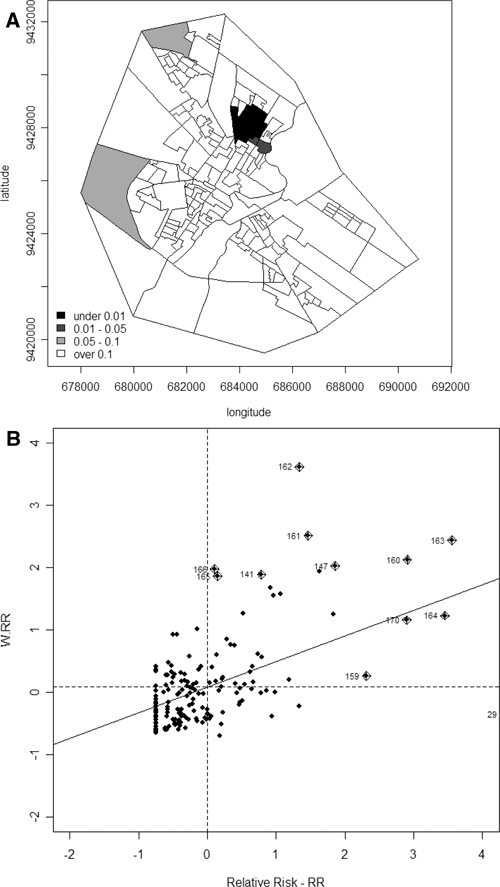
A, Map of the P values (local P value for Moran I) related to the hypothesis tested of no association around each tract. In this map a dark region can be observed, which is the cluster A shown in Figure 4A. Although this cluster resembles cluster A shown in Figure 4A, the cluster B of the same figure cannot be shown by local indicator of spatial association (LISA) because the cluster B is formed by only one tract and therefore it does not present strong association with its neighboring tract. B, Moran scatterplot shows the tracts that present significant association with the neighboring tract. The tracts that are outliers may be easily visualized as points further then two units away from the origin, which are shown in Figure 5A, dark black.

Association of socioeconomic variables in the aggregation of Hansen's disease.

Because high-risk clustering of disease was found, we tested the hypothesis of whether the spatial distribution of Hansen's disease was associated with any socio-economic variables. A high level of multicolinearity was observed among the socio-economic variables. Because this could hide the association between the regressors and the response variable, the model was adjusted with the RR as the response and the three latent factors extracted in a principal component analysis using standard varimax rotation as regressors above the 10 social economic variables. Using this approach, the first factor explained 34.4% of the total variation in the social economic variables; whereas the second and third factors explained 32.5% and 16.2%, respectively, of this variation. This means that these three factors together explained 83% of the total variation observed among the census tracts. The correlations between each variable and each principal factor are shown in Table 1. This analysis showed that the first factor was strongly correlated with the presence of basic sanitation, defined by the existence of piped water, presence of toilets in the house, and trash collection. The second factor represented the level of literacy and income, which was expressed by the mean family income, years of schooling, and number of toilets in the house. Finally, the third factor expressed the level of poverty that can be estimated as the lack of access to banking loans, which in the Brazilian society is a marker of accessibility to formal economy, and the number of people living in a house.

A negative correlation was observed between the lack of access to banking loans and the mean income received by the household head, which can be considered as an indicator of poverty. A spatial linear model was adjusted to estimate the level of association between each principal factor and the RR of disease. A significant association with the factors one and three was detected. Factor 1 had β1 = −0.0978 and P = 0.0331, whereas factor 3 had β₃ = −0.1027 and P = 0.0240. As presented in Table 1, factor 1 had positive correlations with the presence of a water supply (0.7947), household with a toilet (0.7816), and trash collection (0.9390), and negative correlation with dumping the trash outside the household (−0.9054). A high score in this factor indicated better sanitary conditions in the tract, and consequently, a lower RR for Hansen's disease (β1 is negative). In short, the presence of a water supply, of a toilet in the household, and of trash collection reduced the expected risk of Hansen's disease. Conversely, dumping the trash outside the household increased the risk of Hansen's disease. Similar analysis was made considering factor 3. In accordance to the correlations, as shown in Table 1, the greater the score the lower the level of poverty in the tract, the lower the expected RR for Hansen's disease (β₃ is negative). In addition, the lower grade of poverty can be estimated by the lack of access to credit from a bank and increased number of people per household.

The model also showed strong spatial association of the RR (ρ = 0.4919; LR test P < 0.0001). This spatial association is explained by the heterogeneous spatial distribution of the population and possibly by other spatial factors not measured in this study. Although, in general, R² is not an adequate parameter to assess the quality of the adjusted spatial regression model, we found here that it performed better than the OLS model followed by the Wald test (W = 32.126, P < 0.0001). In addition, its residuals lacked autocorrelation in accordance to the LM test (LM = 0.0144, P = 0.9042), indicating that the model used was robust.

Use of the Spatial Scan Statistic and the residual analysis are complimentary methods in determining clustering of diseases, i.e., the residual found by the linear regression model can identify outliers, which in turn could be part of the clusters found by the Spatial Scan Statistic. In this study, 11 outliers from the census tracts were found in the model's estimation as seen in Table 3. These are tracts whose residuals (ɛ) are greater than q₃ + 1.5 (q₃ – q₁), that is beyond the third quartile at least one-and-a-half quartile range. In Table 3, we can see that seven of the tracts are into the clusters detected by the spatial scan statistic, with at least one factor with a score less than its first quartile or close to it, but all have RR greater than the third quartile (1.22). For example, the tract number 29 has RR = 6.50 and score = −1.30 (< q₁ = −0.07) for the factor 2. This tract is the cluster B shown in Figure 4A, which was detected by the spatial scan statistic method. The tract number 146 has the greatest RR of Hansen's disease (RR = 9.39) and a score −1.13 (< q₁ = −0.64) for the factor 1. The tracts of numbers 49, 143, 147, and 159 were not detected by the spatial scan statistic method. They have a low score for at least one factor and were detected by using the residual analysis (Table 3).

Table 3.

Relative risk (RR) and scores^* of the factors of the census tracts considered outliers in the spatial regression model (q₁ = 1st quartile and q₃ = 3rd quartile)

Number of census tract	RR q1 = 0.21 q3 = 1.22	Factor 1q1 = −0.64 q3 = 0.41	Factor 2 q1 = −0.07 q3 = 0.56	Factor 3 q1 = −0.54 q3 = 0.21
29†	6.50	0.44	−1.30	−0.17
49	2.68	2.57	−0.24	0.95
132‡	3.05	−0.45	0.71	0.08
143	3.32	−0.63	0.28	−0.64
146‡	9.39	−1.13	0.24	−0.30
147	3.34	−0.52	0.58	−0.11
159	3.93	−0.07	0.73	−1.11
160‡	4.69	−1.22	0.39	−0.47
163‡	5.53	−1.06	0.43	−0.04
164‡	5.40	−0.85	0.43	−0.03
170‡	4.68	−1.10	0.46	−0.67

^*Scores in bold are smaller than its q₁ or are close to it.

^†Census tract that constitutes the second cluster B detected using the Spatial Scan Statistic.

^‡Census tract into the main cluster A detected using the Spatial Scan Statistic (Kulldorff).

Clinical Hansen's disease.

The clinical presentation of the Hansen's disease cases is shown in Table 4, with 45% of the cases being multibacillary and the remaining paucibacillary. The main cluster of Hansen's disease detected by the Scan Statistic was not a result of the clinical presentation or operational classification of the disease because the rate by type found in and out of the main cluster did not differ significantly. The main cluster is composed of nine census tracts. The distribution of the multibacillary cases was 46.4% in the main cluster and 44.5% outside of the cluster (P = 0.6366). In addition, 26.7% of the cases are tuberculoid pole, with 29.2% within and 25.9% outside of the Main Cluster (P = 0.6049), as detected by the Scan Statistic (Table 4).

Table 4.

Rate of cases by Clinical form and Operational class of leprosy into and out of the main cluster

Clinical form/Operational class	Inside main cluster 9 tracts		Outside main cluster 161 tracts		P value*
	n	Rate	n	Rate
Indeterminate	33	15.79	108	18.37	0.6049
Dimorphous	84	40.19	227	38.61
Tuberculosis	61	29.19	152	25.85
Vichowiana	31	14.83	101	17.18
Total case	209	100.00	588	100.00
Paucibacillary	112	53.59	329	55.48	0.6366
Multibacillary	97	46.41	264	44.52
Total case	209	100.00	593	100.00

^*M–L χ² test, homogeneous distribution.

Discussion

Until 20 years ago, few cases of Hansen's disease were detected yearly in Rio Grande do Norte. More recently, improved active case detection increased detection of hidden cases, leading to an increase in detection rates in some municipalities including the city of Mossoró.³¹ This study was performed based on the analysis of 808 cases of Hansen's disease, which corresponded to 62.5% of all cases of Hansen's disease diagnosed in the study period in Mossoró. Similar to Mossoró, other areas in Brazil have also been showing an increase in case detection.^37,38

The study of leprosy transmission in Mossoró, Brazil, was performed by identification of maps and by geographical epidemiology tools. We tested the hypothesis to determine whether this distribution was random, i.e., whether there was a constant risk of Hansen's disease throughout the areas or whether there was spatial association. Because of the existence of several statistical tools that can be used to test this hypothesis, each one with specific attributes, we chose to use Kernel intensity, Moran's correlogram, LISA indicators, Moran's scatter plot, spatial scan statistics, and SAR modeling to validate the results obtained from each analysis. These combined analyses provided a more consistent diagnostic, with more substantial conclusions, than could have otherwise been obtained by using any one statistical approach alone.²⁸

Kernel intensity was the first tool used to evaluate the intensity of disease from the points map. In an epidemiological setting, the intensity of cases of disease per unit area varies with the population density. One way to correct this is to divide the Kernel by the population density. In our study, there was no need to perform this adjustment because the population was very homogeneous. From our analysis, we concluded that the use of the following three tools provided a good procedure to analyze the spatial association. The Moran's correlogram assessed the global associate in distinct lags. The LISA indicators decomposed the global index in all census tracts and allowed us to visualize clusters of tracts with significant association with their neighbors. Finally, the Moran's scatter plot allowed us to identify tract outliers. As it is known,²⁸ the use of Moran's I as a global indicator of spatial association to rates of regional data merits some precautions, because it can be under the influence of trends in the spatial data and might show an association that is not real. Therefore, we used the correlogram to resolve this problem. The correlogram in Figure 4B shows a quite high positive correlation at lag one, where only neighboring tracts are considered, and a fast decrease at further lags is observed. This may be evidence of spatial association and clustering, rather than regional trends, justifying, for example, the presence of cluster as shown in Figure 4A. Conversely, the scan statistics method validates the clusters found by the previous methods and the SAR model was used as a supplementary approach to help us refine our conclusions, quantifying the nature of the association between spatial referenced RR and a set of others evenly referenced variables. The analysis of its residuals contributed to determining the outliers. In this way, the combination of these methods permitted us to develop a model to analyze clustering of Hansen's disease in Mossoró with consistency. This model can now be used to design strategies for disease control. It also has the potential to be tested in other areas, taking advantage of census information and geographic location of a particular disease.¹⁹

The application of this combination of spatial statistics in Mossoró clearly showed the spatial aggregation of Hansen's disease cases in that city. This lead to rejection of the hypothesis of constant risk of disease throughout the area and showed the existence of two clusters of tracts with significant RR. In addition, the SAR model illustrated that the distribution of disease was clearly associated with poverty and population density. A significant association between Hansen's disease risk and socio-economical factors, such as availability of water supply, trash collection, and level of poverty, was observed in this study. The association of factor 3 with risk of disease indicates that there is higher chance of close contacts being infected, because one of the variables that influences factor 3 is the number of residents in the household, representative of high population density. Similar to this finding, other studies conducted in Brazil have shown that indicators of poverty are usually associated with increased risk of Hansen's disease in endemic areas.^38,39 Contacts of Hansen's disease patients have a higher risk of developing clinical Hansen's disease.^40,41 A study conducted in Bangladesh showed that 67% of the high-risk contacts lived within 10 m from a Hansen's disease case. The GIS used in this study allowed the identification of the high-risk areas, showing the power of this type of technique to determine areas at risk of disease.⁴² The outliers found by the residues of the SAR model confirmed the high-risk areas. Outliers are sectors in which the risk observed is distinct from the expected pattern in conformity to a model.

This type of analysis is an important asset in surveillance for transmissible disease, aiding the design of more focused intervention strategies. The space-time scan statistic may be used for either a single retrospective analysis, using historic data, or for time-periodic prospective surveillance, where the analysis may be repeated yearly.^29,43 Finally, as this study confirms, tools such as GIS and Spatial Statistics Analysis allow a better understanding of the epidemiology of Hansen's disease, and can also be used for other infectious diseases such as tuberculosis^19,44–47 and vector-borne diseases.^48–51 In such studies, the spatial linear regression model can take into account factors related to the vector, environmental characteristics, and landscape coverage.

In summary, our study suggests that a more detailed investigation in highly endemic areas can identify other factors that contribute to Hansen's disease and point out the need for intervention. However, the model tested herein did not explain fully the other additional risk factors involved in clustering of the disease. Other risk factors need to be considered, including human genetic factors. Several studies have shown that there is a genetic risk to developing clinical forms of leprosy.^52–56 Our continuing studies are also designed to apply the power of genome-wide association studies to the analysis of Hansen's disease in this region. This will provide the data that will help determine novel modifiable environmental variables that can be incorporated into analysis of the spatial distribution of disease to understand the risk of developing diseases such as Hansen's disease.^57,58