A Finite Element Inverse Analysis to Assess Functional Improvement during the Fracture Healing Process

Abstract

Assessment of the restoration of load-bearing function is the central goal in the study of fracture healing process. During the fracture healing, two critical aspects affect its analysis: (1) material properties of the callus components, and (2) the spatio-temporal architecture of the callus with respect to cartilage and new bone formation. In this study, an inverse problem methodology is used which takes into account both features and yields material property estimates that can analyze the healing changes. Six stabilized fractured mouse tibias are obtained at two time points during the most active phase of the healing process, respectively 10 days (n=3), and 14 days (n=3) after fracture. Under the same displacement conditions, the inverse procedure estimations of the callus material properties are generated and compared to other fracture healing metrics. The FEA estimated property is the only metric shown to be statistically significant (p=0.0194) in detecting the changes in the stiffness that occur during the healing time points. In addition, simulation studies regarding sensitivity to initial guess and noise are presented; as well as the influence of callus architecture on the FEA estimated material property metric. The finite element model inverse analysis developed can be used to determine the effects of genetics or therapeutic manipulations on fracture healing in rodents.

INTRODUCTION

Approximately 10–20% of the 6.2 million annual bone fractures result in non-unions, causing significant morbidity and mortality (Einhorn, 1995; Marsh, 1998). In long-bones, fracture healing proceeds through the formation of a cartilaginous template that is then replaced by bone that undergoes remodeling (Einhorn, 1998). A critically important function of bone healing is that the healing tissue provides sufficient mechanical stabilization such that a return to functionality is possible. Experimental studies on fracture healing have largely been dependent on rodent models. However, the lack of sensitive methods to monitor and relate the fracture mechanical properties with tissue type renders those studies inadequate to fully evaluate the fracture healing patho-physiology.

Assessment of fracture healing has relied on histological, imaging, and biomechanical testing (BMT) (Gerstenfeld et al., 2005). Histological methods allow the visualization of tissue-specific molecules over histological sections by in-situ hybridization, immunohistochemistry, or specific staining. However, comparisons between sections are difficult and true quantitative assessment is unrealistic. Furthermore, histological methods are limited to post-mortem analysis and cannot provide functional information. Various imaging modalities have been used to assess the fracture healing, such as micro-computed tomography (μCT), magnetic resonance, and positron emission tomography (Cattermole et al., 1996; Grigoryan et al., 2003; Ciprian et al., 2004; Lynch et al., 2004; Severns et al., 2004; Schmidhammer et al., 2006; Hsu et al., 2007; Saran and Hamdy, 2008). μCT imaging is mostly used due to advantages in 3D reconstructions. However, imaging provides no information about tissue types and mechanical properties. BMT remains the gold standard for the functional assessment of fracture healing. Standard BMT analyses use force versus displacement data and analytic calculations based on beam theory to generate mechanical property information. Beam theory calculations rely on the assumption of a homogeneous cross section, but because of the irregular geometry of the callus, these calculations are strongly biased by geometrical factors (van Lenthe et al., 2008).

Some studies have explored coupling μCT imaging with finite element analysis (FEA) to predict the mechanical behavior based on geometrical information. In particular, studies have evaluated μCT attenuation to stiffness value transformations to provide material properties and found empirical power law relationships between modulus and bone mineral content assessed by μCT attenuation/density (Bourne and van der Meulen, 2004; Shefelbine et al., 2005). Shefelbine and colleagues have also reported a weak correlation between predicted and experimental torsional rigidity with a very poor predictive value in calluses studied at early healing stages when mineralization is low (Bourne and van der Meulen, 2004; Shefelbine et al., 2005). It is quite apparent that the direct relationship between μCT attenuation/density and mechanical parameters is unclear and is to some degree unsatisfactory; and when factoring in the potential for variability of this relationship across experimental systems, it is unlikely that the correlation will improve.

In our studies, rather than using a μCT-to-stiffness empirical relationship, we have used an elastographic approach to directly generate values for mechanical parameters. Our approach combines an inverse finite element model of the subject s cartilage/bone geometry (μCT/histological imaging data), data acquired from BMT, and numerical optimization techniques to characterize the callus mechanical properties. This approach does not require calibration per system but rather is an active reconstruction parameter that can be measured experimentally. The concept of an inverse FE analysis method to determine the mechanical parameters to monitor the progression of fibrogenic diseases has been demonstrated. These techniques are more widely referred to as elastography (Ophir et al., 1991; Greenleaf et al., 2003; Washington and Miga, 2004; Miga et al., 2005; Barnes et al., 2007; Samani and Plewes, 2007; Ou et al., 2008). Within this work, the approach is used to evaluate mechanical properties as a biomarker in the assessment of fracture healing progression. Quantifying the change in mechanical properties during the fracture healing process may provide information that: (1) allows to determine when healing has failed to progress, (2) suggests the need for intervention in non-union/slow healing fractures, and (3) evaluates the effectiveness of treatments that aim to enhance the healing process through the formation of more mechanically competent tissue.

METHODS

Generation of the Computational Model

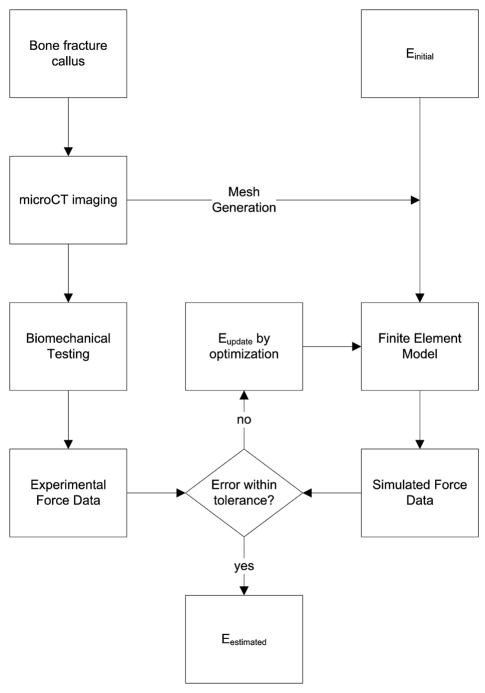
An inverse FEA procedure was developed to determine the stiffness of the callus based on μCT imaging and BMT data. As summarized in Figure 1, the procedure begins with the establishment of an assumed Hookean linear elastic tissue model framework for the bone/callus system. The process continues with the development of a bone/callus computer model of the subject generated from μCT image volumes. A volumetric tetrahedral grid is then generated to represent a FE mesh system.

Figure 1.

General framework of the inverse material property estimation method. The modulus of elasticity is iteratively determined by comparing model calculated forces to BMT forces.

The boundary conditions for the model were chosen to reflect the BMT protocol, in which the top boundary is prescribed a fixed upward normal displacement with no lateral displacement (Dirichlet boundary conditions). The bottom surface was also fixed in both the normal and lateral direction. The remaining boundary conditions for the sides of the model were stress free. The displacement criteria selected for each sample was based on the individual force/displacement curve obtained from BMT. A series of four displacements were taken along the curve at 25%, 50%, 75%, and 100% of the linear elastic limit to reproduce the linear portion of the curve. As pointed out in Figure 5, the linear elastic limit was defined as the point at which the curve exhibited plastic deformation (slope ≤ 0 in our case). Solutions to the elastic system are then generated as reported previously (Barnes et al., 2007). As shown by Barnes and colleagues, the unused Galerkin equations associated with the implementation of the Dirichlet boundary conditions are utilized post model-execution to estimate the local boundary stress (Barnes et al., 2007). This stress is then averaged over the tensile boundary surface and multiplied by the surface area to generate a model-calculated average force (F_calc) applied to the bone surface for the given displacement. The model is solved at each displacement value to generate 4 model-calculated average forces which are compared to the corresponding forces measured from the force/displacement curve in a least squares sense and properties of the callus determined through an iterative optimization process. A further discussion of the inverse problem framework is discussed the Supplemental Material.

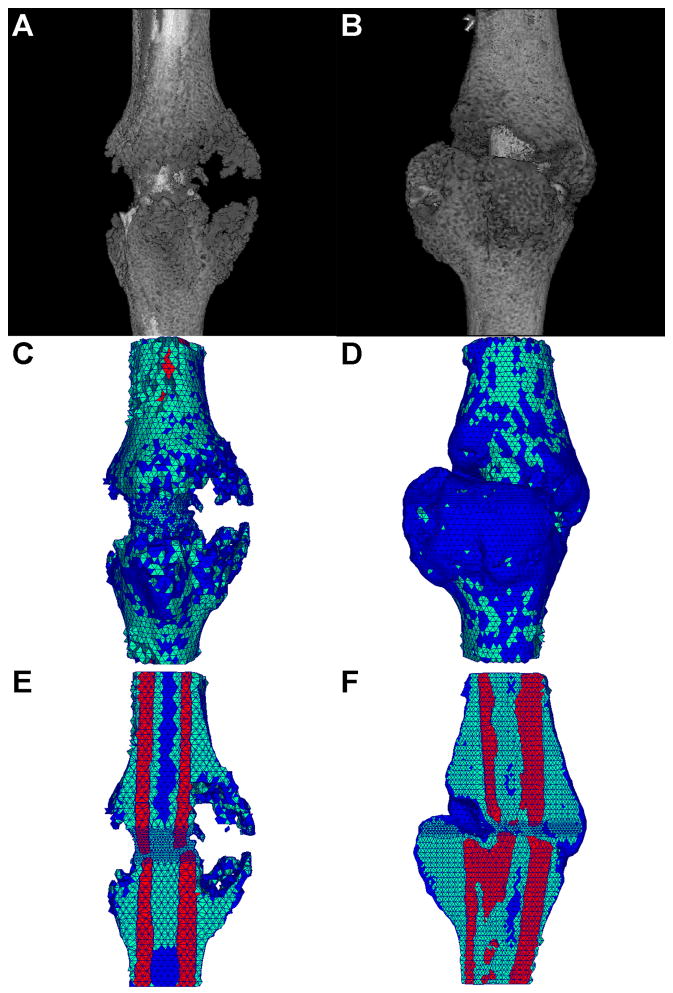
Figure 5.

(a,b) Representative μCT 3-D reconstructions for mouse tibia fracture, (c,d) corresponding tetrahedral FE meshes, (e,f) cut-away images of the tetrahedral FE meshes showing internal elements and material types. Element colors represent material type of bone (red), callus (green), and void (blue). (a,c,e) 10 day post fracture, (b,d,f) 14 day post fracture.

Experimental model

Mouse Stabilized Tibia Fracture Model

Female FVB-NJ mice (Jackson Laboratories) 8–12 weeks old were anesthetized using isofluorane to provide deep anesthesia. Pin stabilized mid-diaphyseal tibia fractures were generated by insertion of a 0.25 mm stainless steel pin (Fine-Science-Tools) through the tibial tuberosity followed by fracture creation using a three-point bending device with a standardized force. Immediately following tibia fracture, 0.5 mg/kg of bupremorphine was administered for pain control. On post-fracture days 10 and 14, mice were euthanized, fractured tibias were dissected and wrapped in PBS soaked gauze and stored at −80 °C until further analysis. Animal studies were approved by the Institutional Animal Care and Use Committee at Vanderbilt University Medical Center and the University of North Carolina at Chapel Hill.

μCT Callus Imaging and μCT/Histological Thresholding Analyses

CT scans were performed using a Scanco μCT 40 scanner (Scanco Medical) and were obtained at 55 kVp, 145 μA, 300 ms integration time using 12 μm voxel resolution along 5.2 mm length centered at the fracture line (Reynolds et al., 2007). μCT reconstructions were used for subsequent FEA and volume measurements. To determine material type (newly mineralized bone, highly mineralized bone and cartilage) and quantify callus volumes from μCT scans, a parametric thresholding study was performed by serial μCT scanning and histological analysis as more extensively reported within the Supplemental Material.

BMT Analyses

Fractured tibia ends were embedded into a polymethylmethacrylate cast using custom designed testing fixtures, leaving the fracture callus exposed. Specimens were kept fully hydrated with PBS during the entire testing procedure. The fixtures were loaded into an Enduratec Electroforce 3100 mechanical tester (Bose, Enduratec Systems Group) and tested in tension at a fixed displacement rate of 0.25 mm/min using a 22 N transducer (Honeywell Sensotec) for force data (Colnot et al., 2003). Displacement and force were recorded until failure and used for subsequent FEA and to determine biomechanical metrics of fracture healing. Additional descriptions can be found in the Supplementary Material.

Generation of Subject Specific FE Models

Subject specific FE models were generated for 6 tibias (three each at 10 and 14 days post-fracture). After using the imaging protocol above, μCT image sets were semi-automatically segmented and boundary descriptions (as described by 3D points and 3D triangular patches) were generated through the use of a marching cubes algorithm in a commercially available image analysis software (Analyze, AnalyzeDirect) for both the entire bone/callus and solely the cortical bone. Boundary descriptions of each were then used to create a heterogeneous FE tetrahedral mesh consisting of two properties (i.e. cortical bone and other material) using custom-built mesh generation methods (Sullivan et al., 1997). Once the 3D mesh is created, an image-to-grid approach is utilized which determines the voxel intensities within each tetrahedral element from the imaging domain and assigns properties based on thresholding.

Values of Poisson s ratio were assumed for all tissue types (0.3 for bone and 0.45 for callus) based on the literature (Shefelbine et al., 2005) and values associated with the near-incompressible nature of soft tissue. In addition, the cartilage and low-mineralized bone were lumped into a single isotropic property. The value of the void space elastic modulus was assumed as 0.1 Pa (many orders of magnitude below callus value). Reported values of the cortical bone modulus range from ~4 GPa to ~21 GPa (Choi et al., 1990; Jamsa et al., 1998; Schriefer et al., 2005). Because of this large variability, we tested the inverse FEA modulus estimations to explore the impact of different cortical bone modulus values using respectively 5, 10 and 15 GPa. As reported in Supplemental Table I, we found that the estimated callus elastic modulus did not change with the assumed cortical bone modulus (maximum of ~4.5% difference, not statistically significant). Thereafter, the 5 GPa value has been used in all the studies performed.

Simulation Studies

A cylinder mesh with three layers was created to simulate a simplified appearance of a bone fracture callus, as seen in Figure 2. The simplified geometry allows analytic comparisons to FEA results. Simulations were then performed on the cylinder mesh to test the accuracy and sensitivity of the inverse FEA procedure upon initial guess, with material properties approximating that of bone and callus (5 GPa and 1 MPa, respectively) and radius and total height of 1 mm and 6 mm, respectively. To gauge accuracy of the simulations, the forward elastic model was used to calculate boundary normal surface forces for a step displacement corresponding to 0.5% strain and compared to an analytic calculation of the surface normal force (derivation in Supplementary Material). The dependence of the elastographic framework on initial guess was also tested by executing simulations with five random initial callus modulus guesses.

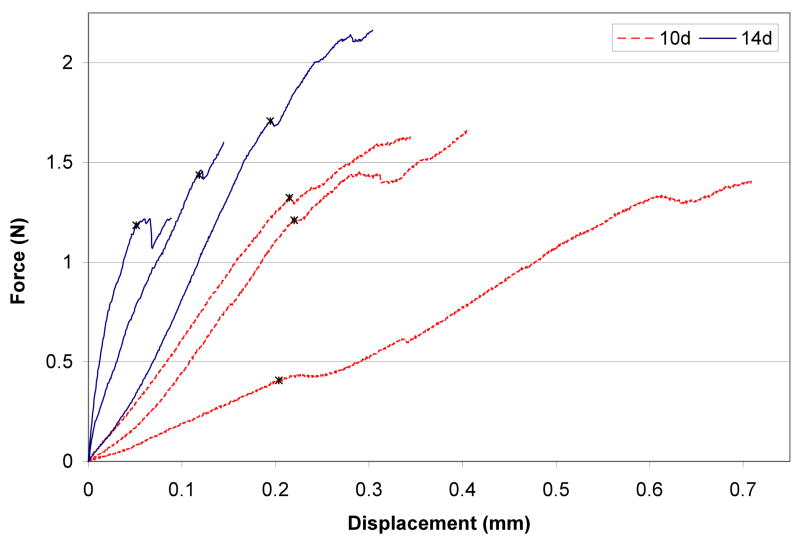
Figure 2.

BMT force versus displacement data of each tibia fracture callus tested at day 10 and day 14 post fracture during tensile testing. Note the wide sample variation within each group, demonstrating confounding geometrical effects. Asterisk denotes linear elastic limit.

In a separate simulation study, two meshes created from μCT imaging of a representative post-fracture day 10 and 14 tibia were used as realistic geometries for further simulation analyses. To examine the effect of mineralization compositional differences in the callus on the estimated lumped elastic modulus parameter, meshes at the two time points (representing two different phases of mineralization) were used to estimate the combined callus modulus. The callus material in the mesh was subdivided into new bone and soft tissue portions and assigned separate Young s modulus values of 10 MPa and 0.1 MPa, respectively (values were arbitrarily selected to fit to actual experimental results, but are based on magnitude differences of 100 fold that have been previously suggested (Shefelbine et al., 2005)). The effect of transducer noise on the inverse FEA method was also examined through the addition of Gaussian noise.

Ex Vivo Studies

Day 10 and 14 post-fracture tibias were subjected to the material property estimation analysis, whereby force versus displacement curves obtained from the mechanical tests were used in conjunction with the meshes generated from μCT scans to determine callus material properties. In addition, the following metrics were analyzed: (1) ultimate load, (2) toughness, (3) apparent stiffness, (3) normalized apparent stiffness, (4) total bone volume, and (5) total callus volume. More details are reported in the Supplementary Material.

Statistics

Data are expressed as mean ± SD. Statistical analyses were performed using unpaired Student s t-test, The Graph-pad Prism Software and the Power and Sample Size package software were used. Statistical significance was set at p<0.05; statistical power was set at 0.9

RESULTS

Simulation 1: Validation of the FEA Model

To validate the FEA model, the simulation cylinder mesh was compared against an analytic calculation. The model was prescribed fixed displacement of 0.5% strain and the average normal surface force was calculated from the forward FEA model as described in the Methods. The average surface normal forces were calculated as 45.0347 mN and 47.1050 mN for the model and analytic calculations, respectively, representing a 4.40 percent error in the model versus the analytic calculation, which is reasonable given the level of discretization and the type of element used.

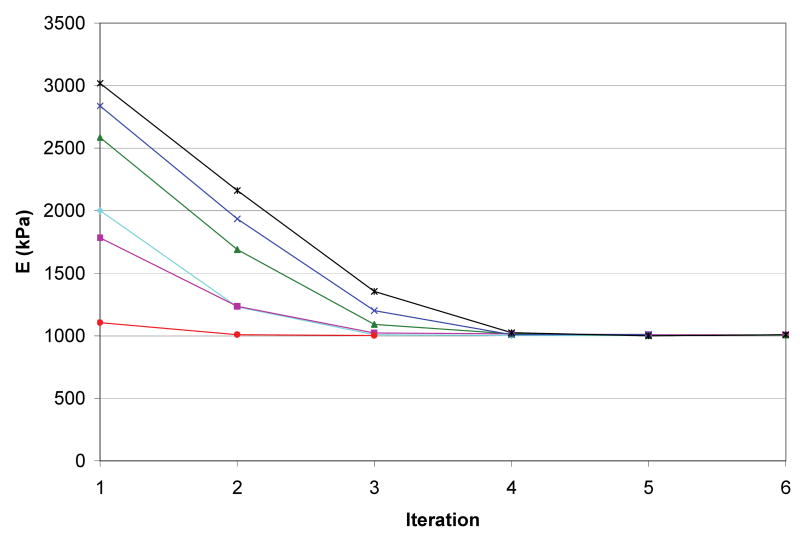
Simulation 2: Sensitivity of Material Property Estimation on Initial Guess

To determine the sensitivity of the material property estimation method, the forward FEA model was run as described in the Methods to generate model calculated average surface normal forces at 4 strain increments (0.5, 1.0, 1.5, and 2.0 percent strain). These results were then used as the “experimental force transducer” input along with multiple random initial guesses for the callus material property. The material property estimation was executed with varying initial guesses to determine the accuracy of the model to converge on the known material property given a random initial material property guess. As shown in Figure 3, the solution to the material property estimation converged to the correct value of 1 MPa (within 1.74 % maximum error) for all initial guesses tested.

Figure 3.

Cylinder mesh representing a simplified appearance of a bone fracture callus used for simulation studies. The proximal and distal layers represent the bone ends (red), while the intermediate layer represents callus (blue). Each geometrically identical layer is assumed to be a homogeneous material of dimension similar to that of a bone fracture callus.

Simulation 3: Lumped Parameter Estimation and Sensitivity of Force Transducer Error

Representative callus meshes from 10 and 14 days post-fracture were used in simulations in which the callus was subdivided into new bone and soft tissue with modulus values as described in the Methods. The forward model was used to determine boundary normal surface forces for displacements of 0.1, 0.2, 0.3, and 0.4 mm, which were then used as the transducer force inputs to the inverse FEA with one lumped parameter corresponding to the total bulk callus modulus of elasticity. As shown in Table I, the estimated callus moduli were 1930 and 3538 kPa for the 10 and 14 day post-fracture callus meshes, respectively. These data demonstrate that changes to the new bone volume fraction (new bone/callus volume) between days 10 and 14 post-fracture result in an estimated bulk modulus of ~ 2 fold. This simulation provides some understanding of how a lumped parametric model is affected by the new bone volume fraction. The effects of transducer noise was simulated by generating noisy data sets through the addition of random Gaussian noise of 0, 1, 2, 4 and 8 standard deviations of the force transducer s listed accuracy [± 0.15 % of full scale (22 N)] to each force data point on the loading curve of the previous simulation. The noisy data sets were used to define the effects of force transducer noise on the estimated material property accuracy. As shown in Table I, the maximum error in the stiffness estimation procedure was observed as 3.89% for the addition of 8 standard deviations of transducer noise (an unreasonable case). For the realistic scenario of 1 standard deviation of noise, the error in estimation was 9.83 kPa and 12.97 kPa, corresponding to 0.51% and 0.37% error for the 10 and 14 day calluses, respectively. This suggests that transducer noise plays little part in the overall error of the method.

Table I.

Simulation results of estimated callus elastic modulus and effects of simulated transducer noise through the addition of 0, 1, 2, 4, and 8 standard deviations of noise.

Standard deviation of noise	Emodel,10d (kPa)	% error in E10d	Emodel,14d (kPa)	% error in E14d
0	1930	0	3538	0
1	1920	0.5094	3525	0.3667
2	1919	0.5870	3543	0.1355
4	1949	0.9651	3553	0.4193
8	1855	3.891	3471	1.903

Simulation 4: Material Property Estimation in Mouse Tibia Fracture Callus

Representative μCT reconstructions, corresponding meshes, and cross-sections of the meshes for both 10-day and 14-day groups are shown in Figure 4. μCT volume quantifications reported in Table II, showed a trend over an increase of callus volume and mineralization in 14 versus 10 days post-fracture. Model generated material property estimations are also compared to other biomechanical fracture healing analysis metrics (apparent stiffness, normalized apparent stiffness, and callus volume). The inverse FEA was the only test to be statistically significant in estimating a modulus that was ~4 fold increased in the 14 days post-fracture calluses compared to day 10 post-fracture (Table II). With 3 mice in each group the inverse FEA had the statistical power to detect a difference (power=0.9, alpha=0.05) between groups. These data indicate that the inverse FEA approach is sensitive to detect architectural changes that occur within the callus during the mineralization process. Although the unprocessed BMT data generated a trend of increasing stiffness for the 14 day over the 10 day post-fracture specimens, this parameter as well as all the others measured did not reach statistical significance. A large data variation was observed between samples, as clearly shown in Figure 5 that depicts the unprocessed BMT data for each sample. This large sample variation persisted following normalization of the apparent stiffness by maximal cross-sectional callus area and length, indicating the inadequacy of these types of normalizations.

Figure 4.

Convergence plot of cylinder mesh simulation with varying initial guess. The modulus of elasticity (E) converged to the optimal solution (1000 kPa) for all initial guesses tested.

Table II.

Comparison of BMT and CT fracture healing analysis metrics with estimated callus elastic modulus for 10 and 14 days post fracture samples. Numbers are expressed as mean +/− SD and P values are reported using unpaired Student’s t-test.

	10 d (n=3)	14 d (n=3)	P Value
Ultimate Load (N)	1.560 ± 0.1370	1.643 ± 0.4888	0.7902
Toughness (N*mm)	0.4059 ± 0.08796	0.1957 ± 0.1567	0.1127
Apparent Stiffness (N/mm)	4.744 ± 2.345	13.95 ± 6.241	0.0751
Normalized Apparent Stiffness (kPa)	3885 ± 1800	8330 ± 4941	0.2170
Total Bone Volume (new bone + cortical bone) (mm^3)	4.051 ± 0.1183	5.894 ± 1.355	0.0788
Total Callus Volume (soft tissue + new bone) (mm^3)	4.391 ± 1.051	8.772 ± 3.772	0.1257
Eestimated (kPa)	797.1 ± 414.3	2908 ± 872.8	0.0194*

^*denotes statistically significant difference.

DISCUSSION

In this study we have developed an inverse FEA procedure to determine the elastic modulus in mouse tibia fracture callus based on μCT/histological threshold data and data acquired from tensile BMT analyses. The FEA showed: 1) less than 5% error compared to the analytic calculations; 2) a sensitivity of material property estimation within 1.74% maximal error; 3) to be appropriately sensitive in estimating the modulus changes expected during two distinct time points of the fracture healing process.

The healing length of the stabilized mouse tibia fracture model is ~28 days (Hiltunen et al., 1993). We have performed our studies at post-fracture days 10 and 14. As assessed by histological analyses in this time window the callus is in its most active healing phase and has not yet reached the remodeling phase (Hiltunen et al., 1993). It is reasonable to assume that the mechanical properties of the callus should become progressively better and more functionally stable over time. As a result, metrics focused at assessing healing should improve between these time points. BMT has been considered the gold-standard technique to assess the mechanical properties of the callus and therefore the healing progression. However, in our studies we found that BMT was not sensitive to detect significant differences in any of thee metrics between the time points studied. It is likely that the mechanical improvement has been masked by confounding geometrical factors that determined a wide data variation, even after maximal cross-sectional area and callus length normalizations. These BMT data, left alone, would have led to the paradoxical conclusion that a rapid healing progression would not be reflected by an improvement in mechanical stability. This lack of BMT sensitivity clearly highlights the need for alternative methods to detect material property changes during the healing process. Since the large variance of the apparent stiffness measurements, it is possible that the inability of this method to detect a difference may be due to the small sample size. We estimated that 6 mice for each group would have been needed to get a statistical power of 0.9. On the other hand, using equal power analysis, only 3 mice for each group were needed to detect a difference between groups using the inverse FEA model. This indicates that because of the small variance, our model is powerful in detecting subtle differences in material properties therefore reducing the usage of mice, experimental time and expenses.

Through simulation studies, the inverse FEA approach developed in this work is shown to accurately calculate surface normal forces and to converge on a preset modulus value using random initial guess in the presence of transducer noise. Through ex vivo specimen analysis, the approach was able to detect a difference in the callus material modulus of ~4 fold from post-fracture day 10 to day 14. Taken together with the simulation analysis of callus meshes with both new bone and cartilaginous tissue material components, these data suggest that between 10 and 14 days post-fracture, there is a significant change in material composition (new bone volume fraction) that results in stiffness increase. In future studies, the inverse FEA approach will allow for establishing the temporal pattern of material property changes throughout the entire course of the healing process in normal and genetically/therapeutically manipulated fracture calluses.

In our model we have only incorporated the linear component of the force/displacement curves, but fracture healing can also be characterized by both geometrical and material nonlinearities. We recognize that our model in lacking the nonlinear component has some limitations, however, as depicted in Figure 5 the linear component accounts for 75 ± 24.2% of the curve(s) indicating that a significant amount of the callus follows a linear modality in force/displacement testing. We acknowledge that this analysis only begins to address the question of constitutive modeling, but, it is important in that it demonstrates that first order approximations of subject specific models offer discriminatory power regarding fracture healing state analysis.