Abstract
To guide development of robotic lower limb exoskeletons, it is necessary to understand how humans adapt to powered assistance. The purposes of this study were to quantify joint moments while healthy subjects adapted to a robotic ankle exoskeleton and to determine if the period of motor adaptation is dependent on the magnitude of robotic assistance. The pneumatically-powered ankle exoskeleton provided plantar flexor torque controlled by the wearer’s soleus electromyography (EMG). Eleven naïve individuals completed two 30-min sessions walking on a split-belt instrumented treadmill at 1.25 m/s while wearing the ankle exoskeleton. After two sessions of practice, subjects reduced their soleus EMG activation by ~36% and walked with total ankle moment patterns similar to their unassisted gait (r2 = 0.98±0.02, THSD, p>0.05). They had substantially different ankle kinematic patterns compared to their unassisted gait (r2 = 0.79±0.12, THSD, p<0.05). Not all of the subjects reached a steady state gait pattern within the two sessions, in contrast to a previous study using a weaker robotic ankle exoskeleton (Gordon and Ferris 2007). Our results strongly suggest that humans aim for similar joint moment patterns when walking with robotic assistance rather than similar kinematic patterns. In addition, greater robotic assistance provided during initial use results in a longer adaptation process than lesser robotic assistance.
Keywords: Gait, powered orthosis, locomotion, inverse dynamics, joint kinetics, EMG
Introduction
Robotic lower limb exoskeletons hold considerable potential to improve human mobility, serve as gait rehabilitation tools, and study the physiology of human locomotion (Ferris, Sawicki et al., 2005; Ferris, Sawicki et al., 2007). In order to guide robotic exoskeleton development, it is critical to identify principles of human motor adaptation and to discover the parameters that affect the rate of motor adaptation to the powered assistance. However, there are only a handful of studies that have quantified the human motor response to powered lower limb exoskeletons compared to the number of different exoskeletons being developed around the world. This is a hurdle to future exoskeleton development that needs to be overcome (Dollar and Herr, 2008).
Being able to predict some gait dynamics parameters that remain fairly invariant with and without exoskeleton assistance would greatly aid in robotic exoskeleton design. This would allow engineers to reliably estimate the mechanical output of the exoskeleton during different tasks. One possible parameter of gait dynamics that could be used for predicting exoskeleton behavior is the overall support moment during stance. Winter (Winter, 1980; Winter, 1989) demonstrated a consistent pattern across a range of speeds when summing extensor moments from the hip, knee and ankle joints during stance in human walking. More generally, it seems that kinetic parameters have better predictability across walking speeds than kinematic parameters (Lelas, Merriman et al., 2003; Shemmell, Johansson et al., 2007). Dynamic torques generated from hip, knee and ankle have been found to be tightly coupled during the swing phase of gait as well (Shemmell, Johansson et al., 2007). The findings from these studies support the idea that joint moments may be intrinsically represented in the neural control of human walking and that they have an important mechanical consequence on the gait dynamics (Winter and Eng, 1995; Prilutsky, Sirota et al., 2005).
In a recent study from our laboratory, we examined how healthy young subjects adjusted to a robotic ankle exoskeleton under proportional myoelectric control (Gordon and Ferris, 2007). When the exoskeleton mechanical assistance was first introduced, subjects walked on the ball of their foot due to the increased plantar flexion torque. By the end of two thirty-minute training sessions, subjects had substantially reduced soleus electromyography (EMG) amplitude by ~35% and reached steady state walking dynamics (Gordon and Ferris, 2007). That study found that subjects had adopted kinematic patterns with exoskeleton assistance that were similar to kinematic patterns without assistance but did not measure joint kinetics via inverse dynamics.
Another important issue related to robotic exoskeletons is the period of motor adaptation required to smoothly use the exoskeleton assistance. In our previous study (Gordon and Ferris, 2007), we measured changes in electromyographic, kinematic, and kinetic parameters during training to determine how much walking practice was required to reach steady state dynamics. Interestingly, we found that using gastrocnemius EMG for control instead of soleus EMG (Kinnaird and Ferris, 2009), or using a kinematic based controller instead of proportional myoelectric control (Cain, Gordon et al., 2007) did not result in different times to reaching steady state in naïve users of the robotic ankle exoskeletons. Thus, it may be that the mechanical capabilities of the robotic exoskeleton are what determine how long it takes to adapt to the robotic assistance.
The purposes of this study were to determine if human subjects walking with a robotic ankle exoskeleton: (1) had similar joint moment profiles during powered versus unpowered walking; and (2) if greater mechanical assistance affected the rate of motor adaptation. We used a robotic ankle exoskeleton similar to that used in previous studies (Cain, Gordon et al., 2007; Gordon and Ferris, 2007; Sawicki and Ferris, 2008; Kinnaird and Ferris, 2009; Sawicki and Ferris, 2009; Sawicki and Ferris, 2009) but with two artificial pneumatic muscles in parallel providing plantar flexor torque in response to the wearer’s soleus muscle activity. Subjects walked on a force-measuring treadmill (Collins, Adamczyk et al., 2009) during two training sessions so we could calculate joint kinetics. We hypothesized that subjects would walk with similar joint moment patterns for powered versus unpowered exoskeleton gait. We also hypothesized that subjects would take a longer time period to reach steady state dynamics with the double-muscle robotic ankle exoskeleton compared to the single-muscle exoskeleton (Gordon and Ferris, 2007) due to the greater mechanical perturbation.
Method
Subjects
11 healthy subjects (6 female, 5 male, age 24±6 years and mass 71.6±14.3 kg, mean±SD) gave written informed consent and participated in the study. The University of Michigan Medical School Institutional Review Board approved the protocol.
Experimental design
We constructed a custom-made exoskeleton (Fig 1) for the left lower limb of each subject. Details of the design and performance of the exoskeleton are documented elsewhere (Ferris, Czerniecki et al., 2005; Ferris, Gordon et al., 2006; Gordon, Sawicki et al., 2006). We implemented proportional myoelectric control (i.e., amplitude and timing) of the artificial muscles through a desktop computer and real-time control board (dSPACE Inc.). A custom real-time computer controller regulated air pressure in the artificial plantar flexor muscles proportional to the processed soleus electromyographic signals (EMG) via a pressure regulator. EMG signal from soleus was high-pass filtered with a second-order Butterworth filter (20-Hz cutoff frequency) to remove movement artifact, full wave rectified, and low-pass filtered with a second-order Butterworth filter (10-Hz cutoff frequency) to smooth the signal.
Fig 1.

Subjects wore a custom made exoskeleton on their left lower limb. The exoskeleton consisted of a carbon fiber shank section and a polypropylene foot section. The exoskeleton was hinged at the ankle to allow free sagittal plane rotation. The exoskeleton had an average weight of 1.08±0.09 kg (mean±SD) and moment arm length of 11.0±1.2 cm that varied and depended on the size of the subject. Electrical signals (EMG) of soleus were recorded and processed to be used to control air pressure in the artificial pneumatic muscles proportionally. As air pressure increased, the artificial muscles started to develop tension and become shortened, allowing the powered exoskeleton to provide plantar flexor torque controlled by soleus muscle activation.
Subjects completed two identical testing sessions approximately 72 hrs apart. During each session, subjects walked with the exoskeleton first without power for 10 min (baseline), with power for 30 min (powered), and without power again for 15 min (post-adaptation) (Gordon and Ferris, 2007).
Data acquisition and analysis
We collected lower body kinematics, artificial muscle force, electromyography (EMG) and three-dimensional ground reaction forces (1200Hz) while subjects walked on a custom-constructed force-measuring split-belt treadmill (Collins, Adamczyk et al., 2009) at 1.25 m/s. The three-dimensional kinematic data were collected by using an 8-camera video system (120 Hz, Motion Analysis Corporation, Santa Rosa, CA). Artificial muscle force data were collected with force transducers (1200 Hz, Omega Engineering) mounted on the bracket of exoskeleton. We estimated the amount of mechanical torque, power and work done by the exoskeleton using the measurement of artificial muscle moment arm and ankle kinematic data. We placed bipolar surface electrodes on the left lower limb to record EMG (1200 Hz, Konigsberg Instruments Inc.) from tibialis anterior (TA), soleus (SOL), medial gastrocnemius (MG), lateral gastrocnemius (LG). We used commercial software (Visual3D, C-Motion Inc., Germantown, MD) to calculate joint angles as well as joint kinetics by inverse dynamics analysis. Lower limb inertial properties were estimated based on anthropometric measurements of subjects (Zatsiorsky, 2002) and the exoskeleton mass.
Ten seconds of data recorded each minute reflected the average of about seven strides of data. All data were time normalized to 100% of stride cycle (i.e., from left heel strike to left heel strike). To quantify changes in muscle activation, we calculated root-mean square (RMS) amplitude of the high-pass filtered (20-Hz cutoff frequency) and rectified EMG for the soleus over the stance phase. We normalized data to the last minute of baseline on a given testing session.
To examine changes in kinematics and kinetics across time for ankle, knee and hip joints, we linearly correlated the average joint angle and torque profiles during the powered condition at each minute to the average angle and torque profiles at the last minute of baseline on a given testing session using Pearson product moment correlation. The common variance (r2) of the linear correlation was used as a quantitative measure of similarity in joint kinematics and torques between every minute’s data and the data at the last minute of baseline (Derrick, Bates et al., 1994). To quantify variability of gait patterns in unpowered and powered walking, we calculated the coefficients of variation (CV) for joint angle and moment profiles (Winter, 1991) during stance phase. Since coefficients of variation are influenced differently by the means of each data profile, we did not directly compare the CVs among data profiles. We compared the CVs between conditions for joint angle and moment profiles, respectively.
To compare the adaptation rate during powered walking to the single-muscle study (Gordon and Ferris, 2007), we used the same method of quantifying motor adaptation (Noble and Prentice, 2006) as the single-muscle study. An envelope of steady-state behavior during the powered walking was defined based on the mean±2SD of the final 15 minutes of day two if linear regression of the data in this period revealed slopes that were not statistically different from zero (t-test, p> 0.05). Statistically significant slopes of linear regression indicate subjects did not reach steady state within the two training sessions. We calculated time to steady state for soleus stance RMS EMG, ankle joint correlation, and exoskeleton positive and negative mechanical work.
Statistics
We used repeated measure ANOVAs to test for differences in normalized EMG RMS (primary outcome variable was soleus stance RMS EMG), joint angle and torque correlation common variances (primary outcome variables were for the ankle joint), and positive and negative exoskeleton work between days and conditions (baseline, powered walking 1, 15, and 30) (2 days × 4 conditions). We analyzed other parameters as secondary outcome variables to provide insight into the overall adaptation. We set the significance level at p<0.05 and used Tukey Honestly Significant Difference (THSD) post hoc tests for pair-wise comparisons if a main effect was detected. We used paired t-test with Bonferroni correction to test for difference in the coefficients of variation (CV) of joint angle and moment profiles for hip, knee and ankle joints between baseline and minute 30 of day 2 (i.e. 6 comparisons).
Results
Joint kinematics
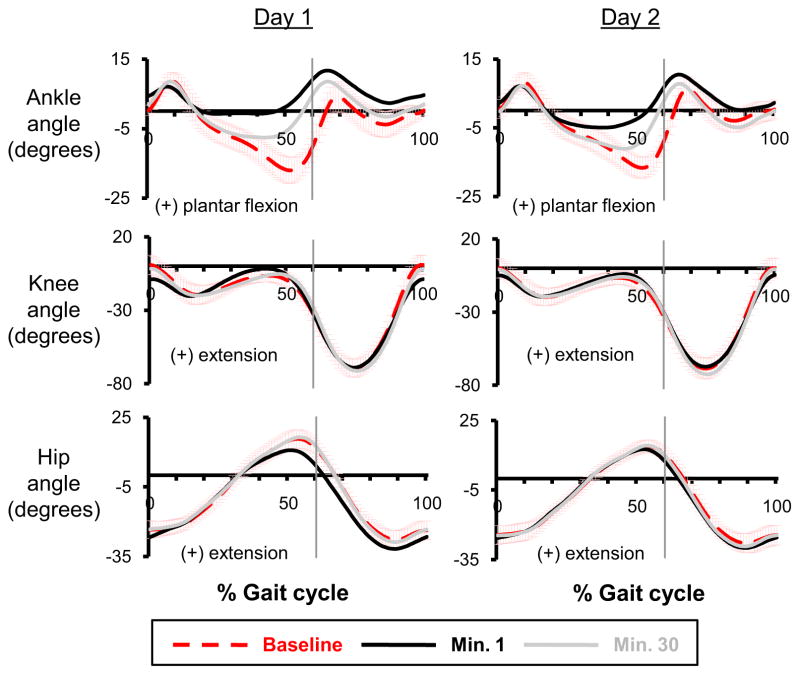
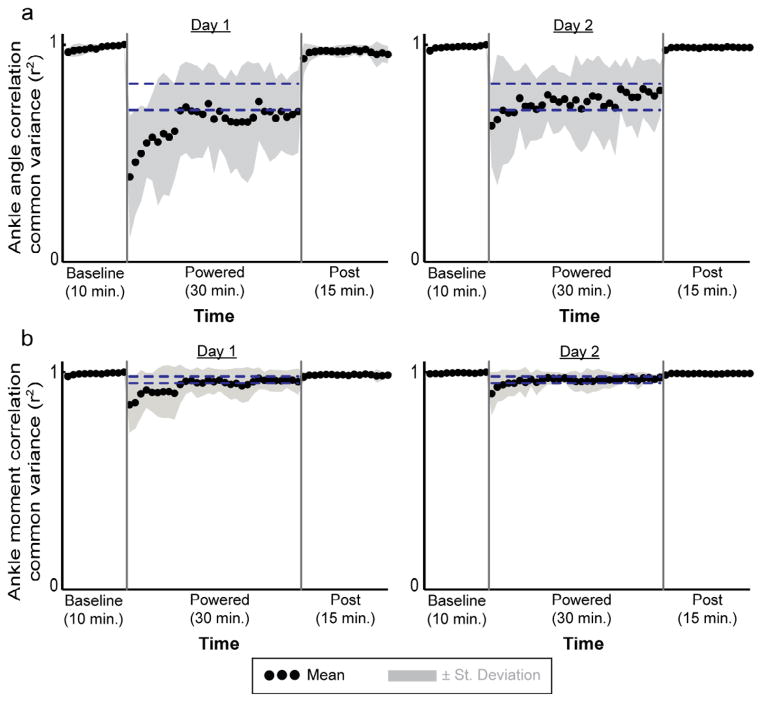
Although subjects showed some adaptation over the two 30-minute sessions, there were still large differences in ankle joint kinematics at the end of the second session compared to baseline (Fig 2). When first walking with the exoskeleton assistance, subjects stayed at plantar flexed posture almost for the whole gait cycle (Fig 2). Correspondingly, the ankle angle correlation common variance (r2) at the first minute was the lowest during all testing (day 1, minute 1: 0.39±0.28, mean±SD) (Fig 4a). After 30 minutes of practice, subjects had similar ankle kinematics during early-to-mid stance and swing but still had greater plantar flexion during mid-to-late stance compared to the baseline condition. The ankle angle correlation common variance (r2) at minute 30 was significantly higher compared to the first minute (day 1, minute 30: 0.69±0.19, THSD, p<0.05). On the second day, ankle angle correlation common variance (r2) at the minute 1 was significantly greater than the value during initial powered walking on day 1 (day2, minute 1: 0.63±0.19, THSD, p<0.05) and increased further with practice. However, the values of ankle angle correlation common variance were still significantly different from baseline by the end of day 2 (day 2, min 30: 0.79± 0.12, THSD, p<0.05).
Fig 2.
Joint kinematics. Ankle, knee and hip joint angle profiles are shown for the last minute of baseline condition (baseline, red dashed line), the first minute of active condition (minute 1, black line), and the last minute of active condition (minute 30, grey line) on the two training sessions. Data are the average of all subjects. ±1 SD of the baseline is displayed by the light red bars. The vertical lines represent the toe-off. Positive values indicate ankle plantar flexion, knee extension and hip extension. Compared to the baseline, the ankle joint angle profiles showed less dorsiflexion during mid-to-late stance during powered walking. The hip and knee joint angle profiles were similar to the baseline by the end of training of each day.
Fig 4.
Ankle joint angle (a) and moment (b) correlation common variance (r2). Mean data (black dots) ± 1 standard deviation (grey area) are shown for each minute. The two horizontal blue lines are the mean±2 standard deviations from the last 15 minutes of active condition on day2, representing steady state dynamics. The steady state envelopes shown above from the average group data are for display purposes. Steady state dynamics were determined for each subject, individually. The values of correlation common variance (r2) increased with practice in the active condition both for joint angle and moment. By the end of active condition on day 2 (day 2, minute), the values of correlation common variance were similar to the baseline for total ankle moment profile (0.98±0.02, THSD, p>0.05) but not for ankle angle profile (0.79±0.12, THSD, p<0.05).
There were no large differences in knee or hip joint kinematics during powered walking. Throughout the active trials, knee and hip angle correlation common variances were always greater than 0.96 and 0.97, respectively. On the second day, there were no significant differences between minute 30 and baseline (THSD, p>0.05) in joint angle correlation common variances for knee (day 2, min 30: 0.98± 0.01) or hip (0.99± 0.01) after 30 minutes of training.
Joint kinetics
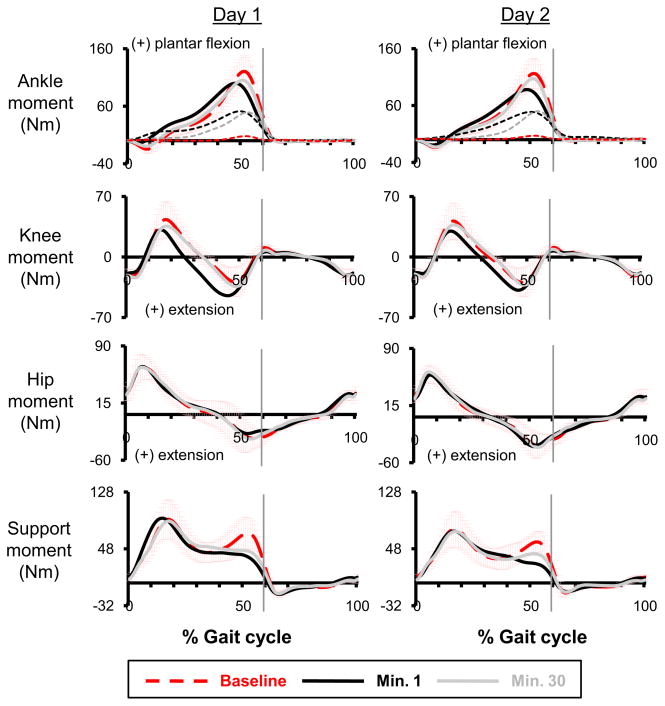
Hip, knee and ankle joint moment profiles at the end of each session were only slightly different compared to the baseline while these small changes resulted in a larger difference in the overall support moment (Fig 3). The values of ankle (Fig 4b), knee and hip moment correlation common variance (r2) were the lowest at minute 1 (ankle: 0.85±0.13; knee: 0.77±0.23, hip: 0.96±0.03). With practice, the correlation common variances (r2) of joint moment profiles increased during the second session. By the end of day 2, subjects walked with similar joint moment profiles during the powered condition as during the baseline condition (Fig 3). Joint moment correlation common variances (r2) for hip (0.98±0.01), knee (0.90±0.16), or ankle (0.98±0.02) at minute 30 of day 2 were not significantly different from the baseline (THSD, p>0.05).
Fig 3.
Joint moments, overall support moment, and exoskeleton mechanical torque. The thicker lines represent the ankle, knee, hip and overall support moment (i.e., sum of the extensor moments across the hip, knee and ankle joints) profiles on the two training sessions. The thinner dashed lines with the ankle joint moment data represent the plantar flexor torque provided by the exoskeleton (calculated from artificial muscle force and muscle moment arm) at the baseline (red), active minute 1 (black) and active minute 30 (grey). Data are the average of all subjects. ±1 SD of the baseline is displayed by the light red bars. At the end of day 2, the peak torque provided by the exoskeleton (50.09±12.05 Nm) was ~43% of peak ankle joint moment at the baseline (116.48±26.10 Nm) or ~47% of peak ankle joint moment at the minute 30 (107.14±23.56 Nm). After two sessions of training, the individual joint moment profiles were similar to the baseline. However, the second peak of overall support moment was smaller than the baseline on day two (baseline: 58.86±12.90 Nm, minute 30: 46.44±17.09 Nm).
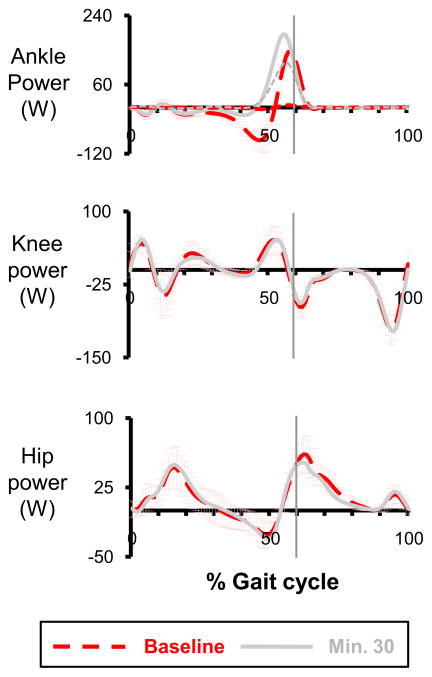
Subjects walked with similar knee and hip joint power profiles but very different ankle joint power profiles (Fig 5) and ankle work during the powered condition. After 30 minutes of training, subjects had greater power generation and less power absorption at the ankle joint on both days. Compared to the baseline, the peak ankle positive power in the powered condition was significantly greater at the end of day 2 (baseline: 152.93± 29.38 W; day 2, minute 30: 203.04±64.90 W, p=0.015). In addition, the total ankle positive work was significantly greater than the ankle positive work at the baseline by ~66% (baseline: 13.07±2.94 J; day 2, minute 30: 21.74±6.83 J, THSD, p<0.05); and the total ankle negative work was ~51% less than the ankle negative work at the baseline (baseline: −15.68±4.27 J; day 2, minute 30: −7.66±4.01 J, THSD, p<0.05).
Fig 5.
Joint powers and the mechanical power provided by the exoskeleton on day 2. The thicker lines represent the ankle, knee and hip joint power profiles. The thinner dashed line with the ankle joint power data represent the mechanical power provided by the exoskeleton (calculated from artificial muscle force, muscle moment arm and ankle joint velocity) at the baseline (red) and powered minute 30 (grey). Data are the average of all subjects. ±1 SD of the baseline is displayed by the light red bars. After two sessions of training, joint power profiles were similar to the baseline except the ankle joint power profile. Throughout the powered condition, subjects had greater power generation and less power absorption at the ankle joint. The exoskeleton produced a peak positive mechanical power of 117 W, about 80% of peak positive ankle joint power at the baseline (147.2±32.97 W) or ~61% of peak ankle joint power at the minute 30 (191.59±64.57 W).
Electromyography (EMG)
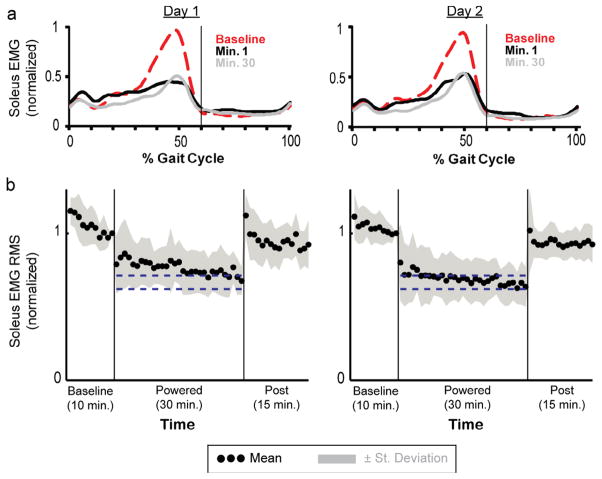
Subjects had substantially smaller soleus EMG activation during powered walking (Fig 6). By the end of day 2, soleus stance RMS EMG amplitude (0.64± 0.14) was significantly lower than the baseline by ~36% (THSD, p<0.05) (Fig 6b). For other lower limb muscles, the muscle activation patterns were similar to the baseline by the end of training.
Fig 6.
Soleus activation patterns (a) and soleus stance EMG RMS amplitudes (b). (a) Soleus EMG linear envelopes (rectified and low-pass filtered EMG with 6-Hz cutoff frequency) were averaged from all subjects. During initial walking with the powered exoskeleton (day 1, minute 1), subjects had lower soleus activation right away. After 30 minutes of practice, soleus activation pattern showed a clear bursting shape similar to the baseline. (b) Soleus EMG RMS amplitudes during stance. Mean data (black dots) ±1 standard deviation (grey area) are shown for each minute. The two horizontal blue lines are the mean±2 standard deviation from the last 15 minutes of active condition on day 2, representing steady state dynamics. The steady state envelopes shown above from the averaged group data are for display purposes. Steady state dynamics were determined by each subject, individually. By the end of day 2 (day 2, minute 30), the soleus stance EMG RMS amplitude was reduced by ~36% (0.64±0.14) compared to the baseline.
Exoskeleton mechanics
The powered exoskeleton with double muscles provided substantial assistance (Fig 3 and 6). The peak plantar flexor torque provided by the exoskeleton (50.09±12.05 Nm) was ~43% of peak ankle plantar flexor moment at the baseline (116.48±26.10 Nm), and ~47% of peak ankle plantar flexor moment at the minute 30 (107.14±23.56 Nm) on day 2 (Fig 3). The peak mechanical power generated by the exoskeleton was 117 W, about 80% of peak positive ankle joint power at the baseline (147.2±32.97 W), and ~61% of peak ankle joint power at the minute 30 (191.59±64.57 W) (Fig 5).
Coefficient of variation (CV)
Subjects had significantly greater variability in ankle joint angle profile during powered than during unpowered walking. Compared to the baseline, subjects had larger coefficients of variation both in joint angle and moment profiles during powered walking. There were significant differences in coefficients of variation for ankle angle profiles between baseline and minute 30 of powered condition (baseline: 0.14±0.04; minute 30: 0.30±0.12, p=0.0008<0.0083) but not for total ankle moment profiles (baseline: 0.13±0.02; minute 30: 0.17±0.05, p=0.07>0.0083) after two sessions of training.
Adaptation period
Not all of the subjects reached steady state dynamics within two training sessions compared to the 100% success rate in the study of single muscle design. The significant slope of linear regression on the data of last 15 minutes of day 2 indicated that five out of eleven subjects did not reach steady state dynamics in soleus RMS EMG.
Discussion
The findings of this study support our hypothesis that subjects would walk with similar joint moment patterns during powered versus unpowered walking. When the robotic assistance was provided, subjects reduced soleus EMG activation by about 36% to walk with a similar total ankle moment pattern (biological plus exoskeleton moment). However, they walked with a substantially different ankle kinematic pattern compared to the unpowered condition. In addition, the variability of total ankle moment profile was similar during powered versus unpowered walking while the variability of ankle angle profile was significantly greater in the powered condition. The results indicate that humans seem to prioritize maintaining invariant ankle moment patterns with and without robotic lower limb assistance.
Another finding of this study is that subjects had significantly different overall support moment at late stance during powered versus unpowered walking. The reduction in the second peak of overall support moment resulted from a small decrease in plantar flexor moment and an increase in knee flexor moment. We found that subjects had slightly greater horizontal ground reaction forces and similar vertical ground reaction forces at late stance in the powered condition. During powered walking, the slight reduction in ankle plantar flexor moment might result from more plantar flexed ankle position at late stance while an increase in knee flexor moment might cause greater horizontal ground reaction forces. This finding suggests that overall support moment pattern is not as consistent with robotic lower limb assistance as has been found without lower limb assistance (Winter, 1980; Winter, 1989).
The powered ankle exoskeleton replaced some of the ankle plantar flexor torque and did not substantially alter the dynamics of the other joints. One of the primary goals for robotic lower limb exoskeletons is to replace some of the mechanical work required for walking in order to reduce metabolic expenditure. The results showed that joint moment profiles of ankle, knee and hip were similar during powered versus unpowered walking. This is particularly notable given that the ankle exoskeleton was providing ~47% of the total ankle joint moment at push-off during the powered condition. This finding supports the concept that a joint kinetic rule of inter-limb coordination may be used in the neural control of human gait (Shemmell, Johansson et al., 2007).
Our results also have important implications for training people to use robotic lower limb assistance during locomotion. Only about half of our subjects reached steady state muscle activation patterns after two 30-minute training sessions. This is in contrast to what was found on a robotic ankle exoskeleton with less mechanical capability (Gordon and Ferris, 2007). Gordon and Ferris (2007) found that their subjects had reached steady state at about 15 minutes of training on the second day. This difference between studies supports the hypothesis that subjects take longer time to reach steady state dynamics when walking with robotic exoskeletons with greater mechanical strength. With a longer training duration, it may be that subjects would have adapted to keep both joint kinematics and joint moments the same during assisted walking and unassisted walking. For facilitating fast adaptation to a robotic exoskeleton, however, it would seem that having too strong of an exoskeleton is disadvantageous for the motor learning process.
Acknowledgments
The authors thank Kristin Carroll, Danielle Sandella, Evelyn Anaka, and members of the Human Neuromechanics Laboratory for assistance in collecting data. We also thank Anne Manier for help with fabricating the exoskeleton. Supported by NIH R21 NS062119 (DPF) and F32 HD055010 (CLL).
Supported by the National Institutes of Health (R21 NS062119).
Footnotes
Conflict of Interest Statement
There are no conflicts of interest in this work.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Cain SM, Gordon KE, Ferris DP. Locomotor adaptation to a powered ankle-foot orthosis depends on control method. Journal of Neuroengineering and Rehabilitation. 2007;4(48) doi: 10.1186/1743-0003-4-48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins SH, Adamczyk PG, Ferris DP, Kuo AD. A simple method for calibrating force plates and force treadmills using an instrumented pole. Gait & Posture. 2009;29(1):59–64. doi: 10.1016/j.gaitpost.2008.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrick TR, Bates BT, Dufek JS. Evaluation of Time-Series Data Sets Using the Pearson Product-Moment Correlation-Coefficient. Medicine and Science in Sports and Exercise. 1994;26(7):919–928. [PubMed] [Google Scholar]
- Dollar AM, Herr H. Lower extremity exoskeletons and active orthoses: Challenges and state-of-the-art. Ieee Transactions on Robotics. 2008;24(1):144–158. [Google Scholar]
- Ferris DP, Czerniecki JM, Hannaford B. An ankle-foot orthosis powered by artificial pneumatic muscles. Journal of Applied Biomechanics. 2005;21(2):189–197. doi: 10.1123/jab.21.2.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferris DP, Gordon KE, Sawicki GS, Peethambaran A. An improved powered ankle-foot orthosis using proportional myoelectric control. Gait and Posture. 2006;23(4):425–8. doi: 10.1016/j.gaitpost.2005.05.004. [DOI] [PubMed] [Google Scholar]
- Ferris DP, Sawicki GS, Daley MA. A physiologist’s perspective on robotic exoskeletons for human locomotion. International Journal of Humanoid Robotics. 2007;4(3):507–528. doi: 10.1142/S0219843607001138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferris DP, Sawicki GS, Domingo A. Powered lower limb orthoses for gait rehabilitation. Topics in Spinal Cord Injury Rehabilitation. 2005;11(2):34–49. doi: 10.1310/6gl4-um7x-519h-9jyd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon KE, Ferris DP. Learning to walk with a robotic ankle exoskeleton. Journal of Biomechanics. 2007;40(12):2636–44. doi: 10.1016/j.jbiomech.2006.12.006. [DOI] [PubMed] [Google Scholar]
- Gordon KE, Sawicki GS, Ferris DP. Mechanical performance of artificial pneumatic muscles to power an ankle-foot orthosis. Journal of Biomechanics. 2006;39(10):1832–41. doi: 10.1016/j.jbiomech.2005.05.018. [DOI] [PubMed] [Google Scholar]
- Kinnaird CR, Ferris DP. Medial gastrocnemius myoelectric control of a robotic ankle exoskeleton for human walking. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2009;17(1):31–37. doi: 10.1109/TNSRE.2008.2008285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lelas JL, Merriman GJ, Riley PO, Kerrigan DC. Predicting peak kinematic and kinetic parameters from gait speed. Gait & Posture. 2003;17(2):106–112. doi: 10.1016/s0966-6362(02)00060-7. [DOI] [PubMed] [Google Scholar]
- Noble JW, Prentice SD. Adaptation to unilateral change in lower limb mechanical properties during human walking. Experimental Brain Research. 2006;169(4):482–95. doi: 10.1007/s00221-005-0162-3. [DOI] [PubMed] [Google Scholar]
- Prilutsky BI, Sirota MG, Gregor RJ, Beloozerova IN. Quantification of motor cortex activity and full-body biomechanics during unconstrained locomotion. Journal of Neurophysiology. 2005;94(4):2959–2969. doi: 10.1152/jn.00704.2004. [DOI] [PubMed] [Google Scholar]
- Sawicki GS, Ferris DP. Mechanics and energetics of level walking with powered ankle exoskeletons. Journal of Experimental Biology. 2008;211(9):1402–1413. doi: 10.1242/jeb.009241. [DOI] [PubMed] [Google Scholar]
- Sawicki GS, Ferris DP. Mechanics and energetics of incline walking with robotic ankle exoskeletons. Journal of Experimental Biology. 2009;212(1):32–41. doi: 10.1242/jeb.017277. [DOI] [PubMed] [Google Scholar]
- Sawicki GS, Ferris DP. Powered ankle exoskeletons reveal the metabolic cost of plantar flexor mechanical work during walking with longer steps at constant step frequency. Journal of Experimental Biology. 2009;212(1):21–31. doi: 10.1242/jeb.017269. [DOI] [PubMed] [Google Scholar]
- Shemmell J, Johansson J, Portra V, Gottlieb GL, Thomas JS, Corcos DM. Control of interjoint coordination during the swing phase of normal gait at different speeds. Journal of Neuroengineering and Rehabilitation. 2007;4(10) doi: 10.1186/1743-0003-4-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winter DA. Overall principle of lower limb support during stance phase of gait. Journal of Biomechanics. 1980;13(11):923–927. doi: 10.1016/0021-9290(80)90162-1. [DOI] [PubMed] [Google Scholar]
- Winter DA. Biomechanics of Normal and Pathological Gait - Implications for Understanding Human Locomotor Control. Journal of Motor Behavior. 1989;21(4):337–355. doi: 10.1080/00222895.1989.10735488. [DOI] [PubMed] [Google Scholar]
- Winter DA. The biomechanics and motor control of human gait: normal, elderly and pathological. Waterloo Biomechanics; Waterloo, Ontario: 1991. [Google Scholar]
- Winter DA, Eng P. Kinetics: our window into the goals and strategies of the central nervous system. Behavioural Brain Research. 1995;67(2):111–20. doi: 10.1016/0166-4328(94)00154-8. [DOI] [PubMed] [Google Scholar]
- Zatsiorsky VM. Kinetics of Human Motion. Human Kinetics; Champaign, IL: 2002. [Google Scholar]