Spatial Implications Associated with Using Euclidean Distance Measurements and Geographic Centroid Imputation in Health Care Research

Abstract

Objective

To determine the effect of using Euclidean measurements and zip-code centroid geo-imputation versus more precise spatial analytical techniques in health care research.

Data Sources

Commercially insured members from a southeastern managed care organization.

Study Design

Distance from admitting inpatient facility to member's home and zip-code centroid (geographic placement) was compared using Euclidean straight-line and shortest-path drive distances (measurement technique).

Data Collection

Administrative claims from October 2005 to September 2006.

Principal Findings

Measurement technique had a greater impact on distance values compared with geographic placement. Drive distance from the geocoded address was highly correlated (r=0.99) with the Euclidean distance from the zip-code centroid.

Conclusions

Actual differences were relatively small. Researchers without capabilities to produce drive distance measurements and/or address geocoding techniques could rely on simple linear regressions to estimate correction factors with a high degree of confidence.

Geographically based health care research commonly utilizes methodologies and measurements attainable using a geographic information system (GIS). The need for measurement precision varies and is relative to the study question and unit of measure within a study. It is often of interest to measure the distance from one point to another (e.g., distance from a patient to a hospital or physician) to estimate, for example, access to care (Mobley and Frech 2000; Noor et al. 2003; Jordan et al. 2004;), hospital market size (Goody 1993; Phibbs and Robinson 1993; Mobley and Frech 2000;), or patient travel times (Mobley and Frech 2000). These distances can be estimated using either Euclidean (i.e., straight-line) distance measurements or drive time analyses (i.e., distance or time traveled over a road network). Geographical access from a source point (e.g., patient) to a target point (e.g., hospital) may be influenced by topological structures (e.g., mountains, rivers, etc.) and associated road networks. Measurements utilizing drive distance or time account for this phenomena, whereas Euclidean measurements do not. Although it has been shown drive time analyses are highly correlated with Euclidean measurements (Phibbs and Luft 1995), increasing measurement precision may be necessary depending on the study question (Jordan et al. 2004). Hospital market areas are often defined using radial circles centered on the hospital with radii defined by Euclidean measurements (Garnick et al. 1987; Goody 1993; Phibbs and Robinson 1993;). Radial and other static areal boundaries (e.g., zip code, county, or metropolitan statistical area) ignore potential geographic barriers (e.g., mountains, rivers, etc.) that may exist. Radial boundaries further assume the hospital is centered within the market (Goody 1993). Advancements in GIS capabilities and drive distance analyses now allow users to define market areas more explicitly.

Another common practice in geographically based research is geographical imputation (geo-imputation) (Henry and Boscoe 2008) to locate point records (e.g., patients, hospitals, and physician office) at the centroid of their corresponding zip code, rather than utilizing street-level geocoding (Goody 1993; Phibbs and Robinson 1993; Luo, Wang, and Douglass 2004;). Justification for utilizing centroids in health care research is often adherence to patient privacy regulations (e.g., Health Insurance Portability and Accountability Act of 1996) and ease of use. Compared with centroid mapping, geocoding to the street address level often requires additional software/extensions, expertise, and processing time. Population-based zip-code centroids are spatially associated with areas of high commercial activity and population density, and therefore may often represent the unit of interest (e.g., physician or hospital locations). However, utilizing geographic-based zip codes as a geographical unit of study may be problematic due to lack of standardization (Grubesic and Matisziw 2006) and variability in spatial structure (i.e., size, shape).

The combinatory effects of using Euclidean measurements and geographic zip-code centroids in health care research is unknown. As the use of GIS and spatially oriented data increase in health care research, it is important to understand the implications that may exist in using these methodologies. The intent of our research is to determine if significant differences in distance values exist using Euclidean measurements and zip-code centroid placement methodologies compared with more precise spatial analytical techniques (i.e., drive distance data and residential geocoded address). The results of this study can be applied to future research efforts within health services research regardless of outcome. If significant differences do exist between methods, future research efforts should consider this phenomenon and address measurements appropriately. If, however, significant differences are not found, this study may be cited as reference for using conventional data collection methods that are less time intensive and easier to obtain.

METHODS

Study Population

To determine eligible patients (hereafter, members) for the study, we extracted inpatient claims data (member data, admitting facility, and date of admission) from a commercially insured member population enrolled in a large southeastern managed care organization for the October 2005–September 2006 time period. The admitting facility was the target point and members were considered source points. Of 76,833 potential observations, we mapped and included in our analyses exactly 66,492 (86.5 percent). We included only members with mappable addresses and excluded all members with post office boxes; therefore, we have no discernable method to collect geographic information on members that were not geocoded.

Geographic Placement and Distance Measurement Techniques

Members' address information at the time of inpatient admission were geocoded to obtain latitude/longitude coordinates. For each member, a coordinate was obtained for (1) the member's geocoded residential address and (2) geographic centroid of zip code for member. For this study, “Centroid” refers to a member being placed at their respective geographic zip-code centroid and “Address” indicates the member placement at their actual residential address. Actual facility (hospital) location addresses were obtained by either world-wide web access or contacting the facility. Urban/rural designations were assigned to members and facilities based on their location either internal (urban) or external (rural) to a metropolitan statistical area. Displacement distance was also calculated and represents the straight-line distance from a member's centroid to their geocoded residential address.

We used two different measurement techniques to calculate distance from the member to the facility at which they had an inpatient admission. For this study, “Euclidean” distance measurements represent the straight-line distance from the member to the admitting facility. “DriveDistance” refers to the shortest path distance traveled over a road network from the member to the admitting facility using Dijkstra's algorithm (Dijkstra 1959). A Euclidean measurement by definition will always be equal to or lesser than a DriveDistance measurement to and from the same locations; however, the magnitude of this difference is unknown.

Comparisons Tests

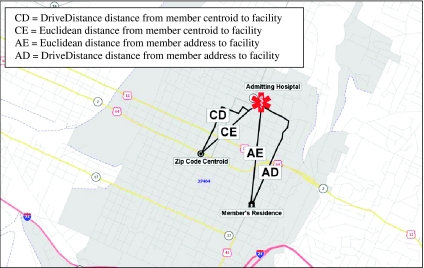
To determine differences in linear distance from members to their corresponding admitting facility, we compared Euclidean straight-line measurements to DriveDistance measurements using member origin locations at (1) residential street address and (2) zip-code centroid. We assigned codes to each unique combination of geographic placement and measurement technique as follows:

1. AE is the Euclidean distance from member address to facility.

2. AD is the DriveDistance distance from member address to facility.

3. CE is the Euclidean distance from member centroid to facility.

4. CD is the DriveDistance distance from member centroid to facility.

Initial tests of data normality failed and therefore nonparametric tests on median values were evaluated. Using Wilcoxon's signed rank sum tests, we tested for significant differences (p<.05) between geographic placement (Centroid [C], Address [A]) and measurement techniques (Euclidean [E], DriveDistance [D]) by examining median distance values from members to the admitting facilities (Figure 1). We conducted four separate signed rank sum tests for rural and urban members (eight total tests) by examining the following geographic placement and measurement technique combinations:

Figure 1.

Example of Four Different Scenarios of Geographic Placement of Member (Centroid, Address) and measurement techniques (Euclidean, DriveDistance)

1. AD versus AE—Difference in Euclidean versus DriveDistance with member placed at Address.

2. CD versus CE—Difference in Euclidean versus DriveDistance with member placed at Centroid.

3. CE versus AE—Euclidean differences associated with member at Centroid versus Address.

4. CD versus AD—DriveDistance differences associated with member at Centroid versus Address.

Lastly, it is assumed that the drive distance from a geocoded location (AD) is the most desirable spatial estimation technique, and the Euclidean distance from a zip-code centroid (CE) is least desirable. Therefore, we conducted a separate signed rank sum test and correlation analysis to estimate the association between AD and CE, as well as correlation analyses to estimate associations between AD–CE and the aforementioned four combinations.

RESULTS

We examined 66,492 members across 117 facilities. Approximately 58 percent of the members and 52 percent of the facilities were classified as urban. The median displacement distance was 3.4 miles for rural members and 2.4 miles for urban members. Variability due to geographic placement (Centroid versus Address) was small relative to measurement technique (DriveDistance versus Euclidean). Median DriveDistance measurements were 2.4 and 2.1 miles longer than Euclidean measures when members were placed at their zip-code centroid and residential address, respectively. Differences were greater for rural members across all tests and comparisons.

Member Level Linear Distances to Facility

Members traveled a median 11.9 miles to an admitting facility when measuring DriveDistance, and 9.5 miles when measuring straight-line Euclidean distance. Overall median differences for the four delta metrics were as follows:

Measurement Technique

1. Difference in Euclidean versus DriveDistance with member placed at Address (2.1 miles).

2. Difference in Euclidean versus DriveDistance with member placed at Centroid (2.4 miles).

Geographic Placement

1. Euclidean differences associated with member at Centroid versus Address (0.5 miles).

2. DriveDistance differences associated with member at Centroid versus Address (0.8 miles).

Measurement technique produced larger actual differences in linear distance to a facility compared with geographic placement of the member. Differences were greater for rural members compared with urban members. Regardless of geographic placement, DriveDistance measurements to the admitting facility were statistically greater (p<.0001) than Euclidean distances for rural and urban members. Distance values were statistically higher when members were placed at their centroid versus their residential address, although actual median values were low (i.e., 0.8 miles or less) for urban and rural members (Table 1).

Table 1.

Summary Information of Comparing Linear Distances from Member to Admitting Facility Using Euclidean Straight-Line Measurements and DriveDistance Measurements with Member Origins at Residential Street Address and Zip-Code Centroid

		Median Distance from Member to Facility When Member Is Placed at				Difference in Median Values (miles)
		Centroid		Address		Most-Desired Method (AD) versus Least-Desired Method (CE)	Measurement Type		Geographic Placement
	N	Euclidian (CE)	DriveDistance (CD)	Euclidian (AE)	DriveDistance (AD)	AD versus CD	AD versus AE	CD versus CE	CE versus AE	CD versus AD
Rural	27,732	14.8	18.9	14.1	18.2	4.5*	4.1*	4.1*	0.7*	0.7*
Urban	38,760	8.1	9.8	7.6	9.0	1.1*	1.4*	1.7*	0.5*	0.8*
Overall	66,492	9.5	11.9	9.0	11.1	1.9	2.1	2.4	0.5	0.8

^*Statistically significant difference at α=0.05 (overall not tested).

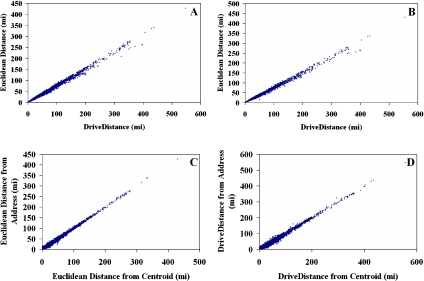
A scatter plot revealed a strong linear relationship existed for each of the four unique combinations of geographic placement and measurement technique, regardless of distance from the facility center (Figure 2). For each of the four delta metrics, the distribution of data ranged from highly negatively skewed for differences related to measurement technique to apparent normal for differences related to geographic placement. Using Euclidean versus DriveDistance measurement techniques, the maximum absolute difference in distance for a member to the admitting facility was approximately 146 miles with high kurtosis (above 36) and negative skewness (>−4). Placing a member at their centroid versus their address produced a maximum absolute difference of 35 miles with low kurtosis (<3) and slightly positive skewness (>0). Geographic placement distributions were not statistically normal, though this may be an artifact of our large sample size rather than actual nonnormality. Distribution relationships were comparable for urban and rural observations.

Figure 2.

Scatter Plot of Distances from Member to Admitting Facility Using Different Measurement Techniques (Euclidean versus DriveDistance) with Member Placed at Address (A) and Centroid (B), and with Different Geographic Placement (Address versus Centroid) using Euclidean (C) and DriveDistance (D) Measurements

The drive distance to the admitting facility from the member's address (AD) was highly correlated (p<.0001; r=0.99) with the Euclidean distance from the member's zip-code centroid (CE). Median distance values of AD versus CE were statistically different for both rural (4.5 miles; z=21.28; p<.0001) and urban (1.1 miles; z=9.60; p<.0001) members (Table 1). All correlations with the four combinations were statistically significant (p<.0001) for rural and urban analyses, and the AD–CE distance was most highly correlated (r=0.95) with the AD–AE comparison.

DISCUSSION

Although DriveDistance and Euclidean distance measurements may be highly correlated with one another (Phibbs and Luft 1995), it was important to test this relationship in our data to quantify this impact. We first compared actual linear distance values associated with using the actual geocoded residential address of the patient rather than zip-code centroids, combined with using actual drive distances rather than straight-line Euclidean distances. Our results suggest measurement technique (Euclidean versus DriveDistance) will influence outcomes comparatively greater than geographical placement (Centroid versus Address).

Overall, differences were greater in rural measures compared with urban. Urban zip codes, by definition, may be smaller on average than rural zip codes because zip code creation is population centered. Spatial displacement of members within an urban zip code is more restricted than rural zip codes, and therefore the geocoded address of an urban member is more likely to be closer to their corresponding centroid. Displacement distances calculated in this study confirmed this as rural members' address–centroid displacement was approximately 1 mile greater than urban members. Population-weighted zip-code centroids are more accurate than geographic-based centroids (Henry and Boscoe 2008) and therefore may perform better especially in more rural zip codes.

As expected, DriveDistance measurements were consistently larger than Euclidean measurements. Larger differences from measurement technique are seemingly related to the complex road network and topography of Tennessee. States with less complex and more grid-like road networks (e.g., Nebraska) may experience smaller differences in DriveDistances versus Euclidean measurements. The strong linear relationships between the combinations of variables suggest that regardless of how far a member is from a point source, measurement technique and geographic placement methods are proportionally equal. The implications of this are important because researchers without the capabilities to produce drive distance measurements and/or exact geocoding techniques could rely on a simple linear regression to estimate a correction factor with a high degree of confidence. In addition, the high correlation between the most desirable (AD) and least desirable (CE) methods suggests a relatively insignificant correction factor could compensate for an inability to estimate distances using drive distances and/or residential geocoding. The AD–CE comparison was quantitatively analogous to a member being placed at their address and using DriveDistance versus Euclidean. This is most likely a result of the relatively small overall displacement distance (∼3 miles) of a member being placed at their zip-code centroid versus their address. Therefore, this comparison reinforces our earlier findings that measurement technique influences error more than geographic placement.

The magnitude of the distributions was unexpected. Although measurement technique created a maximum absolute difference of approximately 146 miles, these values should be considered within the context of the data distributions. That is, 95 percent of the differences associated with measurement technique had values <12 miles; hence, the highly negative skewness of the data. Statistical significance in our results could be attributed to our large sample size. Notwithstanding a statistically significant difference of Euclidean versus DriveDistance measures, an overall median difference of 2.4 and 2.1 miles is not appreciably large. However, study question should determine if the differences observed in this study are geographically meaningful.

CONCLUSIONS

From this study, we conclude measurements of linear distance are more influenced by the measurement type (Euclidean versus DriveDistance) than geographic placement (Centroid versus Address) of the member. However, it is important to note that our study design focused on comparing actual distance values and not phenomena associated with spatial displacement. For example, clustering algorithms (e.g., Getis-Ord local G) (Ord and Getis 1995) that use point locations to determine statistically significant spatial hotspots would perform poorly if a large number of members were located at their centroid versus residential address. Centroid placement would be too granular, would not allow for spatial dispersion and results potentially biased. For the majority of projects utilizing linear distance measurements, it is unlikely the differences we experienced in this study would influence the overall outcome. However, if precision of travel time/distance is important to the study (e.g., measuring coverage of ambulatory services; adequate network coverage of primary care providers), we recommend utilizing drive distance and/or drive time measurements with members geocoded to their residential address rather than the zip-code centroid. If the study area in question is more rural than urban, proper consideration should be given if placing members at the zip-code centroid as this may introduce unwanted bias in estimates.

SUPPORTING INFORMATION

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.