Abstract
Kindergarten to 3rd grade mathematics achievement scores from a prospective study of mathematical development were subjected to latent growth trajectory analyses (n = 306). The four corresponding classes included children with mathematical learning disability (MLD, 6% of sample), and low (LA, 50%), typically (TA, 39%) and high (HA, 5%) achieving children. The groups were administered a battery of intelligence (IQ), working memory, and mathematical-cognition measures in 1st grade. The children with MLD had general deficits in working memory and IQ, and potentially more specific deficits on measures of number sense. The LA children did not have working memory or IQ deficits, but showed moderate deficits on these number sense measures and for addition fact retrieval. The distinguishing features of the HA children were a strong visuospatial working memory, a strong number sense, and frequent use of memory-based processes to solve addition problems. Implications for the early identification of children at risk for poor mathematics achievement are discussed.
About 7% of children and adolescents will experience a substantive learning deficit in at least one area of mathematics (MLD) before graduating from high school (Barbaresi, Katusic, Colligan, Weaver, & Jacobsen 2005; Lewis, Hitch, & Walker, 1994; Ostad, 1998; Shalev, Manor, & Gross-Tsur, 2005), and are accompanied by another 5% to 10% of children and adolescents, and perhaps more, with learning difficulties (for reviews see Berch & Mazzocco, 2007; Dowker, 2005). The latter students have specific difficulties in one more areas of mathematics that are independent of cognitive ability and reading achievement, and in this sense might be considered to have a moderate learning disability in mathematics. It is not known if the factors underlying their difficulties are simply less pervasive or severe as those that appear to underlie MLD or are qualitatively different (e.g., due to poor instruction; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Murphy, Mazzocco, Hanich, & Early, 2007). Thus, we distinguished the two groups and classified the children with moderate difficulties as low achieving (LA), to be consistent with recent studies (e.g., Murphy et al., 2007). Other unresolved issues concern the extent of the grade-to-grade stability of a child’s classification as MLD or LA (Silver, Pennett, Black, Fair, & Balise, 1999) and identification of the early risk factors for long-term inclusion in one or the other of these groups (Gersten, Jordan, & Flojo, 2005).
We addressed each of these issues using data from a longitudinal, prospective study of children’s mathematical learning and learning disability (Geary, in press). Using latent growth trajectory analyses applied to mathematics achievement scores from kindergarten to 3rd grade, we identified stable groups of MLD and LA children. We compared and contrasted the performance of these groups to groups of typically achieving (TA) and high achieving (HA) children on a battery of mathematical cognition, intelligence (IQ), and working memory tasks administered in 1st grade. The approach allowed us to identify early risk for persistent MLD and LA and determine if the cognitive factors contributing to inclusion in these groups represented lower and higher points, respectively, of the same underlying ability continuum or represented qualitatively different patterns of deficit.
Mathematical Cognition
The mathematical tasks were chosen based on areas in which children with MLD or LA children have been found to have deficits or difficulties in earlier studies (Berch & Mazzocco, 2007; Geary, 1993, 2004). The areas assessed include children’s early number sense, their implicit knowledge of counting principles, and the mix of strategies they use to solve addition problems.
Number Sense
Children’s number sense includes a non-verbal and implicit understanding of the absolute and relative magnitude of sets of small numbers of objects and of symbols (e.g., Arabic numerals) that represent these quantities. This implicit knowledge is manifested in their ability to apprehend the quantity of sets of 3 to 4 objects or actions without counting (Starkey & Cooper, 1980: Strauss & Curtis, 1984; Wynn, Bloom, & Chiang, 2002); use of non-verbal processes or counting to quantity small sets of objects and to add and subtract small quantities to and from these sets (Case & Okamoto, 1996; Gelman & Gallistel, 1978; Levine, Jordan, & Huttenlocher, 1992; Starkey, 1992); and, proficiency at estimating the magnitude of sets of objects and the results of simple numerical operations (Dehaene, 1997). We use two measures to capture children’s number sense; specifically, the speed and accuracy of identifying and processing number sets and the ability to represent quantity along a mathematical number line.
Number Sets
Children with MLD have potential deficits in the core non-verbal ability to apprehend the quantity of small sets of objects and in the conceptual insight that numbers are composed of sets of smaller numbers (Butterworth & Reigosa, 2007; Geary et al., 2007; Geary, Bailey, & Hoard, 2009; Koontz & Berch, 1996). Koontz and Berch assessed the ability of 3rd and 4th grade children with MLD and TA children to apprehend, without counting, the quantity of small sets of items or Arabic numeral representations of these sets. As an example, the children were asked to determine if combinations of Arabic numerals and number sets were the same (e.g., 2-▪▪) or different (e.g. 3-▪▪). Reaction time patterns for the TA children indicated fast access to representations of quantities of two and three, regardless of whether the code was an Arabic numeral or number set. The children with MLD showed fast access to numerosity representations for the quantity of two, but appeared to rely on counting to determine quantities of three. The results suggest that some children with MLD might not have an inherent non-verbal representation for numerosities of three or more likely the representational system for three does not allow for reliable discrimination of two from three.
Using the Number Sets Test (described below), we have also found evidence for less fluent (slow and inaccurate) processing of number-set information by children with MLD and, to a lesser extent, LA children (Geary et al., 2007; Geary et al., 2009). The test items require children to match groups of objects and Arabic numerals (e.g., •• 3) to a target number, such as 5. Signal detection methods can be applied to the corresponding number of hits and false alarms to generate sensitivity (d′) and response bias (C) variables (Macmillan, 2002). The d′ variable represents the child’s sensitivity to quantities represented in task items and the C variable represents the child’s tendency to respond to task items, whether they match the target number or not. Children who correctly identify many target quantities and commit few false alarms will have high d′ and low C scores, whereas children who have as many hits as false alarms will have low d′ and high C scores. In the latter case, the high number of correct items is due to the child’s bias to respond and not sensitivity to quantity. We found that higher d′ scores in 1st grade were associated with higher mathematics achievement scores through 3rd grade [rs = .49 to .58 (ps<.001)], and that children at risk for MLD by 3rd grade–as determined by achievement scores less than the 15th national percentile ranking–have lower d′ scores in 1st grade (Geary et al., 2009).
Number Line
The mathematical number line (e.g., the difference between two consecutive numbers is identical regardless of position on the number line) is a core component of many aspects of mathematics and a critical part of basic education in mathematics. Children’s competence with the number line is also theoretically interesting because magnitude representations, including those that support the mathematical number line, may be based on the potentially inherent number-magnitude system that contributes to performance on the Number Sets Test; this system is represented by specific areas in the parietal cortices (Isaacs, Edmonds, Lucas, & Gadian, 2001; Kadosh, Kadosh, Schuhmann, Kaas, Goebel, Henik, & Sack, 2007). Making placements on a physical number line that are based on use of the inherent number-magnitude system results in a pattern that conforms to the natural logarithm (ln) of the number (Feigenson, Dehaene, & Spelke, 2004; Gallistel & Gelman, 1992; Siegler & Booth, 2004; Siegler & Opfer, 2003). More precisely, use of this representation results in placements that are compressed for larger magnitudes such that the perceived distance between 92 and 93 is smaller than the perceived distance between 2 and 3. With instruction on the mathematical number line, children’s placements become linear.
If children with MLD have deficits in the number-magnitude representational system (Koontz & Berch, 1996), then their number line placements might not conform to the natural log model or might show more compression (closer placements) for smaller numbers. We have found several patterns in the number line placements of children with MLD and LA children that suggest these types of deficits (Geary et al., 2007). We found that children with MLD were more heavily reliant on the natural number-magnitude representational system to make their number line placements than were LA and TA children; MLD children were learning the linear mathematical number line more slowly than these other children (Geary, Hoard, Nugent, & Byrd-Craven, 2008). Even when they made placements consistent with use of the natural number-magnitude system, the placements of children with MLD and their LA peers did not conform as precisely to the predicted natural-log pattern as those of the TA children early in 1st grade, before much if any formal instruction on the number line. By the end of 2nd grade, LA children caught up with their TA peers, but the MLD children, though they improved, lagged behind the other children. One possibility is that children with MLD and LA children begin school with a less precise underlying system of natural number-magnitude representations. This system may quickly mature improved ability to discriminate between quantities of near equal value–in LA children and may not mature or do so at a slower rate for children with MLD (Halberda, Mazzocco, & Feigenson, 2008).
Counting
Most school children quickly learn to count by rote, and this in and of itself is not a useful indicator of MLD or LA status. Children’s understanding of the core principles of counting, such as one-one correspondence, and their ability to actively apply counting to solve arithmetic problems are, however, potential sources of poor mathematics achievement. We have explored both of these facets using a task that assesses children’s sensitivity to the violation of counting principles (Briars & Siegler, 1984; Gelman & Gallistel, 1978). More precisely, following Gelman and Meck (1983) and Briars and Siegler, we assess this knowledge by asking the child to monitor a puppet’s counting of objects. If the puppet violates a basic counting principle and the child detects the miscount, we assume the child at least implicitly understands the principle. Children’s knowledge of counting principles and sensitivity to violations of these principles emerge during the preschool years and mature during the early elementary-school years (LeFevre, Smith-Chant, Fast, Skwarchuk, Sargla, Arnup et al., 2006).
Our studies suggest that children with MLD and LA children understand most basic counting principles, but they are sometimes confused when counting deviates from the standard left to right counting of adjacent objects (Geary, Bow-Thomas, & Yao, 1992; Geary, Hoard, Byrd-Craven, & Desoto, 2004). A more consistent finding is that children with MLD, but not LA children, fail to detect errors when the puppet double counts the first object in an array of objects, that is, this single object is tagged “one,” “two”. They detect these double counts when they occur with the last item, indicating they understand one-one correspondence, but have difficulty retaining a notation of the counting error in working memory during the count (Geary et al., 2004; Hoard, Geary, & Hamson, 1999). The forgetting of miscounts is potentially important for children’s learning to use counting to solve arithmetic problems. Ohlsson and Rees (1991) predicted that children who are skilled at detecting counting errors would more readily learn to correct these miscounts and thus eventually commit fewer errors when using counting to solve arithmetic problems. The evidence for this prediction is mixed (Geary et al., 1992; Geary et al., 2004), but detection of these double-counting errors it still a good empirical indicator of risk for MLD (Geary et al., 2007; Gersten et al., 2005).
Arithmetic
Children use a mix of counting strategies and memory-based processes to solve addition problems (Ashcraft, 1982; Siegler & Shrager, 1984). The mix is initially dominated by finger and then verbal (e.g., out loud) counting. With both counting strategies, children tend to use the sum or min procedure (Fuson, 1982; Groen & Parkman, 1972); the former involves counting both addends starting from one and the latter involves stating the cardinal value of the larger addend (e.g., “five”) and counting a number of times equal to the value of the smaller addend (e.g., “six, seven, eight” to solve 5+3). As a result of schooling and practice, the strategy mix changes such that children use the min procedure more often and eventually rely primarily on memory-based processes. The latter include direct retrieval of the answer and decomposition. To solve 7+5, a child might decompose the 7 into 5 and 2, retrieve the answer to 5+5 and then add 2.
In comparison to their TA peers, children with MLD, and LA children to a lesser extent, are delayed in their ability to effectively use counting to solve addition problems. They rely on finger counting for more years, adopt the min procedure at a later age, and commit more counting errors (Geary, 1993; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Montani, 1997; Ostad, 1997). The most consistent finding is that children with MLD show a deficit in the ability to use retrieval-based processes (Barrouillet, Fayol, & Lathuliére, 1997; Geary, 1990; Geary, Hamson, & Hoard, 2000; Jordan, Hanich, & Kaplan, 2003a). It is not that these children never correctly retrieve answers. Rather, they show a persistent difference in the frequency with which they correctly retrieve basic facts, and rarely use decomposition. A similar pattern is found with young LA children, but the grade-to-grade persistence of their retrieval deficit is not currently known.
Intelligence and Working Memory
Intelligence (IQ), working memory, and speed of processing are the central cognitive mechanisms that contribute to learning across academic domains (Baddeley, 1986; Engle, Tuholski, Laughlin, & Conway, 1999; Fry & Hale, 1996; Kail, 1991; Walberg, 1984), including mathematics (e.g., Andersson, 2008; Bull, Johnston, & Roy, 1999; Geary et al., 2004; McLean & Hitch, 1999; Swanson, 1993; Swanson & Sachse-Lee, 2001). The contribution of speed of processing to performance on our mathematical tasks is not substantial, however, when we control for individual differences in working memory (Geary et al., 2007). Thus, our focus here is on IQ and working memory. These two constructs are highly related but capture independent components of ability. The important features of working memory appear to be the attentional and inhibitory control mechanisms of the central executive (Engle et al., 1999), whereas the important feature of IQ may be the ability to logically problem solve (Embretson, 1995).
Geary et al. (2008) found that individual differences in children’s accuracy at making placements on a number line was related to IQ in 1st grade, but improvement in accuracy from 1st to 2nd grade was more strongly related to the central executive than to IQ. The relation between IQ and number line performance in 1st grade is consistent with the ability to think logically and systematically as related to learning the logical structure of the mathematical number line. The attentional and inhibitory control aspects of the central executive may be important during the actual placement of the numbers on the number line and for the inhibition of the natural-magnitude representational system during these placements; access to this system is associated with less accurate placements. The visuospatial sketch pad and phonological loop may also contribute to mathematics learning but in more restricted domains; the visuospatial sketch pad, for instance, may contribute to performance on the Number Sets Test and the number line task.
Current Study
The current study adds to our previous results from the longitudinal project in several ways. The use of four years of achievement scores and the estimation of latent growth trajectories allowed for the identification of stable groups of MLD, LA, TA, and HA children. The procedure obviates the need to use cutoff scores for group classification and thus avoids fluctuations in the diagnosis of MLD due to measurement error in the achievement tests; for instance, a child with scores at the 9th and 14th national percentile ranking for mathematics achievement might be classified as MLD one year and LA the next with no substantive change in cognitive competence. With four years of achievement test data and a battery of IQ, working memory, mathematical-cognition measures administered in 1st grade, we were able to identify the early cognitive predictors of longer-term growth in mathematical achievement, as well as identify potential cognitive mechanisms that contribute to achievement growth differences across groups. The approach does not address growth in the specific forms of mathematical cognition deficit (e.g., Chong & Siegel, 2008; Jordan et al., 2003a), but does allow us to identify groups that are learning mathematics at substantially different rates during the early school years, and the early cognitive profiles of children that will form these achievement groups. Finally, in contrast to our previous analyses from this project, we included the full range of IQ scores when determining achievement groups. The cost was the introduction of IQ as a potential confound to the classification of MLD and LA, but with the benefit of providing a more realistic assessment of achievement groups that emerge in school settings.
Methods
Participants
All kindergarten children from 12 elementary schools were invited to participate in a longitudinal prospective study of MLD. Parental consent and child assent were received for 37% (n = 311) of these children (see Geary et al., 2007), and the latent trajectory analysis included the 306 children (142 male) with at least one year of achievement data. The ethnic composition was mixed (68% White, 12% Black, 5% Asian, 4% Hispanic, 6% of mixed race; the remaining participants did not report ethnicity) and came from schools that served families from a wide range of socioeconomic levels, although schools that have yielded high numbers of children with MLD or LA children in previous studies were oversampled.
Standardized Measures
Intelligence
In 1st grade, the children were administered the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999), and these scores were used to estimate IQ based on norms presented in the manual. For this study, we did not use scores for the Raven’s Coloured Progressive Matrices (Raven, Court, & Raven, 1993), which was administered in kindergarten. The cost was slightly lower mean IQ scores (about 3 points) but the gain was more recent IQ norms that are calibrated with the achievement test norms.
Achievement
During the second semester of each grade, the children were administered the Numerical Operations and Word Reading subtests from the Wechsler Individual Achievement Test-II-Abbreviated (Wechsler, 2001). The Numerical Operations subtest assesses number discrimination, rote counting, number production, basic addition and subtraction, multi-digit addition and subtraction, and some multiplication and division. The Word Reading subtest includes matching and identifying letters, rhyming, beginning and ending sounds, phoneme blending, letter sounds, and word recognition.
Mathematical Tasks
Number sets
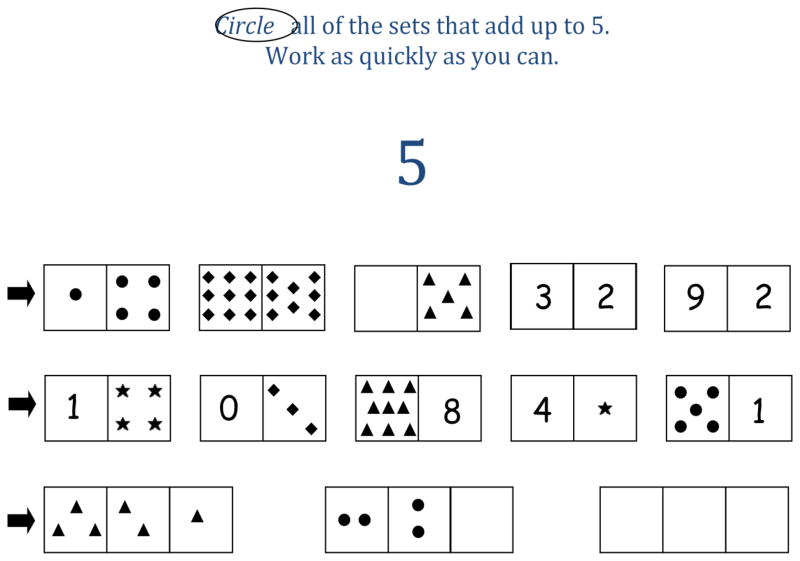
The test was designed as a group-administered paper-and-pencil measure of the speed and accuracy with which children can identify the quantity of sets of objects and combine these with quantities represented by Arabic numerals (Geary et al., 2007). Figure 1 shows several example items from the measure. Two items matching a target number of 4 were first explained for practice. Next, using 3 as the target number, four lines of two sets of items were administered as practice. In these practice lines, one set was a match and one was clearly not a match (3 vs. 9, 10, or 11). Once it was determined that the child understood the task, the experimental items were administered. There are four pages of such items, and the child is instructed to move across each line of the page from left to right without skipping any and to “circle any groups that can be put together to make the top number, five (nine)” and to “work as fast as you can without making many mistakes.” The child is given 60 sec and 90 sec per page for the targets 5 and 9, respectively, and is asked to stop at the time limit. We chose to time the task to avoid ceiling effects and because a timed measure should provide a better assessment of fluency in recognizing number combinations than an untimed measure.
Figure 1.
Example items from the Number Sets Test.
The task yields numbers of hits, misses, correct rejections, and false alarms for each problem type and size. Geary et al. (2007) found that 1st graders’ performance was consistent across target number and item content (e.g., whether the rectangle included Arabic numerals or shapes) and could thus be combined to create an overall frequency of hits (alpha, α = .88), correct rejections (α = .85), misses (α = .70), and false alarms (α = .90). Using a response operator characteristic curve analysis, Geary et al. (2009) derived a sensitivity measure, d′, by subtracting each participant’s z-score for misses from their z-score for hits (Macmillan, 2002). As noted, the value provides a measure of sensitivity to number while controlling for the child’s response bias. We used the d′ measure in the current analyses.
Number line estimation
A series of twenty-four 25cm number lines containing a blank line with two endpoints (0 and 100) was presented, one at a time, to the child with a target number (e.g., 45) in a large font printed above the line. The child’s task was to mark on the line, where the target number should lie; for a detailed description see Siegler and Booth (2004). Accuracy is defined as the absolute difference between the child’s placement and the correct position of the number. For the number 45, placements of 35 and 55 produce difference scores of 10. The overall score is the mean of these differences across trials.
Counting knowledge
The child watched a puppet count a series of alternating red and blue chips at several different counting string lengths. Sometimes the puppet counted correctly and other times did not. The correct counts could be the standard left to right count or could be nonstandard (e.g., right to left), whereas the incorrect counts violated a basic counting principle (e.g., one-one correspondence; Gelman & Gallistel, 1978). The child’s task was to tell the puppet if the way he counted was “OK” or “not OK”, and thus assessed the child’s awareness of counting principles and their understanding of whether variation from the standard left to right counting could still be correct (Briars & Siegler, 1984). Across a series of studies, we have found that children with MLD consistently miss trials on which the first chip in the sequence is double counted (e.g., Geary et al., 1992). Therefore, the variable used in this study was the percentage of trials (out of 3) on which the child correctly detected this particular counting error.
Addition strategy assessment
Fourteen simple (e.g., 3 + 6) and six complex (9 + 15) addition problems were horizontally presented in a large font (about 2 cm tall), one at a time, at the center of a 5″ by 8″ card. The child was asked to solve each problem (without the use of paper and pencil) as quickly as possible without making too many mistakes. It was emphasized that the child could use whatever strategy was easiest get the answer, and was instructed to speak the answer out loud. Based on the child’s description of how they got the answer and the experimenter’s observations, the trial was classified into 1 of 6 strategies; specifically, counting fingers, fingers (i.e., holding up fingers and then retrieving an answer without counting), verbal counting, retrieval, decomposition, or other/mixed strategy (see Geary et al., 2007; Siegler, 1987; Siegler & Shrager, 1984). A mixed trial was one in which the child started using one strategy, but completed the problem using another. The four most commonly used strategies were counting fingers, verbal counting, retrieval, and decomposition.
For the current analyses, we used five variables from the strategy tasks. The first was the percentage of retrieval trials that were correct for simple problems (direct retrieval was uncommon for the complex problems); because this percentage is correlated with mathematics achievement scores (Geary, Bow-Thomas, Liu, & Siegler, 1996) and is an indicator of MLD (Geary, 2004). The second and third variables were based on Geary et al. (2007); specifically, the raw number of problems correctly solved by a memory-based process (i.e., retrieval or decomposition) for simple (MemoryS) and complex problems (MemoryC). The two final variables captured the sophistication and accuracy of the children’s use of backup strategies when they could not correctly use a retrieval-based process. If the number of retrieval errors was greater than the number of problems correctly solved by finger counting or verbal counting, then backup (BackupS for simple problems, BackupC for complex problems) was coded as [0 – number of retrieval errors]. If the number of problems solved correctly by finger counting or verbal counting was greater than the number of retrieval errors, then backup was coded [(2 × Correct Min counts) + (Correct Sum counts) – total counting errors]. Low scores indicated frequent guessing, whereas high scores indicated frequent use of the sophisticated min counting procedure.
Working Memory
The Working Memory Test Battery for Children (WMTB-C; Pickering & Gathercole, 2001) consists of nine subtests that assess the central executive, phonological loop, and visuospatial sketchpad. All of the subtests have six items at each span level. Across subtests, the span levels rang from one to six to one to nine. Passing four items at one level moves the child to the next. At each span level, the number of items (e.g., words) to be remembered is increased by one. Failing three items at one span level terminates the subtest.
Central executive
The central executive is assessed using three dual-task subtests. Listening Recall requires the child to determine if a sentence is true or false, and then recall the last word in a series of sentences. Counting Recall requires the child to count a set of 4, 5, 6, or 7 dots on a card, and then to recall the number of counted dots at the end of a series of cards. Backward Digit Recall is a standard format backward digit span.
Phonological loop
Digit Recall, Word List Recall, and Nonword List Recall are standard span tasks with differing content stimuli; the child’s task is to repeat words spoken by the experimenter in the same order as presented by the experimenter. In the Word List Matching task, a series of words, beginning with two words and adding one word at each successive level, is presented to the child. The same words, but possibly in a different order, are then presented again, and the child’s task is to determine if the second list is in the same or different order than the first list.
Visuospatial sketch pad
Block Recall is another span task, but the stimuli consist of a board with nine raised blocks in what appears to the child as a “random” arrangement. The blocks have numbers on one side that can only be seen from the experimenter’s perspective. The experimenter taps a block (or series of blocks), and the child’s task is to duplicate the tapping in the same order as presented by the experimenter. In the Mazes Memory task, the child is presented a maze with more than one solution, and a picture of an identical maze with a path drawn for one solution. The picture is removed and the child’s task is to duplicate in the path in the response booklet. At each level, the mazes get larger by one wall.
Procedure
All children were tested in the spring of their kindergarten year and in the fall and spring of 1st, 2nd and 3rd grade. The achievement tests were administered each spring and the 1st grade mathematical tasks were administered in the fall. The majority of children were tested in a quiet location at their school site, and occasionally in a testing room on the university campus or in a mobile testing van if the child moved between assessments. The WMTB-C was administered in the testing van or on the university campus during 1st grade. The assessment times and corresponding sample sizes are shown in Table 1; as shown attribution is low after the spring of 1st grade.
Table 1.
Assessment Schedule and Sample Sizes
| Measures | Assessment Schedule | |||||||
|---|---|---|---|---|---|---|---|---|
| Kindergarten | 1st Grade | 2nd Grade | 3rd Grade | |||||
| Fall | Spring | Fall | Spring | Fall | Spring | Fall | Spring | |
| Achievement | X | X | X | X | ||||
| Intelligence | X | |||||||
| Working Memory | X | X | ||||||
| Mathematical | ||||||||
| Cognition | X | |||||||
| Group | Sample Size | |||||||
| MLD | 17 | 16 | 13 | 13 | 14 | |||
| LA | 154 | 141 | 125 | 125 | 123 | |||
| TA | 120 | 117 | 109 | 109 | 108 | |||
| HA | 15 | 15 | 14 | 14 | 14 | |||
Results
The results are organized into three sections. In the first, we describe procedures for determining latent groups, estimating growth trajectories, and corresponding group differences on the achievement, IQ, working memory, and mathematical-cognition measures. In the second and third respective sections, we describe univariate and multivariate ratios for the odds of class membership using IQ, working memory, and the mathematical-cognition measures as predictors.
Latent Class Models
Analyses were performed in Mplus, version 5.1 (Muthén & Muthén, 2008). Growth mixture models and latent class growth analyses were considered (see Jung & Wickrama, 2007), but for various reasons, we chose a latent trajectory analysis solution1. With the latter, individuals were assigned to endogenous categories based on raw mathematics achievement scores at the 4 measurement occasions. The number of classes for the solution was determined based on the interpretability and likely replicability of the classification of individuals as well as model fit indexes. The latter were the Bootstrapped Likelihood Ratio Test, Bayesian Information Criterion (BIC), and the Adjusted Bayesian Information Criterion (ABIC; Nylund, Asparouhov, and Muthén, 2007), and are shown in Table 2. As can be seen, the overall fit of the 4-, 5-, and 6-class solutions is roughly similar. The 6-class solution, however, produced one class representing less than 1% of the sample and we therefore examined the 4- and 5-class solutions. The latter produced a slightly better fit than the former, but consisted of three high-achieving classes that were not clearly distinct from one another based on posterior probabilities. For this reason and because our objective is to identify lower-achieving children, the 4-class model was retained.
Table 2.
Fit Statistics across Numbers of Classes
| No. classes | BLRT p-value | BIC | ABIC | entropy | % in smallest class |
|---|---|---|---|---|---|
| 2 | < .0001 | 5171.10 | 5129.87 | 0.72 | 43% |
| 3 | < .0001 | 5109.64 | 5052.55 | 0.78 | 6% |
| 4 | < .0001 | 5069.43 | 4996.48 | 0.82 | 5% |
| 5 | < .0001 | 5068.49 | 4979.69 | 0.82 | 2% |
| 6 | < .0001 | 5065.67 | 4961.01 | 0.84 | < 1% |
Note. BLRT = Bootstrapped Likelihood Ratio Test, between n classes and (n-1) classes; BIC = Bayesian Information Criterion; ABIC = Bayesian Information Criterion, adjusted for sample size.
The entropy value for the 4-class model–bound between 0 and 1 (with values of 1 indicating a clear delineation between classes; Celeux & Soromenho, 1996)–was 0.82. Values on the diagonal of the posterior probability matrix, which indicate the distinctness of the classification for each of the four respective groups, ranged from 0.88 to 0.94.
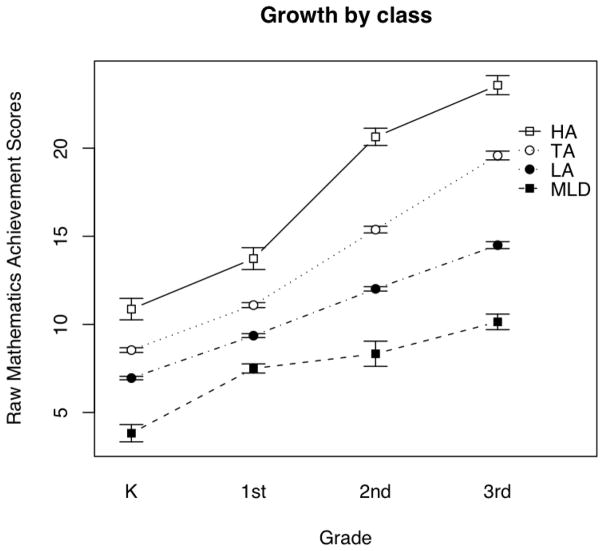
As shown in Figure 2 (produced using the Sciplot package in R, Morales, 2008), the classes show distinct mathematics achievement scores and trajectories across measurement occasions. On the basis of mean achievement scores shown in Table 3, we refer to these classes, from lowest to highest achieving, as MLD, LA, TA, and HA, with prevalence based on most likely class membership: 6% (n = 17), 50% (n = 154), 39% (n = 120), and 5% (n = 15) of the sample belonging to each respective class. The overall achievement trajectory of the LA group suggests a moderate learning difficulty in mathematics, but to be consistent with terms used in recent studies (Geary et al., 2007; Murphy et al., 2007) and because this is likely to be a heterogeneous group of children, we used the term low achieving rather than learning disabled.
Figure 2.
Mathematical achievement raw score growth by class across measurement occasions. HA = high achieving, TA = typically achieving, LA = low achieving, MLD = mathematical learning disability.
Table 3.
Mean IQ, Working Memory, and Achievement Scores for the Four Classes
| Working Memory | Mathematics | Reading | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IQ | CE | PL | VSSP | K | 1st Grade | 2nd Grade | 3rd Grade | K | 1st Grade | 2nd Grade | 3rd Grade | |||||||||||||
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| MLD | 83 | 7 | 83 | 9 | 80 | 12 | 83 | 12 | 11 | 14 | 8 | 6 | 5 | 4 | 2 | 2 | 36 | 25 | 21 | 25 | 17 | 23 | 15 | 19 |
| LA | 95 | 12 | 95 | 13 | 98 | 15 | 97 | 14 | 42 | 20 | 22 | 15 | 20 | 13 | 18 | 12 | 66 | 19 | 51 | 29 | 52 | 28 | 47 | 23 |
| TA | 104 | 13 | 106 | 12 | 104 | 13 | 103 | 14 | 66 | 20 | 44 | 23 | 55 | 23 | 55 | 21 | 80 | 17 | 73 | 24 | 74 | 21 | 66 | 20 |
| HA | 115 | 17 | 116 | 13 | 107 | 13 | 113 | 13 | 85 | 20 | 74 | 24 | 94 | 8 | 84 | 14 | 88 | 12 | 89 | 15 | 86 | 15 | 81 | 16 |
Note. IQ = Intelligence, CE = central executive, PL = phonological loop, VSSP = visuospatial sketchpad. Achievement scores are national percentile rankings.
Independent ANOVAs confirmed significant group differences (ps < 0.001) for IQ, F(3,257) = 23.63, and each of the working memory variables; CE, F(3,265) = 41.16, VSSP, F(3,265) = 16.50, and PL, F(3,265) = 16.27. Follow-up analyses revealed all pairwise comparisons of means to be significant at Tukey-adjusted alpha = 0.05, except for PL differences between HA and TA (p = 0.87) and between HA and LA [p = 0.09].
An ANCOVA with mathematics and reading achievement as within-subjects variables group as a between-subject variable, and IQ as the covariate yielded significant main effects for group and IQ [Fs (1, 253); (3, 253) = 35.89, 94.43, ps < 0.0001], which were qualified by significant test by IQ, F(1, 253) = 11.26, p < 0.001, test by group, F(3, 253) = 14.12, p < 0.0001, time by group [Wilks’ Lambda = 0.87, F(9, 611.02) = 4.04; p < 0.001], and test by time by group [Wilk’s Lambda = 0.90, F(9, 611.02) = 2.95, p < 0.005] interactions. The critical tests confirmed that the class differences for mathematics achievement were not due to class differences in IQ at any grade [Fs (3, 253) = 32.71, 40.48, 97.29, and 113.97, ps < 0.0001].
Univariate Class Diagnoses
Because specific classes are clearly distinct (e.g., MLD vs. TA), individual children are not likely to be misclassified as members of non-adjacent classes; for example, a child with MLD is unlikely to be misclassified as TA. Some children, however, represent borderline cases between adjacent classes; for example, a child with MLD might be misclassified as LA. As a means to address these potentially ambiguous cases, we estimated the odds ratios that a child is a member of one of two adjacent classes for each of the key variables used in this study; specifically, the IQ and working memory measures and the mathematical cognition measures shown in Table 4. Because these variables are continuous, the interpretation of each ratio is the increase in odds that an individual is a member of the first class for each one SD increase in the variable; each variable has been standardized (M = 0, SD = 1). Each of these values represents an odds ratio returned from a single variable diagnostic logistic regression model. Using the IQ variable to illustrate, given that a child is in the region where they could be classified as either HA or TA, a 1 SD increase in IQ was associated with a 1.98 fold increase in the odds of membership in the HA class (95% confidence interval = [1.10, 3.57]; since the interval does not include 1, it is significant at alpha = 0.05). As can be seen, the diagnostic utility of IQ increases as achievement decreases. In the case of a child who is either LA or MLD, a 1 SD increase in IQ is associated with a 30 fold increase in the odds that individual is LA.
Table 4.
Mean Z scores for the Mathematical Cognition Measures for the Four Classes
| d′ | Number Line | Count Error | PCR | MemoryS | MemoryC | BackupS | BackupC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | M | SD | |
| MLD | −1.75 | 1.41 | 1.27 | 0.62 | −1.81 | 1.31 | −0.57 | 1.28 | −0.63 | 0.19 | −0.20 | 0.52 | −1.37 | 0.67 | −1.33 | 0.47 |
| LA | −0.12 | 1.08 | 0.41 | 0.99 | −0.35 | 0.80 | −0.30 | 0.80 | −0.38 | 0.65 | −0.27 | 0.25 | −0.18 | 1.05 | −0.27 | 0.98 |
| TA | 0.36 | 0.44 | −0.51 | 0.67 | 0.55 | 0.63 | 0.28 | 1.05 | 0.33 | 1.02 | 0.12 | 1.08 | 0.43 | 0.72 | 0.46 | 0.80 |
| HA | 0.35 | 0.37 | −0.95 | 0.45 | 0.97 | 0.55 | 1.19 | 0.29 | 1.64 | 1.47 | 1.82 | 2.37 | −0.03 | 0.78 | 0.42 | 0.73 |
Note. All variables were standardized with M = 0 and SD = 1. MLD = mathematical learning disability, LA = low achieving, TA = typically achieving, HA = high achieving. d′ = sensitivity measure from Number Sets Test; Number line = mean of absolute error scores on the number line task, Count Error = percentage of trials detecting double-counting error, PCR = percentage of correct retrieval trials for simple addition, MemoryS = frequency of correct retrieval and decomposition for simple addition, MemoryC = frequency of correct retrieval and decomposition for complex addition, problems, BackupS = backup strategies for simple addition problems, BackupC = backup strategies for complex addition problems.
HA/TA
Examination of the odds ratios in Table 5 indicate that, among IQ and the working memory measures, higher levels IQ, VSSP, and CE increased the odds of belonging to the HA group as opposed to the TA group. Regarding mathematical tasks, higher levels in d′, PCR, MemoryS, and MemoryC increased the odds of belonging to the HA group whereas higher levels in BackupS decreased the odds of belong to this group.
Table 5.
Estimates and 95% Confidence Intervals for Univariate Odds Ratios
| Class/Class | |||
|---|---|---|---|
| Variable | HA/TA | TA/LA | LA/MLD |
| Intelligence and Working Memory | |||
| IQ | 1.98 (1.10, 3.57)* | 2.89 (1.82, 4.60)* | 30.05 (9.18, 98.39)* |
| PL | 1.14 (0.64, 2.02) | 1.91 (1.36, 2.67)* | 4.70 (2.21, 9.97)* |
| VSSP | 2.30 (1.20, 4.42)* | 1.74 (1.24, 2.43)* | 4.66 (1.77, 12.28)* |
| CE | 2.22 (1.15, 4.28)* | 3.86 (2.28, 6.55)* | 12.38 (4.18, 36.72)* |
| Mathematical Tasks | |||
| d′ | 3.37 (1.11, 10.24)* | 17.36 (8.21, 36.69)* | 6.46 (3.00, 13.94)* |
| Number linea | 0.11 (0.005, 2.09) | 0.12 (0.06, 0.24)* | 0.32 (0.15, 0.68)* |
| Count Error | 0.99 (0.33, 2.93) | 2.31 (1.41, 3.78)* | 3.01 (1.62, 5.60)* |
| PCR | 1.94 (1.19, 3.17)* | 2.97 (1.81, 4.87)* | 3.00 (0.86, 10.46) |
| MemoryS | 2.69 (1.54, 4.71)* | 4.74 (2.51, 8.96)* | 5.23 (1.06, 25.92)* |
| MemoryC | 2.02 (1.46, 2.81)* | 3.50 (1.83, 6.56)* | 0.51 (0.13, 2.01) |
| BackupS | 0.45 (0.26, 0.77)* | 2.81 (1.94, 4.07)* | 5.67 (2.80, 11.50)* |
| BackupC | 0.77 (0.43, 1.35) | 3.18 (2.15, 4.71)* | 6.23 (2.71, 14.34)* |
Note. MLD = mathematical learning disability, LA = low achieving, TA = typically achieving, HA = high achieving. d′ = sensitivity measure from Number Sets Test; Number line = mean of absolute error scores on the number line task, Count Error = percentage of trials detecting double-counting error, PCR = percentage of correct retrieval trials for simple addition, MemoryS = frequency of correct retrieval and decomposition for simple addition, MemoryC = frequency of correct retrieval and decomposition for complex addition, problems, BackupS = backup strategies for simple addition problems, BackupC = backup strategies for complex addition problems.
Significant at alpha = 0.05
Lower number line deviation scores indicate more accurate placements and thus the odds ratios are lower than 1
TA/LA
Higher levels of IQ, PL, VSSP, and CE increased the odds of belonging to the TA (compared to the LA) group. Among mathematical tasks, higher levels of d′, Count Error, PCR, MemoryS, MemoryC, BackupS, and BackupC increased the odds of belonging to the TA group; notably, a 1 SD increase in d′ resulted in a more than 17-fold increase in the odds of placement in the TA group. Higher error levels on the Number Line task resulted in roughly an 8.33 decrease in odds of belonging to the TA group.
LA/MLD
Higher levels in all IQ and working memory variables increased the odds of LA group membership compared to MLD group membership. Higher levels in the mathematical tasks of d′, Count Error, MemoryS, BackupS, and BackupC increased the odds of belong to the LA group whereas higher error levels in the Number Line task resulted in decreased odds of belong to this group.
Sex
Although not an a priori aspect of our study, the sex (female coded as 0, male coded as 1) of the child was related to class membership. In all three cases, the odds ratio was significant, indicating different proportions of boys and girls across groups. Given that a child is LA or MLD, the odds of being MLD are 5 times higher for boys. Given that a child is TA or LA, a boy has more than twice the odds of being TA. We could not estimate the ratio for discriminating between the HA and TA classes, because there were no girls in the HA class; therefore, based on these data, girls are more likely to belong to the TA class.
Multiple Regression Analyses
To explore the constellation of strengths and deficits underlying class membership, cognitive variables were entered into logistic regressions predicting dichotomous class membership and linear regressions predicting continuous posterior probability variables; the latter are estimates for the probability of membership in each of the four classes. Models were selected using the backwards stepwise procedure with the AIC as a criterion for model fit (Akaike, 1974). Because each predictor is standardized, the interpretation of the regression weights for the logistic regressions is increase in the natural log (ln) odds of class membership given a one SD increase in the predictor, independent of other predictors. The corresponding odds ratios are provided by eb, where b is the regression coefficient. The interpretation of the regression weights for the linear regressions is increase in the probability of class membership (compared to any other class) given a one SD increase in the predictor, independent of other predictors. Both sets of analyses were based on the 228 children without any missing data; MLD (n = 12), LA (n = 101), TA (n = 103), HA (n = 12).
Logistic regressions
The best fitting equations are shown in Table 6. The individual predictors may not be significant in any particular equation, due to collinearity, but the combination represents the best fitting constellation of variables for predicting membership in the four respective classes. Considering the first equation, it can be seen that being a boy results in a 3.71 fold increase in the odds of classification into the MLD group (vs. LA, TA, or HA class membership), independent of the other predictors. Notably, a 1 SD increase in the degree of error on the number line measure resulted in a 5 fold increase in the odds of MLD. Higher IQ, phonological loop, and visuospatial sketch pad scores were associated with a reduced likelihood of MLD classification. Or stated differently, a 1 SD decrease in visuospatial sketch pad scores, for instance, resulted in a 2.78 (1/.36) fold increase in the odds of MLD.
Table 6.
Best Fitting Multivariate Predictors from Logistic Regression
| Mathematical Learning Disability | |||||
|---|---|---|---|---|---|
| Estimate | Std. Error | z value | Pr(>|z|) | Odds Ratio (eb) | |
| Intercept | −6.59 | 1.54 | −4.27 | 0.000 | --- |
| Sex | 1.31 | 0.94 | 1.39 | 0.163 | 3.71 |
| IQ | −0.81 | 0.53 | −1.52 | 0.129 | 0.44 |
| PL | −0.84 | 0.52 | −1.63 | 0.104 | 0.43 |
| VSSP | −1.01 | 0.58 | −1.76 | 0.078 | 0.36 |
| Number line | 1.62 | 0.66 | 2.45 | 0.014 | 5.05 |
| Count Error | −0.51 | 0.32 | −1.60 | 0.110 | 0.60 |
| Low Achieving | |||||
| Intercept | 0.12 | 0.21 | 0.56 | 0.576 | --- |
| Sex | −0.73 | 0.33 | −2.23 | 0.026 | 0.48 |
| CE | −0.54 | 0.22 | −2.45 | 0.014 | 0.58 |
| PL | 0.31 | 0.20 | 1.59 | 0.126 | 1.36 |
| d′ | −0.45 | 0.24 | −1.90 | 0.058 | 0.64 |
| Number line | 0.32 | 0.22 | 1.49 | 0.136 | 1.38 |
| PCR | −0.39 | 0.20 | −2.01 | 0.045 | 0.68 |
| Typically Achieving | |||||
| Intercept | −0.66 | 0.19 | −3.41 | 0.000 | --- |
| CE | 0.30 | 0.19 | 1.60 | 0.110 | 1.35 |
| d′ | 1.00 | 0.29 | 3.47 | 0.001 | 2.72 |
| Number line | −0.54 | 0.23 | −2.30 | 0.021 | 0.58 |
| Count Error | 0.62 | 0.27 | 2.29 | 0.022 | 1.86 |
| High Achieving | |||||
| Intercept | −8.39 | 2.01 | −4.17 | 0.000 | --- |
| Sex | 2.32 | 1.33 | 1.75 | 0.080 | 10.18 |
| IQ | 0.77 | 0.44 | 1.73 | 0.083 | 2.16 |
| CE | 1.13 | 0.72 | 1.56 | 0.119 | 3.10 |
| VSSP | 1.07 | 0.63 | 1.70 | 0.089 | 2.92 |
| d′ | 1.25 | 0.85 | 1.47 | 0.143 | 3.49 |
| PCR | 1.18 | 0.46 | 2.59 | 0.010 | 3.25 |
A contrast of this first equation with that associated with the LA classification reveals similarities but more importantly many differences. The latter suggests different mechanisms underlying the poor mathematics achievement of these two groups of children. Being a girl is associated with a 2.08 (1/.48) fold increase in the likelihood of LA classification. Cognitive differences emerged in terms of the importance of the central executive, the d′ variable, and the percentage of correct retrieval of simple addition facts (i.e., PCR). A one SD increase in these respective competencies independently result in 1.72 (1/.58), 1.56 (1/.64), and 1.47 (1/.68) fold decrease in the likelihood of LA classification.
Three of the four variables that emerged with the TA classification equation also emerged with the LA equation, suggesting the LA and TA groups may be largely lower and higher ends, respectively, of the same population. Increases in fluency in identifying number sets (d′) and percentage of correct identification of double counting errors increased the likelihood of classification into the TA group, whereas decreased accuracy in number line placements decreased the likelihood of TA class membership. The most notable feature of the final equation is the 10.18 fold increase in the likelihood of a HA classification for boys. Unlike the LA and TA classifications and in inverse the relation to that found for MLD classification, the visuospatial sketch pad emerged as an important predictor for HA (odds ratio = 2.92). A one SD increase in the fluency of identifying number sets (d′) and accuracy in retrieving addition facts from long-term memory independently resulted in more than a three-fold increase in the odds of HA classification.
Linear regressions
As can be seen in Table 7, the predictors in the linear regressions were largely the same as those that emerged in the logistic equations; overall model fits ranged from R2 = .24 to .31, ps<.0001. As an example, independent of other predictors, a one SD decease in the fluency of identifying number sets (d′) and in accuracy in detecting double counting errors respectively resulted in a 5% increase in the probability of an MLD classification. Again, there was considerable overlap in the predictors of the probability of LA and TA classification and, unlike these two groups, the visuospatial sketch pad emerged as a predictor of the probability of a HA classification.
Table 7.
Best Fitting Multivariate Predictors from Linear Regression
| Mathematical Learning Disability | ||||
|---|---|---|---|---|
| Estimate | Std. Error | t value | Pr(>|t|) | |
| Intercept | 0.04 | 0.015 | 2.66 | 0.008 |
| Sex | 0.04 | 0.023 | 1.76 | 0.079 |
| PL | −0.02 | 0.013 | −1.67 | 0.097 |
| VSSP | −0.01 | 0.013 | −0.98 | 0.328 |
| d′ | −0.05 | 0.015 | −3.33 | 0.001 |
| Number Line | 0.03 | 0.016 | 1.63 | 0.105 |
| Count Error | −0.05 | 0.013 | −3.75 | 0.000 |
| Low Achieving | ||||
| Intercept | 0.53 | 0.035 | 15.14 | 0.000 |
| Sex | −0.13 | 0.054 | −2.34 | 0.020 |
| CE | −0.09 | 0.031 | −2.46 | 0.015 |
| d′ | −0.06 | 0.036 | −1.72 | 0.087 |
| Number Line | 0.08 | 0.044 | 2.27 | 0.024 |
| PCR | −0.07 | 0.029 | −2.45 | 0.015 |
| Typically Achieving | ||||
| Intercept | 0.42 | 0.025 | 16.92 | 0.000 |
| CE | 0.06 | 0.030 | 2.18 | 0.030 |
| d′ | 0.11 | 0.034 | 3.08 | 0.002 |
| Number Line | −0.13 | 0.034 | −3.70 | 0.000 |
| High Achieving | ||||
| Intercept | 0.03 | 0.017 | 1.72 | 0.086 |
| Sex | 0.05 | 0.026 | 2.04 | 0.042 |
| IQ | 0.03 | 0.014 | 2.38 | 0.018 |
| PCR | 0.07 | 0.013 | 5.19 | 0.000 |
| VSSP | 0.03 | 0.014 | 2.42 | 0.017 |
Discussion
The central goals of the current study were to identify stable groups of MLD and LA children, determine similarities and differences in the cognitive deficits contributing to group membership, and to identify early cognitive predictors of group membership. We consider each of these issues respectively.
Stability of MLD and LA
In their prospective, longitudinal study of mathematics learning, Murphy et al. (2007) classified children as MLD if their mathematics achievement scores were below the 11th percentile of their sample for at least two years, from kindergarten to 3rd grade, and as LA if their scores were between the 11th and 25th percentiles, inclusive, for at least two of these years. Children in these respective groups not only showed, by definition, lower and higher levels of mathematical performance, but different growth trajectories. The children with MLD started lower on the achievement test and showed more shallow growth, relative to their LA peers and a comparison group of TA children. The two latter groups did not differ in terms of growth in mathematics achievement, but their start points differed by design. Jordan and her colleagues have also identified classes of children with different initial levels of mathematical competence and sometimes with different growth rates (Jordan, Hanich, & Kaplan, 2003b; Jordan, Kaplan, Oláh, & Locuniak, 2006).
Our results confirm Murphy et al.’s (2007) and Jordan et al.’s (2006) findings for the existence of a small number of classes of children with different initial levels of mathematical achievement, and Murphy et al.’s (2007) findings in terms of class differences in the growth trajectories of achievement scores; Jordan et al. (2006) also identified groups with different trajectories across the kindergarten year, but focused on growth on mathematical-cognition tasks, not achievement measures. As with the MLD group identified by Murphy et al., our group of children with MLD showed some grade-to-grade growth on the mathematics test, but their below-average trajectory resulted in declining national percentile scores across grades. Our MLD class and that of Murphy et al. also showed below average IQ and reading achievement scores, but performance in both of these domains was above that found for mathematics achievement. As detailed below, whatever the contributions of IQ and reading competence to their mathematical development, children with MLD appear to have deficits specific to mathematics.
Murphy et al. also found that 2 out of 3 of the children in their MLD group were boys and 2 out of 3 children in their LA group were girls. Although their results were not statistically significant, the same pattern emerged in our study and suggests that low mathematics achievement may manifest differently in boys and girls (see also Barbaresi et al., 2005). Either way, our results add to accumulating evidence for the existence of an identifiable group of at least 5% of children who have a persistent, grade-to-grade learning disability in one or several areas of mathematics that cannot be entirely attributable to IQ or poor reading ability.
Cognitive Profiles of MLD and LA Groups
It has been demonstrated many times that children with MLD score below average on measures that assess one or several working memory systems (Bull et al., 1999; Geary et al., 2004; McLean & Hitch, 1999; Swanson, 1993) and have delayed procedural development in arithmetic and difficulty learning basic arithmetic facts (Chong & Siegel, 2008; Geary, 1993; Jordan et al., 2003a). However, the criterion used to define groups of children with MLD has varied from one study to the next and, as a result, many of these groups included both children with MLD and LA children, as defined here and by Murphy et al. (2007). The conflation of these groups has made it difficult to determine if the same or different mechanisms are underlying their poor mathematical development. There has also been a tendency in this literature to classify children with poor mathematics achievement based on whether the deficits are specific to mathematics (MD-only) or involve poor outcomes in both mathematics and reading (MD/RD; Geary, Hoard, Hamson, 1999; Geary et al., 2000; Hanich et al., 2001; Jordan & Montani, 1997). Children with MD-only and MD/RD appear to be similar to the LA and MLD groups, respectively, identified in this study and by Murphy et al., and thus the following discussion may also apply to the MD-only and MD/RD classifications.
Murphy et al. (2007) identified subtle differences in the working memory deficits of their MLD and LA groups, but there was no specific cognitive or mathematics variable that differentiated the groups. Rather, the groups differed in terms of more or less severe deficits in the same cognitive and mathematical domains. Geary et al. (2007), in contrast, identified a group of average-IQ children with MLD that had substantial working memory deficits and a group of average-IQ LA children with no such working memory deficits. We did not control for IQ in the current analyses, but the same group differences in working memory emerged. The best constellation of variables for predicting membership in the MLD class included IQ and the phonological loop and visuospatial sketch pad scores, the means for all of which were about 1 SD below average (Table 3). However, the central executive variable did not emerge as a significant predictor of MLD class membership in our current analyses, in contrast with Geary et al. (2007), which may have been due to the emergence of the count error variable in these equations and collinearity; specifically, the deficit of children with MLD on this counting variable appears to be mediated by their central executive deficits (Geary et al., 2007). In other words, the central executive deficits of the children with MLD were better captured by the count error variable than by the central executive measure per se.
The emergence of the central executive and phonological loop variables for prediction of LA class membership was not due to deficits in these components of working memory. In fact, controlling for other predictors, higher phonological loop scores were associated with higher odds of classification as LA, potentially due to the over-representation of girls in this class. Lower central executive scores were associated with higher odds of LA classification, despite scores in the average range (Table 3), due to the contrast with the above average central executive scores of the children in the TA and HA groups.
Independent of working memory and IQ scores, the best predictor of membership in the MLD class was the number line variable for the logistic regression and the d′ and count error variables in the linear regression. As stated, the count error variable could be capturing variance in central executive competence, but the emergence of the number line and d′ variables suggest these children have a poor number sense, in support of other findings (Butterworth & Reigosa, 2007; Geary et al., 2009; Koontz & Berch, 1996). The children with MLD also correctly retrieved fewer addition facts than did TA and HA children (Table 4), as is typically found, but this did not emerge in the regressions as their most serious deficit. The number line and d′ measures also emerged as core predictors of membership in the LA class, as did their low frequency of correct addition-fact retrieval. Whether the number sense and retrieval deficits of the children with MLD and LA children represent different cut points along the same underlying ability continuums or different forms of deficit is not clear. For instance, the IQ and working memory deficits might contribute to the poor performance of the children with MLD on these tasks (Geary et al., 2008), but this cannot be the case for the LA children.
In fact, given the unexpectedly large percentage (50%) of children in our overall sample who were classified as LA, it is unlikely that all of them have number sense or fact retrieval deficits of the magnitude that would support a learning disability diagnosis. The poor performance of some proportion of these children may result from instructional practices or lack of early informal exposure to number-information at home. Our planned follow-up analyses of the grade-to-grade changes on the mathematical-cognition measures may provide a means to better separate children in our LA class into those who have actual mathematics cognition deficits from those whose low achievement is the result of experiences that do not support full development of their potential in mathematics.
For this particular sample, the emergence of similar sets of predictors in the regressions and based on the pattern of mean scores, the LA and TA classes appear to represent lower and higher ends, respectively, of largely the same constellation of ability continuums. No doubt the children in the MLD and HA classes vary along the same continuums for individual competencies, but there were several potentially interesting differences within the constellations of variables that best predicted inclusion in these two classes. The children classified into the MLD group had across-the-board deficits in all three working memory systems, if we assume the count error variable is capturing poor central executive abilities. The other notable feature is that the mathematical tasks that emerged in the regressions assess their number sense, and not their competence in procedural execution or addition-fact retrieval. The children with MLD do, in fact, have difficulties in these two latter areas (Table 4), as found in most previous studies (Geary, 2004), but an earlier emerging and potentially more fundamental deficit may exist in their number sense (Butterworth & Reigosa, 2007; Koontz & Berch, 1996); potentially related to the inherent number-magnitude representational system.
In addition to the finding that they were all boys, the most distinct aspect of the regressions for predicting HA class membership was the importance of the visuospatial sketch pad. In an earlier study in which we identified HA children based on IQ scores–mean of 126 as compared to 115 for the current HA–group and not mathematics achievement scores, the key working memory mechanism that contributed to their advantages on most of the mathematical tasks was the central executive (Hoard, Geary, Byrd-Craven, & Nugent, 2008). The central executive is important for the current HA group as well, but the visuospatial sketch pad may contribute as much or more to their growth trajectory in mathematics as the central executive (see also Dark & Benbow, 1991).
Predictors of MLD and LA Status
The results of this study are consistent with those of other studies of early potential predictors of poor outcomes in mathematics (Gersten et al., 2005; Mazzocco & Thompson, 2005) and confirm the importance of an early number sense for mathematical development (Case & Okamoto, 1996). More precisely, the Number Sets Test, the number line task, the double-count error items from the counting knowledge task, and assessment of the ability to correctly retrieve basic addition facts from long-term memory all emerged as important mathematical-cognition variables in the prediction MLD or LA class membership, independent of the contributions of IQ and working memory. The critical distinction between membership in the MLD or LA classes was the below average IQ and working memory competencies of the former group. The implication is that risk assessment for poor long-term outcomes in mathematics should include IQ and working memory measures, as well as measures that assess children’s number sense, their ability to monitor the act of counting, and their knowledge of very simple addition and presumably subtraction facts.
Acknowledgments
Geary acknowledges support from grants R01 HD38283 from the National Institute of Child Health and Human Development (NICHD), and R37 HD045914 co-funded by NICHD and the Institute of Educational Sciences. Little acknowledge training-grant support from T32 AA13526 from the National Institute on Alcohol Abuse and Alcoholism Grants awarded to Kenneth J. Sher. We thank Linda Coutts, Shirley Brewer, Rachel Christensen, Jennifer Byrd-Craven, Kendra Cerveny, Mike Coutts, Sara Ensenberger, Nicholas Geary, Nancy Goodale, Larissa Haggard, Rebecca Hale, DJ Jordan, Mary Lemp, Patrick Maloney, Rehab Mojid, Cy Nadler, Chattavee Numtee, Catherine Ford O’Connor, Amanda Shocklee, Jennifer Smith, Ashley Stickney, Jasmine Tilghman, and Katherine Waller for help on various aspects of the project.
Footnotes
Lower-achieving children’s mathematics achievement scores show a floor effect in kindergarten and 1st grade. Therefore, classes are predicted to grow differently across measurement occasions with respect to an intercept, slope, and quadratic factors. With more measurement occasions, separate linear or even logistic functions might appropriately model growth across measurement occasions, but due to the low number of measurement occasions and the complex nature of observed growth across these occasions, a parsimonious LCA model was chosen.
Odds ratio confidence intervals were estimated using robust estimates based on the Maximum Likelihood estimation function. Confidence intervals based on bootstrap draws for IQ yielded extremely similar results, which did not change any interpretations of statistical significance.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19:716–723. [Google Scholar]
- Andersson U. Working memory as a predictor of written arithmetic skills in children: The importance of central executive functions. British Journal of Educational Psychology. 2008;78:181–203. doi: 10.1348/000709907X209854. [DOI] [PubMed] [Google Scholar]
- Ashcraft MH. The development of mental arithmetic: A chronometric approach. Developmental Review. 1982;2:213–236. [Google Scholar]
- Baddeley AD. Working memory. Oxford: Oxford University Press; 1986. [Google Scholar]
- Barbaresi WJ, Katusic SK, Colligan RC, Weaver AL, Jacobsen SJ. Math learning disorder: Incidence in a population-based birth cohort, 1976–82, Rochester, Minn. Ambulatory Pediatrics. 2005;5:281–289. doi: 10.1367/A04-209R.1. [DOI] [PubMed] [Google Scholar]
- Barrouillet P, Fayol M, Lathuliére E. Selecting between competitors in multiplication tasks: An explanation of the errors produced by adolescents with learning disabilities. International Journal of Behavioral Development. 1997;21:253–275. [Google Scholar]
- Berch DB, Mazzocco MMM, editors. Why is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities. Baltimore, MD: Paul H. Brookes Publishing Co; 2007. [Google Scholar]
- Briars D, Siegler RS. A featural analysis of preschoolers’ counting knowledge. Developmental Psychology. 1984;20:607–618. [Google Scholar]
- Bull R, Johnston RS, Roy JA. Exploring the roles of the visual-spatial sketch pad and central executive in children’s arithmetical skills: Views from cognition and developmental neuropsychology. Developmental Neuropsychology. 1999;15:421–442. [Google Scholar]
- Butterworth B, Reigosa V. Information processing deficits in dyscalculia. In: Berch DB, Mazzocco MMM, editors. Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities. Baltimore, MD: Paul H. Brookes Publishing Co; 2007. pp. 65–81. [Google Scholar]
- Celeux G, Soromenho G. An entropy criterion for assessing the number of clusters in a mixture model. Journal of Classification. 1996;13:195–212. [Google Scholar]
- Case R, Okamoto Y. The role of central conceptual structures in the development of children’s thought. Monographs of the Society for Research in Child Development. 1996;66(1–2) doi: 10.1111/j.1540-5834.1996.tb00536.x. Serial No. 246. [DOI] [PubMed] [Google Scholar]
- Chong SL, Siegel LS. Stability of computational deficits in math learning disability from second through fifth grades. Developmental Neuropsychology. 2008;33:300–317. doi: 10.1080/87565640801982387. [DOI] [PubMed] [Google Scholar]
- Dark VJ, Benbow CP. Differential enhancement of working memory with mathematical versus verbal precocity. Journal of Educational Psychology. 1991;83:48–60. [Google Scholar]
- Dehaene S. The number sense: How the mind creates mathematics. NY: Oxford University Press; 1997. [Google Scholar]
- Dowker A. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, UK: Psychology Press; 2005. [Google Scholar]
- Embretson SE. The role of working memory capacity and general control processes in intelligence. Intelligence. 1995;20:169–189. [Google Scholar]
- Engle RW, Tuholski SW, Laughlin JE, Conway ARA. Working memory, short-term memory, and general fluid intelligence: A latent-variable approach. Journal of Experimental Psychology: General. 1999;128:309–331. doi: 10.1037//0096-3445.128.3.309. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke E. Core systems of number. TRENDS in Cognitive Science. 2004;8:307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Fry AF, Hale S. Processing speed, working memory, and fluid intelligence: Evidence for a developmental cascade. Psychological Science. 1996;7:237–241. [Google Scholar]
- Fuson KC. An analysis of the counting-on solution procedure in addition. In: Carpenter TP, Moser JM, Romberg TA, editors. Addition and subtraction: A cognitive perspective. Hillsdale, NJ: Erlbaum; 1982. pp. 67–81. [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Geary DC. A componential analysis of an early learning deficit in mathematics. Journal of Experimental Child Psychology. 1990;49:363–383. doi: 10.1016/0022-0965(90)90065-g. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematical disabilities: Cognitive, neuropsychological, and genetic components. Psychological Bulletin. 1993;114:345–362. doi: 10.1037/0033-2909.114.2.345. [DOI] [PubMed] [Google Scholar]
- Geary DC. Mathematics and learning disabilities. Journal of Learning Disabilities. 2004;37:4–15. doi: 10.1177/00222194040370010201. [DOI] [PubMed] [Google Scholar]
- Geary DC. Missouri longitudinal study of mathematical development and disability. In: Cowan R, Saxton M, Tolmie A, editors. Understanding number development and number difficulties. Leicester, UK: British Psychological Society; (in press) (No. 7, British Journal of Educational Psychology, Monograph Series II: Psychological Aspects of Education - Current Trends, pp xxx-xxx) [Google Scholar]
- Geary DC, Bailey DH, Hoard MK. Predicting mathematical achievement and mathematical learning disability with a simple screening tool: The Number Sets Test. Journal of Psychoeducational Assessment. 2009;27 doi: 10.1177/0734282908330592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Bow-Thomas CC, Yao Y. Counting knowledge and skill in cognitive addition: A comparison of normal and mathematically disabled children. Journal of Experimental Child Psychology. 1992;54:372–391. doi: 10.1016/0022-0965(92)90026-3. [DOI] [PubMed] [Google Scholar]
- Geary DC, Bow-Thomas CC, Liu F, Siegler RS. Development of arithmetical competencies in Chinese and American children: Influence of age, language, and schooling. Child Development. 1996;67:2022–2044. [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Hamson CO. Numerical and arithmetical cognition: Patterns of functions and deficits in children at risk for a mathematical disability. Journal of Experimental Child Psychology. 1999;74:213–239. doi: 10.1006/jecp.1999.2515. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hamson CO, Hoard MK. Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability. Journal of Experimental Child Psychology. 2000;77:236–263. doi: 10.1006/jecp.2000.2561. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Desoto M. Strategy choices in simple and complex addition: Contributions of working memory and counting knowledge for children with mathematical disability. Journal of Experimental Child Psychology. 2004;88:121–151. doi: 10.1016/j.jecp.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;78:1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, Byrd-Craven J. Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology. 2008;33:277–299. doi: 10.1080/87565640801982361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman R, Gallistel CR. The child’s understanding of number. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Gelman R, Meck E. Preschooler’s counting: Principles before skill. Cognition. 1983;13:343–359. doi: 10.1016/0010-0277(83)90014-8. [DOI] [PubMed] [Google Scholar]
- Gersten R, Jordan NC, Flojo JR. Early identification and interventions for students with mathematics difficulties. Journal of Learning Disabilities. 2005;38:293–304. doi: 10.1177/00222194050380040301. [DOI] [PubMed] [Google Scholar]
- Groen GJ, Parkman JM. A chronometric analysis of simple addition. Psychological Review. 1972;79:329–343. [Google Scholar]
- Halberda J, Mazzocco MMM, Feigenson L. Individual differences in non-verbal number acuity correlate with maths achievement. Nature. 2008 October 2;455:665–669. doi: 10.1038/nature07246. [DOI] [PubMed] [Google Scholar]
- Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology. 2001;93:615–626. [Google Scholar]
- Hoard MK, Geary DC, Byrd-Craven J, Nugent L. Mathematical cognition in intellectually precocious children. Developmental Neuropsychology. 2008;33:251–276. doi: 10.1080/87565640801982338. [DOI] [PubMed] [Google Scholar]
- Hoard MK, Geary DC, Hamson CO. Numerical and arithmetical cognition: Performance of low-and average-IQ children. Mathematical Cognition. 1999;5:65–91. [Google Scholar]
- Isaacs EB, Edmonds CJ, Lucas A, Gadian DG. Calculation difficulties in children of very low birthweight: A neural correlate. Brain. 2001;124:1701–1707. doi: 10.1093/brain/124.9.1701. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. Arithmetic fact mastery in young children: A longitudinal investigation. Journal of Experimental Child Psychology. 2003a;85:103–119. doi: 10.1016/s0022-0965(03)00032-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Hanich LB, Kaplan D. A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties. Child Development. 2003b;74:834–850. doi: 10.1111/1467-8624.00571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan NC, Kaplan D, Oláh LN, Locuniak MN. Number sense growth in kindergarten: A longitudinal investigation of children at risk for mathematics difficulties. Child Development. 2006;77:153–175. doi: 10.1111/j.1467-8624.2006.00862.x. [DOI] [PubMed] [Google Scholar]
- Jordan NC, Montani TO. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997;30:624–634. doi: 10.1177/002221949703000606. [DOI] [PubMed] [Google Scholar]
- Jung T, Wickrama KAS. Recent advances in longitudinal data analysis in social and psychological research: An introduction to latent class growth analysis and growth mixture modeling. Social and Personality Psychology Compass. 2007;2:302–31. [Google Scholar]
- Kadosh RC, Kadosh KC, Schuhmann T, Kaas A, Goebel R, Henik A, Sack AT. Virtual dyscalculia induced by parietal-lobe TMS impairs automatic magnitude processing. Current Biology. 2007;17:689–693. doi: 10.1016/j.cub.2007.02.056. [DOI] [PubMed] [Google Scholar]
- Kail R. Developmental change in speed of processing during childhood and adolescence. Psychological Bulletin. 1991;109:490–501. doi: 10.1037/0033-2909.109.3.490. [DOI] [PubMed] [Google Scholar]
- Koontz KL, Berch DB. Identifying simple numerical stimuli: Processing inefficiencies exhibited by arithmetic learning disabled children. Mathematical Cognition. 1996;2:1–23. [Google Scholar]
- Kail R. Developmental change in speed of processing during childhood and adolescence. Psychological Bulletin. 1991;109:490–501. doi: 10.1037/0033-2909.109.3.490. [DOI] [PubMed] [Google Scholar]
- LeFevre J-A, Smith-Chant BL, Fast L, Skwarchuk S-L, Sargla E, Arnup JS, et al. What counts as knowing? The development of conceptual and procedural knowledge of counting from kindergarten through Grade 2. Journal of Experimental Child Psychology. 2006;93:285–303. doi: 10.1016/j.jecp.2005.11.002. [DOI] [PubMed] [Google Scholar]
- Levine SC, Jordan NC, Huttenlocher J. Development of calculation abilities in young children. Journal of Experimental Child Psychology. 1992;53:72–103. doi: 10.1016/s0022-0965(05)80005-0. [DOI] [PubMed] [Google Scholar]
- Lewis C, Hitch GJ, Walker P. The prevalence of specific arithmetic difficulties and specific reading difficulties in 9-year-old to 10-year-old boys and girls. Journal of Child Psychology and Psychiatry. 1994;35:283–292. doi: 10.1111/j.1469-7610.1994.tb01162.x. [DOI] [PubMed] [Google Scholar]
- MacMillan NA. Signal detection theory. In: Wixted J, Pashler H, editors. Stevens’ Handbook of Experimental Psychology, 3rd Edition, Vol. 4: Methodology in Experimental Psychology. New York: John Wiley & Sons, Inc; 2002. pp. 43–90. [Google Scholar]
- Mazzocco MMM, Thompson RE. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice. 2005;20:142–155. doi: 10.1111/j.1540-5826.2005.00129.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLean JF, Hitch GJ. Working memory impairments in children with specific arithmetic learning difficulties. Journal of Experimental Child Psychology. 1999;74:240–260. doi: 10.1006/jecp.1999.2516. [DOI] [PubMed] [Google Scholar]
- Morales MA. Sciplot: Scientific graphing functions for factorial designs. 2008 R package version 1.0–2. [Google Scholar]
- Murphy MM, Mazzocco MMM, Hanich LB, Early MC. Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. Journal of Learning Disabilities. 2007;40:458–478. doi: 10.1177/00222194070400050901. [DOI] [PubMed] [Google Scholar]
- Nylund KL, Asparouhov T, Muthen B. Deciding on the number of classes in latent class analysis and growth mixture modeling. A Monte Carlo simulation study. Structural Equation Modeling. 2007;14:535–569. [Google Scholar]
- Ohlsson S, Rees E. The function of conceptual understanding in the learning of arithmetic procedures. Cognition and Instruction. 1991;8:103–179. [Google Scholar]
- Ostad SA. Developmental differences in addition strategies: A comparison of mathematically disabled and mathematically normal children. British Journal of Educational Psychology. 1997;67:345–357. doi: 10.1111/j.2044-8279.1997.tb01249.x. [DOI] [PubMed] [Google Scholar]
- Ostad SA. Developmental differences in solving simple arithmetic word problems and simple number-fact problems: A comparison of mathematically normal and mathematically disabled children. Mathematical Cognition. 1998;4:1–19. [Google Scholar]
- Pickering S, Gathercole S. Working Memory Test Battery for Children (WMTB-C) Manual. London: Psychological Corporation Ltd; 2001. [Google Scholar]
- Muthén LK, Muthén BO. Mplus User’s Guide [Computer software and manual] 5. Los Angeles: Muthén & Muthén; 2008. [Google Scholar]
- Raven JC, Court JH, Raven J. Manual for Raven’s Progressive Matrices and Vocabulary Scales. London: H. K. Lewis & Co; 1993. [Google Scholar]
- Shalev RS, Manor O, Gross-Tsur V. Developmental dyscalculia: A prospective six-year follow-up. Developmental Medicine & Child Neurology. 2005;47:121–125. doi: 10.1017/s0012162205000216. [DOI] [PubMed] [Google Scholar]
- Siegler RS. The perils of averaging data over strategies: An example from children’s addition. Journal of Experimental Psychology: General. 1987;116:250–264. [Google Scholar]
- Siegler RS, Booth JL. Development of numerical estimation in young children. Child Development. 2004;75:428–444. doi: 10.1111/j.1467-8624.2004.00684.x. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Opfer J. The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science. 2003;14:237–243. doi: 10.1111/1467-9280.02438. [DOI] [PubMed] [Google Scholar]
- Siegler RS, Shrager J. Strategy choice in addition and subtraction: How do children know what to do? In: Sophian C, editor. Origins of cognitive skills. Hillsdale, NJ: Erlbaum; 1984. pp. 229–293. [Google Scholar]
- Silver CH, Pennett HD-L, Black JL, Fair GW, Balise RR. Stability of arithmetic disability subtypes. Journal of Learning Disabilities. 1999;32:108–119. doi: 10.1177/002221949903200202. [DOI] [PubMed] [Google Scholar]
- Starkey P. The early development of numerical reasoning. Cognition. 1992;43:93–126. doi: 10.1016/0010-0277(92)90034-f. [DOI] [PubMed] [Google Scholar]
- Starkey P, Cooper RG., Jr Perception of numbers by human infants. Science. 1980 November 28;210:1033–1035. doi: 10.1126/science.7434014. [DOI] [PubMed] [Google Scholar]
- Strauss MS, Curtis LE. Development of numerical concepts in infancy. In: Sophian C, editor. Origins of cognitive skills: The eighteenth annual Carnegie symposium on cognition. Hillsdale, NJ: Erlbaum; 1984. pp. 131–155. [Google Scholar]
- Swanson HL. Working memory in learning disability subgroups. Journal of Experimental Child Psychology. 1993;56:87–114. doi: 10.1006/jecp.1993.1027. [DOI] [PubMed] [Google Scholar]
- Swanson HL, Sachse-Lee C. Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important. Journal of Experimental Child Psychology. 2001;79:294–321. doi: 10.1006/jecp.2000.2587. [DOI] [PubMed] [Google Scholar]
- Walberg HJ. Improving the productivity of America’s schools. Educational Leadership. 1984;41:19–27. [Google Scholar]
- Wechsler D. Wechsler Abbreviated Scale of Intelligence. San Antonio, TX: PsychCorp, Harcourt Assessment, Inc; 1999. [Google Scholar]
- Wechsler D. Wechsler Individual Achievement Test II- Abbreviated. San Antonio, TX: The Psychological Corporation, Harcourt Brace & Co; 2001. [Google Scholar]
- Wynn K, Bloom P, Chiang W-C. Enumeration of collective entities by 5-month- old infants. Cognition. 2002;83:B55–B62. doi: 10.1016/s0010-0277(02)00008-2. [DOI] [PubMed] [Google Scholar]