A Multivariate Approach for Integrating Genome-wide Expression Data and Biological Knowledge

Abstract

Motivation

Several statistical methods that combine analysis of differential gene expression with biological knowledge databases have been proposed for a more rapid interpretation of expression data. However, most such methods are based on a series of univariate statistical tests and do not properly account for the complex structure of gene interactions.

Results

We present a simple yet effective multivariate statistical procedure for assessing the correlation between a subspace defined by a group of genes and a binary phenotype. A subspace is deemed significant if the samples corresponding to different phenotypes are well separated in that subspace. The separation is measured using Hotelling’s T² statistic, which captures the covariance structure of the subspace. When the dimension of the subspace is larger than that of the sample space, we project the original data to a smaller orthonormal subspace. We use this method to search through functional pathway subspaces defined by Reactome, KEGG, BioCarta, and Gene Ontology. To demonstrate its performance, we apply this method to the data from two published studies, and we visualize the results in the principal component space.

INTRODUCTION

Microarray technology enables the simultaneous monitoring of expression profiles on a genome-scale and has numerous areas of application. With the identification of differentially expressed genes between different cancer types, for example, the microarray technique can aid in diagnosis (Pomeroy et al., 2002). By correlating expression with phenotypic data such as patient survival time and responsiveness to treatment, it may also help in the prognosis and treatment of diseases (Park et al., 2002; Holleman et al., 2004).

Recently proposed analytical tools for microarray data combine statistical analysis with a priori biological knowledge from expert-curated databases. In general, a univariate statistical score is first computed for each gene. Then a second statistical procedure is used to determine whether a particular category of genes are over-represented among the top-scoring genes. Annotations from different databases provide a multitude of different gene categories for this process. Fisher’s exact statistic, Kolmogorov-Smirnov statistic, and a simple average of univariate statistical scores (e.g., average of negative log p-values) are among the common measures of significance for a group of genes. A large number of tools are available for this type of analysis including MAPPFinder (Doniger et al., 2003), DAVID/EASE (Dennis et al., 2003), Gene Set Enrichment Analysis (GSEA) (Lamb et al., 2003; Mootha et al., 2003; Subramanian et al., 2005), and ermineJ (Pavlidis et al., 2004). Especially notable is GSEA, in which genes are rank-ordered according to a signal-to-noise ratio and the distribution on this list of the genes from a gene set is used to compute the score for each gene set. If a large fraction of genes in a gene set shows up near the top of the ordered list, that gene set gets a high score, as measured by the Kolmogorov-Smirnov test. Model-based methods include global test by Goeman et al. (2004) and the analysis of covariance (ANCOVA) approach by Mansmann and Meister (2005). These two tests are equivalent in the case of independent genes but appear to lose some power for correlated genes (Mansmann and Meister, 2005).

Advantages of the approach combining expression data and biological knowledge are at least two-fold. First, a biological interpretation of the results can be facilitated by categorizing the differentially expressed genes into functional groups. This is especially true when the user is not familiar with the statistically significant genes. Second, a weak effect in a group of genes may be missed when each gene is considered individually, but it may be captured when they are considered together (Mootha et al., 2003).

However, in the simple methods using Fisher’s test or χ² test from a contingency table, one problem has been the instability of the results that depends on the threshold value for statistical significance (Pan et al., 2005). This problem has been alleviated to an extent with some more recent methods, which employ a statistic that considers the entire list of genes and avoids the thresholding. Another shortcoming shared by most current tools, however, is the use of a univariate statistic to score each gene, prior to the calculation of a group score. Genes in a gene set are functionally related and are not independent; the complex structure of gene interactions within a gene set are not fully captured using univariate approaches. Sample groups that do not seem to be separated according to a series of univariate measures may be well separated when a joint distribution is considered.

In this paper, we present a multivariate approach to address this problem. As in other methods, we seek to determine the significance of every pre-defined group of genes in order to choose the most relevant ones. The novelty in the proposed method is that we recast this problem as measuring the separation of the samples by their phenotype in each subspace of genes. Considered this way, it becomes natural to employ a variety of multivariate methods commonly used for class discovery and prediction. In the context of two-group comparison, the t-statistic or some variation based on it is a standard measure of significance. Such a univariate method is used in most of the methods described above. In the proposed method, we instead use Hotelling’s T² (or, equivalently, the Mahalanobis distance, which differs only by a constant). This is the multidimensional analogue of the t-statistic that accounts for the correlation structure. A number of methods, such as the Between-Group Analysis (Culhane et al., 2002) based on correspondence analysis, also attempt to find a subspace in which the samples are maximally separated. In the current work, we use a formal statistic that allows us to compare different subspaces.

Hotelling’s T² has been already employed for identification of differentially expressed genes (Szabo et al., 2003; Kim et al., 2005; Lu et al., 2005). Kim et al. (2005) compared Hotelling’s T² statistic and a univariate procedure in detection of differentially expressed genes and found Hotelling’s T² to be more efficient. Lu et al. (2005) used the same statistic with a search algorithm to identify a set of differentially expressed genes. They reported that Hotelling’s T² gave fewer false positives and false negatives than the univariate t-test when a spike-in data set from Affymetrix was analyzed. One shortcoming in that work, however, was that the number of differentially expressed genes found by T² had to be smaller than the number of samples to avoid singularity in the inversion of the covariance matrix. In this study, we address this problem by transforming the data onto an orthonormal subspace using principal components first. This allows us to calculate the score even for the subspaces whose dimension is larger than that of the samples.

In the following, we describe the methodology in detail and apply it to two data sets of our interest. The first data set on the effect of TOR inhibitor on Akt transgenic mice (Majumder et al., 2004) was originally analyzed using GSEA. In the re-analysis of this data set, we compare the performance of the proposed method to GSEA as well as the global test for a group of genes by Goeman et al. (2004). While we analyze the first data set using a collection of gene sets similar to the one used in the original paper for comparison, we search through a much larger set of subspaces for the second data set on the effect of left ventricular assist device (Hall et al., 2004). These subspaces are defined by several biological knowledge databases. Previously defined sets include those curated from KEGG, BioCarta, and Gene Ontology (GO) (Tian et al., 2005). For this work, we also derived new sets from the Reactome (Joshi-Tope et al., 2005) database. The R source code and the gene sets implemented as an object in R are available from the authors upon request.

METHODS

The current problem is naturally phrased in the language of vector spaces, where n samples are points in a q dimensional space of genes. An element in a gene set is an additional dimension of the vector space. Hence, concepts such as projection and subspaces developed in vector algebra provide a natural framework (Kuruvilla et al., 2002). In the subsequent discussions, we use the term ‘subspace’ in place of ‘gene set’ or ‘functional category’ to emphasize that a statistical test is performed in a multidimensional space where the dimension is the number of genes.

Comparing multivariate means of two groups using Hotelling’s T²

Let X₀ be the data matrix containing expression values, with n₁ samples from first group and n₂ samples from second group. n = n₁ + n₂ columns correspond to samples and p rows correspond to genes. Suppose the subspace that we wish to test is a q × n matrix X that contains q functionally related genes. The null hypothesis is that the multivariate means of the two groups are equal. The covariance matrices of the two groups are assumed to be the same and the pooled within-group covariance matrix is denoted by S.

Our test statistic is based on Hotelling’s T²:

$$T^2=\frac{n_1{n}_2}{n}{({\overline{\mathbf{X}}}_1-{\overline{\mathbf{X}}}_2)}^t{\mathbf{S}}^{-1}({\overline{\mathbf{X}}}_1-{\overline{\mathbf{X}}}_2),$$

where ${\overline{\mathbf{X}}}_i=1/n_i{\sum }_{j=1}^{n_i}{\mathbf{X}}_{ij}$ denotes the mean vector of the ith group obtained by summing over the jth q-dimensional vector X_ij in group i; S denotes the pooled covariance matrix ((n₁ − 1)S₁ + (n₂ − 1)S₂)/(n − 2), where ${\mathbf{S}}_i=1/(n_i-1){\sum }_{j=1}^{n_i}({\mathbf{X}}_{ij}-{\overline{\mathbf{X}}}_i){({\mathbf{X}}_{ij}-{\overline{\mathbf{X}}}_i)}^t$. For the null hypothesis H₀: X̄₁ = X̄₂, the sampling distribution of T² follows (n − 2)q/(n − q − 1)F_q,n−q−1. If the covariance matrix cannot be assumed to be the same, a similar statistic (with S₁/n₁ + S₂/n₂ as the covariance term and a different constant) follows a χ² distribution but only for a large sample size. But the unequal variance case can be easily incorporated since our significance testing is based on permutation. Multiple testing problem is addressed by false discovery rate (FDR) as described previously in Storey and Tibshirani (2003).

Dimensionality Reduction

When the dimension of the subspace is smaller than that of the sample size (q < n − 1), Hotelling’s T² can be applied in a straightforward way. When the dimension of the subspace is larger (q ≥ n − 1), a modification is necessary to deal with the singularity of the within-group covariance matrix S. For the gene set subspaces we compiled, the dimensions vary widely and handling the latter case well is crucial. There are several common ways to deal with this issue. The simplest is to ignore the correlations among genes and to set the off-diagonals in S to be zero, which results in a squared Euclidean distance between the two mean vectors. This is the approach taken in, e.g., von Heydebreck et al. (2001). The correlations among the genes, however, should play a critical role in determining the significance of the subspace, and should not be disregarded. Another way is to regularize S by adding a small constant ε to the diagonal. This has the effect of shifting the eigenvalues by ε. In one simple but effective variation, only the diagonal of S is still used but shrunken centroids for each group are used (Tibshirani et al., 2002). Other sophisticated methods include Regularized Discriminant Analysis (Friedman, 1989), in which the separate covariance matrices as in Quadratic Discriminant Analysis are shrunk toward the pooled covariance matrix, and Penalized Discriminant Analysis (Hastie et al., 1995), in which εS′ is added to S with a small constant ε > 0 and a suitably chosen symmetric and non-negative definite penalty matrix S′.

In our approach, we diagonalize the within-group covariance matrix by projecting the data onto an orthonormal subspace spanned by principal components of the covariance matrix. After this transformation, the coordinates are uncorrelated and each principal component has unit variance. This type of pretreatment of data are common in linear discriminant analysis (LDA) and independent component analysis (ICA). Mathematically, this involves computing the new data matrix

$${\mathbf{X}}^{\prime }={\mathbf{D}}^{-1/2}{\mathbf{U}}^t\mathbf{X},$$

where the diagonal D and orthogonal U matrices are obtained from the decomposition of the covariance matrix S = UDU^t. Since S is singular, only the columns corresponding to the nonzero eigenvalues in D are used for this transformation. Numerically, the eigenvalues decay rapidly in our examples and it is not difficult to find a reasonable threshold (e.g., 10⁻⁴) for determining the rank. We have verified that in working with the transformed data, the transition between the singular and the non-singular cases is smooth and that addition or subtraction of few genes from a subspace does not change the significance of a subspace unexpectedly. We note that a relatively simple method for projecting the data into a lower dimensional space was chosen for this step here and that more sophisticated methods may result in improved performance.

Computationally, the statistic for each subspace can be calculated fast. The data matrix X is generally small (q ≪ p), and, even when we have q ≫ n, the matrix decomposition can be done quickly using a trick. Instead of decomposing q × q matrix S, we adjust X by subtracting their group means and use the singular value decomposition relationship X = UDV^t. Using the fact that the columns of V in are the eigenvectors of a smaller n×n matrix X^tX, we first obtain V and then calculate U by X = UDV^t. It is easy to show that this is the desired U.

RESULTS

Application to the microarray data sets

We used two publicly available gene expression data sets to evaluate our method. For each subspace, Hotelling’s T² statistic was calculated to test the null hypothesis that the two groups are indistinguishable in the subspace. Statistical significance was computed based on the null distribution obtained by permuting the group labels. To differentiate among many highly significant genes, a large number of permutations (20,000) was performed.

For the first data set, nearly the same gene sets used in the original study were used; for the second data set, functional annotations were collected from BioCarta, KEGG, Reactome, and Gene Ontology. The Affymetrix probe sets were mapped to the subspaces through the Entrez Gene identifiers. The conversion from probe set ID to Entrez Gene ID was performed using the annotation packages available through Bioconductor (http://www.bioconductor.org) in the statistical language R. When there were several probe set IDs for a single Entrez Gene ID, all of them were included. The annotations were dated March, 2005.

Effect of mTOR inhibitor on Akt transgenic mice

Target of rapamycin (TOR) is a key protein that regulates the translation of ribosomal proteins in eukaryotes. Pathways upstream of TOR as well as the TOR pathway itself are frequently activated in cancer, and it has been extensively studied as a novel anticancer therapeutic target (Bjornsti and Houghton, 2004). In Majumder et al. (2004), Akt transgenic (Akt-Tg) mice were treated with mTOR inhibitor RAD001 and placebo, and the samples after 12 or 48 hours of RAD001 or placebo treatment in both wild-type and Akt-Tg mice were hybridized to microarrays. From this experiment, they reported that mTOR inhibition induced apoptosis of epithelial cells and a complete reversal of a neoplastic phenotype in the prostate of mice expressing human AKT1 in the ventral prostate. To identify the targets altered by AKT expression and by subsequent mTOR inhibition, they searched BioCarta gene sets and other manually curated gene sets for enriched categories of genes using GSEA. It was found that the main transcriptional response to AKT activation and mTOR inhibition involved the targets of Hif (Hypoxia-Inducible Factor)-1α.

To reanalyze this data set, we downloaded the Mouse 430A gene sets similar to the ones used in the original study from http://www.broad.mit.edu/gsea/msigdb/msigdb_index.html. The two are not exactly the same, as the authors have updated some pathways and added new ones. The current version contains 539 gene sets, which includes 274 BioCarta pathways. We calculated Hotelling’s T² between the RAD001-treated (n = 9) and placebo-treated (n = 10) groups in the subspace defined by each of these pathways. The main results are shown in Table 1. In the original study, the Hif pathway was reported as the only significant gene set, with the p-value 0.034. In our analysis, the Hif pathway was also significant with the permutation p-value 0.0001 (q-value 0.000313) but was ranked 4th among the BioCarta pathways. The most significant pathway was Erk1/Erk2 Mapk Signaling Pathway (‘erkPathway’ in the GSEA result). The second ranked one was Hemoglobin’s Chaperon (‘ahspPathway’), which includes ALAS1/2, Hbs, and GATA1. Its role in Akt-Tg treated with RAD001 was not clear, but the Hif targets were considered to play an important role in the experiment and so the hypoxia-related hemoglobin changes can be expected. We also found that multiple pathways related to carbohydrate metabolism on the top of our list. Six out of the top 10 KEGG gene sets were from carbohydrate metabolism, which includes Glycolysis/Gluconeogenesis (KEGG: MAP00010). Among the BioCarta pathways, 6th ranked Feeder Pathway for Glycolysis (‘feederPathway’) was related to carbohydrate metabolism. This finding is also in accordance with the observations in the original paper.

Table 1.

List of top 10 pathways in BioCarta and KEGG. Among the 539 collected pathways, there are 274 BioCarta, 63 KEGG, and 202 manually curated pathways. The permutation p-value is based on 20,000 permutations of samples labels, and false discovery rates (q-values) were calculated.

Source	Description	No of Probe sets	p-value	q-value
BioCarta
1	Erk1/Erk2 Mapk Signaling pathway	56	< 0.00005	<0.000010
2	Hemoglobin’s Chaperone	19	0.00005	0.000217
3	CXCR4 Signaling Pathway	38	0.00005	0.000217
4	Hypoxia-Inducible Factor in the Cardiovascular System	28	0.00010	0.000313
5	HIV-I Nef: negative effector of Fas and TNF	99	0.00015	0.000384
6	Feeder Pathways for Glycolysis	9	0.00025	0.000500
7	Cadmium induces DNA synthesis and proliferation in macrophages	29	0.00035	0.000658
8	uCalpain and friends in Cell spread	26	0.00050	0.000810
9	CCR3 signaling in Eosinophils	35	0.00075	0.001030
10	SREBP control of lipid synthesis	12	0.00075	0.001030
KEGG
1	MAP00020 Citrate cycle (TCA cycle)	29	< 0.00005	<0.000010
2	MAP00051 Fructose and mannose metabolism	43	< 0.00005	<0.000010
3	MAP00650 Butanoate metabolism	33	< 0.00005	<0.000010
4	MAP00252 Alanine and aspartate metabolism	30	0.00005	0.000217
5	MAP00280 Valine and leucine and isoleucine degradation	44	0.00005	0.000217
6	MAP00030 Pentose phosphate pathway	34	0.00010	0.000313
7	MAP00970 Aminoacyl tRNA biosynthesis	28	0.00015	0.000384
8	MAP00710 Carbon fixation	29	0.00020	0.000470
9	MAP00010 Glycolysis/Gluconeogenesis	85	0.00025	0.000503
10	MAP00052 Galactose metabolism	35	0.00025	0.000503

It is also important to note that our method appears to have much greater statistical power than GSEA, resulting in 234 curated pathways under the significance level of the permutation p-value < 0.05 (The top ones are shown in Table 1). In the original publication using GSEA, only one pathway was found to be significant. We also compared our method to the global test in the generalized linear model setting (Goeman et al., 2004). For this example, the global test appears to detect few more subspaces, e.g., it detected 270 under the permutation p-value of 0.05, while our method detected 234. In this case, the overlap between the two were 152. Important subspaces such as the Erk1/Erk2 Mapk Signaling Pathway, Hif pathway, and KEGG TCA cycle were found in both cases.

Among the significant pathways identified, there often are a large number of shared genes. For instance, the vegfPathway (VEGF, Hypoxia, and Angiogenesis), which was significant with permutation p-value 0.00465 (q-value 0.00305), shares 5 genes (Hif-1α, NOS 3, Vegf, von Hippel-Lindau syndrome, and Arnt) with the Hif pathway. The relationship among pathways that share some of their members and their proper interpretation are subject to further investigation.

Cardiac remodeling by left ventricular mechanical unloading

To investigate the underlying mechanism of cardiac remodeling after mechanical unloading in patients with heart failure, Hall et al. (2004) studied 19 paired human left ventricular apex samples that were harvested at the time of implant of a left ventricular assist device (pre-LVAD) and at the time of explant (post-LVAD). They identified 107 genes with false discovery rate of less than 1% that were differentially regulated in pre-LVAD versus post-LVAD groups. Among down-regulated genes, neurophilin-1 (a VEGF receptor), FGF9, Sprouty 1 (FGFR/EGFR antagonist), stromal-derived factor 1, and endomucin have been implicated in the regulation of vascular organization. Consequently the authors inferred that vascular gene expression is modulated by mechanical unloading. In addition, they found that GATA-4, a central regulator of cardiac gene transcription, was downregulated after mechanical unloading.

We applied our multivariate approach to discover gene subspaces in which gene expression was coordinately regulated between pre-LVAD and post-LVAD conditions. Unlike the previous example in which the same gene sets as in the original publication was used for comparison, we used a much larger database of subspaces. We collected 5,400 gene set subspaces (5000 from Gene Ontology and 400 from Reactome, KEGG, and BioCarta; described in Tian et al. (2005) and available from authors’ website), from which we selected 2,338 subspaces containing 5 to 250 genes for further analysis. The lower limit on size was imposed to eliminate subspaces that were too easily influenced by single genes and did not correspond to a pathway. The upper limit was necessary to avoid categories that were too general to be helpful in interpretation.

Thirty-eight subspaces were significant at permutation p-value 0.01 (Table 2). Compared to the first example in which 119 had p-values <0.01, not as many subspaces were significant and the q-values were relatively high. This is most likely due to the greater heterogeneity expected in the human clinical samples than in transgenic models. The distribution of univariate p-values confirms that the number of differentially expressed genes is much greater for the first data set for any threshold. Interestingly, the BioCarta ‘NFAT and Hypertrophy of the heart transcription in the broken heart’ subspace was ranked 5th (permutation p-value 0.003). As the title suggests, this subspace has multiple genes related to the cardiac hypertrophy and remodeling such as GATA-4, Nkx2.5, MAP kinases, NFAT, IGF, Akt, and calcium/calmodulin-dependent protein kinases. This subspace summarizes the changes of many genes that are known to play a role in the heart failure and cardiac remodeling, and its occurrence supports the ability of our method to identify significantly co-regulated genes many of which are not significant by univariate analysis.

Table 2.

List of significant subspaces from the comparison of pre-LVAD and post-LVAD. 38 subspaces were identified as significant at 0.01. For this data set, 2,338 subspaces of size between 5 and 250 were compiled from BioCarta, KEGG, Reactome, and Biological Processes of GO annotations. Many pathways were related to MAP kinase signaling cascades and their effectors. This result is in agreement with the previously suggested role of MAP kinase pathway in the failing heart.

Source	Description	No of Probe sets	p-value	q-value
BioCarta
1	MAP Kinase inactivation of SMRT Corepressor	28	0.00025	0.244
2	Activation of PKC through G protein coupled receptor	11	0.00220	0.366
3	TACI and BCMA stimulation of B cell immune responses	18	0.00270	0.366
4	Sprouty regulation of tyrosine kinase signals	27	0.00285	0.366
5	NFAT and Hypertrophy of the heart transcription in the broken heart	72	0.00300	0.366
6	Neuropeptides VIP and PACAP inhibit the apoptosis of activated T cells	25	0.00340	0.380
7	Multi step Regulation of Transcription by Pitx2	29	0.00490	0.395
8	Role of EGF Receptor Transactivation by GPCRs in Cardiac Hypertrophy	33	0.00580	0.432
9	TPO Signaling Pathway	45	0.00800	0.475
10	NF-κB activation by Nontypeable Hemophilus influenzae	50	0.00920	0.475
11	Role of FYVE finger proteins in vesicle transport	19	0.00980	0.475
KEGG
1	MAP00460 Cyanoamino acid metabolism	12	0.00105	0.366
2	MAP00630 Glyoxylate and dicarboxylate metabolism	14	0.00440	0.395
3	MAP00010 Glycolysis/Gluconeogenesis	103	0.00490	0.399
4	MAP00531 Glycosaminoglycan degradation	27	0.00735	0.463
Reactome
1	Hsa Phospho-IRS: activated insulin receptor	6	0.00945	0.475
Gene Ontology Biological Process
1	GO:0000185 Activation of MAPKKK	6	< 0.00005	< 0.0001
2	GO:0045786 Negative regulation of cell cycle	28	0.00130	0.366
3	GO:0050790 Regulation of enzyme activity	209	0.00195	0.366
4	GO:0006665 Sphingolipid metabolism	52	0.00205	0.366
5	GO:0030641 Hydrogen ion homeostasis	10	0.00220	0.366
6	GO:0006301 Postreplication repair	5	0.00245	0.366
7	GO:0035088 Establishment/maintenance of apical/basal cell polarity	11	0.00255	0.366
8	GO:0045197 Establishment/maintenance of epithelial cell polarity	11	0.00260	0.366
9	GO:0006816 Calcium ion transport	51	0.00270	0.366
10	GO:0008284 Positive regulation of cell proliferation	191	0.00370	0.380
11	GO:0042828 Response to pathogen	21	0.00370	0.380
12	GO:0007589 Fluid secretion	10	0.00400	0.391
13	GO:0042493 Response to drug	22	0.00450	0.395
14	GO:0019318 Hexose metabolism	109	0.00550	0.430
15	GO:0006968 Cellular defense response	142	0.00625	0.438
16	GO:0045765 Regulation of angiogenesis	19	0.00635	0.438
17	GO:0005996 Monosaccharide metabolism	109	0.00650	0.438
18	GO:0045934 Negative regulation of nucleotide/nucleic acid metabolism	187	0.00735	0.463
19	GO:0000165 MAPKKK cascade	86	0.00825	0.475
20	GO:0030384 Phosphoinositide metabolism	24	0.00875	0.475
21	GO:0006026 Aminoglycan metabolism	7	0.00975	0.475
22	GO:0016477 Cell migration	101	0.00985	0.475

The BioCarta gene subspace ‘MAP Kinase inactivation of SMRT corepressor’ was the most significant. Modulation of MAP kinase cascades was also supported by results from the GO Biological Process subspaces, where ‘GO:000185 activation of MAPKKK’ (permutation p-value < 0.00005) and its parent node ‘GO:0000165 MAPKKK cascade’ (permutation p-value 0.00825) were found to be significant. MAP kinase signaling pathways are pivotal mediators of diverse cellular functions, including growth, differentiation, and apoptosis. MAP kinase pathways are activated in heart failure (Haq et al., 2001), and chronic activation in transgenic over-expression models has been associated with dilated cardiomyopathy and heart failure (reviewed in Liang and Molkentin (2003)).

The third ranked BioCarta pathway was ‘TACI and BCMA stimulation of B cell immune responses.’ As members of the TNF receptor gene family, TACI and BCMA interact with TNF receptor associated factors (TRAFs) to activate NF-κB activation and MAP kinase pathways. The significant rank of this subspace again points to modulation of MAP kinase signaling, and also suggests that myocardial unloading alters TNF signaling. TNF and related cytokines are produced by myocardial cells after injury, and activation of TNF pathways in heart failure is well documented (Mann, 2003). Chronic TNF activation results in cardiomyopathy and detrimental cardiac remodeling (Mann, 2003). NF-κB is a major target of TNF signaling pathways, and it has been found to be activated in failing human myocardium, where it is an important regulator of cardiomyocyte hypertrophy and apoptosis (Purcell and Molkentin, 2003). NF-κB and its negative regulator IKB were also important components of two additional BioCarta pathways with highly significant permutation p-values: ‘Activation of PKC through G protein coupled receptor’ (permutation p-value 0.0022) and ‘NF-κB activation by Nontypeable Hemophilus influenzae’ (permutation p-value 0.0092).

Activation of receptor tyrosine kinases, either by direct stimulation by ligand or by receptor transactivation through G protein coupled receptors, is important for the pathogenesis of heart failure (Asakura et al., 2002; Iwamoto et al., 2003). The BioCarta pathway ‘Role EGF Receptor Transactivation by GPCRs in Cardiac Hypertrophy’ received a highly significant permutation p-value (0.0058), consistent with a significant co-regulation of genes in this subspace during mechanical unloading. This was reinforced by the BioCarta pathway ‘Sprouty regulation of tyrosine kinase signals’, which delineates tyrosine kinase signaling pathways and their negative regulation by Sprouty. Placed in this broader context, the significant upregulation of Sprouty found in the original report may be related to regulation of myocardial receptor tyrosine kinase signaling, which is known to be perturbed in heart failure.

As shown above, a detailed examination of the BioCarta pathways with highly significant permutation p-values reveals a number of signaling pathways that play an important role in the pathogenesis of heart failure, as determined by experimental data from a number of model systems. Identification of these pathways highlights the ability of this approach to identify significant patterns of differential gene expression that are not apparent by single-gene analysis.

For this example, we again compared our method to the global test (Goeman et al., 2004) using their R package, which allows one to iterate through the possible subspaces given by the user easily. The results in this example were more discordant than those of the first. Similar number of subspaces were identified, but a couple of key subspaces were not found by the global test. For example, ‘TACI and BCMA stimulation of B cell immune responses’ had the permutation p-value of 0.0027 in our method but 0.193 in the global test. Similarly, ‘Sprouty regulation of tyrosine kinase signals,’ which was validated in the original paper, obtained the p-value of 0.0029 in our method and it obtained 0.11 in the global test. It is difficult to draw a strong conclusion of this evaluation, but this result appears to favor the proposed method in this example. The bigger advantage of the proposed method may be its simplicity and intuitive interpretation.

DISCUSSION

Our goal in this study was to integrate biological knowledge with microarray data using a multivariate statistical approach. The main advantage of the proposed method is the simple conceptual framework of finding a subspace in which the two groups belonging to different phenotypes are most separated. This method is made possible by the dimensionality step described earlier, in which we project a subspace of high dimension onto a orthonormal space by matrix decomposition and sphering. This step is essential because most subspaces contain more genes than the number of samples in the study. A problem might still arise if the subspace is too large, but most subspaces do not contain more than one or two hundred genes. The proposed method should be intuitively appealing to biologists, many of whom may be already familiar with visualizing the samples in a two- or three-dimensional principal component plots.

A statistical method adjusting for different covariance structure and dimension of subspaces was described previously (Tian et al., 2005), but the current approach has a simpler interpretation, especially with the aid of visualization. The statistical test proposed here is similar to the second of the two null hypothesis described in that paper but is in some sense less aggressive and more omnibus. For example, the current statistic does not distinguish between up- and down-regulated genes. If there is no correlation among genes, the statistic becomes the sum of squared t-statistics. The first null hypothesis in Tian et al. (2005) can still be used in addition if desired but we felt that this was not necessary here. Exactly which features of the subspaces should be considered most relevant from a biological perspective is not yet clear. With respect to other available methods, the proposed method should be able capture those relationship missed by univariate methods. Evidence on the data sets of our interest strongly suggests that the proposed method performs better, but a more extensive comparison is made difficult due to the differences in the set of subspaces used. Due to the evolution of biological databases, the original subspaces are not available for comparison.

The usefulness of this type of analysis depends on the quality of the gene sets as well as the statistical method used. The BioCarta, KEGG, and Reactome databases were curated by human experts and the functional annotation from these databases are considered to be specific and of high quality. The contents of many GO terms, however, are not as accurate, as their annotations come from several different sources with varying degrees of reliability. In particular, those derived by algorithmic approaches and not by human experts tend to be low in accuracy. Some of the inaccuracies may be due to the ambiguities in names and symbols (Weeber et al., 2003). The IEA (Inferred from Electronic Annotation) type especially is regarded as the evidence of lowest quality, but this type of annotation is extremely common: in case of human Biological Process category, only 8,377 out of 20,566 annotations are from non-IEA sources as of April 2005. In addition, the relationships among the three categories, Biological Process, Molecular Function, and Cellular Component are not clear. For this study, we collected the annotations in the Biological Process domain and excluded IEAs. In the current analysis, we also limited the subspace size to between 5 and 250 based on our experience. It is conceivable that a subspace with larger or small dimension can give useful information, but we have found that the difficulty of examining a longer list of gene sets outweighs any potential benefit. The limits are also similar to 5–100 used in Segal et al. (2004) and same as 5–250 used in Pavlidis et al. (2004).

The proposed analysis generates a list of potential pathways but interpreting that list itself can be time-consuming. Understanding the relationship between the significant subspaces then becomes critical to interpretation. The obvious candidates are the complex parent-children relationships in the GO graph. For example, in the result for the second data set, ‘GO:000185 Activation of MAPKKK’ is a part of ‘GO:000165 MAPKKK cascade’ and is also a part of the different GO term ‘GO:0045860 Positive regulation of protein kinase activity.’ In this case, the first two were significant while the third was not. A couple of methods for adjusting statistical significance in such cases have been proposed recently (Alexa et al., 2006; Grossmann et al., 2006). However, we have also noticed that pathways distant in the graph, from different GO graph (e.g., biological function vs. cellular component), or referred to by different names in databases without hierarchical structure can involve significant overlaps. Hence, a tool for facilitating the process of relating different pathways would be helpful. When the relationships between pathways are clarified, the analysis may resemble the method of understanding the data in terms of modules. Defining a network of modules rather than of genes to describe an underlying phenomenon has become popular recently (Segal et al., 2004). By examining the genes contained in each significant pathway, it should be possible to generate a network of interactions by groups of genes.

The idea of identifying a relevant subspace can be particularly helpful in pharmacogenomic screening. By comparing before- and after-treatment data, the pathway targeted by a compound can be more easily identified. The mTOR example was one such example. The proposed approach is general and can be applied to other data types as well as other phenotypes. When the phenotype involves more than two classes, for example, MANOVA (Multiple Analysis of Variance) is the natural extension.

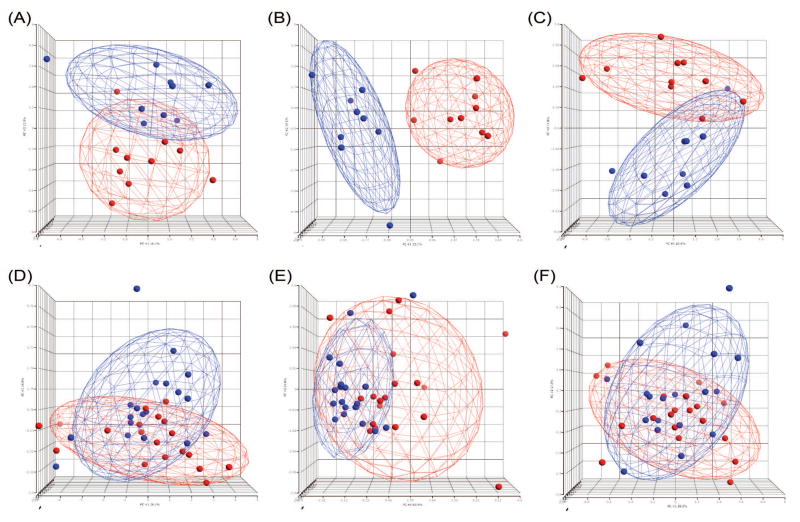
Fig. 1.

The significant subspaces are shown in the principal component analysis plots. All principal components are used for calculation but the data are displayed only in three dimensions. An ellipsoid of 2 standard deviation was generated in each case. The top row corresponds to the top BioCarta and KEGG pathways, and the Hif pathway in the mTOR data set: A) BioCarta: Erk1/Erk2 Mapk Signaling pathway; B) KEGG: MAP00020 Citrate cycle (TCA cycle); C) BioCarta: Hypoxia-Inducible Factor in Cardiovascular System. The red and blue colors denote the RAD001-treated and placebo-treated, respectively. The bottom row contains the three pathways in the cardiac remodeling data set: D) BioCarta: MAP Kinase Inactivation of SMRT Corepressor; E) Gene Ontology Biological Process: Activation of MAPKKK; F) BioCarta: Sprouty regulation of tyrosine kinase signals. The blue and red colors denote pre- and post-LVAD.