Convection driven generation of long-range material gradients

Abstract

Natural materials exhibit anisotropy with variations in soluble factors, cell distribution, and matrix properties. The ability to recreate the heterogeneity of the natural materials is a major challenge for investigating cell-material interactions and for developing biomimetic materials. Here we present a generic fluidic approach using convection and alternating flow to rapidly generate multi-centimeter gradients of biomolecules, polymers, beads and cells and cross-gradients of two species in a microchannel. Accompanying theoretical estimates and simulations of gradient growth provide design criteria over a range of material properties. A poly(ethyleneglycol) hydrogel gradient, a porous collagen gradient and a composite material with a hyaluronic acid/gelatin cross-gradient were generated with continuous variations in material properties and in their ability to regulate cellular response. This simple yet generic fluidic platform should prove useful for creating anisotropic biomimetic materials and high-throughput platforms for investigating cell-microenvironment interaction.

Introduction

Anisotropic materials are highly important for many natural and engineered systems. Examples of anisotropic materials in nature include marbles, tree trunks and squid beaks. Examples of engineered anisotropic materials include the birefringent crystals of prisms, the metal wood head of golf clubs and the aluminum alloys used in aircraft and rockets. Spatial anisotropy in materials is especially prominent in cellular microenvironments in vivo where heterogeneous distributions of cells and molecules exist within spatially varying extracellular matrices (ECM). Molecular concentration gradients play an important role in biological phenomena such as chemotaxis,[1, 2] morphogenesis and wound healing.[3-5] Meanwhile, the graded variations of ECM and cell concentration at the tissue interface (e.g. bone-cartilage interface, dentino-enamel junctions) are nature's solution for connecting mechanically mismatched tissues.[6, 7] Creating chemical and material gradients to mimic the heterogeneity of cellular environments is important for investigating cell-matrix interaction[8] and for developing biomimetic materials for tissue engineering.[9]

Various methods exist to generate molecular and material gradients (Supplementary Table 1). Diffusion-based approaches for gradient generation are limited to diffusible molecules and require long times to create millimetric gradients, since the timescale for pure diffusion scales as length squared. Dispersion-based approaches, which combine primary stretching by flow shear and secondary spreading by diffusion, have been used to generate centimeter long molecular gradients in seconds to minutes.[10-12] However, so far no generic platform employing dispersion to generate material gradients of single or multiple components over long distances have been developed. In this study, we present a generic microfluidic dispersion-based platform for rapidly (seconds to minutes) generating long-range material gradients of molecules, polymers, particles or cells. By using a syringe pump to drive fast alternating flows which continually lengthen the gradient, we have, to our knowledge, for the first time created centimeter scale concentration gradients of cells and microbeads by flow convection. Our work is also the first to generate cross-gradients in particles and hydrogels by using alternating flows to superpose gradients of two species. In particular, we have generated composite materials containing a ‘cross-gradient’ of two hydrogels or two types of microbeads. Our simple yet versatile gradient platform (Fig. S1) should prove useful for a wide range of applications that involve anisotropic material gradients.

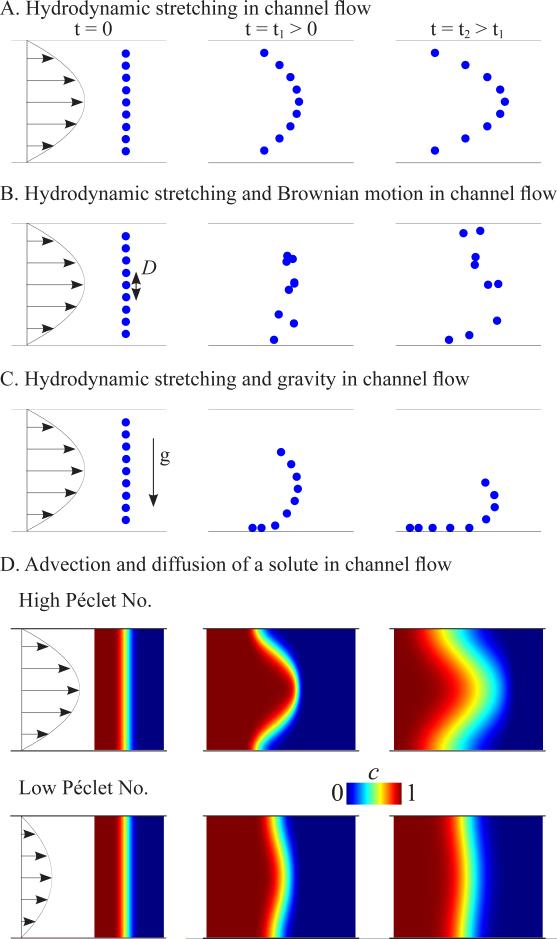
Fluidic shear-driven stretching, also known as convective or hydrodynamic stretching, is the primary mode of gradient generation in the present work. In short, a particle in the center of the channel moves faster than one at the wall and the two spread apart at a rate proportional to the maximum channel velocity. A gradient so forms in the laterally averaged concentration profile (Fig. 1A). Ironically, diffusion acts to suppress hydrodynamic stretching by reducing the mean variation in particle speeds:[13, 14] slowly moving particles near the wall diffuse toward the center and accelerate, while fast moving particles near the center diffuse toward the wall and decelerate (Fig. 1B). For dilute suspensions of micron sized and larger particles moving in viscous flows, diffusion is negligible.[15, 16] However, negatively buoyant particles settle under gravity to the channel bottom (Fig. 1C), whereupon all particles experience the same low velocity and spreading ceases. Thus, high flow rates improve stretching at all scales: for molecules, high flow rates dominate diffusion which acts to suppress hydrodynamic stretching; for microparticles such as microbeads and cells, high flow are imperative to spread the particles before they settle. The latter may explain why centimeter scale gradients of micron sized particles have not been previously generated by convection in microchannels. In the following sections, we demonstrate that high-speed (mm/s) flow shear-driven stretching generated gradients of a wide range of species (molecules, cells, microbeads) along a simple microchannel.

Figure 1. Physical picture of gradient generation in channel flow.

A. Particle spreading due to convection (hydrodynamic stretching). B. Vertical diffusion characterized by a diffusion coefficient D suppresses longitudinal convection-driven spreading. C. Gravitational settling suppresses longitudinal convection-driven spreading. D. Advection and diffusion of dissolved solute in high/low Péclet flows.

Materials and Methods

Materials

Poly(ethelyene glycol-diacrylate) (MW 4000) was purchased from Monomer-Polymer & Dajac Labs. The photo-initiator (PI), 2-hydroxy-1-[4-(hydroxyethoxy)phenyl]-2-methyl-l-propanone (Irgacure D2959), was purchased from Ciba Geigy (Dover, NJ). Polyethylene microtubing (I.D. 0.38 mm, O.D. 1.09 mm) was purchased from Intramedic Clay Adams (Becton Dickinson & Co, MD). Green Fluorescent FITC-microbead and non-fluorescent microbead solutions were purchased from Polysciences (Warrington, PA). Human Umbilical Vein Endothelial cells (HUVECs) and endothelial cell basal medium (EBM-2, Clonetics) supplemented with 0.5mL vascular endothelial growth factor (VEGF), 0.2mL hydrocortisone, 0.5mL epidermal growth factor (rhEGF), 0.5mL ascorbic acid, 2.0mL r-human fibroblast growth factor-B (rhFGF-B), 0.5mL heparin, 0.5mL recomb long R insulin-like growth factor (R3-IGF-1) and 0.5mL gentamicin sulfate amphotericin-B (GA-1000) were obtained from Lonza (Basel, Switzerland). All other reagents were purchased from Sigma-Aldrich (St. Louis, MO) unless otherwise indicated.

Fabrication of microchannel

The microchannel was fabricated by a standard soft lithography method described previously[10] and consisted of a top polydimethylsiloxane (PDMS) fluidic channel that was plasma bonded onto a bottom glass slide. The rectangular channel dimensions were 100μm (height) × 2mm (width) × 50mm (length).

Generation of biomolecule gradient

The microchannel was pre-filled with 1X Dulbecco's Phosphate Buffered Saline (DPBS) solution. 1%wt fluorescein isothiocyanate-dextran (FITC-dextran, MW 10kDa) solution was sequentially pumped (forward flow) and withdrawn (backward flow) into the channel at flow rates between 0.007 and 0.044 ml min⁻¹ with a syringe pump (World Precision Instruments Aladdin 1000, WPI, FL). Forward and backward flows were separated by 30s of downtime. Two flow sequences were used, alternately pumping and withdrawing fluid in the channel: 4.7, 2.0, and 1.3 μL (three flow segments); 5.2, 3.5, 2.9, 2.4, 2.1, 1.8, and 1.6 μL (seven flow segments). Flow rates were calibrated with a flow meter from Gilmont Instruments, IL. The imaging protocol is outlined in Supp. II.4. The diffusion coefficients for several MWs of FITC-dextran dissolved in PBS at 25°C have been measured[17] and give similar results to one study of FITC-dextran in water.[18] Averaging interpolated results from four studies[17-20] that measured the diffusion coefficient D of 10kDa FITC-dextran in water and PBS at 25°C yields D = 1.3×10⁻⁶ cm² s⁻¹. The particular values interpolated from each study ranged from 0.9 to 2.0×10⁻⁶ cm² s⁻¹ due to differences in the degree of branching and polydispersity of the dextrans used in the studies.[17]

Generation of bead/cell gradients

Microbead stock solutions containing microbeads with diameters in 5.0 and 10μm (with a solid fraction of 0.1% w/w) were diluted 10 times in DPBS. 6μL of the microbead solution was pumped at a rate of 0.044ml/min into the channel, followed by 30s of downtime. Subsequent pumping did not alter the gradient. The protocol for generating cell gradients was similar to that for the microbead gradients. HUVECs were cultured in endothelial cell basal medium at 37°C in a humidified incubator. HUVEC medium was used in place of DPBS as the background solution and medium containing HUVECs (5×10⁶/ml) after trypsinization was used in place of the microbead solution.

Generation of PEG-DA hydrogel gradient

The channel was pre-filled with 5wt% PEG-DA solution. A concentration gradient of hydrogel precursor solution (with high concentration of 40wt% PEG-DA in DPBS and 1% PI) was generated at a flow rate of 0.025ml/min using the flow sequence outlined above for FITC-dextran. The hydrogel precursor concentration gradient was cross-linked via photo-polymerization (UV exposure: 10mW/cm² for 20s). For characterization, the resultant hydrogel was air-dried, cut in half with a scalpel blade to obtain a cross section, sputter-coated with gold and imaged using SEM (ZEISS ULTRA 55, Germany). The thickness of the hydrogel was quantified using ImageJ and the scale bars in the SEM images.

Generation of collagen gradient

The channel was pre-filled with 0.5mg/ml collagen solution. A concentration gradient of collagen solution (maximum concentration 3.8mg/ml) was generated at a flow rate of 0.025ml/min using the flow sequence outlined above for FITC-dextran. Collagen fibers formed during gelation for 30min in an incubator (37°C). The channel and collagen gradient were then pre-frozen at −20°C for 10min and the PDMS channel was demoulded from the glass slide. The collagen gradient was further frozen at −80°C for 2h and then freeze-dried in a lyophilizer. The morphology of the collagen gradient was visualized by SEM.

Generation of cross-gradient of FITC-dextran and rhodamine dextran

The channel was pre-filled with solution containing 1wt% FITC-dextran (MW 10kDa). 200μL Rhodamine-B isothiocyanate-dextran (rhodamine dextran, MW 10kDa) solution (1wt%) was pipetted into the outlet port of the channel. A syringe pump connected to the inlet of the channel withdrew 6μL of fluid at a flow rate of 0.025ml/min, drawing the rhodamine dextran into the channel. The 6μL of solution was then pumped forward and backward twice. The channel containing the cross-gradient of the two dyes was allowed to stand (no flow) for at least 30s before visualization. Overlapping fluorescent images were taken along the channel using the green and red filters of a fluorescent microscope. The images were stitched with Photoshop and quantified with ImageJ. The diffusion coefficient of 10kDa FITC was listed above; since 10kDa rhodamine dextran is close to FITC-dextran in mw, size, and shape, its diffusion coefficient should be approximately the same.

Generation of cross-gradient of two types of microbeads

To create the cross gradient of microbeads, 10μm diameter FITC and non-fluorescent microbeads were diluted 20 times. The channel was pre-filled with distilled water. The FITC microbeads were added to the inlet and 6μL of water was pumped into the channel at a flow rate of 0.044ml/min. The beads were allowed to settle. The non-fluorescent microbeads were then added to the outlet and 6 L of water was withdrawn from the channel.

Generation of composite HA-gelatin material cross-gradient

Hyaluronic acid and gelatin were methacrylated to be photo-crosslinkable as described previously.[21, 22] The channel was pre-filled with 2wt% methacrylated HA solution (containing 1wt% PI). 2wt% methacrylated gelatin (1wt% PI) was added to the outlet port of the channel. A cross-gradient of HA and gelatin was formed following the same loading/flow sequence used for the FITC-dextran/rhodamine dextran cross-gradient and was stabilized upon photo-polymerization (UV exposure: 10mW/cm² for 60s). Smooth muscle cells (SMC) were cultured in SMC basal medium (RPIM 1640, Gibco) at 37°C in a humidified incubator. Upon trypsinization, the cells were seeded in a density of 1×10⁴ cells/cm² on the surface of the HA-gelatin composite hydrogels. After 24h of incubation, the hydrogels were rinsed three times with sterile PBS to wash away unattached cells and then fixed with 3.7% formaldehyde solution. Overlapping phase contrast images were taken along the channel with a microscope and then stitched. The stitched image was quantified by counting the number of attached cells with ImageJ. The experiment was repeated twice.

Results and discussion

The spreading of molecular species in a microfluidic channel involves both convection (or advection, hydrodynamic stretching) and diffusion, a combined process known as dispersion (Fig. 1D). The Péclet number Pe = UH/D specifies the ratio of the rates of transport by flow advection at speed U and molecular diffusion D in a channel of height H and ranges from approximately 400 to 4000 in our experiments. In the axial direction, transport is mainly due to advection; in the transverse direction, transport is due to molecular diffusion since the flow velocity is purely axial. A typical flow sequence to spread a diffusible species in our microchannel is illustrated in Figure S1C and Video S1 and proceeded as follows. Dissolved material at uniform concentration entered the channel initially filled only with solvent. The concentration profile was hydrodynamically stretched and the initially short, steep gradient in concentration spread (Fig. S1Ci). The profile stretching was suppressed by lateral molecular diffusion, so that larger spreading was observed for larger Péclet numbers. The flow was stopped before the gradient reached the end of the channel. At this point, as we explain shortly, it was advantageous to keep the fluid at rest for an order H²/(π²D) time (in our case ~ 5-30 s) to allow diffusion to completely mix the solution vertically (Fig. S1Cii). The flow was then reversed and stopped before the gradient reached the opposite end of the channel (Fig. S1Ciii). The cycle was repeated until a gradient of sufficient length was obtained. As the gradient grew and filled the channel, the flow segments became shorter. These short duration flows laterally smoothed the concentration profile by shortening the spatial lags between the wall and centerline concentration profiles.

Theoretical descriptions of dispersion in unidirectional flow are well developed. In a channel of uniform cross-section characterized by a height H and width W ≥ H, three regimes of dispersion exist: a short time regime t << H² / D where diffusion is not important, molecules follow the streamlines, and gradient growth is linear; an intermediate time interval H² / D << t << W² / D over which the molecules spread across the channel height; and a long time regime t << W² / D, called Taylor-Aris dispersion, over which molecules have sampled the entire channel cross-section.[12, 23-25] The current study involves rectangular channels of height H = 100 μm and width W = 2 mm, with molecules of diffusivity D ~ 10⁻⁷ to 10⁻⁶ cm² s⁻¹. Thus the time H²/D is seconds to minutes and W²/D is hours to days. Since our gradients were generated in seconds to minutes, their evolution fell in the early to intermediate dispersion regime. Approximate theoretical descriptions valid for early, intermediate, and late times exist for many geometries, including rectangular channels,[26, 27] cylindrical tubes,[28] and channels with smooth cross-sections.[12, 23] We define the gradient length Δ as the length of the transition zone between 10% and 90% of the maximum concentration, which captures the most linear, and therefore usable, portion of the concentration profile. For flow in tubes of diameter H, Taylor[14] found that at late times,

$$\frac{\Delta }{H}=3.62\sqrt{\tilde{D}\tau }$$ (1)

where τ = tD/H² is the dimensionless diffusive time and D̃ = 1 + Pe²/192 the dimensionless dispersivity. For Poiseuille flow between parallel plates, an approximate formula uniformly valid in time was derived for the dispersivity,[24]

$$\tilde{D}=1+\frac{P{e}^2}{210}\left(1-\frac{1-e^{-4{\pi }^2\tau }}{4{\pi }^2\tau }\right)$$ (2)

For large Péclet numbers and early times τ << 1, the gradient growth is linear; at late times the growth has the familiar square root dependence. In the absence of flow (diffusion only, Pe = 0), the expressions for D̃ reduce to the dimensionless molecular diffusivity, D̃ = 1. The expressions for D̃ imply that gradient growth is faster for higher Péclet numbers, i.e. higher flow speeds and lower molecular diffusivities. In fact, longer gradients are produced for higher Péclet numbers even if the total volume of fluid pumped into the channel is kept constant. To see this note that if a fixed volume of fluid is pumped into the channel at speed U over time t, then Ut is constant regardless of the flow rate. Thus τ = const/Pe and for large Péclet numbers the final gradient length increases with Pe as $\Delta ∕H\sim \sqrt{Pe}$. Expressions for the dispersivity in rectangular microchannels are significantly more complicated and depend on the cross-sectional aspect ratio W/H.[25]

To rationalize our experiments on gradient generation in alternating flows and to provide general design criteria we developed a computational advection-diffusion model to simulate the concentration profile evolution over sequences of forward and backward flows and diffusion-only downtimes. Simulations were run over a wide range of channel geometries, W/H = 1 to 20, and Péclet numbers, Pe = 100 to 10⁴ (Supp. II.3c). The viscous flow in our channel was characterized by Reynolds numbers on the order of 0.1 or less. Thus, throughout the rectangular channel the flow was essentially fully developed laminar Poiseuille flow, a textbook exact solution to the Navier–Stokes equations[29] governing the fluid flow (Fig. S2 and Supp. II.2). Using this exact flow solution, a finite element code (Comsol 3.4) solved the advection-diffusion equation in the microchannel on a rectangular grid (Fig. S3). During downtimes when the fluid was quiescent, molecular species spread via diffusion over the diffusive timescale τ = tD/H². The diffusion in a rectangular channel was calculated from analytical formulas and discrete Fourier transforms (Supp. II.3a). Flow reversal was modelled by initializing the computational model with the concentration profile following the previous flow segment or diffusion-only downtime and running the steady flow in reverse. Further details including computational code and a sensitivity analysis are provided in the Supplementary Information, II.3c. The resulting numerically computed concentration profiles were cross-sectionally averaged and the gradient length Δ was extracted. A user-friendly formula of the form (2) is provided with two tabulated fitting coefficients in the Supplementary Information (II.3c) to make approximate estimates of gradient growth.

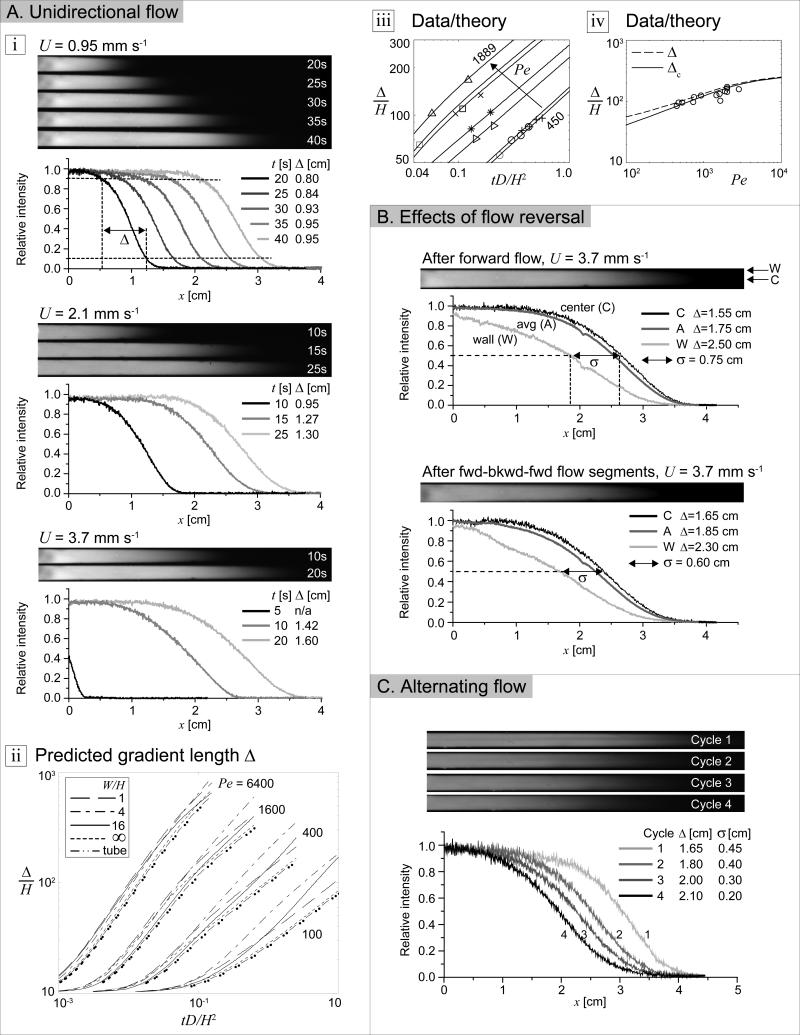
To optimize the flow sequence for gradient generation we produced gradients of FITC-dextran in PBS with different flow rates. The size and molecular weight of 10 kDa FITC-dextran was representative of the various materials we used to form gradients. Fluorescent images of the microchannel were captured at 5s intervals (Fig. 2Ai). Quantification of the fluorescent images illustrated that gradients grow faster and longer with higher flow rates. Our numerical simulations of gradient length showed a similar trend (Fig. 2Aii): higher Péclet numbers were associated with faster gradient growth rates and longer gradients; the channel geometry had a secondary effect. Using a diffusion coefficient of 1.3×10⁻⁶ cm² s⁻¹ for FITC-dextran in PBS, estimated in the Materials and Methods section, our experimental results of gradient growth were compared with our numerical predictions over a wide range of Pe (Fig. 2Aiii-iv). The measured intensities were taken from above and were therefore vertically averaged, by definition. Our numerical results were vertically averaged for comparison. In Figure 2Aiii, the experimentally measured centerline gradient lengths compared well with predictions. To account for variable initial experimental gradient lengths (not controlled), the measurements were moved along the time axis so that the initial measurement coincided with the predicted gradient length profile. Finally, Figure 2Aiv shows that longer measured and predicted centerline gradient lengths were produced by pumping the same volume of fluid at higher flow rates through the channel.

Figure 2. Long-range molecular gradients.

A. Unidirectional flow. i) Time-lapse top-down view of fluorescent FITC-dextran gradient and quantification along channel centerline at average flow speeds U = 0.95, 2.1, 3.7 mm s⁻¹. ii) Simulation of gradient growth vs. time for various Péclet numbers Pe and channel aspect ratios W/H. iii) Gradient growth vs. time for experiments (avg. flow speeds U = 2.5 (△), 1.9 (□), 1.7 (×), 1.1 (*), 0.95 (▷), 0.62 (+), 0.58 (○) mm s⁻¹) and corresponding simulations (W/H = 20, Pe = 1889, 1457, 1333, 884, 734, 476, 450, from left to right). iv) Measured gradient length along centerline of channel after fluid travels x = 2.34 cm (o), simulation of length Δ of gradient in cross-sectionally averaged concentration (− −) and simulation of length Δ_c of gradient in vertically averaged centerline concentration (—). B. Effects of flow reversal. Top-down views of fluorescent FITC-dextran gradient after a one and three flow segments with quantification of centerline (C), wall (W), cross-sectionally averaged (A) gradient profiles, gradient length Δ and spatial lag σ. C. Alternating flow. Top-down view of fluorescent FITC-dextran gradient after seven flow segments (four cycles) with quantification along centerline, including Δ and σ. Cycle 1 had a single forward flow segment. See Materials and Methods for pumping sequences.

For diffusible species in a finite channel, additional gradient growth was achieved by subsequent backward and forward flow segments (Fig. 2B). After the first forward flow segment a second species could be introduced in the outlet to create a second gradient during the backward flow. Since the rapid gradient growth in this study was due to high-speed flow shear-driven stretching, it is important to consider how the concentration profile shape and concomitant gradient length changed during flow reversal. In the absence of diffusion, flow reversal would undo the hydrodynamic stretching and collapse the gradient. The effect of flow reversal on the gradient length was predicted numerically by reversing the flow after a forward flow segment and different durations of diffusion downtime (Fig. S3). If the flow was reversed immediately without any diffusion downtime, gradients shrank as the hydrodynamic stretching of the previous flow segment was partially undone. With even brief diffusion downtimes, in particular those long enough to allow for vertical mixing, (t = 0.1H²/D ≈ H²/(Dπ²) or = 0.1), the gradient shrinking was virtually eliminated for most channel cross-sections. Based on our simulations, we used flow sequences with multiple forward-backward flow cycles and with 30s diffusion downtimes between flow segments to allow for vertical mixing and to eliminate gradient shrinking. After four cycles (four forward segments and three backward segments), we obtained a 3 cm FITC gradient that was nearly laterally uniform (Fig. 2C).

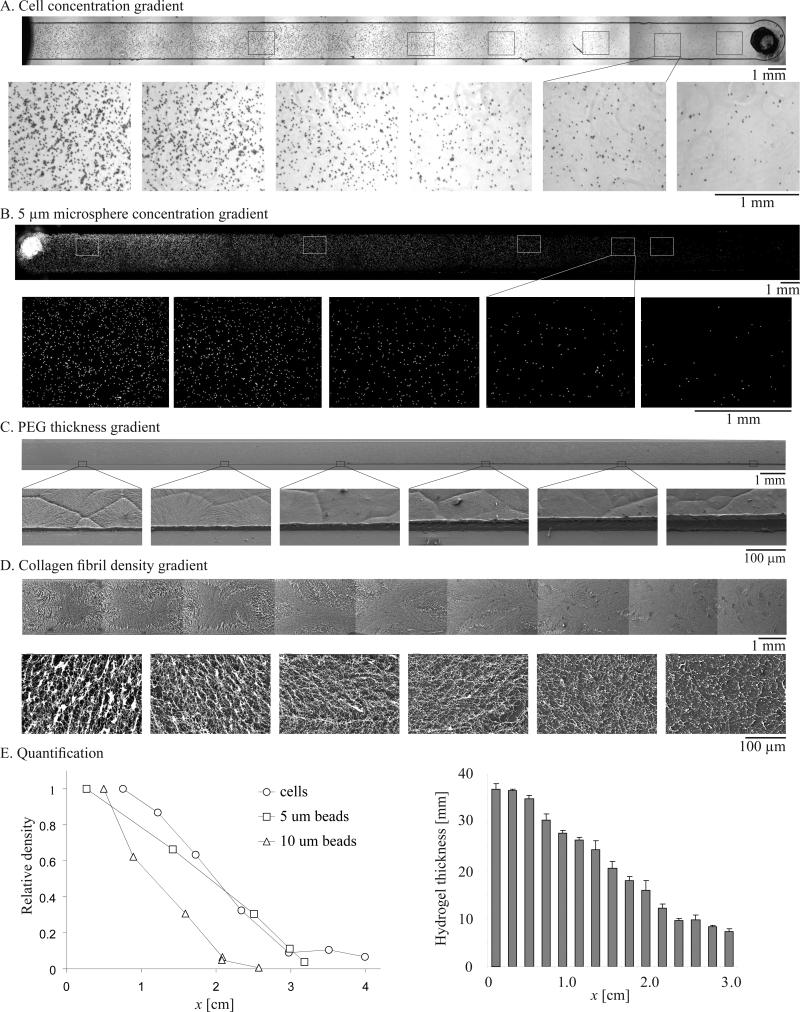
By combining material engineering technologies, our convection-driven gradient generation method was used to create material gradients of synthetic and natural polymers with controlled property variations. In each case, a concentration gradient of precursor solution of a material was first generated and then polymerized by the appropriate cross-linking method. Figure 3A shows SEM images of the air-dried PEGDA hydrogel gradient with a continuous variance in thickness. The concentration gradient of PEG-DA precursor solution was photopolymerized to form the hydrogel gradient. As quantified in Figure 3E, the thickness of the freeze-dried hydrogel gradient gradually increased from ~10 μm in the region formed with 5wt% PEG-DA to ~40 μm in the region with 40wt% PEG-DA. In another example, thermally cross-linked collagen gradients were established and visualized after free-drying. The porous 3D collagen mesh exhibited continuous changes in fibril density (Fig. 3B).

Figure 3. Long-range gradients of particles, cells and materials.

SEM images at low and high magnification of freeze-dried A) PEG-DA hydrogel gradient and B) collagen gradient. Microscope images of C) endothelial cell gradient and D) fluorescent particle gradient (diameter 5 μm). E) Quantification of the continuous variance in thickness of the hydrogel gradient and relative density profiles of endothelial cell gradient and fluorescent particle gradient (with diameters of 5, 10 μm).

The ability to rapidly generate nano/micro particle gradients allows precise control of nano/micro surface morphology to regulate cell behavior[30] and may also be useful to establish a controlled release system to deliver drugs with spatial variations. Gradients with controlled variations in cell density are potentially useful for generating bio-mimetic tissue constructs with heterogeneous cellular density and distribution (e.g. cartilage tissue[31]). Our gradient platform offers a simple, rapid and biocompatible method of producing gradients of microparticles. Using high flow speeds (mm/s), 2-3 cm gradients of endothelial cells and 5 μm and 10 μm microbeads were generated along the channel (Fig. 3C-E). The difference in gradient lengths can be rationalized by considering the degree of settling during gradient formation. Both cells and beads settled under gravity, limiting the extent of gradient growth. We can safely neglect the effects of diffusivity over the length and time scales of interest (Supp. II.3d). For flow between parallel plates, the gradient in particle concentration is generated by pure convection and evolves according to Δ = 1.2Ut (Supp. II.3b). In our cell and bead experiments, 6 μL of fluid was pumped into the channel, so that Ut = 3 cm and a 3.6 cm gradient could be generated in the absence of gravity. The amount of settling is estimated with Stokes’ formula for the terminal fall velocity.[32] The 5 and 10 μm beads of density 1.05 g ml⁻¹ fell at approximately 0.7 and 3 μm/s, respectively, in distilled water. For cells and 10 μm beads, the average flow speed was U = 3.7 mm/s for a duration of 8.1s, and for 5 μm beads, U = 2.1 mm/s for 14.4 s. Thus the 10 μm beads fell approximately a quarter of the channel height while the 5 μm beads fell only on tenth, implying that the effect of settling is smaller for the 5 μm beads than for the 10 μm beads. It is not surprising that the length of the 5 μm bead gradient is 3 cm, close to value of 3.6 cm predicted for pure convection, while the 10 μm bead and cell gradients are approximately 2 cm long (Fig. 3E).

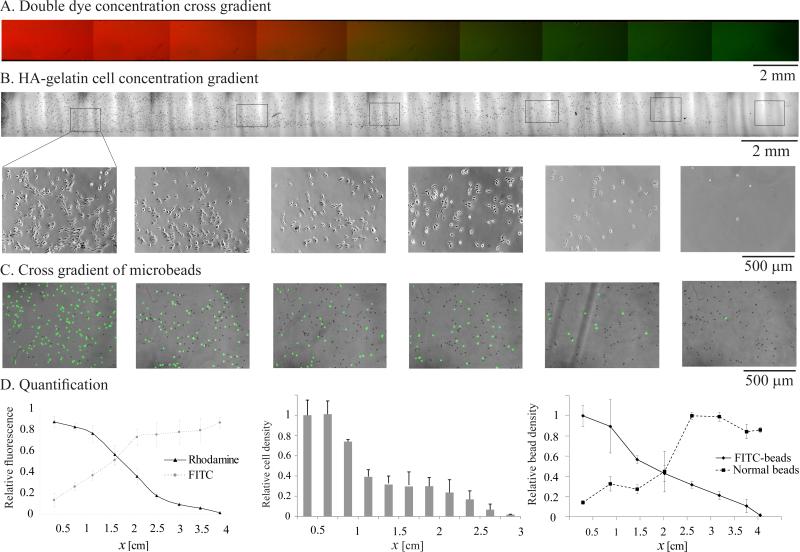
The versatility of our platform allows cross-gradients to be formed by prefilling the channel with one species, loading another species in the outlet port, and simultaneously generating gradients in both species during alternating flow segments. The cross gradient approach can potentially be used to generate composite multi-functional biomaterials with optimal biological, mechanical, and therapeutic properties for tissue engineering applications. Provided the concentrations are dilute and the species do not react with each other, the two gradients evolve and grow independently, as if alone in the channel. Our theoretical and experimental findings on single gradient evolution may therefore be used for each of the crossing gradients. For visualization and testing, the cross-gradient method was used with a four cycle flow sequence to create a 2 cm cross-gradient of the fluorescent dyes FITC-dextran (MW 10kDa) and rhodamine dextran (MW 10kDa) (Fig. 4A,E). The same method and flow sequence were then used to create a cross-gradient of hyaluronic acid (HA) and gelatin, which regulate cell behavior differently.[33] HA is cell repellent,[34, 35] while gelatin is bio-active. Crossing gradients of the precursor solutions of methacrylated HA and gelatin were first formed and polymerized by UV cross-linking. Smooth muscle cells (SMCs) were cultured on the resultant HA-gelatin composite hydrogel to investigate the effect of the composite material on cell adhesion. After 24 h of incubation, the majority of attached SMCs were found on the gelatin dominant region and the number of attached cells gradually decreased along the composite material as the ratio of HA increased (Fig. 4B,D). In addition to the cross-gradient of polymers, we also generated in a similar manner a cross gradient of two types of microbeads. Microbead solutions were loaded into opposite ports on successive flow segments with downtime in between to allow the first type of microbeads to settle. After one flow cycle, the two types of microbeads were well mixed with each other in different ratios along the channel (Figs. 4C,D and S5).

Figure 4. Cross gradients containing two species.

A) Merged fluorescence image of a cross gradient of FITC-dextran (green) and rhodamine dextran (red). B) Phase images (upper: lower magnification; lower: higher magnification) of SMC cultured on a substrate made from a composite material with HA-gelatin cross gradient. C) Merged phase and fluorescence image of a cross gradient of 10μm fluorescent and non-fluorescent microbeads. D) Quantification of the relative fluorescence of the FITC-dextran/rhodamine dextran cross-gradient, relative cell density on the composite HA-gelatin material cross-gradient, and relative number density of the microbead cross-gradient.

While hydrodynamic stretching can create long gradients in seconds, it is important to ensure the gradients are sufficiently laterally uniform for the particular application. The lateral (cross-sectional) uniformity may be quantified by the distance between the x-locations of concentration c = 0.5 at the channel center and at the wall. Figure S6A shows the center, wall, and laterally averaged FITC-dextran concentration profiles after the initial forward flow segments of Figure 2A. In all cases, the laterally averaged concentration profiles were close to the centerline profiles, indicating that the gradients were uniform over the majority of the channel except in narrow regions near the sidewalls. The lag σ increased with flow rate, consistent with the larger shear. The gradient length at the wall was longer than that in the center, consistent with the additional dispersivity near the sidewalls.[25] Our computational simulations showed similar trends and indicated that the channel cross-section had only a secondary effect on the growth of (Fig. S6C). Initially σ grew linearly in time and diffusion eventually slowed its growth. In the absence of flow, diffusion alone could render the concentration profiles uniform over the timescale W²/D (Fig. S7), which for our wide channel was on the order of hours. Fortunately, flow reversal combined with short diffusion downtimes offered a much faster approach to maintain gradient length while reducing non-uniformity (Fig. S6B). In numerical simulations of the backward flow, the separation decreased to 0 and then increased as the hydrodynamic stretching of the previous flow segment was undone; the profile was then stretched in the opposite direction (Fig. S6D). If lateral uniformity is desired, the flow may be stopped when σ reaches zero. An optimal flow sequence may involve a mix of flow segments devoted to growing the gradient and those devoted to improving lateral uniformity. Note that for non-diffusible species, flow reversal merely undoes the hydrodynamic stretching and collapses the gradient, unless the particles are negatively buoyant and have settled, in which case flow reversal has no effect. Lastly, we note the non-uniformity of the concentration profile in our channel was partly due to the inlet tube having an inner diameter less than the width of the channel, which produced a pointed concentration profile at the inlet. For generality, we used a laterally uniform initial concentration profile for our numerical simulations.

It is important to consider how the channel size affects the time required to generate a gradient of a given length Δ. In the absence of diffusion, the gradient length evolves as 1.2Ut, given above, which is independent of the channel dimensions provided the average flow speed U is kept constant. Generating a gradient of length Δ requires Δ/1.2U time. For non-diffusible species, a uniform gradient is formed once the particles settle to the channel bottom, and hence the settling time scales as the channel height. For diffusible species, increasing the smallest dimension of the channel, defined here as the height H, while keeping U constant increases the Péclet number and enhances hydrodynamic stretching. However, achieving a uniform gradient requires lateral diffusive mixing. While flow reversal may be used to render the gradient uniform across the largest lateral dimension of the channel, defined here as the width, to avoid collapsing the gradient diffusive mixing must first complete across the height, which requires a time H²/(π²D). Thus while scaling up may enhance the hydrodynamic stretching, the total time to generate a uniform gradient scales as the channel height H for non-diffusible species and as H² for diffusible species, where H is the smallest dimension of the channel.

For completeness, we comment on the effects of other parameters on gradient evolution. The Reynolds number Re=UH/ν and the scaled channel length L/H do not directly affect the concentration profile and gradient evolution. The analytic solution for the fully developed flow profile has the special property that the convective derivatives in the Navier-Stokes equation vanish and hence so does the dependence on the Reynolds number. Moreover, since the flow solution is independent of the longitudinal coordinate x, the role of the channel length is merely to provide a stopping point once the gradient reaches the end of the channel. Thus while the channel length L/H affects the choice of time sequence, it does not directly affect the concentration profile. Lastly, temperature affects gradient formation through its effect on the diffusion coefficient.

Conclusions

In this study we have presented a simple yet versatile platform to generate centimeter scale gradients of species from the molecular to micron scale in seconds to minutes. Microbead and cell concentration gradients were produced by high-speed flows offering high fluidic shear in a simple microfluidic channel. For diffusible species, flow sequences were developed to generate long and laterally uniform gradients, and were tested to produce 2-3 cm gradients of fluorescent dyes. Similar flow sequences were then used to create gradients of PEG hydrogel, collagen and a cross gradient composite material of HA-gelatin which possessed a gradient in cell-attachment. Accompanying scaling arguments and numerical simulations of the gradient evolution in alternating flows generalized our results to a wide range of Péclet numbers and channel geometries. Our simple, versatile gradient platform should be accessible to a broad range of experimenters in the materials science and biomedical fields.