Rapid Pupil-Based Assessment of Glaucomatous Damage

Abstract

Purpose

To investigate the ability of a technique employing pupillometry and functionally-shaped stimuli to assess loss of visual function due to glaucomatous optic neuropathy.

Methods

Pairs of large stimuli, mirror images about the horizontal meridian, were displayed alternately in the upper and lower visual field. Pupil diameter was recorded and analyzed in terms of the “contrast balance” (relative sensitivity to the upper and lower stimuli), and the pupil constriction amplitude to upper and lower stimuli separately. A group of 40 patients with glaucoma was tested twice in a first session, and twice more in a second session, 1 to 3 weeks later. A group of 40 normal subjects was tested with the same protocol.

Results

Results for the normal subjects indicated functional symmetry in upper/lower retina, on average. Contrast balance results for the patients with glaucoma differed from normal: half the normal subjects had contrast balance within 0.06 log unit of equality and 80% had contrast balance within 0.1 log unit. Half the patients had contrast balances more than 0.1 log unit from equality. Patient contrast balances were moderately correlated with predictions from perimetric data (r = 0.37, p < 0.00001). Contrast balances correctly classified visual field damage in 28 patients (70%), and response amplitudes correctly classified 24 patients (60%). When contrast balance and response amplitude were combined, receiver operating characteristic area for discriminating glaucoma from normal was 0.83.

Conclusions

Pupillary evaluation of retinal asymmetry provides a rapid method for detecting and classifying visual field defects. In this patient population, classification agreed with perimetry in 70% of eyes.

The pupillary light reflex (PLR) has been recognized as an indicator of retinal status for decades,¹ and the swinging flashlight test² has been a widely used clinical test to evaluate relative afferent pupillary defects in optic neuropathy from various etiologies. Measurement of pupil responses to light stimuli provides an objective test of visual function, in contrast to the various forms of perimetry, which require subjective judgements on the part of patients.³ However, there has been limited progress in quantitative application of the PLR in clinical settings, because of test duration, test complexity, fluctuation of the pupil response with internal sympathetic/parasympathetic state variation, external ambient light, and contamination of the pupil response by scattered light.

In previous work, a method was developed for comparing the PLR to relatively large superior and inferior stimuli.⁴ In normal eyes there was functional near-symmetry between superior and inferior retina, whereas patients with hemifield perimetric defects showed functional asymmetry. Functional glaucomatous loss is often asymmetric about the horizontal meridian,^5–8 so pupillary assessment of functional asymmetry may be helpful in detecting and identifying patterns of glaucomatous visual loss.

In the present work, pupillary responses of a group of 40 patients with glaucoma and a group of 40 age-similar control subjects were tested to evaluate the ability of the technique to detect and classify eyes with glaucomatous damage.

METHODS

Pupillometric Technique

The basic technique is described in detail elsewhere⁴; the following gives a brief summary of those methods. Stimuli were presented on a cathode ray display controlled by a computer. Horizontal pupil diameter was recorded (60 samples/sec) using a computer-based pupillometer.

Three stimulus pairs were employed, each pair designed to capture areas of the visual field with a high likelihood of glaucomatous damage. Each pair consisted of two component stimuli which were mirror images about the horizontal meridian. Taken together, the three stimulus pairs covered most of a region of central visual field subtending an area 20 deg in vertical extent (10 deg superior to 10 deg inferior) by 30 deg in horizontal extent (20 deg nasal to 10 deg temporal). The three stimulus pairs were named “paracentral” (the smallest stimulus pair, nearest to fixation and near the horizontal meridian between fixation and the blind spot), “Bjerrum” (a larger stimulus pair, further from fixation and covering much of the Bjerrum area), and “peripheral” (furthest from fixation and extending 20 deg into the nasal field).⁴ The stimuli are shown as insets in Fig. 1.

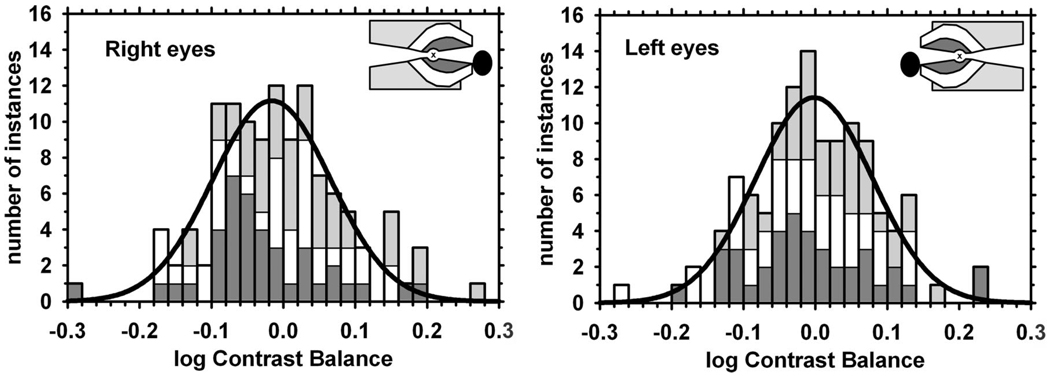
FIGURE 1.

Distributions of all weighted mean values of log contrast balance for the right and left eyes of normal subjects. Means: −0.009, −0.003; SDs: 0.094, 0.100. The distributions are normal according to both K-S and S-W tests. Histograms are shown for the data; smooth curves are the best-fit normal distributions. Insets are scale diagrams of the three stimulus pairs for right and left eyes, indicating the fixation target (“x”) and the blind spot. Histogram and stimulus shading indicate: paracentral stimulus (dark gray), Bjerrum stimulus (white), peripheral stimulus (light gray).

In a single trial, the two component stimuli of one stimulus pair were presented alternately for 1 s each. The “on” luminance of the lower member of the pair was fixed at 36 cd/m²; the on luminance of the upper member of the pair was cycled through three luminance levels: 24, 36, and 54 cd/m². On the next presentation after the brightest, the sequence began again at 24 cd/m². The “off” luminances for all stimuli were the same—approximately 0.01 cd/m². Outside the boundaries of the stimulus pair in use on a given trial, the background luminance was 5.5 cd/m². A single trial was recorded for 18 s, during which time the 6 s sequence of stimulus presentations described above was repeated three times. The three repeat segments of data were averaged together.

In a single session two complete sets of trials were performed, each set presenting the three stimulus pairs to both eyes (one set contained six trials). The two sets of trials were separated by a break of approximately 30 min. A second session with the same subject took place 1 to 3 weeks later. The stimulus sequence, and the order of eye tested, were counterbalanced to minimize any effect of sequence (e.g., fatigue or practice effects).

For each trial, data analysis produced two indices per stimulus: the contrast balance and the response amplitudes. The “contrast balance” is an estimate of the relative upper/lower stimulus contrasts required to produce pupil responses of equal amplitudes; this is expressed as the log of the ratio of upper to lower stimulus contrasts. A value of zero indicates symmetry, positive values indicate greater sensitivity for superior retina, and negative values indicate greater sensitivity for inferior retina. Determination of the contrast balance for a given set of trials involved fitting a function to data for different stimulus luminances, and the square root of the mean squared deviation of the data from the fitted function (“SRMSD”) was used as a measure of reliability of the log contrast balance. Data from trials with SRMSD > 0.5 were considered unreliable, giving rejection rates of 11% of trials for the patient group and 8% of trials for the control group. This rate of trial rejection did not generally prevent data acquisition. Only one patient, who fit the inclusion/exclusion criteria, was accepted into the study and subsequently failed to provide useable data (due to relatively immobile pupils).

For the final estimate of the contrast balance value for a stimulus in a particular subject (typically determined from four repeat trials, two from each session), a weighted mean of the values was employed, where the weighting factor for each trial was 0.5 minus the SRMSD for that trial. This procedure assigns greater weight to values determined from trials on which the fitted function provided a good description of the response balance values. The distribution of log contrast balance values for the normal older subjects based on the arithmetic mean and on the weighted mean were, in fact, very similar. Values reported here are weighted means. As an indicator of the quality and number of the fits underlying the final mean values, a figure of merit was determined that was equal to the sum of the weighting factors in a given weighted mean. This could have a value between zero and two, the latter reflecting perfect fits.

In the present experiments, the stimuli (upper = 24, 36, 54 cd/m²; lower = 36 cd/m²) had a range of upper/lower stimulus contrast of −0.18 to +0.18 log units. Log contrast balance values were determined (by interpolation or extrapolation) over approximately twice this range, beyond which the values were posted at −0.40 or +0.40 log units, depending on the direction of the imbalance. Occasional individual trials of control subjects (1%) were posted in this manner. The posting acknowledges uncertainty in extrapolation beyond this range, while retaining the clear indication of imbalance.

In addition to the log contrast balance, separate averages of response amplitudes to upper and lower stimulus presentations were determined, and abnormalities were detected in patients by comparison with values from control subjects.

Subjects

Two groups of subjects were recruited, a group of 40 patients with glaucoma and a group of 40 age-similar control subjects. Subjects in both groups were required to have spherical refractive error within the range ± 5D, cylindrical refractive error no > 3D, have no significant media opacity or other ocular disorders (other than glaucoma in the patient group), have no systemic conditions known to affect the eye or visual pathway (e.g., cerebral-vascular disease), and not be using medications that affect pupil size.

Patients with glaucoma (17 males, 24 females), aged 42 to 82 years old (62.2 ± 9.0) were recruited from patients undergoing treatment at the Glaucoma Institute of SUNY State College of Optometry. Patients included in the study were adherent to treatment protocols and follow-up for a period of at least 2 years, and showed no clinically significant changes in structural or functional analysis suggestive of progression of glaucoma over the 12 months preceding the study. Patients were recruited who had a wide range of degrees of loss; the visual fields had mean deviation values ranging from −0.7 to −32.4 dB (mean: −7.4 dB; median: −5.1 dB) and pattern standard deviation (PSD) ranging from 1.2 to 14.5 dB (mean: 5.7 dB; median 4.4 dB). Both eyes of included patients had been diagnosed with primary open angle glaucoma. Patients were required to have best corrected visual acuity no worse than 20/40 and no significant field loss within 1 deg of fixation.

Age-similar control subjects (16 males; 24 females), aged 44 to 62 years old (52.0 ± 5.4) were recruited from the community at the SUNY State College of Optometry. All subjects had received a comprehensive ocular examination in the University Optometric Center at SUNY College of Optometry; they were found to have normal intraocular pressures and no indications of ocular disease. Best corrected visual acuity for control subjects was required to be 20/20 or better. They were also required to have no first degree relatives with a history of glaucoma.

The research adhered to the tenets of the declaration of Helsinki and was approved by the SUNY State College of Optometry Institutional Review Board. After the nature of the experiment was explained, written informed consent was obtained from each subject prior to testing.

Comparison of Perimetric Data and Pupil Data

For each patient, the results of several visual field tests in their clinic records were selected which were gathered close in time to the pupil experiment, using the Humphrey Visual Field Analyzer, Model 750 (Carl Zeiss Meditec, San Leandro, California) and either 24-2 or 10-2 test patterns.

Most patients with moderate or advanced glaucoma had been tested with the 24-2 pattern, whereas patients with severe visual field loss had usually been tested with the 10-2 test pattern, which is useful for comparison with data gathered with the paracentral and Bjerrum stimuli (which were largely confined to the area within 10 deg of fixation); for such subjects recent 24-2 test results were used for comparison with the peripheral stimulus data (which falls primarily outside the region of the 10-2 test pattern). Comparisons of pupil data with visual field data were generally based on the average results of between two and four visual fields, taken within 1 to 1.5 years of the date of the pupil experiment.

To compare visual field data and pupillary contrast balance values, an index of visual field asymmetry was computed for each eye and stimulus using perimetric data for locations within the boundaries of each stimulus pair. The sensitivity corresponding to a single (upper or lower) stimulus was computed with an arithmetic mean of perimetric sensitivities (the perimetric sensitivities in decibels were transformed to linear sensitivity units and averaged across stimulus locations^9,10), and the predicted contrast balance was computed as the logarithm of the ratio for upper and lower sensitivities. The logarithm of that ratio was used for comparison with the log contrast balance.

In some cases there were few test locations within a stimulus outline (e.g., the 24-2 test pattern only has two locations within a paracentral stimulus), so moderate variations in visual field results could cause large fluctuations in predictions. To reduce this effect, several fields were averaged together, 10-2 data were employed when possible, and a modified prediction was introduced as follows: a computational grid was defined with points spaced 0.25 deg apart and sensitivities were estimated over the fine grid using bilinear interpolation¹¹ from the coarser-grid visual field data. Because many fine-grid locations fall inside the stimulus outlines, the fine-grid approach allows sensitivity values outside the boundaries of a stimulus to influence the average for that stimulus. Predictions made in this manner were found to fluctuate less from one visual field to another than the original predictions.

In eyes with substantial glaucomatous field damage, estimates of the perimetric asymmetry may be as large as two or more log units, while pupillary estimates of asymmetry were limited to ± 0.4 log unit (see above). To facilitate comparison of these quantities, the predictions made from visual fields were limited to ± 0.4 log unit from balance.

The comparison of visual field findings with pupil amplitude data used the separate arithmetic means for perimetric sensitivity in the upper and lower stimulus areas, and compared log sensitivity corresponding to a given stimulus with the log of the amplitude of the pupillary response to this stimulus.

Grayscale Representation of Pupil Defects

To provide a simple graphic basis for comparing pupil data to visual fields, a grayscale representation was developed and pupil results using this representation are presented together with the corresponding visual fields.

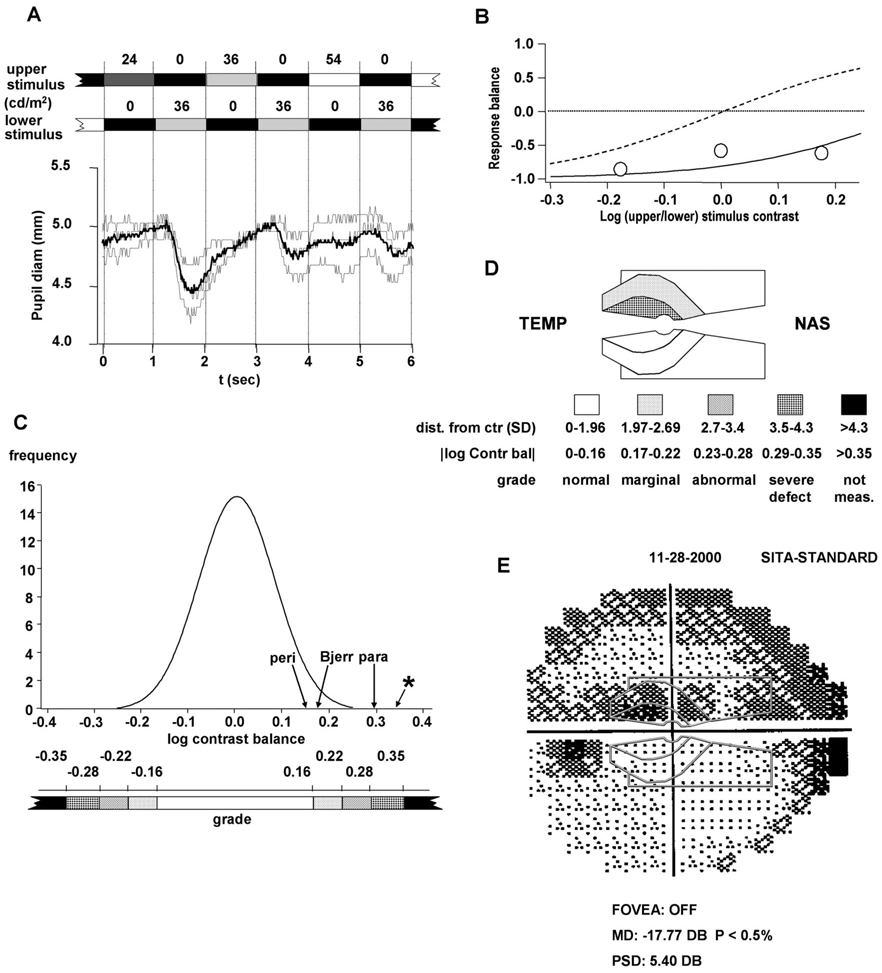
The grayscale representation for pupil defects was based on the distribution of log contrast balance values determined for the normal older subjects. The distribution was determined using the weighted mean value of log contrast balance for each stimulus condition (see above). A log contrast balance value determined for an eye was compared with this distribution; values within ± 1.96 standard deviation (SD) of the center of the distribution were considered to be in the normal range. This corresponds to the 95% confidence interval (CI) for the distribution. Log contrast balance values further from the center were graded from marginal to “not measurable” at intervals of approximately 0.7 SD, and assigned a corresponding grayscale level (Fig. 2C, D). The weighted mean value for each stimulus condition was assigned a grayscale value according to this scheme.

FIGURE 2.

Transformation of experimental data from the group of patients into a grayscale representation. (A) Raw data for one trial (left eye, paracentral stimulus). Thin traces show individual cycles; thick trace shows average. (B) The three experimental values of response balance (circles) determined for the trial in A, plotted against log stimulus contrast. (The “response balance” measures relative pupil response to the three upper/lower pairs of stimulus presentations in one trial—one for each luminance of the upper stimulus—and is equal to [(R_U − R_L)/(R_U − R_L)], where R_U and R_L are response amplitude for the upper and lower stimulus, respectively). Solid curve: sigmoid function fitted to the response data. Dashed curve: average sigmoid function for all normal eyes and all stimuli. The sigmoid functions were of the form F(x) = [((x/x₀)^a − 1)/((x/x₀)^a + 1)], where x is the contrast of upper stimulus relative to lower, x₀ is the contrast that gives equal responses to upper and lower stimuli (the contrast balance), and “a” is related to the slope. (C) The curve is the best-fit normal distribution for the normal subjects. The weighted mean values of log contrast balance determined for the eye in A are indicated by arrows; the single-trial value for the trial shown in A and B is indicated by an asterisk. Details of the steps from raw data to contrast balance are given in ref. 4. Below the axis, the grayscale used for contrast balance is indicated. (D) Grayscale representation of pupil defects for the eye in A and B, based on the weighted mean log contrast balance values indicated by arrows in C. Below the representation, the grayscale intervals and labels are indicated. (E) Perimetric results for the same eye. Outlines of the pupil stimuli are superimposed at the same scale.

A simple grayscale for amplitude data was also employed, based on the distribution of log amplitude values for the normal group. The distribution of amplitudes was determined separately for left and right eyes, for each stimulus and for upper vs. lower visual field. The amplitudes were treated as response amplitude values (in millimeter) and these were converted to Z-scores for log amplitude; these distributions were similar enough that a single distribution of Z-scores was employed for interpretation of all results. The criteria for abnormality were then taken as 2.5 and 3 SD below the center of the normal subject distribution (99.4% and 99.9% CIs for a one-sided distribution). These are higher CI values than used for contrast balance; with six areas per eye, the goal was to keep the false positive rate reasonably low (for six areas per eye, a 2.5 SD criterion corresponds to a 5% probability of at least one area falling outside the interval). A value 3 SD below the center of the normal distribution is approximately the limit of resolution of a response (which depends on the details of a particular record); hence, data with a Z-score less than −3 was clipped and posted at −3.25.

Statistics

All analyses were conducted separately for left eyes and right eyes. The frequency distributions of normal log contrast balance values were evaluated with the Kolmogorov-Smirnov normality test (K-S test) (D < 1.36/√N indicates a normal distribution at the level of p = 0.05), and with the Shapiro-Wilk test (S-W test) (W values significant with p < 0.05 indicate normality should be rejected with 95% probability).

Test-retest variability was studied by means of analysis of agreement. ¹² Within-session variability was measured as the difference in log contrast balance between the two test trials for the same condition performed in the same session. Between-session variability was measured as the difference between the average values for the two sessions.

For patients with glaucoma, pupil data were compared with visual field results, as described above, and tested for correlation by means of linear regression (p < 0.05) and also using non-parametric Spearman rank order correlation. For comparisons with global indices from perimetry, a global index for pupillometry was computed as the magnitude of the contrast balance for the stimulus showing the largest asymmetry.

RESULTS

Normal Retinal Balance

The distributions of pupillometric contrast balance values for the normal subjects are plotted in Fig. 1A. The distributions were Gaussian according to both K-S and S-W tests. The right and left eye distributions were very similar, and for subsequent analyses they have been pooled into a single distribution for all normal eyes with center = 0.00 log units, SD = 0.08 log units, and 95% CI (± 1.96 SD from the mean) of ±0.16 log units. Across the three stimuli and both eyes, there were 240 contrast balances, of which only five (2%) fell outside the 99% confidence limits.

Distributions for within-session differences in contrast balance were normal for both right and left eyes; the centers were −0.02 and +0.04 (R, L eyes, respectively) and the SDs were 0.16 and 0.17. Distributions for between-session differences were also normal; the centers were 0.01 and 0.01 and the SDs were 0.12 and 0.13. The absolute values of the differences were 0.11 log units for within-session variation (same for both eyes) and 0.09 and 0.08 log units for between-session variation (R, L eyes).

Functional Retinal Imbalance in Patients

Of the 240 contrast balances from the patients, 60 (25%) fell outside the 99% confidence limits for normal. An example is shown in detail in Fig. 2, where panel A shows raw pupil data from a single trial performed on one eye of a patient with glaucoma, using the paracentral stimulus. The response to the upper stimulus was consistently smaller than the response to the lower stimulus, even for the brightest upper stimulus (54 cd/m²). Fig. 2B shows a plot of the three values of upper/lower response balance for the trial of Fig. 2A, and the sigmoid function fitted to the response balances.⁴ The sigmoid is displaced to the right relative to the average curve for normal subjects (shown as the dashed curve). The log contrast balance for this trial was extrapolated to 0.35 (where the sigmoid curve crosses zero). The SRMSD of the sigmoid fit for this trial was 0.152. Fig. 2C shows the contrast balances for this eye for the three stimuli, as arrows on the distribution from the normal group (the individual trial of Fig. 2A is indicated with an asterisk). These were converted to Z-scores of 1.87, 2.05, and 3.61 for the peripheral, Bjerrum, and paracentral stimuli, respectively. Also shown in Fig. 2C is a grayscale for use in describing the pupil data graphically (see Methods), and the results for the same eye are shown graphically in Fig. 2D. Fig. 2E shows perimetric data for the same eye, with the pupil stimulus outlines superimposed at the same scale. There appears to be substantial agreement between the two.

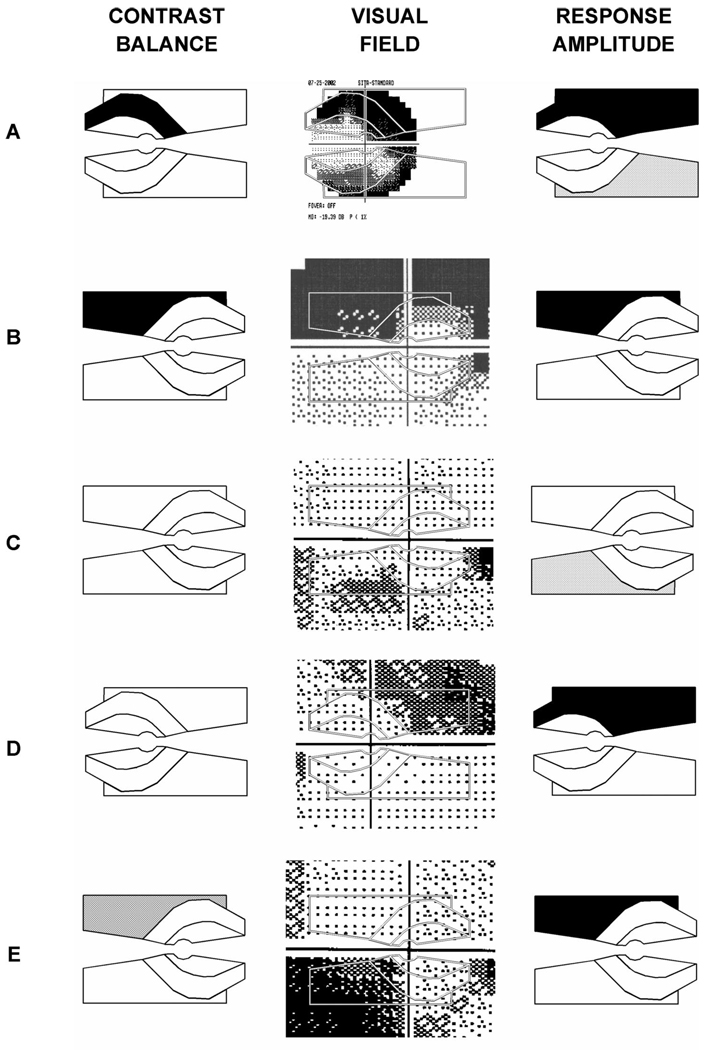
Fig. 3 shows five more examples from patients, with grayscales for log contrast balance (left column), visual fields (middle column), and response amplitudes (right column). In many eyes tested, the pupil data appeared to agree reasonably well with the corresponding visual field data [e.g., Fig. 2, Fig. 3A (particularly for the Bjerrum stimulus), B (particularly for the peripheral stimulus)]. In eyes where agreement was less clear, visual field changes were approximately the same over a pair of stimuli, either with mild loss [e.g., Fig. 3C, D (Bjerrum stimulus)], or with more substantial loss [e.g., Fig. 3A (peripheral stimulus)]. In many of these cases the amplitude grayscale identified reduced response amplitudes to both stimuli. In every instance where both contrast balance and amplitude measures indicated abnormality, the two were in agreement. In one out of 79 eyes a consistent pupil defect appeared to be opposite to a consistent visual field defect (Fig. 3E).

FIGURE 3.

Five examples of grayscale representations of pupil defects from patients (left column), compared with visual field data (center column). Right column shows amplitude results for the same eyes (see text). The example shown at the bottom is the only case in 79 eyes where the pupil defect was clearly opposite to the prediction from perimetry.

The distribution of response amplitudes for the control group were best described in terms of the logarithm of the amplitudes, for which the data conformed to Gaussian distributions with centers at 0.12 mm (−0.92 log(mm); paracentral stimulus) or 0.18 mm (−0.74 log(mm); Bjerrum and peripheral stimuli) and SDs of 0.2 to 0.3 log units. The actual data distributions ended fairly abruptly at approximately 1 SD above the Gaussian centers, corresponding to physical constraints and non-linearities in the pupil system. However, in the present work only smaller responses than normal were treated as abnormal, so it only matters that the lower limbs of the Gaussian distributions provided good descriptions of the lower portion of the log amplitude distributions. The distributions of response amplitudes in the patient group showed a distinct shift toward smaller amplitudes, with the means shifting by 1 SD. Testing the left and right eye groups separately (patients vs. normal), two-sample t-tests assuming unequal variances indicated negligible probability that the two distributions were drawn from the same population (p < 0.00001).

Perimetric and Pupillometric Measures of Asymmetry and Sensitivity

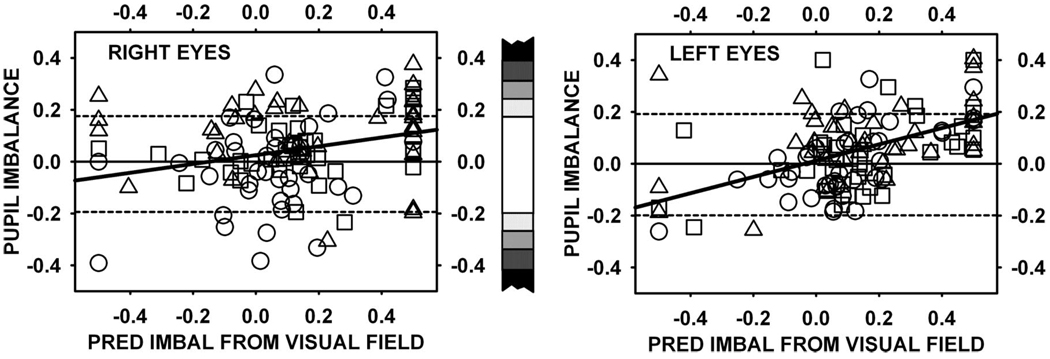
In Fig. 2 and Fig. 3, a few examples of comparisons between perimetric and pupillometric measures of retinal asymmetry were presented. In Fig. 4, a broader comparison was made on a more quantitative basis: the contrast balance was plotted against the prediction made from the corresponding visual field; correlations were moderate (R eyes: r = 0.20, p = 0.03; L eyes: r = 0.38, p < 0.0001). Spearman rank order correlations were stronger for the left eyes (R eyes: r = 0.20, p < 0.05; L eyes: r = 0.47, p < 0.05).

FIGURE 4.

Scatter plots of observed pupil response imbalance (weighted mean log contrast balance) plotted against predicted imbalance (difference in average sensitivity determined from perimetry) for the same eyes. Data for right and left eyes are plotted separately.

The global index for pupillometric asymmetry was moderately correlated with global indices derived from visual fields, the glaucoma hemifield test (GHT) and the PSD. GHT results are given as within normal limits, borderline, or outside normal limits, whereas PSD is a continuous variable. For the PSD, the correlations were r = 0.49 (p = 0.002) and r = 0.50 (p = 0.001) for right and left eyes, respectively (rank order correlations: r = 0.56 and 0.64 for right and left eyes, respectively, both with p < 0.05). Similar results were obtained for the GHT (rank order correlations: 0.55 and 0.40, both with p < 0.05).

In addition to the above comparisons, pupil amplitude data were compared with visual field sensitivities: the Z-scores of log(response amplitude(mm)) were plotted against average sensitivity determined from visual fields. Correlations were again modest and were slightly greater for the right eyes than for the left eyes (0.35 vs. 0.30). Rank order correlations were similar (0.33 and 0.27 for right and left eyes, both with p < 0.05). Although the data were some-what noisy, it is worth noting that when sensitivity was less than about 25 dB, virtually all Z-scores were negative (zero is the center of the truncated normal distribution fitted to the control subject data).

Within-and Between-Session Variability for Patients with Glaucoma

Within-and between-session variability in patients were analyzed by means of Bland-Altman analysis.¹² The frequency distributions of both within-and between-session variation were normal according to both K-S and S-W tests. The centers of the within-session distributions were 0.03 and −0.02 (R and L eyes, respectively) and the SDs were 0.16 and 0.12. The between-session distributions had centers 0.03 and −0.01, with SDs 0.13 and 0.12. The centers of all these distributions did not differ significantly from zero. Linear regression did not indicate significant correlation between magnitude of variation and contrast balance (right eyes: r = 0.06, p = 0.50 within session, r = 0.03, p = 0.72 between sessions; left eyes: r = 0.15, p = 0.11 within session, r = 0.07, p = 0.48 between sessions). In addition, when the within-subject SD of log contrast balance for repeats of each stimulus was plotted against average perimetric sensitivity over upper and lower parts of the same stimulus in the same eye, there was no significant correlation.

A two-way analysis of variance was carried out to test for effects of stimulus type (paracentral, Bjerrum, and peripheral) or group (patient vs. normal) on variability (right and left eyes were treated separately). There was no significant effect of group or stimulus type on either within-or between-session variability (F < 3.7, p > 0.05) (the only exception was that the Bjerrum stimulus was associated with greater between-session variability for the right eyes; F > 5.0; p < 0.01).

DISCUSSION

Contrast Balance for Normal Older Subjects

The distributions of log contrast balance for the normal group center at approximately zero, similar to earlier observations with young normal subjects.⁴ Although visual sensitivity tests, including conventional perimetry, generally indicate a decline in visual sensitivity with age,^13–17 contrast balance measures relative defects; age-related decreases that occur equally in upper and lower retina will tend to cancel out. The results therefore suggest that the overall average change is approximately the same in upper and lower retina.

Contrast Balance and Amplitude as Indicators of Visual Field Loss in Patients with Glaucoma

When pupil defects were revealed by the contrast balance values, there was frequently a degree of consonance between the findings and the visual field defects found with conventional perimetry (Fig. 3, left and middle columns; Fig. 4). In cases where contrast balance findings were not clearly correlated with visual field defects, response amplitude was sometimes helpful in determining the presence of reduced retinal sensitivity (Fig. 3, right column). It appears plausible that using both measures could increase overall discrimination capability, and preliminary results using receiver operating characteristic analysis supported this view: contrast balance alone gave an area of 0.83, while combining it with amplitude gave an area of 0.88 (larger samples would be required to establish the significance of any difference in receiver operating characteristic area).

The correlation between contrast balance and imbalance predicted from visual fields was found to be somewhat different for right vs. left eyes (Fig. 4). To determine the extent to which this might depend on relatively poor sigmoid fits, the effect of excluding data with figures of merit < 0.5 was examined. The correlation for right eyes increased from r = 0.15 (r² = 0.023) to r = 0.19 (r² = 0.036); the correlation for left eyes remained unchanged at r = 0.53 (r² = 0.28). Thus, the sigmoid fit does not seem to be a critical factor in the low correlation for right eyes. One difference between right and left eyes in the present study was that there were more right eyes with substantial damage (there were 15 right eyes and nine left eyes with mean deviation < −10, and 18 right and 10 left eyes with PSD > 6). The correlations for different stimuli were also examined; the correlation was lowest for the peripheral stimulus and this was especially marked for right eyes: r= −0.18 (p = 0.26). Correlations for other stimulus/eye combinations were more significant [right Bjerrum: r = 0.35 (p = 0.025); right paracentral: r = 0.28 (p = 0.076); left Bjerrum: r = 0.64 (p = 0.00001); left paracentral: r = 0.58 (p = 0.0001); left peripheral: r = 0.40 (p = 0.01)]. It is possible that the lower correlations for the peripheral stimuli could result from scatter of light outside the overall area of the present stimuli (due to limitations of monitor size, the 5.4 cd/m² background did not extend beyond the outer edges of the peripheral stimulus. In a planned future version of the system, the angular subtense of the stimulus display will be large enough to provide a “frame” of background luminance, surrounding the peripheral stimulus.

A particularly interesting finding was that, even for severely damaged areas (e.g., areas with all test points having visual sensitivities of “<0” dB), some pupil constriction could often be elicited with the present stimuli. A detailed analysis of issues relating to scattered light has led us to argue against the possibility that the present stimuli give spurious findings due to scatter.⁴ If the stimuli were much brighter, this might not be the case; however, the background was only 1 log unit dimmer than the brightest stimulus. Brindley and Westheimer¹⁸ showed that keeping stimulus luminance within 1.2 log units of a large background prevented stray light contamination of the electroretinogram (ERG). In agreement with this, it was confirmed that in the absence of a background, a 2°, 54 cd/m² stimulus centered on the blind spot elicited pupil responses; however, no responses were observed with the 5.4 cd/m² background used in the present experiments.

Assuming that genuine “survival” of pupil sensitivity can occur in some severely damaged areas, this might be at least partly due to the large stimuli used. Although the pupil stimuli are very large, the prediction of imbalance from perimetry is based on tests performed with small stimuli. Increasing stimulus size in perimetry has been shown to increase stimulus visibility for normal subjects, and even more for glaucoma patients.^19–23 It seems possible that even patients with severe loss might be able to see very large stimuli, if they were used in a conventional perimetric test.

An additional effect of the large size of the present stimuli is that defocus up to 6 D does not markedly affect the responses (unpublished results).

Within-and Between-Session Variability

A difficulty with conventional perimetry is that the test-retest variability at locations with advanced visual field defects is greater than the variability at locations with mild defects.^24–29 This makes it difficult to determine whether glaucomatous defects are progressing, especially in the case of deeper defects. Among the patients with glaucoma in the present study, within-and between-session variability of pupil results was no greater at retinal locations with advanced defects than at locations with mild defects.

The finding that variability was not dependent on local sensitivity might be due to the large stimuli used in the present test. Large stimuli have been found to reduce variability in conventional perimetry for normal subjects, and even more so for patients with glaucoma.^30–33 The finding that variability of results with frequency doubling perimetry (FDP) does not appear to depend on the depth of glaucomatous defects may also be in part due to the larger stimulus used.^25,27,34 The Bjerrum and peripheral stimuli used in the present study cover areas of approximately 80 and 130 deg², respectively, which are comparable to the stimulus size used by the FDP tests (approximately 25 to 100 deg²),^34,35 and which are larger than stimuli used in techniques such as chromatic and contrast sensitivity perimetry.^36–38

Some approximate comparisons with static automated perimetry (SAP) may be useful. For the pupil, the normal range (95% CI) for log contrast balance extends from 0 to 0.16 log units (Fig. 2C); thus, the test-retest difference values of 0.12 to 0.16 log units for log contrast balance amounts to 75 to 100% of this range. This is the difference of two samples, suggesting that SDs based on multiple repeats would be approximately 0.08 to 0.11 log units or 50 to 70% of the relevant range. For SAP, if 5 dB (0.5 log units) below mean normal is taken as the edge of “normal,” the variability observed for normal eyes by Heijl et al.¹⁴ (SD of multiple thresholds = 0.16 to 0.45 log units) amounts to 30 to 90% of this range. Thus, for normal subjects, variabilities of pupil contrast balance and SAP are roughly comparable percentages of the normal range. Pupil responses approximately average over the stimulus area, which is likely to reduce variability. The effect of averaging on variability was assessed using 10-2 and 24-2 perimetric data from normal subjects, and found to reduce variability by 0.03 to 0.04 log units (0.3 to 0.4 dB). This would suggest that 24 to 82% may be more appropriate SAP percentages to compare.

In the case of a deep visual field defect (say 10 to 15 dB SAP sensitivity), SAP variability equals ~ 0.6 log units or 6 dB^29,39; i.e., > 100% of the 5 dB change taken to indicate a significant shift from the status quo, and values extend from 0 to mean normal. In the same situation, the variability of log contrast balance is unchanged, so pupil variability should still be at about 50 to 70% of the range for no change from status quo. This assumes that a 0.16 log unit change in balance indicates a change in glaucomatous eyes, which remains to be determined.

It should be noted that the scale for log contrast balance only extends to ± 0.4 log units, whereas the sensitivity scale (for the Humphrey Field Analyzer) extends over a range of about 3.5 log units; thus, SAP can potentially quantify sensitivity over a much larger range. However, the balance measure can continue to make direct sensitivity comparisons even when the average sensitivity is well below normal. In the case of the pupil response amplitude measure, the distance from normal to the outer edge of normal is approximately 2.5 log units, and the range extends 0.5 log units further. Amplitude test-retest variability is approximately 50 to 100% of the average value for all average values (unpublished results). Thus, it could be suggested that variabilities of pupil and SAP measures are grossly similar.

Modeling studies have suggested that increased test-retest variability in visual field defects might be a consequence of cortical inputs made sparser by glaucoma.^33,40 It was also suggested that large stimuli could be less susceptible to such an effect. Conceivably, similar effects could take place in the pretectal olivary nuclei, which receive signals from retinal pupillary ganglion cells in the monkey. An additional proposal regarding test-retest variability is that small eye movements play a substantial role.^33,41,42 To the extent that small eye movements cause visual field test-retest variability, they would not be expected to cause much variability in the present experiments because the retinal territory covered by one of the large stimuli would be relatively unchanged by a small eye movement.

Relationship Between Perimetry and the PLR

The relationship between the afferent pupillary and visual pathways has long been of interest (discussed in detail in ref. 43). Experiments testing the relationship are difficult; owing to the effects of scattered light, the use of background illumination is necessary (as employed in the present work). At present, it is believed that at least some pupillomotor ganglion cells (projecting to the pretectal olivary nucleus) are distinct from visual ganglion cells (projecting to the lateral geniculate nucleus).^44–47 In addition, it appears that at least some of the pupillomotor ganglion cells possess intrinsic photosensitivity, relating to the presence of melanopsin, in addition to receiving input from rods and cones.^48–53

The key question in comparing pupil loss with visual loss is: how similar are the pathways from a visual ganglion cell and a pupillo-motor ganglion cell? For there to be a correlation, the pathways must be similar as far as the lesion site. In the case of glaucoma, for which there is substantial agreement that damage to axons probably occurs at the level of the lamina cribrosa, the similarity of pathway need only extend from ganglion cell to the lamina. Although one of the authors has suggested that minor differences between the courses of some visual axons might exist early in the afferent pathway,⁵⁴ there is no reason to expect the early pathways of pupillomotor and visual ganglion cells to differ substantially. On a related matter, a recent report characterized a population of presumptive pupillomotor ganglion cells in primate as “giant,” with dendritic trees up to 400 µm across in central retina.⁵² Although giant by retinal standards, this dendritic extent corresponds to < 1.5 deg of visual angle, so it would have little effect on the relationship between visual perimetry and “pupil perimetry,” and even less on responses to the large stimuli used in the present experiments.

It is also worth noting that pupil responses via intrinsically photosensitive ganglion cells operate with much slower dynamics than responses to inputs through the photoreceptors, and therefore are unlikely to be active in the present experiments.

Generally speaking, the spatial agreement between visual field defects (mapped with perimetry) and pupillary field defects (mapped with pupil perimetry) is consistent with the argument that damage to visual retinal ganglion cells or their axons is correlated with damage to pupillary ganglion cells or their axons, when afferent lesions lie in or distal to the optic tract.^55–60 This correlation may well be imperfect; however, it should be noted that in assessment of glaucomatous damage, correlations between various types of visual field measurements and/or various structural measures also tend to be limited in strength.^61–65

Application of the Present Method to Glaucoma Testing

Although the properties of ganglion cells subserving the PLR are of interest in relating visual loss to pupil loss, the potential usefulness of a pupil-based test does not depend on strict similarity between the two cell populations. The norms for the pupil-based test are determined from pupil responses of normal eyes and, at least for contrast balance, the controls are partly determined from the same eye that is being tested. In like fashion, determination of a relative afferent pupillary defect is based on a comparison of two eyes of a patient who is not normal. The stimulus geometry design was based on knowledge of early visual loss in glaucoma,^4,5 and it is possible that the geometry might be improved if there are indications that pupil loss pattern differs significantly from visual loss pattern. At this time, there are no clear indications of such differences, although one study has suggested that elevated intraocular pressure may be somewhat less injurious to melanopsin-containing ganglion cells than to other ganglion cells.⁶⁶

It seems possible that the speed and ease of the present methods might lead to a useful testing modality; however, the specific uses (e.g., screening, assessment of progression, etc.) will require further assessment when cross-sectional and longitudinal data from larger numbers of normal subjects and patients become available.