New “Golden” Ratios for Facial Beauty

Abstract

In four experiments, we tested the existence of an ideal facial feature arrangement that could optimize the attractiveness of any face given its facial features. Participants made paired comparisons of attractiveness between faces with identical facial features but different eye-mouth distances and different interocular distances. We found that although different faces have varying attractiveness, individual attractiveness is optimized when the face’s vertical distance between the eyes and the mouth is approximately 36% of its length, and the horizontal distance between the eyes is approximately 46% of the face’s width. These “new” golden ratios match those of an average face.

Humans prefer attractive faces over unattractive ones (Dion, Berscheid & Walster, 1972; Eagly, Ashmore, Makhijani & Longo, 1991; Griffin & Langlois, 2006). Our preference for attractive faces exists from early infancy and is robust across age, gender and ethnicity (Rubenstein, Langlois & Roggman, 2002). The quest to define facial beauty either by the size or shape of isolated facial features (e.g., eyes or lips) or by the spatial relations between facial features dates back to antiquity, when the Ancient Greeks believed beauty was represented by a golden ratio of 1:1.618 (Atalay, 2006). Although there is little support for the golden ratio (Green, 1995), studies have shown that averaging a group of faces results in a synthetic face more attractive than any of the originals (Langlois & Roggman, 1990; Rhodes, 2006). Furthermore, a sufficiently large increase in the distance between the eyes and mouth of an individual face can make the face appear grotesque (Searcy & Bartlett, 1996). Together, these findings suggest that any individual’s facial attractiveness can be optimized when the spatial relations between facial features approximate those of the average face. However, no evidence to date has confirmed this suggestion. Here we tested this hypothesis.

Two types of alterations can be made to the spatial relations between facial features of any individual face. One may alter the vertical distance between the eyes and the mouth; this alteration results in a change in the ratio of this distance to the face length, which is measured by the distance between the hairline and the chin. The ratio is henceforth referred to as the length ratio. The other alteration is to change the horizontal distance between the pupils; this change alters the ratio between this distance and the face width, which is measured between the inner edges of the ears. This ratio is henceforth referred to as the width ratio. Here we used four experiments to obtain the optimal length and width ratios to an individual’s facial attractiveness.

Experiment 1

Experiment 1 assessed the contribution of vertical feature spacing to perceived attractiveness of an individual face. We tested the hypothesis that although different individual faces vary in attractiveness, each face has its own optimal attractiveness state defined by length ratio, and this ratio is constant across faces.

Methods

Participants

Twenty students (16 female) from the University of California, San Diego participated in exchange for course credit.

Material & Procedure

We obtained a color photograph of a Caucasian female face (320 × 240 pixels) and used Adobe Photoshop to increase or decrease the distance between the eyes and mouth of this face by 10%, 20%, 30%, 40% or 50% of the original eye-to-mouth distance. This produced 10 new faces that differed only in terms of their vertical distances between the eyes and the mouth. The internal and external facial features remain constant (i.e., identical eyes, mouth, nose, face contour, and hair). The length ratio for each of the 10 derived faces and the original face was obtained by dividing each face’s eye-to-mouth distance by its face length (measured by the distance between the hairline and the chin). The 10 derived faces and the original face were then paired with each other to create 110 face pairs with identical facial features but different length ratios. Figure 1 contains example face stimuli.

Figure 1.

Example faces with different length and width ratios; faces with an average length or width ratio are framed in black.

We repeated this procedure with an additional 9 original Caucasian female faces. Note that because each original face had a different face length and different eye-to-mouth distance, the same percentage of eye-to-mouth distance change resulted in different length ratios in each original face.

For each trial, faces were presented side by side on a 51 cm CRT-monitor with a black background at a resolution of 600 × 800 pixels and a distance of 90 cm, with each face in the pair presented once on the right and once on the left to counter balance display location. Participants judged which face in each randomly presented pair appeared more attractive. Each face pair remained on display until the participant responded. Because we were interested in whether there exists an optimal length ratio for each individual face given its unique facial features, participants never judged the relative attractiveness of faces with different facial features.

Paired comparison data for each original face and its 10 derivations were converted to an attractiveness score on a Thurstonian scale, a well-established psychophysical metric for measuring attitudes (Thurstone, 1972). The attractiveness scores thus represented the relative attractiveness of the original faces and their derived faces, with higher scores indicating greater attractiveness. Because a Thurstonian score is standardized, the attractiveness scores for one original face and its 10 derived faces with identical facial features are comparable with those of another original face and its derived faces even though each set of faces had different facial features.

Results & Discussion

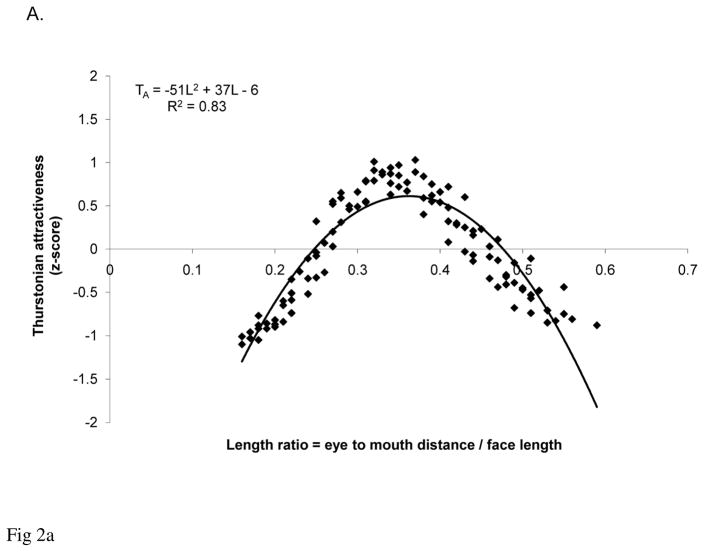
Using a regression analysis to determine the exact relation between the attractiveness score and length ratio, we found that facial attractiveness follows a curvilinear function with length ratio. This is displayed in Figure 2A. When L represents a given length ratio, the Thurstonian attractiveness (T_A) is represented by

Figure 2.

Figure 2A. Thurstonian attractiveness scores as a function of length ratios in Experiment 1.

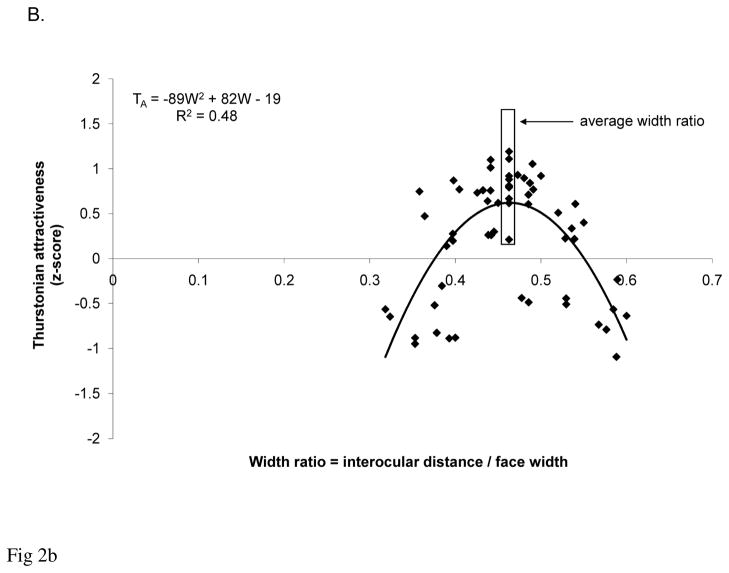
Figure 2B. Thurstonian attractiveness scores as a function of width ratios while holding the length ratio constant at the optimal level in Experiment 3.

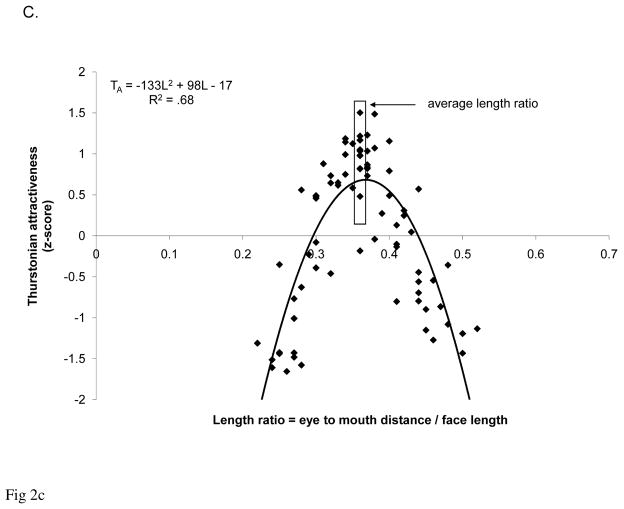
Figure 2C. Thurstonian attractiveness scores as a function of length ratios while holding the width ratio constant at the optimal level in Experiment 4.

$${\text{T}}_{\text{A}}=-51{\text{L}}^2+37\text{L}-6$$ (Equation 1)

This function was a strong predictor of Thurstonian attractiveness, F (107, 2) = 252, R² = .83, p < .001. The length ratio for the maximally attractive face according to Equation 1 was .36. This ratio is also the length ratio obtained by averaging the length ratios of 40 Caucasian female faces, M = .36, SD = .017. This suggests that the observed optimal length ratio for each individual face may reflect participants’ preference for an average vertical spacing between facial features. However, we needed direct evidence to support this suggestion because participants were never asked to judge the attractiveness of faces with a length ratio of .36. Therefore, we ran Experiment 2 on a new set of faces including average length ratios to address this issue directly.

Experiment 2

Methods

Participants

Thirty-four university students participated (30 female).

Material & Procedure

The procedure for Experiment 2 was identical to that of Experiment 1 except for the face stimuli. Here we applied the procedure from Experiment 1 to 10 new Caucasian female faces (320 × 240 pixels). For each original face, we increased or decreased the eye-to-mouth distance by 10%, 20%, or 30% of the original face’s eye-to-mouth distance to create 6 new faces with different length ratios. We obtained an additional face by setting the length ratio at .36, the average length ratio based on 40 Caucasian female faces as described above. Thus, we created 7 new faces for each original face. Then, the 7 derived faces and the original face were paired with each other as in Experiment 1.

Results & Discussion

Experiment 2 completely replicated the findings of Experiment 1: Attractiveness scores again followed a curvilinear function with the length ratio,

$${\text{T}}_{\text{A}}=-90{\text{L}}^2+66\text{L}-12$$ (Equation 2)

Length ratio and length ratio² were significant predictors of attractiveness, F (77, 2) = 84, R² = .69, p < .001. The optimal length ratio for attractiveness was .37, despite differences in facial features. This ratio was not significantly different from the average length ratio of .36, p > .05. Faces with an average length ratio tended to be rated as more attractive than faces with other length ratios. This is further supported by the finding that attractiveness scores for faces without an average length ratio were significantly less than the mean attractiveness score for the faces with an average length ratio, t (69) = −9.7, p < .001.

Experiments 3

Experiments 3 & 4 examined whether there exists an optimally attractive state for an individual face in terms of both length and width ratios. To test this possibility, in Experiment 3, we systematically varied width ratio by altering the horizontal distance between the eyes while keeping the length ratio constant at the optimal level of .36.

Methods

Participants

Thirty university students (21 female) participated.

Material & Procedure

The procedure was identical to that used in Experiment 1 except for the face stimuli. First we selected the 10 faces from Experiment 2 with average length ratios (.36) but different facial features. For each of these faces, we increased or decreased the horizontal distance between the eyes by 10% or 20% of the original interocular distance. We also created an additional face with the average width ratio of .46 (based on 40 Caucasian female faces: M = .46, SD = .022). This resulted in 5 faces plus the original one, each with the same facial features and length ratio but different width ratios. Faces were then paired as in Experiment 1.

Results & Discussion

Figure 2B displays the relation between deviation from the average width ratio and attractiveness when the length ratio was held constant at the optimal level. Results indicated that facial attractiveness also follows a curvilinear function with the width ratio, F (57, 2) = 26, R² = .48, p < .001. When the width ratio is represented by W,

$${\text{T}}_{\text{A}}=-89{\text{W}}^2+82\text{W}-19$$ (Equation 3)

Based on Equation 3, when an individual face’s length ratio is already optimal, the optimal width ratio maximizing its attractiveness is .46, the same as the average width ratio. Similar to Experiment 2, attractiveness scores for faces without an average width ratio were significantly less than the mean attractiveness score for the faces with an average width ratio, t (49) = −7.0, p < .001.

Experiment 4

In Experiment 4, we systematically varied the length ratios of faces by altering the vertical distance between the eyes and the mouth while keeping the width ratio constant at the optimal level of .46.

Methods

Participants

Forty-two university students (25 female) participated.

Material & Procedure

The procedure was identical to that of Experiment 1 except for the face stimuli. We first altered the horizontal distance between the eyes of each of the 10 original faces used in Experiment 2 to make 10 faces with a width ratio of .46, the width ratio of an average face based on 40 Caucasian female faces as described above. After setting each face to the optimal width ratio, we then applied the changes in eye-to-mouth distances from Experiment 2 to derive face stimuli with different length ratios but identical facial features.

Results & Discussion

Figure 2C displays the relation between deviation from the average length ratio and attractiveness when the width ratio is held constant at .46. Results completely replicated those of Experiment 2 - facial attractiveness followed a curvilinear function with length ratio, F (77, 2) = 80.00, R² = .68, p < .001,

$${\text{T}}_{\text{A}}=-133{\text{L}}^2+98\text{L}-17$$ (Equation 4)

This equation revealed that when an individual face’s width ratio is already optimal, the optimal length ratio that maximizes its attractiveness is .37. This ratio did not differ significantly from .36, the average length ratio, p > .05. Attractiveness scores for faces without an average length ratio were significantly less than the mean attractiveness score for the faces with an average length ratio, t (69) = −9.1, p < .001. Given that the R² values also did not greatly vary between the current experiment and Experiment 2 (.68 vs. .69), these results further suggest that preference for an ideal length ratio is independent of the width ratio.

General Discussion

In four experiments, we revealed that for each individual face, there exists an optimally attractive state in terms of both length and width ratios. When the face’s eye-to-mouth distance is 36% of the face length and interocular distance is 46% of the face width, the face reaches its optimal attractiveness given its unique facial features. Further, although the absolute level of attractiveness may vary with differences in facial features, the optimal length and width ratios remain constant. These optimal, “golden” ratios correspond with those of an average face. Critically, since we never collapsed the data across faces, this preference for average ratios reflects a true preference for the average and not a regression toward the mean. These results may explain some basic daily observations, such as why some hairstyles can make an unattractive face appear more attractive or vice versa. Changing one’s hairstyle may alter the perceived face length or face width, as well as their related length and width ratios, therefore affecting the perceived attractiveness of the face.

The present findings provide an important step forward in our understanding of facial attractiveness. Many previous experiments on attractiveness involved comparing faces that differed in both facial features and spatial relations. But the presence of features that vary in attractiveness could obscure any effect of variation in feature spatial relation on attractiveness. Also, prior research comparing an average face to individual faces failed to discover the ideal length and width ratios for any individual face because the averaging process tends to not only average the spatial relations between facial features but also smoothes the facial features and skin texture (Rhodes, 2006). This smoothing effect could artificially increase the attractiveness of the average face, obscuring the effect of average spatial relations on facial attractiveness.

Our study is uniquely able to demonstrate the optimal ratios for attractiveness of individual faces because we make attractiveness comparisons between faces with the same features but different spatial relations, thus controlling for the attractiveness of individual features. Specifically, in each experiment we used Thurstonian scaling to create an attractiveness score for each original face and each of the subsequent derived faces. These scores are similar to z-scores. Therefore, each identity had attractiveness scores associated with low length or width ratios, typical length or width ratios, and high length or width ratios. Then we plotted the attractiveness score by the length or width ratio for each face and fit a curvilinear function to the data. With the use of this procedure, we were able to identify the optimal length and width ratios for individual facial beauty, which have attracted a tremendous amount of pursuit but yet eluded discovery for centuries. Furthermore, the present findings suggest that although different faces vary greatly in absolute attractiveness, for any particular face, there is an optimal spatial relation between facial features that will reveal its intrinsic beauty.

The ancient Greeks believed the golden ratio, or phi, represented the essence of beauty. Yet here we find a new golden ratio, that is the average length and width ratios. So how do our ratios compare to a face with the classic golden ratios? To test this we created a face with classic “golden sections” based on the face shown in Figure 1. This occurred when the face’s length minus its eye to mouth distance, divided by the eye to mouth distance equalled phi or approximately 1.16. A similar golden ratio existed for interocular distance and face width. In this face, both the length and width classic golden ratios equalled .38. A one-sample t-test confirmed that our preferred length ratios from Experiments 1, 2, and 4 were significantly different from the classic golden ratio of .38, t(2) = −8.63, p < .05, and our preferred width ratio of .46 was also significantly different from the classic golden ratio of .38. Therefore, our optimal length and width ratios truly are the “new” golden ratios.

It should be noted that the optimal spatial relations found in the present study can also coexist with preferences for sexually dimorphic features. A woman who has large lips, suggesting a strong mating potential, with average length and width ratios will always be more attractive than a woman with narrow lips and average length and width ratios. It is unknown, however, whether the preference for average length and width ratios is stronger than the desire for a pronounced sexually dimorphic trait. In other words, a woman with large lips and unattractive length and width ratios may or may not be preferred to a woman with narrow lips and ideal length and width ratios. Future research is necessary to assess the nature of this trade-off.

Since our ideal length and width ratios were obtained only in female faces it is possible that they represent a preference for average female ratios only, with a separate ratio preferred for males. Similarly, variations in the average across race and age may also produce different ideal length and width ratios. In addition, adaptation can cause a shift in perceived attractiveness that is thought to correspond with a shift in the perceived average (Rhodes, Jeffery, Watson, Clifford & Nakayama, 2003). Therefore, we would also expect the optimal ratios to shift with adaptation. In support of different ideal ratios for male and female faces, Danel and Pawlowski (2007) reported that eye-mouth-eye angle is a sexually dimorphic trait in which smaller angles are preferred in male faces, while larger angles are preferred in female faces. Unfortunately, ideal eye-mouth-eye angles were never obtained. Only the average female and average male eye-mouth-eye angles were assessed, so it is unknown whether eye-mouth-eye angle is truly a sexually dimorphic feature (i.e. angles greater than average are preferred for females while angles less than average preferred for males).

By definition, eye-mouth-eye angle involves both horizontal and vertical components. Yet, our results suggest that the preference for an average length ratio is independent of the width ratio. Therefore, it is important to note that despite the similarity between the two measures, they may actually measure two very different aspects of the face. While eye-mouth-eye angle provides information on the spatial relations between internal facial features, our measures assess the relation between the internal features and the external facial contour. Since faces are perceived holistically, it is important to consider the facial elements in the context of the whole face. It is possible for the length and width ratios to vary, while eye-mouth-eye angle stays the same, and vice versa. Therefore, we suggest that in the context of the whole face length ratios and width ratios appear independent, but within the localized area of the eyes and mouth, there may be an interaction between length and width.

Why should we find a face with an average length and width ratio attractive? Two existing theories provide explanations at two different levels (Langlois & Roggman, 1990). At the evolutionary level, it has been suggested that humans prefer to reproduce with other healthy mates (Jones, Little, Penton-Voak, Tiddeman, Burt & Perrett, 2001). Generations of healthy mate selection may act as an evolutionary “averaging” process. This process leads to the propagation of healthy individuals with physical characteristics, including faces that approximate the population average. As a result, we are biologically predisposed to find average faces attractive. At the cognitive level, it is well established that after exposure to a series of exemplars from one object category, we form a prototype (i.e., an average) for this category. One robust consequence of prototype formation is that we find the prototype more attractive than any individual category members because the prototype is easier to process. Due to this same cognitive averaging mechanism, the average face is perceived as more attractive than any individual face (Rubenstein, Kalakanis & Langlois, 1999). We suggest that while the two theories provide different levels of explanation, they may work together to account for our preferences for the optimal length and width ratios for facial beauty. The evolutionary process predisposes us to find average length and width ratios attractive; the cognitive process prescribes what the average length and width ratios are by averaging the ratios of individual faces we have encountered to date.

It should be noted that further studies are needed to confirm the last suggestion because 40 faces are little compared to several decades of exposure to female faces. However, evidence does suggest that an average of so few faces may function as a proxy for the facial prototype (e.g. Langlois & Roggman, 1990; Levin, 2000; Perrett, Lee, Penton-Voak, Rowland, Yoshikawa, Burt, Henzi, Castles & Akamatsu, 1998; Rhodes & Jeffery, 2006; Rhodes, Lee, Palermo, Weiss, Yoshikawa, Clissa, Williams, Peters, Winkler & Jeffery, 2005; Rubenstein et al., 1999; Valenzano, Mennucci, Tartarelli & Cellerino, 2006). For example, Langlois and Roggman (1990) demonstrated than an average of 32 faces or 16 faces is perceived as more attractive than any individual face – regardless of the faces used to create the average. The same, however, cannot be said for composites involving fewer than 16 faces. Thus, our participants’ preference for faces with length and width ratios corresponding to those of a 40 face average suggests that these ratios may indeed approximate those of a female face prototype.