A RICIAN MIXTURE MODEL CLASSIFICATION ALGORITHM FOR MAGNETIC RESONANCE IMAGES

Abstract

Tissue classification algorithms developed for magnetic resonance images commonly assume a Gaussian model on the statistics of noise in the image. While this is approximately true for voxels having large intensities, it is less true as the underlying intensity becomes smaller. In this paper, the Gaussian model is replaced with a Rician model, which is a better approximation to the observed signal. A new classification algorithm based on a finite mixture model of Rician signals is presented wherein the expectation maximization algorithm is used to find the joint maximum likelihood estimates of the unknown mixture parameters. Improved accuracy of tissue classification is demonstrated on several sample data sets. It is also shown that classification repeatability for the same subject under different MR acquisitions is improved using the new method.

1. INTRODUCTION

Classification methods based on parametric statistical models have been previously proposed and are in widespread use to classify magnetic resonance (MR) brain images into three dominant tissue classes: cerebrospinal fluid (CSF), gray matter (GM), and white matter (WM) [1]. Finite mixture models (FMM’s), upon which these methods are based, use the assumption that the intensity of any voxel is derived from a discrete set of conditional distributions. For MR images, it is most commonly assumed that the distributions are Gaussian with their means, variances, and prior probabilities assumed to be deterministic but unknown variables. After estimating the model parameters using maximum likelihood, one can generate a posterior probability of a voxel belonging to each tissue class, which can then be used as an estimate of a “soft segmentation” of the voxels or can be maximized to establish a “hard segmentation”.

Practical application of these principles is best carried out using a model of spatial smoothness, most notably a Markov random field (MRF) [2], the expectation maximization algorithm [3] for numerical efficiency, and a model of intensity inhomogeneity to model the radio frequency coil inhomogeneity [4]. The Expectation Maximization Segmentation (EMS) [5] and FMRIB’s Automated Segmentation Tool (FAST) [6] are two highly successful implementations of these principles. Though not based on the strict probabilistic model of these noted methods, the approach called FANTASM [7] incorporates similar principles within a fuzzy C-means (FCM) [8] framework and yields similar results.

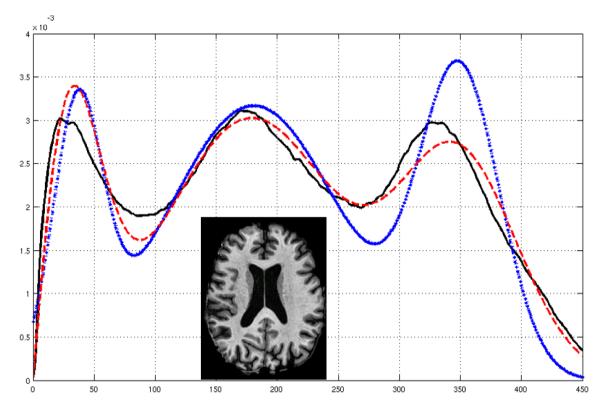
It is well known that signals in MR images are Rician in distribution [9], and therefore the standard Gaussian model really only applies in the high signal-to-noise ratio (SNR) regime [10]. For example, Fig. 1 demonstrates visually that the Rician FMM fit is a better fit than that of a Gaussian FMM for the histogram of a real MR image. Quantitatively, this is confirmed using the Kullback-Leibler (KL) distance between the fit and the true histogram, which in this example yields 0.0418 for the Gaussian FMM and 0.0097 for the Rician FMM.

Fig. 1.

Histogram, shown in solid black, of an MP-RAGE image (inset) overlapped with a fitted Gaussian pdf (dotted blue) and a Rician pdf (dashed red).

In this paper, we present a new classification method that follows the principles of an Expectation-Maximization (EM) algorithm—including bias field correction and an MRF model—with a Rician FMM model for the observed image. In a validation study involving 20 normal subjects, we show that our method performs better than both FAST and FANTASM. In a second validation study involving five normal subjects, we demonstrate improved consistency in segmentation when MR images are acquired from the same subject using two different T1-weighted pulse sequences (SPGR and MP-RAGE).

2. BACKGROUND

MR image intensities are in fact the magnitudes of underlying complex data that are acquired in separate in-phase and quadrature channels. The real and imaginary parts are modeled as being independently distributed Gaussians with means A_R and A_I, respectively, with the same variance σ². Thus, the image intensity y is a Rician random variable with probability density function (pdf)

$$f_R(y\mid v,\sigma )=\frac{y}{{\sigma }^2}{e}^{-\left(\frac{y^2+v^2}{2{\sigma }^2}\right)}{I}_0\left(\frac{yv}{{\sigma }^2}\right),y>0,$$ (1)

where $v=\sqrt{{A_R}^2+{A_I}^2}$ and I_p is the modified p^th order Bessel function of the first kind. We substitute y_i for y, with i referring to the i^th voxel. Let z_ij be the indicator function for the i^th voxel being in the j^th class for j = 1, …, K. In our case the classes are CSF, GM, and WM and therefore K = 3. We also have v_j and σ_j for each class and the collection of such parameters for all classes is ɵ = {v_j, σ_j}.

The classification problem can now be represented as an estimation problem where the underlying segmentation z_ij is calculated from the observed intensity y_i. The segmentation can be computed if v_j and σ_j are known, while v_j and σ_j is known only when z_ij is known. This setup leads naturally to use of the EM algorithm to find the maximum likelihood (ML) estimate $\widehat{\Theta }=\underset{\Theta }{\mathrm{argmax}}\log f(y_i\mid \Theta )$. The EM algorithm iteratively estimates the segmentation z_ij based on current estimates of the parameters and then updates the parameters using the current estimate of z_ij. This is described in the two-step process:E Step : At the m^th iteration, we compute,

$$Q(\Theta \mid {\Theta }^{\left(m\right)})=E\left[\log f(z\mid \Theta )\mid y,{\Theta }^{\left(m\right)}\right]$$

M Step : Find new estimation of parameters from

$${\Theta }^{(m+1)}=\underset{\Theta }{\mathrm{argmax}}Q(\Theta \mid (\Theta {)}^{\left(m\right)})$$

The algorithm converges based on the difference of successive total log-likelihoods being small.

3. RICIAN MIXTURE MODEL

We now develop the EM classification algorithm for the Rician mixture model given by

$$f(y_i\mid \Theta ,z)=\prod _{j=1}^K{\left[{\pi }_{ij}{f}_R(y_i\mid \Theta )\right]}^{z_{ij}},$$ (2)

where f_R is given in (1) and π_ij is the prior probability of the i^th voxel belonging to the j^th class. We can incorporate spatial regularization and bias field correction into the likelihood function as follows

$$f(y_i\mid \Theta ,z)=\prod _{j=1}^K{\left[f(z_{ij}\mid z_{N_i},\Theta )f_R(b_i{y}_i\mid \Theta )\right]}^{z_{ij}},$$ (3)

where N_i is a neighborhood of the i^th voxel. Here b_i is a low frequency smoothly varying polynomial field used for bias correction and is defined by $\sum _{s=0}^L{\alpha }_s{P}_s\left(i\right)$, where P_s(i) is an s^th order orthogonal polynomial family, L is the maximum order (taken as 3 in our experiments), and α_s are bias field correction coefficients. Spatial consistency is achieved by replacing the fixed prior probability π_ij with the spatially varying prior f(z_ij|z_Ni, ɵ) [11], defined as:

$$\frac{1}{\sqrt{2\pi }{\beta }_j}\exp \left\{-\frac{\sum _{k\in N_i}{\left(\right(z_{ij}-z_{ik}\left)z_{ij}\right)}^2}{2{\beta }_j^2}\right\},$$ (4)

where β_j controls the smoothness of the MRF for the j^th class. If the segmentation of the i^th voxel is the same as the segmentation of the voxels in N_i, then f(z_ij|y_Ni, ɵ) ≈ 1. Otherwise, the i^th voxel becomes a potential noisy one. A large spatial prior is imposed if z_ij is small, and conversely a small spatial prior for large z_ij. We note the expanded collection of variables ɵ = {v_j, σ_j, β_j, α_s}.

We use a mean field approach [5], to solve our EM algorithm. The E step requires computation of E[z_ij|y_i, ɵ]. Since z_ij is a binary random variable with values 0 or 1, its expectation is the probability of i^th voxel belonging to the j^th class P(z_ij = 1|y_i, ɵ), which is the same as the conditional expectation w_ij, defined as $w_{ij}^{\left(m\right)}\equiv E[z_{ij}\mid y_i,{\Theta }^{\left(m\right)}]$ for the m^th iteration of the EM algorithm. Thus, the E step becomes:

$$w_{ij}^{(m+1)}\approx \frac{\widehat{f}\left(z_{ij}\mid z_{N_i},{\Theta }^{\left(m\right)}\right)f_R\left(y_i\mid {\Theta }^{\left(m\right)}\right)}{\sum _{j=1}^K\widehat{f}\left(z_{ij}\mid z_{N_i},{\Theta }^{\left(m\right)}\right)f_R\left(y_i\mid {\Theta }^{\left(m\right)}\right)},$$

where $\widehat{f}(z_{ij}\mid z_N,{\Theta }^{\left(m\right)})$ is modified from (4) by the mean field idiom and is given by

$$\frac{1}{\sqrt{2\pi }{{\beta }_j}^{\left(m\right)}}\exp \left\{-\frac{\sum _{k\in N_i}{\left((w_{ij}^{\left(m\right)}-w_{ik}^{\left(m\right)})w_{ij}^{\left(m\right)}\right)}^2}{2{\beta }_j^{{\left(m\right)}^2}}\right\}.$$

In essence this replaces $z_{ij}^{\left(m\right)}$ in (4) with its expectation $w_{ij}^{\left(m\right)}$.

In the M step, of the EM algorithm, we update ɵ, thus updating $v_j^{(m+1)}$, ${\sigma }_j^{(m+1)}$, and ${\beta }_j^{(m+1)}$ with,

$$v_j^{(m+1)}=\frac{\sum _i{w}_{ij}^{\left(m\right)}{y}_i{b}_i^{\left(m\right)}{\gamma }_{ij}^{\left(m\right)}}{\sum _i{w}_{ij}^{\left(m\right)}}$$ (5)

$$\begin{array}{cc}\hfill & {\sigma }_j^{{(m+1)}^2}=\hfill \\ \hfill & \frac{\sum _i{w}_{ij}^{\left(m\right)}\left(b_i^{{\left(m\right)}^2}{y}_i^2+v_j^{{(m+1)}^2}-2y_i{b}_i^{\left(m\right)}{v}_j^{(m+1)}{\gamma }_{ij}^{\left(m\right)}\right)}{2\sum _i{w}_{ij}^{\left(m\right)}}\hfill \end{array}$$ (6)

$${\beta }_j^{\left(m\right)}=\sqrt{\frac{\sum _i\left(\sum _{k\in N_i}{\left((w_{ij}^{\left(m\right)}-w_{ik}^{\left(m\right)})w_{ij}^{\left(m\right)}\right)}^2\right)}{N}}$$ (7)

Here, N is the number of voxels in the image domain and

$${\gamma }_{ij}^{\left(m\right)}=\frac{I_1\left({\iota }_{ij}^{\left(m\right)}\right)}{I_0\left({\iota }_{ij}^{\left(m\right)}\right)}\text{where}{\iota }_{ij}^{\left(m\right)}=\frac{y_i{b}_i^{\left(m\right)}{v}_j^{\left(m\right)}}{{\sigma }_j^{{\left(m\right)}^2}}.$$

To update the bias field coefficients ${\alpha }_s^{(m+1)}$, we solve a set of linear equations generated by setting the first derivative of the log-likelihood with respect to α_s to zero. For each s = 0, …, L, the linear equations are given by:

$$\begin{array}{cc}\hfill \sum _{t=0}^L{\alpha }_t^{(m+1)}& \sum _i{y}_i^2{P}_s\left(i\right)P_t\left(i\right)\sum _{j=1}^K\frac{w_{ij}^{\left(m\right)}}{{\sigma }_j^{{\left(m\right)}^2}}=\hfill \\ \hfill & \sum _i\left[\frac{1}{b_i^{\left(m\right)}}+y_i\sum _{j=1}^k{w}_{ij}^{\left(m\right)}\frac{v_j^{\left(m\right)}{\gamma }_{ij}^{\left(m\right)}}{{\sigma }_j^{{\left(m\right)}^2}}\right]P_s\left(i\right)\hfill \end{array}$$

We solve these equations simultaneously to determine the ${\alpha }_s^{(m+1)}$ values. We continue iterating through the EM algorithm until the increases in log-likelihood, of successive iterations, are below a threshold. The final values of the w_ij’s are the desired soft classification for the i^th voxel with respect to the j^th class. The hard segmentation for the i^th voxel is given by $z_i=\underset{j}{\max }\left\{w_{ij}\right\}$.

4. VALIDATION

We conducted two experiments to validate our method. The first experiment involves T1-weighted images of 20 normal healthy subjects from the Internet Brain Segmentation Repository (IBSR) [12]. These data sets have manual whole head segmentations, which we used to compare against the hard segmentations of FAST, FANTASM, and our Rician mixture model Classifier (RC). Tab. 1 shows the Dice coefficients between the manual segmentations and the hard segmentation from each algorithm. The IBSR data pool formed two very distinct groups, which we call Group 1 and Group 2. In Group 1, comprising 16 subjects, all three methods performed well though RC performed slightly better. In Group 2, comprising 4 subjects, the WM Dice coefficients were below 0.60 for all methods indicating a gross failure for all three methods, although RC was still the best. Further investigation revealed that the inhomogeneity fields for Group 2 subjects were not smoothly varying, which led to gross bias field estimation errors as well as classification errors. With the Group 1 population, we considered the null hypothesis that the Dice coefficient of RC is less than that of FANTASM. The resultant p-values of a t-test for GM, WM, and WT are 0.000005, 0.0009, and 0.0002, respectively. A similar hypothesis and comparison between our Rician mixture model and FAST yields p-values of 0.0018, 0.3371, and 0.0381. Thus, RC yields statistically significant improvement on overall tissue segmentation.

Table 1.

IBSR comparison between GM, WM, and a volume weighted total (WT) for Dice coefficients between manual segmentations and hard segmentation by each of FAST (FT), FANTASM (FN), and our Rician mixture model Classifier (RC).

		Group 1		Group 2
		Mean	Std. Dev.	Mean	Std. Dev.
GM	FT	0.9002	0.0279	0.5860	0.1642
	FN	0.8941	0.0343	0.6081	0.1575
	RC	0.9132	0.0313	0.6115	0.1578
WM	FT	0.8272	0.0325	0.3478	0.1055
	FN	0.8095	0.0832	0.3239	0.1239
	RC	0.8320	0.0660	0.3452	0.1172
WT	FT	0.8738	0.0306	0.5162	0.1106
	FN	0.8642	0.0484	0.5271	0.1254
	RC	0.8842	0.0420	0.5327	0.1212

We demonstrate repeatability of our method in the second experiment, by using two different acquisitions, one SPGR and one MP-RAGE, of five normal healthy subjects. Ideally, we expect to be able to generate identical segmentations for the same subject on the differing acquisitions. Tab. 2 shows the Dice coefficients between the SPGR and MP-RAGE segmentations. The p-values of the CSF, GM, and WM Dice coefficients for FAST and RC comparison are 0.0129, 0.017, and 0.0324. Between FANTASM and RC the p-values are 0.0003, 0.0003, and 0.0002, which again demonstrates statistically significant improvement. Tab. 2 also shows that the CSF segmentation has improved substantially on MP-RAGE, while it is nominally so on SPGR.

Table 2.

CSF, GM, and WM Dice coefficients between SPGR and MP-RAGE hard segmentations of five subjects, see Tab. 1 for abbreviations.

		Subject
		1	2	3	4	5
CSF	FT	0.800	0.176	0.169	0.155	0.148
	FN	0.632	0.626	0.570	0.590	0.394
	RC	0.823	0.813	0.799	0.785	0.712
GM	FT	0.859	0.468	0.340	0.290	0.319
	FN	0.691	0.714	0.698	0.681	0.603
	RC	0.848	0.843	0.852	0.820	0.832
WM	FT	0.923	0.889	0.872	0.884	0.864
	FN	0.880	0.918	0.880	0.878	0.855
	RC	0.918	0.942	0.921	0.912	0.891

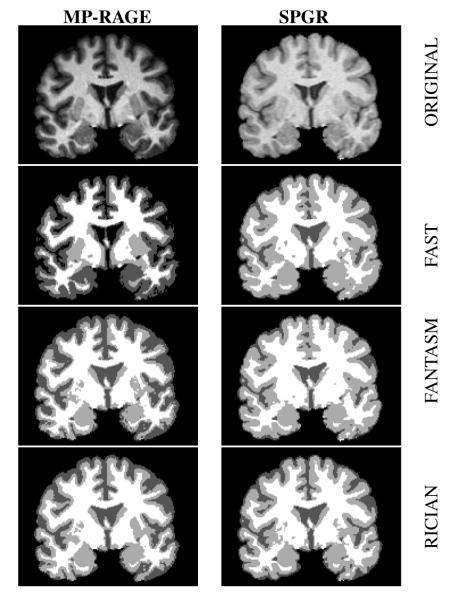
It is observed in Tab. 2 that the Dice coefficients are generally very small in the FT and FN estimates of CSF. The reason for this is that the intensity of CSF is very small in the MP-RAGE images (see Fig. 2). As a result, the Gaussian approximation is particularly inappropriate in this case yielding poor results. RC is a better model for this case, yielding better, and more consistent, results.

Fig. 2.

SPGR and MP-RAGE data for a subject in our second experiment and the resultant hard segmentations from FAST, FANTASM, and our Rician mixture model.

5. CONCLUSION

We proposed a fully automatic Rician mixture model classification algorithm and demonstrated its usefulness for tissue classification. It was shown to be superior, especially on MP-RAGE images, to existing state of the art segmentation algorithms which use an underlying Gaussian (or Gaussian-like in the case of FANTASM) distribution model. It was also shown to be more consistent at segmenting different T1-weighted acquisitions of the same subject.