Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2009 Nov 27;105(2):233–247. doi: 10.1093/aob/mcp278

Are the common assimilate pool and trophic relationships appropriate for dealing with the observed plasticity of grapevine development?

B Pallas 1,2, A Christophe 3, J Lecoeur 1,*
PMCID: PMC2814752  PMID: 19946042

Abstract

Background and Aims

Models based on the consideration of plant development as the result of source–sink relationships between organs suffer from an inherent lack of quantification of the effect of trophic competition on organ growth processes. The ‘common assimilate pool theory’ underlying many such models is highly debatable.

Methods

Six experiments were carried out in a greenhouse and outdoors with two grapevine cultivars and with 12 management systems, resulting in different types of plant architecture. Ten variables were used to quantify the impact of variations in assimilate supply and topological distances between sources and sinks on organogenesis, morphogenesis and biomass growth.

Key Results

A hierarchy of the responses of these processes to variations in assimilate supply was identified. Organ size seemed to be independent of assimilate supply, whereas both organogenesis and biomass growth were affected by variations in assimilate supply. Lower levels of organ biomass growth in response to the depletion of assimilate supplies seemed to be the principal mechanism underlying the plasticity of plant development in different environments. Defoliation or axis ablation resulted in changes in the relationship between growth processes and assimilate supply, highlighting the influence of non-trophic determinants. The findings cast doubt on the relevance of ‘the common assimilate pool theory’ for modelling the development of grapevine.

Conclusions

The results of this study suggest new formalisms for increasing the ability of models to take plant plasticity into account. The combination of an ecophysiological model for morphogenesis taking environmental signals into account and a biomass driven model for organogenesis and biomass allocation taking the topological distances between the sources and the sinks into account appears to be a promising approach. Moreover, in order to simulate the impact of agronomic practices, it will be necessary to take into account the non-trophic determinants of plant development such as hormonal signaletics.

Key words: Biomass growth, branching system, common assimilate pool, morphogenesis, organogenesis, source–sink, grapevine, Vitis vinifera

INTRODUCTION

Plant development is strongly affected by trophic competition, through the source–sink relationships between organs (Wardlaw, 1990). Trophic competition affects all processes of organ development, including organogenesis (Valantin et al., 1999), morphogenesis (Costes et al., 2000) and biomass accumulation (Heuvelink and Buiskool, 1995). Recently, several functional structural plant models, such as GreenLab (Letort et al., 2008) and Ecomeristem (Luquet et al., 2006), have been proposed for the modelling of plant development in response to trophic competition through the existing source–sink relationships at the organ scale. Nevertheless, most of these models do not take into account the impact of trophic competition on the various developmental processes. This quantification of the effect of trophic competition is necessary to improve model performance, because the development of the entire plant system is the result of different growth processes operating at different levels of organization (Fourcaud et al., 2008; Mathieu et al., 2009). This quantification is of particular interest for grapevine, which has been shown to display highly plastic development in response to trophic competition (Lebon et al., 2004; Pallas et al., 2008). Grapevine shoots have a hierarchical structure (primary and secondary axes), with complex connections between the various organs tending to modify the effects of trophic competition (Pallas et al., 2009). Finally, in vineyards, grapevine development is strongly modified by agronomic practices, which tend to modify the existing relationships between the different organs (Rives, 2000).

In several modelling approaches, the effect of trophic competition in plants is considered to be identical for all the developing organs. These models do not take into account the topological distance between the sources and sinks of assimilates in the simulation of biomass fluxes (e.g. Letort et al., 2008). In this approach, based on the so-called ‘common assimilate pool’ (Heuvelink, 1995), the ability of developing organs to attract the available plant biomass does not depend on their topological position on the plant. Assimilate partitioning between organs is considered to depend principally on sink strength (i.e. the ability to attract assimilates; Ho, 1988), and the timing of development (Letort et al., 2008). Nevertheless, previous studies have shown that the partitioning of assimilates may also depend on the topological distance between sources and sinks (Lacointe, 2000). Studies in grapevine have highlighted the importance of this source–sink distance for the estimation of biomass fluxes (Hale and Weaver, 1962). Nevertheless, the impact of source–sink distance on organ development has yet to be definitively demonstrated and quantified. For grapevine, there seems to be a need to increase our knowledge of this aspect, to improve our understanding of the impact of the agronomic practices modifying these distances (Jackson and Lombard, 1993).

In several models (Drouet and Pagès, 2006; Luquet et al., 2006; Letort et al., 2008) the development of vegetative organs has been broken down into three different processes: initiation (organogenesis), elongation or expansion (morphogenesis) and biomass growth. Organogenesis processes have been studied in detail in grapevine, and have been described using a constant rate and a duration of development for all axes (Lebon et al., 2004; Louarn et al., 2007). As observed in many species, the number of organs initiated and expanded on the primary axis is linearly correlated with temperature (for Pisum sativus, Turc and Lecoeur, 1997). No effect of trophic competition induced by differences in cluster loads or environmental conditions has been observed for primary axis development (Lebon et al., 2006; Pallas et al., 2008). By contrast, secondary axis development is strongly affected by trophic competition (Pallas et al., 2008). Morphogenetic processes have also been analysed in studies of internode and leaf development in many species, based on analyses of the duration and rate of development (for grapevine, Schultz and Matthews, 1988; for sunflower, Helianthus annuus, Dosio et al., 2003). These morphogenetic processes appear to be affected by trophic competition in many species with a determinate pattern of development (for Arabidopsis thaliana, Christophe et al., 2008). For grapevine, no clear effect of trophic competition on organ morphogenesis has yet been identified (Lebon et al., 2004; Pallas et al., 2008). The relative plasticity of organogenesis and morphogenesis therefore seem to depend on the species. In plants with indeterminate patterns of development, such as pea (Turc and Lecoeur, 1997), kiwi fruit (Seleznyova et al., 2002) and white clover (Belaygue et al., 1996), total leaf area depends more on leaf number than on individual leaf area. In plants with determinate patterns of development, such as maize (Fournier and Andrieu, 2000) and sunflower (Dosio et al., 2003), total leaf area seems to be highly dependent on individual leaf area. Organ biomass growth has been less intensively studied than organ morphogenesis, due to its apparently lower interest for plant development. Indeed, leaf area or axis length are generally considered the principal traits for studies of whole-plant development (Granier and Tardieu, 2009). Thus, in modelling approaches, organ mass and size are generally connected through simple allometric relationships (Letort et al., 2008). Secondary growth of the internodes is modelled principally with the ‘pipe model theory’ in functional structural plant models (Mäkelä, 1986), making it possible to connect internode mass to plant leaf area without considering the trophic status of the plant. In many functional structural plant models, specific leaf area depends on the position of the leaf on the plant (Luquet et al., 2006) or on its age (Christophe et al., 2008). Few modelling approaches (e.g. Drouet and Pagès, 2006) take into account the impact of plant trophic status on specific leaf area. Nevertheless, organ biomass growth has been shown to be a major underlying process modulating the impact of trophic competition in plants by affecting specific leaf area or internode linear weight (Sultan, 2000). The plasticity of these underlying variables makes it possible for plants to develop in many different environments, for example, by increasing specific leaf area when levels of photosynthetically active radiation are low (Meziane and Shipley, 1999) or by decreasing internode linear weight in conditions of high population density (Donohue et al., 2000).

In this study, the aim was to analyse the impact of variations in source–sink relationships on grapevine plant development by acting directly on the source activity. A wide range of experimental conditions was set up by varying levels of photosynthetically active radiation, to evaluate the plasticity of the various processes (organogenesis, morphogenesis and biomass growth) in response to trophic competition. These processes were studied for internodes, leaves, roots and clusters. Local defoliation was also carried out to quantify the relative contribution of assimilate supply and changes in architecture to the observed plasticity of the growth processes. These modifications to plant architecture were made with the aim of evaluating the relevance of the ‘common assimilate pool’ assumption to model grapevine development. Two cultivars used worldwide – ‘Grenache N.’ and ‘Syrah’ – were studied, to identify possible phenotypic variability in the response to trophic competition.

MATERIALS AND METHODS

Plant material and growing conditions

Six experiments were carried out at the Montpellier-SupAgro Campus (43°38'N, 3°53'E) from 2007 to 2009, resulting in nine different sets of experimental conditions. The plants studied were 3-year-old grapevines (Vitis vinifera L.) of two cultivars ‘Syrah’ and ‘Grenache N.’ grafted onto Fercal rootstocks. In expts 1–6, respectively, 44, 51, 48, 36, 55 and 22 plants of each cultivar (except expt 6, in which only ‘Grenache N.’ was grown) were studied. Plants were grown outdoors in expts 1–3 and in a greenhouse in expts 4–6. They were grown in different seasons: summer (expts 1–3), spring (expt 4), autumn (expt 5) or winter (expt 6). In all experiments, plants were grown in 6-L PVC pots filled with a 1:1:1 (v/v/v) mixture of topsoil, sand and organic compost. Pots placed outdoors (expts 1–3) were watered daily and treated every 2 weeks with 15 g of complex fertilizer (Osmocote 18 % :11 % :10 % NPK; Heerlen, The Netherlands) supplemented with 10 g of ammonium nitrate fertilizer (33 % N) and 7 g of phosphorus/potassium fertilizer (18 %:10 % PK). Pots placed in the greenhouse (expts 4–6) were watered with Hoagland (N/5) nutrient solution, the pH of which was adjusted to 5·5 with HNO3, resulting in a final [NO3–] of 2·8 mol m−3. In all experiments, transpirable soil water content was maintained above 75 % of pot capacity. This value is higher than the thresholds of 35–55 % defined as limiting physiological or developmental processes for grapevine (Lebon et al., 2006).

Experimental design

Impact of source–sink relationship variation on the growth of an individual shoot

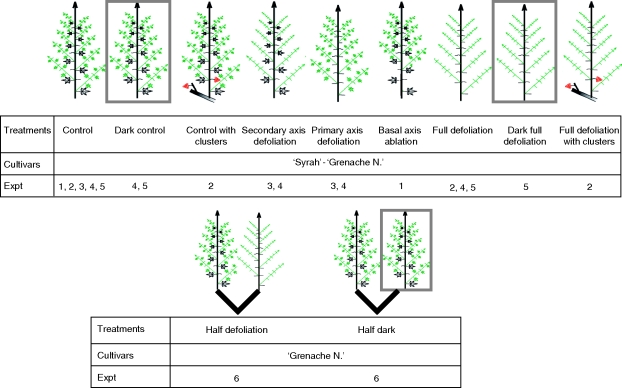
In expts 1–5, at the ‘five separated leaves’ stage (stage 12 on the modified Eichorn and Lorenz scale; Coombe, 1995), plants were pruned to a single shoot and all the clusters were removed. The remaining shoot was trained vertically, and allowed to continue its vegetative development until 25 leaves appeared on the primary axis. Thereafter, the various treatments were applied (Fig. 1).

Fig. 1.

Fig. 1

Open in a new tab

Schematic diagram of the treatments in the experiments.

On one set of plants, the architecture of the plant was not modified in any other way and the remaining shoot was allowed to undergo normal vegetative development in the same growing conditions (outdoors or in the greenhouse; ‘control’ treatments, expts 1–5). In expts 4 and 5, a set of plants subjected to the same shoot management procedure was placed in the dark under a polyester shelter (‘dark control’ treatments, expts 4 and 5) (Fig. 1). These treatments (‘control’ and ‘dark control’) resulted in plants with a similar shoot architecture but subject to a broad range of light conditions ranged from 0 to 53·5 mol m−2 d−1 of photosynthetic active radiation (Table 1). They were used to analyse the impact of photoassimilate supply on potential plant growth.

Table 1.

Environmental conditions in different experiments or experimental conditions: daily photosynthetically active radiation (PAR) and daily mean VPD (vapour pressure deficit)

Daily mean temperature (°C)
 Daily cumulative PAR (mol m2 d−1)
 Daily mean VPD (kPa)
Expt Experimental conditions Location Cultivars Year Date Min Max Mean Min Max Mean Min Max Mean
1 1 Outdoors Syrah–Grenache N. 2007 01 Aug to 13 Sept 18·6 27·9 22·6 18·9 58·2 43·6 0·7 2·3 1·4
2 2 Outdoors Syrah–Grenache N. 2008 30 June to 08 Aug 20·4 28·7 24·4 24·3 65·7 53·5 0·6 2·4 1·6
3 3 Outdoors Syrah–Grenache N. 2008 05 Aug to 18 Sept 16·4 28·2 22·3 9·3 57·8 39·6 0·6 2·4 1·3
4 4a Greenhouse Syrah–Grenache N. 2008 9 Apr to 26 May 17·4 24·0 21·2 3·8 22·8 12·6 0·5 2·1 1·0
4 4b Greenhouse–shelter Syrah–Grenache N. 2008 9 Apr to 26 May 17·9 25·4 22·4 0·3 0·4 0·3 0·4 2·1 1·1
5 5a Greenhouse Syrah–Grenache N. 2008 3 Nov to 17 Dec 19·5 22·6 21·1 4·1 7·4 6·3 0·8 2·0 1·4
5 5b Greenhouse–shelter Syrah–Grenache N. 2008 3 Nov to 17 Dec 18·6 21·1 20·1 0·0 0·1 0·0 0·6 1·5 1·1
6 6a Greenhouse Grenache N. 2009 9 Jan to 29 Jan 20·7 23·1 22·3 5·6 11·1 8·2 0·8 1·7 1·2
6 6b Greenhouse–shelter Grenache N. 2009 9 Jan to 29 Jan 16·7 18·7 17·5 0·0 0·2 0·0 0·7 1·6 1·1
Open in a new tab

The values (minimal, maximal and mean) were observed from the start of treatment to the end of the experiments.

Different architectural management practices were applied to four other sets of plants. These practices included defoliation or axis ablation on the remaining shoot. In one set of plants, all the leaves on all axes were removed (‘full defoliation’ treatments, expts 2, 4 and 5). In another set of plants, all the secondary axes on the shoots were defoliated (‘secondary axis defoliation’ treatments, expts 3 and 4) and in a third set of plants the primary axis on the shoots were defoliated (‘primary axis defoliation’ treatments, expts 3 and 4). In expt 1, the secondary axes at the base of the shoot (below insertion rank 15 on the primary axis) were pulled out in one set of plants (‘basal axis ablation’ treatments, expt 1) (Fig. 1). Plants subjected to these various defoliation and axis ablation treatments were compared with plants without axis ablation or defoliation (‘control’ treatments), to assess the impact of shoot structure on plant development.

In addition, in expt 5, the remaining shoot was completely defoliated and placed in the dark under the polyester shelter (‘dark full defoliation’ treatments, expt 5) in one set of plants (Fig. 1). This treatment was used to assess interactions between photoassimilate supply and architectural shoot management, by comparing treatments ‘control’, ‘dark control’, ‘full defoliation’ and ‘dark full defoliation’ treatments.

Impact of variations in source–sink relationships on the growth of two shoots

In expt 6, at the ‘five separated leaves’ stage (Coombe, 1995), the plants were pruned to two annual shoots per plant and all the clusters were removed. These two shoots were then trained vertically and allowed to continue their vegetative development until 25 leaves had appeared on each primary axis. Thereafter, various treatments were applied to the two remaining shoots. The two shoots of the plant subjected to ‘half defoliation’ treatments (Fig. 1) were grown in the same climatic conditions (in the greenhouse), but one shoot was completely defoliated, whereas the second was allowed to grow without any additional modification. This treatment management led to the development of two shoots subjected to two different treatments on each plant: ‘full defoliation’ and ‘control’. In a second set of plants, no defoliation treatment was applied to either of the two shoots. However, one shoot was grown in the same light conditions as before, whereas the second was grown in the dark under a polyester shelter. The plants of these treatments are referred to as ‘half dark’ treatments. This treatment management led to the development of two shoots subjected to two different treatments on each plant: ‘dark control’ and ‘control’.

Impact of source–sink relationship variations on cluster development

In expt 2, at the ‘five separated leaves’ stage, plants were pruned to two annual shoots per plant and two clusters were retained. One cluster (the C1 cluster) was retained on one shoot, and another cluster (the C2 cluster) was retained on the other shoot, which was pruned above the insertion rank of the cluster. All the leaves on this shoot were pulled out during the experiment. The shoot with leaves was then trained vertically and allowed to continue its vegetative development until 25 leaves had appeared on the primary axis. From this point onwards, two treatments were applied to the shoot with leaves. No other intervention was performed for the ‘control with clusters’ treatment, and the shoot with leaves was completely defoliated for the ‘full defoliation with cluster’ treatment. Defoliation treatments were carried out when 25 leaves had already appeared on the primary axis, to prevent the abortion of berries in clusters. Indeed, after the ‘25 leaves separated’ stage (corresponding to stage 27 on the modified Eichorn and Lorenz scale; Coombe, 1995), no further berry abortion occurs (Coombe, 1995).

Microclimate and thermal time calculation

Air temperature and relative humidity were measured with a capacitive hygrometer (HMP35A Vaisala; Oy, Helsinki, Finland) protected from direct radiation and placed at a height of 1·5 m (expts 4–6) or at a height of 2·5 m (expts 1–3). Photosynthetic photon flux density (PPFD) was measured with a PPFD sensor (LI-190SB; LI-COR, Lincoln, NE, USA). Data were collected every 30 s, averaged over 1800 s and stored in a datalogger (CR10X; Campbell Scientific Ltd, Shepshed, Leics, UK). Thermal time was calculated by daily integration of air temperature minus the base temperature of 10 °C common to both cultivars (Lebon et al., 2004) and is expressed in degree-days (°Cd).

All the values presented for microclimate variables (Table 1) are those obtained during the measurement period (i.e. from the beginning of treatment when the 25th leaf appeared on the primary axis until the end of the experiment). For the experiments carried out in the greenhouse (expts 4–6), two sets of environmental conditions were established, based on the growth of the plants in the greenhouse (experimental conditions a) or under the shelter (experimental conditions b). In the various experiments, a range of photosynthetic active radiation (PAR) values was established with mean values ranging from 0 (below the shelter, experimental conditions 4b, 5b, 6b) to 53·5 mol m−2 d−1 (outdoors, expt 3). In the various environments, mean temperature ranged from 17·5 °C (experimental conditions 6b) to 24·4 °C (expt 2), with mean maximal values of 18·7 (experimental conditions 6b) to 28·7 °C (expt 2) and mean minimal values of 16·7 (experimental conditions 6b) to 20·7 °C (experimental conditions 6a) (Table 1). Mean vapour presure deficit ranged from 1·0 (expt 4a) to 1·6 kPa (expt 2).

Plant measurements and variables

For each treatment (except for expt 6), four plants were harvested at each of three stages of development (Table 2). The first harvest was performed when there were 25 leaves on the primary axis. The second and third harvests were carried out approx. 250 and 500 °Cd later, respectively (Table 2). All organs were removed and oven-dried at 80 °C for 48 h. The root system and trunk were also extracted and dried. They were subsequently considered together as the ‘reserve’. The dry weight of each organ on the primary axis (leaf, internode, cluster) was determined. For each secondary axis, the total dry weight of each type of organ (leaf, internode) was also determined. The total dry weights of the clusters and ‘reserve’ were also determined. The organs on the primary and secondary axes were assigned to two categories on the basis of their date of appearance. The phytomers appearing before the first harvest were classified as ‘old’ and those appearing during the measurement period were classified as ‘new’. At each harvest date, internode and leaf lamina lengths were measured for each phytomer of the primary axis. The number of berries on the clusters was also evaluated. For secondary axes, the total length of the axis was recorded. During expt 6, no organs were harvested from the plants. From the first harvest to the end of experiment (Table 2), the number of phytomers on the various axes (primary and secondary) was recorded twice weekly for all the plants in each experiment. The secondary axes were distinguished on the basis of their insertion rank on the primary axis.

Table 2.

Times of start of treatment, end of the experiment and harvest for the various experiments and experimental conditions

Experimental conditions Time at start of treatment and 1st harvest (°Cd after budburst) 2nd harvest time (°Cd after budburst) Time at the end of experiment and 3rd harvest (°Cd after budburst)
1 556 834 1128
2 591 877 1158
3 541 857 1076
4 561 824 1077
4a 561 858 1166
5a 710 951 1210
5b 710 942 1161
6a 462 (no harvest) – 743 (no harvest)
6b 462 (no harvest) – 716 (no harvest)
Open in a new tab

Ten variables were analysed and classified according to the three processes studied: organogenesis, morphogenesis and biomass growth. For organogenesis, the variables studied were: the rate of phytomer appearance on the primary axis (phytomer Cd−1) and the rate of phytomer appearance on the secondary axes (phytomer Cd−1). For morphogenesis, the variables studied were: the length of ‘newly’ formed internodes on each axis (for the primary axis and for the secondary axes), and the individual leaf area of ‘newly’ formed leaves on the primary axis (cm2). For biomass growth, the variables studied were: the increase in whole-plant biomass (mg Cd−1), and the increase in ‘reserve’ biomass (mg Cd−1) during the measurement period, the linear internode weight of ‘newly’ formed internodes (mg cm−1) on each primary and secondary axis, and the area leaf weight of each ‘newly’ formed leaf on the primary axis (mg cm−2).

Concerning the increases in whole-plant and ‘reserve’ biomass, the total biomass increase during the experiments was divided by the duration of the experiments to avoid potential bias due to variations in experiment durations (Table 2).

The rate of appearance of phytomers on the axes was determined as the slope of the regression between the number of phytomers and thermal time throughout the duration of the experiment. The average phytomer appearance rate of all the secondary axes was determined for each treatment.

Individual leaf areas on the primary axis (Sf,I) were estimated from a quadratic relationship between the length of the leaf lamina Ll and the corresponding leaf area, as described by Pallas et al. (2008).

graphic file with name mcp278eqn1.jpg 1

where a = 0·011 and 0·0091 and b = 0·149 and 0·254 for ‘Syrah’ and ‘Grenache N., respectively (Sf, cm2; Ll, mm).

The total leaf area of each secondary axis of insertion rank i on the primary axis (SII,i) was estimated with an allometric relationship linking the leaf area on the secondary axis to the corresponding number of leaves (NII,i), as follows (Pallas et al., 2008):

graphic file with name mcp278eqn2.jpg 2

where a = 0·93 and 1·03 and b = 56·63 and 52·68 for ‘Syrah’ and ‘Grenache N.’, respectively (cm2).

Internode linear weight (mg cm−1) was calculated for each internode as the ratio between its dry mass and its length for the primary axis and secondary axes. Area leaf weight (mg cm−2) of each leaf on the primary axis was calculated as the ratio of the dry mass of the leaf to its area.

The relative variation of the mean value for each observed variable X was calculated as follows for all observed variables:

graphic file with name mcp278eqn3.jpg 3

where X is the value of the considered variable and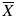Inline graphic is the mean value of the variable observed in the experiments.

Statistical analysis

The coefficient of variation (CV) of each observed variable was calculated as follows:

graphic file with name mcp278eqn4.jpg 4

with σ the observed standard deviation of the variable X.

Correlations between the variables were analysed by calculating the mean observed values of the variables for each plant in each experiment. The Pearson coefficient was determined and its significance tested. The ANOVA procedure of Statistica 8·0 (Statsoft, Tulsa, OK, USA) was used to test for significant differences between treatments. Newman–Keul's test was used as a post hoc test for subgroups. The ANOVA/MANOVA procedure of Statistica 8·0 (Statsoft) was used to check for significant differences between means. The differences in slopes and intercepts of linear regressions between datasets were assessed by comparing ΣSSi (sum of the residual sum of squares for individual fits to each dataset) with SSc (residual sum of squares for a common fit to the whole dataset), as follows:

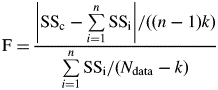graphic file with name mcp278eqn5.jpg 5

which follows Fisher's law with (n − 1)k and (Ndata – k) degrees of freedom. Ndata is the total number of data points, n is the number of individual regressions and k is the number of fitted parameters for each regression.

RESULTS

Variability of observed plants

Before treatment initiation, no difference in shoot leaf area was observed between cultivars in all experiments, except expt 5, in which the shoot leaf area of ‘Grenache N.’ was significantly (P < 0·05) greater than that of ‘Syrah’ (Table 3). Significant differences in shoot leaf area were observed between the different experiments. The shoot leaf area of plants (before treatment initiation) grown outdoors (expts 1–3) tended to be greater than that of plants grown in the greenhouse (expts 4–6). In all experiments, the shoot leaf area of the plants subjected to different treatments did not differ significantly before the initiation of the treatments.

Table 3.

Mean shoot leaf area before and after the treatment (see Fig. 1 for treatment description and Table 2 for the treatment start times)

Syrah
 Grenache N.
Expt Treatment Shoot treatment Leaf area before treatment (m2) Leaf area after treatment (m2) Leaf area before treatment (m2) Leaf area after treatment (m2)
1 Control 0·79 0·79a 0·71 0·71a
Basal axis ablation 0·72 0·35b 0·72 0·27b
Treatment effect n.s. *** n.s. ***
2† Control 0·68 0·68 0·67 0·67
Control with clusters 0·64 0·64 0·64 0·64
Full defoliation 0·63 – 0·63 –
Full defoliation with clusters 0·65 – 0·67 –
Treatment effect n.s. n.s. n.s. n.s.
3 Control 0·55 0·55a 0·51 0·51a
Primary axis defoliation 0·54 0·17c 0·51 0·15c
Secondary axis defoliation 0·56 0·37b 0·49 0·35b
Treatment effect n.s. *** n.s. ***
4 Control 0·42 0·42a 0·47 0·47a
Dark control 0·43 0·43a 0·45 0·45a
Primary axis defoliation 0·41 0·30b 0·46 0·31b
Secondary axis defoliation 0·44 0·13c 0·47 0·15c
Full defoliation 0·42 – 0·46 –
Treatment effect n.s. *** n.s. ***
5 Control 0·32 0·32 0·45 0·45
Dark control 0·32 0·32 0·45 0·45
Full defoliation 0·31 – 0·44 –
Full defoliation dark 0·32 – 0·45 –
Treatment effect n.s. n.s. n.s. n.s.
6‡ Half defoliation Control 0·31 0·31
Full defoliation 0·32 –
Half dark Control 0·31 0·31
Dark control 0·27 0·27
Treatment effect n.s. n.s.
Open in a new tab

***, Significant at P < 0·001; n.s., not significant. Values followed by different letters were significantly different,

† Data for expt 2 are those for the unpruned shoot. ‡ In expt 6, only Grenache N. cultivar was grown.

Defoliation and axis ablation modified the total leaf area of the shoots. Shoots subjected to full defoliation on primary and secondary axes (expts 3 and 4), and with ablation of secondary axes at the base of the shoot (expt 1) had a significantly lower leaf area than the shoots with no defoliation or axis ablation (‘control’, ‘dark control’, ‘control with clusters’ treatments). The ablation of secondary axes at the base of the shoot (below insertion rank 15) (‘basal axis ablation’ treatment) led to a decrease in shoot leaf area (56 and 62 % for ‘Syrah’ and ‘Grenache N.’, respectively). In expt 3, shoot leaf area was significantly greater for ‘secondary axis defoliation’ treatment (0·37 and 0·35 m2 for ‘Syrah’ and ‘Grenache N.’, respectively) than for ‘primary axis defoliation’ treatment (0·17 and 0·15 m2 for ‘Syrah’ and ‘Grenache N.’, respectively). Conversely, in expt 4, the shoots of plants subjected to defoliation on the secondary axes had a significantly greater leaf area (0·30 and 0·31 m2 for ‘Syrah’ and ‘Grenache N.’, respectively) than the shoots of plants subjected to defoliation on the primary axis (0·13 and 0·15 m2 for ‘Syrah’ and ‘Grenache N.’, respectively).

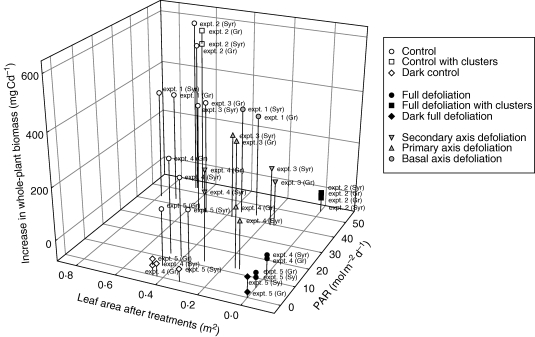
Considerable variability in the increase in whole-plant biomass throughout the experiments was observed between different experiments and treatments (Fig. 2). In ‘control’ treatments, the plants grown outdoors (expts 1–3) had a significantly greater increase in whole-plant biomass than plants grown in the greenhouse (expts 4 and 5). The plants subjected to ‘control’ treatments in expt 2 had the highest increase in whole-plant biomass (587 and 503 mg Cd−1, for Syrah and Grenache N., respectively), whereas the plants grown in expt 5 had the lowest increase (139 and 156 mg Cd−1, for Syrah and Grenache N., respectively). In expt 2, plants subjected to ‘control’ and ‘control with clusters’ treatments had similar whole-plant biomass increase, for both cultivars (P = 0·35). If treatments without defoliation or axis ablation only (‘control’, ‘dark control’, ‘control with clusters’, white points in Fig. 2) are considered, the plants subjected to ‘dark control’ treatments (expts 4 and 5) had the lowest increase of whole-plant biomass. If the treatments with defoliation or axis ablation are considered, the completely defoliated plants (‘full defoliation’, ‘full defoliation with clusters’, ‘dark full defoliation’ treatments, closed symbols in Fig. 2) had the lowest increase in whole-plant biomass, these values being below 0. Partial defoliation or axis ablation (‘primary axis defoliation’, ‘secondary axis defoliation’ and ‘basal axis ablation’ treatments, shaded symbols in Fig. 2) resulted in a lower increase in whole-plant biomass than for the corresponding ‘control’ treatments. No significant difference in increase in whole-plant biomass was observed between the two cultivars, in any of the experiments other than expt 4 (for ‘secondary axis defoliation’ treatments).

Fig. 2.

Fig. 2

Open in a new tab

Increase in whole-plant biomass during the experiments as a function of the amount of incident PAR and the initial leaf area of the plants after treatment initiation. Each point represents the observed mean value for a treatment.

The mean, minimum and maximum values of the ten variables analysed are presented in Table 4. The CV was calculated to make it possible to compare the relative dispersion of variables between each experiment and treatment. The variables related to biomass growth in individual plants had the highest CV (1·42 for the increase in ‘reserve’ biomass and 1·18 for the increase in whole-plant biomass). For internodes and leaves, the CV for variables related to morphogenesis processes were lower than those related to organ biomass growth. For morphogenesis and biomass growth, a similar range of variation was observed for these variables on the primary and secondary axes. Secondary axis organogenesis displayed a range of variation similar to that for morphogenetic processes, whereas primary axis organogenesis had the lowest CV.

Table 4.

Maximum, minimum, mean values and coefficient of variation observed for the ten variables studied

Processes Variable Mean observed values Maximum observed values Minimum observed values CV* (no units)
Whole-plant Biomass accumulation Increase in whole-plant biomass (mg Cd−1) 172 587·2 −42·1 1·18
Increase in ‘reserve’ biomass (mg Cd−1) 42·7 144·2 −28·2 1·42
Primary axis Organogenesis Phytomer appearance rate (phytomer Cd−1) 0·036 0·047 0·017 0·23
Morphogenesis Internode length (cm) 5·1 9·1 0·8 0·63
Individual leaf area (cm2) 96·2 141·2 12·3 0·52
Biomass growth Internode linear weight (mg cm−1) 52·8 136·7 1·6 0·86
Area leaf weight (mg cm−2) 3·9 6·3 0·3 0·69
Secondary axis Organogenesis Phytomer appearance rate (phytomer Cd−1) 0·01 0·021 0·001 0·61
Morphogenesis Internode length (cm) 1·4 2·5 0·5 0·51
Biomass growth Internode linear weight (mg cm−1) 10·9 25·9 3·4 0·78
Open in a new tab

* The coefficient of variation for each variable was calculated as the ratio of the observed s.d. to the observed mean value for the whole dataset.

Data were collected in expts 1–5.

Impact of variations in photoassimilate supply on the various vegetative growth processes

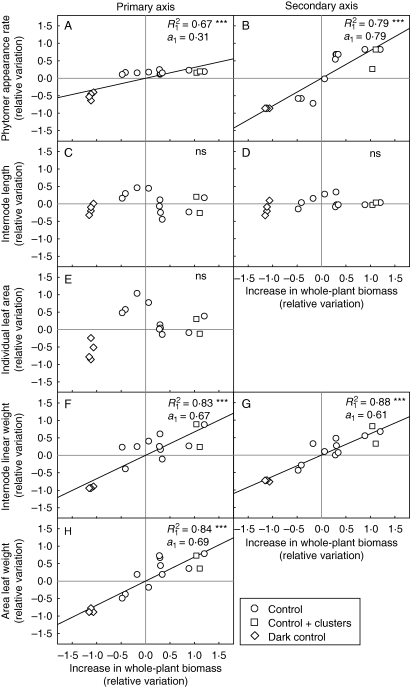
The impact of variations of photoassimilate supply on plant development was analysed with the plants with no defoliation or axis ablation (‘control’, ‘control with clusters’ and ‘dark control’ treatments) to assess the potential for shoot development in the different environmental conditions established in expts 1–5. The significance of correlations between the relative variations of the organogenesis (phytomer appearance rate), morphogenesis (internode length and individual leaf area), biomass growth variables (internode linear weight and area leaf weight) and the relative variations of increase in whole-plant biomass was assessed (Fig. 3). No significant correlation was found between the morphogenesis variables and the relative increase in whole-plant biomass (Fig. 3C–E). If ‘control’, ‘control with clusters’ and ‘dark control’ treatments are considered, significant correlations (P < 0·001) were found between the organogenesis and biomass growth variables and the relative increase in whole-plant biomass (Fig. 3A–H). The slopes of the regression lines for the relative variation of phytomer appearance rate on secondary axes and for biomass growth variables were significantly greater than those for phytomer appearance rate on primary axis (at P = 0·05; F1,32 = 4·15; 3·42; 3·51; 3·63, respectively). Similar results were obtained if the two cultivars were considered separately (data not shown).

Fig. 3.

Fig. 3

Open in a new tab

Relative variation around the observed mean values for phytomer appearance rate, individual leaf area, internode length, internode linear weight and area leaf weight (for the description of the variables, see Table 4), as a function of variation around the mean for increase in whole-plant biomass for ‘control’, ‘control with clusters’ and ‘dark control’ treatments. The lines represent the linear regression for ‘control’, ‘dark control’ and ‘control with clusters’ treatments. Each point corresponds to the mean value for plants subjected to the same treatment in each experiment (except in expt 6). R12 is the coefficient of determination for the linear regressions, and a1 is the slope of the linear regression line. The significance of the regressions was assessed with Pearson's test: ***, significant at P < 0·001; n.s., not significant.

Impact of architectural management practices and of darkness on the various vegetative growth processes

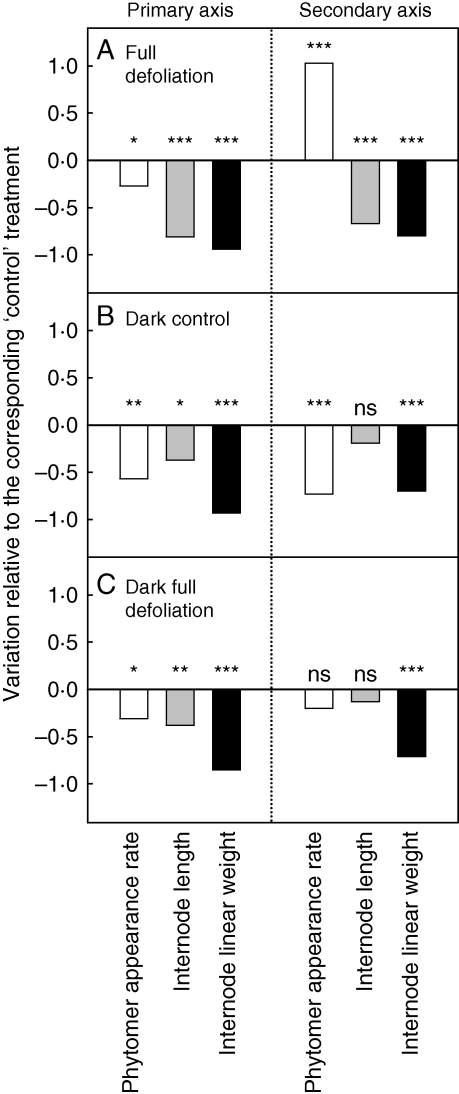
The impact of complete defoliation, and of darkness on axis development was analysed by comparing the development of the plants subjected to ‘full defoliation’, ‘dark control’ and ‘dark full defoliation’ treatments with plants subjected to ‘control’ treatments (Fig. 4). Significant decreases (P < 0·05) in phytomer appearance rate, internode length and internode linear weight on primary axis was observed for the three treatments compared with the value observed for the ‘control’ treatments. Internode length was more reduced for ‘full defoliation’ treatment (−72 %, Fig. 4A) than for ‘dark full defoliation’ and ‘dark control’ treatments (−38 and −28 %, respectively; Fig. 4B, C). Except for the phytomer appearance rate, the same trends were observed for secondary axes with an absence of a significant decrease in internode length for ‘dark control’ and ‘dark full defoliation’ treatments. For secondary axes, in comparison to the values observed for ‘control’ treatments, the phytomer appearance rate significantly decreased (−71 %) for ‘dark control’ treatments (Fig. 4B) and significantly increased (+111 %) for ‘full defoliation’ treatments (Fig. 4A). ‘Dark full defoliation’ treatments (Fig. 4C) involved no change in phytomer appearance rate on secondary axes.

Fig. 4.

Fig. 4.

Open in a new tab

Relative phytomer appearance rate, internode length and internode linear weight on primary and secondary axes normalized using the observed values for the corresponding ‘control’ treatments in each experiment for (A) ‘full defoliation’, (B) ‘dark control’, and (C) ‘dark full defoliation’ treatments. ***, Significant at P < 0·001; **, significant at P < 0·01; *, significant at P < 0·05; n.s., not significant.

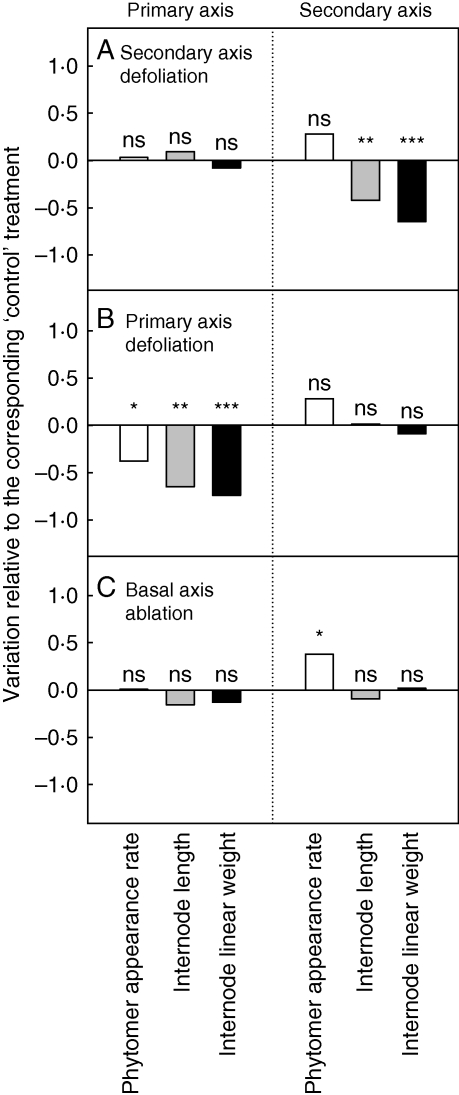
The impact of partial defoliation and ablation on axis development was analysed by comparing the development of plants subjected to ‘secondary axis defoliation’, ‘primary axis defoliation’ and ‘basal axis ablation’ treatments with plants subjected to ‘control’ treatments (Fig. 5). No change in primary axis development was observed for ‘secondary axis defoliation’ and ‘basal axis ablation’ treatments compared with the values observed for ‘control’ treatments (Fig. 5A, C). Conversely for the primary axis, phytomer appearance rate, internode length and internode linear weight were significantly decreased for ‘primary axis defoliation’ treatments (Fig. 5B). Complete defoliation of the primary axis involved no change in secondary axis development (Fig. 5B) whereas complete defoliation of secondary axes (Fig. 5A) led to a decrease in the length and the linear mass of the internode on the secondary axes. Basal axis ablation (Fig. 5C) involved a significant (+31 %) increase in phytomer appearance rate of secondary axes. No significant difference in morphogenesis and biomass growth processes on secondary axes was observed between ‘basal axis ablation’ and ‘control’ treatments.

Fig. 5.

Fig. 5

Open in a new tab

Relative phytomer appearance rate, internode length and internode linear weight on primary and secondary axes normalized using the observed values for the corresponding ‘control’ treatments in each experiment for (A) ‘secondary axis defoliation’, (B) ‘primary axis defoliation’, and (C) ‘basal axis ablation’ treatments. ***, Significant at P < 0·001; **, significant at P < 0·01; *, significant at P < 0·05; n.s., not significant.

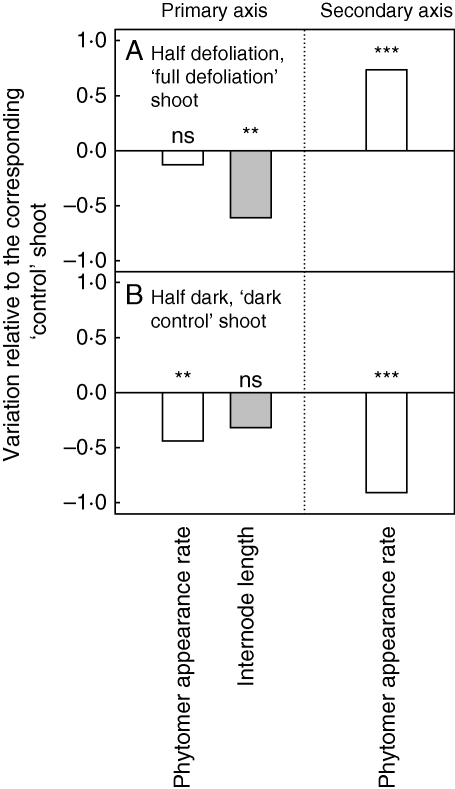
In expt 6 (Fig. 6), the development of the two shoots of each plant was compared. For the ‘half defoliation’ treatment, for each plant, the development of the completely defoliated shoot (afterwards called ‘full defoliation’ shoot) was compared with the development of the ‘control’ shoot (Fig. 6A). For the ‘half dark’ treatment, for each plant, the development of the ‘dark control’ shoot was compared with the development of the ‘control’ shoot (Fig. 6B). In treatment ‘half dark’, the phytomer appearance rates on primary and secondary axes were significantly (P < 0·01) lower for the ‘dark control’ shoots than for the ‘control’ shoots (Fig. 6B). No difference in internode length on the primary axis was observed between the two shoots (‘control’ or ‘dark control’) of the plants subjected to the ‘half dark’ treatment. For the ‘half defoliation’ treatment, the phytomer appearance rate on the secondary axes was significantly higher for the ‘full defoliation’ shoots than for the corresponding ‘control’ shoots. For this treatment (‘half defoliation’), no significant difference was observed between the two shoots for phytomer appearance rate on primary axis (Fig. 6A). Internode length was significantly shorter (−62 %) for the ‘full defiolation’ shoots than for the corresponding ‘control’ shoots.

Fig. 6.

Fig. 6

Open in a new tab

Relative variation of phytomer appearance rate on primary and secondary axes and of internode length on primary axis for (A) the ‘full defoliation’ shoot (‘half defoliation’ treatments at the whole-plant level), and (B) for the ‘dark control’ shoot (‘half dark’ treatments at the whole-plant level) normalized using the observed values for the corresponding ‘control’ shoots for both treatments. ***, Significant at P < 0·001; **, significant at P < 0·01; n.s., not significant.

Root development

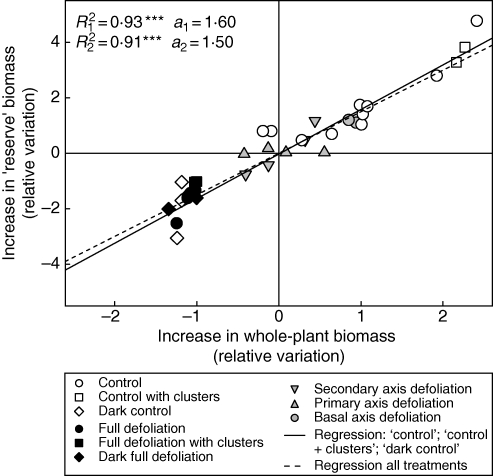
The impact on root development of modifying photoassimilate supply was investigated by analysing the correlation between the relative increase in whole-plant biomass increase and the relative increase in ‘reserve’ biomass increase. The correlation analysis for the whole dataset was carried out to assess the differences in root development associated with changes in architecture. Significant correlations were observed (P < 0·001) (Fig. 7) if plants without axis ablation or defoliation were only considered (‘control’, ‘control with clusters’ and ‘dark control’ treatments, R12 = 0·93) or if the whole dataset was considered (R22 = 0·91). The slopes of the two linear regression lines (a1 = 1·60 and a2 = 1·50) were not significantly different (F2,78 = 2·14). No significant difference was observed between the two cultivars in terms of the significance of the correlation or the slopes of the regression lines obtained (data not shown).

Fig. 7.

Fig. 7

Open in a new tab

Variation around the observed mean values for the increase in reserve biomass (for a description of the variables, see Table 4) as a function of variation around the mean for whole-plant biomass increase. The continuous line represents the linear regression for ‘control’, ‘control with clusters’ and ‘dark control’ treatments and the dashed line represents the same regression for the whole dataset. Each point corresponds to the mean value for the same treatment in each experiment (except expt 6). R12 is the coefficient of determination of the linear regression for the plants subjected to ‘control’, ‘control with clusters’ and ‘dark control’ treatments and R22 is the equivalent coefficient of determination for the whole dataset. a1 and a2 are the slopes of the regression lines. The significance of the regressions was assessed with Pearson's test: ***, significant at P < 0·001; n.s., not significant.

Cluster development

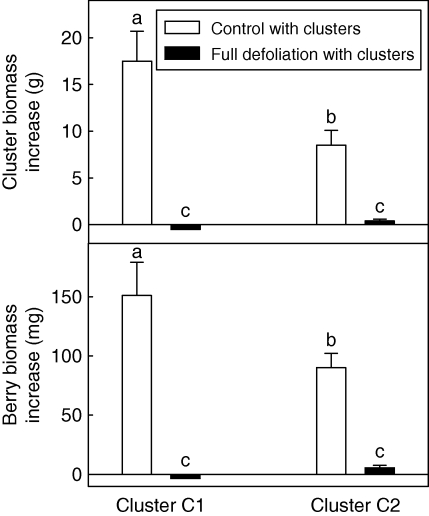
The development of clusters and berries was investigated in expt 2, for ‘control with clusters’ and ‘full defoliation with clusters’ treatments (Fig. 8). Two clusters were retained on each plant (Fig. 1), one cluster (C1) on a shoot with unmodified vegetative development for ‘control with clusters’ treatment, or on a completely defoliated shoot for treatment ‘full defoliation with clusters’ treatment. The other cluster (C2) was retained on a completely defoliated and pruned shoot for both treatments (Fig. 1). No significant difference in the number of berries per cluster or cluster biomass was observed between cultivars. Furthermore, no significant differences in the number of berries was found between the two treatments, for either cluster position (P = 0·35). The increase in cluster or berry biomass throughout the experiment was almost zero for both clusters of the ‘full defoliation with clusters’ treatment. For the ‘control with clusters’ treatment, the increase in cluster (Fig. 8A) and berry biomass (Fig. 8B) was significantly (P < 0·05) greater for C1 than for C2 clusters.

Fig. 8.

Fig. 8

Open in a new tab

Increase in cluster biomass (A) and in berry biomass (B) for the two clusters for ‘control with clusters’ and ‘full defoliation with clusters’ treatments in expt 2, for both cultivars. Cluster 1 (C1) was located on an unpruned shoot and cluster 2 (C2) was located on the pruned shoot (see Fig. 1 for treatment description). Values with different letters were significantly different at P < 0·05; errors bars represent the s.d.

DISCUSSION

Plasticity of plant development

Considerable variability in microclimatic conditions (9; Table 1), coupled with various architectural management practices (11; Fig. 1) and resulting in 40 sets of conditions defined in terms of the combination of initial plant leaf area and level of photosynthetic active radiation, was observed in the experiments (Table 3 and Fig. 2). The impact of these experimental combinations on plant development was analysed as a function of the variation of ten growth variables. These variables were related to various plant growth processes, such as organogenesis, morphogenesis, biomass production and biomass allocation. These processes were studied at different scales: the whole-plant scale for variations of total and ‘reserve’ biomass, and at the scale of the organ for organogenesis, morphogenesis and biomass growth processes on primary and secondary axes. Based on the extent of the variation in these variables, biomass accumulation at whole-plant level seemed to be the most plastic variable (Table 4). The variables operating at whole-plant level displayed twice as much variation as the processes operating at the organ level. For processes operating at the organ level, a hierarchy was observed as a function of two criteria: process and type of axis (Table 4). For comparisons of similar processes, less variation was observed for the primary axis than for the secondary axes. Variability depended also on the nature of the process, with an increasing gradient from organogenesis to morphogenesis to biomass growth. The various experimental designs resulted in a wide range of assimilate supply among the treatments (Fig. 2). The assimilate supply for each plant was quantified by assessing the increase in whole-plant biomass (Fig. 2), which is equivalent to the net carbon balance (Monteith, 1977).

A co-ordinated system of regulation for growth processes allows plant development in fluctuating radiative environments

The responses of growth processes to assimilate supply in the absence of defoliation or axis ablation were classified (Figs 3 and 7). The following hierarchy was obtained: primary axis organogenesis < internode linear weight = area leaf weight < secondary axis organogenesis < reserve biomass accumulation. Organ morphogenesis was not included in this hierarchy because it was not correlated with assimilate supply and may be considered as partially independent of the level of assimilate supply within the observed range. No significant difference in the response to variations in assimilate supply was observed between cultivars, as previously reported for the response to variations in trophic competition (Pallas et al., 2009).

Primary axis organogenesis was maintained at a sustained rate even in situations in which the assimilate supply was low, including situations with no incident PAR. This finding highlights the predominance of the production of new phytomers by the primary axis meristem over the other processes (Table 4). Conversely, a marked decrease in secondary axis organogenesis was observed in situations of strong trophic competition (Lebon et al., 2006; Pallas et al., 2008). This finding confirms that the decrease in total leaf area observed in the absence of assimilate results mostly from a decrease in the number of leaves on the secondary axes (Lebon et al., 2006; Pallas et al., 2008).

The lower area leaf weight recorded in low-irradiance conditions was associated with an increase in leaf area with respect to biomass allocation to the leaves. Similarly, the lower linear internode weight was associated with an increase in the length of internodes with respect to biomass allocation to the internodes. This finding is consistent with other studies reporting lower organ weights relative to their sizes for plants grown in low-irradiance conditions (Meziane and Shipley, 1999; Chenu et al., 2007, Bell and Galloway, 2008). Allometric changes in plant organs can be analysed as an adaptive property partly counterbalancing the lower level of total plant growth under conditions of resource limitation (Sultan, 2000; Chenu et al., 2007). In individual plants, this adaptation results from the regulation of signalling (Pigliucci and Schmitt, 1999) during plant development, to promote the growth of organs involved in resource capture (Sultan, 2000). However, other authors have interpreted variations in the weight of the organs relative to their sizes as being a result of source–sink equilibrum unrelated to the functional adaptation of plants. In the first of these two theories, the decrease in area leaf weight results from a change in leaf morphology during leaf expansion, particularly as concerns the thickness of the mesophyllum (Granier and Tardieu, 2009). This change leads to both a decrease in photosynthetic activity per unit leaf area and an increase in total leaf area for a given amount of biomass allocated to leaves. The overall advantage at the scale of the plant depends on the cumulative photosynthesis response. This increase in plant leaf area and internode length appears to be advantageous for young plants competing with other plants, as it increases the amount of light intercepted (Violle et al., 2009). However, its potential advantages are less clear for large plants with a high level of self-shading, because an increase in plant leaf area does not result in an increase in the amount of intercepted light.

In the second theory, variations in organ weight are linked only to the existence of a transient carbohydrate reserve pool in these organs. The potential size of this pool is determined by organ size, regardless of the level of trophic competition, and the amount of carbon in this pool is determined by the level of trophic competition in the plants (Thornley and Hurd, 1974; Bertin et al., 1999).

Consequently, two alternative points of view are possible to analyse the absence of a link between organ morphogenesis and assimilate supply. These two points of view differ in terms of the status of specific organ weight, which may be either a controlled variable or dependent on organ morphogenesis and trophic competition. In the first case, area leaf weight is determined by environmental signals, such as incident PAR or light quality, regardless of trophic competition. Organ size is determined by the amount of biomass allocated to the organ, divided by the specific weight of the organ. The resulting organ size therefore depends on the relative decreases in specific organ weight and allocated biomass. No relationship is found between organ size and biomass production (Fig. 3) if the decrease in biomass production is perfectly compensated by changes in specific organ weights in response to incident PAR. Secondly, many authors have suggested that organ morphogenesis is determined by variations in the rate and duration of organ expansion in response to environmental conditions, in a process mediated by non-trophic signalling (e.g. Tardieu et al., 1999). This would suggest that organ size determines the capacity of the transient reserve pool of the organ and that trophic competition determines the level to which this pool is filled. Indeed, a number of relationships have consistently been identified, establishing a link between the rate and duration of organ morphogenesis on the one hand and environmental variables on the other. For example, leaf expansion has consistently been shown to be very sensitive to soil water status (Lecoeur et al., 1995; Lechner et al., 2008), temperature (Fournier and Andrieu, 2000), vapour pressure deficit (Chenu et al., 2008) and light quality (Christophe et al., 2006). Going beyond analyses of the correlations between organ expansion and environmental conditions, organ size development seems to be linked to a system of genetic regulation (Reymond et al., 2003) in response to microclimatic variations, ensuring robust plant development in various environments.

The absence of a decrease in the root : shoot ratio in response to decreasing assimilate supply (Fig. 7) is not consistent with an adaptive response promoting leaf development in conditions in which assimilate is lacking, similar to that observed for herbaceous species (Shipley and Meziane, 2002). The observed difference between the present results and the predictions of this theory may be linked to the higher level of priority accorded to the storing of reserves in young perennial plants (Keller et al., 1995).

Defoliation, axis ablation and darkness involve changes in the relationships between growth processes

Defoliation, axis ablation or darkness treatments resulted in many changes in the relationships between growth variables and assimilate supply that could not be directly attributed to source–sink relationships (Figs 4–6). This was particularly true for secondary axis organogenesis (Figs 4–6). The increase in the rate of organ production on the defoliated secondary axes of shoots subjected to the ‘full defoliation’ and ‘primary axis defoliation’ treatments highlights the existence of a non-trophic determinant of axis development. This increase probably resulted from a hormonal signal that increased axis organogenesis by decreasing abscisic acid synthesis (Abo Hamed et al., 1981). Indeed, in natural conditions, the production of abscisic acid by leaves has been observed, leading to a decrease in meristem activity (Neales and McLeod, 1991). The absence of such an increase for primary axis organogenesis in ‘full defoliation’ and ‘secondary axis defoliation’ treatments clearly emphasizes the fact that the phyllochron of the primary axis is really stable and cannot be superior to a value of 0·044 phytomer Cd−1 for both cultivars (Pallas et al., 2008). The absence of an increase in the rate of phytomer production on secondary axes for the shoots subjected to ‘dark full defoliation’ and ‘dark control’ treatments, which had the same photosynthetic activity as ‘full defoliation’ shoots, also highlights the existence of a light-mediated signal-regulating meristem activity (Robin et al., 1994; Warnasooriya and Montgomery, 2009; Fig. 4). The existence of this light-mediated signal has been confirmed by the internode length differences between the shoots subjected to ‘full defoliation’, ‘dark control’ and ‘dark full defoliation’ treatments. The darkness led to an increase in internode length relative to the amount of assimilate allocated to the internode. Conversely, a trophic approach could be used to analyse the results for plants subjected to the ‘basal axis ablation’ treatment. Based on the changes in the source : sink ratio (Pallas et al., 2009), axis ablation at the base of the shoot leads to an increase in development of the remaining axes, due to a decrease in trophic competition between the secondary axes (Fig. 5).

Is the common assimilate pool assumption appropriate?

Models of carbon production and allocation are generally based on one of two hypotheses: (1) the ‘common assimilate pool’ assumption (e.g. Letort et al., 2008) or (2) ‘the transport-resistance’ assumption (e.g. Deuleuze and Houllier, 1997). The transport-resistance assumption arose from physiological studies of phloem transport (Münch, 1930), in which assimilate fluxes were found to be proportional to an osmotic gradient between the sources and sinks of the assimilates, divided by a transport-resistance factor (Thornley, 1976). The ‘common assimilate pool’ theory has been used in various modelling approaches and is supported by experimental evidence. For instance, Heuvelink (1995) showed that the distance between leaves and trusses had no impact on truss development in tomato plants. The total amount of assimilate in the plant was the only factor determining final truss weight. Most of the results obtained in the present study suggest that this assumption is not appropriate for studies of the plasticity of grapevine development. According to this theory, in expt 2, the two clusters on the shoots with and without leaves should have displayed similar patterns of development regardless of their positions on the plant (Fig. 8). In expt 6, the two shoots corresponding to the ‘half defoliation’ and ‘half dark’ treatments should have displayed similar patterns of development (Fig. 6). The results of these two experiments go against expectations based on the common assimilate pool theory. Thus, the common assimilate pool appears to be an inadequate simplification for the modelling of grapevine development. The observed differences between tomato and grapevine may be linked to the rate of assimilate circulation in the phloem, with a greater impact of topological distance in larger plants. This hypothesis appears to be relevant to the transport-resistance theory approaches used to model tree development (e.g. Allen et al., 2005). The ‘common assimilate pool’ assumption may, however, be appropriate for descriptions of biomass allocation in such complex systems, provided they are broken down into smaller subunits, such as individual axes, to which the ‘common assimilate pool’ assumption could then be applied. According to the results of this study, it appears that a representation of grapevine as a sum of independent axes could be relevant in term of biomass partitioning (Sprugel et al., 1991; Lacointe et al., 2004). Indeed, the biomass growth of the secondary axes (respectively, primary axis) in the plants subjected to primary axis defoliation (respectively, secondary axis) was the same as in ‘control’ plants. The relevance of this theory remains unclear and needs to be further evaluated, using, for example, 14C labels in order to evaluate the ratio of photo-assimilates produced inside an axis and allocated to another one. A dynamic study of these fluxes could be relevant, if each axis is considered as an independent unit, to determine the carbon balance of each axis and the transition time between the heterotrophic and the autotrophic phase of its development (Bosc, 2000).

Conclusions

Many of the results of this study clearly highlight the inadequacy of some of the hypotheses of the models based on carbon partitioning to model grapevine development. In these models, all plant developmental processes are considered to be a consequence of the source–sink relationships between organs (Letort et al., 2008). Many other non-trophic effects and compensatory growth mechanisms were observed in this study, showing that plant development is driven by a combination of trophic and of non-trophic determinants. Moreover, in many models, carbon partitioning depends purely on the sink strength of organs, with the topological distances between the organs not taken into account (Luquet et al., 2006; Letort et al., 2008). The results of the present study suggest that it is essential to take into account the topological distances between the sources and the sinks of assimilates for grapevine. Some of the quantifications in this study also suggest new formalisms for increasing the ability of models to take plant phenotypic plasticity into account. The combination of both an ecophysiological model for morphogenesis taking environmental signals into account and a biomass-driven model for organogenesis and biomass allocation appears to be a promising approach.

ACKNOWLEDGEMENTS

The authors thank M. Kawamata, C. Pons, A. Dardou, J. Mineau, M. Ferrand, E. T. Sumer, D. Merabet, D. Rablat, A. Seguard, B. Suard and H. Mallié for their technical assistance during experiments. B. Pallas received fundings from the Ecole Centrale de Paris.

LITERATURE CITED

  1. Abo-Hamed S, Hardwick K, Collin HA. Biochemical and physiological aspects of leaf development in cocoa (Theobroma cacao L.). VI. Hormonal interactions between mature leaves and the shoot apex. New Phytologist. 1981;89:191–200. [Google Scholar]
  2. Allen MT, Prusinkiewicz P, De Jong TM. Using L-systems for modelling source–sink interactions, architecture and physiology of growing trees: the L-PEACH model. New Phytologist. 2005;166:869–880. doi: 10.1111/j.1469-8137.2005.01348.x. [DOI] [PubMed] [Google Scholar]
  3. Belaygue C, Wery J, Cowan AA, Tardieu F. Contribution of leaf expansion, rate of leaf appearance, and stolon branching to growth of plant leaf area under water deficit in white clover. Crop Science. 1996;36:1240–1246. [Google Scholar]
  4. Bell DL, Galloway LF. Population differentiation for plasticity to light in an annual herb: adaptation and cost. American Journal of Botany. 2008;95:59–65. doi: 10.3732/ajb.95.1.59. [DOI] [PubMed] [Google Scholar]
  5. Bertin N, Tchamtichian M, Baldet P, Devaux C, Brunel B, Gary C. Contribution of carbohydrate pools to the variations in leaf mass per area within a tomato plant. New Phytologist. 1999;143:53–61. [Google Scholar]
  6. Bosc A. EMILION, a tree functional-structural model: presentation and first application to the analysis of branch carbon balance. Annals of Forest Sciences. 2000;57:555–569. [Google Scholar]
  7. Chenu K, Franck N, Lecoeur J. Simulations of virtual plants reveal a role for SERRATE in the response of leaf development to light in Arabidopsis thaliana. New Phytologist. 2007;175:472–481. doi: 10.1111/j.1469-8137.2007.02123.x. [DOI] [PubMed] [Google Scholar]
  8. Chenu K, Chapman SC, Hammer Gl, et al. Short-term response of leaf growth rate to water deficit scale up to whole-plant and crop levels: an integrated modelling approach in maize. Plant, Cell and Environment. 2008;31:378–391. doi: 10.1111/j.1365-3040.2007.01772.x. [DOI] [PubMed] [Google Scholar]
  9. Christophe A, Moulia B, Varlet-Grancher C. Quantitative contributions of blue light and PAR to the photocontrol of plant morphogenesis in Trifolium repens (L.) Journal of Experimental Botany. 2006;57:2379–2390. doi: 10.1093/jxb/erj210. [DOI] [PubMed] [Google Scholar]
  10. Christophe A, Letort V, Hummel I, Cournede PH, de Reffye P, Lecoeur J. A model-based analysis of the dynamics of carbon balance at the whole-plant level in Arabidopsis thaliana. Functional Plant Biology. 2008;35:1–16. doi: 10.1071/FP08099. [DOI] [PubMed] [Google Scholar]
  11. Coombe BG. Adoption of a system for identifying grapevine growth stages. Australian Journal of Grape and Wine Research. 1995;1:100–110. [Google Scholar]
  12. Costes E, Fournier D, Salles JC. Changes in primary and secondary growth as influenced by crop load in ‘Fantasme®’ apricot trees. Journal of Horticultural Science and Biotechnology. 2000;75:510–519. [Google Scholar]
  13. Deleuze C, Houiller F. A transport model for tree ring width. Silva Fennica. 1997;31:113–120. [Google Scholar]
  14. Donohue K, Messiqua D, Pyle EH, Heschel MS, Schmitt J. Evidence of adaptive divergence in plasticity: site-dependent selection on shade-avoidance responses in Impatiens capensis. Evolution. 2000;54:1956–1968. doi: 10.1111/j.0014-3820.2000.tb01240.x. [DOI] [PubMed] [Google Scholar]
  15. Dosio AG, Rey H, Lecoeur J, et al. A whole-plant analysis of the dynamics of expansion of individual leaves of two sunflower hybrids. Journal of Experimental Botany. 2003;54:2541–2552. doi: 10.1093/jxb/erg279. [DOI] [PubMed] [Google Scholar]
  16. Drouet JL, Pagès L. GRAAL-CN: a model of growth, architectural and allocation for carbon and nitrogen dynamics within whole plants formalised at the organ level. Ecological Modelling. 2006;206:231–249. [Google Scholar]
  17. Fourcaud T, Zhang X, Stockes A, Lambers H, Korner C. Plant growth modelling and application: the increasing importance of plant architecture in growth models. Annals of Botany. 2008;101:1053–1063. doi: 10.1093/aob/mcn050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fournier C, Andrieu B. Dynamics of the elongation of internodes in maize (Zea mays L.): analysis of phases of elongation and their relationships to phytomer development. Annals of Botany. 2000;86:551–563. [Google Scholar]
  19. Granier C, Tardieu F. Multi-scale phenotyping of leaf expansion in response to environmental changes: the whole is more than the sum of parts. Plant, Cell and Environment. 2009;32:1175–1184. doi: 10.1111/j.1365-3040.2009.01955.x. [DOI] [PubMed] [Google Scholar]
  20. Hale RC, Weaver RJ. The effect of developmental stage on direction of translocation of photosynthetase in Vitis vinifera. Hilgardia. 1962;33:89–131. [Google Scholar]
  21. Heuvelink E. Dry matter partitioning in a tomato plant: one common assimilate pool? Journal of Experimental Botany. 1995;46:1025–1033. [Google Scholar]
  22. Heuvelink E, Buiskool RPM. Influence of sink-source interaction on dry matter production in tomato. Annals of Botany. 1995;75:381–389. [Google Scholar]
  23. Ho LC. Metabolism and compartmentation of imported sugars in sink organs in relation to sink strength. Annual Review of Plant Molecular Biology. 1988;39:355–378. [Google Scholar]
  24. Jackson DI, Lombard PB. Environmental and management practices affecting cluster composition and wine quality: a review. American Journal of Enology and Viticulture. 1993;44:409–430. [Google Scholar]
  25. Keller M, Hess B, Schwager H, Schärer H, Koblet W. Carbon and nitrogen partitioning in Vitis vinifera L.: responses to nitrogen supply and limiting irradiance. Vitis. 1995;34:19–26. [Google Scholar]
  26. Lacointe A. Carbon allocation among tree organs: a review of basic processes and representation in functional-structural tree models. Annals of Forest Science. 2000;57:521–533. [Google Scholar]
  27. Lacointe A, Deleens E, Ameglio T, et al. Testing the branch autonomy theory: a 13C/14C double-labelling experiment on differentially shaded branches. Plant, Cell and Environment. 2004;27:1159–1168. [Google Scholar]
  28. Lebon E, Pellegrino A, Tardieu F, Lecoeur J. Shoot development in grapevine (Vitis vinifera L.) is affected by the modular branching pattern of the stem and intra–inter-shoot trophic competition. Annals of Botany. 2004;46:1093–1101. doi: 10.1093/aob/mch038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lebon E, Pellegrino A, Louarn G, Lecoeur J. Branch development controls leaf area dynamics in grapevine (Vitis vinifera) growing in drying soil. Annals of Botany. 2006;98:175–185. doi: 10.1093/aob/mcl085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lechner L, Pereyra-Irujo GA, Granier C, Aguirrezabal LAN. Rewatering plants after a long water-deficit treatment reveals that leaf epidermal cells retain their ability to expand after the leaf has apparently reached its final size. Annals of Botany. 2008;101:1007–1015. doi: 10.1093/aob/mcn029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lecoeur J, Wery J, Turc O, Tardieu F. Expansion of pea leaves subjected to short water deficit: cell number and cell size are sensitive to stress at different periods of leaf development. Journal of Experimental Botany. 1995;46:1093–1101. [Google Scholar]
  32. Letort V, Cournède PH, Mathieu A, de Reffye P, Constant T. Parametric identification of a functional–structural tree growth model and application to beech trees. Functional Plant Biology. 2008;35:951–968. doi: 10.1071/FP08065. [DOI] [PubMed] [Google Scholar]
  33. Louarn G, Guedon Y, Lecoeur J, Lebon E. Quantitative analysis of the phenotypic variability of shoot architecture in two grapevine cultivars (Vitis vinifera L.) Annals of Botany. 2007;99:425–437. doi: 10.1093/aob/mcl276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Luquet D, Dingkun M, Kim H, Tambour L, Clement-Vidal A. EcoMeristem, a model of morphogenesis and competition among sinks in rice. 1. Concept, validation and sensitivity analysis. Functional Plant Biology. 2006;33:309–323. doi: 10.1071/FP05266. [DOI] [PubMed] [Google Scholar]
  35. Mäkelä A. Implications of the pipe-model theory on dry matter partitioning and height growth in trees. Journal of Theoretical Biology. 1986;123:103–120. [Google Scholar]
  36. Mathieu A, Cournède P-H, Letort V, Barthélémy D, de Reffye P. A dynamic model of plant growth with interaction between development and functional mechanisms to study plant structural plasticity related to trophic competition. Annals of Botany. 2009;103:1173–1186. doi: 10.1093/aob/mcp054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Meziane D, Shipley B. Interaction determinants of specific leaf area in 22 herbaceous species: effects of irradiance and nutrient availability. Plant, Cell and Environment. 1999;22:447–459. [Google Scholar]
  38. Monteith JL. Climate and the efficiency of crop production in Britain. Philosophical Transactions of the Royal Society of London. 1977;281:277–294. [Google Scholar]
  39. Münch E. Jena: Gustav Fisher; 1930. Die Stoffbewegungen in der Pflanze. [Google Scholar]
  40. Neales TF, McLeod AL. Do leaves contribute to the abscisic acid present in the xylem sap of ‘draughted’ sunflower plants? Plant, Cell and Environment. 1991;14:979–986. [Google Scholar]
  41. Pallas B, Louarn G, Christophe A, Lebon E, Lecoeur J. Influence of intra-shoot trophic competition on shoot development in two grapevine cultivars (Vitis vinifera L.) Physiologia Plantarum. 2008;134:49–63. doi: 10.1111/j.1399-3054.2008.01100.x. [DOI] [PubMed] [Google Scholar]
  42. Pallas B, Christophe A, Cournède PH, Lecoeur J. Using a mathematical model to evaluate the trophic and non trophic determinants of axis development in grapevine. Functional Plant Biology. 2009;36:156–170. doi: 10.1071/FP08178. [DOI] [PubMed] [Google Scholar]
  43. Pigliucci M, Schmitt J. Genes affecting phenotypic plasticity in Arabidopsis: pleiotropic effects and reproductive fitness of photomorphogenic mutants. Journal of Evolutionary Biology. 1999;12:551–562. [Google Scholar]
  44. Reymond M, Muller B, Leonardi A, Charcosset A, Tardieu F. Combining QTL analysis and an ecophysiological model to analyse the genetic variability of the responses of maize leaf growth to temperature and water deficit. Plant Physiology. 2003;131:664–675. doi: 10.1104/pp.013839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Rives M. Vigour, pruning, cropping in the grapevine (Vitis vinifera L.). I. A literature review. Agronomie. 2000;20:79–91. [Google Scholar]
  46. Robin C, Hay MJM, Newton PCD, Greer DH. Effect of light quality (red : far red ratio) at the apical bud of the main stolon on morphogenesis of Trifolium repens L. Annals of Botany. 1994;74:119–123. [Google Scholar]
  47. Schultz HR, Matthews MA. Vegetative growth distribution during water deficit in Vitis vinifera L. Australian Journal of Plant Physiology. 1988;15:641–656. [Google Scholar]
  48. Seleznyova AN, Thorp TG, Barnett AM, Costes E. Quantitative analysis of shoot development and branching patterns in Actinidia. Annals of Botany. 2002;89:471–482. doi: 10.1093/aob/mcf069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Shipley B, Meziane D. The balanced-growth hypothesis and the allometry of leaf and root biomass allocation. Functional Ecology. 2002;16:326–331. [Google Scholar]
  50. Sprugel DG, Hinckley TM, Schaap W. The theory and practice of branch autonomy. Annual Review of Ecological Systems. 1991;22:309–334. [Google Scholar]
  51. Sultan ES. Phenotypic plasticity for plant development, function and life history. Trends in Plant Science. 2000;5:537–542. doi: 10.1016/s1360-1385(00)01797-0. [DOI] [PubMed] [Google Scholar]
  52. Tardieu F, Granier C, Muller B. Modelling leaf expansion in a fluctuating environment: are changes in specific leaf area a consequence of changes in expansion rate? New Phytologist. 1999;143:33–43. [Google Scholar]
  53. Thornley JHM. London: Academic Press; 1976. Mathematical models in plant physiology: a quantitative approach to problems in plant and crop physiology. [Google Scholar]
  54. Thornley JHM, Hurd RG. An analysis of the growth of young tomato plants in water culture at different light integrals and CO2 concentrations. II. A mathematical model. Annals of Botany. 1974;38:389–400. [Google Scholar]
  55. Turc O, Lecoeur J. Leaf primordium initiation and expanded leaf production are co-ordinated responses to air temperature in pea (Pisum sativum L.) Annals of Botany. 1997;80:265–273. [Google Scholar]
  56. Valantin M, Gary C, Vaissière BM, Frossard JS. Effect of fruit load on partitioning of dry matter and energy in cantaloupe (Cucumis melo L.) Annals of Botany. 1999;84:173–181. [Google Scholar]
  57. Violle C, Garnier E, Lecoeur J, et al. Competition, resource depletion and plant traits in herbaceous communities. Oecologica. 2009;160:747–755. doi: 10.1007/s00442-009-1333-x. [DOI] [PubMed] [Google Scholar]
  58. Wardlaw IF. The control of carbon partitioning in plants. Translay review no. 27. New Phytologist. 1990;116:341–381. doi: 10.1111/j.1469-8137.1990.tb00524.x. [DOI] [PubMed] [Google Scholar]
  59. Warnasooriya NS, Montgomery BL. Detection of spatial-specific phytochrome responses using targeted expression of biliverdin reductase in Arabidopsis. Plant Physiology. 2009;149:424–433. doi: 10.1104/pp.108.127050. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES