The subjective value of delayed and probabilistic outcomes: Outcome size matters for gains but not for losses

Abstract

The subjective value of a reward (gain) is related to factors such as its size, the delay to its receipt and the probability of its receipt. We examined whether the subjective value of losses was similarly affected by these factors in 128 adults. Participants chose between immediate/certain gains or losses and larger delayed/probabilistic gains or losses. Rewards of $100 were devalued as a function of their delay (“discounted”) relatively less than $10 gains while probabilistic $100 rewards were discounted relatively more than $10 rewards. However, there was no effect of outcome size on discounting of delayed or probabilistic losses. For delayed outcomes of each size, the degree to which gains were discounted was positively correlated with the degree to which losses were discounted, whereas for probabilistic outcomes, no such correlation was observed. These results suggest that the processes underlying the subjective valuation of losses are different from those underlying the subjective valuation of gains.

Introduction

Decision-making often involves comparing outcomes that differ along several dimensions, for example, choosing between using vacation time to take a short, local trip and accumulating vacation time to permit a longer, more extensive holiday. Several procedures have been developed to quantify choice patterns between smaller, more immediate gains and larger, delayed gains (e.g., Rachlin, Brown & Cross, 2000; Richards, Zhang, Mitchell & de Wit, 1999). A typical procedure involves estimating the subjective value of a larger, delayed monetary reward by identifying the amount at which individuals are indifferent between a smaller, immediate amount of money and that larger amount of delayed money. A similar procedure of varying the amount of certain (p = 1.0) money can be used to identify the indifference point for larger, probabilistic monetary rewards. Almost invariably, studies have shown that the subjective value of monetary rewards (e.g., Rachlin, Raineri & Cross, 1991) or other commodities (e.g., Chapman & Weber, 2006; Odum & Rainaud, 2003) decreases with increases in the length of the delay or the odds against their receipt. The area under the empirical discounting curve can be used to quantify individual differences in sensitivity to delay or probability: a person with less area under the curve discounts the objective value of delayed or probabilistic gains more than someone with greater area under the curve (Myerson, Green & Warusawitharana, 2001).

Research has demonstrated that individual differences in discounting are related to an individual’s personality and other lifestyle characteristics, such as drug use (see Bickel & Marsch, 2001 and Reynolds, 2006 for reviews). Other studies have focused on the stimulus and task variables influencing the discount function. Numerous studies have indicated that larger delayed gains are discounted relatively less steeply than smaller delayed gains (for review see Green & Myerson, 2004). For example, the subjective value of $10,000 decreases with delay less steeply than the value of $1,000 decreases with delay (e.g., Benizon, Rapaport & Yagel, 1989; Green, Myerson & McFadden, 1997; Myerson, Green, Hanson, Holt & Estle, 2003). In contrast, the subjective value of larger probabilistic gains decreases more steeply as a function of the odds against their receipt than smaller probabilistic gains (e.g., Green, Myerson & Ostaszewski, 1999). The psychological mechanism underlying this difference is unclear.

Recently, interest has been increasing in the subjective value calculation associated with delayed or probabilistic negative outcomes (losses). Many decisions involve choices between negative outcomes, such as deciding whether to have a possibly uncomfortable medical procedure now or running the risk of having a disorder that will be more serious when diagnosed or contracted later. One example would be deciding to receive a ‘flu shot now versus risking contracting the influenza virus later (Chapman & Coups, 1999). Relatively few studies have examined discounting of losses. These have shown that different size losses were discounted at the same rate using hypothetical monetary rewards that were either delayed or probabilistic (Estle, Green, Myerson & Holt, 2006; Holt, Green, Myerson & Estle, 2008; also see Murphy, Vuchinich & Simpson, 2001) and delayed hypothetical monetary or cigarette rewards (Baker, Johnson & Bickel, 2003). Such data have important ramifications. They suggest that the immediate costs that individuals will be prepared to incur to avoid a delayed/probabilistic negative outcome will be driven by the delay or probability of the negative outcome, but that discounting rate will not vary as a function of the magnitude of the outcome.

The current study expands on the previous research by comparing both delay and probability discounting for gains and for losses within and between individuals. Thus, in addition to examining whether delay and probability discounting are affected by the size of a projected loss of money in a manner similar to that for an anticipated gain, we also examine whether individual differences in performance are correlated across different tasks. A lack of consistent individual differences would imply that somewhat different factors control behavior on delay and probability discounting tasks, and behavior towards gains and losses. For example, recent research using functional magnetic resonance imaging has implied that the brain encodes gains and losses differently (e.g., Cooper & Knutson, 2008; Seymour, Daw, Dayan, Singer & Dolan, 2007), but behavioral data characterizing the impact of these differences is lacking.

Method

Participants

Participants were 64 males and 64 females, mean age 29.93 years (SD 9.33), recruited using flyers, advertisements on the web and word-of-mouth. The local Institutional Review Board approved the protocol, and participants were treated according to the “Ethical Principles of Psychologists and Code of Conduct” (American Psychological Association, 2002). Participants were debriefed at the end of the study and received $15 as compensation.

Procedure

Participants were initially screened over the phone to ensure that they were age 18 or older, had a high school diploma or equivalent, were not pregnant, were not taking any prescription drugs (except birth control), and were fluent English speakers. At a face-to-face screening interview, participants completed a health questionnaire including medical and drug use history. Exclusion criteria were (1) a history of substance use disorder except nicotine dependence (DSM-IV criteria: American Psychiatric Association, 1994), (2) current physical or psychiatric problems, and (3) a history of serious psychiatric disorder (DSM-IV, Axis 1 disorders). Participants provided breath and urine samples to verify abstinence from alcohol and illicit drugs that might impact cognition. Afterwards, eligible participants completed the discounting tasks and several questionnaires (data not reported) in a counterbalanced order.

Discounting tasks

Eight computerized tasks were created to measure preference for hypothetical gains and losses (see Table 1). For tasks examining hypothetical gains, the computer asked “At this moment, what would you prefer?” then participants used the computer mouse to select one of two alternatives presented side by side on the computer screen. One alternative was always an amount of money ($10 or $100) available either in D days or with a P% chance. The other alternative was always an amount of money available either “now” or “for sure”. The value of the immediate/certain alternative was selected randomly without replacement for each value of the delayed/probabilistic alternative. For example, participants would be asked: “At this moment, what do you prefer? $8.50 now vs. $10 in 365 days” or “At this moment, what do you prefer? $40.00 for sure vs. $100 with a 75% chance”. Questions were similar for tasks examining hypothetical losses, for example, participants would be asked: “At this moment, what do you prefer to pay? $10 in 365 days vs. $8.50 now” or “At this moment, what do you prefer to pay? $100 with a 75% chance vs. $40.00 for sure”.

Table 1.

Schematic of the discounting tasks used in the study.

		Loss: At this moment, what would you prefer to pay?	Gain: At this moment, what would you prefer?
Delay	$10	Money now OR $10 in D days	Money now OR $10 in D days
	$100	Money now OR $100 in D days	Money now OR $100 in D days
Probability	$10	Money for sure OR $10 with a P% chance	Money for sure OR $10 with a P% chance
	$100	Money for sure OR $100 with a P% chance	Money for sure OR $100 with a P% chance

Notes.

D values were: 0, 7, 30, 90, 180, 365 days.

P values were: 100, 90, 75, 50, 25, 10, i.e., probabilities of 1.0, 0.9, 0.75, 0.50, 0.25, 0.10. Amounts of Money now or Money for sure were: $0.00, $0.25, and $0.50 to $10.50 in $0.50 increments for $10 tasks, and 0.00, $2.50, and $5.00 to $105.00 in $5.00 increments for $100 tasks.

Each participant was assigned at random to one of four groups (N = 32/group) and each group completed four of the computerized tasks. The tasks completed by each group were selected so that groups differed in whether the discounting factor (delay or probability) was the same or whether the outcome amount was the same:

Group 1: same discounting factor - delay (i.e., $10 delayed gain, $10 delayed loss, $100 delayed gain, and $100 delayed loss)

Group 2: same discounting factor - probability (i.e., $10 probabilistic gain, $10 probabilistic loss, $100 probabilistic gain, and $100 probabilistic loss)

Group 3: same outcome amount - $10 (i.e., $10 delayed gain, $10 delayed loss, $10 probabilistic gain, and $10 probabilistic loss)

Group 4: same outcome amount - $100 (i.e., $100 delayed gain, $100 delayed loss, $100 probabilistic gain, and $100 probabilistic loss).

This arrangement resulted in each task being completed by 64 participants. For example, the $10 delayed gain and the $10 delayed loss tasks were both completed by Group 1 and by Group 3. However, the maximum number of participants from whom data was available for within-subject comparisons of amount (e.g., $10 delayed gain vs. $100 delayed gain) was 32.

Dependent variables

The main dependent variable was the amount of money at which each participant was indifferent between the immediate/certain alternative and the $10/$100 alternative at each delay (0, 7, 30, 90, 180 and 365 days) or probability (1.0, 0.9, 0.75, 0.5, 0.25, 0.1 [odds against: 0, 0.1, 0.3, 1, 3, 9]). The indifference point may be viewed as indexing the subjective value of the delayed/probabilistic alternative. This point was operationally defined as being midway between the smallest value of the immediate/certain alternative accepted and the largest value that was rejected (see Mitchell, 1999 for additional details). Note that, for the gain tasks, values of the immediate/certain reward that are larger than the indifference point are preferred over the delay/probabilistic rewards, while values smaller than the indifference point are rejected and the delayed/probabilistic reward is preferred. In contrast, for loss tasks, values of the immediate/certain loss that are larger than the indifference point are rejected and the delay/probabilistic loss is preferred, while values smaller than the indifference point are preferred over the delayed/probabilistic loss.

Data for a single individual were excluded because indifference points could not determined; on the $10 and $100 probabilistic gain tasks he never selected the probabilistic alternative and on the $10 and $100 probabilistic loss tasks he never selected the certain alternative. Data from all other participants were included.

To assess discounting for the delayed or probabilistic outcome we calculated the area under the indifference points (see Myerson et al., 2001 for a full description of this method). The area takes on values from zero to one, whereby smaller areas indicate a greater preference for the immediate or certain rewards for gain tasks and a lesser preference for the immediate/certain rewards for the loss tasks. This measure has the advantage of not making any assumptions about the form of the discounting function. Further, these areas are normally distributed, making transformations unnecessary.

Results

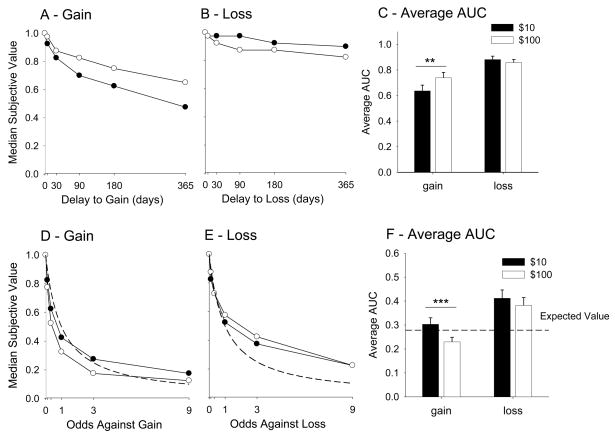
Most individuals discounted the value of delayed gains and probabilistic gains (see Figure 1). In other words, the subjective value as measured by the indifference point at the 365 day delay or at the 0.10 probability (odds against = 9) was less than the objective value of the reward ($10 or $100). To provide an estimate of the number of subjects who exhibited very shallow delay or probability discounting functions, the number of participants for each task who discounted the objective amount of the outcome ($10 or $100) by less than 10% at the longest delay or lowest probability was counted. That is, the indifference point at the longest delay or smallest probability was more than 90% of the value of the delayed/probabilistic outcome (more than $9 or $90). Using this criterion, 9 of the 64 subjects who completed the delayed $10 gain task had very shallow discount functions, as did 12 of those who completed the $100 delayed gain task. In comparison, 32 and 24 participants exhibited very shallow discounting functions for the delayed $10 and $100 loss tasks. Indeed, some of these individuals preferred to pay the full amount now rather than waiting ($10: N = 17; $100: N = 12). Of the 63 participants who completed the probability discounting tasks, no one had very shallow functions for the probabilistic gain tasks, and few participants discounted the lowest probability loss ($10 or $100) by less than 10%: 4 and 8, respectively. In addition, some participants exhibited “reverse discounting” ($10: N = 7; $100: N = 12) in the probabilistic loss tasks. That is, as the probability of the loss increased, the amount that the individual would forfeit “for sure” rather than risking the loss increased.

Figure 1.

Median indifference points (A and B) and the average AUC values (C) for the $10 and $100 delayed gain and loss tasks. Median indifference points (D and E) and the average AUC values (F) for the $10 and $100 probabilistic gain and loss tasks. Dashed line indicates the expected value of the gamble (size of gain or loss × probability of gain or loss). Notice that data are normalized, that is, all indifference points are expressed as proportions to facilitate comparisons because ANOVAs revealed that the absolute indifference points for $10 tasks were all significantly lower than indifference points for $100 tasks at the corresponding delay and probability levels.

** p ≤ 0.01 using a within subjects t-test on AUC

*** p ≤ 0.001 using a within subjects t-test on AUC

Participants with very shallow discount functions or reverse discount functions were included in the area under the curve analyses presented below. In preliminary analyses we examined the effects of removing these individuals, as well as the effects of removing individuals exhibiting nonsystematic discounting (Johnson & Bickel, 2008: criterion 1, i.e., an indifference point that was larger than the indifferent point for the next smallest delay/odds against value by more than 20% of the size of the delayed or probabilistic reward). Neither analysis yielded results that were qualitatively different from the relationships observed when all subjects were included.

Based on calculations of the area under the curve (Figure 1C, 1F) combined with visual inspection of the data, a within subjects t-test revealed that larger delayed gains were discounted less than smaller delayed gains, i.e., the area under the curve was larger for larger rewards (t[31] = −3.18, p = 0.003). The opposite was the case for probabilistic gains, i.e., large probabilistic gains were discounted more steeply than smaller probabilistic gains (t[30] = 4.24, p < 0.001). In contrast, the size of the loss did not affect discounting of delayed losses (t[31] = 0.94, p > 0.05), nor did it affect discounting of probabilistic losses (t[30] = 0.97, p > 0.05).

Performance on delay tasks featuring different monetary amounts was positively correlated. Individuals who discounted the value of the delayed outcome more steeply in the $10 delayed gain task also discounted more steeply in the $100 delayed gain task. Individuals who discounted the $10 delayed loss more steeply also discounted the $100 delayed loss more steeply (Table 2). A positive relationship also held for the probability tasks: individuals who were more risk averse when offered a probabilistic $10 were also more risk averse when offered a probabilistic $100. Similarly, individuals who were more risk averse when facing a probabilistic $10 loss were also more risk averse when facing a probabilistic $100 loss. The extent to which individuals discounted delayed gains and losses of the same monetary size was positively correlated. In other words, individuals who exhibited a relative preference for immediate rewards (smaller area under the curve, less likely to defer gains and more impulsive) also exhibited a relative preference for delayed losses (smaller area under the curve, more likely to defer losses). However, we did not see this positive correlation when we compared the probabilistic loss and gain tasks. The small negative, but nonsignificant, correlation between discounting of probabilistic losses and probabilistic gains indicated that participants who were the most risk prone for losses tended to be the most risk averse for gains. For individuals who completed both delayed and probabilistic tasks, discounting was unrelated (r = −0.31 to 0.22, ps > 0.05).

Table 2.

Pearson’s product moment correlations between AUC values for the eight discounting tasks.

		Delay		Probability
Relationship of interest	Tasks compared	r	N	r	N
Amount	Gain: 10 and 100	0.73***	32	0.77***	31
Amount	Loss: 10 and 100	0.54**	32	0.60***	31
Gain-Loss	$10: Gain and Loss	0.39**	64	−0.20	63
Gain-Loss	$100: Gain and Loss	0.51***	64	−0.08	63

Notes.

^**p < 0.01

^***p < 0.001

Discussion

The area under the curve analyses indicated that the $100 delayed gain was discounted less than the $10 delayed gain, while the $10 probabilistic gain was discounted less than the $100 probabilistic gain. These results replicate a number of prior observations (e.g., Green et al., 1997). However, currently there is no parsimonious explanation for the magnitude effects that have been observed in numerous studies.

One theory to explain the magnitude effect for gains is that different amounts are assigned to different mental “accounts” based on their purchasing power (Lowenstein & Thaler, 1989). This causes the utility of different amounts of money to be qualitatively, as well as quantitatively, different (e.g., lunch for $10 compared with electronic gadget for $100). The similar discounting rates for the losses would suggest that when money is to be paid, it must come from the same mental account whether it is $10 or $100 and that people assess the value of losses in terms of the purchasing power of to-be-forfeited money. We should note, however, that there are three problems associated with adopting this accounting explanation. First, it is difficult to apply when an amount effect is observed for nonmonetary rewards (e.g., Baker, Johnson & Bickel, 2003), which presumably are not assigned to mental accounts based on their purchasing power. Second, it is unclear how this accounting process accommodates the possibility of not receiving money, a factor known to influence the subjective value of probabilistic gains and demonstrated in the current study. Third, the evidence suggests that discounting rate appears to increase continuously with amount of delayed reward up to about $20,000 (e.g., Green et al., 1999), which would mean multiple mental accounts for amounts in this range.

An alternative theory can be constructed based on the idea that different emotions are generated in anticipation of receiving a reward or not, and that these can influence choice between reward alternatives (e.g., Mellers et al., 1999). However, to use emotion-based choice theories to explain the difference in magnitude effects for the different tasks used in the current study requires numerous assumptions about the types of emotions experienced, their interactive effects and how these interactions impinge on the subjective value of alternatives. Such speculation is beyond the scope of the data. Especially difficult is the extension of such a theory to loss discounting, where no amount effect on discounting was found in the current study for either the delayed losses or the probabilistic losses, which replicates other research (Estle et al., 2006).

As shown in Figure 1, the median indifference points were lower for delayed gains than for delayed losses. Similarly, probabilistic gains were discounted more steeply than probabilistic losses. The results replicate data described by Kahneman and Tversky (1979): participants tended to be risk averse for gains and risk prone for losses. These asymmetries, as well as the asymmetrical amount effect, imply that the cognitive and neurological processes used to evaluate the subjective value of an outcome do not function identically for gains and losses, or for delayed and probabilistic rewards (e.g., Cooper & Knutson, 2008; Gehring & Willoughby, 2002). Understanding the different neural substrates of these processes is critical to develop a fuller understanding of economic decision making.

The relatively shallower curves and larger AUCs for the delayed loss tasks relative to the delayed gains tasks (Figure 1) in large part reflected the greater number of participants who discounted very little. Choices made by these individuals suggested that they would rather pay the full amount now than the $10 or $100 after a delay; although their discount functions for gains were indistinguishable from the gain functions of participants who discounted future losses to a greater degree. Demographic data were limited and it did not indicate that these individuals differed in a qualitative way to participants who exhibited some discounting. Further, it is unclear whether this behavioral difference is also observed outside the laboratory, and what the implications are for real world purchasing behavior. A substantial number exhibited “reverse” discounting, that is, as the probability of losing money decreased from 1 to 0.1, the amount of money they were willing to forfeit to avoid the gamble increased. For example, one individual was willing to pay $8 rather than accept a gamble of losing $10 with a probability of 0.1, but would only pay $3 rather than accept a gamble of losing $10 with a probability of 0.9. These data suggest visual representations of probability data should be used to help participants understanding alternatives more clearly. However, these “reverse” discounting individuals performed similarly to other participants in gain tasks, indicating that any possible misunderstanding of the task was confined to the loss scenario for these individuals. Such possibilities for misunderstanding tasks framed in terms of losses suggest that reframing health messages in terms of losses rather than gains so that their impact will not be discounted should only be done with caution (Ortendahl & Fries, 2005).

There were some consistent individual differences in choices on the different tasks. Individuals who steeply discounted delayed gains also steeply discounted delayed losses, suggesting that their time horizon is circumscribed similarly for positive and negative events, and that precommitment strategies that reduce impulsive choices of gains (e.g., Rachlin & Green, 1972) would be equally effective to reduce the tendency to defer bill payment. For probabilistic rewards, though not statistically significant, the opposite relationship tended to be observed: those who discounted probabilistic gains to a large extent, discounted probabilistic losses to a small extent. In other words, the more risk averse one is for gains the more risk prone one is for losses. One practical implication of this result is that reframing of situations to emphasize gains rather than losses may alter risk-taking behavior. For example, campaigns to persuade smokers to quit might focus on the probable health gains associated with smoking cessation like lower blood pressure, improved fitness, heightened sense of taste, rather than on possible changes in lifestyle that could be perceived as losses, such as no longer needing to go outside for a “smoke break”.

In conclusion, while hyperbolic functions relating the subjective value of delayed or probabilistic gains and losses share the same mathematical form, the current study has shown two important differences. First, there are robust effects of the size of the gain on discounting but no effects of the size of the loss. Second, individual differences in response to delay and probability are consistent for tasks in which the amount of gain or loss is varied, and consistent for delay tasks, but performance on a probabilistic gain task does not permit us to predict performance of a probabilistic loss task. No neuropsychological model of decision-making that accommodates these differences is yet available but one precondition for such a model is that different processes must underlie discounting of gains and losses and delayed and probabilistic outcomes.